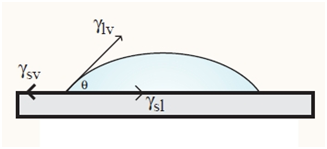
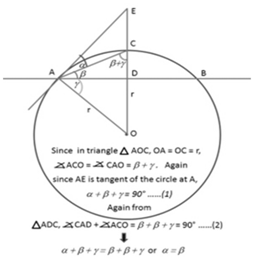
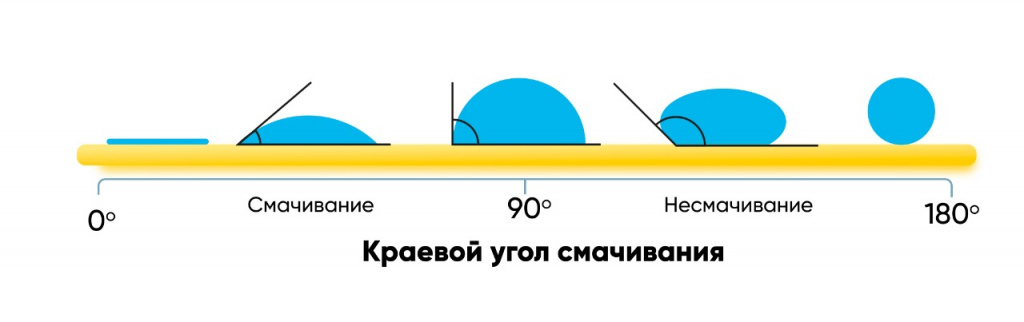
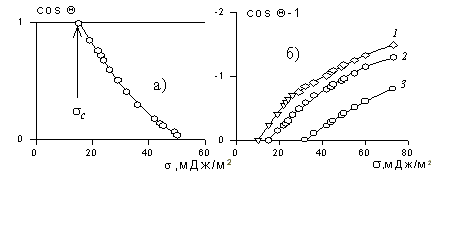Краевой угол смачивания или угол контакта θс. γSL, γLG, γSG обозначены соответственно как удельные свободные поверхностные энергии на границе раздела фаз: твёрдое тело-жидкость (SL), жидкость-газ (LG) и твёрдое тело-газ (SG).
Краевой угол смачивания, также угол смачивания, угол контакта (англ. Contact angle) — угол, который образуется между касательной, проведённой к поверхности фазы жидкость-газ и твёрдой поверхностью с вершиной, располагающейся в точке контакта трёх фаз, и условно измеряемый всегда внутрь жидкой фазы[1]. Обозначается греческой буквой тета — θ.
Краевой угол смачивания является количественной характеристикой процесса смачивания, его величина определяет межмолекулярное (атомное, ионное) взаимодействие частиц поверхности твёрдых тел с жидкостями.
Физическое описание[править | править код]
Наглядный пример смачивания жидкостью твёрдой поверхности. А — краевой угол много больше 90° и, как следствие плохое смачивание (капля имеет почти шарообразную форму и слабое взаимодействие с твёрдой поверхностью — происходит уменьшение площади контакта жидкости с ней), В и С — краевой угол меньше θ<90°, капли жидкости приобретают менискообразную форму (лучшее взаимодействие с твёрдой поверхностью, площадь контакта жидкости больше, чем в примере А), S — краевой угол θ=0°(по сути его нет) — полное смачивание, происходит растекание жидкости по твёрдой поверхности, площадь контакта жидкости с твёрдой поверхностью в данном случае максимальна. Процесс растекания жидкости является предельным случаем смачивания.
Считается, что если величина краевого угла меньше θ<90°, то происходит смачивание жидкостью твёрдой поверхности, а сама поверхность называется лиофильной (в случае, если жидкостью является вода — гидрофильной), в случае, если величина краевого угла больше θ>90°, то твёрдая поверхность не смачивается жидкостью и является лиофобной (в случае воды — гидрофобной). При полном или абсолютном смачивании (растекании) краевой угол равен нулю, при полном или абсолютном несмачивании — 180°, последнее значение не наблюдается в природе. Равновесный краевой угол вычисляется по закону Юнга:

где 


Величина косинуса краевого угла определяет смачивается ли твёрдая поверхность жидкостью или нет. Значения косинусов контактного угла приведена в таблице:
| Значение cosθ | Значение θ | Описание |
|---|---|---|
| 1 | 0° | При данном значении косинуса, жидкость полностью растекается по поверхности твёрдого тела, такие поверхности называются сверхгидрофильными. |
| 1/2 | 60° | Жидкость на поверхности твёрдого тела образует менискообразные капли. Площадь контакта жидкости с поверхностью уменьшается. Такие поверхности называют гидрофильными |
| 0 | 90° | Жидкость приобретает полукруглую форму, площадь контакта с поверхностью ещё меньше. |
| -1 | 180° | Жидкость на поверхности твёрдого тела образует сферические капли, однако, такое значение контактного угла в природе не наблюдается. |
На фотографии отчётливо видно, что ртуть плохо смачивает стекло (Θ>90°), вследствие слабого взаимодействия с ним (работа сил адгезии меньше работы когезии) и принимает каплеобразную форму (снижается площадь контакта).
Величина краевого угла зависит от работы адгезии и когезии. С работой адгезии контактный угол связан уравнением Дюпре-Юнга:

где σ12 — поверхностное натяжение на границе раздела двух фаз (жидкость-газ), cosθ — косинус краевого угла смачивания, Wa — обратимая работа адгезии. Это уравнение можно представить в следующем виде:

Если уравнение разделить на 2, то можно получить зависимость работы сил адгезии и когезии от величины угла смачивания:

На диаграмме представлены направления действия сил когезии молекул жидкости (образование мениска).
Работа адгезии — Wa направлена на растекание жидкости по поверхности твёрдого тела, посредством растяжения. В то же время, работа когезионных сил — Wк противоположна работе адгезии и способствует стягиванию жидкости в каплеобразную форму, предотвращая растекание. Из этого следует, что чем выше значения Wa, и чем ниже Wк, тем сильнее твёрдая поверхность будет смачиваться жидкостью (как следствие, величина θ<90°) и наоборот. Иными словами для того, чтобы усилить смачивание твёрдой поверхности жидкостью, необходимо увеличить работу адгезии и снизить работу когезии.
Гистерезис смачивания[править | править код]
Гистерезисом смачивания называют гистерезис, возникающий в результате различных значений углов смачивания в точках соприкосновения взаимодействующих фаз (т. н. углы натекания и оттекания). Иными словами гистерезис смачивания это задержка в установлении равновесного угла. Разница краевых углов обусловлена тем, что угол в точке соприкосновения поверхности жидкости с сухой поверхностью твёрдого тела имеет значение величины большую, чем при соприкосновении с поверхностью того же тела, предварительно смоченной.
Существует два типа гистерезиса:
- кинетический
- статический.
Кинетический тип гистерезиса смачивания возникает при перемещении (изменении) значений углов смачивания — разность углов натекания (всегда больше равновесного угла) и оттекания (всегда меньше равновесного угла).
Статистический тип обусловлен снижением периметра смачивания. Рассчитывается как разность между равновесным углом и углом, вычисленным.
Методы измерения[править | править код]
Существует несколько методов измерения краевого угла смачивания.
Измерение краевого угла смачивания по методу сидячей капли, производится с помощью специального гониометра.
Одним из наиболее распространённых является метод сидячей капли. Сущность метода заключается в том, что каплю воды наносят на ровную горизонтальную твёрдую поверхность, фотографируют и по профилю капли определяют краевой угол. Однако полученные таким образом статические углы не являются, строго говоря, углами оттекания θот или натекания θнт воды. Иногда статический угол сидячей капли называют равновесным.
Видоизменённый метод сидячей капли — метод прижатой капли. Используя данный метод можно получить непосредственно углы натекания и оттекания. Однако эти углы зависят от силы прижатия капли.
Супергидрофобность[править | править код]
Супергидрофобностью или сверхгидрофобностью называется явление очень слабого взаимодействия частиц поверхности твёрдых тел с жидкостями, в частности, с водой. Значения контактного угла составляет больше 150°. Вследствие слабых сил взаимодействия (значения Wa << Wк) с таким родом поверхности и высокому значению поверхностного натяжения, капля воды принимает сферическую форму, тем самым, уменьшая площадь контакта с супергидрофобной поверхностью. В природе явление супергидрофобности известно как эффект лотоса.
Примечания[править | править код]
- ↑ А.Шварц, Дж Перри. Поверхностно активные вещества. — М.: Иностранной литературы, 1953. — С. 250. — 550 с.
- ↑ Начинкин О.И. Полимерные микрофильтры. — М.: Химия, 1985. — С. 65. — 216 с.
Краевой угол смачивания: понятие, методы измерения

Краевым углом смачивания называется угол между твердой поверхностью и каплей жидкости в точке контакта трех фаз – твердой, жидкой и газообразной.
Величина угла смачивания показывает степень межмолекулярного взаимодействия частиц жидкости и поверхности твердого тела.
Смачиванием называется такое взаимодействие твердого тела и жидкости, при котором последняя растекается по поверхности. Площадь контакта капли и тела при смачивании максимальна.
Это происходит из-за неравенства сил адгезии и когезии.
Адгезия действует на сцепление молекул разнородных материалов: жидкого и твердого. Она направлена противоположно когезии, которая действует на сцепление молекул внутри капли жидкости.
Когда адгезия превышает когезию, происходит растяжение капли по поверхности твердого тела. При этом угол смачивания оказывается острым.
Если угол равен или приближен к 0, то говорят о полном смачивании поверхности и ее супергидрофильности.

Менискообразные капли, соответствующие углу смачивания около 60 градусов, образуются на гидрофильных поверхностях. Такие капли формируются при попадании воды на стекло, ртути на цинковую поверхность.
Если когезионное взаимодействие молекул внутри капли жидкости превышает силы адгезии, то капля стремится приобрести шарообразную форму, а площадь ее контакта с твердым телом уменьшается.
Поверхности, при попадании на которые жидкости приобретают полукруглую форму, называются гидрофобными. Угол смачивания в таком случае равен или превышает 90 градусов.
На сверхгидрофобных поверхностях жидкость приобретает форму шара, краевой угол смачивания стремится к 180 градусам. В природе таких явлений не наблюдается.
Термины гидрофильность и гидрофобность применяются в случаях взаимодействия твердых поверхностей и воды. Смачиваемость или несмачиваемость другими жидкостями называются лиофильностью и лиофобностью.
Один из самых простых и распространенных способов измерения краевого узла смачивания – фотофиксация.
Капля воды или другой жидкости наносится на горизонтальную поверхность, после чего проводится фотосъемка. Угол определяют по полученному изображению.
Данный способ измерения также называют методом «сидячей капли».
Для более профессионального и точного измерения угла смачивания используются специальные приборы.
Они состоят из нескольких камер, регистрирующих каплю с разных ракурсов, дозирующих систем, подающих жидкость, программного обеспечения для автоматического определения не только краевого угла смачивания, в том числе под давлением, но и расчета свободной энергии поверхности, поверхностного и межфазного натяжения.

Существуют устройства с измерением угла смачивания методом отраженного света. Они позволяют измерить краевой угол смачивания на поверхности со сложным рельефом, не разрушая ее.
Наблюдение за каплей в этом случае происходит сверху. Краевой угол рассчитывается на основании расстояния между двумя точками отраженного света с кривой поверхности капли. Фиксация осуществляется в формате видео. Камера передает отраженный свет на компьютер, где осуществляется расчет.
Такие приборы позволяют также выявить неоднородность смачивания за счет наблюдения сверху.
Измерение угла смачивания необходимо для создания и модернизации гидрофобных покрытий. Сегодня они находят очень широкое применение.
Гидрофобное покрытие – это материал, который наносится на поверхности для обеспечения их водонепроницаемости и несмачиваемости.
Они защищают поверхности от разрушающего воздействия влаги и намокания.
В быту такие материалы применяются на стеклах и частях корпусов автомобилей, обуви, тканях, экранах гаджетов для обеспечения стекания капель воды без удерживания на поверхности.

Более широкое использование они получили в промышленности.
При строительстве конструкций гидрофобные пропитки позволяют предотвратить разрушение пористых материалов под воздействием влаги и увеличить надежность и срок их эксплуатации.
На деталях оборудования они выполняют ряд важных функций: защита от коррозии, обледенения, увеличение срока службы.
Например, для узлов промышленного оборудования разработано гидрофобное покрытие MODENGY 1009.
В его состав включен политетрафторэтилен. Он обладает низкой адгезией к большинству материалов. Данное вещество также обеспечивает низкий коэффициент трения, благодаря чему сфера применения покрытия очень широка.
Например, покрытие MODENGY 1009 наносится на механизмы оборудования, работающего при отрицательных температурах. За счет предотвращения задерживания конденсата материал защищает от примерзания и обеспечивает штатное срабатывание устройств.
Также покрытие эффективно работает на механизмах, эксплуатируемых в агрессивных средах, таких как морской климат. Оно защищает обработанные поверхности от воздействия соляного тумана и предотвращает оседание капель соленой воды. Благодаря этому обеспечивается длительная защита от коррозионного разрушения.
Свойства гидрофобных покрытий полезны на производствах, оборудование которых работает с расплавленными полимерными материалами. Это станки по упаковке изделий в пленку, термоформовочные аппараты, экструзионные линии, форсунки для подачи расплавленного пластика, формообразующая оснастка.
Применение покрытия позволяет предотвратить прилипание и нагар разогретых полимеров, благодаря чему повышаются срок службы оборудования и качество продукции, ускоряется процесс производства.
Возврат к списку
Угол контакта
Угол контакта (θ) – это угол, который образуется между каплей жидкости и поверхностью твердой или иной фазы.
Равновесие сил, воздействующих на угол контакта (θ)
Равновесное уравнение: γsv = γsl + γlv cosθ
γlv –равновесное состояние между жидкостью и газовой фазой;
γsv –равновесное состояние между твердой фазой и газовой фазы;
γsl – равновесное состояние между твердой и жидкой фазами.
Статический угол контакта
Статический угол контакта измеряется в том случае, когда капля жидкости находится в неподвижном состоянии на твердой поверхности.
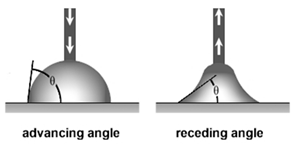
Динамический угол контакта
Динамический угол контакта измеряется в том случае, когда граница раздела фаз движется и происходит изменение статического угла контакта во времени. Динамический угол контакта бывает двух типов – наступающий и отступающий. Измерение может быть произведено двумя методами – метод изменения объема капли и метод наклона подставки.
Наступающий угол смачивания θa : наибольший угол контакта достигается путем увеличения межфазной поверхности при добавлении дополнительного количества жидкости.
Отступающий угол смачивания θr: возникает при уменьшении объема жидкой капли.
Угол гистерезиса θH: является разницей между наступающим и отступающим углами θH = θa – θr
Наклонный метод: совмещает как наступающий, так и отступающий угол контакта в одной капле. Капля помещается на рабочий столик, который постепенно начинает наклоняться. Наступающий угол измеряется в нижней части капли (на картинке слева), когда она начинает двигаться. Отступающий угол контакта измеряется в верхней части капли (на картинке справа).
Методы измерения и расчета угла смачивания лежачей капли
Существует 4 метода измерения и расчета угла смачивания лежачей капли:
- 1. Полуугловой метод
- 2. Круговой метод
- 3. Эллиптический метод
- 4. Тангенциальный метод
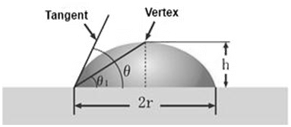
Полуугловой метод
Если размер капли мал, то ее можно представить как часть сферы и профиль капли в двух измерениях, т.е. в виде круга.
Здесь h – высота, а r – половина ширины базовой линии. Таким образом, θ1 = tan-1h/r. И в случае простой геометрии угол смачивания можно выразить следующим образом θ = 2θ1. (см. рисунок). Рассчитав h и r при помощи анализа изображения, далее можно рассчитать угол контакта θ.
Этот метод подходит для капель симметричной формы и меньшего размера. Для капель большего размера и тяжести можно снизить высоту вершины.
Круговой метод
Стадии расчета угла контакта круговым методом:
- Захват и сохранение изображения с упавшей каплей.
- Распознавание базовой линии
- Выберите 3 или более точек на краю криволинейного профиля капли.
- По кривой с данными точками можно найти уравнение окружности.
- Угол смачивания представляет собой угол между касательной и базовой линией.
Данный метод является наиболее распространенным при вычислении угла контакта.
Эллиптический метод
В эллиптическом методе применяется построение кривой профиля капли. В этом отношении данный метод похож на круговой.
- Захват и сохранение изображения с упавшей каплей.
- Распознавание базовой линии
- Выделение 6 базовых точек на кривой
- Вычисляется уравнение эллипса
- Угол смачивания представляет собой угол между касательной и базовой линией
По сравнению с другими данный метод является достаточно сложным. Поэтому он используется для вычисления угла смачивания по методу лежачей капли в диапазоне 0 – 130°С.
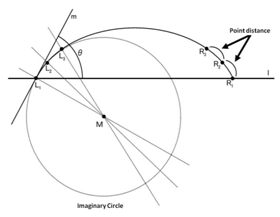
Тангенциальный метод
Форма капли представляется как часть контура предполагаемой окружности. В данном методе определяется центр предполагаемой окружности, и угол контакта представляет собой угол между касательной и окружностью.
Три точки L1, L2 и L3 образуются на представляемой окружности. Левый гол контакта – угол между касательной m и базовой линией l. Правый угол контакта может быть измерен таким же образом при помощи точек R1, R2, и R3.
Измерение краевого угла
1. Подготовка образца
Образцы должны быть подготовлены заранее, и их поверхности должны быть надлежащим образом очищены непосредственно перед измерениями угла контакта. Образец следует размещать строго в горизонтальном положении. Необходимо тщательно очистить иглу шприца. Это важно потому, что жидкость, выходящая из иглы, может немного подниматься вверх по наружной поверхности иглы в ходе эксперимента. Желательно натереть кончик иглы водоотталкивающим составом.
2. Обеспечение условий влажности / уровни пара
Образец должен быть помещен в измерительную ячейку, заполненную рабочей жидкостью. Эти операции проводятся за несколько минут до измерения угла контакта. На данном этапе необходимо закрепить шприц, заполненный рабочей жидкостью, и выровнять иглу по отношению к поверхности образца.
3. Измерение статического угла контакта
После выхода жидкости из иглы должна появиться капля. Диаметр капли должен быть больше диаметра иглы в 3-4 раза. Подача жидкости должна осуществляться до того момента, пока целая капля не выйдет из иглы. Далее игла должна быть удалена. Нужно выждать 1-3 минуты для стабилизации капли, после чего можно померить статический угол контакта.
4. Измерение наступающего угла контакта
Игла должна быть перемещена назад к капле и необходимо добавлять жидкость до того момента, пока не растечется база. Далее игла снимается и измеряется наступающий угол контакта. Эта операция повторяется 3-5 раз, после чего берется среднее значение.
5. Измерение убывающего угла контакта
Игла погружается в каплю для того, чтобы начать втягивать жидкость обратно, уменьшив тем самым размер капли. Данную операцию следует проводить аккуратно, не меняя, диаметра капли. После аккуратного удаления иглы можно измерить убывающий угол контакта. Измерение следует провести 3-5 раз, усреднив в конечном итоге результат.
6. Воспроизведение результатов
Измерение угла контакта необходимо повторить либо на 3 – 5 точках одного и того же образца, либо на других таких же образцах, прошедших те же стадии очистки.
Поверхностное
натяжение твердого тела непосредственно
измерить трудно. Поэтому для
исследования процессов взаимодействия
твердых тел с жидкостями и газом
пользуются косвенными методами
изучения поверхностных явлений,
протекающих на контактах между твердыми
и жидкими телами. К таким методам
относятся измерение работы адгезии
(Адгезия измеряется работой, которую
надо затратить, чтобы оторвать твердое
тело от жидкости в направлении нормали
к поверхности раздела), исследование
теплоты смачивания и углов избирательного
смачивания и т. д.
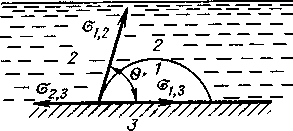
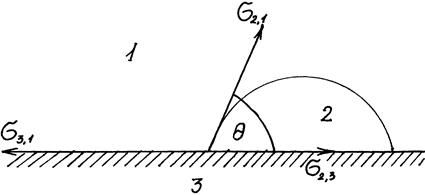
Е
сли
на поверхность твердого тела нанести
каплю жидкости, то под действием
молекулярных сил она растекается по
поверхности твердого тела и принимает
форму линзы (рис. VI.4).
Рис VI4 Форма
капли, обусловленная поверхностными
натяжениями на различных границах
соприкасающихся фаз
Угол ,
образованный касательной к капле в
точках ее периметра, зависит от
поверхностных натяжений 1,3,
1,2
и 2,3
на разделах фаз 1-3, 1-2 и 2-3. (В нефтяной
литературе принято условно обозначать
цифрой 1 водную фазу, цифрой 2 —
углеводородную жидкость или газ и цифрой
3 — твердое тело). Угол всегда отсчитывают
от касательной в сторону фазы 1 (в сторону
более полярной фазы).
Из условия равновесия
векторов (предполагается, что краевой
угол
отвечает термодинамическому равновесию)
получим уравнения, выведенные впервые
Юнгом, 2,3
=1,3
+ 1,2cos (VI.2)
откуда cos=
(VI.3)
В этих уравнениях
2,3
и 1,3
практически неизвестны. Поэтому о
соотношении поверхностных натяжений
3,2
и 3,1
(т. е. о процессах, происходящих на границе
твердого тела с другими фазами) судят
по углу ,
который служит мерой смачивания
жидкостями поверхности твердого тела
и косвенно характеризует взаимодействие
твердого тела с другими фазами.
Значение ,
если исключить влияние силы тяжести,
не зависит от размеров капли и определяется
лишь молекулярными свойствами поверхности
твёрдого тела и соприкасающихся фаз.
Поэтому, исходя из теории поверхностных
явлений, можно установить связь
краевого угла смачивания
с поверхностным натяжением между
твердым телом и жидкостью. Например,
поверхность должна лучше смачиваться
той жидкостью, которая обладает
меньшей разностью полярностей между
твердым телом и жидкостью, т.е. меньшим
значением поверхностного натяжения на
их разделе (см. рис. VI.4). Высокополярные
жидкости, т. е. жидкости с высоким
поверхностным натяжением, хуже смачивают
твердую поверхность, чем жидкости
малополярные (т. е. обладающие меньшим
поверхностным натяжением). Например,
такая высокополярная жидкость, как
ртуть, смачивает только некоторые
металлы; вода — жидкость, менее полярная,
чем ртуть, смачивает кроме металлов,
многие минералы и кристаллические
соли; малополярные масла смачивают на
границе с воздухом все известные твердые
тела.
По углу избирательного
смачивания, образующегося при контакте
воды, нефти и породы, наряду с другими
параметрами можно судить о качестве
вод и их отмывающей и нефтевымывающей
способностях. Лучше отмывают нефть
воды, хорошо смачивающие породу. Поэтому
изучению явлений смачивания в
нефтепромысловом деле уделяется большое
внимание.
Угол смачивания
зависит от множества факторов:
механического строения поверхности,
адсорбции на ней газов, поверхностно-активных
и других веществ, от ее загрязнения,
электрического заряда и т. д
Особо большое
влияние на угол смачивания оказывают
процессы адсорбции в связи с изменением
химического строения поверхности
твердого тела. Если при этом к поверхности
ориентирована неполярная углеводородная
цепь поверхностно-активных веществ,
то гидрофильные радикалы (—ОН, —СООН,
—СО, —СОН и др.), обращенные в сторону
жидкости, способствуют смачиванию
поверхности водой. При обратной
ориентации поверхность гидрофобизуется.
Интересно отметить,
что радикалы, свободно ориентировавшиеся
на поверхности жидкости, в зависимости
от свойств фаз сохраняют эту ориентировку
при быстром переходе жидкости в твердую
фазу. В опытах Дево, например, воск и
парафин, расплавленные и охлажденные
на воздухе, давали гидрофобную поверхность,
а охлажденные на границе с водой —
гидрофильную. Точно так же поверхность
стеариновой кислоты, полученная на
границе с воздухом, гидрофобна, а
полученная на границе с водой и стеклом
— гидрофильна.
Адсорбция полярных
молекул на поверхности горных пород
имеет большое значение при избирательном
смачивании их водой и нефтью. Кварц,
известняк и другие минералы, которыми
в основном представлены нефтесодержащие
породы, по своей природе гидрофильны.
Несмотря на это, все нефтесодержащие
породы в значительной степени
гидрофобизованы нефтью и часто очень
плохо смачиваются водой или же обладают,
по-видимому, устойчивой гидрофобной
поверхностью.
С процессами
адсорбции тесно связаны явления
статического гистерезиса смачивания,
заключающиеся в задержке установления
равновесного значения смачивания
вследствие трения при перемещении
периметра капли по поверхности твердого
тела. Мерой статического гистерезиса
смачивания может служить разность
косинусов углов B
= B2,1—В1,2,
см. формулу (VI.3). Эта разность получается
при различном порядке смачивания
твердой поверхности жидкостями 1 и 2, т.
е. от того, какой средой (1 или 2) вначале
была смочена поверхность. В присутствии
адсорбционного слоя статический
гистерезис смачивания резко возрастает.
В соответствии с
изменением молекулярно-поверхностных
характеристик жидкостей на различных
поверхностях раздела с увеличением
давления и температуры изменяется также
угол смачивания. По результатам
исследований Н. Д. Таирова и М. М. Кусакова,
краевой угол избирательного смачивания
кварца растворами нефти на границе с
водой при насыщении углеводородной
жидкости и воды азотом (т. е. малорастворимым
газом) не зависит от давления. Аналогичная
закономерность наблюдается в данных
условиях и для поверхностного натяжения
нефти на границе с водой.
При растворении
в нефти углеводородного газа, обладающего
значительно лучшей растворимостью, чем
азот, в нефти, с одной стороны, увеличивается
относительное содержание неполярной
части; это сопровождается уменьшением
адсорбции и гидрофобизации поверхности.
В результате вода лучше избирательно
смачивает кварц при контакте с нефтью.
С другой стороны, вследствие адсорбции
поверхностно-активных веществ на
поверхности породы увеличивается угол
смачивания
при повышении давления. В совокупности
зависимость
= f(р)
с ростом давления от преобладания того
или иного фактора может иметь разный
характер, а d/dp
может быть положительной или
отрицательной.
Щелочные воды
лучше смачивают поверхность кварца и
других минералов, слагающих пласт, чем
морская и дистиллированная воды. Это
связано с омылением, органических кислот
щелочами воды. Мыла, адсорбируясь на
поверхности раздела нефть — вода и
нефть — порода — вода, способствуют
гидрофилизации поверхности, т. е.
уменьшению угла избирательного
смачивания.
В атмосферных
условиях значение угла смачивания
пропорционально поверхностной
активности нефти. При высоких давлениях
это условие нарушается.
Кроме измерения
углов смачивания, взаимодействие жидких
и твердых тел может быть исследовано
путем изучения работы адгезии и теплот
смачивания.
Работа адгезии по
уравнению Дюпре Wa=2,3+1,2-1,3,
(VI.4)
где 1,2
— поверхностное натяжение жидкости на
границе с воздухом; 2,3
и 1,3
—поверхностные натяжения твердого
тела на границе с воздухом и с жидкой
фазой.
Неизвестные
величины 2,3
и 1,3
из (VI.4) можно исключить, если использовать
соотношения (VI.3) и (VI.2). Подставляя в
уравнение Дюпре вместо 2,3
и 1,3
их значения из (VI.2), получим уравнение
Дюпре—Юнга Wa=1,2(1+cos).
(VI.5)
Из
соотношения 2,3—1,3=1,2cos
следует, что при
смачивании свободная энергия единицы
поверхности твердого тела уменьшается
на 1,2cos.
Величину 1,2cos
принято называть натяжением смачивания.
Работа WK
когезии, как известно, характеризует
энергетические изменения поверхностей
раздела при взаимодействии частиц одной
фазы.
Из уравнения (VI.5)
следует, что на отрыв жидкости от
поверхности твердого тела при полном
смачивании, когда cos=1,
затрачивается работа, необходимая для
образования двух жидких поверхностей
— 2жг,
т. е. WК=2жг,
где жг
— поверхностное натяжение жидкости на
границе с газом.
Это значит, что
при полном смачивании жидкость не
отрывается от поверхности твердого
тела, а происходит разрыв самой
жидкости т. е. при полном смачивании
1,21,3.
Для гидрофобных
поверхностей характерно соотношение
1,2>1,3,
т. е. жидкость может отрываться от
поверхности. При =180,
т. е. при полной несмачиваемости жидкостью
поверхности твердого тела, работа
адгезии равна нулю. Следовательно,
работа адгезии может служить показателем
смачиваемости или прилипаемости
жидкостей к поверхности твердого тела.
Подставив в
уравнение Юнга значения работ адгезии
и когезии, получим
(VI.6)
Это уравнение
позволяет оценить смачиваемость твердого
тела в зависимости от соотношения сил
притяжения жидкости к твердому телу и
взаимного притяжения частиц жидкости.
Например, твердое тело будет смачиваться
жидкостью (cos
положителен) при Wa>0,5WK.
При Wa<0,5WK
значение cos
будет иметь отрицательный знак, т.
е. жидкость не смачивает поверхность.
Из формулы (VI.6) следует, что полная
несмачиваемость (cos=-1)
может быть только при условии Wa=0.
Это условие на практике никогда не может
быть выполнено, ибо между телами с любыми
свойствами всегда существуют силы
молекулярного притяжения, и работа
адгезии имеет всегда положительный
знак.
Из уравнения (VI.6)
следует, что смачиваемость жидкостью
твердого тела тем лучше, чем меньше
работа когезии WK
(и поверхностное натяжение жидкости
на границе с газом).
Для характеристики
смачивающих свойств жидкости может
быть использована также относительная
работа адгезии z = Wa/WK,
при увеличении которой смачивающие
свойства улучшаются. Из (VI.6) следует,
что при z=1,
Wa=WK
cos=1.
Строго говоря,
уравнение (VI.6) теряет смысл в условиях
полного смачивания, так как краевой
угол не устанавливается. При этом в
качестве термодинамической характеристики
взаимодействующих фаз используют
коэффициент растекания
S=тг—тж—жг.
где тг,
тж,
жг
— поверхностные натяжения соответственно
твердого тела на границе с газом с
жидкостью и жидкости на границе с газом.
Учитывая соотношения
Дюпре (VI.4) и коэффициент растекания,
можно написать S=
Wа-2жг.
Следовательно,
для полного растекания необходимо,
чтобы работа адгезии была более, чем
в два раза больше величины жг.
Уравнение Юнга
(VI.3) можно записать так cos=(Wa—жг)жг.
Это уравнение
интересно тем, что в отличие от формулы
Юнга входящие в него величины в ряде
случаев могут быть измерены.
Адгезию можно
установить экспериментально. Опыты
показывают, что при медленном отрыве,
когда поверхностные силы успевают
прийти в состояние равновесия, значения
работы отрыва, подсчитанные по
уравнению Дюпре — Юнга и определенные
экспериментально, совпадают. С увеличением
скорости отрыва работа адгезии
возрастает, по-видимому, за счет
возникающих электростатических сил.
При этом заряды двойного слоя не успевают
нейтрализоваться и электрические силы
суммируются с силами адгезии.
Установлено, что
при смачивании твердого тела жидкостью
наблюдается выделение тепла, так как
разность полярностей на границе твердое
тело — жидкость меньше, чем на границе
с воздухом. Для пористых и порошкообразных
тел теплота смачивания обычно имеет
значение от 1 до 125 кДж/кг и зависит
от степени дисперсности твердого тела
и от полярности жидкости.
Теплота смачивания
характеризует степень дисперсности
твердого тела и природу его поверхности.
Большее количество теплоты выделяется
при смачивании той жидкостью, которая
лучше смачивает твердую поверхность.
Поэтому отношение теплот смачивания
жидкости служит термической характеристикой
смачиваемости этой поверхности.
Более определенно
степень гидрофильности или гидрофобности
поверхности горных пород оценивают
путем сравнения теплоты смачивания
керна водой с теплотами смачивания
полностью гидрофобизованной и
гидрофилизованной породы. Средняя
теплота смачивания нефтенасыщенных
кернов ряда нефтяных месторождений
Западной Сибири колеблется от 6,3 до 24,4
кДж/кг. Этот параметр оценивается в
калориметрах высокой точности.
Поверхность горных
пород отличается значительной
неоднородностью по смачиваемости,
что можно объяснить многими причинами.
Большое влияние на свойства поверхностей
оказывают процессы адсорбции, которые
зависят от многообразия факторов,
связанных как с составом пластовых
жидкостей и пород, так и с условиями их
контакта в пласте. Свойства поверхности
минералов, кроме явлений адсорбции,
зависят и от процессов химического
взаимодействия жидкостей и минералов,
ионного обмена, растворения и
электрокинетических явлений.
Значительно влияет на эти процессы
сложное строение самой поверхности
минералов. Вследствие влияния на свойства
поверхности горных пород большого числа
факторов избирательная смачиваемость
их пластовыми жидкостями может изменяться
в широких пределах. Некоторые породы,
по-видимому, полностью гидрофобизованы
нефтью. Большинство же исследованных
коллекторов газовых месторождений
сложены гидрофильными породами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ГЛАВА ХI. АДГЕЗИЯ, СМАЧИВАНИЕ И РАСТЕКАНИЕ ЖИДКОСТЕЙ
Адгезия и работа адгезии
Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы называют адгезией(прилипанием). Адгезия обеспечивает между двумя телами соединение определенной прочности, обусловленное межмолекулярными силами.
Различают адгезию между двумя жидкостями, между жидкостью и твердым телом и между двумя твердыми телами.
Явления адгезии и смачивания широко распространены. Склеивание материалов, нанесение покрытий, получение материалов на основе связующих и наполнителей (бетон, резина, стеклопластики и т. п.), сварка и паяние металлов, печатание – все эти процессы связаны с адгезией и смачиванием, которые в значительной степени определяют качество материалов и изделий.
Рис.27. К выводу соотношения между работой адгезии и поверхностными натяжениями взаимодействующих компонентов (уравнения Дюпре): 1 – газ; 2 – жидкость; 3 ‑ твердое тело
Из-за сложности протекающих процессов, рассматриваемые в данном разделе межфазные явления до сих пор недостаточно изучены. Поэтому основное внимание будет уделено системам, в которых имеется хотя бы одна жидкая фаза, что позволяет обеспечивать равновесные обратимые условия и соответственно использовать термодинамические соотношения.
Адгезия – результат стремления системы к уменьшению поверхностной энергии. Поэтому адгезия является самопроизвольным процессом.
Работа адгезии Wад (по аналогии с работой когезии) определяется как работа изотермического обратимого разделения двух конденсированных фаз вдоль межфазной поверхности единичной площади.
При таком разделении образуются свободные поверхности раздела обеих конденсированных фаз с газом, имеющие энергии 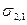
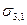
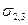
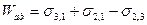
Это уравнение Дюпре. Оно отражает закон сохранения энергии при адгезии. Из него следует, что работа адгезии тем больше, чем больше поверхностные натяжения исходных компонентов и чем меньше межфазное натяжение.
Величина Wад характеризует родственность контактирующих фаз, т. е. степень насыщения нескомпенсированных поверхностных сил при контакте. Межфазная энергия 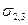
Она измеряется в тех же единицах, что и поверхностное натяжение (Дж/м 2 ).
Работу адгезии экспериментально определяют при непосредственном разрушении соединения. Работу адгезии можно определить и косвенными методами, которые особенно удобны, если хотя бы одной из взаимодействующих фаз является жидкость и можно измерить, например, краевой угол.
Смачивание и краевой угол. Закон Юнга
Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом).
Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания).
При нанесении небольшого количества жидкости, например, капли на поверхность другой жидкости, имеющей большую плотность, или на поверхность твёрдого тела можно наблюдать два процесса, если приводимые в контакт вещества взаимно нерастворимы. В одном случае нанесенная жидкость остается на поверхности другой фазы в виде капли, принявшей при установившемся равновесии определенную форму. В другом случае капля растекается по поверхности. Вначале рассмотрим первый процесс, когда капля не растекается полностью по поверхности другого тела.
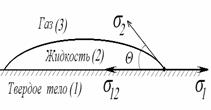
Рис.28. К выводу уравнения для краевого угла (закона Юнга).
Рис.28 иллюстрирует состояние капли жидкости на поверхности твёрдого тела в условиях равновесия. Поверхностная энергия твёрдого тела, стремясь уменьшиться, вызывает растяжение капли по поверхности. Эта энергия равна поверхностному натяжению твёрдого тела на границе с воздухом s3, 1. Межфазная энергия на границе твёрдого тела с жидкостью s2, 3 стремится, наоборот, сжать каплю, т. е. поверхностная энергия уменьшается за счет снижения площади поверхности. Растеканию препятствуют когезионные силы, действующие внутри капли. Действие когезионных сил направлено от границы между твёрдой, жидкой и газообразной фазами по касательной к сферической поверхности капли и равно s2, 1 (силы гравитации не учитываются). Угол q, который образован касательными к межфазным поверхностям, ограничивающим смачивающую жидкость, имеющий вершину на линии раздела трех фаз, называется краевым углом смачивания.

Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил. При равновесии между ними соблюдается следующее соотношение:
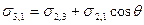
Полученное соотношение называется законом Юнга. Отсюда количественную характеристику смачивания – косинус краевого угла можно выразить через поверхностные и межфазное натяжения:
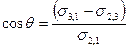
Чем меньше угол q и соответственно больше cos q, тем лучше смачивается поверхность. При остром угле q, т. е. при cos q > 0, поверхность считают хорошо смачиваемой данной жидкостью. Если угол q тупой, т. е. cos q
Поверхностные явления и адсорбция
Кандидат химических наук, доцент
Тема 1. Поверхностные явления и адсорбция
Занятие 2. Поверхностные явления
2. Смачивание и растекание.
3. Основные понятия и характеристики адсорбции.
4. Изотермы и изобары адсорбции
ЛИТЕРАТУРА
1. Фролов коллоидной химии. – М.: Химия, 1989. – С. 25-31, 78-96.
2. Коллоидная химия. – СПб.: «Лань», 2003. – С. 70-76.
НАГЛЯДНЫЕ ПОСОБИЯ И ПРИЛОЖЕНИЯ
Работа когезии и адгезии
Краевой угол смачивания
Критерии смачивания и несмачивания
ВВЕДЕНИЕ
Изучение поведения жидкостей на твердых и жидких поверхностях представляет большой интерес в связи с широкой распространенностью явлений смачивания и растекания как в природе, так и в различных отраслях народного хозяйства. Явления смачивания и растекания лежат в основе процессов отмывания жидких загрязнений с твердых покрытий. Начнем с изучения понятий адгезии и когезии.
1. АДГЕЗИЯ И КОГЕЗИЯ
Когезия характеризует взаимное притяжение частиц (атомов, молекул) однородного тела, обусловленное силами межмолекулярного взаимодейст-вия, действующими внутри тела.
Когезия характеризует прочность тел на разрыв. Она сильна в твердых телах, меньше в жидкостях.
Адгезия характеризует взаимное притяжение частиц различных тел в области их соприкосновения (т. е. на поверхности раздела фаз), обусловленное силами межмолекулярного взаимодействия, действующими между этими телами.
Количественно когезия и адгезия характеризуются соответственно работой когезии Wк и работой адгезии Wa. Эти величины измеряются в тех же единицах, что и поверхностное натяжение (Дж/м2, Н/м), и они связаны с поверхностным натяжением (рис. 1).
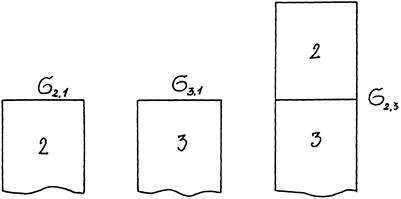
Работа когезии Wк – работа, которую надо совершить для разрыва однородного тела по сечению с единичной площадью на две части. Эта работа затрачивается на разрыв межмолекулярных связей внутри тела. Представим мысленно цилиндр из какой-либо жидкости с единичной площадью сечения S (рис. 1). Разорвем этот цилиндр на 2 части.
Рис. 1. К выводу соотношения между когезией и
Образовалась новая поверхность площадью 2S на границе жидкость – газ. Если вспомнить физический смысл поверхностного натяжения (это работа, которую надо совершить, чтобы увеличить на единицу площадь поверхности раздела фаз), то можно записать
где Wк – работа когезии, Дж/м2;
sЖ-Г – поверхностное натяжение на границе раздела
жидкость – газ, Дж/м2.
При разрыве твердого тела на две части работа когезии соответственно равна
где sТ-Г – поверхностное натяжение на границе раздела
твердое тело – газ, Дж/м2.
сразу можно отметить, что работа когезии тем больше, чем больше величина поверхностного натяжения.
Работа адгезии Wa – работа, которую надо совершить для разрыва двух соприкасающихся тел с единичной площадью контакта. Эта работа затрачивается на разрыв межмолекулярных связей, возникающих на границе раздела фаз.
Рис. 2. К выводу соотношения между адгезией и
Пусть в соприкосновении находятся две несмешивающиеся жидкости с единичной площадью контакта. Граница раздела фаз характеризуется поверхностным натяжением sЖ1- Ж2. После разрыва исчезла граница раздела фаз ж1-ж2, но появились две новые площади поверхности, которые характеризуются поверхностным натяжением sЖ1- Г и sЖ2 – Г.
Очевидно, что работу адгезии можно рассчитать по формуле
Wa = sЖ1- Г + sЖ2 – Г – sЖ1- Ж2 (3)
Это выражение называется уравнением Дюпре.
По аналогии при отрыве жидкости от твердой поверхности совершается работа адгезии, равная:
Wa = sЖ – Г + sТ – Г – sТ – Ж (4)
По уравнению (3) работу адгезии вычислить достаточно легко, поскольку все входящие в него величины определяются экспериментально.
По уравнению (4) рассчитать Wа практически невозможно, т. к. определение поверхностного натяжения на границе с твердым телом представляет собой сложную экспериментальную задачу.
Силы когезии и адгезии играют большую роль в процессах смачивания и несмачивания жидкостями твердых тел, склеивания материалов, нанесения лакокрасочных и других покрытий, печатания, крашения.
2. СМАЧИВАНИЕ И РАСТЕКАНИЕ
Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом).
При нанесении капли жидкости на поверхность твердого тела (или другой жидкости) можно наблюдать разные явления. В одном случае нанесенная жидкость сохраняет форму капли, в другом случае капля растекается по поверхности. Рассмотрим первый случай (рис. 3)
Рис. 3. Смачивание жидкостью твердого тела
Линия соприкосновения трех фаз называется периметром смачивания. Угол q называется краевым углом смачивания. Он отсчитывается со стороны жидкости. Поскольку капля находится в состоянии равновесия, действие сил на нее скомпенсировано. Рассмотрим эти силы. Как известно, силы поверхностного натяжения направлены на сокращение площади контакта фаз и действуют по касательной к поверхности. На рис. 3 эти силы представлены векторами, выходящими из точки соприкосновения всех трех фаз.
sТ-Г – стремиться уменьшить площадь контакта твердого тела с газом, поэтому растягивает пленку жидкости по твердому телу.
sТ-Ж – стремится уменьшить площадь контакта твердого тела с жидкостью, поэтому стягивает каплю жидкости в шарик.
sЖ-Г – стремится уменьшить площадь контакта жидкости с газом, поэтому стягивает каплю жидкости в шарик (шарообразная поверхность имеет наименьшую площадь).
Рассмотрим равнодействующую сил, действующих на каплю в точке О вдоль поверхности твердого тела. Эти силы поверхностного натяжения sТ-Г, sТ-Ж, а также проекция sЖ-Г на выбранную ось 
В состоянии равновесия равнодействующая сил равна 0:
sТ-Г = sТ-Ж + sЖ-Г. cosq (5)
Полученное соотношение (5) называется законом Юнга.
Краевой угол смачивания q или cosq являются количественной характеристикой смачивания. Чем меньше угол q и соответственно больше cosq, тем лучше смачивается поверхность.
Закон Юнга позволяет выразить cosq через поверхностные межфазные натяжения:

Сочетание уравнения Дюпре (4) с законом Юнга (5) позволяет выразить работу адгезии Wa через косинус краевого угла смачивания q.
Из уравнения (5) выразим разность
sТ-Г – sТ-Ж = sЖ-Г. cosq
Полученную разность подставим в уравнение 4
Wa = sЖ-Г + sЖ-Г. cosq = sЖ-Г(1 + cosq) (7)
Уравнение (7) называют уравнением Дюпре – Юнга. Оно позволяет рассчитать работу адгезии, если известно поверхностное натяжение жидкости и краевой угол смачивания. Обе эти величины сравнительно легко определяются экспериментально: q определяют путем проектирования капли на экран (с помощью несложной установки) и измерения краевого угла на проекции капли. С помощью уравнения Дюпре – Юнга (7) легко найти соотношение между работой когезии смачивающей жидкости и работой адгезии между жидкостью и смачиваемым телом.
Краевой угол смачивания (или косинус краевого угла) является характеристикой способности жидкости смачивать твердую или жидкую поверхность. В таблице 1 представлены возможные случаи поведения жидкости на твердой или жидкой поверхности. Смачивание или несмачивание зависит от соотношения работы когезии и работы адгезии.
Таблица 1. Критерии смачивания, несмачивания и растекания
q > 900 (тупой угол)
Смачивание жидкостью поверхности
Капиллярное поднятие или опускание жидкостей связано с возникновением кривизны поверхности (выпуклый или вогнутый мениск). В свою очередь появление кривизны поверхности связано с процессами смачивания (q 900, выпуклый мениск) жидкостями стенок капилляров.
Растекание жидкостей по поверхности
Особо остановимся на предельном случае смачивания – растекании жидкости по поверхности, которое наблюдается при q = 00, когда работа адгезии равна работе когезии (Wa = Wк). Очевидно, что чем больше преобладает работа адгезии над работой когезии, тем лучше будет растекаться жидкость по поверхности. Величина
называется коэффициентом растекания или критерием Гаркинса.
Если f > 0 – жидкость растекается (Wa > Wк)
Изотермы полимолекулярной адсорбции (рис.7) характерны для адсорбции газов и паров на твердых адсорбентах. Изотерма вида а (s-образная изотерма) при невысоких давлениях напоминает изотерму мономолекулярной адсорбции (участок Р1), т. е. на поверхности образуется один слой молекул адсорбтива. При дальнейшем увеличении давление газа на первый слой может сесть второй, третий и т. д. слой молекул, происходит полимолекулярная адсорбция, поэтому адсорбция резко возрастает.
Первый слой молекул удерживается на адсорбенте силами взаимодействия адсорбент – адсорбтив, а второй, третий слои удерживаются силами притяжения между молекулами адсорбтива. Концентрирование адсорбтива на поверхности приводит к тому, что газ (пар) конденсируется и образуется жидкий слой конденсата на поверхности адсорбента.
Рис.7. Изотермы полимолекулярной адсорбции
Рs – давление насыщенного пара
Изотермы адсорбции с капиллярной конденсацией (рис.8) характерны для газов (паров), адсорбирующихся на пористых адсорбентах. Эти изотермы сходны с изотермами полимолекулярной адсорбции, но имеют и некоторые отличия. Пористые адсорбенты имеют многочисленные поры, которые представляют из себя капилляры. При образовании полимолекулярного слоя на стенках пор возникает искривленная (вогнутая) поверхность раздела фаз жидкость – пар, давление насыщенного пара над которой меньше, чем над плоской поверхностью. Поэтому в пористых материалах пар конденсируется при более низких давлениях и конденсация идет до заполнения всех пор. Этот процесс заканчивается раньше, чем достигается давление насыщенного пара. Поэтому изотерма адсорбции выходит на предельное значение (все поры заполнены, адсорбция не идет).
Рис.8. Изотермы полимолекулярной адсорбции,
осложненной капиллярной конденсацией
Рs – давление насыщенного пара
Изобары и изопикны адсорбции
Изобарой адсорбции называется зависимость величины адсорбции газа (или пара) на твердом адсорбенте от температуры при постоянном парциальном давлении газа (пара) А = fр(Т)
Изопикной адсорбции называется зависимость величины адсорбции растворенного вещества от температуры при постоянной концентрации растворенного вещества А = fc(Т)
Процесс адсорбции экзотермичен и, следовательно, в соответствии с принципом Ле-Шателье с ростом температуры величина физической адсорбции уменьшается (рис.9). При повышении температуры колебания адсорбированных поверхностью частиц усиливаются, они отрываются от поверхности, равновесие сдвигается в сторону процесса десорбции.
Рис.9. Изобара (Р = const) или изопикна (С = const) адсорбции.
Описание взаимодействия молекул адсорбтива и молекул адсорбента представляет собой весьма сложную и до сих пор до конца неразрешенную задачу. Рассмотрению некоторых теорий адсорбции будет посвящена следующая лекция.
Сегодня мы познакомились с основными видами поверхностных явлений: смачиванием, растеканием и адсорбцией. Следующая лекция будет посвящена подробному рассмотрению явлений адсорбции, которые играют значительную роль в природе, технологических процессах.
2.3.2. Смачивание и растекание на границе твердое тело – жидкость – газ
В большинстве случаев жидкость на поверхности твердого тела остается в виде капли, большей или меньшей толщины, контактирующей с твердым телом под определенным углом, который называется краевым углом смачивания и обозначается буквой Q (рис. 1.24). Растекание капли по поверхности прекратится при достижении равновесия, которое без учета сил тяжести может быть описано уравнением Юнга:

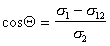
где индексы 1, 2, 3 – обозначают, соответственно, твердую, жидкую и газовую фазы.
Работа адгезии выражается уравнением Дюпре:
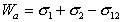
Рис. 1.24. Капля жидкости на поверхности твердого тела (схема)
Работа адгезии при 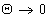
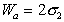
Следует помнить, что определение работы адгезии в реальных системах предполагает равновесие фаз, насыщенных относительно друг друга.
Кроме того, твердая поверхность, по которой происходит растекание жидкости, не свободна. Она обычно покрыта пленкой вещества, адсорбированного из газо-паровой фазы. Эта пленка имеет поверхностное давление p, поэтому
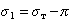
Смачивание неоднородных, пористых или шероховатых поверхностей сопровождается запиранием пузырьков воздуха в неровностях. В результате этого краевые углы смачивания сухой и предварительно увлажненной поверхностей различаются. Такое явление носит название «гистерезис смачивания». Гистерезис смачивания проявляется также при загрязнении поверхности, в результате чего она становится неоднородной при закреплении на ней твердых частиц или жировых пленок. В этом случае поверхность ведет себя как составная.
Шероховатость поверхности учитывается введением коэффициента шероховатости r, представляющего отношение площади поверхности реального тела к площади идеально гладкой поверхности, тогда
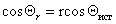
Можно отметить, что если краевой угол смачивания гладкой поверхности, например полимерной пленки, меньше 90 o , то шероховатость (ткань из волокон этого полимера) уменьшает его, если же он больше 90 o , то шероховатость его увеличивает. Для составной поверхности, которая специфична для большинства текстильных материалов, наличие участков различной природы может быть учтено введением коэффициентов x, характеризующих долю поверхности с различными свойствами. Например, если текстильный материал изготовлен из волокон двух видов 1 и 2, то
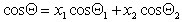
Если переплетение нитей таково, что получается сетчатый или дырчатый материал, то уравнение (2.50) принимает вид
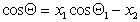
где х2 – доля открытой поверхности.
Как мы обсуждали выше, поверхностное натяжение можно разделить на компоненты дисперсионных и полярных сил, а при нахождении межфазового натяжения для многих жидких границ можно ограничиться лишь дисперсионной составляющей. Такое ограничение позволяет провести обсуждение явления смачивания (по крайней мере, низкоэнергетических поверхностей, к каковым можно отнести подавляющее большинство волокнообразующих полимеров), в рамках теории дисперсионных сил.
Как показал Н. В. Чураев смачивание неполярной жидкостью твердой поверхности возможно, если будет соблюдаться условие смачивания, которое выражается уравнением
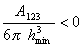
где А123 – составная постоянная Гамакера при взаимодействии жидкости (фаза 2) с твердым телом (фаза 1) на границе с воздухом (фаза 3); hmin – наименьшая толщина пленки, которая фактически соответствует Ван-дер-Ваальсову расстоянию, т.е. hmin = (0,22¸0,24) нм. Например, для воды на поверхности тефлона А123 = -7·10 – 21 Дж.
Учет только дисперсионных сил приводит к уравнению
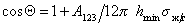
При расчетах углов смачивания твердых поверхностей следует учитывать поверхностное давление пленки, образованной при адсорбции из газо-паровой фазы. Тогда с учетом уравнения (1.2.48), уравнение Юнга (1.2.45) следует записать в виде
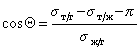
Способ расчета поверхностного давления предложили Бэнгхэм и Разорук:
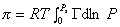
где P – равновесное давление, Г– равновесная адсорбция газа (пара), Ps – давление насыщения.
При больших углах смачивания и слабом взаимодействии жидкости с твердым телом поверхностное давление обычно не учитывают.
Для неполярных жидкостей на низкоэнергетической поверхности твердого тела для работы адгезии было получено выражение
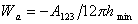
Поэтому уравнение Дюпре (1.2.46) можно записать
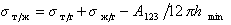
Для дисперсионной составляющей жидкости
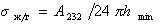
где А232 – постоянная Гамакера взаимодействия жидкости через прослойку газа (пара).
Сочетая уравнения (1.2.47), (1.2.55) и (1.2.56), получаем
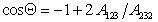
Очевидно, что Q = 0, т.е. при полном смачивании, cosQ = 1, если
Уравнение (1.2.57) позволяет прогнозировать вероятность смачивания (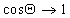
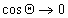
Чаще, однако, прибегают к определению постоянной Гамакера по известному значению межфазового натяжения на границе «твердое тело – газ». Эту характеристику поверхности твердого тела находят при распространении подхода Джирифалько и Гуда, рассмотренного нами выше для границы двух жидкостей, на поверхность раздела «жидкость – твердое тело», уравнения (1.2.23), (1.2.35).
Так приложение уравнения (1.2.34) к уравнению Юнга для случая смачивания неполярной жидкостью поверхности полимерного материала позволяет получить уравнение, известное как уравнение Фоукса, при
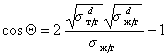
Если жидкости неполярны и 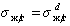
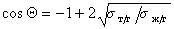
Уравнение (1.2.59) Зисман предложил использовать для определения поверхностного натяжения твердых тел. Очевидно, что при 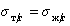
Естественно, что метод Зисмана ограничен некоторыми условиями, в частности, из уравнения (1.2.57) следует, что полное смачивание возможно при дисперсионной неразличимости твердого тела и жидкости, т.е. при А232= А123.
В действительности такого условия никогда невозможно достигнуть хотя бы потому, что если жидкость и твердое тело будут иметь одинаковый химический состав, их постоянные Гамакера будут различаться из-за различий в плотности.
Другое ограничение, связанное с применением метода Зисмана, основано на том, что использовать для измерения краевых углов смачивания следует лишь неполярные жидкости. Наиболее целесообразно применять гомологические ряды жидкостей. При величине поверхностного натяжения жидкостей более 35 мДж/м 2 метод Зисмана уже дает высокую погрешность, так как необходимо учитывать вклад полярных сил, которые в отличие от дисперсионной составляющей могут иметь и отрицательное значение. С другой стороны, приложение для смачивания твердых тел полярными жидкостями уравнения Ву (1.2.36) позволяет рассчитать полярную составляющую поверхностного натяжения жидкости, если для одной из неполярных жидкостей измерить краевой угол смачивания. Для расчета используют уравнение
Рис. 1.25. Зависимость смачивания поверхностей от поверхностного натяжения жидкостей. Материал поверхности: 1- FC-721; 2- ПТФЭ (тефлон); 3 – полиэтилен
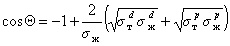
Этот метод позволил разделить величину поверхностного натяжения жидкостей на полярную и дисперсионную компоненты и определить поверхностное натяжение многих волокнообразующих полимеров.
Пример зависимости косинуса угла смачивания поверхности пленок различными жидкостями приведен на рис.1.25. Для описания этих зависимостей Зисман предложил использовать эмпирическое уравнение
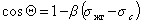
где bэмпирическая постоянная, sс – «критическое» поверхностное натяжение твердого тела, при котором происходит полное смачивание твердого тела жидкостью. Очевидно, что cos Q =1 при условии sжг = sс .
Как мы обсуждали выше, этот критерий в известной мере является условным, хотя и отражает энергетическое состояние поверхности твердого тела.
Реальное значение поверхностного натяжения твердого тела экспериментально определить невозможно, также как и рассчитать его теоретически. В этой связи метод Зисмана нашел широкое применение в практике исследования полимерных материалов, а также полимерных покрытий тканей, используемых в качестве отделочных материалов
[spoiler title=”источники:”]
http://pandia.ru/text/78/062/79852.php
http://xumuk.ru/colloidchem/35.html
[/spoiler]