Как найти крайние в уравнение

• Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
• Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
• Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax 2 + c = 0, при b = 0;
• ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

1. Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

• перенесем c в правую часть: ax 2 = – c,
• разделим обе части на a: x 2 = – c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 2 = – c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = – c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = – c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = – c/а. Ура, больше у этого уравнения нет корней.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

• не имеет корней при — c/а 0.

В двух словах

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,
х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b 2 −4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

1. Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Произведем равносильные преобразования. Умножим обе части на −1

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Преобразуем уравнение так, чтобы появились множители

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

Найдем дискриминант по формуле

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 – 4ac = 4n 2 — 4ac = 4(n 2 – ac) и подставим в формулу корней:

2 + 2nx + c = 0″ height=”705″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png” width=”588″>

Для удобства вычислений обозначим выражение n 2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n 2 – ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n 2 – ac;
• если D₁ 0, значит можно найти два действительных корня по формуле

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=”215″ src=”https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE” width=”393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=”52″ src=”https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG” width=”125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=”52″ src=”https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo” width=”112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

2 − 6x + 8 = 0″ height=”59″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png” width=”117″>

Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x 2 – 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 – 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 – 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

Теоретический материал по теме “10 способов решений квадратных уравнений”

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

10 способов решения квадратных уравнений

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Многие практические задачи решаются с их помощью. Например, квадратное уравнение позволяет рассчитать тормозной путь автомобиля, мощность ракеты для вывода на орбиту космического корабля, траектории движения различных физических объектов – от элементарных частиц до звёзд.

В школе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения. Предлагаю 10.

Определение 1. Квадратным уравнением называют уравнение вида ах 2 + b х + с = 0, где коэффициенты а, в, с- действительные числа, а ≠ 0.

Определение 2 . Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых т.е. коэффициенты в и с отличны от нуля.

Неполное квадратное уравнение — это уравнение, в котором хотя бы один из коэффициентов в или, с равен нулю.

Определение 3. Корнем квадратного уравнения ах 2 + вх + с = 0 называют всякое значение переменной х, при котором квадратный трехчлен ах 2 + вх + с обращается в нуль.

Определение 4 . Решить квадратное уравнение — значит найти все его

корни или установить, что корней нет.

Разложение левой части уравнения на множители.

Решим уравнение х 2 + 10х – 24 = 0 .

Разложим левую часть на множители:

х 2 + 10х – 24 = х 2 + 12х – 2х – 24 = х(х + 12) – 2(х + 12) = (х + 12)(х – 2).

Следовательно, уравнение можно переписать так:

Произведение множителей равно нулю, если по крайней мере, один из его множителей равен нулю.

х + 12= 0 или х – 2=0

2. Метод выделения полного квадрата двучлена.

Решим уравнение х 2 + 6х – 7 = 0 .

Выделим в левой части полный квадрат:

тогда, данное уравнение можно записать так:

х + 3=4 или х + 3 = -4

3.Решение квадратных уравнений по формулам.

а) Решим уравнение:

б) Решим уравнение:

в) Решим уравнение: 2х 2 + 3х + 4 = 0,

Данное уравнение корней не имеет.

Ответ: корней нет.

4. Решение уравнений с использованием теоремы Виета.

Чтобы квадратное уравнение привести к приведенному виду, нужно все его члены разделить на a ,, тогда

сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

5. Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение

Умножая обе его части на а, получаем уравнение а 2 х 2 + а b х + ас = 0.

Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению у 2 + by + ас = 0,

Его корни у ₁ и у ₂ найдем с помощью теоремы Виета и окончательно:

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Решим уравнение 2х 2 – 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

Согласно теореме Виета

6. Свойства коэффициентов квадратного уравнения.

1. Пусть дано квадратное уравнение ах 2 + b х + с = 0, где а ≠ 0.

Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю),

А. Решим уравнение 345х 2 – 137х – 208 = 0.

Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то

Б. Решим уравнение 132х 2 – 247х + 115 = 0.

Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то

2) Решим уравнение 2х 2 + 3х +1= 0. Так как 2 – 3+1=0, значит х ₁ = – 1, х ₂ = -с/а= -1/2

Данный метод удобно применять к квадратным уравнениям с большими коэффициентами.

2. Если второй коэффициент уравнения b = 2 k – четное число, то формулу корней можно записать в виде

Решим уравнение 3х 2 — 14х + 16 = 0 .

Приведенное уравнение х 2 + рх + q = 0 совпадает с уравнением общего вида, в котором а = 1 , b = р и с = q . Поэтому для приведенного квадратного уравнения формула корней принимает вид

Формулу ( ) удобно использовать, когда р — четное число.

Пример. Решим уравнение х 2 – 14х – 15 = 0.

Решение. Имеем а=1, в =-14, (к=-7),с=-15.

7.Графическое решение квадратного уравнения.

И спользуя знания о квадратичной и линейной функциях и их графиках, можно решить квадратное уравнение так называемым функционально-графическим методом. Причем некоторые квадратные уравнения можно решить различными способами, рассмотрим эти способы на примере одного квадратного уравнения.

Пример. Решить уравнение =0

1способ . Построим график функции , воспользовавшись алгоритмом.

Значит, вершиной параболы служит точка (1;-4), а осью параболы – прямая x=1

2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки рис.2

х= -1 и х=3, тогда f (-1)= f (3)=0.

3) Через точки (-1;0) , (1;-4), (3;0) проводим параболу (рис 2).

Корнями уравнений являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения

Преобразуем уравнение к виду .

Построим в одной системе координат графики функций и (рис 3 ).

Они пересекаются в двух точках A(-1;1) и B(3;9). Корнями уравнения служат абсциссы точек A и B , значит, .

3 способ

Преобразуем уравнения к виду.

Построим в одной системе координат графики функций и (рис.4) Они пересекаются в двух точках A(-1;-2) и В (3;6). Корнями уравнения являются абсциссы точек А и В, поэтому .

Преобразуем уравнение к виду , затем т.е.

Построим в одной системе координат параболу и прямую . Они пересекаются в точках А(-1;4) и В(3;4). Корнями уравнений служат абсциссы точек А и В, поэтому (рис.5) .

Рис.5

Разделим почленно обе части уравнения на x, получим:

Построим в одной системе координат гиперболу и прямую (рис.6). Они пересекаются в двух точках А(-1;-3) и В(3;1). Корнями уравнений являются абсциссы точек А и В, следовательно, .

Первые четыре способа применимы к любым уравнениям вида

ах 2 + b х + с = 0, а пятый- только к тем, у которых с не равно нулю.

Графические способы решения квадратных уравнений красивы, но не дают стопроцентной гарантии решения любого квадратного уравнения.

8. Решение квадратных уравнений с помощью циркуля и

Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + b х + с = 0 с помощью циркуля и линейки (рис.7 ).

Допустим, что искомая окружность пересекает ось

Центр окружности находится в точке пересечения перпендикуляров SF и SK , восстановленных в серединах хорд AC и BD , поэтому

Итак:

1) построим точки (центр окружности) и A (0; 1) ;

2) проведем окружность с радиусом SA ;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

2) Радиус окружности равен ординате центра ( AS = SB , или R = a + c /2 a ) , окружность касается оси Ох (рис.8б) в точке В(х ₁ ; 0) , где х ₁ – корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра

окружность не имеет общих точек с осью абсцисс (рис 8в), в этом случае уравнение не имеет решения.

Решим уравнение х 2 – 2х – 3 = 0 (рис.9).

Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA , где А (0; 1).

9. Решение квадратных уравнений с помощью

Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. – М., Просвещение, 1990.

Таблица XXII . Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен-

там определить корни уравнения.

Криволинейная шкала номограммы построена

по формулам (рис.10):

Полагая ОС = р, ED = q , ОЕ = а (все в см.), из

подобия треугольников САН и CDF получим

откуда после подстановок и упрощений вытекает уравнение

причем буква z означает метку любой точки криволинейной шкалы.

2) Решим с помощью номограммы уравнение

Разделим коэффициенты этого уравнения на 2,

3) Для уравнения z 2 – 25 z + 66 = 0 коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5 t , получим уравнение t 2 – 5 t + 2,64 = 0,

10. Геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал – Хорезми.

1) Решим уравнение х 2 + 10х = 39.

В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.12).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD , достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25) , т.е. S = х 2 + 10х + 25. Заменяя

х 2 + 10х числом 39 , получим, что S = 39 + 25 = 64 , откуда следует, что сторона квадрата ABCD , т.е. отрезок АВ = 8 . Для искомой стороны х первоначального квадрата получим

2) А вот, например, как древние греки решали уравнение у 2 + 6у – 16 = 0 .

Решение представлено на рис 13. где

Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой

один и тот же квадрат, а исходное уравнение у 2 + 6у – 16 + 9 – 9 = 0 – одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у ₁ = 2, у ₂ = – 8 (рис. .

3) Решить геометрически уравнение у 2 – 6у – 16 = 0.

Преобразуя уравнение, получаем

На рис 14. находим «изображения» выражения у 2 – 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3 . Значит, если к выражению у 2 – 6у прибавить 9 , то получим площадь квадрата со стороной у – 3 . Заменяя выражение у 2 – 6у равным ему числом 16,

получаем: (у – 3) 2 = 16 + 9, т.е. у – 3 = ± √25 , или у – 3 = ± 5, где у ₁ = 8 и у ₂ = – 2.

Решение пропорций

Рассмотрим решение пропорций на конкретных примерах.

Решить уравнения с пропорцией:

1) 25 : x = 10 : 18

Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции , произведение крайних членов разделим на известный средний член:

25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.

Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:

При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.

Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:

В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:

Сокращаем 24 и 6 на 6, 10 и 45 — на 5:

Еще раз сокращаем 4 и 2 на 2:

Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.

Чтобы найти неизвестный крайний член пропорции, произведение средних членов разделим на известный крайний член:

При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.

Произведение крайних членов пропорции равно произведению средних членов:

Здесь удобно упростить уравнение, разделив обе части на 5:

Произведение крайних членов пропорции равно произведению ее средних членов:

Для упрощения вычислений удобно умножить каждую часть уравнения на 10:

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

[spoiler title=”источники:”]

http://infourok.ru/teoreticheskij-material-po-teme-10-sposobov-reshenij-kvadratnyh-uravnenij-4034975.html

[/spoiler]

Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию.
Например, рассмотрим такое уравнение.

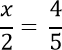
Для решения уравнения с пропорцией используют правило пропорции или,
как его называют по-другому, правило креста.

Подробно понятие пропорции мы рассматривали в уроке
«Пропорции».
В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.

Правило пропорции или правило креста

По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции,
то произведения членов пропорции, которые лежат на концах креста, равны .

Вернемся к нашему уравнению. Решим его, использую правило пропорции.
Нарисуем поверх пропорции крест.

Теперь по правилу пропорции (правило креста) запишем пропорцию
в виде равенства произведений крайних и средних членов пропорции.

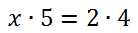
Вспомним правило деления и
решим уравнение до конца.
В ответе не забудем выделить целую часть у дроби.

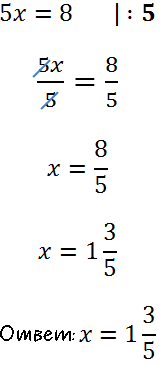
Рассмотрим другой пример уравнения с пропорцией.

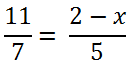
Такое уравнение также решается с помощью правила пропорции.

Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда
будете использовать правило пропорции.

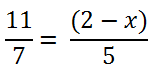
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции
для дальнейшего решения.

Теперь раскроем скобки с помощью
правила раскрытия
скобок.

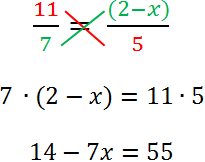
Из урока «Решение линейных уравнений» используем
правило переноса и
правило деления для уравнений.

Не забудем при делении на отрицательное число, использовать
правило знаков.

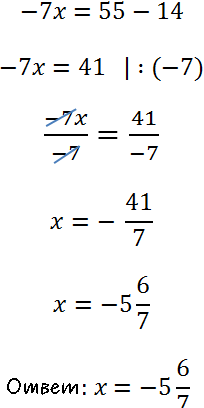
Иногда уравнения с пропорцией могут быть представлены следующим образом:

Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение,
в общем для пропорции виде.

Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.

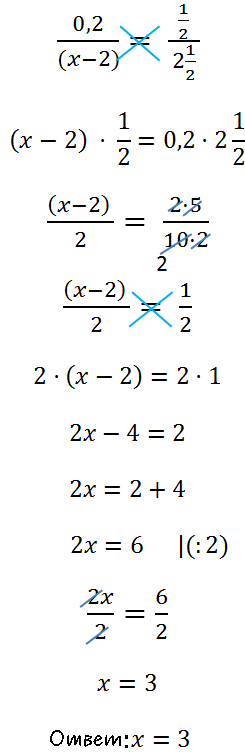
Другие примеры решения уравнений с пропорцией

• =
  
  18 · x = 6 · 3x
  18x = 18x
  18x − 18x = 0
  0 = 0
  
  Ответ: x — любое число

  ---

• =

  3x · 6,8 = 0,21 · 1,7

  20,4 x=

  ·

  20

  x =
  =

  204x · 1000 = 21 · 17 · 10         |:(204 · 1000)

  x =

  x =

  x =

  x =

  x =

  
  Ответ: x =

---

Ваши комментарии

Оставить комментарий:

---

Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x² − 8x + 12 = 0;
2. 5x² + 3x + 7 = 0;
3. x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

1. x² − 2x − 3 = 0;
2. 15 − 2x − x² = 0;
3. x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]

Наконец, третье уравнение:
x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

[x=frac{-12+sqrt{0}}{2cdot 1}=-6]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x² + 9x = 0;
2. x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x² − 7x = 0;
2. 5x² + 30 = 0;
3. 4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

1. Теорема Виета
2. Следствия из теоремы Виета
3. Тест на тему «Значащая часть числа»
4. Метод коэффициентов, часть 1
5. Однородные тригонометрические уравнения: общая схема решения
6. Задача B4: строительные бригады

Решение простых уравнений  — одна из базовых тем для усвоения, при этом они являются достаточно мощным инструментом для решения большинства задач. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.

Уравнение — это равенство, содержащее в себе переменную. Значение данной переменной требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.

Переменную, входящую в уравнение, еще называют неизвестным.

Примеры:

• выражение 3+2=5 является равенством, так как при вычислении получаем 5=5
• выражение 3+х=5 является уравнением, так как содержит переменную х, значение которой можно найти.

Решить уравнение — значит найти такое значение х, чтобы равенство было верным.
То есть, в уравнении 3+х=5 значение будет равно 2 (х=2), чтобы получилось верное равенство.
При этом говорят, что 2 — это корень уравнения или решение уравнения 3+х=5.

Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.

Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.

Компоненты

Компонентами называются числа и переменные, которые входят в равенство:

• компоненты сложения — слагаемые и сумма;
• компоненты вычитания — уменьшаемое, вычитаемое и разность;
• компоненты умножения — множители и произведение;
• компоненты деления — делимое, делитель и частное.

Правила нахождения неизвестных

Чтобы выразить переменную через другие числа, нужно переменную оставить (или перенести) в левой части выражения, а все числа перенести в правую часть.

Решение простых уравнений подразумевает применение следующих правил:

1. чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
2. чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
3. чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
4. чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
5. чтобы найти неизвестное делимое, нужно частное умножить на делитель;
6. чтобы найти неизвестный делитель, нужно делимое разделить на частное.

Примеры:

1. 3+х=5.
   Нужно задать вопрос: что сделать с числами 5 и 3, чтобы получить переменную х.
   Чтобы найти слагаемое, нужно из суммы вычесть известное слагаемое: х=5-3.
2. х-3=7
   Нужно задать вопрос: что сделать с числами 3 и 7, чтобы получить переменную х.
   Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое: х=7+3.
3. 8-х=6
   Нужно задать вопрос: что сделать с числами 8 и 6, чтобы получить переменную х.
   Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность: х=8-6.
4. 3×а=6 (а-переменная)
   Нужно задать вопрос: что сделать с числами 3 и 6, чтобы получить переменную а.
   Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель
5. а:4=3(а-переменная)
   Нужно задать вопрос: что сделать с числами 4 и 3, чтобы получить переменную а.
   Чтобы найти неизвестное делимое, нужно частное умножить на делитель: а=3*4
6. 12:а=3(а-переменная)
   Нужно задать вопрос: что сделать с числами 12 и 3, чтобы получить переменную а.
   Чтобы найти неизвестный делитель, нужно делимое разделить на частное: а=12:3.

Если неизвестное имеет коэффициент

Решение простых уравнений сводится к тому, что неизвестное нужно выразить через другие числа. Но чаще всего задаются уравнения, в которых неизвестное имеет коэффициент, например: 2х, 5х и т.д. В таких случаях неизвестное нельзя выразить сразу, поскольку оно содержит коэффициент. Поэтому нужно привести это уравнение к виду, в котором переменная будет выражена.

Рассмотрим пример: 2х+4=8.
В данном примере: 2x — первое слагаемое, 4 — второе слагаемое, 8 — сумма.

• Принимает слагаемое 2х за неизвестное слагаемое. Применяем правило нахождения неизвестного слагаемого: вычитаем из суммы известное слагаемое. Получаем: 2х=8-4 или 2*х=4.
• Мы получили новое уравнение . Теперь мы имеем дело с умножением. Применяем правило нахождения неизвестного множителя: произведение делим на известный множитель. Получаем: х=4:2; х=2
• Вычислим правую часть, получим значение переменной х.
• Проверяем: 2*2+4=8. Равенство верное.

Если уравнение имеет неизвестные с разными коэффициентами

Рассмотрим пример: a+2a+3a=30.
Cразу выразить неизвестное нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить. Для этого нужно сложить все неизвестные величины с коэффициентами: 1а+2а+3а=6а (а — это переменная с коэффициентом 1. который не пишется).
Получаем уравнение вида: 6*а=30. Его можно решить как простое уравнение. Получаем корень: а=5.

Равносильные уравнения

Уравнения называют равносильными, если их корни совпадают.

Из предыдущего примера: уравнение a+2a+3a=30 и уравнение 6а=30 являются равносильными.
Проверим это. Подставим корень сначала в уравнение a+2a+3a=30, а затем в уравнение 6а=30, которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства.

Для удобства решения можно любое уравнение преобразовать в равносильное. Для этого можно применить законы математики и свойства уравнений.

Свойства уравнений

• Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
• Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.

Пример. Решить уравнение 5х-10=20.
Вычтем из обеих частей уравнения число 10, получим: 5х=20-10 или 5х=10.
В результате получилось равносильное уравнение , корень которого равен 2.

Пример. Решить уравнение 4(х+3)=20.
Раскроем скобки: 4х+12=20.
Вычтем из обеих частей уравнения число 12, получим: 4х=20-12 или 4х=8.
В результате получилось равносильное уравнение , корень которого равен 2.

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.

Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные числа.

Пример. Решить уравнение (1/4)х+5=6,5

• При решении уравнений, содержащих дробные выражения, сначала  принято упростить это уравнение.
• Для упрощения обе части уравнения можно умножить на 4: 4*(1/4)х+4*5=4*6,5 или х+20=26.
• В результате останется простейшее уравнение. Получаем, что корень равен 6.
• Вернемся к исходному уравнению  и подставим вместо x найденное значение. Получается верное числовое равенство. Значит уравнение решено правильно.

Пример. Решить уравнение 8х+16=56

• Для упрощения обе части уравнения можно разделить на 8: 8х:8+16:8=56:8 или х+2=7.
• В результате останется простейшее уравнение. Получаем, что корень равен 5.
• Вернемся к исходному уравнению  и подставим вместо x найденное значение. Получается верное числовое равенство. Значит уравнение решено правильно.

Если обе части уравнения умножить на минус единицу (поменять знаки), то получится уравнение равносильное данному.

Это правило следует из того, что если обе части уравнения умножить или разделить на одно и тоже число, не равное нулю, то получится равносильное уравнение. Иногда это нужно для того, чтобы получить равносильное уравнение, которое проще решать.

Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.

При этом минус, стоящий перед переменной x, относится не к самой переменной x, а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать.

Пример. Решить уравнение: 2х-5х+10=4.

• Приведем подобные слагаемые:  -3х+10=4
• Перенесем второе слагаемое в правую часть: -3х=-6
• Для удобства умножим обе части на (-1). получим: 3х=6.
• Корень: х=2.

Уравнение имеет несколько корней

Уравнение может иметь несколько корней.

Рассмотрим уравнение: x(x + 9) = 0.
Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из множителей равен нулю.
То есть в уравнении x(x + 9) = 0 равенство будет выполняться, если x будет равен нулю или (x + 9) будет равно нулю. Таким образом, уравнение имеет два корня: 0 и −9.

Уравнение имеет бесконечно много корней

Уравнение может иметь бесконечно много корней, когда при подстановке подставив в такое уравнение любого числа, мы получим верное равенство.

Например: рассмотрим простое уравнение 6*(х+2)=6х+12. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 6х+12= 6х+12. Это равенство будет выполняться при любом х.

Уравнение не имеет корней

Бывает и так, что уравнение совсем не имеет  корней.

Например: уравнение х+2=х.
Данное уравнение не имеет корней, так как при любом значении х, левая часть уравнения всегда будет больше правой на 2.

Таким образом, мы рассмотрели в статье решение разных видов простых уравнений. Решение более сложных уравнений без знания данного материала практически невозможно.

Далее вы можете переходить к решению квадратных уравнений и решению систем линейных уравнений. 

Для решения уравнений вам также могут понадобится темы: раскрытие скобок и порядок действий в примерах.

15 способов решения квадратных уравнений

Содержание

1. История развития квадратных уравнений 1

1.1 Квадратные уравнения в Древнем Вавилоне 1

1.2 Как составлял и решал Диофант квадратные уравнения. 1

1.3 Квадратные уравнения в Индии 2

1.4 Квадратные уравнения у ал – Хорезми 2

1.5 Квадратные уравнения в Европе XIII – XVII вв 3

1.6 О теореме Виета 3

2. Способы решения квадратных уравнений 4

1. СПОСОБ: Разложение левой части уравнения на множители. 4

2. СПОСОБ: Метод выделения полного квадрата (классический метод). 4

3. СПОСОБ: Метод выделения полного квадрата (применение формулы выделения полного квадрата (метод Надь А. В.). 5

4. СПОСОБ: Решение квадратных уравнений по формуле. 6

5. СПОСОБ: Решение уравнений с использованием теоремы Виета. 7

6. СПОСОБ: Решение уравнений способом «переброски». 8

7. СПОСОБ: Свойства коэффициентов квадратного уравнения 8

8. СПОСОБ: Другая формула дискриминанта (основанная по формуле выделения полного квадрата (метод Надь А. В.)). 10

9. СПОСОБ: Приведенное квадратное уравнение (метод Надь А. В). 11

10. СПОСОБ: Графическое решение квадратного уравнения. 11

11. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки. 13

12. СПОСОБ: Решение квадратных уравнений с помощью номограммы. 15

13. СПОСОБ: Геометрический способ решения квадратных уравнений. 16

14. СПОСОБ: Способ замены переменной при решения квадратных уравнений 18

15. СПОСОБ: Способ замены переменной при решения квадратных уравнений (метод среднеарифметического корней уравнения) (метод Надь А. В.). 19

Заключение 21

Литература: 21

1. История развития квадратных уравнений 1.1 Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

X² + X = ¾; X² – X = 14,5

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

1.2 Как составлял и решал Диофант квадратные уравнения.

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение – 96»

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 – х. Разность между ними 2х.

Отсюда уравнение:

(10 + х)(10 – х) = 96

или же:

100 – х² = 96

х² – 4 = 0 (1)

Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения

у(20 – у) = 96,

у² – 20у + 96 = 0. (2)

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).

1.3 Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ах² + bх = с, а 0. (1)

В уравнении (1) коэфиценты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XII в. Бхаскары.

Задача 13.

«Обезьянок резвых стая А двенадцать по лианам…

Власть поевши, развлекалась. Стали прыгать, повисая…

Их в квадрате часть восьмая Сколько ж было обезьянок,

На поляне забавлялась. Ты скажи мне, в этой стае?»

Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 3).

Соответствующее задаче 13 уравнение:

(x/8)² + 12 = x

Бхаскара пишет под видом:

х² – 64х = -768

и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32², получая затем:

х² – 64х + 32² = -768 + 1024,

(х – 32)² = 256,

х – 32 = ± 16,

х₁ = 16, х₂ = 48.

1.4 Квадратные уравнения у ал – Хорезми

В алгебраическом трактате ал – Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корнями», т.е. ах² + с = bх.

2) «Квадраты равны числу», т.е. ах² = с.

3) «Корни равны числу», т.е. ах = с.

4) «Квадраты и числа равны корням», т.е. ах² + с = bх.

5) «Квадраты и корни равны числу», т.е. ах² + bx = с.

6) «Корни и числа равны квадратам», т.е. bx + с = ах².

Для ал – Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал – джабр и ал – мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида

ал – Хорезми, как и все математики до XVII в., е учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал – Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.

Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х² + 21 = 10х).

Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.

Трактат ал – Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.

1.5 Квадратные уравнения в Европе XIII – XVII вв

Формулы решения квадратных уравнений по образцу ал – Хорезми в Европе были впервые изложены в « Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI – XVII вв. и частично XVIII.

Общее правило решения квадратных уравнений, приведенных к единому каноническому виду:

х² + bx = с,

при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

1.6 О теореме Виета

Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D, умноженное на A – A², равно BD, то A равно В и равно D».

Чтобы понять Виета, следует вспомнить, что А, как и всякая гласная буква, означало у него неизвестное (наше х), гласные же В,D – коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место

(а + b)х – х² = ab,

т.е.

х² – (а + b)х + аb = 0,

то

х₁ = а, х₂ = b.

Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и по этому при решении уравнений рассматривал лишь случаи, когда все корни положительны.

2. Способы решения квадратных уравнений

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.

1. СПОСОБ

: Разложение левой части уравнения на множители.

Решим уравнение

Разложим левую часть на множители:

Следовательно, уравнение можно переписать так:

Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = – 13. Это означает, что число 2 и – 13 являются корнями уравнения х² + 11х – 26 = 0.

2. СПОСОБ

: Метод выделения полного квадрата (классический метод).

Решим уравнение

Выделим в левой части полный квадрат.

Для этого запишем выражение х² + 6х в следующем виде:

х² + 8х -9= х² + 2• х • 4-9.

В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3. Поэтому чтобы получить полный квадрат, нужно прибавить 3², так как

Преобразуем теперь левую часть уравнения

прибавляя к ней и вычитая 4². Имеем:

Таким образом, данное уравнение можно записать так:

Следовательно,.

3. СПОСОБ

: Метод выделения полного квадрата (применение формулы выделения полного квадрата (метод Надь А. В.).

Сделаем вывод формулы в общем виде

Данная операция является обратной операцией для

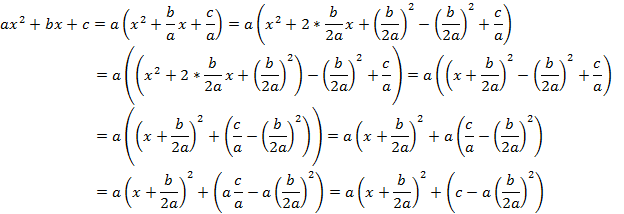
Обозначим

При этом получили метод выделения полного квадрата

Подсчитываем

и записываем полный квадрат уравнения

пример

или более короче

4. СПОСОБ

: Решение квадратных уравнений по формуле.

Умножим обе части уравнения

ах² + bх + с = 0, а ≠ 0

на 4а и последовательно имеем:

4а²х² + 4аbх + 4ас = 0,

((2ах)² + 2ах • b + b²) – b² + 4ac = 0,

(2ax + b)² = b² – 4ac,

2ax + b = ± √ b² – 4ac,

2ax = – b ± √ b² – 4ac,

Примеры.

а) Решим уравнение: 4х² + 7х + 3 = 0.

а = 4, b = 7, с = 3, D = b² – 4ac = 7² – 4 • 4 • 3 = 49 – 48 = 1,

D 0, два разных корня;

Таким образом, в случае положительного дискриминанта, т.е. при

b² – 4ac 0, уравнение ах² + bх + с = 0 имеет два различных корня.

б) Решим уравнение:

D = 0, один корень (два одинаковых корня);

Итак, если дискриминант равен нулю, т.е. b² – 4ac = 0, то уравнение

ах² + bх + с = 0 имеет единственный корень (два повторяющих корня (кратный корень кратности 2)),

в) Решим уравнение: 2х² + 3х + 4 = 0,

а = 2, b = 3, с = 4, D = b² – 4ac = 3² – 4 • 2 • 4 = 9 – 32 = – 13 , D

Данное уравнение корней не имеет.

Итак, если дискриминант отрицателен, т.е. b² – 4ac ,

уравнение ах² + bх + с = 0 не имеет корней.

Формула (1) корней квадратного уравнения ах² + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.

5. СПОСОБ: Решение уравнений с использованием теоремы Виета.

Как известно, приведенное квадратное уравнение имеет вид

х² + px + c = 0. (1)

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если сводный член q приведенного уравнения (1) положителен (q 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р , то оба корня отрицательны, если р , то оба корня положительны.

Например,

x² – 3x + 2 = 0; x₁ = 2 и x₂ = 1, так как q = 2 0 и p = – 3

x² + 8x + 7 = 0; x₁ = – 7 и x₂ = – 1, так как q = 7 0 и p= 8 0.

б) Если свободный член q приведенного уравнения (1) отрицателен (q ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p 0 .

Например,

x² + 4x – 5 = 0; x₁ = – 5 и x₂ = 1, так как q= – 5 и p = 4 0;

x² – 8x – 9 = 0; x₁ = 9 и x₂ = – 1, так как q = – 9 и p = – 8

6. СПОСОБ: Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение

ах² + bх + с = 0, где, а ≠ 0.

Умножая обе его части на, а, получаем уравнение

а²х² + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению

у² + by + ас = 0,

равносильно данному. Его корни у₁ и у₂ найдем с помощью теоремы Виета.

Окончательно получаем

х₁ = у₁/а и х₁ = у₂/а.

При этом способе коэффициент, а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Пример.

Решим уравнение 2х² – 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у² – 11у + 30 = 0.

Согласно теореме Виета

у² – 11у + 30 = 0.

Ответ: 2,5; 3.

7. СПОСОБ: Свойства коэффициентов квадратного уравнения.

А. Пусть дано квадратное уравнение

ах² + bх + с = 0, где а ≠ 0.

1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х₁ = 1,

х₂ = с/а.

Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение

x² + b/a • x + c/a = 0.

Согласно теореме Виета

По условию а – b + с = 0, откуда b = а + с. Таким образом,

x₁ + x₂ = – а + b/a= -1 – c/a,

x₁x₂ = – 1• ( – c/a),

т.е. х₁ = -1 и х₂ = c/a, что и требовалось доказать.

Примеры.

1. Решим уравнение 345х² – 137х – 208 = 0.

Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то

х₁ = 1, х₂ = c/a = -208/345.

Ответ: 1; -208/345.

2) Решим уравнение 132х² – 247х + 115 = 0.

Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то

х₁ = 1, х₂ = c/a = 115/132.

Ответ: 1; 115/132.

Б. Если второй коэффициент b = 2k – четное число, то формулу корней

можно записать в виде

Пример.

Решим уравнение 3х2 — 14х + 16 = 0.

Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;

D = k² – ac = (- 7)² – 3 • 16 = 49 – 48 = 1, D 0, два различных корня;

Ответ: 2; 8/3

В. Приведенное уравнение

х² + рх + q= 0

совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней

или,

или

принимает вид:

Формулу (3) особенно удобно использовать, когда р — четное число.

Пример. Решим уравнение х² – 14х – 15 = 0.

Решение. Имеем:

х_1,2 =7±8

Ответ: х₁ = 15; х₂ = -1.

8. СПОСОБ: Другая формула дискриминанта (основанная по формуле выделения полного квадрата (метод Надь А. В.)).

9. СПОСОБ: Приведенное квадратное уравнение (метод Надь А. В).

Приведенное уравнение

х² + рх + q= 0

совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней

10. СПОСОБ: Графическое решение квадратного уравнения.

Если в уравнении

х² + px + q = 0

перенести второй и третий члены в правую часть, то получим

х² = – px – q.

Построим графики зависимости у = х² и у = – px – q.

График первой зависимости – парабола, проходящая через начало координат. График второй зависимости –

прямая (рис.1). Возможны следующие случаи:

– прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;

– прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;

– прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.

Примеры.

1) Решим графически уравнение х² – 3х – 4 = 0 (рис. 2).

Решение. Запишем уравнение в виде х² = 3х + 4.

Построим параболу у = х² и прямую у = 3х + 4. Прямую

у = 3х + 4 можно построить по двум точкам М (0; 4) и

N (3; 13). Прямая и парабола пересекаются в двух точках

А и В с абсциссами х₁ = – 1 и х₂ = 4. Ответ: х₁ = – 1;

х₂ = 4.

2) Решим графически уравнение (рис. 3) х² – 2х + 1 = 0.

Решение. Запишем уравнение в виде х² = 2х – 1.

Построим параболу у = х² и прямую у = 2х – 1.

Прямую у = 2х – 1 построим по двум точкам М (0; – 1)

и N(1/2; 0). Прямая и парабола пересекаются в точке А с

абсциссой х = 1. Ответ: х = 1.

3) Решим графически уравнение х² – 2х + 5 = 0 (рис. 4).

Решение. Запишем уравнение в виде х² = 5х – 5. Построим параболу у = х² и прямую у = 2х – 5. Прямую у = 2х – 5 построим по двум точкам М(0; – 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.

Ответ. Уравнение х² – 2х + 5 = 0 корней не имеет.

11. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки.

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.

Предлагаю следующий способ нахождения корней квадратного уравнения ах² + bх + с = 0 с помощью циркуля и линейки (рис. 5).

Допустим, что искомая окружность пересекает ось

абсцисс в точках В(х₁; 0 ) и D (х₂; 0), где х₁ и х₂ – корни уравнения ах² + bх + с = 0, и проходит через точки

А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х₁х₂/ 1 = c/a.

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому

Итак,

1) построим точки (центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

1) Радиус окружности больше ординаты центра (AS SK, или R a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х₁; 0) и D(х₂; 0), где х₁ и х₂ – корни квадратного уравнения ах² + bх + с = 0.

2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х₁; 0), где х₁ – корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.

Пример.

Решим уравнение х² – 2х – 3 = 0 (рис. 7).

Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA, где А (0; 1).

Ответ: х₁ = – 1; х₂ = 3.

12. СПОСОБ: Решение квадратных уравнений с помощью номограммы.

Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. – М., Просвещение, 1990).

Таблица XXII. Номограмма для решения уравнения z² + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен там определить корни уравнения.

Криволинейная шкала номограммы построена по формулам (рис.11):

Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение

z² + pz + q = 0,

причем буква z означает метку любой точки криволинейной шкалы.

Примеры.

1) Для уравнения z² – 9z + 8 = 0 номограмма дает корни

z₁ = 8,0 и z₂ = 1,0 (рис.12).

2) Решим с помощью номограммы уравнение

2z² – 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение

z² – 4,5z + 1 = 0.

Номограмма дает корни z₁ = 4 и z₂ = 0,5.

3) Для уравнения

z² – 25z + 66 = 0

коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение

t² – 5t + 2,64 = 0,

которое решаем посредством номограммы и получим t₁ = 0,6 и t₂ = 4,4, откуда z₁ = 5t₁ = 3,0 и z₂ = 5t₂ = 22,0.

13. СПОСОБ: Геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал – Хорезми.

Примеры.

1) Решим уравнение х² + 10х = 39.

В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х², четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х² + 10х + 25. Заменяя

х² + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

2) А вот, например, как древние греки решали уравнение у² + 6у – 16 = 0.

Решение представлено на рис. 16, где

у² + 6у = 16, или у² + 6у + 9 = 16 + 9.

Решение. Выражения у² + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у² + 6у – 16 + 9 – 9 = 0 – одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у₁ = 2, у₂ = – 8 (рис.16).

3) Решить геометрически уравнение у² – 6у – 16 = 0.

Преобразуя уравнение, получаем

у² – 6у = 16.

На рис. 17 находим «изображения» выражения у² – 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у² – 6у прибавить 9, то получим площадь квадрата со стороной у – 3. Заменяя выражение у² – 6у равным ему числом 16,

получаем: (у – 3)² = 16 + 9, т.е. у – 3 = ± √25, или у – 3 = ± 5, где у₁ = 8 и у₂ = – 2.

14. СПОСОБ: Способ замены переменной при решения квадратных уравнений.

введем новую переменную

пример

Ответ: ;

15. СПОСОБ: Способ замены переменной при решения квадратных уравнений (метод среднеарифметического корней уравнения) (метод Надь А. В.).

введем новую переменную

пример

Ответ: ;

Заключение

Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.

Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.

Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена вообще, просто ею не занимаются, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.

Здесь можно остановиться на вопросе решения квадратных уравнений, а что, если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое. Но это вопросы уже следующих работ.

Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни.

Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников. Моя работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.

Литература:

1. Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классовой средней школы. – М., Просвещение, 1981.

2. Брадис В.М. Четырехзначные математические таблицы для средней школы.Изд. 57-е. – М., Просвещение, 1990. С. 83.

3. Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. – М., высшая школа, 1969.

4. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. – М., Просвещение, 1972.

5. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. – М., Квант, № 4/72. С. 34.

6. Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. – 4-е, дополн. – М., Высшая школа, 1973.

7. Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. – М., Просвещение, 1970.

8. Реутова Е. В., Патрикеева Г. А. с., Копьевская сельская СОШ, Копьево, 2007.