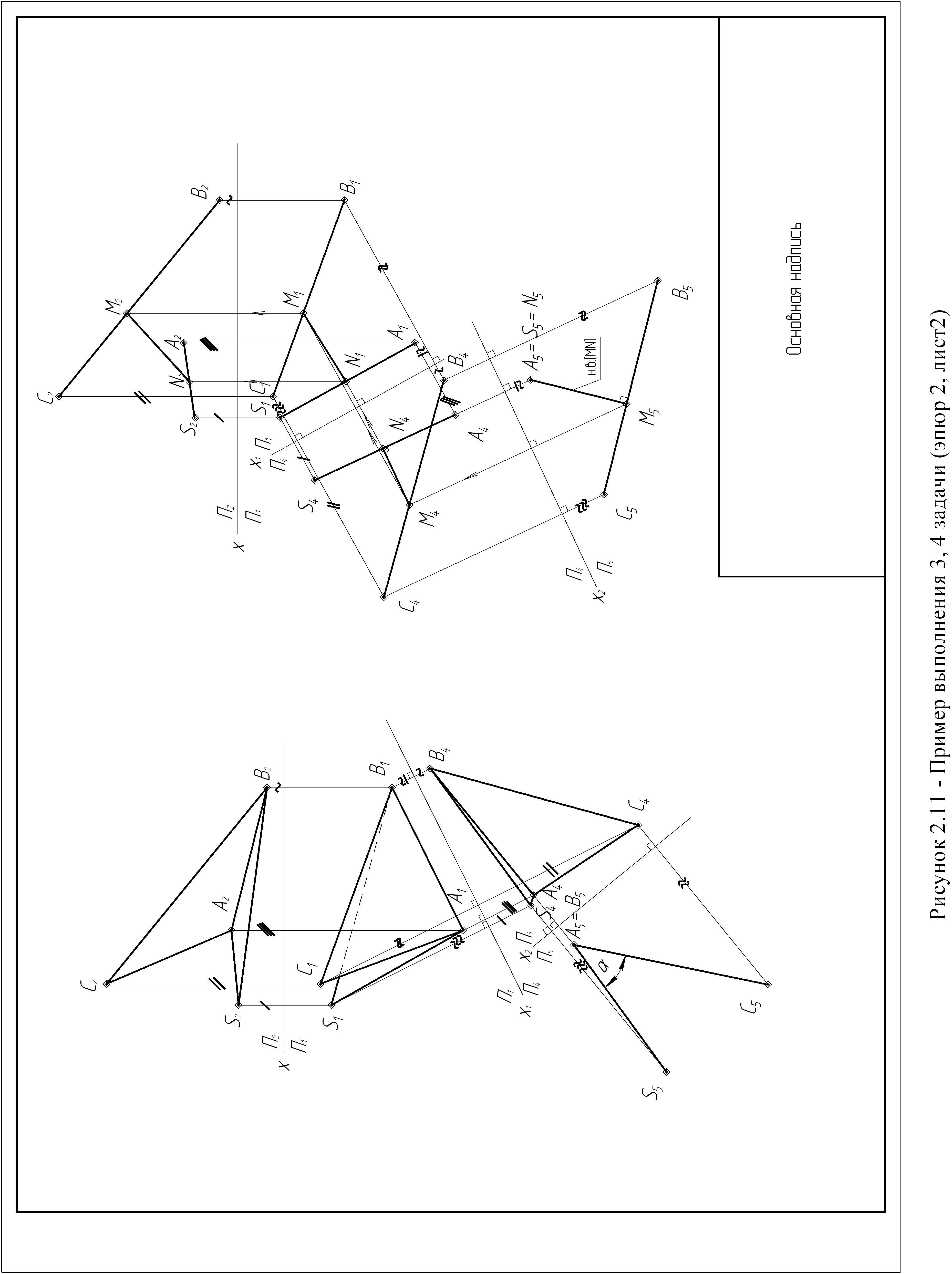
Как найти кратчайшее расстояние между ребрами - Сайт, где вы сможете решить свои вопросы

2.1. Содержание эпюра:

Дано:
Координаты вершин пирамиды SABC.

Требуется:

задача
1 – определить
натуральную величину основания пирамиды
АВС.

задача
2 – определить
расстояние от вершины пирамиды S
до плоскости ее основания АВС.

задача
3 – найти
кратчайшее расстояние между ребрами
пирамиды SА
и ВС.

задача
4 – определить
величину двугранного угла при ребре
пирамиды АВ.

Рекомендации
по выполнению эпюра:

Чертеж
должен быть выполнен в соответствии с
ГОСТми: 2.301 – 68^*
(Форматы), 2.302 – 68^*
(Масштабы), 2.303 – 68^*
(Линии), 2.304 – 81 (Шрифты) (приложение 4);

2. После выполнения
чертежа выполнить его обводку (возможно
оформление в цвете):

исходный чертеж
(цвет черный) и результат построений
(цвет красный) выполнить сплошными
основными толстыми линиями;
промежуточные
построения (цвет синий) – сплошными
тонкими;
невидимые линии
– штриховой.

Указания
к выполнению эпюра:

1.
Студенты факультета МСХ выполняют
задачи 1 – 4 на двух форматах А3. Задачи
1, 2 совместить на первом листе эпюра,
задачи 3, 4 – на втором. Студенты факультета
ПГС выполняют задачи 1 – 3 на двух форматах
А3.

2.
Данные для выполнения эпюра взять из
таблицы 2 в соответствии с вариантом.
Координаты точек даны в миллиметрах.
Все задания выполнить в масштабе 1:1.
Основная надпись выбирается в соответствии
с факультетом из приложения 3.

Задачи
эпюра должны быть решены следующими
способами:

– плоскопараллельное
перемещение (задача 2);

– вращение
вокруг горизонтали или фронтали (задача
1);

– замена
плоскостей проекций (задачи 3, 4).

Примечание:
при решении задач 3 и 4 расстояния
переносимые из одной плоскости в другую
отмечать засечками или другими знаками
(рисунки 2.8, 2.9).

Внимание!
Не разрешается все задачи решать одним
способом.

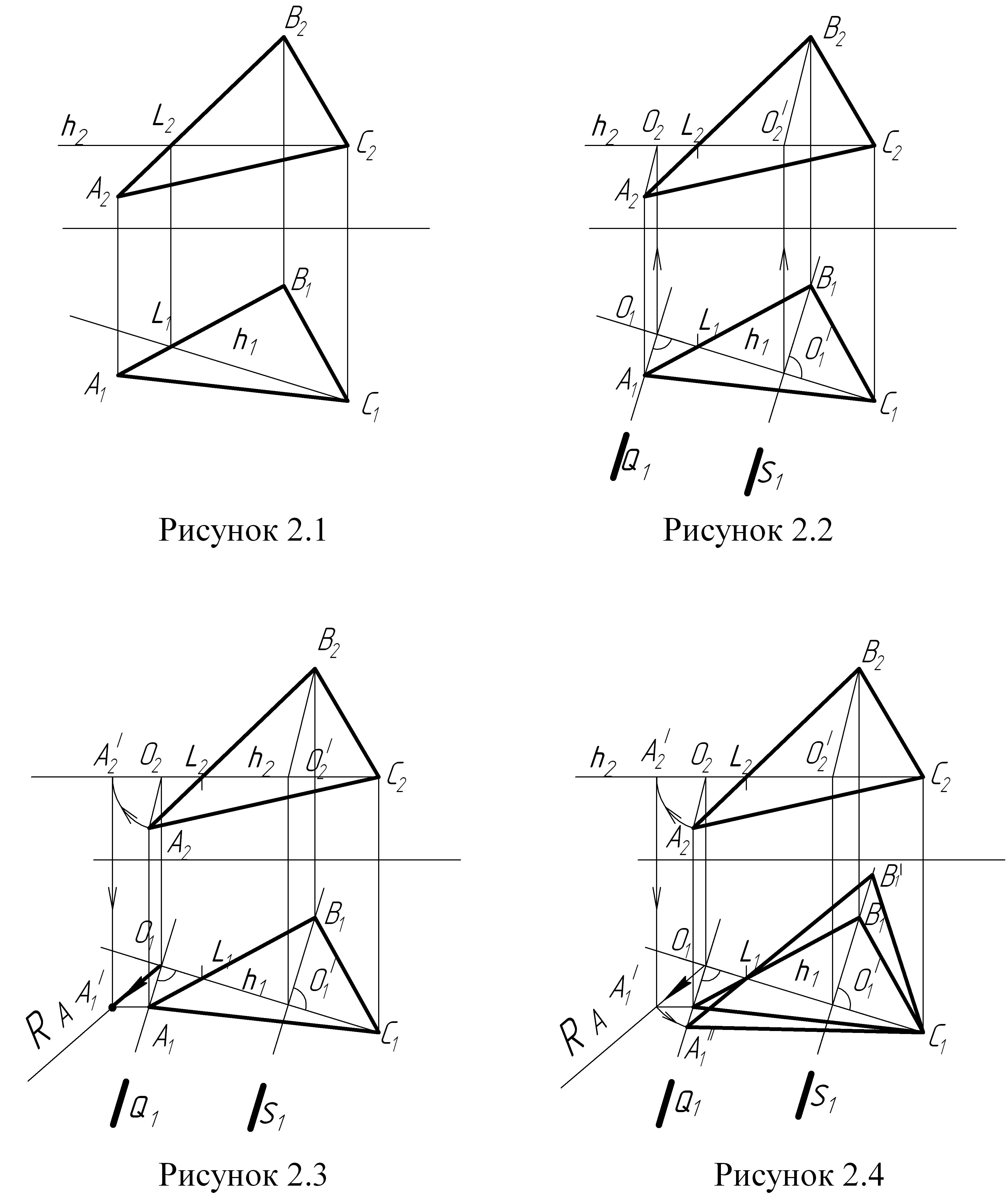
2.2. Порядок выполнения эпюра

Задача
1 (рисунки
2.1, 2.2, 2.3, 2.4)

Для решения задачи 1 необходимо
преобразовать чертеж так, чтобы основание
пирамиды (треугольник {АВС}), представляющее
собой плоскость общего положения, в
результате вращения оказалось параллельным
одной из плоскостей проекций.

За
ось вращения принимаем горизонталь СL
(С₂L₂,
С₁L₁).
Каждая точка треугольника {АВС},
вращаясь вокруг горизонтали СL, будет
описывать дугу окружности в плоскости,
перпендикулярной к этой горизонтали,
а следовательно, и к плоскости П₁.

Окружности,
которые описывают вершины А и В
треугольника АВС, находясь в горизонтально
– проецирующих плоскостях Q
и S,
спроецируются на плоскость П₁
в виде прямых, совмещенных со следами
Q₁
и S₁
плоскостей Q и S.

Центры
вращения точек А и В будут лежать на
оси вращения (горизонтали CL). Для вершины
А– точка О ( О₁,О₂
), для вершины В – точка О´( О₁´,О₂´
).

Когда
плоскость треугольника АВС будет
параллельна плоскости П₁,
горизонтальная проекция каждой из
перемещающихся вершин окажется удаленной
от оси вращения (горизонтали СL)
на расстояние, равное радиусу вращения
данной точки.

Порядок
построения:

По
координатам точек А, В, С строим проекции
треугольника {АВС};
В
плоскости треугольника {АВС}
проводим
горизонталь СL
(С₂L₂,
С₁L₁)
являющуюся осью вращения треугольника
{АВС} (
рисунок 2.1 );
Из
горизонтальных проекций вершин А и В
проводим прямые, перпендикулярные
горизонтали СL,
по которым будут перемещаться
горизонтальные проекции вращающихся
точек ( рисунок 2.2);
Отмечаем
проекции центров вращения вершин
треугольника. Для вершины А–точка О
( О₁,О₂
), для вершины В – точка О´( О₁´,О₂´
). Радиус вращения вершины А – [АО]
([А₁О₁],
[А₂О₂]),
радиус вращения вершины В – [ВО’]
([В₁О₁‘],
[В₂О₂‘]);
По
двум проекциям определяем натуральную
величину R_А
радиуса вращения вершины А (рисунок
2.3). Натуральная величина R_А
определяется способом вращения отрезка
[АО] вокруг оси , проходящей через точку
О перпендикулярно плоскости П₂;
Отрезок
R_А
откладываем от точки О₁
вдоль прямой, по которой
перемещается горизонтальная проекция
вершины А₁.
Получим точку А₁”;
Через
полученную точку В₁‘
и точку L₁
проводим прямую до пересечения с прямой,
по которой перемещается горизонтальная
проекция вершины В;
Получим
точку В₁‘
( рисунок 2.4);
Соединяя
найденные точки А₁”
и В₁‘
с вершиной С₁
, получаем новую горизонтальную проекцию
треугольника {А₁”В₁‘С₁}.
Эта проекция определяет натуральную
величину плоскости треугольника {АВС}.

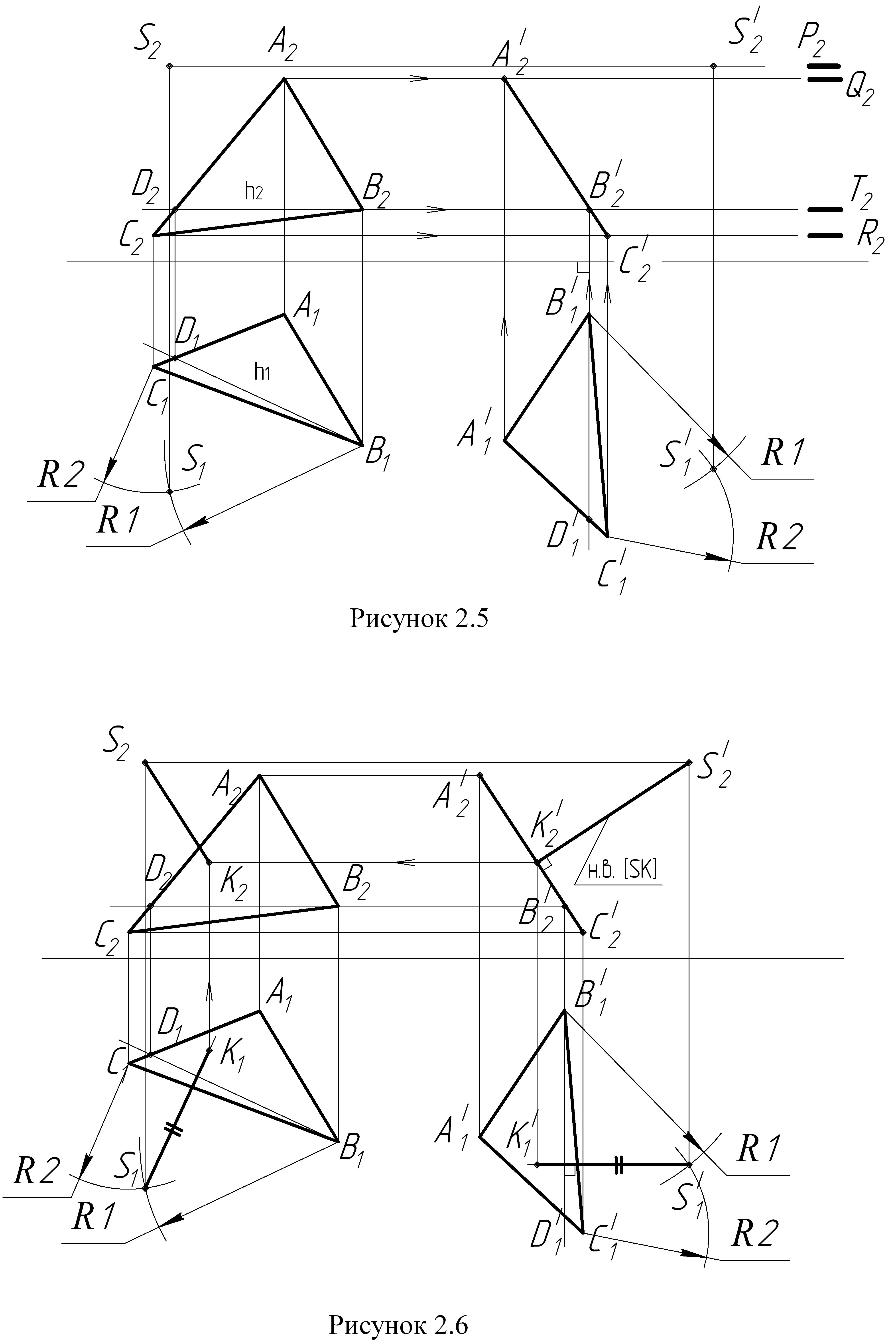
Задача
2 (рисунки
2.5, 2.6)

Для
решения задачи 2 необходимо преобразовать
чертеж так, чтобы основание пирамиды –
треугольник {АВС},
представляющий собой плоскость общего
положения, в результате перемещения
оказалось перпендикулярным плоскости
П₂
(плоскости П₁),
т.е. стало фронтально – проецирующей
плоскостью (горизонтально – проецирующей
плоскостью).

Порядок построения:

По
координатам точек S,
A,
B,
C
строим проекции основания пирамиды
треугольника {АВС}
и ее вершину
точки S;
В
плоскости треугольника {АВС}
проводим
горизонталь ВД (В₁Д₁,
В₂Д₂)
(рисунок 2.5);
По
координатам точек S,
A,
B,
C
строим проекции основания пирамиды
треугольника {АВС}
и ее вершину
точки S;
В
плоскости треугольника {АВС}
проводим
горизонталь ВД (В₁Д₁,
В₂Д₂)
(рисунок 2.5);
Переместим
треугольник {АВС}
так, чтобы
горизонтальная проекция В₁Д₁горизонтали
заняла положение перпендикулярное оси
Х, а фронтальная проекция треугольника
{А₂В₂С₂}
превратилась
в прямую линию, т.е. треугольник {АВС}
станет
фронтально – проецирующей плоскостью;
Найдем
новое положение точки S
(при помощи засечек);
Перпендикуляр
из точки S
к фронтально проецирующей плоскости
будет искомым расстоянием (рисунок
2.6);
Покажем
перпендикуляр [SК]
в исходных проекциях;
Определить
видимость перпендикуляра [SK].

Примечание:
задачу можно решать, преобразовав
треугольник АВС в горизонтально –
проецирующую плоскость, тогда в плоскости
треугольника необходимо построить
фронталь.

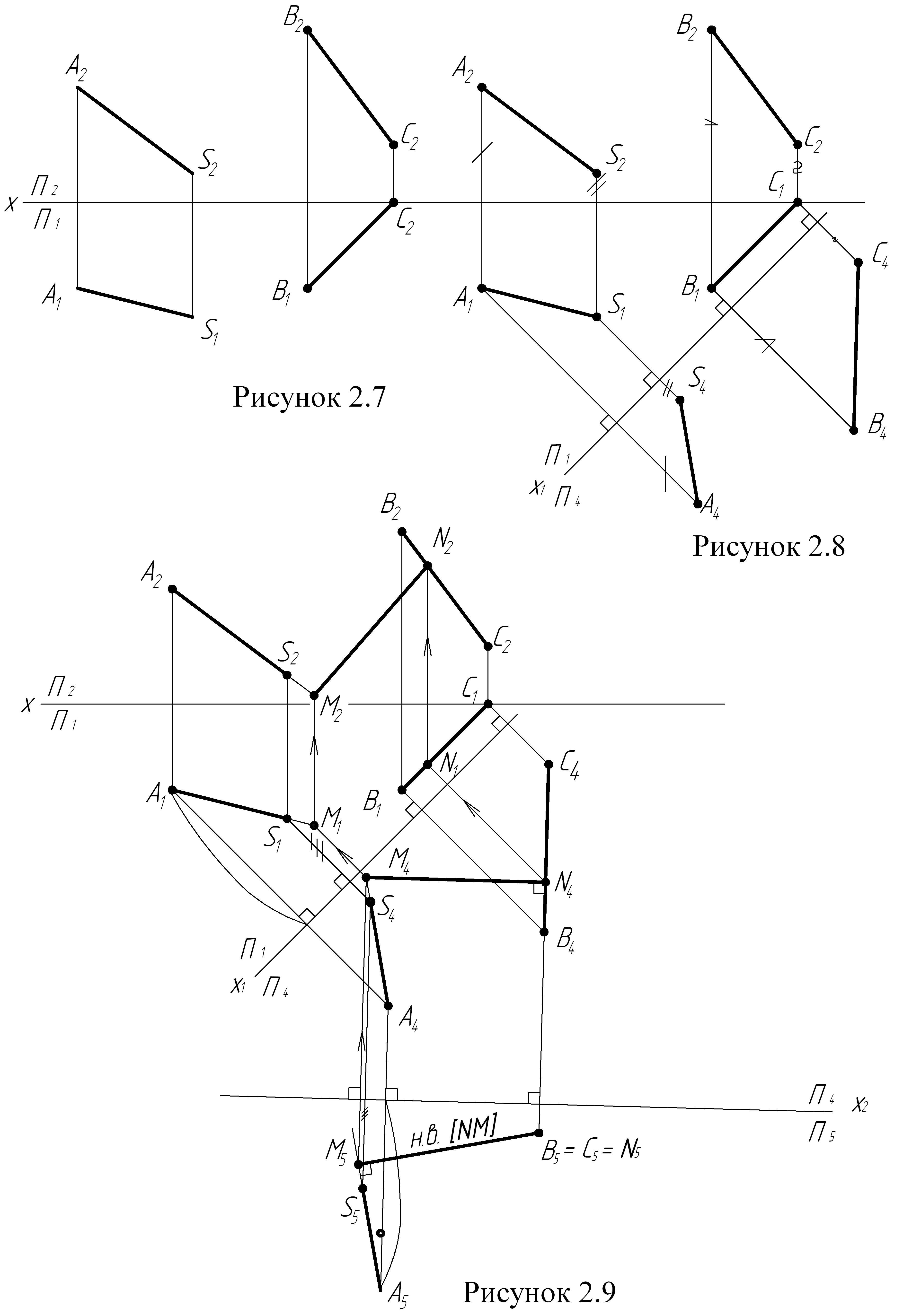
Задача
3 (рисунки
2.7, 2.8, 2.9)

Если
одна из заданных прямых является
проецирующей прямой, то кратчайшее
расстояние между такими прямыми
измеряется длиной перпендикуляра [MN],
общего к заданным прямым. В этом случае
перпендикуляр [MN] будет параллелен одной
из плоскостей проекций и равен длине
его проекции на эту плоскость.

Для
решения данной задачи необходимо одну
из прямых общего положения (SA)
или (BC)
преобразовать в прямую проецирующую,
применив две замены плоскостей проекций.

Порядок
построения:

По
координатам точек S,
A,
B,
C
построить проекции ребра пирамиды
SA
и проекцию стороны основания BC
(рисунок 2.7);
При
первой замене чертеж преобразуем так,
чтобы прямая общего положения
(ВС) оказалась параллельной одной из
плоскостей проекций, для этого вводим
новую плоскость П₄,
перпендикулярную плоскости П₁
и параллельную отрезку [ВС]. Ось Х₁
проведем параллельно [В₁С₁].
Измеряя расстояния от оси х до точек
А₂,
S₂,
В₂
и С₂
и откладывая их в плоскости П₄
от оси х₁,
получаем проекции [S₄A₄]
и [В₄C₄]
прямых (SA)
и (ВС) (рисунок 2.8);
При
второй замене чертеж преобразуем так,
чтобы отрезок прямой [ВС], параллельный
в системе П₄/П₁
плоскости П₄,
стал перпендикулярен плоскости П₅
в системе П₄/П₅
(рисунок 2.9);
Вводим
новую плоскость П₅,
перпендикулярно плоскости П₄
и отрезку [ВС], т.е. ось Х₂
пройдет перпендикулярно [В₄С₄].
Измерив расстояния от оси Х₁
до точек А₁,
S₁,
В₁,
С₁
и отложить их в плоскости П₅
от оси Х₂
на соответствующих линиях связи, получим
проекции [В₅С₅]
и [S₅А₅];
Находим
кратчайшее расстояние [МN]
между прямыми (SА)
и (ВС). Кратчайшим расстоянием будет
являться перпендикуляр, опущенный из
точки В₅=С₅
на проекцию [S₅А₅];
По
линиям связи находим проекции кратчайшего
расстояния между прямыми (SА)
и (ВС) в исходных проекциях.

Примечание:
данную задачу
можно решить, используя только одну
замену плоскостей проекций, если одна
из данных прямых (AS)
или (BC)
является прямой уровня.

Задача
4

Если
двугранный угол образован проецирующими
плоскостями и ребро АВ двугранного угла
перпендикулярно этой плоскости, то
двугранный угол спроецируется в
натуральную величину.

Для
решения данной задачи необходимо ребро
АВ (прямую общего положения) преобразовать
в проецирующую прямую, применив две
замены плоскостей проекций.

Порядок
построения:

По
координатам точек S,
А, В, С строим проекции двугранного
угла;
При
первой замене чертеж преобразуем так,
чтобы ребро АВ двугранного угла оказалось
параллельным одной из плоскостей
проекций, т.е. вводим новую плоскость
П₄,
перпендикулярно плоскости П₂
и параллельно ребру АВ; ось Х₁
пройдет параллельно [А₁В₁]
(рисунок 2.11);
По
линиям связи, перпендикулярным оси Х₁,
двугранный угол проецируем на плоскость
П₄.
Получаем проекцию S₄А₄В₄С₄
двугранного угла SАВС.
При
второй замене чертеж преобразуем так,
чтобы ребро АВ стало перпендикулярно
новой плоскости П₅;
Вводим
новую плоскость П₅
перпендикулярно плоскости П₄
и ребру АВ, т.е. ось Х₂
пойдет перпендикулярно А₄В₄.
По линиям связи, перпендикулярным оси
Х₂,
проецируем двугранный угол SАВС
на плоскость П₅.
Получаем проекцию двугранного угла на
плоскости П₅;
Натуральной
величиной двугранного угла будет угол
α, между проекциями сторон двугранного
угла [А₅=В₅
S₅]
и [А₅=В₅
С₅].

Примечание:
если ребро
АВ двугранного угла является прямой
уровня, то задача решается с помощью
одной замены плоскостей проекций.

Таблица
2 – Индивидуальные
задания к эпюру 2.

№

вар.

Точки

Координаты

№

вар.

Точки

Координаты

Продолжение
таблицы 2

Продолжение таблицы
2

Продолжение
таблицы 2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Часто для приведения прямой, плоской фигуры или пространственной
формы в то частное положение, которое требуется для решения задачи, приходится
заменять обе плоскости проекций. Переход от заданной системы плоскостей V/H
к новой V₁/H₁ может быть осуществлен по одной из
приведенных ниже схем:

V/H → V₁/H → V₁/H₁ или V/H → V/H₁ → V₁/H₁.

На рисунке 12 задана точка A в системе V/H. Затем
осуществлен переход от системы V/H к системе V₁/H₁:
проведена новая ось проекций Х₁, найдена новая проекция а’₁
точки А. Далее система V₁/H заменена новой
системой плоскостей проекции V₁/H₁ —вместо
горизонтальной плоскости проекций введена новая плоскость Н₁.

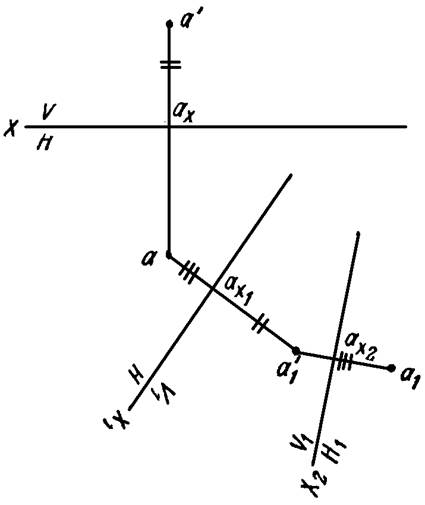
Рисунок 12

Положение
новых осей проекций выбирается в соответствии с конкретными условиями задачи.

Рассмотрим
примеры.

Пример 6. Определить
истинную фигуру треугольника ABC (рисунок 13).

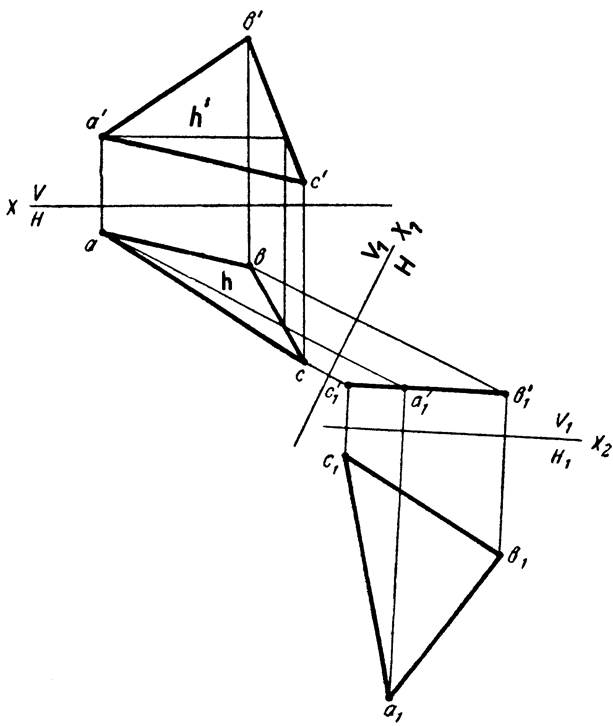
Рисунок 13

Треугольник
спроектируется в натуральную величину на какую-либо плоскость проекций, если он
окажется параллельным этой плоскости. Для того чтобы треугольник АВС оказался
параллельным одной из плоскостей проекций, необходимо выполнить двойную замену
плоскостей.

Сначала заменим
плоскость V на плоскость V₁. Плоскость V₁ выберем перпендикулярно плоскости
треугольника АВС — новая ось проекций x₁должна быть перпендикулярна горизонтальной проекции горизонтали h. На новую фронтальную плоскость проекций
треугольник cпроектируетcя в виде прямой линии c’₁a’₁b’₁.
Затем введем новую плоскость проекций H₁ параллельно
плоскости треугольника.

Горизонтальная
проекция a₁b₁c₁ треугольника ABC в
новой системе — истинная величина его.

Пример 7. Дана пирамида SАВС (рисунок 14). Определить величину
двугранного угла при ребре АВ.

Задача
сводится к построению проекции данного угла на плоскость проекций,
перпендикулярную к его ребру.

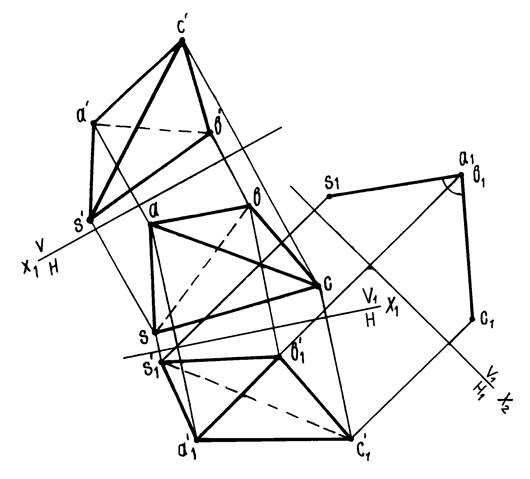
Рисунок 14

Так
как ребро АВ — прямая общего положения, то необходимо произвести две
последовательные замены плоскостей проекций. Плоскость V заменяем
плоскостью V₁, параллельной отрезку АВ.

Находим
новую фронтальную проекцию s’₁a’₁b’₁c’₁
пирамиды SАВС на новой фронтальной плоскости проекций. Затем от
системы V₁/H перейдем к системе V₁/H₁. Плоскость H₁
расположим перпендикулярно отрезку АВ. На плоскость Н₁ ребро
АВ спроектируется в точку, а грани SАВ и САВ — в прямые.
Угол s₁a₁c₁ будет искомым.

Пример 8. Дана пирамида SАВС (рисунок 15).
Определить кратчайшее расстояние между ребрами SА и ВС.

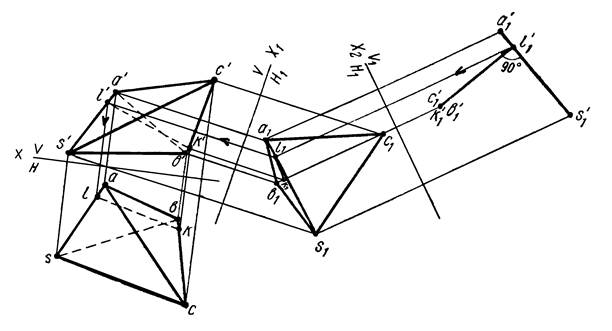
Рисунок 15

Прямые
SА и ВС являются скрещивающимися. Следовательно, задача сводится к
определению кратчайшего расстояния между двумя скрещивающимися прямыми. Для
решения задачи необходимо произвести такую замену плоскостей проекций, чтобы в
новой системе одна из прямых, например ВС (рисунок 16), оказалась
перпендикулярной к какой-либо плоскости проекций. Замену плоскостей проекций
осуществляем по схеме V/H → V/H₁ → V₁/H₁.

Следовательно, решение задач методами преобразования
сводится к выполнению четырех основных этапов:

1) преобразование прямой общего положения в прямую
уровня (определение углов наклона прямой к плоскостям проекций и натуральной
величины отрезков);

2. преобразование прямой уровня в проецирующую прямую
(определение величины двугранного угла, расстояния между прямыми);

3. преобразование плоскости общего положения в
проецирующую плоскость (определение углов наклона плоскости к плоскостям
проекций, расстояния от точки до плоскости);

4. преобразование плоскости проецирующей в плоскость
уровня (определяется натуральная величина плоскости).

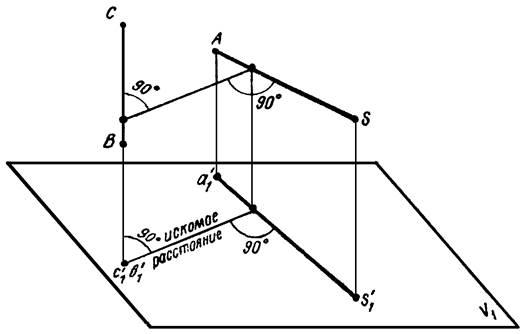
Рисунок 16

В системе V₁H₁ прямая ВС
(см. рисунок 15) проектируется в точку. Отрезок k’₁l’₁
— кратчайшее расстояние между ребрами АS и ВС. Для построения
проекций кратчайшего расстояния в системе V/H находим по линии связи
точку l₁ и проводим l₁k₁ параллельно
оси проекций Х₂ , после чего при помощи линий связи
находим основные проекции kl и k’l’.

СПОСОБЫ ВРАЩЕНИЯ

Сущность способов вращения заключается в том, что
заданная геометрическая форма путем вращения вокруг некоторой оси перемещается
в пространстве до тех пор, пока она не займет частное положение по отношению к
неизменной системе плоскостей проекций.

В зависимости от положения оси вращения по отношению к
плоскостям проекций различают следующие способы вращения:

а) вращение вокруг осей, перпендикулярных
к плоскостям проекций;

б) то же без указания положения осей
вращения;

в) вращение вокруг горизонтали или
фронтали;

г) вращение вокруг одного из следов
плоскости (совмещение).

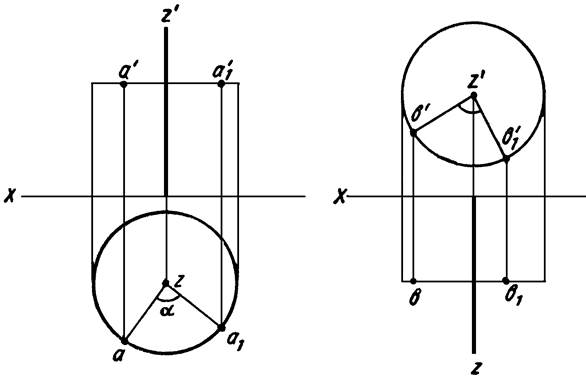
Рисунок 17 Рисунок
18

На
эпюре (рисунок 17) изображена точка А и ось вращения Z, перпендикулярная
к плоскости проекций H. При вращении вокруг оси Z точка А будет
перемещаться по окружности, лежащей в плоскости, перпендикулярной оси вращения
(параллельной плоскости проекций H). Если точку А переместить из
положения А в положение A₁ т. е. повернуть ее вокруг
оси Z, на некоторый угол α , то ее горизонтальная проекция (а)
займет положение a₁, описав при этом дугу радиуса za (za
— радиус вращения), а фронтальная проекция (а’) точки переместится
по прямой a’a’₁, параллельной оси X.

Если
ось вращения Z (рисунок 18) перпендикулярна к плоскости проекций V, то
при вращении точки В вокруг этой оси фронтальная проекция траектории её
перемещения будет окружностью, а горизонтальная — прямой, параллельной оси X.

Рассмотрим
пример.

Пример 9. Совместить
точку А с плоскостью Р путем вращения ее вокруг заданной оси Z
(рисунок 19).

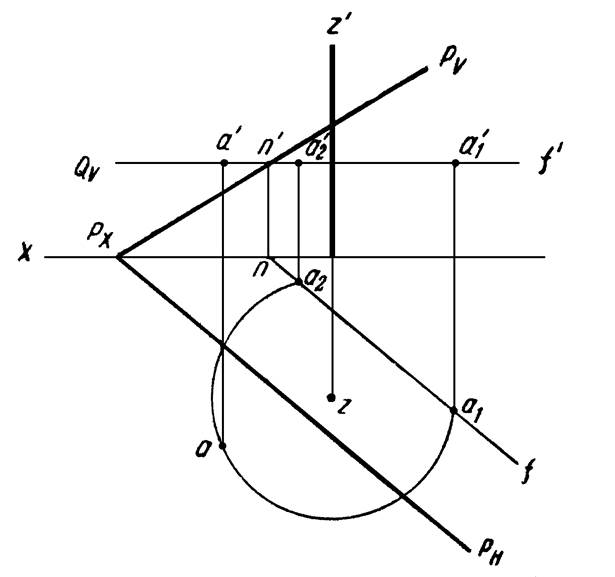
Рисунок 19

При
вращении вокруг оси Z, точка А опишет окружность в плоскости Q,
перпендикулярной этой оси. Плоскость Q пересечет заданную плоскость Р
по горизонтали NF. Очевидно, точка А окажется в плоскости Р
тогда, когда окружность, описываемая точкой А, пересечет горизонталь NF.
Задача, как видно из чертежа, имеет два решения.

Чтобы повернуть прямую АВ (рисунок 20) на некоторый угол α,
достаточно повернуть на заданный угол две принадлежащие, ей точки. Из чертежа
видно, что треугольники abz и a₁b₁z₁
равны между собой (по двум сторонам и углу между ними), а из их равенства
следует, что ab = a₁b₁, т. е. величина
горизонтальной проекции отрезка при вращении его вокруг оси, перпендикулярной Н,
не изменяется, изменяется только ее положение относительно оси проекций.
Это обстоятельство позволяет упростить построения при решении приведенного
примера

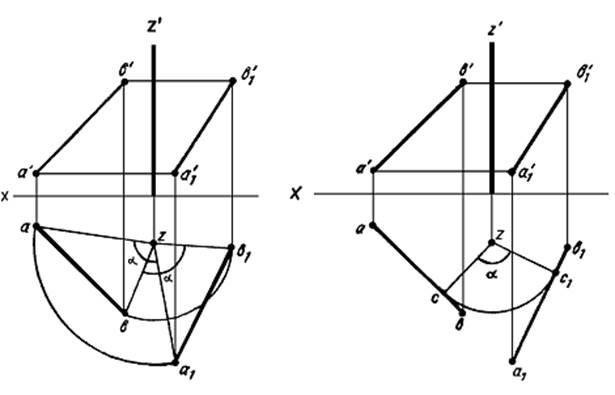
Рисунок 20 Рисунок
21

На рисунке 21 для поворота прямой АВ вокруг оси Z на
угол α из z, опущен перпендикуляр на ab. Затем точка с повернута
на заданный угол α, через точку c₁ проведена прямая,
перпендикулярная радиусу c₁z, и отложены отрезки c₁a₁=са
и c₁b₁=cb.

Вращение
плоскости вокруг оси, перпендикулярной плоскости проекций, осуществляется путем
вращения на один и тот же угол в одном и том же направлении точек и прямых,
которыми задана плоскость.

На
рисунке 22 плоскость, заданная треугольником АВС, повернута вокруг оси Z.
в положение, перпендикулярное фронтальной плоскости проекций
(горизонтальная проекция горизонтали А1 заняла положение,
перпендикулярное оси X).

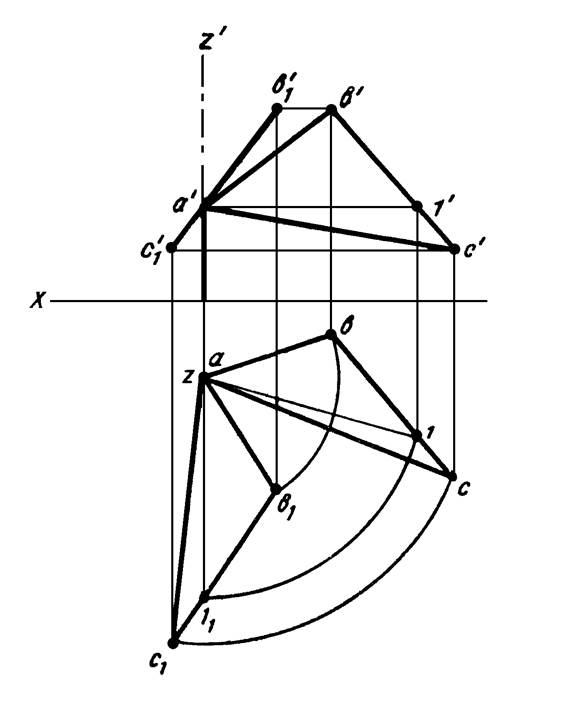
Рисунок 22

Если же плоскость задана следами, то для поворота плоскости на
некоторый угол необходимо повернуть на заданный угол один из ее следов и
горизонталь или фронталь этой плоскости (рисунок 23).

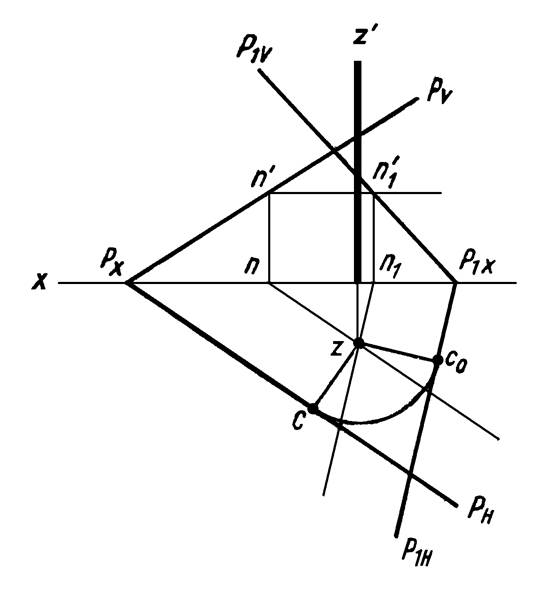
Рисунок 23

Таким
образом, при вращении любой пространственной формы около оси, перпендикулярной
одной из плоскостей проекций, проекция ее на эту плоскость по своей величине не
изменится. Изменится лишь положение этой проекции относительно оси проекций.
Пользуясь этим, для решения той или иной задачи можно применять способ
вращения, не изображая на чертеже осей вращения.

Источник

Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.

Кратчайшие пути в графе

Рассмотрим взвешенный граф, то есть у всех его ребер есть вес – некоторое число. Можно представить, что это цена, за которую мы можем по нему проехать.

Как его хранить? Давайте просто в списке смежности вместо номеров вершин соседа хранить пару (номер соседа, вес ребра до него).

Давайте решать задачу посика кратчайшего пути в графе – мы хотим за наименьшую стоимость проехать из вершины (A) в (B).

Обычно будем считать, что в графе нет циклов отрицательного веса – иначе кратчайшее расстояниие может быть равно минус бесконечности.

Для данной задачи есть несколько алгоритмов решения.

Алгоритм Флойда

Мы с вами уже знаем динамическое программирование, давайте рассмотри следующую динамику:

(d_{i j}^k) – это длина кратчайшего пути от вершины (i) до (j), используя как промежуточные только вершины из первых (k) = (d_{i j}^k) (напоминает рюкзак).

База динамики ((k = 0)) определяется только путями из одного ребра. Если есть ребро из (i) в (j) стоимостью (c), то (d_{i j}^{0}) = (c). Если таких ребер несколько, то, конечно, надо взять минимум.

Если мы хотим посчитать (d_{i j}^{k}), то у нас есть два варианта

Не брать на пути нигде (k)-ую вершину, тогда (d_{i j}^{k}) = (d_{i j}^{k – 1})
Взять где-нибудь в пути k-ую вершину, тогда путь разбивается на две части – от (i) до (k) и от (k) до (j), раз итоговый путь кратчайший, то и и эти два пути должны быть кратчайшми, а значит формула (d_{i j}^{k}) = (d_{i k}^{k – 1}) + (d_{k j}^{k – 1})

В результате ответ – (d_{A B}^{n}),

Можете подумать, как по такой динамике восстановить сам путь.

Также заметим, что вместо трехмерной динамики в этом алгоритме можно использовать двухмерную, храня в (dp_{ij}) последнее известное значение из (dp_{ij}^0), (dp_{ij}^1) (dp_{ij}^2), (ldots), (dp_{ij}^n).

for(int k = 0; k < n; k++){
    for(int i = 0; i < n; i++){
        for(int j = 0; j < n; j++){
            a[i][j] = min(a[i][j], a[i][k] + a[k][j]);
        }
    }
}

Теоретическое задание

Подумайте, как находить циклы отрицательного веса с помощью Флойда.

Плюсы алгоритма в том, что он находит расстояние сразу от всех вершин графа до остальных, а минус – алгоритм работает за (O(N^3));

Практическое задание

Первые две задачи на алгоритм Флойда.

Алгоритм Дейкстры

Для этого алгоритма придется рассматривать только графы без отрицательных рёбер.

Алгоритм Дейкстры решает немного другую задачу: он находит расстояние от одной вершины (A) до каждой вершины. Давайте для каждой вершины хранить расстояние до нее из вершины (A) в массиве (d). Например: * (d[A] = 0) * (d[x] = infty), если x не достижима из A

Назовем релаксацией обновление ответа для вершины (b) через ребро ((a, b, c)) таким способом: (d[b] = min(d[b], d[a] + c)).

При таком действии ответ не может стать лучше, чем кратчайшее расстояние до (b), так как мы просто пользуемся путем для вершины (a) и продлеваем его в (b).
Если мы прорелаксировали все ребра в кратчайшем пути в правильном порядке до вершины (b), то мы получим кратчайший путь до (b).

Теперь давайте каждый раз доставать вершину, для которой расстояние от А сейчас минимально, и мы еще ее не смотрели и затем обновлять всех ее соседей. Допустим вершина с минимальным расстоянием – x, тогда надо прорелаксировать все ребра из нее.

Давайте докажем корректность алгоритма по индукции:

База) Первой вершиной мы всегда рассмотрим (A), но для нее верно, что расстояние от (А) до (А) = 0;

Шаг) Мы достали вершину (i), нам известно, что для всех ее предков ответ – корректен, но тогда, допустим, что для (i)-ой вершины мы нашли ответ больший, чем надо, тогда это значит, что мы должны прийти из еще не рассмотренной вершины, но так как ребер отрицательного веса в графе нет, то такое невозможно (Rightarrow) мы доказали

https://visualgo.net/en/sssp?slide=1

Есть две возможные реализации алгоритма

реализация помощью нахождения минимального расстояния внутри массива за линию. Так как мы для каждого шага находим минимальную вершину, то мы сделаем не более (N) шагов, но при этом на каждом шаге мы находим минимум за линию, то есть алгоритм работает за (O(N^2)).

for (int i = 0; i < n; ++i){
    int uk = -1;
    for (int j = 0; j < n; j++){
        if ((mark[j] == 0) && ((uk == -1) || (d[j] < d[uk]))){
                uk = j;
        }
    }
    for (int j = 0; j < n; j++){
        if ((j != uk) && (g[uk][j] != -1)) d[j] = min(d[j], g[uk][j] + d[uk]);
    }
    mark[uk] = 1;
}

Реализация за (O(MlognN + NlogN)) с помощью нахождения минимального расстояния внутри кучи/сета за логарифм. Так как для каждой вершины мы сделаем не более одного извлекания из структуры + каждое ребро мы используем максимум два раза. Для этого давайте в выбранной структуре хранить пару (расстояние, вершина); Первый код реализован с set, второй с кучей. Так как в куче нет компаратора на возрастание, то надо либо сделать свой, либо домножить расстояние на -1;

while (used.size()) {
    int v = (*(used.begin())).second;
    for (int i = 0; i < g[v].size(); i++) {
        int to = g[v][i].first, c = g[v][i].second;
        if (dist[v] + c < dist[to]) {
            used.erase({dist[to], to});
            dist[to] = dist[v] + to;
            used.insert({dist[to], to});
        }
    }
    used.erase({dist[v], v});
}

while (!q.empty()) {
        int v = q.top().second;
        q.pop();
    for (int j = 0; j < g[v].size(); ++j) {
        int to = g[v][j].first, c = g[v][j].second;
        if (d[v] + c < d[to]) {
            d[to] = d[v] + c;
            q.push({-d[to], to});
        }
    }
}

Из асимптотики понятно, что при большом количестве ребер первый алгоритм писать лучше, иначе второй.

Теоретическое задание

Приведите примеры, когда каждый из алгоритмов работает лучше.

Недостаток алгоритма Дейкстры всего один – он не работает, если в графе есть ребра отрицательного веса.

Практическое задание

3-5 Задача на алгоритм Дейкстры.

Форд-Беллман

Этот алгоритм решает ту же задачу, что и Дейкстра, но зато может работать с отрицательными ребрами!

Давайте заведем массив расстояний, как и в дейкстре, для стартовой вершины расстояние = 0. Алгоритм состоит в релаксации каждого ребра в графе (N-1) раз.

Это работает потому, что в кратчайшем пути не больше, чем (N-1) ребро, и если мы прорелаксируем их в таком порядке, этот путь найдется. После (N-1) прохода по всем ребрам и их релаксации мы точно это сделаем и найдем кратчайший путь.

Также в этом случае удобнее хранить список ребер явно вместо списка смежности.

int from[m], to[m], cost[m];
for (int i = 0; i < n - 1; ++i) {
        for (int j = 0; j < m; ++j) {
                d[to[j]] = min(d[to[j]], d[from[j]] + cost[j]);
    }
}

Теоретическое задание

Подумайте, как найти цикл отрицательного веса с помощью этого алгоритма.

Практическое задание

Решите задачи 6 и 7.

Ссылка на контест

https://informatics.msk.ru/mod/statements/view.php?id=33380#1

Источник

2.1. Содержание эпюра:

2.2. Порядок выполнения эпюра

Кратчайшие пути в графе

Алгоритм Флойда

Теоретическое задание

Практическое задание

Алгоритм Дейкстры

Из асимптотики понятно, что при большом количестве ребер первый алгоритм писать лучше, иначе второй.

Теоретическое задание

Практическое задание

Форд-Беллман

Теоретическое задание

Практическое задание

Ссылка на контест

Вам также может понравиться

Как исправить полинявшие джинсы

Как составить кодекс чести женщины

Как исправить приложение вот лаунчер

Добавить комментарий Отменить ответ