Алгоритм Дейкстры. Разбор Задач
Время на прочтение
7 мин
Количество просмотров 34K
Поиск оптимального пути в графе. Такая задача встречается довольно часто и в повседневной жизни, и в мире технологий. Справиться с такими вызовами помогает подход, который должен быть в арсенале каждого программиста — алгоритм Дейкстры.
Если вы хотите найти ответить на вопросы, чем этот алгоритм лучше BFS (поиска в ширину), при каких условиях алгоритм применим, и какие теоретические и практические задачи можно с его помощью решать, читайте далее.
Введение
Алгоритм Дейкстры работает на ориентированных (с некоторыми дополнениями и на неориентированных) графах, и призван искать кратчайшие пути между заданной вершиной и всеми остальными вершинами в графе.
Как правило, граф обозначают как набор вершин и рёбер где число рёбер может быть задано
, а вершин числом
Для каждого ребра в графе задан неотрицательный вес , а также вершина, из которой осуществляется поиск оптимальных путей.
Алгоритм Дейкстры может найти кратчайший путь между вершинами и
в графе, только если существует хотя бы один путь между этими вершинами. Если это условие не выполняется, то алгоритм отработает корректно, вернув значение “бесконечность” для пары несвязанных вершин.
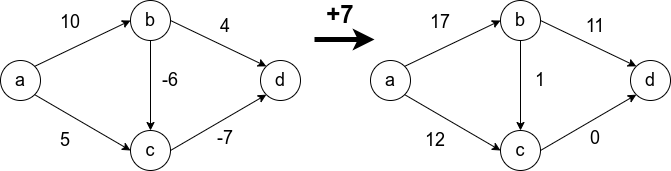
Условие неотрицательности весов рёбер крайне важно и от него нельзя просто избавиться. Не получится свести задачу к решаемой алгоритмом Дейкстры, прибавив наибольший по модулю вес ко всем рёбрам. Это может изменить оптимальный маршрут. На рисунке видно, что в первом случае оптимальный путь между и
(сумма рёбер на пути наименьшая) изменяется при такой манипуляции. В оригинале путь проходит через
, а после добавления семёрки ко всем рёбрам, оптимальный путь проходит через
Как ведёт себя алгоритм Дейкстры на исходном графе, мы разберём, когда выпишем алгоритм. Но для начала зададимся другим вопросом: “почему не применить поиск в ширину для нашего графа?”. Известно, что метод BFS находит оптимальный путь от произвольной вершины в ориентированном графе до любой другой вершины, но это справедливо только для рёбер с единичным весом.
Свести задачу к решаемой BFS можно, но если заменить все рёбра неединичной длины рёбрами длины
, то граф очень разрастётся, и это приведёт к огромному числу действий при вычислении оптимального маршрута.
Чтобы этого избежать предлагается использовать алгоритм Дейкстры. Опишем его:
Инициализация:
Основный цикл алгоритма:
- Пока все вершины не исследованы (или формально
), повторяем:
В итоге исполнения этого алгоритма, массив будет содержать все оптимальные пути, исходящие из
.
Примеры работы
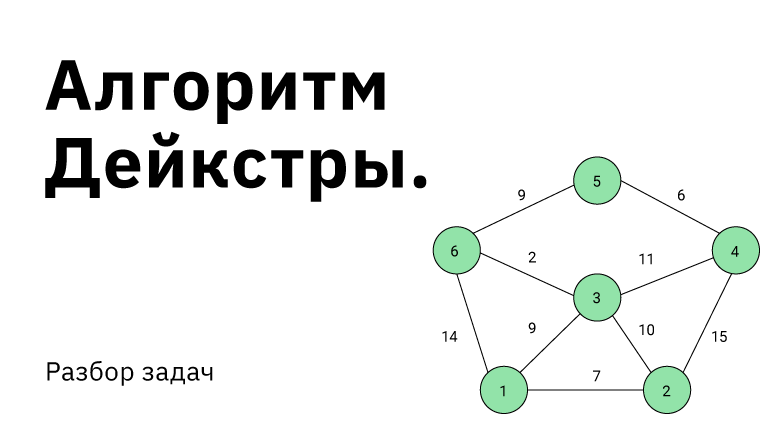
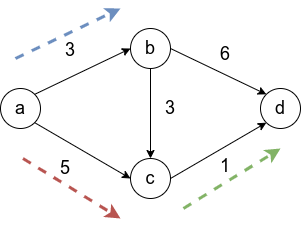
Рассмотрим граф выше, в нём будем искать пути от до всего остального.
Первый шаг алгоритма определит, что кратчайший путь до проходит по направлению синей стрелки и зафиксирует кратчайший путь. Второй шаг рассмотрит, все возможные варианты
и окажется, что оптимальный вариант двигаться вдоль красной стрелки, поскольку
меньше, чем
и
Добавляется длина кратчайшего пути до
. И наконец, третьим шагом, когда три вершины
уже лежат в
, остается рассмотреть только два ребра и выбрать, лежащее вдоль зеленой стрелки.
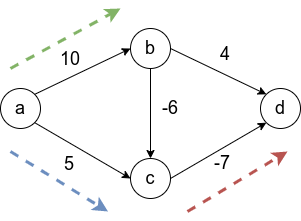
Теперь рассмотрим граф с отрицательными весами, упомянутый выше. Напомню, алгоритм Дейкстры на таком графе может работать некорректно.
Первым шагом отбирается ребро вдоль синей стрелки, поскольку это ребро наименьшего веса из исходной вершины. Затем выбирается ребро Это зафиксирует навсегда неверный путь от
к
, в то время как оптимальный путь проходит через центр с отрицательным весом. Последним шагом, будет добавлена вершина
.
Оценка сложности алгоритма
К этому моменту мы разобрали сам алгоритм, ограничения, накладываемые на его работу и ряд примеров его применения. Давайте упомянем какова вычислительная сложность этого алгоритма, поскольку это пригодится нам для решения задач, ради которых затевалась эта статья.
Базовый подход, основанный на циклах, предполагает проход по всем рёбрам каждого узла, что приводит к сложности .
Эффективная реализация предполагает использование кучи. Об этой структуре данных можно сказать коротко: она позволяет выполнять две операции за логарифмическое время. Первая операция — получение узла в дереве, с наименьшим ключом, и, вторая операция, вставка нового узла в дерево с новым ключом.
Что еще можно сказать о куче:
- это сбалансированное бинарное дерево,
- ключ текущего узла всегда меньше, либо равен ключей дочерних узлов.
Интересную задачу с использованием куч я разбирал ранее в этом посте.
Используя кучу в алгоритме Дейкстры, где в качестве ключей используются расстояния от вершины в неисследованной части графа (в алгоритме это ), до ближайшей вершины в уже покрытом (это множество вершин
), можно сократить вычислительную сложность до
Доказательство справедливости этих оценок я оставляю за пределами этой статьи.
Далее перейдём к разбору задач!
Задача №1
Будем называть узким местом пути в графе ребро максимальной длины в этом пути. Путём с минимальным узким местом назовём такой путь между вершинами и
, что не существует другого пути
, чьё узкое место меньше по длине. Требуется построить алгоритм, который вычисляет путь с минимальным узким местом для двух данных вершин в графе. Асимптотическая сложность такого алгоритма должна быть
Решение
По условию задачи ребро с большим весом трактуется как узкое место. Вес в этом случае можно воспринимать как цену за проход по ребру. В результате решения задачи хотелось бы получить алгоритм, способный строить маршруты между узлами так, чтобы, если мы захотим провести любой другой путь, он будет содержать более тяжелые рёбра.
В случае классической задачи, поиска пути минимальной длины между двумя вершинами графа, мы поддерживаем в каждой посещенной алгоритмом вершине графа минимальную длину пути до этой вершины. Здесь стоит оговориться, что будем именовать множество посещенными вершинами, а
часть графа, для которой еще нужно найти величину пути или узкого места.
В отличии от классического алгоритма, решение этой задачи должно поддерживать величину актуального узкого места пути, приводящего в вершину . А при добавлении новой вершины из
, мы должны смотреть не увеличивает ли ребро
величину узкого места пути, которое теперь приводит в
.
Если ребро увеличивает узкое место, то лучше рассмотреть вершину
, ребро
до которой легче
. Поиск неувеличивающих узкое место ребёр нужно осуществлять не только среди соседей определенного узла
, но и среди всех
, поскольку отдавая предпочтение вершине, путь в которую имеет наименьшее узкое место в данный момент, мы гарантируем, что мы не ухудшаем ситуацию для других вершин.
Последнее можно проиллюстрировать примером: если путь, оканчивающийся в вершине имеет узкое место величины
, и есть вершина
с ребром
веса
, и
с ребром
веса
, то предпочтение отдаётся
, алгоритм даст верный результат в обоих случая, если существует
веса
или веса
.
В результате разбора выше, предлагается руководствоваться следующей формулой при выборе очередной вершины из непосещенных и обновлении величин, которые мы поддерживаем.
Стоит пояснить, что поиск по осуществляется, только для существующих связей
а
это вес ребра
.
Задача №2
Предлагается решить более практическую задачу. Пусть городов, между ними существуют пути, заданные массивом
edges[i] = [city_a, city_b, distance_ab], а также дано целое число mileage.
Требуется найти такой город из данных, из которого можно добраться до наименьшего числа городов не превысив mileage.
Стоит отметить, что граф неориентированый, т.е. по пути между городами можно двигаться в обе стороны, а длина пути между городами a и c может быть получена как сумма длин путей a -> b и b -> c, если есть маршрут a -> b -> c
Решение
С решением данной проблемы нам поможет алгоритм Дейкстры и описанная выше реализация с помощью кучи. Поставщиком этой структуры данных станет библиотека heapq в Python.
Будем использовать алгоритм Дейкстры для того, чтобы подсчитать количество соседних городов, расстояние до которых меньше mileage, для каждого из городов. Соберем количества соседей в в одном месте и найдем минимум из них.
Поскольку наш граф неориентированный, то из любой его вершины можно добраться до произвольной вершины
. Будем использовать алгоритм Дейкстры для того, чтобы для каждого из городов в графе построить кратчайшие пути до всех остальных городов, мы это уже умеем делать в теории. И чтобы, оптимизировать этот процесс, будем в его течении сразу отвергать пути, которые превышают
mileage, а не делать постфактум, когда все пути получены.
Давайте опишем функцию решения:
def least_reachable_city(n, edges, mileage):
"""
входные параметры:
n --- количество городов,
edges --- тройки (a, b, distance_ab),
mileage --- максимально допустимое расстояние между городами
для соседства
"""
# заполняем список смежности (adjacency list), в нашем случае это
# словарь, в котором ключи это города, а значения --- пары
# (<другой_город>, <расстояние_до_него>)
graph = {}
for u, v, w in edges:
if graph.get(u, None) is None:
graph[u] = [(v, w)]
else:
graph[u].append((v, w))
if graph.get(v, None) is None:
graph[v] = [(u, w)]
else:
graph[v].append((u, w))
# локально объявим функцию, которая будет считать кратчайшие пути в
# графе от вершины, до всех вершин, удовлетворяющих условию
def num_reachable_neighbors(city):
# создаем кучу, из одного элемента с парой, задающей нулевую
# длину пути до самого исходного города
heap = [(0, city)]
# и массив, содержащий города и кратчайшие
# расстояния до них от исходного
distances = {}
# затем, пока куча не пуста, извлекаем ближайший
# от посещенных городов город
while heap:
currDist, neighb = heapq.heappop(heap)
# если кратчайшее ребро ведет к городу, где мы уже знаем
# оптимальный маршрут, то завершаем итерацию
if neighb in distances:
continue
# в остальных случаях, и если сосед не является отправным
# городом, мы добавляем новую запись в массив кратчайших расстояний
if neighb != city:
distances[neighb] = currDist
# обрабатываем всех смежных городов с соседом, добавляя их в кучу
# но только если: а) до них еще не известен кратчайший маршрут и б) путь до них через neighb не выходит за пределы mileage
for node, d in graph[neighb]:
if node in distances:
continue
if currDist + d <= mileage:
heapq.heappush(heap, (currDist + d, node))
# возвращаем количество городов, прошедших проверку
return len(distances)
# выполним поиск соседей для каждого из городов
cities_neighbors = {num_reachable_neighbors(city): city for city in range(n)}
# вернём номер города, у которого наименьшее число соседей
# в пределах досигаемости
return cities_neighbors[min(cities_neighbors)]
В функции выше, в комментариях, подробно описывается, как метод Дейкстры, реализованный на куче позволяет найти расстояния до всех городов, в пределах `mileage`. Основную сложность для понимания предстваляет цикл, работающий с кучей.
Заключение
Алгоритм Дейкстры это мощный инструмент в мире работы с графами, область применения его крайне широка. С его помощью можно оценить даже целесообразность добавления новой ветки метро, новой дороги или маршрута в компьютерной сети. Он прост в исполнении и интуитивно понятен, как другие жадные (greedy) алгоритмы. Вычислительная сложность решений задач с его помощью зачастую не выше . При некоторых условиях может достигать линейной сложности (существует алгоритм линейной сложности, решающий первую задачу, при условии, что граф неориентированный).
Стоит еще раз отметить, что алгоритм не работает, когда в графе существуют отрицательные веса. Для этого существует подход динамического программирования — алгоритм Беллмана – Форда, что может послужить темой другой статьи. Несмотря на это, алгоритм Дейкстры является представителем идеального баланса простоты и мощи, для решения прикладных задач.
Статья подготовлена в преддверии старта курса «Алгоритмы для разработчиков». Узнать о курсе подробнее, а также зарегистрироваться на бесплатный демоурок можно по ссылке.
Информация
[1] Условия задач взяты из книги «Algorithms Illuminated: Part 2: Graph Algorithms and Data Structures» от Tim Roughgarden,
[2] и с сайта leetcode.com.
[3] Решения авторские.
Всем привет, меня зовут Елена и мы продолжаем разбирать задачи из ЕГЭ по информатике.
В прошлой статье мы рассмотрели азы теории графов, научились решать задачи на сопоставление двух информационных моделей – графа и таблицы. В конце были приведены задачи для самостоятельного разбора.
Все ли удалось?) Если есть какие-то вопросы по задачам, пишите в комментарии, дам подсказку или разберу сложную задачу подробно.
В этой статье опишу алгоритм, позволяющий решать остальные задачи первого типа, подробно рассмотрим его работу на примере. Приведу блок-схему алгоритма и дам подборку задач ЕГЭ по теме.
Заметка для сдающих ОГЭ
С помощью этого алгоритма вы сможете решать задачи типа 4. Возможно, алгоритм покажется вам сложным, но не бойтесь разобраться с ним. Помните, что привыкание – ключ к пониманию. Вернитесь к описанию алгоритма, разберите несколько номеров, двигаясь по блок-схеме. У вас получится!
Алгоритм Дейкстры
Область применения
Сегодня разберем задачи первого типа на поиск кратчайшего пути. Для этого используют алгоритм Дейкстры. Он хорошо описан на Википедии, можете почитать по ссылке. Единственное – мне не очень нравится схема, которой они пользуются при решении, я рекомендую использовать немного другую.
Будем решать задачу из примера на Википедии (чтобы сравнить ответ), используя мою схему.
Формулировка условия
Требуется найти кратчайшие пути от 1й вершины до всех остальных.
Решение
Будем на основе приведенного графа строить другой граф с кратчайшими путями. Рядом с каждым пунктом будем ставить метки – известную кратчайшую длину маршрута до него от начального пункта. В ходе решения задачи значение метки может меняться.
Пока запоминаем следующие правила:
- начальному пункту всегда присваиваем значение 0.
- чтобы найти метку для пункта B, нужно к значению метки для пункта A прибавить длину дороги AB.
На мой взгляд, формальное описание алгоритма сложновато для восприятия, поэтому сначала рассмотрим его работу на примере.
Рисуем следующую схему. Располагаем начальный пункт сверху, рисуем от него три стрелки – дороги в соседние пункты (2, 3 и 6, оранжевым написаны длины этих дорог). Рядом с ними ставим метки (отмечены фиолетовым цветом) – длину маршрута до пункта.
Пункт 1 можно считать посещенным – всю возможную информацию из него мы вытянули (далее отмечен крестиком). Переходим к следующему пункту. К какому? Непосещенному с минимальной меткой. В нашем примере это пункт 2 с меткой 7.
Обрабатываем соседние с пунктом 2 вершины:
- вершина 1 посещенная, ничего делать не нужно;
- вершина 3. Проверяем, будет ли путь к пункту 3 через 2 короче, чем стоящая у пункта 3 метка (метка пункта 3 равна 9, длина пути в п.3 через п.2 будет равен сумме метки п.2 и длины дороги из 2 в 3: 7+10 = 17 > 9. Видим, что длина дороги 1-3 короче, чем длина пути 1-2-3. Метку у пункта 3 менять не нужно. Дорогу рисуем пунктиром – чтобы видеть, что мы ее обрабатывали);
- вершины 4 еще нет на нашей схеме, добавляем, считаем метку для нее: к метке п.2 прибавляем длину дороги 2-4, получаем 7+15=22.
После этого отмечаем вершину 2 как посещенную.
Снова переходим к непосещенной вершине с минимальной меткой – вершине 3.
Соседние с ней вершины: 1, 2, 4, 6.
- Вершины 1 и 2 посещенные.
- Вершина 4. Проверяем сумму метки п.3 и дороги 3-4: 9+11 = 20 < 22. Получается, что более короткий путь до вершины 4 проходит через п.3. Тогда дорога 2-4 на нашей схеме лишняя, вычеркиваем ее (я отметила ее пунктиром). Метку у вершины 4 меняем на 20.
- Вершина 6. Проверяем сумму метки п.3 и дороги 3-6: 9 + 2 = 11 < 14. Вычеркиваем дорогу 1-6, меняем значение метки п.6 на 11.
Теперь непосещенной вершиной с минимальной меткой является п.6. Его соседи – вершины 1, 3 (посещенные) и 5 (не отмечен на нашей схеме). Добавляем п.5 на схему, считаем его метку. Вычеркиваем п.6 как посещенный.
Осталось два непосещенных пункта – 4 и 5. Можем обрабатывать их в любом порядке.
Рассмотрим п.4. Он связан с вершинами 2, 3 (посещенные) и 5. Если попробуем пройти в п.5 через п.4, дорога займет 20 + 6 = 26 > 20 – метку у п.5 менять не нужно, п.4 отмечаем как посещенный.
Остался пункт 5. Все пункты, с которыми он связан, посещены, обрабатывать нечего. Отмечаем п.5 как посещенный и завершаем алгоритм. После этого метки, стоящие у пунктов, являются длинами кратчайших маршрутов из п.1 в остальные пункты.
Хотите пройтись по алгоритму еще раз? Для вашего удобства повторю в галерее все шаги:
Если вы все-таки заглянете в Википедию, то увидите, что в ней предлагают решать задачу, ставя метки на исходном графе. Мой способ кажется мне предпочтительнее по нескольким причинам:
- Исходный граф может иметь много вершин, что затрудняет решение задачи (придется делать много перекрывающих друг друга пометок).
- Но главное: при решении задачи моим способом (не авторским, а подсмотренным где-то на просторах интернета) мы сразу можем ответить на вопросы в нескольких формулировках, предлагаемых в заданиях для подготовки к ЕГЭ (через сколько пунктов проходит кратчайший путь из пункта А в пункт К? Какова длина самой длинной дороги кратчайшего пути? Перечислите все пункты, через которые проходит кратчайший маршрут).
Блок-схема алгоритма Дейкстры
Я не сильна в обозначениях блок-схем, поэтому надеюсь, что ни у кого не будет дергаться глаз от того, что я стрелочку не туда воткнула или поставила блок не той формы)) Главное, что алгоритм четко расписан.
Домашнее задание
Не вижу смысла решать здесь какую-то задачу из ЕГЭ, так как алгоритм решения будет точно такой, как и в рассмотренном примере. Лучше дам список задач для самостоятельной отработки. Если возникают сложности – пишите в комментариях, постараюсь помочь. Также буду рада обратной связи по материалу. Все ли понятно? Может, что-то нуждается в большей подробности?
Домашка! Заходим на сайт К.Полякова, находим номера №№ 1591, 1596, 3641, 1601, 5026, 92, 86. Успехов!
Напоминалочка
Если вам нужна помощь в подготовке к ЕГЭ или ОГЭ по информатике, пишите, у меня еще есть окошки! Провожу занятия офлайн с использованием графического планшета, записи с занятия высылаю pdf-файлом.
Информатика, 11 класс. Урок № 7.
Тема — Моделирование на графах
Цели и задачи урока:
- Получить знания о графах, их видах, свойствах.
- Получить навыки преобразования весовой матрицы (табличной формы представления информации) в граф.
- Сформировать навык построения путей в графе и поиска кратчайшего пути.
На уроке вы узнаете:
- Что такое граф, как наглядное средство представления и состава системы.
- Как применять графы при решении различных задач.
- Как представлять информацию на графах.
- Как находить кратчайший путь по графу.
Давайте рассмотрим, пожалуй, самую известную головоломку, придуманную аж в XVIII веке, и захватившую умы человечества на многие годы. Называется она задача о семи Кёнигсбергских мостах. В Кёнигсберге начиная с XIV было построено 7 мостов: Медовый мост, Лавочный мост, Зелёный мост, Рабочий мост, Кузнечный мост, Деревянный мост и Высокий мост, соединяющий остров и полуострова в единый город. Тогда и возникла головоломка: «Как пройти по всем мостам, не проходя ни по одному дважды?»
Десятилетиям жители города пытались решить эту задачу как практически (гуляя по городу), так и теоретически.
И только Леонард Эйлер, введя новое понятие — ГРАФ, смог решить ее раз и навсегда.
Граф — абстрактный математический объект, представляющий собой множество вершин графа (обозначены красным цветом) и набор рёбер (обозначены синим), то есть соединений между парами вершин. При этом каждое ребро представляет собой отношение двух вершин.
Графы делятся на:
— Неориентированные и ориентированные (когда движение по ребру возможно только в одну сторону).
— Взвешенными (когда у вершины или у ребра есть вес, отличающий его от другого) и невзвешенный.
— И другие более сложные графы (мультиграф, псевдограф, изоморфный граф и другие).
Эйлер установил, что:
1. Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно или не может существовать граф, который имел бы нечётное число нечётных вершин.
2. Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
3. Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
ВЫВОД: пройти только один раз по каждому мосту невозможно.
Графы находят широкое применение во многих сферах нашей жизни. Например, с их помощью можно планировать оптимальные транспортные маршруты, упростить решение математических задач, визуализировать решения компьютерных программ, визуализировать различную информацию (схема метро, карта звездного неба и т. д.).
Очень часто для решения задач требуется найти кратчайший путь между двумя вершинами.
Кратчайшим путем мы будем называть путь, если: эти вершины соединены минимальным числом ребер (в случае, если граф невзвешенный); сумма ребер, соединяющих эти вершины, минимальна (для взвешенного графа).
Существует огромное количество алгоритмов, находящих кратчайший путь и один из них — это алгоритм Дейсктры.
Алгоритм заключается в том, что надо пошагово перебрать все вершины графа, вычеркивая их, которые будут являются известным минимальным расстоянием от вершины «начала» до конкретной вершины.
Для примера возьмем следующий взвешенный ориентированный граф и попытаемся найти кратчайший путь от вершины A до F. Пошагово переберём все вершины графа, вычеркивая их, которые будут являются известным минимальным расстоянием от вершины «начала» до конкретной вершины.
Первым шагом: присвоим вершине А метку равную 0, потому как эта вершина — начало. Остальным вершинам присвоим метки равные бесконечности.
Вторым шагом: выберем не вычеркнутую вершину, вес которой является минимальным («источник»). Сейчас это вершина А. Вычисляем сумму веса вершины источника и веса ребра
То есть для:
B=0+2=2
C=0+5
D=0+7
F=0+10.
Если она окажется меньше веса вершины приемника, то изменим вес этой вершины.
Третьим шагом: вычеркнем вершину-«источник».
Повторим шаги 1, 2, 3 до тех пор, пока не будут вычеркнуты все вершины.
Еще один способом нахождения кратчайшего пути может служить «метод динамического программирования».
Пусть дан некоторый лабиринт, соединяющий комнаты в виде графа. При этом заходя в каждую комнату, нужно заплатить пошлину. Необходимо пройти по нему от точки А до точки В, потратив наименьшее количество денег.
Составим таблицу, в которой каждая ячейка будет соответствовать определенной ячейке. Числа в ячейках будут равны минимальному числу пошлины, которое можно получить, пройдя от начала (A) до соответствующей клетки.
На уроке рассмотрен материал для подготовки к огэ по информатике, 4 задание разбор
Содержание:
- Объяснение 4 задания ОГЭ по информатике
- Поиск кратчайшего пути (перебор)
- ОГЭ информатика разбор задания 4
- Актуальное
- Тренировочные
4-е задание: «Формальные описания реальных объектов и процессов»
Уровень сложности — базовый,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
* до 2020 г — это задание № 3 ОГЭ
Графы
Иногда очень трудно структурировать информацию описанными структурами из-за сложных «взаимоотношений» между объектами. Тогда можно использовать графы:
Граф – это набор вершин и связей между ними, называющихся рёбрами:
Граф, отображающий дороги между поселками
Матрица и список смежности
Связный граф – это граф, между любыми вершинами которого существует путь.
Связный граф
Дерево – это связный граф без циклов (замкнутых участков).
Дерево — связный граф без циклов
Взвешенные графы и весовая матрица
У взвешенных графов указан «вес ребра»:
Из взвешенных графов получается весовая матрица, обратное преобразование тоже возможно.
Весовая матрица
Поиск кратчайшего пути (перебор)
Определение кратчайшего пути между пунктами A и D
- В заданиях ОГЭ этой темы чаще всего используются две информационные модели — таблицы и схемы.
- Информация в таблице строится по следующим правилам: на пересечении строки и столбца находится информация, характеризующая комбинацию этой строки и столбца.
- На схеме информация строится по следующему правилу: если между объектами схемы имеется связь, то она отображается линией, соединяющей названия этих объектов на схеме.
ОГЭ информатика разбор задания 4
Подробный видеоразбор по ОГЭ 4 задания:
📹 Видеорешение на RuTube здесь
Актуальное
Рассмотрим, как решать 4 задание по информатике ОГЭ.
Разбор задания 4.5. Демонстрационный вариант ОГЭ 2022 г ФИПИ:
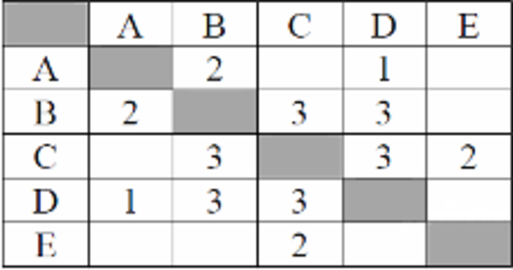
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт С.
Передвигаться можно только по дорогам, протяжённость которых указана в таблице. Каждый пункт можно посетить только один раз.
✍ Решение:
- Построим дерево протяженности дорог, на ветвях будем отображать протяженность. Учтем, что каждая ветвь, должна включить узел пересечения с С:
Ответ: 8
Разбор задания 4.6
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых (в километрах) приведена в таблице.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 5 | 8 | 4 | 1 | ||
| B | 5 | 3 | 3 | 4 | ||
| C | 8 | 3 | 2 | 15 | ||
| D | 4 | 2 | 4 | 12 | ||
| E | 1 | 3 | 4 | 7 | ||
| F | 4 | 15 | 12 | 7 |
Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт С.
Передвигаться можно только по дорогам, протяжённость которых указана в таблице. Каждый пункт можно посетить только один раз.
✍ Решение:
- Найдём все варианты маршрутов из
AвF, проходящих через пунктС, и выберем самый короткий. - Пройдемся по таблице построчно слева-направо сверху-вниз:
A—B—C—D—E--F: длина маршрута 25 км. A—B—C—D--F: длина маршрута 29 км. A—B—C--F: длина маршрута 28 км. пропустим B: A—C--F: длина маршрута 23 км. A—C—D—E--F: длина маршрута 20 км. пропустим и D: A—C—E--F: длина маршрута 16 км. пропустим и E: A—C—D--F: длина маршрута 24 км. A—C--F: длина маршрута 23 км. поменяем следование маршрута, исключая пункты с большим числом км: A—C—B--F: длина маршрута 15 км. A—D—С—B--F: длина маршрута 13 км.
A—D—С—B--F. Длина маршрута 13 км.Ответ: 13
Тренировочные
Разбор задания 4.1:
В таблице приведена стоимость перевозок между соседними железнодорожными станциями, укажите схему, соответствующую таблице:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 2 | 7 | 4 | ||
| B | 2 | ||||
| C | 7 | 3 | 5 | ||
| D | 3 | 3 | |||
| E | 4 | 5 | 3 |
✍ Решение:
- Необходимо рассмотреть каждую схему и подсчитать количество ребер, выходящих из каждой вершины. В скобках будем указывать соответствующую данному «ребру» стоимость:
1 схема:
A: B(2), C(7), E(4) B: A(2), C(4) Здесь уже можно остановиться, т.к. для вершины B по схеме два ребра, а по таблице одно значение (B->A=2 )
2 схема:
A: B(2), C(7), E(4) B: A(2) C: A(7), D(5), E(3) Здесь уже можно остановиться, т.к. для вершины C стоимость по схеме и по таблице различается: по схеме C->D = 5, а по таблице на пересечении C и D цифра 3.
3 схема:
A: B(2), C(7), E(4) B: A(2) C: A(7), D(3), E(5) D: C(3), E(3) E: A(4), C(5), D(3) Данные на схеме полностью совпадают с табличными!
Ответ: 3
Разбор задания 4.2:
На схеме приведена стоимость перевозок между соседними железнодорожными станциями, укажите таблицу, соответствующую схеме:
1.
|
2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.
|
4.
|
Подобные задания для тренировки
✍ Решение:
- Необходимо рассмотреть каждую таблицу и подсчитать количество пересечений для каждой строки, т.е. для каждой ж.д. станции. В скобках будем указывать соответствующую данной станции стоимость:
1 таблица:
A: B(3), E(2), F(2) Здесь уже можно остановиться, т.к. для станции A по схеме два ребра у вершины А, а по таблице уже три значения
2 таблица:
A: B(3), F(2) B: A(3), C(3), E(5), F(4) C: B(3), D(2), E(5) D: C(2), E(3) F: A(2), B(4) Данные на схеме полностью совпадают с табличными!
Ответ: 2
Разбор задания 4.3:
В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите таблицу, для которой минимальное расстояние от точки A до точки F больше 8.
1.
|
2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.
|
4.
|
✍ Решение:
- Для каждой из таблиц построим дерево перевозок, на ветвях будем отображать суммарную стоимость:
- По дереву 1-й таблицы видно, что каждая из ветвей в результате возвращает сумму большую 8. То есть таблица 1 соответствует искомому результату.
1 таблица:
Ответ: 1
Разбор задания 4.4:
Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых (в километрах) приведена в таблице:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 5 | 5 | 4 | |||
| B | 5 | 2 | ||||
| C | 5 | 2 | 1 | |||
| D | 4 | 1 | 3 | |||
| E | 1 | 1 | ||||
| F | 1 | 3 | 1 |
Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5
2) 6
3) 7
4) 8
Подобные задания для тренировки
✍ Решение:
- Решать такое задание лучше с помощью дерева:
- Среди приведенных ответов кратчайший путь, равный 6 км, находится под номером 2.
Ответ: 2
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Простейшие задачи на графы
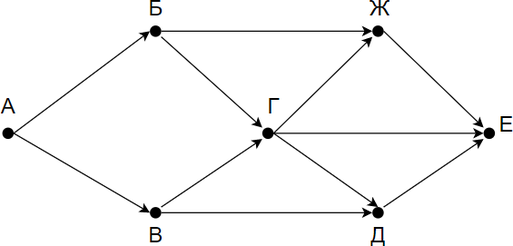
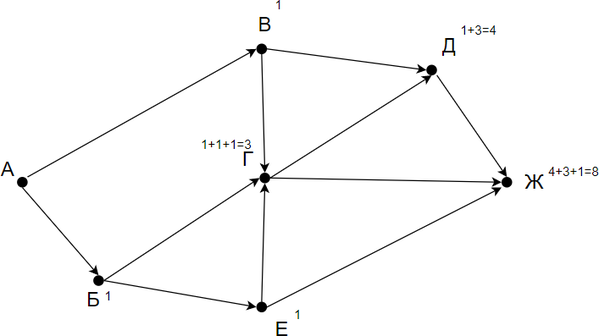
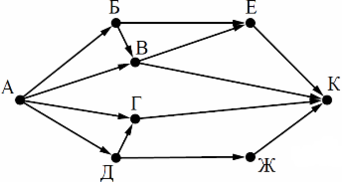
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е?
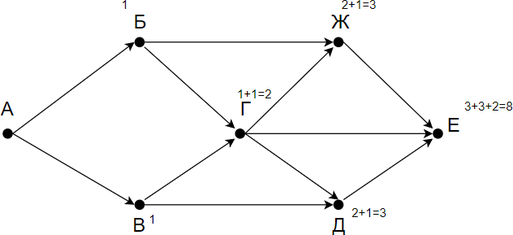
Заметим, что количество путей в город Е является суммой путей в города Ж, Г и Д. Количество путей в город Ж — сумма путей в города Г и Б. Таким образом получаем:
Г = Б + В
Д = Г + В
Ж = Б + Г
Е = Ж + Г + Д
Заметим, что в пункты Б и В можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
Ответ: 8
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Заметим, что количество путей в город Ж является суммой путей в города Д, Г и Е. Количество путей в город Г — сумма путей в город В, Б и Е. Таким образом получаем:
Г = Б + В + Е
Д = В + Г
Ж = Д + Г + Е
Заметим, что в пункты Б, В и Е можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
Ответ: 8
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, D.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 7 км.
A—D—B—C—E: длина маршрута 9 км.
A—D—C—E: длина маршрута 6 км.
Самый короткий путь: A—D—C—E. Длина маршрута 6 км.
Ответ: 6
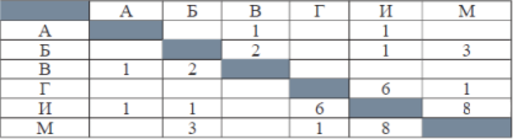
Геральт спешит выручить Цири из плена Кагыра. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого короткого участка кратчайшего пути от Геральта до Цири (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице:
Найдём все варианты маршрутов из И в М и выберем самый короткий.
Из пункта И можно попасть в пункты А, Б, Г, М.
Из пункта Г можно попасть в пункты И, М.
Из пункта В можно попасть в пункты А, Б.
Из пункта Б можно попасть в пункты В, И, М.
И—А—В—Б—М: длина маршрута 7 км.
И—Б—М: длина маршрута 4 км.
И—Г—М: длина маршрута 7 км.
И—М: длина маршрута 8 км.
Самый короткий путь: И—Б—М. Длина маршрута 4 км. Самый короткий участок этого пути равен 1 км.
Ответ: 1
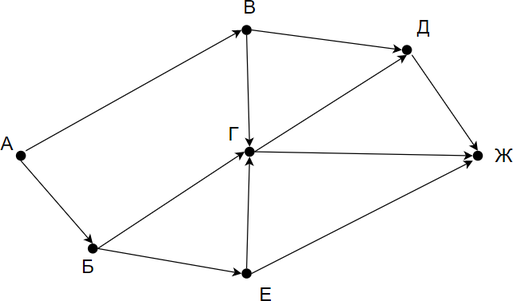
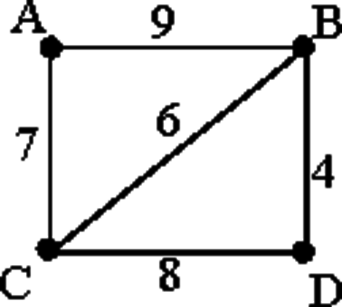
На схеме нарисованы дороги между четырьмя населёнными пунктами A, B, C, D и указаны протяжённости данных дорог.
Определите, какие два пункта наиболее удалены друг от друга (при условии, что передвигаться можно только по указанным на схеме дорогам). В ответе укажите кратчайшее расстояние между этими пунктами.
Заметим, что наиболее удалены друг от друга пункты A и D. Найдём все варианты маршрутов из A в D и выберем самый короткий.
A—B—D: длина маршрута 13 км.
A—C—D: длина маршрута 15 км.
A—B—C—D: длина маршрута 23 км.
A—C—B—D: длина маршрута 17 км.
Заметим, что кратчайшее расстояние между пунктами A и D равняется 13.
Ответ: 13
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, В, Г или Ж, поэтому N = NК = NЕ + NВ + N Г + NЖ (*).
Аналогично:
NЕ = NБ + NВ = 1 + 2 = 3;
NЖ = NД = 1;
NВ = NА + NБ = 1 + 1 = 2;
NГ = NА + NД = 1 + 1 = 2;
NД = NА = 1;
NБ = NА = 1.
Подставим в формулу (*): N = 3 + 2 + 2 + 1 = 8.
Ответ: 8
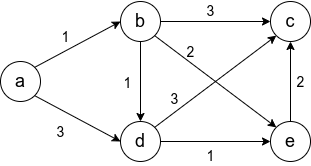
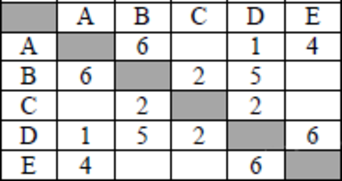
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами B и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Проанализируем некоторые возможные маршруты.
Маршрут B—D—E, длина 11 км.
Маршрут B—C—D—E, длина 10 км.
Маршрут B—С—D—A—E, длина 9 км.
Любые другие маршруты будут длиннее маршрута B—С—D—A—E. Самый короткий путь: B—С—D—A—E. Длина маршрута 9 км.
Ответ: 9

УСТАЛ? Просто отдохни