Алгоритм Дейкстры лежит в основе многих востребованных современных сервисов, к числу которых относятся GPS навигация и маршрутизация состояния канала сетевого уровня. Используя некоторые базовые структуры данных, мы разберемся, что именно он делает, каким образом достигает цель и как реализовать алгоритм в Python.
Что делает алгоритм Дейкстры
Алгоритм Дейкстры находит кратчайший путь между двумя вершинами графа. Следовательно, если математические задачи моделируется при помощи графа, используя алгоритм Дейкстры, можно найти кратчайший путь между вершинами.
Создание графа для алгоритмы Дейкстры
Важно понимать, граф представляет собой множество узлов (nodes), соединенных ребрами (edges).
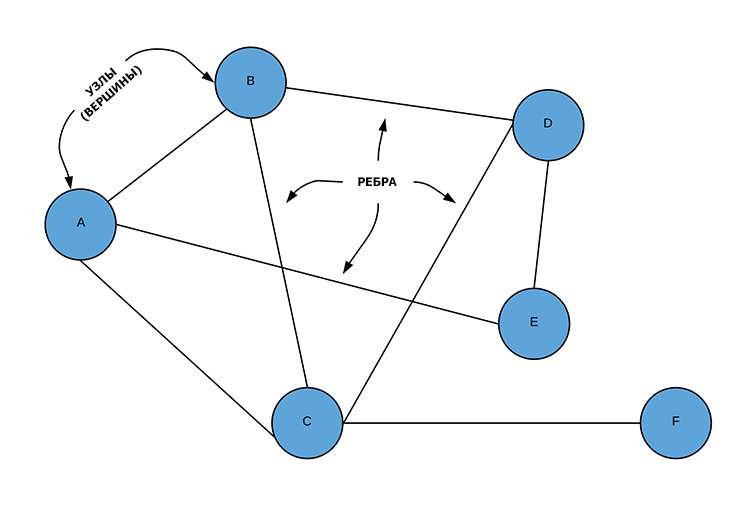
Узел — это просто какой-то объект, а ребро — это связь между двумя узлами. Выше представлен неориентированный граф, то есть без четких направлений, и здешние ребра являются двунаправленными. Существуют также ориентированные графы, у ребер которых есть конкретно указанное направление.
Как узлы, так и ребра могут быть носителями информации. К примеру, граф выше представляет собой систему зданий, которые соединены между собой туннелями. В узлах может находиться информация о названии здания (например, строка «Библиотека»), в то время, как ребро может содержать информацию о длине туннеля.
Есть вопросы по Python?
На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!
Telegram Чат & Канал
Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!
Паблик VK
Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!
Графам можно найти удачное применение в огромном количестве востребованных областей: веб-страницы (узлы) с ссылками на другие страницы (ребра), маршрутизация пакетов в сетях, социальные сети, приложения для создания карт улиц, моделирование молекулярных связей, различные области математики, лингвистика, социология. В общем и целом, это может быть любая система, в которой оперируют связанные между собой объекты.
Данный этап немного выходит за рамки темы, рассматриваемой в статье, поэтому мы не будем вдаваться в подробности. Два самых популярных способа реализации графа — через матрицу смежности или через список смежности. У каждого метода есть свои преимущества и недостатки. Сначала рассмотрим реализацию через матрицу смежности, так как его проще представить визуально и понять на интуитивном уровне. Позже станет яснее, отчего определение базовой реализации оказывает сильное влияние на время выполнения. Любая реализация может задействовать алгоритм Дейкстры, а пока важно различать API, или абстракции (методы), которые могут взаимодействовать с графом. Кратко осветим реализацию матрицы смежности на примере кода Python. Для ознакомления с реализацией списка смежности хорошим стартом станет данная статья.
Ниже представлена матрица смежности для предыдущего графа. Каждый ряд представляет один узел графа, как и каждый столбец. В данном случае ряд 0 и столбец 0 представляют узел «А»; ряд 1 и столбец 1 — узел «B», ряд 2 и столбец 2 — узел «C» и так далее, принцип понятен. Каждый локальный элемент {ряд, столбец} представляет ребро. Таким образом, каждый ряд показывает связь между одним узлом и всеми прочими узлами. Элемент «0» указывает на отсутствие ребра, в то время как «1» указывает на присутствие ребра, связывающего row_node и column_node в направлении row_node → column_node. Поскольку граф в примере является неориентированным, данная матрица равна его транспонированию (то есть матрица симметричная), поскольку каждая связь двунаправленная. Вы могли заметить, что главная диагональ матрицы представлена только нулями, а все оттого, что ни один узел не связан сам с собой. Таким образом, пространственная сложность данного представления нерасчетлива.
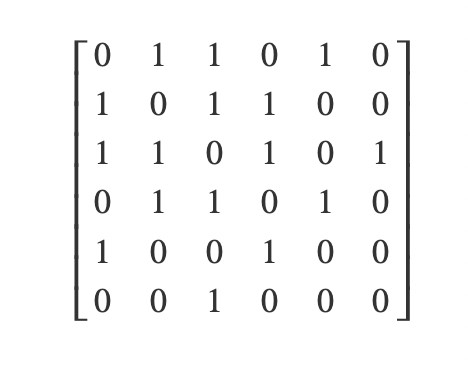
Теперь разберемся с кодом. Обратите внимание, что здесь задействовано немного экстра-данных — так как нам было нужно, чтобы реальные объекты узлов содержали определенную информацию, в классе Graph был реализован массив объектов узлов, индексы которых соответствуют номеру их ряда (столбца) в матрице смежности. В Graph также был добавлен вспомогательный метод, который позволяет использовать либо номера индекса узла, либо объект узда в качестве аргументов для методов класса Graph. Данные классы нельзя считать примерами элегантности, однако они хорошо выполняют свою работу, излишне не усложняя процесс:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
class Node: def __init__(self, data, indexloc = None): self.data = data self.index = indexloc class Graph: @classmethod def create_from_nodes(self, nodes): return Graph(len(nodes), len(nodes), nodes) def __init__(self, row, col, nodes = None): # установка матрица смежности self.adj_mat = [[0] * col for _ in range(row)] self.nodes = nodes for i in range(len(self.nodes)): self.nodes[i].index = i # Связывает node1 с node2 # Обратите внимание, что ряд – источник, а столбец – назначение # Обновлен для поддержки взвешенных ребер (поддержка алгоритма Дейкстры) def connect_dir(self, node1, node2, weight = 1): node1, node2 = self.get_index_from_node(node1), self.get_index_from_node(node2) self.adj_mat[node1][node2] = weight # Опциональный весовой аргумент для поддержки алгоритма Дейкстры def connect(self, node1, node2, weight = 1): self.connect_dir(node1, node2, weight) self.connect_dir(node2, node1, weight) # Получает ряд узла, отметить ненулевые объекты с их узлами в массиве self.nodes # Выбирает любые ненулевые элементы, оставляя массив узлов # которые являются connections_to (для ориентированного графа) # Возвращает значение: массив кортежей (узел, вес) def connections_from(self, node): node = self.get_index_from_node(node) return [(self.nodes[col_num], self.adj_mat[node][col_num]) for col_num in range(len(self.adj_mat[node])) if self.adj_mat[node][col_num] != 0] # Проводит матрицу к столбцу узлов # Проводит любые ненулевые элементы узлу данного индекса ряда # Выбирает только ненулевые элементы # Обратите внимание, что для неориентированного графа # используется connections_to ИЛИ connections_from # Возвращает значение: массив кортежей (узел, вес) def connections_to(self, node): node = self.get_index_from_node(node) column = [row[node] for row in self.adj_mat] return [(self.nodes[row_num], column[row_num]) for row_num in range(len(column)) if column[row_num] != 0] def print_adj_mat(self): for row in self.adj_mat: print(row) def node(self, index): return self.nodes[index] def remove_conn(self, node1, node2): self.remove_conn_dir(node1, node2) self.remove_conn_dir(node2, node1) # Убирает связь в направленной манере (nod1 к node2) # Может принять номер индекса ИЛИ объект узла def remove_conn_dir(self, node1, node2): node1, node2 = self.get_index_from_node(node1), self.get_index_from_node(node2) self.adj_mat[node1][node2] = 0 # Может пройти от node1 к node2 def can_traverse_dir(self, node1, node2): node1, node2 = self.get_index_from_node(node1), self.get_index_from_node(node2) return self.adj_mat[node1][node2] != 0 def has_conn(self, node1, node2): return self.can_traverse_dir(node1, node2) or self.can_traverse_dir(node2, node1) def add_node(self,node): self.nodes.append(node) node.index = len(self.nodes) – 1 for row in self.adj_mat: row.append(0) self.adj_mat.append([0] * (len(self.adj_mat) + 1)) # Получает вес, представленный перемещением от n1 # к n2. Принимает номера индексов ИЛИ объекты узлов def get_weight(self, n1, n2): node1, node2 = self.get_index_from_node(n1), self.get_index_from_node(n2) return self.adj_mat[node1][node2] # Разрешает проводить узлы ИЛИ индексы узлов def get_index_from_node(self, node): if not isinstance(node, Node) and not isinstance(node, int): raise ValueError(“node must be an integer or a Node object”) if isinstance(node, int): return node else: return node.index |
Здесь классы Node и Graph будут использованы для описания данного примера графа. Поместим вышеуказанный граф в код и посмотрим, получится ли в итоге верная матрица смежности:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
a = Node(“A”) b = Node(“B”) c = Node(“C”) d = Node(“D”) e = Node(“E”) f = Node(“F”) graph = Graph.create_from_nodes([a,b,c,d,e,f]) graph.connect(a, b) graph.connect(a, c) graph.connect(a, e) graph.connect(b, c) graph.connect(b, d) graph.connect(c, d) graph.connect(c, f) graph.connect(d, e) graph.print_adj_mat() |
Матрицы смежности, полученная в выводе (из graph.print_adj_mat()) после запуска кода, такая же, как и та, что была рассчитана ранее:
|
[0, 1, 1, 0, 1, 0] [1, 0, 1, 1, 0, 0] [1, 1, 0, 1, 0, 1] [0, 1, 1, 0, 1, 0] [1, 0, 0, 1, 0, 0] [0, 0, 1, 0, 0, 0] |
При желании добавить расстояние ребрам графа нужно просто заменить единицы в данной матрице смежности на значения нужного расстояния. На данный момент класс Graph поддерживает данную функциональность, доказательством чему является код ниже. Для ясности демонстрации были добавлены произвольные значения длины:
|
w_graph = Graph.create_from_nodes([a,b,c,d,e,f]) w_graph.connect(a, b, 5) w_graph.connect(a, c, 10) w_graph.connect(a, e, 2) w_graph.connect(b, c, 2) w_graph.connect(b, d, 4) w_graph.connect(c, d, 7) w_graph.connect(c, f, 10) w_graph.connect(d, e, 3) w_graph.print_adj_mat() |
В результате выводится следующая матрица смежности:
|
[0 , 5 , 10, 0, 2, 0] [5 , 0 , 2 , 4 , 0 , 0] [10, 2, 0, 7, 0, 10] [0 , 4 , 7 , 0 , 3 , 0] [2 , 0 , 0 , 3 , 0 , 0] [0, 0 , 10, 0 , 0 , 0] |
Визуально данный граф будет представлен следующим образом:
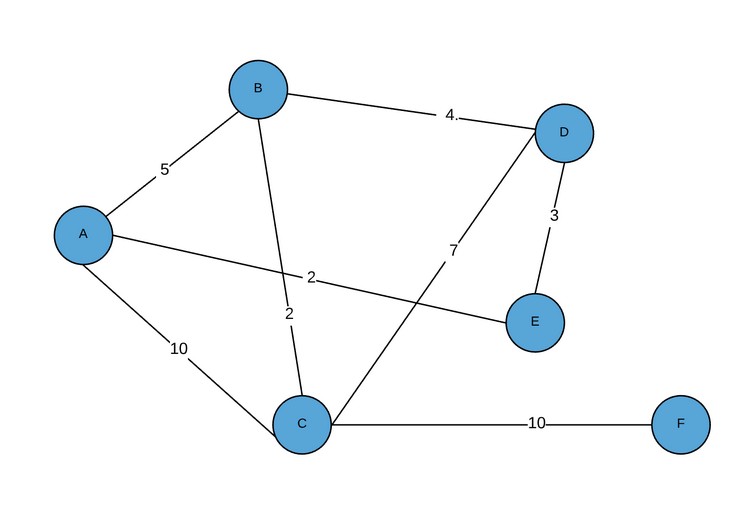
Для того чтобы ребра содержали больше информации, нужно чтобы матрица содержала объекты ребер вместо простых целых чисел.
Алгоритм Дейкстры
Перед непосредственным составлением кода, осветим ключевые моменты темы:
- Главное условие: отрицательных длин ребер не бывает.
- Алгоритм Дейкстры изначально создавался для поиска кратчайшего пути между двумя конкретными узлами. Однако сегодня он также широко используется для поиска кратчайших путей между узлом источника и всеми остальными узлами. В статье будет рассмотрен второй вариант. Для осуществления первого случая понадобится просто остановить алгоритм сразу после того, как узел назначения будет добавлен в набор
seen. По ходу дела все станет намного понятнее.
Окей, примемся за дело. Нам нужно найти исходным узлом и всеми другими узлами (или узлом назначения), однако проверять КАЖДУЮ возможную комбинацию отправления-назначения не хочется. При наличии крупного графа на это потребуется огромное количество времени, и большая часть проверенных путей в конечном итоге окажется ненужной. По этой причине, пойдем напролом и задействуем жадный подход. Наслаждайтесь моментом, ведь это тот редкий случай, когда жадность будет вознаграждена.
Итак, что мы понимаем под жадным алгоритмом? По сути, это значит, что принятые решения будут обусловлены самым оптимальным выбором на данный конкретный момент времени. Метод подойдет далеко не для каждого случая. К примеру, при реализации шахматного бота фокус точно не пройдет — зачем брать враждебного ферзя, если через ход это обернется шахом со стороны противника. Для таких ситуаций больше подойдет minimax. В рассматриваемом сейчас случае жадный алгоритм действительно является наилучшим вариантом, который значительно сокращает число проверок, что нужно совершить без потери точности. Как?
Скажем, мы находимся в исходном узле. Предположим, что начальное предварительное расстояние от узла источника до каждого другого узла в графе является бесконечностью (перепроверим позже). Известно, что по умолчанию расстояние от узла источника до этого же узла источника минимально (0), ведь отрицательных длин ребер быть не может. Наш исходный узел осматривает все соседние узлы и обновляет предварительное расстояние от узла источника до длины ребра от узла источника до конкретного соседнего элемента (плюс 0). Обратите внимание, что НУЖНО проверить каждого ближайшего соседа, этого никак не пропустить. Затем алгоритм делает тот самый жадный выбор для следующей оценки узла, который находится на ближайшем расстоянии к источнику. У нас исходный узел отмечен как visited, поэтому к нему можно не возвращаться и сразу перейти к следующему узлу.
Теперь задумаемся, где мы сейчас находимся в плане логики, так как это важно для реализации. Узел, что сейчас оценивается (ближайший к источнику) больше НИКОГДА не будет оцениваться вновь в плане кратчайшего пути от исходного узла. Его предварительное расстояние теперь стало точным расстоянием. Хотя вполне возможно, что пути от исходного узла к данному узлу могут проходить через иные маршруты, можно с уверенностью сказать, что они будут затратнее, нежели текущий путь. Он был выбран ввиду того, что был кратчайшим по сравнению с любым другим узлом, связанным с источником. Следовательно, любой другой путь будет длиннее, чем текущее расстояние от исходного узла до рассматриваемого узла.
При использовании графика из примера в случае установки исходного узла как А, мы бы назначили предварительные расстояния для узлов B, C и E. Поскольку у E было кратчайшее расстояние от A, после этого был посещен узел E. И теперь, хотя наверняка есть несколько других способов добраться из А до Е, они будут затратнее, нежели текущее расстояние А → Е. Другие маршруты должны проходить через B или С, а в результате проверки стало ясно, что они дальше от A, чем E. Жадный выбор был сделан, а это ограничивает общее количество проверок, которые нам нужно сделать, и при этом точность не теряется. Неплохо.
Продолжим логическую цепочку с использованием графа из примера. Просто повторим для E действия, сделанные для A. Обновляются все ближайшие соседние элементы к E с предварительным расстоянием, равным length(A у E) + edge_length(E к соседнему элементу). Это верно в том случае, ЕСЛИ данное расстояние меньше, чем текущее предварительное расстояние, или же предварительное расстояние еще не было установлено.
Обратите внимание: Для достижения данной функциональности здесь просто инициализируются все предварительные расстояния до бесконечности.
Далее делается жадный выбор касательно того, какой узел должен оцениваться следующим. Выбирается один узел из графа с наименьшим предварительным расстоянием, и добавляется E к набору seen nodes. Теперь он повторно оцениваться не будет. У данного нового узла та же гарантия, что что и E — его предварительное расстояние от A является определенным минимальным расстоянием от A. Чтобы понять это, давайте оценим возможности (хотя они могут не соответствовать графу примера, для ясности используем те же названия). Если следующий узел является соседом E, но не A, то он будет выбран, потому что его временное расстояние все еще короче, чем любого другого прямого соседа A. По этой причине нет другого возможного кратчайшего пути, только через E. Если следующий выбранный узел будет непосредственным соседом A, то есть вероятность, что этот узел обеспечит более короткий путь к некоторым из соседей E, чем сам E.
Обзор кода алгоритма Дейкстры на Python
Давайте более четко и формально рассмотрим процесс реализации алгоритма Дейкстры.
ИНИЦИАЛИЗАЦИЯ
- Установите
provisional_distanceдля всех узлов от исходного узла до бесконечности. - Определите пустой набор
seen_nodes. Данный набор гарантирует, что узел, у которого уже есть кратчайший путь, не будет повторно рассмотрен, а также то, что не будут рассматриваться пути через узел, у которого более короткий путь к источнику, чем текущий путь. Помните, что узлы входят вseen_nodesтолько после доказательства того, что в наличии есть абсолютное кратчайшее расстояние (а не только предварительное расстояние). Набор используется для получения времени поискаO(1)вместо многократного выполнения поиска через массивO(n). - Установите
provisional_distanceдля исходного узла со значением 0, и массив, представляющий перескоки для простого включения самого исходного кода. Это будет полезно позже, когда мы проследим выбранный для графа путь для расчета минимального расстояния.
ПРОЦЕДУРА ИТЕРАЦИИ
- Пока (while) все узлы увидеть (
seen) не удалось. Или, в случае поиска одного узла назначения, пока не удалось увидеть (seen) данный узел назначения. - Установите
current_nodeдля узла c самым малым предварительным расстояниемprovisional_distanceво всем графе. Обратите внимание, что для первой итерации это будет исходный узелsource_node, так как предварительное расстояниеprovisional_distanceустановлено на 0. - Добавьте текущий узел
current_nodeк набору просмотренных узловseen_nodes. - Обновите
provisional_distanceкаждого соседнего элементаcurrent_nodeдо (абсолютного) расстояния отcurrent_nodeдоsource_nodeвдобавок к длине ребра отcurrent_nodeк данному соседнему элементу, ЕСЛИ данное значение меньше, чем текущее значение соседнегоprovisional_distance. Если у соседнего элемента еще не было набора предварительного расстояния, помните, что он инициализирован до бесконечности, и по этой причине должен быть больше, чем данная сумма. При обновленииprovisional_distanceтакже обновляются «перескоки», которые были сделаны для получения расстояния, задействуя конкатенацию перескоковcurrent_nodeк исходному узлу с самимcurrent_node. - Завершение цикла while.
Алгоритм Дейкстры через схемы и изображения
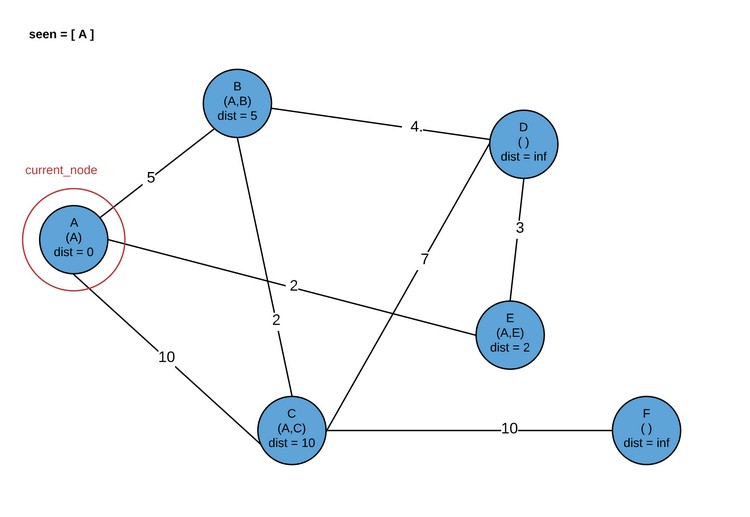
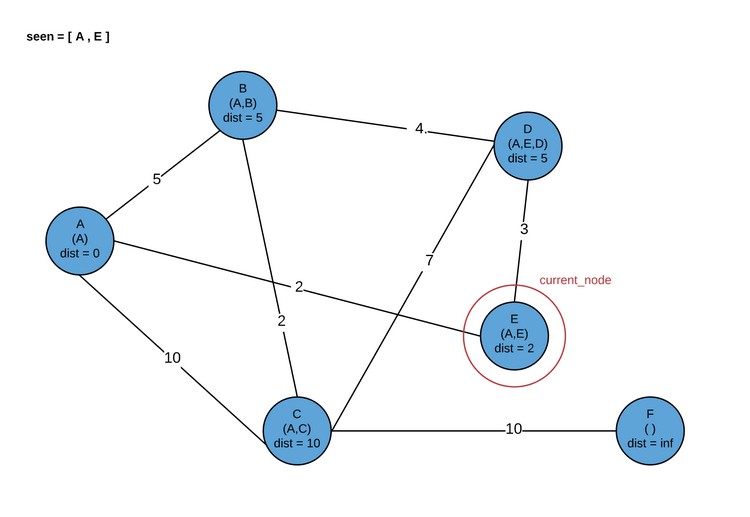
Обратите внимание, что в дальнейшем можно посетить либо D, либо B. Сейчас мы посетим B.
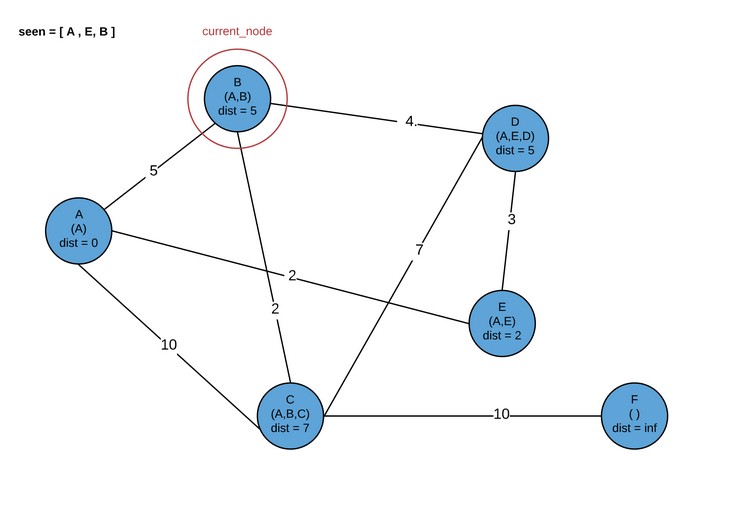
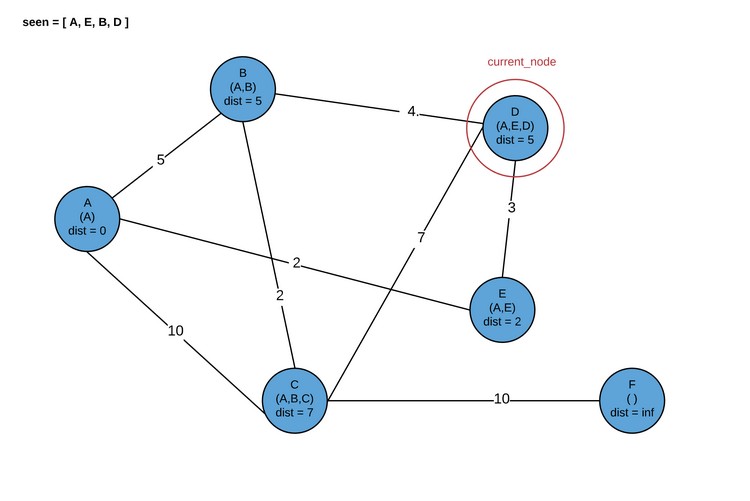
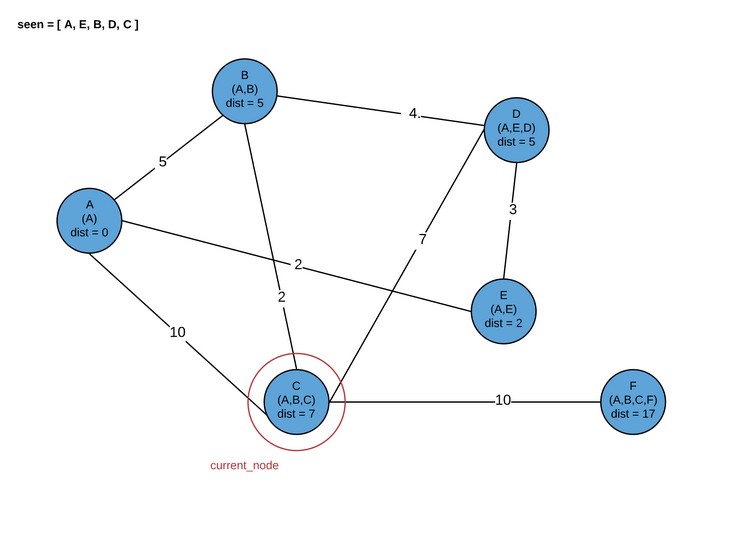
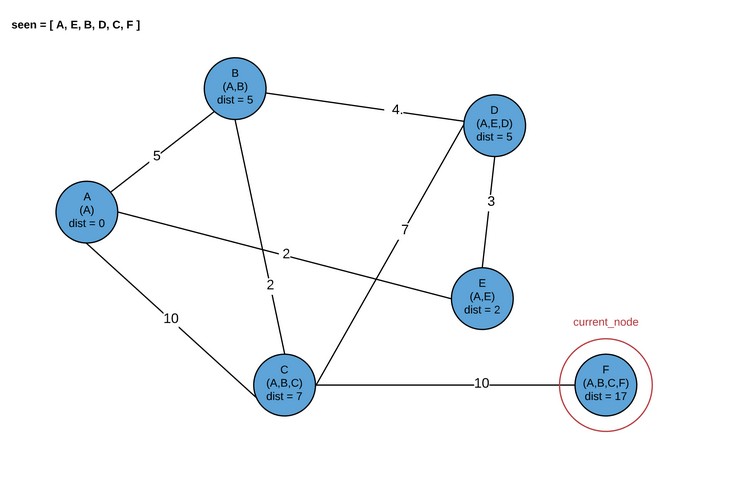
Здесь программа завершается. В результате мы получаем кратчайшие пути для каждого узла графа.
Python код для алгоритма Дейкстры
Посмотрим, как будет выглядеть реализация алгоритма Дейстры в Python. Это экземпляр метода внутри раннее используемого класса Graph, который задействует преимущества других методов и структуры:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
def dijkstra(self, node): # Получает индекс узла (или поддерживает передачу int) nodenum = self.get_index_from_node(node) # Заставляет массив отслеживать расстояние от одного до любого узла # в self.nodes. Инициализирует до бесконечности для всех узлов, кроме # начального узла, сохраняет “путь”, связанный с расстоянием. # Индекс 0 = расстояние, индекс 1 = перескоки узла dist = [None] * len(self.nodes) for i in range(len(dist)): dist[i] = [float(“inf”)] dist[i].append([self.nodes[nodenum]]) dist[nodenum][0] = 0 # Добавляет в очередь все узлы графа # Отмечает целые числа в очереди, соответствующие индексам узла # локаций в массиве self.nodes queue = [i for i in range(len(self.nodes))] # Набор увиденных на данный момент номеров seen = set() while len(queue) > 0: # Получает узел в очереди, который еще не был рассмотрен # и который находится на кратчайшем расстоянии от источника min_dist = float(“inf”) min_node = None for n in queue: if dist[n][0] < min_dist and n not in seen: min_dist = dist[n][0] min_node = n # Добавляет мин. расстояние узла до увиденного, убирает очередь queue.remove(min_node) seen.add(min_node) # Получает все следующие перескоки connections = self.connections_from(min_node) # Для каждой связи обновляет путь и полное расстояние от # исходного узла, если полное расстояние меньше # чем текущее расстояние в массиве dist for (node, weight) in connections: tot_dist = weight + min_dist if tot_dist < dist[node.index][0]: dist[node.index][0] = tot_dist dist[node.index][1] = list(dist[min_node][1]) dist[node.index][1].append(node) return dist |
При использовании данного метода можно протестировать нашу картинку:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
a = Node(“A”) b = Node(“B”) c = Node(“C”) d = Node(“D”) e = Node(“E”) f = Node(“F”) w_graph = Graph.create_from_nodes([a,b,c,d,e,f]) w_graph.connect(a,b,5) w_graph.connect(a,c,10) w_graph.connect(a,e,2) w_graph.connect(b,c,2) w_graph.connect(b,d,4) w_graph.connect(c,d,7) w_graph.connect(c,f,10) w_graph.connect(d,e,3) print([(weight, [n.data for n in node]) for (weight, node) in w_graph.dijkstra(a)]) |
Для получения читабельного для людей вывода нужно отметить объекты узла в их data. Результат станет следующим:
|
[(0, [‘A’]), (5, [‘A’, ‘B’]), (7, [‘A’, ‘B’, ‘C’]), (5, [‘A’, ‘E’, ‘D’]), (2, [‘A’, ‘E’]), (17, [‘A’, ‘B’, ‘C’, ‘F’])] |
Здесь каждый кортеж — (total_distance, [hop_path]). Это совпадает с рассматриваемой картинкой.
Быстрый способ реализации алгоритма Дейкстры в Python
На данный момент тем, кто заинтересован только в функциональности, хватит предоставленного материала. Однако, тем, кому важна скорость стоит продолжить чтение.
Остановимся на одном довольно важном моменте. В каждой итерации нам нужно найти узел с кратчайшим предварительным расстоянием, что требуется для следующего жадного решения. Сейчас осматривается list, вызывая queue (используя данные значения в dist) с целью получения желаемого. У данного queue может быть максимальная длина n, что является числом узлов. Итерация по этому списку является операцией O(n), которую мы выполняем в каждой итерации цикла while. Так как цикл while продолжается до тех пор, пока не будет просмотрен (seen) каждый узел, сейчас операция O(n) совершается n раз. Наш алгоритм — O(n2). Это не очень хорошо, но и это не все.
Если взглянуть на реализацию матрицы смежности в Graph, можно заметить, что для нахождения связи нам пришлось осмотреть весь ряд (размера n). Это еще одна операция O(n) в цикле while. Как это исправить? Во-первых, можно использовать кучу для получения минимального предварительного расстояния в O(lg(n)) времени вместо O(n) времени (при бинарной куче — отметьте, что куча Фибоначчи способна на это в O(1)). Во-вторых, можно реализовать граф при помощи списка смежности, где у каждого узла есть список связанных узлов. Получается, что осматривать все узлы на наличие существующей связи не потребуется. Это показывает, почему важно понимать то, как мы представляем структуры данных. В случае реализаци кучи при помощи представления матрицы смежности асимптомическое время выполнения запуска алгоритма изменено не будет. (На заметку: Если вам не знакома нотация big-O, можете просмотреть данную статью).
Кучи в Python
Такая структура данных, как куча, обычно используется для реализации очереди с приоритетом. По сути, они эффективны во время ситуаций, когда нужно быстро получить элемент с наивысшим приоритетом. В нашем случае элемент с высоким приоритетом — это наименьшее предварительное расстояние (provisional distance) от оставшихся нерассмотренных узлов. Вместо того, чтобы каждый раз осматривать весь массив в поисках наименьшего предварительного расстояния (provisional distance), можно использовать находящуюся там кучу, что готова передать узел с наименьшим предварительным расстоянием (provisional distance). Как только расстояние будет извлечено из кучи, она быстро перестоится, будучи готовой к передаче нового значения в тот момент, когда оно будет нужно. Довольно неплохо! Для практики можете попробовать реализовать очень быструю Фибоначчиеву кучу. А далее мы попробуем реализовать Binary MinHeap, что поможет разрешить наши задачи.
По сути бинарная куча является полным бинарным деревом, что обладает свойством кучи. Что это значит?
Полное бинарное дерево — это структура в виде дерева данных, где у КАЖДОГО родителя узла есть ровно два дочерних узла. Если дочерних узлов недостаточно, чтобы в последнем ряду родительских узлов было по 2 дочерних узла, дочерние узлы будут заполняться слева направо.
Как это будет выглядеть?
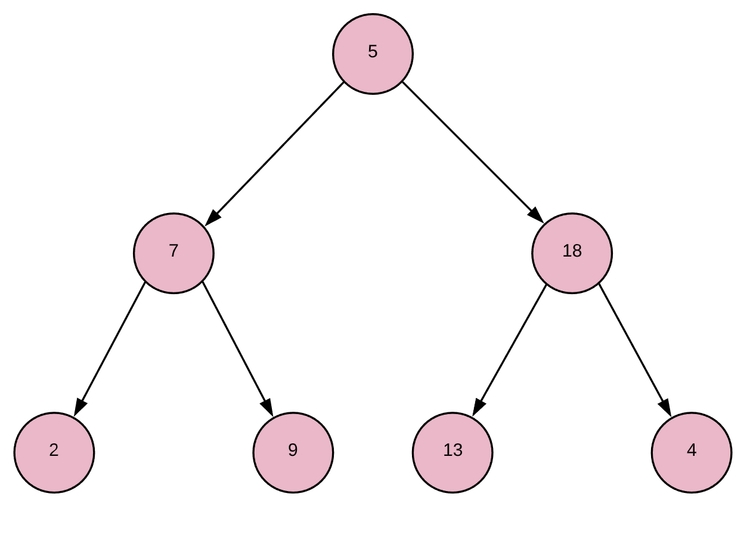
Свойство кучи (для минимальной кучи) Каждый родитель ДОЛЖЕН быть меньше или равен обоим дочерним элементам.
Применив данный принцип к указанному выше полному бинарному дереву, мы получим следующий результат:
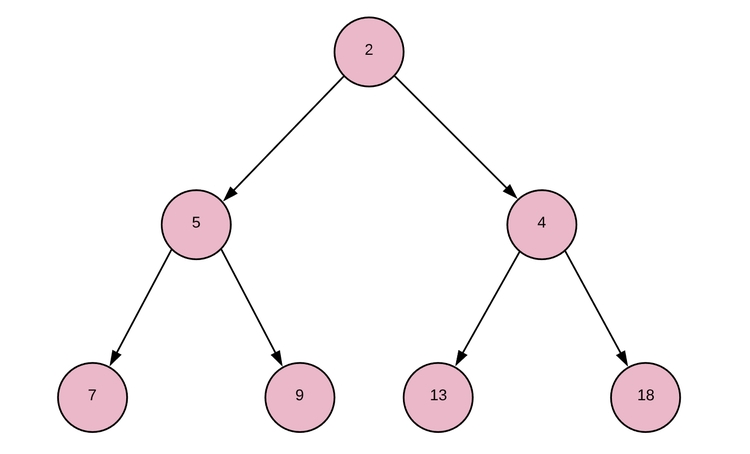
Здесь представлен базовый массив [2, 5, 4, 7, 9, 13, 18]. Как видите, сортировка сделана наполовину, но в данном случае нам и не нужна полная сортировка. Через минуту данный базовый массив станет намного понятнее.
Теперь у нас есть представление о том, что из себя представлят куча. Напишем код и посмотрим, как используются дополнительные методы для реализации требуемых пользователю действий.
Так как бинарная куча является специальной реализацией бинарного дерева, начнем с создания класса BinaryTree, у которого будет наследовать рассматриваемая куча. Для реализации бинарного дерева нужно создать базовую структуру данных в виде массива, после чего структура дерева будет рассчитана через индексы узлов внутри массива. К примеру, у начального бинарного дерева (первое изображение полного бинарного дерева) базовый массив будет [5, 7, 18, 2, 9, 13, 4]. Мы обозначим связи между узлами при определении индекса узла в базовом массиве. Известно, что у каждого родителя ровно два дочерних элемента. Нулевой индекс является корнем в основе, индекс 1 — левый ребенок, а индекс 2 — правый ребенок. Если обобщить, левый ребенок индекса i будет обладать индексом 2*i + 1, а правый — 2*i + 2. У узла индекса i родительский индекс — floor((i-1) / 2).
Итак, класс BinaryTree будет выглядеть следующим образом:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
class BinaryTree: def __init__(self, nodes = []): self.nodes = nodes def root(self): return self.nodes[0] def iparent(self, i): return (i – 1) // 2 def ileft(self, i): return 2*i + 1 def iright(self, i): return 2*i + 2 def left(self, i): return self.node_at_index(self.ileft(i)) def right(self, i): return self.node_at_index(self.iright(i)) def parent(self, i): return self.node_at_index(self.iparent(i)) def node_at_index(self, i): return self.nodes[i] def size(self): return len(self.nodes) |
Теперь MinHeap может наследовать BinaryTree и задействовать требуемую функциональность. Теперь BinaryTree можно будет вновь использовать в иных контекстах.
Окей, мы практически у финала. Сейчас нужно будет идентифицировать способности класса, который должны быть у класса MinHeap, а затем реализовать их. Необходимо, чтобы куча могла:
- Измениться, вместо неупорядученного бинарного дерева став минимальной кучей. Это делается через конкретизацию кучи;
- Получите минимальное значение, а затем реструктурироваться для сохранения своих свойств. Это будет использоваться при посещении следующего узла;
- Обновить (уменьшить) значение узла, сохранив свойство кучи. Это будет использоваться при обновлении предварительных расстояний.
Для осуществления данных условий начнем с создания блока, который сыграет важную роль при реализации первых двух функций. Напишем метод под названием min_heapify_subtree. Данный метод будет рассматривать всю кучу как heapified (то есть при этом поддерживая свойство кучи), кроме единственного узла 3-го поддерева. Мы будем рекурсивно накапливать это поддерево, идентифицируя его индекс родительского узла в точке i и давая возможность правильно размещенному узлу найти верную позицию в куче. Для этого проверяем, меньше ли дочерние узлы, чем родительский. Если да, заменяем наименьший дочерний узел с родительским. Затем рекурсивно вызываем метод по индексу замененного родителя (который теперь является дочерним), чтобы убедиться, что он помещен в позицию для поддержки свойства кучи. Вот псевдокод:
|
FUNCTION min_heapify_subtree(i) index_of_min = i IF left_child exists AND left_child < node[index_of_min] index_of_min = left_child_index ENDIF IF right_child exists AND right_child < node[index_of_min] index_of_min = right_child_index ENDIF IF index_of_min != i swap(nodes[i], nodes[index_of_min]) min_heapify_subtree(index_of_min) ENDIF END |
В худшем случае метод начинается с индекса 0 и рекурсивно распространит корневой узел вплоть до нижнего листа. Поскольку здесь куча является бинарным деревом, у нас есть уровни lg(n), где n — общее количество узлов. Поскольку каждая рекурсия метода выполняет фиксированное количество операций, то есть O(1), классификация времени выполнения min_heapify_subtree — O(lg (n)).
Для превращения совершенно случайного массива в правильную кучу, просто нужно вызвать min_heapify_subtree на каждом узле, начиная с нижних листьев. Задействуем метод min_heapify:
|
FUNCTION min_heapify FOR index from last_index to first_index min_heapify_subtree(index) ENDFOR END |
Данный метод выполняет метод O(lg(n)) n раз, поэтому его время выполнения будет O(n*lg(n)).
Нам нужно извлечь минимальное значение из кучи. Значение можно принять время за O(1), потому что оно всегда будет корневым узлом минимальной кучи (т.е. индекс 0 базового массива), но просто прочитать недостаточно. Требуется удаление, А ТАКЖЕ подтверждение того, что куча остается нагроможденной. Для этого удаляем корневой узел и заменяем его последним листом, а затем min_heapify_subtree индексом 0, чтобы обеспечить сохранение свойства кучи:
|
FUNCTION pop min_node = nodes[0] IF heap_size > 1 nodes[0] = nodes[nodes.length – 1] nodes.pop() // remove the last element from our nodes array min_heapify_subtree(0) ELSE IF heap_size == 1 nodes.pop() ELSE return NIL // the heap is empty, so return NIL value ENDIF return min_node END |
Метод выполняется за постоянное время, за исключением min_heapify_subtree. Можно сказать, что этот метод также O(lg (n)).
Отлично! На последнем этапе нужно будет добиться получения возможности обновления значний кучи (уменьшать их, поскольку обновляются предварительные расстояния (provisional distance) до более низких значений), сохраняя свойство кучи.
Итак, создадим метод под названием decrease_key, который принимает значение индекса обновляемого узла и новое значение. Мы хотим обновить значение этого узла, а затем добавить его туда, где он должен будет находиться, если станет меньше родителя. Таким образом, пока он не станет меньше родительского узла, поменяем его на родительский узел:
|
FUNCTION decrease_key(index, value) nodes[index] = value parent_node_index = parent_index(index) WHILE index != 0 AND nodes[parent_node_index] > nodes[index] swap(nodes[i], nodes[parent_node_index]) index = parent_node_index parent_node_index = parent_index(index) ENDWHILE END |
Окей, посмотрим, как все вышеперечисленное будет выглядеть в виде кода на Python:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
class MinHeap(BinaryTree): def __init__(self, nodes): BinaryTree.__init__(self, nodes) self.min_heapify() # Преобразует в кучу узлы, рассматривая, что все поддеревья уже кучи def min_heapify_subtree(self, i): size = self.size() ileft = self.ileft(i) iright = self.iright(i) imin = i if( ileft < size and self.nodes[ileft] < self.nodes[imin]): imin = ileft if( iright < size and self.nodes[iright] < self.nodes[imin]): imin = iright if( imin != i): self.nodes[i], self.nodes[imin] = self.nodes[imin], self.nodes[i] self.min_heapify_subtree(imin) # Преобразует в кучу массив, который ей не является def min_heapify(self): for i in range(len(self.nodes), –1, –1): self.min_heapify_subtree(i) def min(self): return self.nodes[0] def pop(self): min = self.nodes[0] if self.size() > 1: self.nodes[0] = self.nodes[–1] self.nodes.pop() self.min_heapify_subtree(0) elif self.size() == 1: self.nodes.pop() else: return None return min # Обновляет значение узла, изменяя его для сохранения свойства кучи def decrease_key(self, i, val): self.nodes[i] = val iparent = self.iparent(i) while( i != 0 and self.nodes[iparent] > self.nodes[i]): self.nodes[iparent], self.nodes[i] = self.nodes[i], self.nodes[iparent] i = iparent iparent = self.iparent(i) if i > 0 else None |
Хорошо, время для последнего шага. Теперь уже точно! Нам просто нужно выяснить, как внедрить структуру данных MinHeap в метод dijsktra в Graph, который теперь должен быть реализован с помощью списка смежности. Нужно реализовать его, полностью используя преимущества среды выполнения кучи, при этом поддерживая класс MinHeap настолько гибким, насколько это возможно. Это нужно для повторного использования в будущем.
Итак, сначала разберемся с реализацией списка смежности. Вместо матрицы, представляющей соединения между узлами, требуется, чтобы каждый узел соответствовал списку узлов, к которым он подключен. Таким образом, если мы выполняем итерацию по соединениям узла, нам не нужно проверять ВСЕ узлы, чтобы увидеть, какие из них подключены — в списке этого узла находятся только подключенные узлы.
Уже знакомый нам граф:
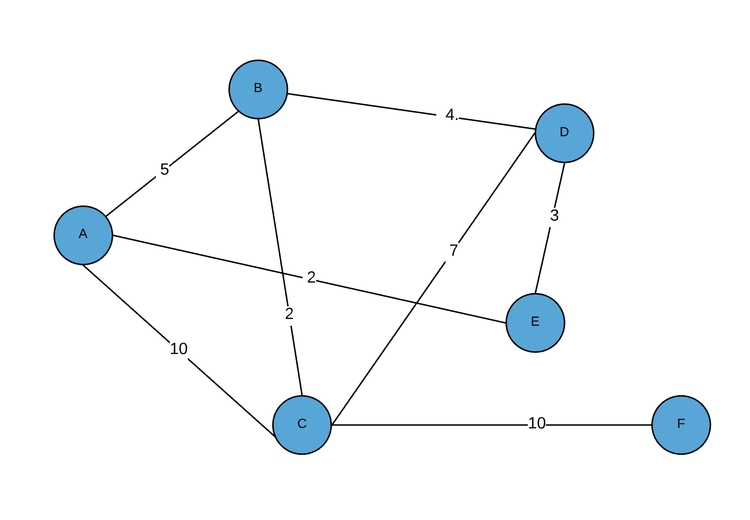
Список смежности графа будет выглядеть приблизительно следующим образом:
|
[ [ NodeA, [(NodeB, 5), (NodeC, 10), (NodeE, 2)] ], [ NodeB, [(NodeA, 5), (NodeC, 2), (NodeD, 4)] ], [ NodeC, [(NodeA, 10), (NodeB, 2), (NodeD, 7), (NodeF, 10)] ], [ NodeD, [(NodeB, 4), (NodeC, 7), (NodeE, 3)] ], [ NodeE, [(NodeA, 2), (NodeD, 3)] ], [ NodeF, [(NodeC, 10)] ] |
Как видите, для получения определенной связи узлов нам больше не нужно проверять ВСЕ прочие узлы. Оставим API относительно простым, ради ясности оставим класс простым:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
class Graph: def __init__(self, nodes): self.adj_list = [ [node, []] for node in nodes ] for i in range(len(nodes)): nodes[i].index = i def connect_dir(self, node1, node2, weight = 1): node1, node2 = self.get_index_from_node(node1), self.get_index_from_node(node2) # Обратите внимание, что указанное ниже не защищает от добавления связи дважды self.adj_list[node1][1].append((node2, weight)) def connect(self, node1, node2, weight = 1): self.connect_dir(node1, node2, weight) self.connect_dir(node2, node1, weight) def connections(self, node): node = self.get_index_from_node(node) return self.adj_list[node][1] def get_index_from_node(self, node): if not isinstance(node, Node) and not isinstance(node, int): raise ValueError(“node must be an integer or a Node object”) if isinstance(node, int): return node else: return node.index |
Далее сосредоточимся на реализации кучи для достижения лучшего алгоритма, чем текущий алгоритм O(n²). Если вспомним метод dijsktra, в классе Graph матрицы смежности, то увидим, что мы перебираем всю очередь, чтобы найти минимальное предварительное расстояние provisional distance (время выполнения O(n)), используя узел с минимальным значением для установки текущего посещаемого узла. Затем перебираем все соединения узла и при необходимости сбрасываем их предварительное расстояние provisional distance (проверьте метод connections_to или connections_from; вы увидите, что его время выполнения O(n)). Эти два алгоритма O(n) сводятся к времени выполнения O(n), потому что O(2n) = O (n). Делаем это для каждого узла графа, поэтому выполняем O(n) алгоритм n раз, тем самым получая время выполнения O(n²). Вместо этого сокращаем время выполнения до O((n + e) lg (n)), где n — количество узлов, а e — количество ребер.
В реализации списка смежности внешнему циклу while все еще нужно выполнять итерацию по всем узлам (n итераций), но чтобы получить ребра для текущего узла внутренний цикл просто должен итерировать ТОЛЬКО по ребрам для данного конкретного узла. Таким образом, внутренний цикл, повторяющийся по краям узла, будет выполняться только O(n + e) раз. Внутри данного внутреннего цикла нужно обновить предварительное расстояние для каждого из связанных узлов. Для этого будет использован метод decrease_key кучи, который мы уже рассматривали, как O(lg (n)). Таким образом, общее время выполнения будет равно O((n + e) lg (n)).
Новый алгоритм:
ИНИЦИАЛИЗАЦИЯ
- Установите
provisional_distanceвсех узлов от источника до бесконечности, за исключением нашего исходного узла, значением которого будет0. Добавьте данные к минимальной куче. - Вместо сохранения набора
seen_nodesопределите, есть ли у вас осмотренные узлы. Это будет зависеть от того, что осталось в куче. Помните, что при использованииpop()для узла, он удаляется из кучи. Следовательно, в соответствии с логикой он будет рассматриваться, как «увиденный».
ПРОЦЕДУРА ИТЕРАЦИИ
- Цикл while выполняется до тех пор, пока куча > 0: (выполняется
nраз) - Установите
current_nodeдля возвращения значенияheap.pop(). - Для
nвcurrent_node.connectionsиспользуйтеheap.decrease_key, если данная связь все еще в куче (то есть не была рассмотрена), А ТАКЖЕ если текущее значениеprovisional distanceбольше, чем предварительное расстояниеcurrent_nodeвместе с весом соседнего элемента. Данный цикл for в общем будет выполнятьсяn + eраз, а его временную сложность можно представить, какO(lg(n)). - Конец цикла while.
Есть две задачи, которые нужно решить при данной реализации:
Задача 1: Код написан таким образом, что куча работает с массивом чисел. Однако нам нужна инкапсуляция предварительного расстояния provisional distance (метрики, которая использовалась при преобразовании в кучу), перескоков И узла, которому соответствует расстояние.
Задача 2: Нужно проверить, находится ли узел внутри кучи, А ТАКЖЕ обновить его provisional distance, используя метод decrease_key, для которого требуется индекс данного узла в куче. Для сохранения своих свойств куча постоянно меняет индексы. Нужно убедиться, что данная задача не будет решена простым анализом кучи в поисках точного места узла. Данная операция O(n) будет выполняться (n + e) раз, следовательно, создание кучи и реализация списка смежности ни к чему не приведут, ведь нам нужно со всем управиться за O(1) раз.
Решение 1: Нам нужно сохранить реализацию кучи максимально гибкой. Чтобы принимать любой тип данных в качестве элементов в базовом массиве, можно просто принять необязательные анонимные функции (например, лямбда-выражения) при создании экземпляра, которые предоставляются пользователем, чтобы указать, как он должен обращаться с элементами внутри массива, если эти элементы не являются простым целым числом. Значением по умолчанию для лямбд может быть функция, которая работает, если элементы массива являются просто числами. Таким образом, если требуется простая куча с числами, пользователю не нужно вставлять лямбды. Данные настраиваемые процедуры потребуются для сравнения элементов, а также для возможности уменьшить значение элемента. Можно назвать лямбду сравнения is_less_than, и ее значение по умолчанию должно быть: a, b: a < b. Лямбда-функция для возврата обновленного узла с новым значением может называться update_node, и ее значение по умолчанию должно быть просто lambda node, newval: newval. При передаче узла и нового значения пользователю дается возможность определить лямбду, которая обновляет существующий объект ИЛИ заменяет значение, которое там находится. В контексте реализации старого Graph, поскольку узлы имели бы значения [ provisional_distance, [nodes, in, hop, path]] лямбда is_less_than могла бы выглядеть следующим образом: lambda a,b: a[0] < b[0]. Здесь можно было бы оставить значение второй лямбды по умолчанию и передать вложенный массив в decrease_key.
Тем не менее, вскоре станет ясно, что существует довольно простое решение вопроса, при котором создаются настраиваемые объекты узлы node и передаются в MinHeap. Гибкость, которая недавно упоминалась, позволит легко воплотить это элегантное решение. В частности, в приведенном ниже коде вы увидите, что лямбда is_less_than превратиться в: lambda a, b: a.prov_dist < b.prov_dist, а лямбда update_node станет: lambda node, data: node.update_data (data), что намного аккуратнее использования вложенных массивы.
Решение 2: Есть несколько способов решить данную задачу, но давайте попробуем выбрать тот, который идет рука об руку с Решением 1. Учитывая гибкость, которой мы добились в Решении 1, мы можем продолжать использовать эту стратегию для реализации дополняющего решения и здесь. Можно реализовать дополнительный массив внутри класса MinHeap, который отображает исходный порядок вставленных узлов в их текущий порядок внутри массива узлов. Назовем этот список order_mapping. Поддерживая этот список, мы можем получить любой узел из кучи за время O(1), учитывая, что мы знаем исходный порядок, в котором узел был вставлен в кучу. Таким образом, если порядок узлов, в котором создаётся куча, совпадает с номером индекса узлов Graph, теперь у нас есть отображение узла Graph до относительного местоположения этого узла в MinHeap в постоянном времени! Чтобы иметь возможность поддерживать это отображение в актуальном состоянии за время O(1), все элементы, передаваемые в MinHeap как узлы, должны каким-то образом «знать» свой исходный индекс, а MinHeap необходимо знать, как считывать исходный индекс с этих узлов. Это требуется для того чтобы он мог обновить значение order_mapping по номеру индекса свойства индекса узла index до значения текущей позиции этого узла в списке узлов MinHeap. Поскольку нам нужно разрешить использование MinHeap, тем, кто не нуждается в этом отображении, А ТАКЖЕ нам нужно, чтобы любые типы данных были узлами кучи, мы можем снова разрешить добавление лямбда-выражения пользователем. Оно сообщит MinHeap, как получить номер индекса из любого типа данных, что добавляются в кучу — его названием будет get_index.
Например, если бы данные для каждого элемента в куче были списком структуры [data, index], лямбда get_index была бы: lambda el: el [1]. Кроме того, мы можем установить для get_index значение по умолчанию None, и доверить ему принятие решений, поддерживается или нет массив order_mapping. Таким образом, если пользователь не вводит лямбду, чтобы сообщить куче, как получить индекс из элемента, куча не будет отслеживать order_mapping, что позволяет пользователю использовать кучу без этой функциональности только с базовыми типами данных, такими как целые числа. Лямбда get_index, что будет в итоге использоваться, так как будет задействован пользовательский объект узла, будет очень простой: lambda node: node.index ().
Результатом совмещения решений 1 и 2 является одно чистое решение. Создается класс DijkstraNodeDecorator для декорирования всех узлов, составляющих граф. Этот декоратор предоставит дополнительные данные о provisional distance (инициализированном в бесконечность) и hoop list (инициализированном в пустой массив). Кроме того, он будет реализован с помощью метода, который позволит объекту обновляться самому. Потом это можно использовать в лямбда-выражении для decrease_key. DijkstraNodeDecorator сможет получить доступ к индексу декорируемого узла, и мы воспользуемся этим фактом, указав куче, как получить индекс узла при помощи лямбды get_index из Решения 2.
Финальный код алгоритма Дейкстры Python:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
class DijkstraNodeDecorator: def __init__(self, node): self.node = node self.prov_dist = float(‘inf’) self.hops = [] def index(self): return self.node.index def data(self): return self.node.data def update_data(self, data): self.prov_dist = data[‘prov_dist’] self.hops = data[‘hops’] return self |
Использоваля для декорирования узлов в реализации Graph ниже.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class MinHeap(BinaryTree): def __init__(self, nodes, is_less_than = lambda a,b: a < b, get_index = None, update_node = lambda node, newval: newval): BinaryTree.__init__(self, nodes) self.order_mapping = list(range(len(nodes))) self.is_less_than, self.get_index, self.update_node = is_less_than, get_index, update_node self.min_heapify() # Изменение в кучу узлов, предполагается, что все поддеревья уже кучи def min_heapify_subtree(self, i): size = self.size() ileft = self.ileft(i) iright = self.iright(i) imin = i if( ileft < size and self.is_less_than(self.nodes[ileft], self.nodes[imin])): imin = ileft if( iright < size and self.is_less_than(self.nodes[iright], self.nodes[imin])): imin = iright if( imin != i): self.nodes[i], self.nodes[imin] = self.nodes[imin], self.nodes[i] # Если есть лямбда для получения абсолютного индекса узла # обновляет массив order_mapping для указания, где находится индекс # в массиве узлов (осмотр для этого индекса будет 0(1)) if self.get_index is not None: self.order_mapping[self.get_index(self.nodes[imin])] = imin self.order_mapping[self.get_index(self.nodes[i])] = i self.min_heapify_subtree(imin) # Превращает в кучу массив, который еще ей не является def min_heapify(self): for i in range(len(self.nodes), –1, –1): self.min_heapify_subtree(i) def min(self): return self.nodes[0] def pop(self): min = self.nodes[0] if self.size() > 1: self.nodes[0] = self.nodes[–1] self.nodes.pop() # Обновляет order_mapping, если можно if self.get_index is not None: self.order_mapping[self.get_index(self.nodes[0])] = 0 self.min_heapify_subtree(0) elif self.size() == 1: self.nodes.pop() else: return None # Если self.get_index существует, обновляет self.order_mapping для указания, что # узел индекса больше не в куче if self.get_index is not None: # Устанавливает значение None для self.order_mapping для обозначения непринадлежности к куче self.order_mapping[self.get_index(min)] = None return min # Обновляет значение узла и подстраивает его, если нужно, чтобы сохранить свойства кучи def decrease_key(self, i, val): self.nodes[i] = self.update_node(self.nodes[i], val) iparent = self.iparent(i) while( i != 0 and not self.is_less_than(self.nodes[iparent], self.nodes[i])): self.nodes[iparent], self.nodes[i] = self.nodes[i], self.nodes[iparent] # Если есть лямбда для получения индекса узла # обновляет массив order_mapping для указания, где именно находится индекс # в массиве узлов (осмотр этого индекса O(1)) if self.get_index is not None: self.order_mapping[self.get_index(self.nodes[iparent])] = iparent self.order_mapping[self.get_index(self.nodes[i])] = i i = iparent iparent = self.iparent(i) if i > 0 else None def index_of_node_at(self, i): return self.get_index(self.nodes[i]) |
MinHeap модифицирован с лямбдой, что позволяет любому типу данных использоваться в виде узла.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class Graph: def __init__(self, nodes): self.adj_list = [ [node, []] for node in nodes ] for i in range(len(nodes)): nodes[i].index = i def connect_dir(self, node1, node2, weight = 1): node1, node2 = self.get_index_from_node(node1), self.get_index_from_node(node2) # Отмечает, что нижеуказанное не предотвращает от добавления связи дважды self.adj_list[node1][1].append((node2, weight)) def connect(self, node1, node2, weight = 1): self.connect_dir(node1, node2, weight) self.connect_dir(node2, node1, weight) def connections(self, node): node = self.get_index_from_node(node) return self.adj_list[node][1] def get_index_from_node(self, node): if not isinstance(node, Node) and not isinstance(node, int): raise ValueError(“node must be an integer or a Node object”) if isinstance(node, int): return node else: return node.index def dijkstra(self, src): src_index = self.get_index_from_node(src) # Указывает узлы к DijkstraNodeDecorators # Это инициализирует все предварительные расстояния до бесконечности dnodes = [ DijkstraNodeDecorator(node_edges[0]) for node_edges in self.adj_list ] # Устанавливает предварительное расстояние исходного узла до 0 и его массив перескоков к его узлу dnodes[src_index].prov_dist = 0 dnodes[src_index].hops.append(dnodes[src_index].node) # Устанавливает все методы настройки кучи is_less_than = lambda a, b: a.prov_dist < b.prov_dist get_index = lambda node: node.index() update_node = lambda node, data: node.update_data(data) # Подтверждает работу кучи с DijkstraNodeDecorators с узлами heap = MinHeap(dnodes, is_less_than, get_index, update_node) min_dist_list = [] while heap.size() > 0: # Получает узел кучи, что еще не просматривался (‘seen’) # и находится на минимальном расстоянии от исходного узла min_decorated_node = heap.pop() min_dist = min_decorated_node.prov_dist hops = min_decorated_node.hops min_dist_list.append([min_dist, hops]) # Получает все следующие перескоки. Это больше не O(n^2) операция connections = self.connections(min_decorated_node.node) # Для каждой связи обновляет ее путь и полное расстояние от # исходного узла, если общее расстояние меньше, чем текущее расстояние # в массиве dist for (inode, weight) in connections: node = self.adj_list[inode][0] heap_location = heap.order_mapping[inode] if(heap_location is not None): tot_dist = weight + min_dist if tot_dist < heap.nodes[heap_location].prov_dist: hops_cpy = list(hops) hops_cpy.append(node) data = {‘prov_dist’: tot_dist, ‘hops’: hops_cpy} heap.decrease_key(heap_location, data) return min_dist_list |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
a = Node(‘a’) b = Node(‘b’) c = Node(‘c’) d = Node(‘d’) e = Node(‘e’) f = Node(‘f’) g = Graph([a,b,c,d,e,f]) g.connect(a,b,5) g.connect(a,c,10) g.connect(a,e,2) g.connect(b,c,2) g.connect(b,d,4) g.connect(c,d,7) g.connect(c,f,10) g.connect(d,e,3) print([(weight, [n.data for n in node]) for (weight, node) in g.dijkstra(a)]) |
Результат вывода финального кода:
|
[(0, [‘a’]), (2, [‘a’, ‘e’]), (5, [‘a’, ‘e’, ‘d’]), (5, [‘a’, ‘b’]), (7, [‘a’, ‘b’, ‘c’]), (17, [‘a’, ‘b’, ‘c’, ‘f’])] |
Как видите, вывод такой же, как и в прошлом варианте реализации алгоритма. Сам код выглядит теперь намного аккуратнее. Кроме того, сейчас нам удалось добиться реализации алгоритма Дейкстры за время O((n + e)lg(n)).

Являюсь администратором нескольких порталов по обучению языков программирования Python, Golang и Kotlin. В составе небольшой команды единомышленников, мы занимаемся популяризацией языков программирования на русскоязычную аудиторию. Большая часть статей была адаптирована нами на русский язык и распространяется бесплатно.
E-mail: vasile.buldumac@ati.utm.md
Образование
Universitatea Tehnică a Moldovei (utm.md)
- 2014 — 2018 Технический Университет Молдовы, ИТ-Инженер. Тема дипломной работы «Автоматизация покупки и продажи криптовалюты используя технический анализ»
- 2018 — 2020 Технический Университет Молдовы, Магистр, Магистерская диссертация «Идентификация человека в киберпространстве по фотографии лица»
Что общего у устройств GPS‑навигации с веб‑сайтами для бронирования рейсов? Оказывается, очень много! Во‑первых, обе технологии используют алгоритм Дейкстры для поиска кратчайшего пути.
В этой статье я познаколю вас с алгоритмом Дейкстры и покажу его простую реализацию на Python. После простого русского языка, на котором всё будет понятно, вы увидите, что кодирование на Python не представляет больших сложностей.
Что такое алгоритм Дейкстры?
В 1956 году у голландского программиста Эдсгера В. Дейкстры возникла практическая задача — найти самый короткий путь из Роттердама в Гронинген. Однако, он не просто сверился с картой для рассчёта расстояния, которые ему нужно было пройти, использую длину дорог. Вместо этого, Дейкстра поступил, как информатикએ: он абстрагировался от проблемы, отбросив такие мелочи, как путешествие из города А в город Б. Он сформулировал более общую проблему поиска по графу. Вот так и родился алгоритм Дейкстрыએ.
Алгоритм Дейкстры — это популярный алгоритм поиска, используемый для определения кратчайшего пути между двумя узлами в графе. В исходном сценарии граф представлял Нидерланды, узлы графа представляли разные голландские города, а рёбра представляли дороги между городами. Алгоритм Дейкстры можно использовать для решения любой задачи, которая может быть представлена в виде графа. Предложения друзей в социальных сетях, маршрутизация пакетов через Интернет или поиск пути через лабиринт — все это может сделать алгоритмом Дейкстры. Но как на самом деле это работает?
Напомним, что алгоритм Дейкстры для графов, а это означает, что он может решить проблему, только если она может быть представлена в графоподобном виде. Пример, который будет здесь показан, возможно, самый интуитивно понятный — кратчайший путь между двумя городами.
Мы будем работать с картой, показаной ниже, для поиска налучшего маршрута между двумя европейскими городами Рейкьявиком и Белградом. Для простоты представим, что все города связаны дорогами (реальный маршрут должен включать как минимум один паром).
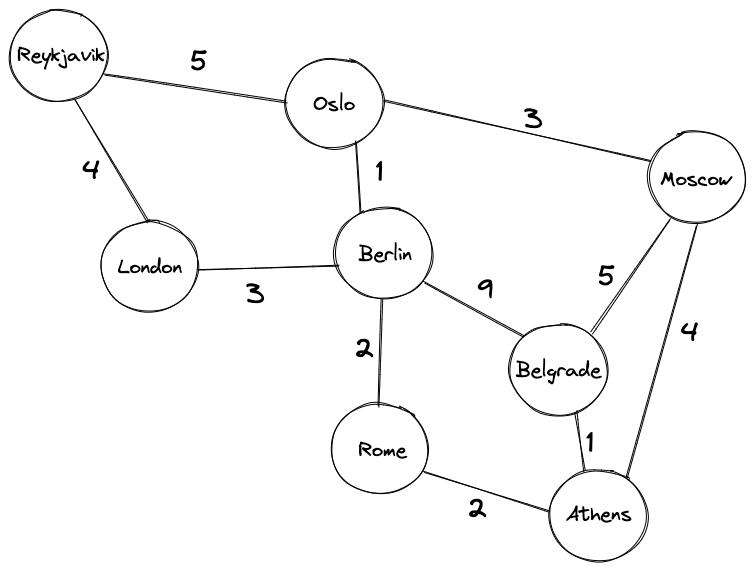
Обратите внимание на следующее:
- Каждый город — это узел.
- Каждая дорога — это ребро.
- У каждой дороги есть своя ценность. Это может быть расстояние между городами, плата за проезд или интенсивностью движения. Как правило, мы отдаем предпочтение рёбрам с более низкими значениями. В нашем конкретном случае связанное значение определяется расстоянием между двумя городами.
Вы должны уже заметить, что добраться из Рейкьявика до Белграда напрямую невозможно. Это сделало бы наши упражнения бессмысленными. Но есть несколько путей из Рейкьявика в Белград, которые проходят через другие города:
- Reykjavik → Oslo → Berlin → Belgrade
- Reykjavik → London → Berlin → Rome → Athens → Belgrade
- Reykjavik → London → Berlin → Rome → Athens → Moscow → Belgrade
Каждый из этих путей заканчивается в Белграде, но все они имеют разные ценности. Мы можем использовать алгоритм Дейкстры, чтобы найти путь с наименьшим общим значением.
Прежде чем погрузиться в код, посмотрим на алгоритм Дейкстры с высоты птичьего полета.
Сначала инициализируем алгоритм:
- Устанавливаем Рейкьявик в качестве начального узла.
- Устанавливаем расстояния между Рейкьявиком и всеми другими городами в ∞ (бесконечность), за исключением расстояния между Рейкьявиком и самим собой, которое принимаем равным 0.
После этого, итеративно выполняем следующие шаги:
- Выбираем узел с наименьшим значением в качестве «текущего узла» и посещаем всех соседей. При посещении каждого соседа, обновляем их ориентировочное расстояние от начального узла.
- Как только мы посетим всех соседей текущего узла и обновили их расстояния, помечаем текущий узел как «visited» «посещенный»). Отметка узла как «посещенного» означает, что найдена его окончательная ценность.
- Вернемся к первому шагу и повторяем до тех пор, пока не посетим все узлы графа.
В нашем примере начинаем с отметки Рейкьявика, поскольку его значение равно 0, как «текущего узла». Далее посетим два соседних узла Рейкьявика: Лондон и Осло. В начале алгоритма их значения устанавливаются на бесконечность, но, когда мы посещаем узлы, то обновляем значение для Лондона до 4 и Осло до 5.
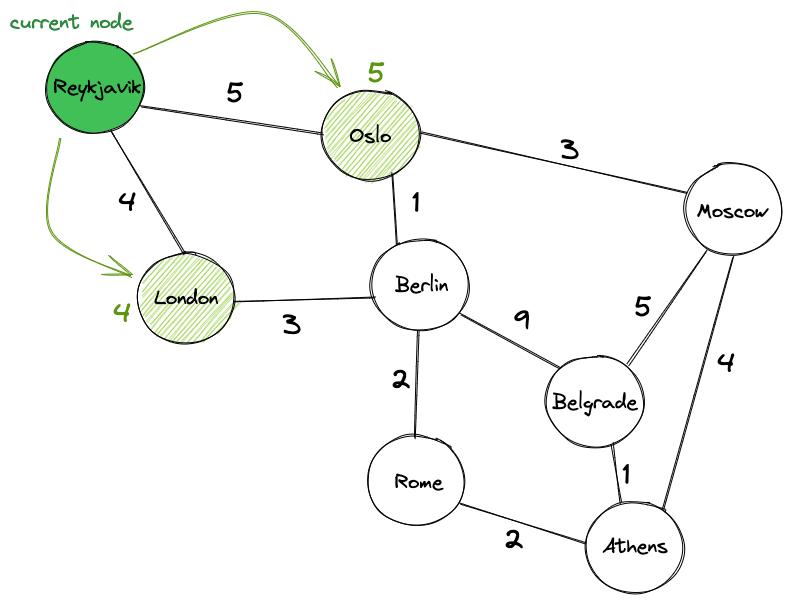
Затем отмечаем Рейкьявик как «посещенный». Мы знаем, что его окончательная стоимость равна нулю, и нам больше не нужно его посещать. Продолжаем со следующего узла с наименьшим значением, которым является Лондон.
Посещаем все соседние узлы Лондона, которые не помечены как «посещенные». Соседи Лондона — Рейкьявик и Берлин. Но мы игнорируем Рейкьявик, потому что мы уже были в нем. Вместо этого обновляем значение Берлина, добавляя значение ребра, соединяющего Лондон и Берлин (3), к значению Лондона (4), что дает нам значение 7.
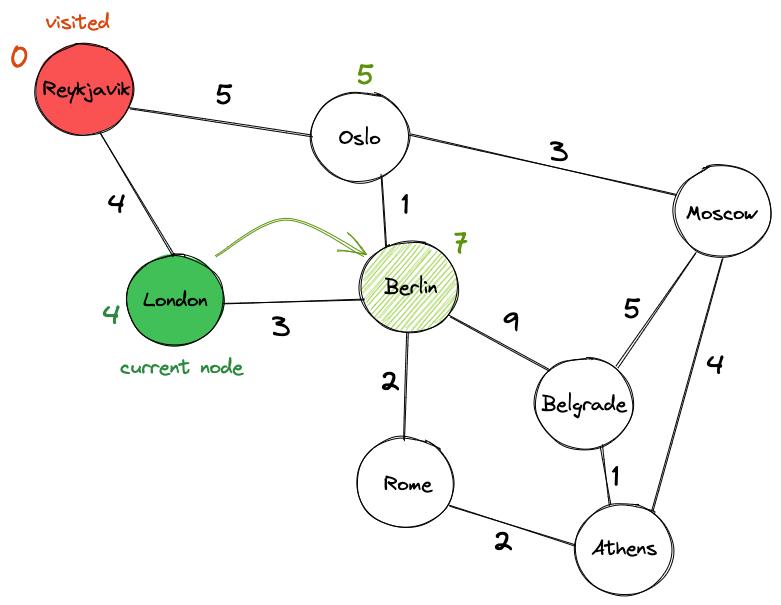
Отмечаем Лондон как посещенный и выбираем следующий узел — Осло. Посещаем соседей Осло и обновляем их ценности. Оказывается, можно лучше добраться до Берлина через Осло (со значением 6), чем через Лондон, поэтому соответствующим образом обновляем его значение. Также обновляем текущее значение Москвы с бесконечности до 8.
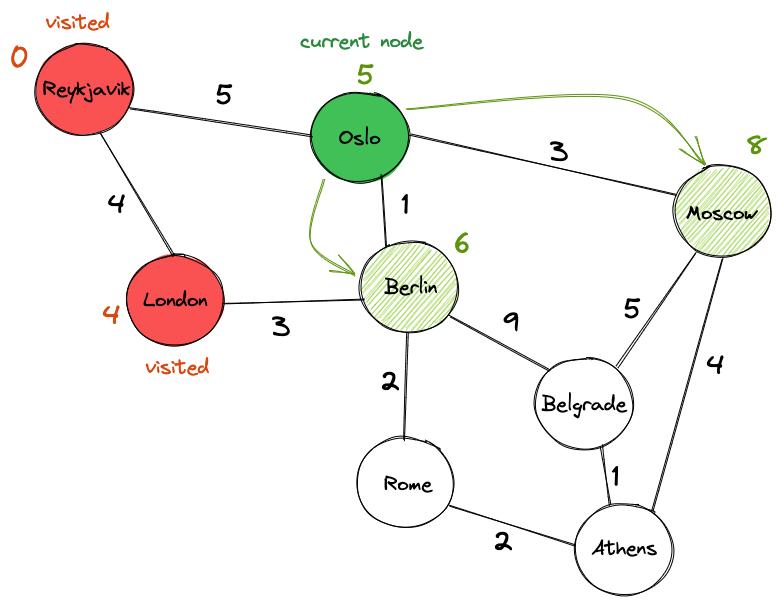
Отмечаем Осло как «посещенный» и обновляем его окончательное значение до 5. Между Берлином и Москвой выбираем Берлин в качестве следующего узла, потому что его значение (6) ниже, чем у Москвы (8). Действуем так же, как и раньше: посещаем Рим и Белград и обновляем их предварительные значения, прежде чем пометить Берлин как «посещенный» и перейти к следующему городу.
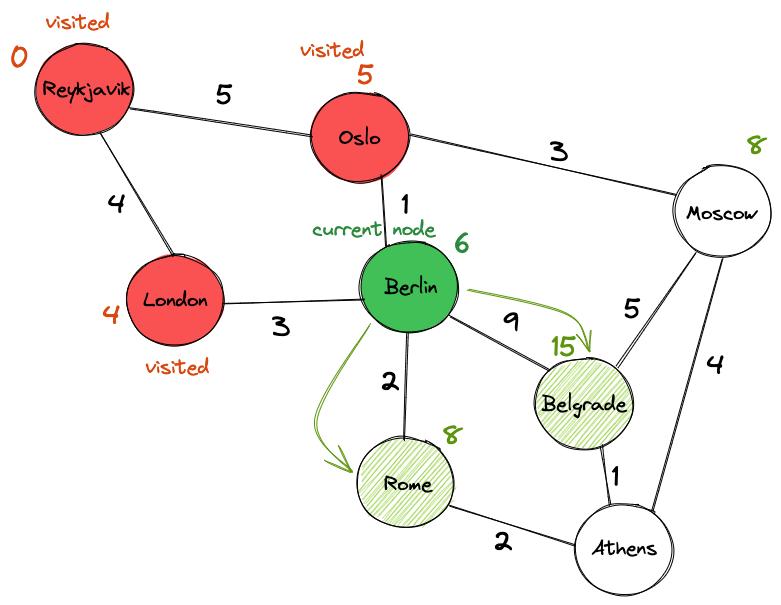
Обратите внимание, что мы уже нашли путь из Рейкьявика в Белград со значением 15! Но лучший ли он?
В конце концов, это не так. Пропустим остальные шаги, а для вас это упражнение. Лучшим путем оказывается Рейкьявик → Осло → Берлин → Рим → Афины → Белград со значением 11.
Теперь, посмотрим, как это реализовать на Python.
1) Класс Graph
Сначала создадим класс Graph. Этот класс не охватывает никакой логики алгоритма Дейкстры, но сделает реализацию алгоритма более лаконичной.
Реализуем граф как словарь Python. Ключи словаря будут соответствовать городам, а его значения будут соответствовать рёбрам, где записывают расстояния до других городов на графе.
import sys
class Graph(object):
def __init__(self, nodes, init_graph):
self.nodes = nodes
self.graph = self.construct_graph(nodes, init_graph)
def construct_graph(self, nodes, init_graph):
'''
Этот метод обеспечивает симметричность графика. Другими словами, если существует путь от узла A к B со значением V, должен быть путь от узла B к узлу A со значением V.
'''
graph = {}
for node in nodes:
graph[node] = {}
graph.update(init_graph)
for node, edges in graph.items():
for adjacent_node, value in edges.items():
if graph[adjacent_node].get(node, False) == False:
graph[adjacent_node][node] = value
return graph
def get_nodes(self):
"Возвращает узлы графа"
return self.nodes
def get_outgoing_edges(self, node):
"Возвращает соседей узла"
connections = []
for out_node in self.nodes:
if self.graph[node].get(out_node, False) != False:
connections.append(out_node)
return connections
def value(self, node1, node2):
"Возвращает значение ребра между двумя узлами."
return self.graph[node1][node2]
2) Алгоритм Дейкстры
Далее реализуем алгоритм Дейкстры. Начнем с определения функции.
def dijkstra_algorithm(graph, start_node):
Функция принимает два аргумента: graph и start_node. graph — это экземпляр класса Graph, который мы создали на предыдущем шаге, тогда как start_node — это узел, с которого мы начнем вычисления. Мы вызовем метод get_nodes() для инициализации списка непосещенных узлов:
unvisited_nodes = list(graph.get_nodes())
Затем создадим два словаря, shorttest_path и previous_nodes:
Shorttest_pathбудет хранить наиболее известную стоимость посещения каждого города на графике, начиная с start_node. Вначале стоимость начинается с бесконечности, но мы будем обновлять значения по мере продвижения по графику.previous_nodesбудет хранить траекторию текущего наиболее известного пути для каждого узла. Например, если нам известен лучший способ добраться до Берлина через Осло, previous_nodes[«Берлин»] вернет «Осло», а previous_nodes[«Осло»] вернет «Рейкьявик». Мы будем использовать этот словарь, чтобы найти кратчайший путь.
shortest_path = {}
previous_nodes = {}
# Мы будем использовать max_value для инициализации значения "бесконечности" непосещенных узлов
max_value = sys.maxsize
for node in unvisited_nodes:
shortest_path[node] = max_value
# Однако мы инициализируем значение начального узла 0
shortest_path[start_node] = 0
Теперь можно запустить алгоритм. Помните, что алгоритм Дейкстры выполняется до тех пор, пока не посетит все узлы в графе, поэтому представим это как условие выхода из цикла while.
while unvisited_nodes:
Теперь алгоритм может начать посещать узлы. Приведенный ниже блок кода сначала инструктирует алгоритм найти узел с наименьшим значением.
current_min_node = None
for node in unvisited_nodes: # Iterate over the nodes
if current_min_node == None:
current_min_node = node
elif shortest_path[node] < shortest_path[current_min_node]:
current_min_node = node
После этого алгоритм посещает всех соседей узла, которые еще не посещены. Если новый путь к соседу лучше, чем текущий лучший путь, алгоритм вносит корректировки в словари shorttest_path и previous_nodes.
# Приведенный ниже блок кода извлекает соседей текущего узла и обновляет их расстояния.
neighbors = graph.get_outgoing_edges(current_min_node)
for neighbor in neighbors:
tentative_value = shortest_path[current_min_node] + graph.value(current_min_node, neighbor)
if tentative_value < shortest_path[neighbor]:
shortest_path[neighbor] = tentative_value
# Мы также обновляем лучший путь к текущему узлу
previous_nodes[neighbor] = current_min_node
После посещения всех его соседей мы можем пометить текущий узел как «посещенный»:
unvisited_nodes.remove(current_min_node
Наконец, мы можем вернуть два словаря:
return previous_nodes, shortest_path
3) Вспомогательная функция
Наконец, нам нужно создать функцию, которая печатает результаты. Эта функция будет принимать два словаря, возвращаемые функцией dijskstra_algorithm, а также имена начального и целевого узлов. Он будет использовать два словаря, чтобы найти лучший путь и сделать его оценку.
def print_result(previous_nodes, shortest_path, start_node, target_node):
path = []
node = target_node
while node != start_node:
path.append(node)
node = previous_nodes[node]
# Add the start node manually
path.append(start_node)
print("Найден следующий лучший маршрут {}.".format(shortest_path[target_node]))
print(" -> ".join(reversed(path)))
Алгоритм в действии
Теперь посмотрим, как работает алгоритм. Dручную инициализируем узлы и их рёбра.
nodes = ["Reykjavik", "Oslo", "Moscow", "London", "Rome", "Berlin", "Belgrade", "Athens"]
init_graph = {}
for node in nodes:
init_graph[node] = {}
init_graph["Reykjavik"]["Oslo"] = 5
init_graph["Reykjavik"]["London"] = 4
init_graph["Oslo"]["Berlin"] = 1
init_graph["Oslo"]["Moscow"] = 3
init_graph["Moscow"]["Belgrade"] = 5
init_graph["Moscow"]["Athens"] = 4
init_graph["Athens"]["Belgrade"] = 1
init_graph["Rome"]["Berlin"] = 2
init_graph["Rome"]["Athens"] = 2
Будем использовать эти значения для создания объекта класса Graph.
graph = Graph(nodes, init_graph)
Когда наш граф полностью построен, можно передать его функции dijkstra_algorithm().
previous_nodes, shortest_path = dijkstra_algorithm(graph=graph, start_node="Reykjavik")
А теперь распечатываем результаты:
print_result(previous_nodes, shortest_path, start_node="Reykjavik", target_node="Belgrade")
Вот и все! Не стесняйтесь экспериментировать с кодом. Например, можно добавить больше узлов к графу, настроить значения ребер или выбрать разные начальный и конечный города, считать города и расстояния из файла или базы данных.
Полный код приложения для проверки алгоритма Дейкстры
import sys
class Graph(object):
def __init__(self, nodes, init_graph):
self.nodes = nodes
self.graph = self.construct_graph(nodes, init_graph)
def construct_graph(self, nodes, init_graph):
'''
Этот метод обеспечивает симметричность графика. Другими словами, если существует путь от узла A к B со значением V, должен быть путь от узла B к узлу A со значением V.
'''
graph = {}
for node in nodes:
graph[node] = {}
graph.update(init_graph)
for node, edges in graph.items():
for adjacent_node, value in edges.items():
if graph[adjacent_node].get(node, False) == False:
graph[adjacent_node][node] = value
return graph
def get_nodes(self):
"Возвращает узлы графа"
return self.nodes
def get_outgoing_edges(self, node):
"Возвращает соседей узла"
connections = []
for out_node in self.nodes:
if self.graph[node].get(out_node, False) != False:
connections.append(out_node)
return connections
def value(self, node1, node2):
"Возвращает значение ребра между двумя узлами."
return self.graph[node1][node2]
def dijkstra_algorithm(graph, start_node):
unvisited_nodes = list(graph.get_nodes())
# Мы будем использовать этот словарь, чтобы сэкономить на посещении каждого узла и обновлять его по мере продвижения по графику
shortest_path = {}
# Мы будем использовать этот dict, чтобы сохранить кратчайший известный путь к найденному узлу
previous_nodes = {}
# Мы будем использовать max_value для инициализации значения "бесконечности" непосещенных узлов
max_value = sys.maxsize
for node in unvisited_nodes:
shortest_path[node] = max_value
# Однако мы инициализируем значение начального узла 0
shortest_path[start_node] = 0
# Алгоритм выполняется до тех пор, пока мы не посетим все узлы
while unvisited_nodes:
# Приведенный ниже блок кода находит узел с наименьшей оценкой
current_min_node = None
for node in unvisited_nodes: # Iterate over the nodes
if current_min_node == None:
current_min_node = node
elif shortest_path[node] < shortest_path[current_min_node]:
current_min_node = node
# Приведенный ниже блок кода извлекает соседей текущего узла и обновляет их расстояния
neighbors = graph.get_outgoing_edges(current_min_node)
for neighbor in neighbors:
tentative_value = shortest_path[current_min_node] + graph.value(current_min_node, neighbor)
if tentative_value < shortest_path[neighbor]:
shortest_path[neighbor] = tentative_value
# We also update the best path to the current node
previous_nodes[neighbor] = current_min_node
# После посещения его соседей мы отмечаем узел как "посещенный"
unvisited_nodes.remove(current_min_node)
return previous_nodes, shortest_path
def print_result(previous_nodes, shortest_path, start_node, target_node):
path = []
node = target_node
while node != start_node:
path.append(node)
node = previous_nodes[node]
# Добавить начальный узел вручную
path.append(start_node)
print("Найден следующий лучший маршрут с ценностью {}.".format(shortest_path[target_node]))
print(" -> ".join(reversed(path)))
nodes = ["Reykjavik", "Oslo", "Moscow", "London", "Rome", "Berlin", "Belgrade", "Athens"]
init_graph = {}
for node in nodes:
init_graph[node] = {}
init_graph["Reykjavik"]["Oslo"] = 5
init_graph["Reykjavik"]["London"] = 4
init_graph["Oslo"]["Berlin"] = 1
init_graph["Oslo"]["Moscow"] = 3
init_graph["Moscow"]["Belgrade"] = 5
init_graph["Moscow"]["Athens"] = 4
init_graph["Athens"]["Belgrade"] = 1
init_graph["Rome"]["Berlin"] = 2
init_graph["Rome"]["Athens"] = 2
graph = Graph(nodes, init_graph)
previous_nodes, shortest_path = dijkstra_algorithm(graph=graph, start_node="Reykjavik")
print_result(previous_nodes, shortest_path, start_node="Reykjavik", target_node="Belgrade")
Мотиватор Implementing Dijkstra’s Algorithm in Python

class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
def printSolution(self, dist):
print("Vertex t Distance from Source")
for node in range(self.V):
print(node, "tt", dist[node])
def minDistance(self, dist, sptSet):
min = 1e7
for v in range(self.V):
if dist[v] < min and sptSet[v] == False:
min = dist[v]
min_index = v
return min_index
def dijkstra(self, src):
dist = [1e7] * self.V
dist[src] = 0
sptSet = [False] * self.V
for cout in range(self.V):
u = self.minDistance(dist, sptSet)
sptSet[u] = True
for v in range(self.V):
if (self.graph[u][v] > 0 and
sptSet[v] == False and
dist[v] > dist[u] + self.graph[u][v]):
dist[v] = dist[u] + self.graph[u][v]
self.printSolution(dist)
g = Graph(9)
g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]
]
g.dijkstra(0)
Графы: разные виды представления графов. Алгоритмы Дейкстры и Флойда: реализация на Python. Минимальное остовное
дерево
Раскрашивание графов
Обход вершин графа
Поиск в глубину – ПВГ (Depth First Search – DFS)
Метод обхода графа при котором в первую очередь переход делается из последней посещённой вершины (вершины
хранятся в
стеке). Обход в глубину получается естественным образом при рекурсивном обходе графа.

# Смежность вершин
inc = {
1: [2, 8],
2: [1, 3, 8],
3: [2, 4, 8],
4: [3, 7, 9],
5: [6, 7],
6: [5],
7: [4, 5, 8],
8: [1, 2, 3, 7],
9: [4],
}
visited = set() # Посещена ли вершина?
# Поиск в глубину - ПВГ (Depth First Search - DFS)
def dfs(v):
if v in visited: # Если вершина уже посещена, выходим
return
visited.add(v) # Посетили вершину v
for i in inc[v]: # Все смежные с v вершины
if not i in visited:
dfs(i)
start = 1
dfs(start) # start - начальная вершина обхода
print(visited)
Поиск в ширину – ПВШ (Breadth First Search – BFS)
Метод обхода графа при котором в первую очередь переход делается из первой вершины, из которой мы ещё не ходили
(вершины хранятся в очереди). Обход в глубину получается естественным образов при рекурсивном
обходе
графа.
Порядок обхода вершин при поиске в ширину

# Смежность вершин
inc = {
1: [2, 8],
2: [1, 3, 8],
3: [2, 4, 8],
4: [3, 7, 9],
5: [6, 7],
6: [5],
7: [4, 5, 8],
8: [1, 2, 3, 7],
9: [4],
}
visited = set() # Посещена ли вершина?
Q = [] # Очередь
BFS = []
# Поиск в ширину - ПВШ (Breadth First Search - BFS)
def bfs(v):
if v in visited: # Если вершина уже посещена, выходим
return
visited.add(v) # Посетили вершину v
BFS.append(v) # Запоминаем порядок обхода
# print("v = %d" % v)
for i in inc[v]: # Все смежные с v вершины
if not i in visited:
Q.append(i)
while Q:
bfs(Q.pop(0))
start = 1
bfs(start) # start - начальная вершина обхода
print(BFS) # Выводится: [1, 2, 8, 3, 7, 4, 5, 9, 6]
Поиск кратчайших путей в графах (объединение разделов по Дейкстре и Флойду)
Алгоритм Дейкстры
Алгоритм Дейкстры (Dijkstra’s algorithm) —
алгоритм на графах,
находящий кратчайшее расстояние от одной из вершин графа до всех остальных.
Алгоритм работает только для графов без рёбер отрицательного веса (без рёбер с отрицательной “длиной”).
Примеры формулировки задачи
Вариант 1. Дана сеть автомобильных дорог, соединяющих города. Некоторые дороги односторонние.
Найти кратчайшие пути от заданного города до каждого другого города (если двигаться можно только по
дорогам).
Вариант 2. Имеется некоторое количество авиарейсов между городами мира,
для каждого известна стоимость. Стоимость перелёта из A в B может быть не равна стоимости перелёта из B в A.
Найти маршрут минимальной стоимости (возможно, с пересадками) от Копенгагена до Барнаула.

Идея алгоритма Дейкстры
Алгоритм состоит и 2 повторяющихся шагов:
- Добавление новой вершины (“Расти” – GROW)
- “Релаксация”, т.е. пересчёт расстояний до других вершин с учётом добавленной вершины
(RELAX).
Более подробное описание:
Обозначения:
Граф $G = (V,E)$, где $V$ – вершины, $E$ – рёбра.
$v_0$ – начальная вершина (от которой мы ищем кратчайшее растояние до всех остальных)
$R_i$ – известное нам расстояние от вершиеы $v_0$ до вершины $i$-ой.
$D$ – множество вершин до которых мы знаем кратчайшее расстояние от $v_0$.
Граф $G=(V,E)$, где $V$ – вершины, $E$ – рёбра.
$v_0$ – начальная вершина
$R_i$ – кратчайщее расстояние от $v_0$ до $i$-ой вершины
$v=v_0$
$D = [v_0]$
Повторять
Инициализация алгоритма:
$D = {}$ – пустое множество.
$R_{v_0} = 0$ – расстояние от $v_0$ до $v_0$ = 0.
$v = v_0$ – расти будем от вершины $v$.
Повторять (общий шаг алгоритма)
$GROW(V/D,v)$ – Добавляем вершину $v$ из множества $V/D$ в множество $D$.
$RELAX(V/D,v)$ – пробегаем достижимые из $v$ вершины до которых мы ещё не знаем кратчайшее расстояние
и
обновляем расстояния $R_i$ от вершины $v$.
$v$ – вершина с минимальным $R$ из множества $V/D$.
Пока удаётся расти (операция $GROW$ добавляет вершину).
Алгоритм
Каждой вершине $v$ из $V$ сопоставим значение $a[v]$ — минимальное известное расстояние от
этой
вершины до начальной $s$.
Алгоритм работает пошагово — на каждом шаге он рассматривает одну вершину и пытается улучшить текущее
расстояние
до
этой вершины.
Работа алгоритма завершается, когда все вершины посещены, либо когда вычислены расстояния до всех вершин,
достижимых
из начальной.
Инициализация. Значение $a[s]$ самой начальной вершины полагается равным 0, значение
остальных вершин —
бесконечности (в программировании это реализуется присваиванием большого, к примеру, максимально возможного
для
данного типа, значения).
Это отражает то, что расстояния от $s$ до других вершин пока неизвестны.
Шаг алгоритма.
Если все вершины посещены, алгоритм завершается.
В противном случае, из ещё не посещённых вершин выбирается вершина v, имеющая минимальное расстояние
от
начальной вершины $s$ и добавляется в список посещенных. Эта вершина находится, используя перебор всех
непосещенных вершин. При этом суммируется расстояние от старта до одной из посещенных вершин u до
непосещенной $v$. Для первого шага $s$ – единственная посещенная вершина с расстоянием от старта
(то
есть от себя самой), равным 0.
const MaxN = 1000; { Максимальное количество вершин }
var
a : array [1..MaxN] of extended; { Найденные кратчайшие расстояния }
b : array [1..MaxN] of boolean; { Вычислено ли кратчайшее расстояние до вершины }
p : array [1..MaxN,1..MaxN] of extended; { Матрица смежности }
begin
{ До всех вершин расстояние - бесконечность }
for i := 1 to n do a[i] := Inf;
a[s] := 0.0; { И только до начальной вершины расстояние 0 }
for i := 1 to n do b[i] := false; { Ни до одной вершины мы ещё не нашли кратчайшее расстояние }
j := s; { Добавляемая вершина (стартовая) }
repeat
l := j;
b[l] := True; { Добавили вершину }
{ Оббегаем все вершины смежные с только что добавленной }
min := Inf; { Будем искать вершину с минимальным расстоянием от стартовой }
for i := 1 to n do
if not b[i] then begin
{ Если есть путь короче чем известный в i-ую вершину через l-тую, то запоминаем его }
if a[i] < a[l] + p[l][i] then a[i] := a[l] + p[l][i];
{ Если расстояние в эту вершину минимально, то запоминаем её как следующий кандидат на добавление }
if a[i] < min then begin min := a[i]; j := i; end;
end;
until min = Inf;
for i := 1 to n do
if a[i] >= Inf then
write('-1 ') { Вершины нельзя достичь из начальной }
else
write(a[i],' '); { Расстояние от начальной вершины = a[i] }
end;
Алгоритм Флойда
Алгоритм Флойда — Уоршелла —
динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного
графа. Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом.
Пусть вершины графа пронумерованы от 1 до $n$ и введено обозначение $d_{ij}^k$ для длины кратчайшего пути от $i$
до
$j$, который кроме самих вершин $i,; j$ проходит только через вершины $1 ldots k$.
Очевидно, что $d_{i j}^{0}$ – длина (вес) ребра $(i,;j)$, если таковое существует (в противном случае его длина
может быть обозначена как $infty$)
Существует два варианта значения $d_{i j}^{k},;k in mathbb (1,;ldots,;n)$:
- Кратчайший путь между $i,;j$ не проходит через вершину $k$, тогда $d_{i j}^{k}=d_{i j}^{k-1}$
- Существует более короткий путь между $i,;j$, проходящий через $k$, тогда он сначала идёт от $i$ до $k$, а
потом от $k$ до $j$. В этом случае, очевидно, $d_{i j}^{k}=d_{i k}^{k-1} + d_{k j}^{k-1}$
Таким образом, для нахождения значения функции достаточно выбрать минимум из двух обозначенных значений.
Тогда рекуррентная формула для $d_{i j}^k$ имеет вид:
$d_{i j}^0$ – длина ребра $(i,;j)$
$d_{i j}^{k} = min (d_{i j}^{k-1},; d_{i k}^{k-1} + d_{k j}^{k-1})$
Алгоритм Флойда – Уоршелла последовательно вычисляет все значения $d_{i j}^{k}$,
$forall i,; j$ для $k$ от 1 до $n$.
Полученные значения $d_{i j}^{n}$ являются длинами кратчайших путей между вершинами $i,; j$.
for k := 1 to n do { k - промежуточная вершина }
for i := 1 to n do { из i-ой вершины }
for j := 1 to n do { в j-ую вершину }
W[i][j] = min(W[i][j], W[i][k] + W[k][j]);
Алгоритм Прима
Алгоритм Прима — алгоритм построения минимального остовного дерева взвешенного связного
неориентированного графа. Алгоритм впервые был открыт в 1930 году чешским математиком Войцехом Ярником, позже
переоткрыт Робертом Примом в 1957 году, и, независимо от них, Э. Дейкстрой в 1959 году.
Построение начинается с дерева, включающего в себя одну (произвольную) вершину. В течение работы алгоритма дерево
разрастается, пока не охватит все вершины исходного графа. На каждом шаге алгоритма к текущему дереву
присоединяется
самое лёгкое из рёбер, соединяющих вершину из построенного дерева, и вершину не из дерева.
Вход: Связный неориентированный граф $G(V,E)$
Выход: Множество $T$ рёбер минимального остовного дерева
Обозначения:
- $d_i$ — расстояние от $i$-й вершины до построенной части дерева
- $p_i$ — предок $i$-й вершины, то есть такая вершина $u$, что $(i,u)$ самое короткое рёбро соединяющее $i$ с
вершиной из построенного дерева. - $w(i,j)$ — вес ребра $(i,j)$
- $Q$ — приоритетная очередь вершин графа, где ключ – $d_i$
- $T$ — множество ребер минимального остовного дерева
Псевдокод:
$T gets $ {}
Для каждой вершины $i in V$: $d_i gets infty$, $p_i gets nil$
$d_1 gets 0$
$Q gets V$
$v gets Extract.min(Q) $
Пока $Q$ не пуста:
Для каждой вершины $u$ смежной с $v$:
Если $u in Q$ и $w(v,u) < d[u]$: $d_u gets w(v,u)$, $p_u gets v$
$ v gets Extract.Min(Q)$
$ T gets T+(p[v],v)$
Поиск особых путей в графах
Поиск эйлерова цикла в графе
Поиск гамильтонова цикла в графе
Топологическая сортировка
Реализация через DFS.

Учимся находить кратчайший путь через простой двумерный алгоритм на Python
Как именно мы находим выход из лабиринта? Как быстрее всего проехать из точки А в ближайшую пиццерию? Можем ли мы провести игрового персонажа к выходу так, чтобы он не уперся в стену?
Поиск пути – типичная задача программирования, решаемая в самых разных ситуациях. Она известна в основном из навигационных задач и разработки игр. Но, изучив ключевые алгоритмы поиска пути, вы узнаете, что они применимы к более абстрактным задачам оптимизации и построения последовательностей.
В этом руководстве рассмотрен простейший алгоритм поиска пути, основанный на алгоритме Дейкстры. Этот алгоритм также известен под названием поиск по первому наилучшему совпадению, ключевая логика у него общая со многими другими алгоритмами, например, A*, заливка методом наводнения и диаграммы Вороного.
Здесь мы рассмотрим практическое применение этого алгоритма. Вам понадобятся базовые знания программирования и языка Python.
Настройка Python
Весь код к этому посту находится в репозитории path-finding. Его нужно клонировать и переключиться в ветку tutorial_1. Также установите пакет pygame, он понадобится нам для графики.
python3 -m pip install -U pygame
git clone git@github.com:mortoray/path-finding.git
cd path-finding
git checkout path_finding_1Теперь проверим, все ли сделали правильно:
python3 find-basic.pyДолжно появиться окно с клетками, а в клетках – цифры. Теперь можете закрыть это окно. Мы вернемся к нему позже.

Лабиринт
Поиск пути – это продвижение из точки А в точку B. Алгоритм может описывать прогулку человека по парку, движение автомобиля по городу, либо курс персонажа, который преследует вас в игре. Давайте сведем все эти окружения к абстракции, которую назовем «лабиринт».
В этом руководстве создается Евклидов алгоритм, представляющий собой двумерную решетку клеток. В таком лабиринте можно двигаться лишь в четырех направлениях, перемещаясь в клетку, смежную с данной. Необходимо перейти из начальной точки в конечную.

На схеме стартовая клетка обозначена желтым цветом, в ней стоит “0”. Все допустимые шаги обозначены как “1”. Мы должны перейти в зеленую клетку, это наша цель.
Запускаем код
В коде предоставлена функция, создающая за нас простейший лабиринт. Нужно разобраться, как использовать алгоритм поиска пути для генерации гораздо более интересных лабиринтов, но пока давайте просто вызовем функцию create_wall_maze.
import mortoray_path_finding as mpf
maze = mpf.create_wall_maze( 20, 12 )Мы создали лабиринт размером 20x12. Поле maze.board – это решетка из объектов Cell. Нам нужен способ отобразить наш лабиринт.
finder = mpf.Finder()
finder.set_board(maze.board)
finder.run()Исходный файл: tutorial_1_1.py
Finder – это утилита, отображающая за нас лабиринт. Серые клетки свободны, то есть, путь может пройти через них. Коричневые клетки – это стены, через них путь пройти не может. В каждой из клеток также записан ноль, это значение Cell.count для данной позиции. Оно пригодится нам при поиске пути.

Измерение расстояния
Поиск пути во многом основан на исходном алгоритме Дейкстры. Существует множество его вариаций, например, алгоритм Флойда-Уоршелла, он же B*. Они действуют по схожему принципу: в них используются списки узлов и подсчитывается расстояние. Для разных ситуаций можно сочетать различные приемы.
Алгоритм, который мы сейчас рассматриваем, действует так: мы измеряем расстояние от стартовой позиции. Посещая клетки, мы отслеживаем, сколько шагов нам потребовалось, чтобы добраться до клетки, и на каждой итерации алгоритма подсчитывается расстояние. В конечном итоге, мы либо находим расстояние до целевой клетки, либо измерим расстояния до всех клеток в решетке.
Ниже в общих чертах изложен весь процесс. Каждый шаг взаимосвязан со всеми прочими, поэтому понять шаги в отдельности может быть сложно. Ниже приведен список, к которому вы, возможно, несколько раз вернетесь, чтобы понять, как согласуются друг с другом все эти шаги.
-
Получаем из списка открытых узлов тот узел, от которого нас отделяет наименьшее расстояние
-
Вычисляем расстояние до каждого из соседних узлов
-
Если расстояние до соседнего узла меньше, чем вычисленное – то добавляем этот узел в список открытых
Термины
Для начала рассмотрим некоторые термины, поскольку они могут быть вам неизвестны.
«Узел» – это общий термин, применимый в графах любых типов. Узел может представлять собой пересечение дорог на карте или, в нашем случае, стык клеток в лабиринте. У каждого узла есть местоположение, и от узла прокладываются пути к ближайшим узлам. В теории графов узлы также называются «вершинами».
Узлы, которые можно соединить, проложив между ними путь, являются соседними. Путь между узлами-соседями характеризуется расстоянием, для которого есть более общий термин «стоимость». В теории графов путь называют «ребром».
«Список открытых узлов» – это в буквальном смысле список узлов. «Открытые» узлы – это узлы, которые алгоритм все равно должен проверить. Например, если вы ищете елочные игрушки, разложенные в ящиках у вас в подвале, то вы просматриваете каждый из ящиков и отмечаете его в списке. Если внутри большого ящика обнаружатся более мелкие, то их также можно добавить в список.
Алгоритм
Алгоритм, реализованный в этой функции, называется fill_shortest_path. Держите его перед глазами, читая это объяснение. Эта функция непосредственно не находит кратчайший путь, а измеряет расстояние от стартовой позиции до других клеток в лабиринте. Позже мы рассмотрим, как эта информация используется для генерации пути.
def fill_shortest_path(board, start, end, max_distance = math.inf):
nboard = board.clone()
nboard.clear_count(math.inf)“Список открытых узлов” – это вектор позиций в решетке. В нем содержатся все местоположения, необходимые нам для поиска пути. Инициализируем список стартовой позицией лабиринта. Также мы должны установить счетчик в 0, поскольку на старте расстояние равно нулю.
nboard.at( start ).count = 0
open_list = [ start ]Этого достаточно, чтобы запустить алгоритм. Перебираем узлы, пока open_list не опустеет.
while open_list:
cur_pos = open_list.pop(0)
cur_cell = nboard.at( cur_pos )Подождите, разве алгоритм не требует перейти к узлу, расстояние до которого является наименьшим? Этот код просто берет следующий узел в списке. Он работает, даже если взять случайный узел, даже если временная сложность в таком случае оказывается гораздо выше. В нашем коде это не важно, так как следующий узел – как раз тот, расстояние до которого является наименьшим. Почему так – будет показано позже.
Для каждого узла рассмотрим всех его соседей.
# (x,y) смещения от текущей клетки
neighbours = [ [-1,0], [1,0], [0,-1], [0,1] ]
for neighbour in neighbours:
ncell_pos = mpf.add_point(cur_pos, neighbour)
if not nboard.is_valid_point(ncell_pos):
continue
cell = nboard.at( ncell_pos )Каждый элемент в neighbors – это Евклидово смещение от текущей клетки до соседней. Например, [-1,0] – это сосед слева. Если cur_pos равно [ 5, 7 ], то сложив его с [-1, 0] получим [4, 7], то есть, ход на клетку влево. Аналогично, [1,0] – это движение в положительном направлении по оси x, то есть, на клетку вправо. [0,-1] влияет только на y и является переходом на одну позицию вверх, тогда как [0,1] – на одну вниз.
Пользуясь численными абстракциями направлений, можно в рамках данного алгоритма точно так же обработать любые другие переходы. Можно учесть и другие направления, например, [1,1], это ход по диагонали вверх и далее вправо. Но при этом мы должны держать в уме и края решетки, за что и отвечает is_valid_point. Например, если мы дойдем до правого края решетки, то смещение [1,0], соответствующее одному переходу вправо, выведет нас за пределы графа, поэтому мы такой ход пропустим.
Также будем пропускать все непустые клетки, поскольку это стены лабиринта, и пройти через них мы не можем.
if cell.type != mpf.CellType.Empty:
continueПереходим к вычислению расстояния.
dist = cur_cell.count + 1Поскольку мы все время движемся по прямой, клетка за клеткой, здесь можно вспомнить о «Манхэттенском расстоянии», то есть, расстояниями между двумя точками, которое можно покрывать лишь в направлении x или y, причем, ни в один ход нельзя перейти сразу по двум осям. Название обусловлено тем, как пересекаются улицы на Манхэттене, образующие именно такую сетку. Манхэттенское расстояние применимо к Евклидовой геометрии, например, к такой сетке, с которой мы здесь работаем.
Если это расстояние меньше, чем до соседа, то мы укажем нового соседа и добавим его в список открытых узлов.
if cell.count > dist:
cell.count = dist
cell.path_from = cur_cell
open_list.append(ncell_pos)Используем обобщенное поле cell.count для измерения расстояния, а также обновим поле path_from, указывающее, каким путем мы пришли в данную точку.
Ранее мы говорили, что первым в open_list всегда идет узел с наименьшим значением count. Уже понятно, почему, ведь каждый соседний узел удален от нас ровно на 1. Стартовый узел считается как 0, поэтому добавляем в список открытых несколько узлов, значения которых равны 1. Теперь, поскольку все узлы мы обрабатываем по порядку, добавляем в список несколько двоек, пока не будут охвачены все единицы. В итоге у нас в списке останутся двойки. Продолжим охватывать двойки, также добавляя в список некоторые тройки.
Этот простой эффект гарантирует качественное решение. Но, расширяя вычисление расстояния и добавляя в него эвристику, мы не сможем полагаться только на это. В более сложном случае алгоритм особо не изменился бы, но мы использовали бы для open_list не вектор, а очередь с приоритетами.
Визуализируем
Давайте уделим немного времени визуализации. Вызовем fill_shortest_path из кода, входящего в дистрибутив.
import mortoray_path_finding as mpf
maze = mpf.maze.create_wall_maze( 20, 12 )
filled = mpf.tutorial_1.fill_shortest_path(maze.board, maze.start, maze.end)
finder = mpf.draw.Finder()
finder.set_board(filled)
finder.run()Исходник: tutorial_1_2.py
Откроется такое окно, как показано ниже. Стартовая клетка обозначена желтым, в ней стоит 0. Числа увеличиваются по мере отдаления от этой точки, с инкрементом в единицу. Все клетки в решетке обозначены в соответствии с манхэттенским расстоянием от стартовой точки до них. Находим клетку, обозначенную зеленым, и вычисляем, каково расстояние от стартовой точки до нее.

Получение пути
Кратчайшего пути у нас пока нет, но есть пара способов, которыми его можно получить.
Можно найти обратный путь от узла назначения к начальному, просматривая всех соседей и всякий раз находя соседа с наименьшим числом. От этого узла операция повторяется, и так пока не дойдем до старта. Поскольку числа обозначают расстояние до старта, мы, каждый раз переходя к наименьшему числу, найдем кратчайший путь назад.
Могут найтись и такие точки, из которых у нас будет несколько вариантов перехода. Например, вы можете находиться в десятке, к которой прилегают две девятки – возможно, оба пути через девятки окажутся в равной степени хороши.
Альтернативный способ – отслеживать путь, заполняя расстояния. Это именно тот код, который мы пока игнорировали.
if cell.count > dist:
cell.count = dist
cell.path_from = cur_cell
open_list.append(ncell_pos)Всякий раз, добавляя узел в список открытых узлов, мы также устанавливаем cell.path_from. Здесь хранятся записи о кратчайшем входящем пути, что упрощает отслеживание обратного курса от места назначения.
def backtrack_to_start(board, end):
""" Возвращает путь до конечной точки, при этом предполагается, что поле заполнялось при помощи алгоритма fill_shortest_path """
cell = board.at( end )
path = []
while cell != None:
path.append(cell)
cell = cell.path_from
return pathВ главном коде можно добавить вызов этой функции, чтобы в окне выводился путь от начальной до конечной точки.
import mortoray_path_finding as mpf
maze = mpf.maze.create_wall_maze( 20, 12 )
filled = mpf.tutorial_1.fill_shortest_path(maze.board, maze.start, maze.end)
path = mpf.tutorial_1.backtrack_to_start(filled, maze.end)
finder = mpf.draw.Finder()
finder.set_board(filled)
finder.set_path(path)
finder.run()Исходник: tutorial_1_3.py

Здесь есть любопытный момент: функция fill_shortest_path вычисляет расстояние «от старта» для каждой клетки, а не только для конечной. Тот же самый код для отслеживания обратного пути до любого узла. Оказывается, такие исчерпывающие знания могут во многих отношениях пригодиться при поиске пути. Но, если наша приоритетная цель – оптимизация, то мы адаптируем алгоритм так, чтобы он прекращал поиск, как только найдет выход из лабиринта. Также есть алгоритм A*, использующий эвристику, которая позволяет обходиться без сканирования всей карты.
Заключение
В этом руководстве было рассмотрено, как найти выход из простого двумерного лабиринта. Ключевой алгоритм ведет список открытых узлов, измеряя расстояние от узла до соседних ему узлов и обновляя информацию о кратчайших маршрутах. В данной логике наиболее важен гибкий поиск маршрута. Алгоритм применим к решению многих задач, например, эвристического поиска пути, заполнения методом заливки и работы с диаграммами Вороного.
