Как найти кратчайший путь в ориентированном графе

Как найти кратчайший путь в ориентированном графе

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 августа 2021 года; проверки требуют 7 правок.

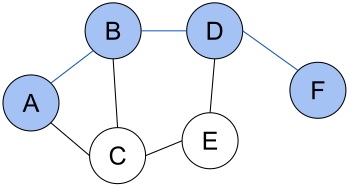
Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.

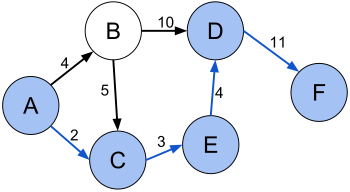
Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.

Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь.

Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для её решения[⇨].

У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.

Значимость данной задачи определяется её различными практическими применениями[⇨]. Например, в GPS-навигаторах осуществляется поиск кратчайшего пути между точкой отправления и точкой назначения. В качестве вершин выступают перекрёстки, а дороги являются рёбрами, которые лежат между ними. Если сумма длин дорог между перекрёстками минимальна, тогда найденный путь самый короткий.

Определение[править | править код]

Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.

Граф представляет собой совокупность непустого множества вершин и рёбер (наборов пар вершин). Две вершины на графе смежны, если они соединяются общим ребром. Путь в неориентированном графе представляет собой последовательность вершин P=(v_{1},v_{2},ldots ,v_{n})in Vtimes Vtimes ldots times V, таких что v_{i} смежна с v_{{i+1}} для 1leq i<n. Такой путь P называется путём длиной n из вершины v_{1} в v_{n} (i указывает на номер вершины пути и не имеет никакого отношения к нумерации вершин на графе).

Пусть e_{{i,j}} — ребро соединяющее две вершины: v_{i} и v_{j}. Дана весовая функция f:Erightarrow {mathbb {R}}, которая отображает ребра на их веса, значения которых выражаются действительными числами, и неориентированный граф G. Тогда кратчайшим путём из вершины v в вершину v' будет называться путь P=(v_{1},v_{2},ldots ,v_{n}) (где v_{1}=v и v_{n}=v'), который имеет минимальное значение суммы sum _{{i=1}}^{{n-1}}f(e_{{i,i+1}}). Если все ребра в графе имеют единичный вес, то задача сводится к определению наименьшего количества обходимых ребер.

Существуют различные постановки задачи о кратчайшем пути:

  • Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
  • Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
  • Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.

В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объём затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).

Задача о кратчайшем пути с учётом дополнительных ограничений[править | править код]

Задача о кратчайшем пути очень часто встречается в ситуации, когда необходимо учитывать дополнительные ограничения. Наличие их может значительно повысить сложность задачи[1]. Примеры таких задач:

  1. Кратчайший путь, проходящий через заданное множество вершин. Можно рассматривать два ограничения: кратчайший путь должен проходить через выделенное множество вершин, и кратчайший путь должен содержать как можно меньше невыделенных вершин. Первое из них хорошо известна в теории исследования операций[2].
  2. Минимальное покрытие вершин ориентированного графа путями. Осуществляется поиск минимального по числу путей покрытия графа, а именно подмножества всех s-t путей, таких что, каждая вершина ориентированного графа принадлежит хотя бы одному такому пути[3].
  3. Задача о требуемых путях. Требуется найти минимальное по мощности множество s-t путей P={p_{1},dots ,p_{m}} такое, что для любого t_{i}in R найдется путь p_{j}in P, накрывающий его. R={t_{1},dots ,t_{k}} — множество некоторых путей в ориентированном графе G[4].
  4. Минимальное покрытие дуг ориентированного графа путями. Задача состоит в отыскании минимального по числу путей подмножества всех путей, такого, что каждая дуга принадлежит хотя бы одному такому пути. При этом возможно дополнительное требование о том, чтобы все пути исходили из одной вершины[5].

Алгоритмы[править | править код]

В связи с тем, что существует множество различных постановок данной задачи, есть
наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:

  • Алгоритм Дейкстры находит кратчайший путь от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса[6].
  • Алгоритм Беллмана — Форда находит кратчайшие пути от одной вершины графа до всех остальных во взвешенном графе. Вес рёбер может быть отрицательным.
  • Алгоритм поиска A* находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), используя алгоритм поиска по первому наилучшему совпадению на графе.
  • Алгоритм Флойда — Уоршелла находит кратчайшие пути между всеми вершинами взвешенного ориентированного графа[6].
  • Алгоритм Джонсона находит кратчайшие пути между всеми парами вершин взвешенного ориентированного графа.
  • Алгоритм Ли (волновой алгоритм) основан на методе поиска в ширину. Находит путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (рёбер). Основное применение — трассировки электрических соединений на кристаллах микросхем и на печатных платах. Также используется для поиска кратчайшего расстояния на карте в стратегических играх.
  • Поиск кратчайшего пути на основе алгоритма Килдала[7].

В работе (Черкасский и др., 1993)[8] представлено ещё несколько алгоритмов для решения этой задачи.

Задача поиска кратчайшего пути из одной вершины во все остальные[править | править код]

В такой постановке задачи осуществляется поиск кратчайшего пути из вершины v во все остальные вершины на графе.

Невзвешенный ориентированный граф[править | править код]

Алгоритм Сложность Автор
Поиск в ширину O(V+E)

Ориентированный граф с неотрицательными весами[править | править код]

Алгоритм Сложность Автор
– O(V2EL) Форд 1956
Алгоритм Беллмана — Форда O(VE) Беллман 1958[9], Мур 1957[10]
– O(V2 log V) Данциг 1958, Данциг 1960, Minty (cf. Pollack&Wiebenson 1960), Whiting&Hillier 1960
Алгоритм Дейкстры со списком. O(V2) Leyzorek et al. 1957[11], Дейкстра 1959[12]
Алгоритм Дейкстры с модифицированной двоичной кучей O((E + V) log V) –
. . . . . . . . .
Алгоритм Дейкстры с использованием фибоначчиевой кучи O(E + V log V) Фридман&Тарьян 1984[13], Фридман&Тарьян 1987[14]
– O(E log log L) Джонсон 1982, Карлссон&Поблете 1983
Алгоритм Габова O(E logE/V L) Габов 1983, Габов 1985
– O(E + V√log L) Ахуджа et al. 1990

Ориентированный граф с произвольными весами[править | править код]

Алгоритм Сложность Автор
Алгоритм Беллмана — Форда O(VE) Беллман[9], Мур[10]
Алгоритм Левита O(VE)

Задача о кратчайшем пути между всеми парами вершин[править | править код]

Задача о кратчайшем пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена Симбелом в 1953 году[15], который обнаружил, что она может быть решена за линейное количество манипуляций (умножения) с матрицей. Сложность такого алгоритма O(V4).

Так же для решения данной задачи существуют другие более быстрые алгоритмы, такие как Алгоритм Флойда — Уоршелла со сложностью O(V3), и
Алгоритм Джонсона (является комбинацией алгоритмов Бэллмана-Форда и Дейкстры) со сложностью O(VE + V2 log V).

Применение[править | править код]

Задача о поиске кратчайшего пути на графе может быть интерпретирована по-разному и применяться в различных областях. Далее приведены примеры различных применений задачи. Другие применения изучаются в дисциплине, которая занимается исследованием операций[16].

Картографические сервисы[править | править код]

Алгоритмы нахождения кратчайшего пути на графе применяются для нахождения путей между физическими объектами на таких картографических сервисах, как карты Google или OpenStreetMap. В обучающем видео от Google можно узнать различные эффективные алгоритмы, которые применяются в данной сфере[17].

Недетерминированная машина[править | править код]

Если представить недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра определяют возможные переходы, тогда алгоритмы поиска кратчайшего пути могут быть применены для поиска оптимальной последовательности решений для достижения главной цели. Например, если вершинами являются состояния Кубика Рубика, а ребром представляет собой одно действие над кубиком, тогда алгоритм может быть применён для поиска решения с минимальным количеством ходов.

Сети дорог[править | править код]

Задача поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог.

Сеть дорог можно представить в виде графа с положительными весами. Вершины являются дорожными развязками, а ребра дорогами, которые их соединяют. Веса рёбер могут соответствовать протяжённости данного участка, времени необходимому для его преодоления или стоимости путешествия по нему. Ориентированные ребра можно использовать для представления односторонних улиц. В таком графе можно ввести характеристику, которая указывает на то, что одни дороги важнее других для длительных путешествий (например автомагистрали). Она была формализована в понятии (идее) о магистралях[18].

Для реализации подхода, где одни дороги важнее других, существует множество алгоритмов. Они решают задачу поиска кратчайшего пути намного быстрее, чем аналогичные на обычных графах.
Подобные алгоритмы состоят из двух этапов:

  1. этап предобработки. Производится предварительная обработка графа без учёта начальной и конечной вершины (может длиться до нескольких дней, если работать с реальными данными). Обычно выполняется один раз и потом используются полученные данные.
  2. этап запроса. Осуществляется запрос и поиск кратчайшего пути, при этом известны начальная и конечная вершина.

Самый быстрый алгоритм может решить данную задачу на дорогах Европы или Америки за доли микросекунды[19].

Другие подходы (техники), которые применяются в данной сфере:

  • ALT
  • Arc Flags
  • Contraction hierarchies
  • Transit Node Routing
  • Reach based Pruning
  • Labeling

Похожие задачи[править | править код]

Существуют задачи, которые похожи на задачу поиска кратчайшего пути на графе.

  • Поиск кратчайшего пути в вычислительной геометрии (см. евклидов кратчайший путь).
  • Задача коммивояжёра. Требуется найти кратчайший маршрут, проходящий через указанные города (вершины) хотя бы по одному разу с последующим возвратом в исходный город. Данная задача относится к классу NP-трудных задач в отличие от задачи поиска кратчайшего пути, которая может быть решена за полиномиальное время в графах без циклов. Задача коммивояжёра решается неэффективно для больших наборов данных.
  • Задача канадского путешественника и задача стохастического поиска кратчайшего пути являются обобщением рассматриваемой задачи, в которых обходимый граф заранее полностью неизвестен и изменяется во времени или следующий проход по графу вычисляется на основе вероятностей.
  • Задача поиска кратчайшего пути, когда в графе происходят преобразования. Например, изменяется вес ребра или удаляется вершина[20].

Постановка задачи линейного программирования[править | править код]

Пусть дан направленный граф (V, A), где V — множество вершин и A — множество рёбер, с начальной вершиной обхода s, конечной t и весами wij для каждого ребра (i, j) в A. Вес каждого ребра соответствует переменной программы xij.

Тогда задача ставится следующим образом: найти минимум функции F=sum _{{ijin A}}w_{{ij}}x_{{ij}}, где x_{{ij}}geq 0, при условии что для всех i и j выполняется следующее неравенство: sum _{j}x_{{ij}}-sum _{j}x_{{ji}}={begin{cases}1,&{text{if }}i=s;\-1,&{text{if }}i=t;\0,&{text{ otherwise.}}end{cases}}

См. также[править | править код]

  • IEEE 802.1aq
  • Транспортная сеть
  • Двунаправленный поиск

Примечания[править | править код]

  1. ↑ Применение теории графов в программировании, 1985.
  2. ↑ Применение теории графов в программировании, 1985, с. 138—139.
  3. ↑ Применение теории графов в программировании, 1985, с. 139—142.
  4. ↑ Применение теории графов в программировании, 1985, с. 144—145.
  5. ↑ Применение теории графов в программировании, 1985, с. 145—148.
  6. ↑ 1 2 Дискретная математика. Комбинаторная оптимизация на графах, 2003.
  7. ↑ Применение теории графов в программировании, 1985, с. 130—131.
  8. ↑ Cherkassky, Goldberg, Radzik, 1996.
  9. ↑ 1 2 Bellman Richard, 1958.
  10. ↑ 1 2 Moore, 1957.
  11. ↑ M. Leyzorek, 1957.
  12. ↑ Dijkstra, 1959.
  13. ↑ Michael Fredman Lawrence, 1984.
  14. ↑ Fredman Michael, 1987.
  15. ↑ Shimbel, 1953.
  16. ↑ Developing algorithms and software for geometric path planning problems, 1996.
  17. ↑ Fast route planning.
  18. ↑ Highway Dimension, 2010.
  19. ↑ A Hub-Based Labeling Algorithm, 2011.
  20. ↑ Ladyzhensky Y., Popoff Y. Algorithm, 2006.

Литература[править | править код]

  • Евстигнеев В. А. Глава 3. Итеративные алгоритмы глобального анализа графов. Пути и покрытия // Применение теории графов в программировании / Под ред. А. П. Ершова. — Москва: Наука. Главная редакция физико-математической литературы, 1985. — С. 138—150. — 352 с.
  • Алексеев В.Е., Таланов В.А. Глава 3.4. Нахождения кратчайших путей в графе // Графы. Модели вычислений. Структуры данных. — Нижний Новгород: Издательство Нижегородского гос. университета, 2005. — С. 236—237. — 307 с. — ISBN 5–85747–810–8. Архивная копия от 13 декабря 2013 на Wayback Machine
  • Галкина В.А. Глава 4. Построение кратчайших путей в ориентированном графе // Дискретная математика. Комбинаторная оптимизация на графах. — Москва: Издательство “Гелиос АРВ”, 2003. — С. 75—94. — 232 с. — ISBN 5–85438–069–2.
  • Берж К. Глава 7. Задача о кратчайшем пути // Теория графов и её применения = Theorie des graphes et ses applications / Под ред. И. А. Вайнштейна. — Москва: Издательство иностранной литературы, 1962. — С. 75—81. — 320 с.
  • Ойстин Оре. Теория графов / Под ред. И. М. Овчинниковой. — Издательство наука, 1980. — 336 с. Архивная копия от 15 декабря 2013 на Wayback Machine
  • Виталий Осипов, Поиск кратчайших путей в дорожных сетях: от теории к реализации на YouTube.
  • Харари Ф. Глава 2. Графы // Теория графов / под ред. Г. П. Гаврилов — М.: Мир, 1973. — С. 27. — 301 с.
  • Cherkassky B. V., Goldberg A. V., Radzik T. Shortest paths algorithms: Theory and experimental evaluation (англ.) // Mathematical Programming — Springer Science+Business Media, 1996. — Vol. 73, Iss. 2. — P. 129–174. — ISSN 0025-5610; 1436-4646 — doi:10.1007/BF02592101
  • Ричард Беллман. On a routing problem // Quarterly of Applied Mathematics. — 1958. — Т. 16. — С. 87—90.
  • Dijkstra E. W. A note on two problems in connexion with graphs (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1959. — Vol. 1, Iss. 1. — P. 269—271. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01386390
  • Moore E. F. The shortest path through a maze (англ.) // Proceedings of an International Symposium on the Theory of Switching (Cambridge, Massachusetts, 2–5 April 1957) — Harvard University Press, 1959. — Vol. 2. — P. 285—292. — 345 p. — (Annals of the Computation Laboratory of Harvard University; Vol. 30) — ISSN 0073-0750
  • M. Leyzorek, R. S. Gray, A. A. Gray, W. C. Ladew, S. R. Meaker, R. M. Petry, R. N. Seitz. Investigation of Model Techniques — First Annual Report — 6 June 1956 — 1 July 1957 — A Study of Model Techniques for Communication Systems (англ.). — Cleveland, Ohio: Case Institute of Technology, 1957.
  • Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) : journal. — Институт инженеров электротехники и электроники, 1984. — P. 338—346. — ISBN 0-8186-0591-X. — doi:10.1109/SFCS.1984.715934. Архивировано 11 октября 2012 года.
  • Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) // Journal of the Association for Computing Machinery : journal. — 1987. — Vol. 34, no. 3. — P. 596—615. — doi:10.1145/28869.28874.
  • Shimbel, Alfonso. Structural parameters of communication networks // Bulletin of Mathematical Biophysics. — 1953. — Т. 15, № 4. — С. 501—507. — doi:10.1007/BF02476438.
  • Sanders, Peter. Fast route planning. — Google Tech Talk, 2009. — 23 марта.. — «Шаблон:Inconsistent citations».
  • Chen, Danny Z. Developing algorithms and software for geometric path planning problems (англ.) // ACM Computing Surveys  (англ.) (рус. : journal. — 1996. — December (vol. 28, no. 4es). — P. 18. — doi:10.1145/242224.242246.
  • Abraham, Ittai; Fiat, Amos; Goldberg, Andrew V.; Werneck, Renato F. Highway Dimension, Shortest Paths, and Provably Efficient Algorithms (англ.) // ACM-SIAM Symposium on Discrete Algorithms : journal. — 2010. — P. 782—793.
  • Abraham, Ittai; Delling, Daniel; Goldberg, Andrew V.; Werneck, Renato F. A Hub-Based Labeling Algorithm for Shortest Paths on Road Networks. Symposium on Experimental Algorithms] (англ.) : journal. — 2011. — P. 230—241.
  • Kroger, Martin. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems (англ.) // Computer Physics Communications  (англ.) (рус. : journal. — 2005. — Vol. 168, no. 168. — P. 209—232. — doi:10.1016/j.cpc.2005.01.020.
  • Ladyzhensky Y., Popoff Y. Algorithm to define the shortest paths between all nodes in a graph after compressing of two nodes. Proceedings of Donetsk national technical university, Computing and automation. Vol.107. Donetsk (англ.) : journal. — 2006. — P. 68—75..[источник не указан 925 дней]
Источник

import java.util.ArrayList;

import java.util.HashSet;

import java.util.List;

import java.util.Set;

class Pair {

    int first, second;

    public Pair(int first, int second)

    {

        this.first = first;

        this.second = second;

    }

}

public class GFG {

    static final int infi = 1000000000;

    static class Node {

        int vertexNumber;

        List<Pair> children;

        Node(int vertexNumber)

        {

            this.vertexNumber = vertexNumber;

            children = new ArrayList<>();

        }

        void add_child(int vNumber, int length)

        {

            Pair p = new Pair(vNumber, length);

            children.add(p);

        }

    }

    static int[] dijkstraDist(List<Node> g, int s,

                              int[] path)

    {

        int[] dist = new int[g.size()];

        boolean[] visited = new boolean[g.size()];

        for (int i = 0; i < g.size(); i++) {

            visited[i] = false;

            path[i] = -1;

            dist[i] = infi;

        }

        dist[s] = 0;

        path[s] = -1;

        int current = s;

        Set<Integer> sett = new HashSet<>();

        while (true) {

            visited[current] = true;

            for (int i = 0;

                 i < g.get(current).children.size(); i++) {

                int v

                    = g.get(current).children.get(i).first;

                if (visited[v])

                    continue;

                sett.add(v);

                int alt = dist[current]

                          + g.get(current)

                                .children.get(i)

                                .second;

                if (alt < dist[v]) {

                    dist[v] = alt;

                    path[v] = current;

                }

            }

            sett.remove(current);

            if (sett.isEmpty())

                break;

            int minDist = infi;

            int index = 0;

            for (int a : sett) {

                if (dist[a] < minDist) {

                    minDist = dist[a];

                    index = a;

                }

            }

            current = index;

        }

        return dist;

    }

    void printPath(int[] path, int i, int s)

    {

        if (i != s) {

            if (path[i] == -1) {

                System.out.println("Path not found!!");

                return;

            }

            printPath(path, path[i], s);

            System.out.print(path[i] + " ");

        }

    }

    public static void main(String[] args)

    {

        List<Node> v = new ArrayList<>();

        int n = 4, s = 0, e = 5;

        for (int i = 0; i < n; i++) {

            Node a = new Node(i);

            v.add(a);

        }

        v.get(0).add_child(1, 1);

        v.get(0).add_child(2, 4);

        v.get(1).add_child(2, 2);

        v.get(1).add_child(3, 6);

        v.get(2).add_child(3, 3);

        int[] path = new int[v.size()];

        int[] dist = dijkstraDist(v, s, path);

        for (int i = 0; i < dist.length; i++) {

            if (dist[i] == infi) {

                System.out.printf("%d and %d are not "

                                      + "connectedn",

                                  i, s);

                continue;

            }

            System.out.printf(

                "Distance of %dth vertex "

                    + "from source vertex %d is: %dn",

                i, s, dist[i]);

        }

    }

}

Источник

Кратчайшие пути в графах. BFS. Dijkstra.

Задача

Дан ориентированный граф $G = (V, E)$, а также вершина $s$.
Найти длину кратчайшего пути от $s$ до каждой из вершин графа. Длина пути — количество рёбер в нём.

BFS

BFS — breadth-first search, или же поиск в ширину.

Этот алгоритм позволяет решать следующую задачу.

Алгоритм работает следующим образом.

  1. Создадим массив $dist$ расстояний. Изначально $dist[s] = 0$ (поскольку расстояний от вершины до самой себя равно $0$) и $dist[v] = infty$ для $v neq s$.
  2. Создадим очередь $q$. Изначально в $q$ добавим вершину $s$.
  3. Пока очередь $q$ непуста, делаем следующее:
    1. Извлекаем вершину $v$ из очереди.
    2. Рассматриваем все рёбра $(v, u) in E$. Для каждого такого ребра пытаемся сделать релаксацию: если $dist[v] + 1 &lt; dist[u]$, то мы делаем присвоение $dist[u] = dist[v] + 1$ и добавляем вершину $u$ в очередь.

Визуализации:

  • https://visualgo.net/mn/dfsbfs

  • https://www.hackerearth.com/practice/algorithms/graphs/breadth-first-search/visualize/

Интуитивное понимание алгоритма

Можно представить, что мы поджигаем вершину $s$. Каждый шаг алгоритма — это распространение огня на соседние вершины. Понятно, что огонь доберётся до вершины по кратчайшему пути.

Заметьте, что этот алгоритм очень похож на DFS — достаточно заменить очередь на стек и поиск в ширину станет поиском в глубину. Действительно, оба алгоритма при обработке вершины просто записывают всех непосещенных соседей, в которые из неё есть ребро, в структуру данных, и после этого выбирает следующую вершину для обработки в структуре данных. В DFS это стек (благодаря рекурсии), поэтому мы сначала записываем соседа, идем в обрабатываем его полностью, а потом начинаем обрабатывать следующего соседа. В BFS это очередь, поэтому мы кидаем сразу всех соседей, а потом начинаем обрабатывать вообще другую вершину – ту непосещенную, которую мы положили в очередь раньше всего.

Оба алгоритма позволяют обойти граф целиком – посетить каждую вершину ровно один раз. Поэтому они оба подходят для таких задач как:

  • поиск компонент связности
  • проверка графа на двудольность
  • построение остова

Реализация на C++

n — количество вершин в графе; adj — список смежности

vector<int> bfs(int s) {
    // длина любого кратчайшего пути не превосходит n - 1,
    // поэтому n - достаточное значение для "бесконечности";
    // после работы алгоритма dist[v] = n, если v недостижима из s
    vector<int> dist(n, n);
    dist[s] = 0;
    queue<int> q;
    q.push(s);

    while (!q.empty()) {
        int v = q.front();
        q.pop();
        for (int u : adj[v]) {
            if (dist[u] > dist[v] + 1) {
                dist[u] = dist[v] + 1;
                q.push(u);
            }
        }
    }

    return dist;
}

Свойства кратчайших путей

Обозначение: $d(v)$ — длина кратчайшего пути от $s$ до $v$.

Лемма 1.

Пусть $(u, v) in E$, тогда $d(v) leq d(u) + 1$.

Действительно, существует путь из $s$ в $u$ длины $d(u)$, а также есть ребро $(u, v)$, следовательно, существует путь из $s$ в $v$ длины $d(u) + 1$. А значит кратчайший путь из $s$ в $v$ имеет длину не более $d(u) + 1$,

Лемма 2.

Рассмотрим кратчайший путь от $s$ до $v$. Обозначим его как $u_1, u_2, dots u_k$ ($u_1 = s$ и $u_k = v$, а также $k = d(v) + 1$).
Тогда $forall (i &lt; k): d(u_i) + 1 = d(u_{i + 1})$.

Действительно, пусть для какого-то $i &lt; k$ это не так. Тогда, используя лемму 1, имеем: $d(u_i) + 1 &gt; d(u_{i + 1})$. Тогда мы можем заменить первые $i + 1$ вершин пути на вершины из кратчайшего пути из $s$ в $u_{i + 1}$. Полученный путь стал короче, но мы рассматривали кратчайший путь — противоречие.

Корректность

Утверждение.

  1. Расстояния до тех вершин, которые были добавлены в очередь, посчитаны корректно.
  2. Вершины лежат в очереди в порядке неубывания расстояния, притом разность между кратчайшими расстояними до вершин в очереди не превосходит $1$.

Докажем это по индукции по количеству итераций алгоритма (итерация — извлечение вершины из очереди и дальнейшая релаксация).

База очевидна.
Переход. Сначала докажем первую часть. Предположим, что $dist[v] + 1 &lt; dist[u]$, но $dist[v] + 1$ — некорректное расстояние до вершины $u$, то есть $dist[v] + 1 neq d(u)$. Тогда по лемме 1: $d(u) &lt; dist[v] + 1$. Рассмотрим предпоследнюю вершину $w$ на кратчайшем пути от $s$ до $u$. Тогда по лемме 2: $d(w) + 1 = d(u)$. Следовательно, $d(w) + 1 &lt; dist[v] + 1$ и $d(w) &lt; dist[v]$. Но тогда по предположению индукции $w$ была извлечена раньше $v$, следовательно, при релаксации из неё в очередь должна была быть добавлена вершина $u$ с уже корректным расстоянием. Противоречие.
Теперь докажем вторую часть. По предположению индукции в очереди лежали некоторые вершины $u_1, u_2, dots u_k$, для которых выполнялось следующее: $dist[u_1] leq dist[u_2] leq dots leq dist[u_k]$ и $dist[u_k] – dist[u_1] leq 1$. Мы извлекли вершину $v = u_1$ и могли добавить в конец очереди какие-то вершины с расстоянием $dist[v] + 1$. Если $k = 1$, то утверждение очевидно. В противном случае имеем $dist[u_k] – dist[u_1] leq 1 leftrightarrow dist[u_k] – dist[v] leq 1 leftrightarrow dist[u_k] leq dist[v] + 1$, то есть упорядоченность сохранилась. Осталось показать, что $(dist[v] + 1) – dist[u_2] leq 1$, но это равносильно $dist[v] leq dist[u_2]$, что, как мы знаем, верно.

Время работы

Из доказанного следует, что каждая достижимая из $s$ вершина будет добавлена в очередь ровно $1$ раз, недостижимые вершины добавлены не будут. Каждое ребро, соединяющее достижимые вершины, будет рассмотрено ровно $2$ раза. Таким образом, алгоритм работает за $O(V+ E)$ времени, при условии, что граф хранится в виде списка смежности.

Неориентированные графы

Если дан неориентированный граф, его можно рассматривать как ориентированный граф с двумя обратными друг другу ориентированными рёбрами.

Восстановление пути

Пусть теперь заданы 2 вершины $s$ и $t$, и необходимо не только найти длину кратчайшего пути из $s$ в $t$, но и восстановить какой-нибудь из кратчайших путей между ними. Всё ещё можно воспользоваться алгоритмом BFS, но необходимо ещё и поддерживать массив предков $p$, в котором для каждой вершины будет храниться предыдущая вершина на кратчайшем пути.

Поддерживать этот массив просто: при релаксации нужно просто запоминать, из какой вершины мы прорелаксировали в данную. Также будем считать, что $p[s] = -1$: у стартовой вершины предок — некоторая несуществующая вершина.

Восстановление пути делается с конца. Мы знаем последнюю вершину пути — это $t$. Далее, мы сводим задачу к меньшей, переходя к нахождению пути из $s$ в $p[t]$.

Реализация BFS с восстановлением пути

// теперь bfs принимает 2 вершины, между которыми ищется пути
// bfs возвращает кратчайший путь из s в t, или же пустой vector, если пути нет
vector<int> bfs(int s, int t) {
    vector<int> dist(n, n);
    vector<int> p(n, -1);
    dist[s] = 0;
    queue<int> q;
    q.push(s);

    while (!q.empty()) {
        int v = q.front();
        q.pop();
        for (int u : adj[v]) {
            if (dist[u] > dist[v] + 1) {
                p[u] = v;
                dist[u] = dist[v] + 1;
                q.push(u);
            }
        }
    }
    
    // если пути не существует, возвращаем пустой vector
    if (dist[t] == n) {
        return {};
    }

    vector<int> path;
    while (t != -1) {
        path.push_back(t);
        t = p[t];
    }
    
    // путь был рассмотрен в обратном порядке, поэтому его нужно перевернуть
    reverse(path.begin(), path.end());
    return path;
}

Проверка принадлежности вершины кратчайшему пути

Дан ориентированный граф $G$, найти все вершины, которые принадлежат хотя бы одному кратчайшему пути из $s$ в $t$.

Запустим из вершины $s$ в графе $G$ BFS — найдём расстояния $d_1$. Построим транспонированный граф $G^T$ — граф, в котором каждое ребро заменено на противоположное. Запустим из вершины $t$ в графе $G^T$ BFS — найдём расстояния $d_2$.

Теперь очевидно, что $v$ принадлежит хотя бы одному кратчайшему пути из $s$ в $t$ тогда и только тогда, когда $d_1(v) + d_2(v) = d_1(t)$ — это значит, что есть путь из $s$ в $v$ длины $d_1(v)$, а затем есть путь из $v$ в $t$ длины $d_2(v)$, и их суммарная длина совпадает с длиной кратчайшего пути из $s$ в $t$.

Кратчайший цикл в ориентированном графе

Найти цикл минимальной длины в ориентированном графе.

Попытаемся из каждой вершины найти кратчайший цикл, проходящий через неё, с помощью BFS. Это делается аналогично обычному BFS: мы должны найти расстояний от вершины до самой себя, при этом не считая, что оно равно $0$.

Итого, у нас $|V|$ запусков BFS, и каждый запуск работает за $O(|V| + |E|)$. Тогда общее время работы составляет $O(|V|^2 + |V| |E|)$. Если инициализировать массив $dist$ единожды, а после каждого запуска BFS возвращать исходные значения только для достижимых вершин, решение будет работать за $O(|V||E|)$.

Задача

Дан взвешенный ориентированный граф $G = (V, E)$, а также вершина $s$. Длина ребра $(u, v)$ равна $w(u, v)$. Длины всех рёбер неотрицательные.
Найти длину кратчайшего пути от $s$ до каждой из вершин графа. Длина пути — сумма длин рёбер в нём.

Алгоритм Дейкстры

Алгоритм Дейкстры решает приведённую выше задачу. Он работает следующим образом.

  1. Создать массив $dist$ расстояний. Изначально $dist[s] = 0$ и $dist[v] = infty$ для $v neq s$.
  2. Создать булёв массив $used$, $used[v] = 0$ для всех вершин $v$ — в нём мы будем отмечать, совершалась ли релаксация из вершины.
  3. Пока существует вершина $v$ такая, что $used[v] = 0$ и $dist[v] neq infty$, притом, если таких вершин несколько, то $v$ — вершина с минимальным $dist[v]$, делать следующее:
    1. Пометить, что мы совершали релаксацию из вершины $v$, то есть присвоить $used[v] = 1$.
    2. Рассматриваем все рёбра $(v, u) in E$. Для каждого ребра пытаемся сделать релаксацию: если $dist[v] + w(v, u) &lt; dist[u]$, присвоить $dist[u] = dist[v] + w(v, u)$.

Иными словами, алгоритм на каждом шаге находит вершину, до которой расстояние сейчас минимально и из которой ещё не была произведена релаксация, и делает её.

Посчитаем, за сколько работает алгоритм. Мы $V$ раз ищем вершину минимальным $dist$, поиск минимума у нас линейный за $O(V)$, отсюда $O(V^2)$. Обработка ребер у нас происходит суммарно за $O(E)$, потому что на каждое ребро мы тратим $O(1)$ действий. Так мы находим финальную асимптотику: $O(V^2 + E)$.

Реализация на C++

Рёбра будем хранить как pair<int, int>, где первое число пары — куда оно ведёт; а второе — длина ребра.

// INF - infinity - бесконечность
const long long INF = (long long) 1e18 + 1;

vector<long long> dijkstra(int s) {
    vector<long long> dist(n, INF);
    dist[s] = 0;
    vector<bool> used(n);
    
    while (true) {
        // находим вершину, из которой будем релаксировать
        int v = -1;
        for (int i = 0; i < n; i++) {
            if (!used[i] && (v == -1 || dist[i] < dist[v])) {
                v = i;
            }
        }
        
        // если не нашли подходящую вершину, прекращаем работу алгоритма
        if (v == -1) {
            break;
        }
        
        for (auto &e : adj[v]) {
            int u = e.first;
            int len = e.second;
            if (dist[u] > dist[v] + len) {
                dist[u] = dist[v] + len;
            }
        }
    }
    
    return dist;
}

Восстановление пути

Восстановление пути в алгоритме Дейкстры делается аналогично восстановлению пути в BFS (и любой динамике).

Дейкстра на сете

Искать вершину с минимальным $dist$ можно гораздо быстрее, используя такую структуру данных как очередь с приоритетом. Нам нужно хранить пары $(dist, index)$ и уметь делать такие операции:

  • Извлечь минимум (чтобы обработать новую вершину)
  • Удалить вершину по индексу (чтобы уменьшить $dist$ до какого-то соседа)
  • Добавить новую вершину (чтобы уменьшить $dist$ до какого-то соседа)

Для этого используют, например, кучу или сет. Удобно помимо сета хранить сам массив dist, который его дублирует, но хранит элементы по порядку. Тогда, чтобы заменить значение $(dist_1, u)$ на $(dist_2, u)$, нужно удалить из сета значение $(dist[u], u)$, сделать $dist[u] = dist_2;$ и добавить в сет $(dist[u], u)$.

Данный алгоритм будет работать за $V O(log V)$ извлечений минимума и $O(E log V)$ операций уменьшения расстояния до вершины (может быть сделано после каждого ребра). Поэтому алгоритм работает за $O(E log V)$.

Заметьте, что этот алгоритм не лучше и не хуже, чем без сета, который работает за $O(V^2 + E)$. Ведь если $E = O(V^2)$ (граф почти полный), то Дейкстра без сета работает быстрее, а если, наример, $E = O(V)$, то Дейкстра на сете работает быстрее. Учитывайте это, когда выбираете алгоритм.

Источник

Алгоритм Флойда (алгоритм Флойда–Уоршелла) — алгоритм нахождения длин кратчайших путей между всеми парами вершин во взвешенном ориентированном графе. Работает корректно, если в графе нет циклов отрицательной величины, а в случае, когда такой цикл есть, позволяет найти хотя бы один такой цикл. Алгоритм работает за времени и использует памяти. Разработан в 1962 году.

Содержание

  • 1 Алгоритм
    • 1.1 Постановка задачи
    • 1.2 Описание
    • 1.3 Код (в первом приближении)
    • 1.4 Код (окончательный)
    • 1.5 Пример работы
  • 2 Вывод кратчайшего пути
    • 2.1 Модифицированный алгоритм
  • 3 Нахождение отрицательного цикла
  • 4 Построение транзитивного замыкания
    • 4.1 Псевдокод
    • 4.2 Доказательство
    • 4.3 Оптимизация с помощью битовых масок
  • 5 Источники информации

Алгоритм

Постановка задачи

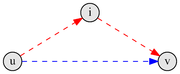
Текущий (синий) путь и потенциально более короткий (красный)

Дан взвешенный ориентированный граф , в котором вершины пронумерованы от до .

Требуется найти матрицу кратчайших расстояний , в которой элемент либо равен длине кратчайшего пути из в , либо равен , если вершина не достижима из .

Описание

Обозначим длину кратчайшего пути между вершинами и , содержащего, помимо и , только вершины из множества как , .

На каждом шаге алгоритма, мы будем брать очередную вершину (пусть её номер — ) и для всех пар вершин и вычислять . То есть, если кратчайший путь из в , содержащий только вершины из множества , проходит через вершину , то кратчайшим путем из в является кратчайший путь из в , объединенный с кратчайшим путем из в . В противном случае, когда этот путь не содержит вершины , кратчайший путь из в , содержащий только вершины из множества является кратчайшим путем из в , содержащим только вершины из множества .

Код (в первом приближении)

for 
    for 
        for

В итоге получаем, что матрица и является искомой матрицей кратчайших путей, поскольку содержит в себе длины кратчайших путей между всеми парами вершин, имеющих в качестве промежуточных вершин вершины из множества , что есть попросту все вершины графа. Такая реализация работает за времени и использует памяти.

Код (окончательный)

Утверждается, что можно избавиться от одной размерности в массиве , т.е. использовать двумерный массив . В процессе работы алгоритма поддерживается инвариант , а, поскольку, после выполнения работы алгоритма , то тогда будет выполняться и .

Утверждение:

В течение работы алгоритма Флойда выполняются неравенства: .

После инициализации все неравенства, очевидно, выполняются. Далее, массив может измениться только в строчке 5.

Докажем второе неравенство индукцией по итерациям алгоритма.

Пусть также — значение сразу после итерации.

Покажем, что , зная, что .

Рассмотрим два случая:

  • Значение стало меньше, чем . Тогда (выполняется на шаге , по индукционному предположению) (в силу выполнения 7-ой строчки алгоритма на -ой итерации и невозрастания элементов массива ) .
  • В ином случае всё очевидно: , и неравенство тривиально.

Докажем первое неравенство от противного.

Пусть неравенство было нарушено, рассмотрим момент, когда оно было нарушено впервые. Пусть это была -ая итерация и в этот момент изменилось значение и выполнилось . Так как изменилось, то (так как ранее ) (по неравенству треугольника) .

Итак — противоречие. 

func floyd(w):
    d =                 // изначально 
    for 
        for 
            for 
                d[u][v] = min(d[u][v], d[u][i] + d[i][v])

Данная реализация работает за время , но требует уже памяти. В целом, алгоритм Флойда очень прост, и, поскольку в нем используются только простые операции, константа, скрытая в определении весьма мала.

Пример работы

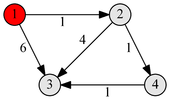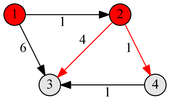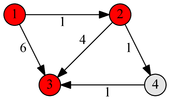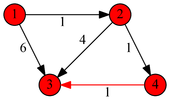
0.png Floyd 1.png Floyd 2.png Floyd algo 3.png Floyd 4.png

Вывод кратчайшего пути

Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив , в котором будет храниться номер вершины, в которую надо пойти следующей, чтобы дойти из в по кратчайшему пути.

Модифицированный алгоритм

func floyd(w):
    d =                // изначально 
    for 
        for 
            for 
                if d[u][i] + d[i][v] < d[u][v]
                    d[u][v] = d[u][i] + d[i][v]
                    next[u][v] = next[u][i]

func getShortestPath(u, v):
    if d[u][v] == 
        print "No path found"                 // между вершинами u и v нет пути
    c = u
    while c != v
        print c
        c = next[c][v]
    print v

Нахождение отрицательного цикла

Утверждение:

При наличии цикла отрицательного веса в матрице появятся отрицательные числа на главной диагонали.
Так как алгоритм Флойда последовательно релаксирует расстояния между всеми парами вершин , в том числе и теми, у которых , а начальное расстояние между парой вершин равно нулю, то релаксация может произойти только при наличии вершины такой, что , что эквивалентно наличию отрицательного цикла, проходящего через вершину .

Из доказательства следует, что для поиска цикла отрицательного веса необходимо, после завершения работы алгоритма, найти вершину , для которой , и вывести кратчайший путь между парой вершин . При этом стоит учитывать, что при наличии отрицательного цикла расстояния могут уменьшаться экспоненциально. Для предотвращения переполнения все вычисления стоит ограничивать снизу величиной , либо проверять наличие отрицательных чисел на главной диагонали во время подсчета.

Построение транзитивного замыкания

Сформулируем нашу задачу в терминах графов: рассмотрим граф , соответствующий отношению . Тогда необходимо найти все пары вершин , соединенных некоторым путем.
Иными словами, требуется построить новое отношение , которое будет состоять из всех пар таких, что найдется последовательность , где .

Псевдокод

Изначально матрица заполняется соответственно отношению , то есть . Затем внешним циклом перебираются все элементы множества и для каждого из них, если он может использоваться, как промежуточный для соединения двух элементов и , отношение расширяется добавлением в него пары . 

for k = 1 to n
    for i = 1 to n
        for j = 1 to n
            W[i][j] = W[i][j] or (W[i][k] and W[k][j])

Доказательство

<wikitex>Назовем промежуточной вершину некоторого пути $p = left langle v_0, v_1, dots, v_k right rangle$, принадлежащую множеству вершин этого пути и отличающуюся от начальной и конечной вершин, то есть принадлежащую $left { v_1, v_2, dots, v_{k-1} right }$. Рассмотрим произвольную пару вершин $i, j in V$ и все пути между ними, промежуточные вершины которых принадлежат множеству вершин с номерами $left { 1, 2, dots, k right }$. Пусть $p$ — некоторый из этих путей. Докажем по индукции (по числу промежуточных вершин в пути), что после $i$-ой итерации внешнего цикла будет верно утверждение — если в построенном графе между выбранной парой вершин есть путь, содержащий в качестве промежуточных только вершины из множества вершин с номерами $left { v_1, v_2, dots, v_{i} right }$, то между ними будет ребро.

  • База индукции. Если у нас нет промежуточных вершин, что соответствует начальной матрице смежности, то утверждение выполнено: либо есть ребро (путь не содержит промежуточных вершин), либо его нет.
  • Индуктивный переход. Пусть предположение выполнено для $i = k – 1$. Докажем, что оно верно и для $i = k$ Рассмотрим случаи (далее под вершиной будем понимать ее номер для простоты изложения):
    • $k$ не является промежуточной вершиной пути $p$. Тогда все его промежуточные пути принадлежат множеству вершин с номерами $left { 1, 2, dots, k-1 right } subset left { 1, 2, dots, k right }$, то есть существует путь с промежуточными вершинами в исходном множестве. Это значит $W[i][j]$ будет истиной. В противном случае $W[i][j]$ будет ложью и на k-ом шаге ею и останется.
    • $k$ является промежуточной вершиной предполагаемого пути $p$. Тогда этот путь можно разбить на два пути: $i xrightarrow{p_1} k xrightarrow{p_2} j$. Пусть как $p_1$, так и $p_2$ существуют. Тогда они содержат в качестве промежуточных вершины из множества $left { 1, 2, dots, k-1 right } subset left { 1, 2, dots, k right }$ (так как вершина $k$ — либо конечная, либо начальная, то она не может быть в множестве по нашему определению). Тогда $W[i][k]$ и $W[k][j]$ истинны и по индуктивному предположению посчитаны верно. Тогда и $W[i][j]$ тоже истина. Пусть какого-то пути не существует. Тогда пути $p$ тоже не может существовать, так как добраться, например, от вершины $i$ до $k$ по вершинам из множества $left { 1, 2, dots, k right }$ невозможно по индуктивному предположению. Тогда вся конъюнкция будет ложной, то есть такого пути нет, откуда $W[i][j]$ после итерации будет ложью.

Таким образом, после завершения внешнего цикла у нас будет $W[i][j] = true$, если между этими вершинами есть путь, содержащий в качестве промежуточных вершин из множества всех остальных вершин графа, что и есть транзитивное замыкание.
</wikitex>

Оптимизация с помощью битовых масок

Строки матрицы можно хранить с помощью массива битовых масок длиной . Тогда последний цикл будет выполняться в раз быстрее и сложность алгоритма снижается до .
Пример реализации оптимизации с помощью битмасок: 

unsigned int W[N][N / 32 + 1]           

func transitiveClosure(W):
    for k = 1 to n
        for i = 1 to n
            if бит с номером (k % 32) в маске a[i][k / 32] единичный
                for j = 1 to n / 32 + 1
                    W[i][j] = W[i][j] or W[k][j]

В данной реализации длина битовой маски равна битам. Последний цикл делает в раза меньше операций — сложность алгоритма .

Источники информации

  • Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд — М.: Издательский дом «Вильямс», 2009. — ISBN 978-5-8459-0857-5.
  • Романовский И. В. Дискретный анализ: Учебное пособие для студентов, специализирующихся по прикладной математике и информатике. Изд. 3-е. — СПб.: Невский диалект, 2003. — 320 с. — ISBN 5-7940-0114-3.
  • Википедия – Алгоритм Флойда — Уоршелла
  • Wikipedia – Floyd–Warshall algorithm
Источник

Добавить комментарий