Базовые алгоритмы нахождения кратчайших путей во взвешенных графах
Время на прочтение
5 мин
Количество просмотров 240K
Наверняка многим из гейм-девелоперов (или просто людям, увлекающимися програмировагнием) будет интересно услышать эти четыре важнейших алгоритма, решающих задачи о кратчайших путях.
Сформулируем определения и задачу.
Графом будем называть несколько точек (вершин), некоторые пары которых соединены отрезками (рёбрами). Граф связный, если от каждой вершины можно дойти до любой другой по этим отрезкам. Циклом назовём какой-то путь по рёбрам графа, начинающегося и заканчивающегося в одной и той же вершине. И ещё граф называется взвешенным, если каждому ребру соответствует какое-то число (вес). Не может быть двух рёбер, соединяющих одни и те же вершины.
Каждый из алгоритмов будет решать какую-то задачу о кратчайших путях на взвешенном связном. Кратчайший путь из одной вершины в другую — это такой путь по рёбрам, что сумма весов рёбер, по которым мы прошли будет минимальна.
Для ясности приведу пример такой задачи в реальной жизни. Пусть, в стране есть несколько городов и дорог, соединяющих эти города. При этом у каждой дороги есть длина. Вы хотите попасть из одного города в другой, проехав как можно меньший путь.
Считаем, что в графе n вершин и m рёбер.
Пойдём от простого к сложному.
Алгоритм Флойда-Уоршелла
Находит расстояние от каждой вершины до каждой за количество операций порядка n^3. Веса могут быть отрицательными, но у нас не может быть циклов с отрицательной суммой весов рёбер (иначе мы можем ходить по нему сколько душе угодно и каждый раз уменьшать сумму, так не интересно).
В массиве d[0… n — 1][0… n — 1] на i-ой итерации будем хранить ответ на исходную задачу с ограничением на то, что в качестве «пересадочных» в пути мы будем использовать вершины с номером строго меньше i — 1 (вершины нумеруем с нуля). Пусть идёт i-ая итерация, и мы хотим обновить массив до i + 1-ой. Для этого для каждой пары вершин просто попытаемся взять в качестве пересадочной i — 1-ую вершину, и если это улучшает ответ, то так и оставим. Всего сделаем n + 1 итерацию, после её завершения в качестве «пересадочных» мы сможем использовать любую, и массив d будет являться ответом.
n итераций по n итераций по n итераций, итого порядка n^3 операций.
Псевдокод:
прочитать g // g[0 ... n - 1][0 ... n - 1] - массив, в котором хранятся веса рёбер, g[i][j] = 2000000000, если ребра между i и j нет
d = g
for i = 1 ... n + 1
for j = 0 ... n - 1
for k = 0 ... n - 1
if d[j][k] > d[j][i - 1] + d[i - 1][k]
d[j][k] = d[j][i - 1] + d[i - 1][k]
вывести d
Алгоритм Форда-Беллмана
Находит расстояние от одной вершины (дадим ей номер 0) до всех остальных за количество операций порядка n * m. Аналогично предыдущему алгоритму, веса могут быть отрицательными, но у нас не может быть циклов с отрицательной суммой весов рёбер.
Заведём массив d[0… n — 1], в котором на i-ой итерации будем хранить ответ на исходную задачу с ограничением на то, что в путь должно входить строго меньше i рёбер. Если таких путей до вершины j нет, то d[j] = 2000000000 (это должна быть какая-то недостижимая константа, «бесконечность»). В самом начале d заполнен 2000000000. Чтобы обновлять на i-ой итерации массив, надо просто пройти по каждому ребру и попробовать улучшить расстояние до вершин, которые оно соединяет. Кратчайшие пути не содержат циклов, так как все циклы неотрицательны, и мы можем убрать цикл из путя, при этом длина пути не ухудшится (хочется также отметить, что именно так можно найти отрицательные циклы в графе: надо сделать ещё одну итерацию и посмотреть, не улучшилось ли расстояние до какой-нибудь вершины). Поэтому длина кратчайшего пути не больше n — 1, значит, после n-ой итерации d будет ответом на задачу.
n итераций по m итераций, итого порядка n * m операций.
Псевдокод:
прочитать e // e[0 ... m - 1] - массив, в котором хранятся рёбра и их веса (first, second - вершины, соединяемые ребром, value - вес ребра)
for i = 0 ... n - 1
d[i] = 2000000000
d[0] = 0
for i = 1 ... n
for j = 0 ... m - 1
if d[e[j].second] > d[e[j].first] + e[j].value
d[e[j].second] = d[e[j].first] + e[j].value
if d[e[j].first] > d[e[j].second] + e[j].value
d[e[j].first] = d[e[j].second] + e[j].value
вывести d
Алгоритм Дейкстры
Находит расстояние от одной вершины (дадим ей номер 0) до всех остальных за количество операций порядка n^2. Все веса неотрицательны.
На каждой итерации какие-то вершины будут помечены, а какие-то нет. Заведём два массива: mark[0… n — 1] — True, если вершина помечена, False иначе, d[0… n — 1] — для каждой вершины будет храниться длина кратчайшего пути, проходящего только по помеченным вершинам в качестве «пересадочных». Также поддерживается инвариант того, что для помеченных вершин длина, указанная в d, и есть ответ. Сначала помечена только вершина 0, а g[i] равно x, если 0 и i соединяет ребро весом x, равно 2000000000, если их не соединяет ребро, и равно 0, если i = 0.
На каждой итерации мы находим вершину, с наименьшим значением в d среди непомеченных, пусть это вершина v. Тогда значение d[v] является ответом для v. Докажем. Пусть, кратчайший путь до v из 0 проходит не только по помеченным вершинам в качестве «пересадочных», и при этом он короче d[v]. Возьмём первую встретившуюся непомеченную вершину на этом пути, назовём её u. Длина пройденной части пути (от 0 до u) — d[u]. len >= d[u], где len — длина кратчайшего пути из 0 до v (т. к. отрицательных рёбер нет), но по нашему предположению len меньше d[v]. Значит, d[v] > len >= d[u]. Но тогда v не подходит под своё описание — у неё не наименьшее значение d[v] среди непомеченных. Противоречие.
Теперь смело помечаем вершину v и пересчитываем d. Так делаем, пока все вершины не станут помеченными, и d не станет ответом на задачу.
n итераций по n итераций (на поиск вершины v), итого порядка n^2 операций.
Псевдокод:
прочитать g // g[0 ... n - 1][0 ... n - 1] - массив, в котором хранятся веса рёбер, g[i][j] = 2000000000, если ребра между i и j нет
d = g
d[0] = 0
mark[0] = True
for i = 1 ... n - 1
mark[i] = False
for i = 1 ... n - 1
v = -1
for i = 0 ... n - 1
if (not mark[i]) and ((v == -1) or (d[v] > d[i]))
v = i
mark[v] = True
for i = 0 ... n - 1
if d[i] > d[v] + g[v][i]
d[i] = d[v] + g[v][i]
вывести d
Алгоритм Дейкстры для разреженных графов
Делает то же самое, что и алгоритм Дейкстры, но за количество операций порядка m * log(n). Следует заметить, что m может быть порядка n^2, то есть эта вариация алгоритма Дейкстры не всегда быстрее классической, а только при маленьких m.
Что нам нужно в алгоритме Дейкстры? Нам нужно уметь находить по значению d минимальную вершину и уметь обновлять значение d в какой-то вершине. В классической реализации мы пользуемся простым массивом, находить минимальную по d вершину мы можем за порядка n операций, а обновлять — за 1 операцию. Воспользуемся двоичной кучей (во многих объектно-ориентированных языках она встроена). Куча поддерживает операции: добавить в кучу элемент (за порядка log(n) операций), найти минимальный элемент (за 1 операцию), удалить минимальный элемент (за порядка log(n) операций), где n — количество элементов в куче.
Создадим массив d[0… n — 1] (его значение то же самое, что и раньше) и кучу q. В куче будем хранить пары из номера вершины v и d[v] (сравниваться пары должны по d[v]). Также в куче могут быть фиктивные элементы. Так происходит, потому что значение d[v] обновляется, но мы не можем изменить его в куче. Поэтому в куче могут быть несколько элементов с одинаковым номером вершины, но с разным значением d (но всего вершин в куче будет не более m, я гарантирую это). Когда мы берём минимальное значение в куче, надо проверить, является ли этот элемент фиктивным. Для этого достаточно сравнить значение d в куче и реальное его значение. А ещё для записи графа вместо двоичного массива используем массив списков.
m раз добавляем элемент в кучу, получаем порядка m * log(n) операций.
Псевдокод:
прочитать g // g[0 ... n - 1] - массив списков, в i-ом списке хранятся пары: first - вершина, соединённая с i-ой вершиной ребром, second - вес этого ребра
d[0] = 0
for i = 0 ... n - 1
d[i] = 2000000000
for i in g[0] // python style
d[i.first] = i.second
q.add(pair(i.second, i.first))
for i = 1 ... n - 1
v = -1
while (v = -1) or (d[v] != val)
v = q.top.second
val = q.top.first
q.removeTop
mark[v] = true
for i in g[v]
if d[i.first] > d[v] + i.second
d[i.first] = d[v] + i.second
q.add(pair(d[i.first], i.first))
вывести d
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 августа 2021 года; проверки требуют 7 правок.
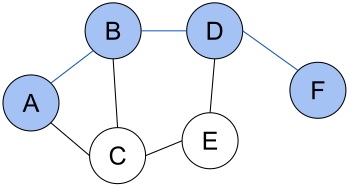
Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.
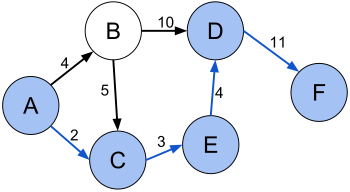
Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.
Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь.
Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для её решения[⇨].
У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.
Значимость данной задачи определяется её различными практическими применениями[⇨]. Например, в GPS-навигаторах осуществляется поиск кратчайшего пути между точкой отправления и точкой назначения. В качестве вершин выступают перекрёстки, а дороги являются рёбрами, которые лежат между ними. Если сумма длин дорог между перекрёстками минимальна, тогда найденный путь самый короткий.
Определение[править | править код]
Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.
Граф представляет собой совокупность непустого множества вершин и рёбер (наборов пар вершин). Две вершины на графе смежны, если они соединяются общим ребром. Путь в неориентированном графе представляет собой последовательность вершин 








Пусть 










Существуют различные постановки задачи о кратчайшем пути:
- Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
- Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
- Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.
В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объём затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).
Задача о кратчайшем пути с учётом дополнительных ограничений[править | править код]
Задача о кратчайшем пути очень часто встречается в ситуации, когда необходимо учитывать дополнительные ограничения. Наличие их может значительно повысить сложность задачи[1]. Примеры таких задач:
- Кратчайший путь, проходящий через заданное множество вершин. Можно рассматривать два ограничения: кратчайший путь должен проходить через выделенное множество вершин, и кратчайший путь должен содержать как можно меньше невыделенных вершин. Первое из них хорошо известна в теории исследования операций[2].
- Минимальное покрытие вершин ориентированного графа путями. Осуществляется поиск минимального по числу путей покрытия графа, а именно подмножества всех s-t путей, таких что, каждая вершина ориентированного графа принадлежит хотя бы одному такому пути[3].
- Задача о требуемых путях. Требуется найти минимальное по мощности множество s-t путей
такое, что для любого
найдется путь
, накрывающий его.
— множество некоторых путей в ориентированном графе G[4].
- Минимальное покрытие дуг ориентированного графа путями. Задача состоит в отыскании минимального по числу путей подмножества всех путей, такого, что каждая дуга принадлежит хотя бы одному такому пути. При этом возможно дополнительное требование о том, чтобы все пути исходили из одной вершины[5].
Алгоритмы[править | править код]
В связи с тем, что существует множество различных постановок данной задачи, есть
наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:
- Алгоритм Дейкстры находит кратчайший путь от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса[6].
- Алгоритм Беллмана — Форда находит кратчайшие пути от одной вершины графа до всех остальных во взвешенном графе. Вес рёбер может быть отрицательным.
- Алгоритм поиска A* находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), используя алгоритм поиска по первому наилучшему совпадению на графе.
- Алгоритм Флойда — Уоршелла находит кратчайшие пути между всеми вершинами взвешенного ориентированного графа[6].
- Алгоритм Джонсона находит кратчайшие пути между всеми парами вершин взвешенного ориентированного графа.
- Алгоритм Ли (волновой алгоритм) основан на методе поиска в ширину. Находит путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (рёбер). Основное применение — трассировки электрических соединений на кристаллах микросхем и на печатных платах. Также используется для поиска кратчайшего расстояния на карте в стратегических играх.
- Поиск кратчайшего пути на основе алгоритма Килдала[7].
В работе (Черкасский и др., 1993)[8] представлено ещё несколько алгоритмов для решения этой задачи.
Задача поиска кратчайшего пути из одной вершины во все остальные[править | править код]
В такой постановке задачи осуществляется поиск кратчайшего пути из вершины v во все остальные вершины на графе.
Невзвешенный ориентированный граф[править | править код]
| Алгоритм | Сложность | Автор |
|---|---|---|
| Поиск в ширину | O(V+E) |
Ориентированный граф с неотрицательными весами[править | править код]
| Алгоритм | Сложность | Автор |
|---|---|---|
| – | O(V2EL) | Форд 1956 |
| Алгоритм Беллмана — Форда | O(VE) | Беллман 1958[9], Мур 1957[10] |
| – | O(V2 log V) | Данциг 1958, Данциг 1960, Minty (cf. Pollack&Wiebenson 1960), Whiting&Hillier 1960 |
| Алгоритм Дейкстры со списком. | O(V2) | Leyzorek et al. 1957[11], Дейкстра 1959[12] |
| Алгоритм Дейкстры с модифицированной двоичной кучей | O((E + V) log V) | – |
| . . . | . . . | . . . |
| Алгоритм Дейкстры с использованием фибоначчиевой кучи | O(E + V log V) | Фридман&Тарьян 1984[13], Фридман&Тарьян 1987[14] |
| – | O(E log log L) | Джонсон 1982, Карлссон&Поблете 1983 |
| Алгоритм Габова | O(E logE/V L) | Габов 1983, Габов 1985 |
| – | O(E + V√log L) | Ахуджа et al. 1990 |
Ориентированный граф с произвольными весами[править | править код]
| Алгоритм | Сложность | Автор |
|---|---|---|
| Алгоритм Беллмана — Форда | O(VE) | Беллман[9], Мур[10] |
| Алгоритм Левита | O(VE) |
Задача о кратчайшем пути между всеми парами вершин[править | править код]
Задача о кратчайшем пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена Симбелом в 1953 году[15], который обнаружил, что она может быть решена за линейное количество манипуляций (умножения) с матрицей. Сложность такого алгоритма O(V4).
Так же для решения данной задачи существуют другие более быстрые алгоритмы, такие как Алгоритм Флойда — Уоршелла со сложностью O(V3), и
Алгоритм Джонсона (является комбинацией алгоритмов Бэллмана-Форда и Дейкстры) со сложностью O(VE + V2 log V).
Применение[править | править код]
Задача о поиске кратчайшего пути на графе может быть интерпретирована по-разному и применяться в различных областях. Далее приведены примеры различных применений задачи. Другие применения изучаются в дисциплине, которая занимается исследованием операций[16].
Картографические сервисы[править | править код]
Алгоритмы нахождения кратчайшего пути на графе применяются для нахождения путей между физическими объектами на таких картографических сервисах, как карты Google или OpenStreetMap. В обучающем видео от Google можно узнать различные эффективные алгоритмы, которые применяются в данной сфере[17].
Недетерминированная машина[править | править код]
Если представить недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра определяют возможные переходы, тогда алгоритмы поиска кратчайшего пути могут быть применены для поиска оптимальной последовательности решений для достижения главной цели. Например, если вершинами являются состояния Кубика Рубика, а ребром представляет собой одно действие над кубиком, тогда алгоритм может быть применён для поиска решения с минимальным количеством ходов.
Сети дорог[править | править код]
Задача поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог.
Сеть дорог можно представить в виде графа с положительными весами. Вершины являются дорожными развязками, а ребра дорогами, которые их соединяют. Веса рёбер могут соответствовать протяжённости данного участка, времени необходимому для его преодоления или стоимости путешествия по нему. Ориентированные ребра можно использовать для представления односторонних улиц. В таком графе можно ввести характеристику, которая указывает на то, что одни дороги важнее других для длительных путешествий (например автомагистрали). Она была формализована в понятии (идее) о магистралях[18].
Для реализации подхода, где одни дороги важнее других, существует множество алгоритмов. Они решают задачу поиска кратчайшего пути намного быстрее, чем аналогичные на обычных графах.
Подобные алгоритмы состоят из двух этапов:
- этап предобработки. Производится предварительная обработка графа без учёта начальной и конечной вершины (может длиться до нескольких дней, если работать с реальными данными). Обычно выполняется один раз и потом используются полученные данные.
- этап запроса. Осуществляется запрос и поиск кратчайшего пути, при этом известны начальная и конечная вершина.
Самый быстрый алгоритм может решить данную задачу на дорогах Европы или Америки за доли микросекунды[19].
Другие подходы (техники), которые применяются в данной сфере:
- ALT
- Arc Flags
- Contraction hierarchies
- Transit Node Routing
- Reach based Pruning
- Labeling
Похожие задачи[править | править код]
Существуют задачи, которые похожи на задачу поиска кратчайшего пути на графе.
- Поиск кратчайшего пути в вычислительной геометрии (см. евклидов кратчайший путь).
- Задача коммивояжёра. Требуется найти кратчайший маршрут, проходящий через указанные города (вершины) хотя бы по одному разу с последующим возвратом в исходный город. Данная задача относится к классу NP-трудных задач в отличие от задачи поиска кратчайшего пути, которая может быть решена за полиномиальное время в графах без циклов. Задача коммивояжёра решается неэффективно для больших наборов данных.
- Задача канадского путешественника и задача стохастического поиска кратчайшего пути являются обобщением рассматриваемой задачи, в которых обходимый граф заранее полностью неизвестен и изменяется во времени или следующий проход по графу вычисляется на основе вероятностей.
- Задача поиска кратчайшего пути, когда в графе происходят преобразования. Например, изменяется вес ребра или удаляется вершина[20].
Постановка задачи линейного программирования[править | править код]
Пусть дан направленный граф (V, A), где V — множество вершин и A — множество рёбер, с начальной вершиной обхода s, конечной t и весами wij для каждого ребра (i, j) в A. Вес каждого ребра соответствует переменной программы xij.
Тогда задача ставится следующим образом: найти минимум функции 


См. также[править | править код]
- IEEE 802.1aq
- Транспортная сеть
- Двунаправленный поиск
Примечания[править | править код]
- ↑ Применение теории графов в программировании, 1985.
- ↑ Применение теории графов в программировании, 1985, с. 138—139.
- ↑ Применение теории графов в программировании, 1985, с. 139—142.
- ↑ Применение теории графов в программировании, 1985, с. 144—145.
- ↑ Применение теории графов в программировании, 1985, с. 145—148.
- ↑ 1 2 Дискретная математика. Комбинаторная оптимизация на графах, 2003.
- ↑ Применение теории графов в программировании, 1985, с. 130—131.
- ↑ Cherkassky, Goldberg, Radzik, 1996.
- ↑ 1 2 Bellman Richard, 1958.
- ↑ 1 2 Moore, 1957.
- ↑ M. Leyzorek, 1957.
- ↑ Dijkstra, 1959.
- ↑ Michael Fredman Lawrence, 1984.
- ↑ Fredman Michael, 1987.
- ↑ Shimbel, 1953.
- ↑ Developing algorithms and software for geometric path planning problems, 1996.
- ↑ Fast route planning.
- ↑ Highway Dimension, 2010.
- ↑ A Hub-Based Labeling Algorithm, 2011.
- ↑ Ladyzhensky Y., Popoff Y. Algorithm, 2006.
Литература[править | править код]
- Евстигнеев В. А. Глава 3. Итеративные алгоритмы глобального анализа графов. Пути и покрытия // Применение теории графов в программировании / Под ред. А. П. Ершова. — Москва: Наука. Главная редакция физико-математической литературы, 1985. — С. 138—150. — 352 с.
- Алексеев В.Е., Таланов В.А. Глава 3.4. Нахождения кратчайших путей в графе // Графы. Модели вычислений. Структуры данных. — Нижний Новгород: Издательство Нижегородского гос. университета, 2005. — С. 236—237. — 307 с. — ISBN 5–85747–810–8. Архивная копия от 13 декабря 2013 на Wayback Machine
- Галкина В.А. Глава 4. Построение кратчайших путей в ориентированном графе // Дискретная математика. Комбинаторная оптимизация на графах. — Москва: Издательство “Гелиос АРВ”, 2003. — С. 75—94. — 232 с. — ISBN 5–85438–069–2.
- Берж К. Глава 7. Задача о кратчайшем пути // Теория графов и её применения = Theorie des graphes et ses applications / Под ред. И. А. Вайнштейна. — Москва: Издательство иностранной литературы, 1962. — С. 75—81. — 320 с.
- Ойстин Оре. Теория графов / Под ред. И. М. Овчинниковой. — Издательство наука, 1980. — 336 с. Архивная копия от 15 декабря 2013 на Wayback Machine
- Виталий Осипов, Поиск кратчайших путей в дорожных сетях: от теории к реализации на YouTube.
- Харари Ф. Глава 2. Графы // Теория графов / под ред. Г. П. Гаврилов — М.: Мир, 1973. — С. 27. — 301 с.
- Cherkassky B. V., Goldberg A. V., Radzik T. Shortest paths algorithms: Theory and experimental evaluation (англ.) // Mathematical Programming — Springer Science+Business Media, 1996. — Vol. 73, Iss. 2. — P. 129–174. — ISSN 0025-5610; 1436-4646 — doi:10.1007/BF02592101
- Ричард Беллман. On a routing problem // Quarterly of Applied Mathematics. — 1958. — Т. 16. — С. 87—90.
- Dijkstra E. W. A note on two problems in connexion with graphs (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1959. — Vol. 1, Iss. 1. — P. 269—271. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01386390
- Moore E. F. The shortest path through a maze (англ.) // Proceedings of an International Symposium on the Theory of Switching (Cambridge, Massachusetts, 2–5 April 1957) — Harvard University Press, 1959. — Vol. 2. — P. 285—292. — 345 p. — (Annals of the Computation Laboratory of Harvard University; Vol. 30) — ISSN 0073-0750
- M. Leyzorek, R. S. Gray, A. A. Gray, W. C. Ladew, S. R. Meaker, R. M. Petry, R. N. Seitz. Investigation of Model Techniques — First Annual Report — 6 June 1956 — 1 July 1957 — A Study of Model Techniques for Communication Systems (англ.). — Cleveland, Ohio: Case Institute of Technology, 1957.
- Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) : journal. — Институт инженеров электротехники и электроники, 1984. — P. 338—346. — ISBN 0-8186-0591-X. — doi:10.1109/SFCS.1984.715934. Архивировано 11 октября 2012 года.
- Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) // Journal of the Association for Computing Machinery : journal. — 1987. — Vol. 34, no. 3. — P. 596—615. — doi:10.1145/28869.28874.
- Shimbel, Alfonso. Structural parameters of communication networks // Bulletin of Mathematical Biophysics. — 1953. — Т. 15, № 4. — С. 501—507. — doi:10.1007/BF02476438.
- Sanders, Peter. Fast route planning. — Google Tech Talk, 2009. — 23 марта.. — «Шаблон:Inconsistent citations».
- Chen, Danny Z. Developing algorithms and software for geometric path planning problems (англ.) // ACM Computing Surveys (англ.) (рус. : journal. — 1996. — December (vol. 28, no. 4es). — P. 18. — doi:10.1145/242224.242246.
- Abraham, Ittai; Fiat, Amos; Goldberg, Andrew V.; Werneck, Renato F. Highway Dimension, Shortest Paths, and Provably Efficient Algorithms (англ.) // ACM-SIAM Symposium on Discrete Algorithms : journal. — 2010. — P. 782—793.
- Abraham, Ittai; Delling, Daniel; Goldberg, Andrew V.; Werneck, Renato F. A Hub-Based Labeling Algorithm for Shortest Paths on Road Networks. Symposium on Experimental Algorithms] (англ.) : journal. — 2011. — P. 230—241.
- Kroger, Martin. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems (англ.) // Computer Physics Communications (англ.) (рус. : journal. — 2005. — Vol. 168, no. 168. — P. 209—232. — doi:10.1016/j.cpc.2005.01.020.
- Ladyzhensky Y., Popoff Y. Algorithm to define the shortest paths between all nodes in a graph after compressing of two nodes. Proceedings of Donetsk national technical university, Computing and automation. Vol.107. Donetsk (англ.) : journal. — 2006. — P. 68—75..[источник не указан 925 дней]
Каждому пути во взвешенном орграфе можно сопоставить вес пути (path weight) – величину, равную сумме весов ребер, составляющих этот путь. Эта важная мера позволяет сформулировать задачи наподобие ” найти путь между двумя заданными вершинами, имеющий минимальный вес ” . Эти задачи о кратчайших путях (shortest-path problem) и являются темой данной главы. Такие задачи не только естественно возникают во многих приложениях, но и знакомят нас с областью алгоритмов решения общих задач, применимых к широкому кругу реальных приложений.
Некоторые из рассматриваемых в данной главе алгоритмов непосредственно связаны с алгоритмами, изученными в лекциях 17-20. Здесь полностью применима наша базовая парадигма поиска на графе, а в основе решения задач о кратчайших путях лежат некоторые специальные механизмы, которые были использованы в
“Виды графов и их свойства”
и
“Орграфы и DAG-графы”
для решения задач связности в графах и орграфах.
Для краткости мы будем называть взвешенные орграфы сетями (network). На
рис.
21.1 показан пример сети и ее стандартные представления. В
“Минимальные остовные деревья”
уже был разработан интерфейс АТД сети с представлениями матрицей смежности и списками смежности. При вызове конструктора достаточно задать второй аргумент равным true, и класс будет содержать лишь одно представление каждого ребра – как при получении представлений орграфов в
“Орграфы и DAG-графы”
из представлений неориентированных графов из главы 17
“Виды графов и их свойства”
(см. программы 20.1-20.4).
Как было подробно разъяснено в
“Минимальные остовные деревья”
, при работе со взвешенными орграфами мы используем указатели на абстрактные ребра, чтобы расширить применимость полученных реализаций. У этого подхода для орграфов имеются некоторые отличия по сравнению с неориентированными графами (см.
“Минимальные остовные деревья”
). Во-первых, имеется только одно представление каждого ребра, и поэтому при использовании итератора не нужна функция from из класса edge (см. программу 20.1): в орграфе значение e->from(v) истинно для любого указателя на ребро e, возвращаемого итератором для v. Во-вторых, как было показано в
“Орграфы и DAG-графы”
, часто при обработке орграфа полезно иметь возможность работать с обратным ему графом, но сейчас нам потребуется подход, отличный от принятого в программе 19.1, поскольку там при создании обратного графа создаются ребра, а здесь предполагается, что клиенты АТД графа, предоставляющие указатели на ребра, не должны сами создавать ребра (см. упражнение 21.3).
В приложениях или системах, где могут потребоваться любые типы графов, нетрудно определить такой АТД сети, от которого можно породить АТД для невзвешенных неориентированных графов из глав 17 и 18, невзвешенных орграфов из
“Орграфы и DAG-графы”
или взвешенных неориентированных графов из
“Минимальные остовные деревья”
(см. упражнение 21.10).

Рис.
21.1.
Пример сети и ее представления
Здесь показана сеть (взвешенный орграф) и четыре ее представления: список ребер, графический вид, матрица смежности и списки смежности (слева направо). Как и для алгоритмов вычисления MST, веса указываются в элементах матрицы и в узлах списков, но в программах используются указатели на ребра. На рисунках длины ребер часто изображаются пропорциональными их весам (как и для алгоритмов вычисления MST), но мы не настаиваем на этом правиле, поскольку большинство алгоритмов поиска кратчайших путей могут работать с произвольными неотрицательными весами (хотя отрицательные веса могут усложнить ситуацию). Матрица смежности несимметрична, а списки смежности содержат по одному узлу для каждого ребра (как в невзвешенном орграфе). Несуществующие ребра представляются пустыми указателями в матрице (незаполненные места на рисунке) и вообще отсутствуют в списках. Петли нулевой длины введены для упрощения реализации алгоритмов поиска кратчайших путей. Они не представлены в списке ребер слева – для экономии места и чтобы продемонстрировать типичную ситуацию, когда они добавляются при создании представления матрицей смежности или списками смежности.
При работе с сетями обычно удобно оставлять петли во всех представлениях. При таком соглашении для указания, что никакая вершина не достижима из себя самой, в алгоритмах можно использовать сигнальный вес (с максимальным значением). В наших примерах мы будем использовать петли нулевого веса, хотя зачастую имеют смысл петли с положительным весом. Во многих приложениях также требуется наличие параллельных ребер – возможно, с различными весами. Как было сказано в
“Минимальные остовные деревья”
, в различных приложениях удобны разные варианты игнорирования или объединения таких ребер. Однако в этой главе для простоты ни в одном из наших примеров параллельные ребра не применяются, в представлении матрицей смежности параллельные ребра не допускаются, и мы выполняем проверку наличия параллельных ребер или их удаление в списках смежности.
Все свойства связности ориентированных графов, рассмотренные в
“Орграфы и DAG-графы”
, справедливы и для сетей. Только там мы выясняли, возможно ли достижение одной вершины из другой, а в этой главе мы учитываем веса и пытаемся найти наилучший путь из одной вершины в другую.
Определение 21.1. Кратчайшим путем между двумя вершинами s и t в сети называется такой направленный простой путь из s в t, что никакой другой путь не имеет меньшего веса.
Лаконичность этого определения скрывает некоторые важные моменты. Во-первых, если t не достижима из s, то не существует вообще никакого пути, поэтому нет и кратчайшего пути. Для удобства рассматриваемые алгоритмы часто трактуют этот случай как наличие между s и t пути с бесконечным весом. Во-вторых, как и в случае алгоритмов вычисления MST, в наших примерах сетей веса ребер пропорциональны их длинам,
хотя определение этого не требует, и в алгоритмах (кроме одного в разделе 21.5) это не предполагается. Вообще-то алгоритмы поиска кратчайшего пути запросто находят неочевидные обходы – например, путь между двумя вершинами, который проходит через несколько других вершин, но имеет общий вес меньше веса ребра, непосредственно соединяющего эти вершины. В-третьих, может существовать несколько путей из одной вершины в другую с одним и тем же весом – обычно достаточно найти один из них. На
рис.
21.2 показан пример, иллюстрирующий эти моменты.
В определении требуется, чтобы путь был простым, хотя для сетей, содержащих ребра с неотрицательными весами, это несущественно, поскольку в такой сети можно удалить из пути любой цикл и получить не более длинный путь (даже более короткий, если цикл не состоит из ребер с нулевым весом). Но в случае сетей с ребрами, которые могут иметь отрицательный вес, необходимость ограничиться простыми путями понятна: ведь если в сети есть цикл с отрицательным весом, то понятие кратчайшего пути теряет смысл. Например, предположим, что ребро 3-5 в сети на
рис.
21.1 имеет вес -0.38, а ребро
5-1 – вес -0.31. Тогда вес цикла 1-4-3-5-1 равен 0.32 + 0.36 – 0.38 – 0.31 = -0.01. Можно кружить по этому циклу, порождая все более короткие пути. Учтите, что не обязательно, как и в данном примере, чтобы все ребра в таком цикле имели отрицательные веса; значение имеет лишь сумма весов ребер. Для краткости ориентированные циклы с общим отрицательным весом мы будем называть отрицательными циклами.
Предположим, что в определении одна из вершин на пути из s в t принадлежит также некоторому отрицательному циклу. В этом случае существование (непростого) кратчайшего пути из s в t бессмысленно, поскольку можно использовать цикл для создания пути с весом, меньшим любого заданного значения. Чтобы избежать таких моментов, в данном определении мы ограничиваемся простыми путями – тогда понятие кратчайшего пути можно строго определить для любой сети. До раздела 21.7 мы не будем рассматривать отрицательные циклы в сетях, поскольку, как мы увидим, они представляют собой принципиальное препятствие на пути решения задачи поиска кратчайших путей.
Чтобы найти кратчайшие пути во взвешенном неориентированном графе, можно построить сеть с теми же вершинами и с двумя ребрами (по одному в каждом направлении), которые соответствуют каждому ребру в исходном графе.
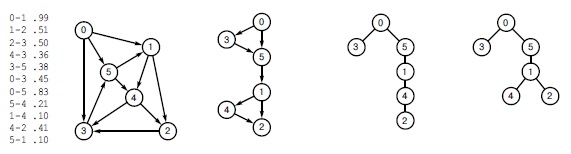
Рис.
21.2.
Деревья кратчайших путей
Дерево кратчайших путей (SPT) определяет наиболее короткие пути из корня в другие вершины (см. определение 21.2). В общем случае различные пути могут иметь одинаковую длину, поэтому может существовать несколько SPT, определяющих кратчайшие пути из заданной вершины. В сети, приведенной слева, все кратчайшие пути из 0 являются подграфами DAG-графа, показанного справа от сети. Дерево с корнем в 0 является остовом этого DAG тогда и только тогда, когда оно является SPT-деревом для вершины 0. Два таких дерева приведены справа.
Существует взаимно однозначное соответствие между простыми путями в сети и простыми путями в графе, и стоимости этих путей совпадают; значит, совпадают и задачи поиска кратчайших путей для них. При построении стандартного представления списками смежности или матрицей смежности для взвешенного неориентированного графа (см., например,
рис.
20.3) получается точно такая же сеть. Это построение бесполезно, если веса могут быть отрицательными, поскольку в сети при этом получаются отрицательные циклы, а мы не знаем, как решать задачи поиска кратчайших путей в сетях с отрицательными циклами (см. раздел 21.7). В остальных случаях алгоритмы для сетей, которые рассматриваются в этой главе, работают и для взвешенных неориентированных графов.
В некоторых приложениях удобно вместо ребер либо наряду с ребрами присваивать веса вершинам; можно также рассмотреть более сложные задачи, где имеют значение как количество ребер в пути, так и общий вес пути. Подобные задачи можно решать, приводя их к сетям со взвешенными ребрами (см., например, упражнение 21.4) или несколько расширяя базовые алгоритмы (см., например, упражнение 21.52).
Поскольку из контекста и так все понятно, мы не вводим специальную терминологию, позволяющую отличать кратчайшие пути во взвешенных графах от кратчайших путей в графах без весов (где вес пути просто равен количеству составляющих его ребер – см.
“Виды графов и их свойства”
). Общепринятая терминология относится к сетям (со взвешенными ребрами), как в данной главе, т.к. особые случаи для неориентированных или невзвешенных графов легко решаются с помощью тех же алгоритмов, что и для сетей.
Мы будем рассматривать те же базовые задачи, которые были определены в
“Поиск на графе”
для неориентированных и невзвешенных графов. Мы вновь формулируем их здесь, обращая внимание на то, что определение 21.1 неявно обобщает их, учитывая веса в сетях.
Кратчайший путь из истока в сток. Для заданных начальной вершины s и конечной вершины t нужно найти кратчайший путь в графе из s в t. Начальную вершину мы называем истоком (source), а конечную вершину – стоком (sink), за исключением тех ситуаций, где такое использование терминов противоречит другому определению истоков (вершин без входящих ребер) и стоков (вершин без исходящих ребер) в орграфах.
Кратчайшие пути из одного истока. Для заданной начальной вершины s нужно найти кратчайшие пути из s во все остальные вершины графа.

Рис.
21.3.
Все кратчайшие пути
В этой таблице приведены все кратчайшие пути в сети с
рис.
21.1 вместе с их длинами. Поскольку данная сеть является сильно связной, в ней существуют пути, соединяющие каждую пару вершин. Цель алгоритма поиска кратчайшего пути из истока в сток – вычисление одного из элементов этой таблицы; цель алгоритма поиска кратчайшего пути из одного истока – вычисление одной из строк этой таблицы; а цель алгоритма поиска кратчайших путей между всеми парами вершин – вычисление всей таблицы. Обычно мы используем более компактные представления, которые содержат по существу ту же информацию и позволяют клиентам обойти любой путь за время, пропорциональное количеству его ребер (см.
рис.
21.8).
Кратчайшие пути между всеми парами вершин. Нужно найти кратчайшие пути, соединяющие каждую пару вершин в графе. Иногда для краткости это множество V2 путей мы будем называть термином все кратчайшие пути.
Если имеется несколько кратчайших путей, соединяющих любую заданную пару вершин, мы выбираем любой из них. Поскольку пути имеют различное количество ребер, наши реализации предоставляют функции-члены, которые позволяют клиентам обходить пути за время, пропорциональное длинам путей. Любой кратчайший путь неявно содержит и собственную длину, но наши реализации выдают длины явно. Итак, уточним: в приведенных выше постановках задач выражение ” найти кратчайший путь ” означает ” вычислить длину кратчайшего пути и способ обхода конкретного пути за время, пропорциональное его длине ” .
На
рис.
21.3 показаны кратчайшие пути для сети с
рис.
21.1. В сетях с V вершинами для решения задачи с одним истоком необходимо указать V путей, а для решения задачи для всех пар вершин – V2 путей. В наших реализациях мы используем более компактное представление, чем эти списки путей; об этом уже было упомянуто в
“Поиск на графе”
и будет подробно рассказано в разделе 21.1.
В реализациях на C++ мы строим алгоритмические решения этих задач в виде реализаций АТД, позволяющих создавать эффективные клиентские программы, которые могут решать разнообразные практические задачи обработки графов. Например, как показано в разделе 21.3, мы реализуем решения задач кратчайших путей для всех пар вершин в виде конструкторов внутри классов, которые отвечают на запросы кратчайшего пути за постоянное (линейное) время. Мы также построим классы для решения задачи с одним истоком, чтобы клиенты, которым нужно вычислить кратчайшие пути из заданной вершины (или небольшого множества вершин) могли не вычислять кратчайшие пути для других вершин. Внимательное рассмотрение таких моментов и надлежащее использование изучаемых здесь алгоритмов может преодолеть разницу между эффективным решением и настолько трудоемким решением, что никакой клиент не сможет воспользоваться им.
Задачи о кратчайших путях в различных вариантах возникают в широком спектре приложений. Многие приложения допускают наглядную геометрическую интерпретацию, но многие другие обрабатывают структуры с произвольными стоимостями. Как и в случае минимальных остовных деревьев (MST, см.
“Минимальные остовные деревья”
), мы иногда будем обращаться к геометрической интерпретации, чтобы облегчить понимание алгоритмов решения этих задач – постоянно помня, что наши алгоритмы способны работать и в более общих условиях. В разделе 21.5 мы рассмотрим специализированные алгоритмы для евклидовых сетей. А в разделах 21.6 и 21.7 будет показано, что базовые алгоритмы эффективны для многочисленных приложений, в которых сети представляют абстрактную модель вычислений.
Дорожные карты. Во многих дорожных картах есть замечательная вещь – таблицы с расстояниями между всеми парами главных городов. Мы считаем, что составитель карты позаботился о том, чтобы эти расстояния кратчайшими, но это предположение не всегда верно (см., например, упражнение 21.11). Обычно такие таблицы составляются для неориентированных графов, которые можно рассматривать как сети с двунаправленными ребрами, соответствующими каждой дороге, хотя в них можно включать улицы с односторонним движением на карте города и некоторые другие аналогичные моменты. Как будет показано в разделе 21.3, нетрудно предоставлять и другую полезную информацию – например, таблицу с инструкцией о прохождении кратчайших путей (см.
рис.
21.4). Современные встроенные системы в автомобилях и других транспортных системах предоставляют такие возможности. Карты являются евклидовыми графами, и в разделе 21.4 мы рассмотрим алгоритмы поиска кратчайших путей, которые при поиске кратчайших путей учитывают позицию вершины.
Авиарейсы. Карты маршрутов и расписания для авиалиний или других транспортных систем могут быть представлены в виде сетей, для которых важны различные задачи о кратчайших путях. Например, может потребоваться минимизировать время перелета между двумя городами, или же стоимость путешествия. Стоимости в таких сетях могут включать функции от времени, финансовых затрат или других интегральных ресурсов. Например, из-за преобладающих ветров перелеты между двумя городами обычно занимают больше времени в одном направлении, чем в другом. Авиапассажиры также знают, что стоимость перелета не обязательно является простой функцией расстояния между городами – очень часто встречаются ситуации, когда окольный маршрут (с пересадками) дешевле прямого перелета. Такие усложнения могут быть обработаны базовыми алгоритмами поиска кратчайших путей, которые мы рассматриваем в этой главе; эти алгоритмы предназначены для работы с любыми положительными стоимостями.
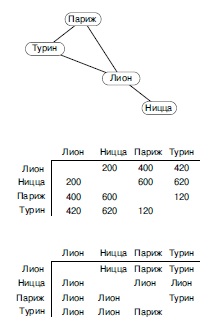
Рис.
21.4.
Расстояния и пути
Дорожные карты обычно содержат таблицы расстояний наподобие приведенной в центрери-сунка для небольшого подмножества французских городов. Соединяющие их автострады показаны в виде графа в верхней части рисунка. Может быть полезна, хотя и редко встречается на картах, таблица наподобие приведенной внизу: в ней отмечены пункты, лежащие на кратчайшем пути. Например, из этой таблицы видно, как добраться из Парижа в Ниццу: первым на пути следования должен быть Лион.
Фундаментальные вычисления кратчайших путей, предлагаемые этими приложениями – это лишь небольшая часть области применимости алгоритмов для вычисления кратчайших путей. В разделе 21.6 мы рассмотрим задачи из прикладных областей, которые с виду не имеют отношения к данной тематике. В этом нам поможет сведение – формальный механизм для доказательства связи между задачами. Мы решаем задачи для этих приложений, трансформируя их в абстрактные задачи поиска кратчайших путей, которые не имеют очевидной геометрической связи с описанными задачами. Некоторые приложения приводят к задачам о кратчайших путях в сетях с отрицательными весами. Такие задачи могут оказаться намного более трудными, чем задачи, где отрицательные веса невозможны. Задачи о кратчайших путях для таких приложений не только заполняют промежуток между элементарными алгоритмами и алгоритмически неразрешимыми задачами, но и приводят нас к мощным и общим механизмам принятия решений.
Как и в случае алгоритмов вычисления MST из
“Минимальные остовные деревья”
, мы часто смешиваем понятия веса, стоимости и расстояния. Здесь мы обычно также используем естественную геометрическую наглядность, даже работая с более общими постановками и с произвольными весами ребер. Поэтому мы говорим о ” длине ” путей и ребер вместо ” веса ” , и говорим, что один путь ” короче ” другого, вместо выражения ” имеет меньший вес ” . Мы также можем сказать, что вершина v находится ” ближе ” к s, чем w, вместо ” ориентированный путь наименьшего веса из s в v имеет меньший вес, чем вес ориентированного пути наименьшего веса из s в w ” , и т.д. Это проявляется и в стандартном использовании термина ” кратчайшие пути ” и выглядит естественно, даже если веса не связаны с расстояниями (см.
рис.
21.2). Однако в разделе 21.6, при расширении наших алгоритмов на отрицательные веса, от этого придется отказаться.
Эта глава организована следующим образом. После знакомства с фундаментальными принципами в разделе 21.1, в разделах 21.2 и 21.3 мы рассмотрим базовые алгоритмы для задач поиска кратчайших путей из одного истока и между всеми парами вершин. После этого в разделе 21.4 мы изучим ациклические сети (или, короче, взвешенные DAG-графы), а в разделе 21.5 – методы использования геометрических свойств для решения задачи с одним истоком и стоком в евклидовых графах. Затем в разделах 21.6 и 21.7 мы переключимся на более общие задачи, где алгоритмы поиска кратчайших путей (возможно, на сетях с отрицательными весами) будут использованы как высокоуровневое средство решения задач.
Упражнения
21.1. Пометьте следующие точки на плоскости цифрами от 0 до 5, соответственно:
(1, 3) (2, 1) (6, 5) (3, 4) (3, 7) (5, 3).
Считая длины ребер весами, рассмотрите сеть, определяемую ребрами
1-03-55-23-45-10-30-44-22-3.
Нарисуйте сеть и приведите структуру списков смежности, которая формируется программой 20.5.
21.2. Покажите в стиле
рис.
21.3 все кратчайшие пути в сети, определенной в упражнении 21.1.
21.3. Разработайте реализацию класса сети, который представляет обращение взвешенного орграфа, который определяется вставленными ребрами. Включите в реализацию конструктор ” обратного копирования ” , который принимает в качестве аргумента граф и использует все ребра этого графа для построения обращения.
21.4. Покажите, что для вычисления кратчайших путей в сетях с неотрицательными весами и в вершинах, и на ребрах (где вес пути определяется как сумма весов вершин и ребер на этом пути), достаточно построения АТД сети с весами только на ребрах.
21.5. Найдите в инернете какую-либо доступную большую сеть, содержащую расстояния или стоимости – возможно, географическую базу данных с информацией о дорогах, соединяющих города, либо расписания движения самолетов или поездов.
21.6. Напишите генератор разреженных случайных сетей на основе программы 17.12. Для присваивания весов ребрам определите АТД ребер случайного веса и напишите две реализации: одну для генерации равномерно распределенных весов, а другую – для нормально распределенных. Напишите клиентские программы, генерирующие разреженные случайные сети для обоих распределений весов с таким множеством значений V и E, чтобы их можно было использовать для выполнения эмпирических тестов на графах.
21.7. Напишите генератор насыщенных случайных сетей на основе программы 17.13 и генератора ребер случайного веса из упражнения 21.6. Напишите клиентские программы, генерирующие случайные сети для обоих распределений весов с таким множеством значений V и E, чтобы их можно было использовать для выполнения эмпирических тестов на графах.
21.8. Реализуйте независимую от представления сети клиентскую функцию, которая строит сеть, получая ребра с весами (пары целых чисел из диапазона от 0 до V- 1 с весами от 0 до 1) из стандартного ввода.
21.9. Напишите программу, которая генерирует V случайных точек на плоскости, затем строит сеть с (двунаправленными) ребрами, соединяющими все пары точек, расстояние между которыми не превышает заданное значение d (см. упражнение 17.74), и устанавливает вес каждого ребра равным расстоянию между концами этого ребра. Определите, каким должно быть d, чтобы ожидаемое количество ребер было равно E.
21.10. Напишите базовый класс и производные классы, реализующие абстрактные типы данных для графов, которые могут быть неориентироваными или ориентированными, взвешенными или невзвешенными и насыщенными или разреженными.
21.11. Приведенная ниже таблица из опубликованной дорожной карты содержит длины кратчайших маршрутов, соединяющих города. Найдите в таблице ошибку и исправьте ее. Составьте также таблицу в стиле
рис.
21.4, которая показывает, как проследовать по кратчайшему маршруту.
| Провиденс | Вестерли | Нью-Лондон | Норвич | |
|---|---|---|---|---|
| Провиденс | – | 53 | 54 | 48 |
| Вестерли | 53 | – | 18 | 101 |
| Нью-Лондон | 54 | 18 | – | 12 |
| Норвич | 48 | 101 | 12 | – |
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Задача
Дан ориентированный граф (G = (V, E)), а также вершина (s).
Найти длину кратчайшего пути от (s) до каждой из вершин графа. Длина пути — количество рёбер в нём.
BFS
BFS — breadth-first search, или же поиск в ширину.
Этот алгоритм позволяет решать следующую задачу.
Алгоритм работает следующим образом.
- Создадим массив (dist) расстояний. Изначально (dist[s] = 0) (поскольку расстояний от вершины до самой себя равно (0)) и (dist[v] = infty) для (v neq s).
- Создадим очередь (q). Изначально в (q) добавим вершину (s).
- Пока очередь (q) непуста, делаем следующее:
- Извлекаем вершину (v) из очереди.
- Рассматриваем все рёбра ((v, u) in E). Для каждого такого ребра пытаемся сделать релаксацию: если (dist[v] + 1 < dist[u]), то мы делаем присвоение (dist[u] = dist[v] + 1) и добавляем вершину (u) в очередь.
Визуализации:
-
https://visualgo.net/mn/dfsbfs
-
https://www.hackerearth.com/practice/algorithms/graphs/breadth-first-search/visualize/
Интуитивное понимание алгоритма
Можно представить, что мы поджигаем вершину (s). Каждый шаг алгоритма — это распространение огня на соседние вершины. Понятно, что огонь доберётся до вершины по кратчайшему пути.
Заметьте, что этот алгоритм очень похож на DFS — достаточно заменить очередь на стек и поиск в ширину станет поиском в глубину. Действительно, оба алгоритма при обработке вершины просто записывают всех непосещенных соседей, в которые из неё есть ребро, в структуру данных, и после этого выбирает следующую вершину для обработки в структуре данных. В DFS это стек (благодаря рекурсии), поэтому мы сначала записываем соседа, идем в обрабатываем его полностью, а потом начинаем обрабатывать следующего соседа. В BFS это очередь, поэтому мы кидаем сразу всех соседей, а потом начинаем обрабатывать вообще другую вершину – ту непосещенную, которую мы положили в очередь раньше всего.
Оба алгоритма позволяют обойти граф целиком – посетить каждую вершину ровно один раз. Поэтому они оба подходят для таких задач как: * поиск компонент связности * проверка графа на двудольность * построение остова
Реализация на C++
n — количество вершин в графе; adj — список смежности
vector<int> bfs(int s) {
// длина любого кратчайшего пути не превосходит n - 1,
// поэтому n - достаточное значение для "бесконечности";
// после работы алгоритма dist[v] = n, если v недостижима из s
vector<int> dist(n, n);
dist[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (dist[u] > dist[v] + 1) {
dist[u] = dist[v] + 1;
q.push(u);
}
}
}
return dist;
}Свойства кратчайших путей
Обозначение: (d(v)) — длина кратчайшего пути от (s) до (v).
Лемма 1. > Пусть ((u, v) in E), тогда (d(v) leq d(u) + 1).
Действительно, существует путь из (s) в (u) длины (d(u)), а также есть ребро ((u, v)), следовательно, существует путь из (s) в (v) длины (d(u) + 1). А значит кратчайший путь из (s) в (v) имеет длину не более (d(u) + 1),
Лемма 2. > Рассмотрим кратчайший путь от (s) до (v). Обозначим его как (u_1, u_2, dots u_k) ((u_1 = s) и (u_k = v), а также (k = d(v) + 1)).
> Тогда (forall (i < k): d(u_i) + 1 = d(u_{i + 1})).
Действительно, пусть для какого-то (i < k) это не так. Тогда, используя лемму 1, имеем: (d(u_i) + 1 > d(u_{i + 1})). Тогда мы можем заменить первые (i + 1) вершин пути на вершины из кратчайшего пути из (s) в (u_{i + 1}). Полученный путь стал короче, но мы рассматривали кратчайший путь — противоречие.
Корректность
Утверждение. > 1. Расстояния до тех вершин, которые были добавлены в очередь, посчитаны корректно. > 2. Вершины лежат в очереди в порядке неубывания расстояния, притом разность между кратчайшими расстояними до вершин в очереди не превосходит (1).
Докажем это по индукции по количеству итераций алгоритма (итерация — извлечение вершины из очереди и дальнейшая релаксация).
База очевидна.
Переход. Сначала докажем первую часть. Предположим, что (dist[v] + 1 < dist[u]), но (dist[v] + 1) — некорректное расстояние до вершины (u), то есть (dist[v] + 1 neq d(u)). Тогда по лемме 1: (d(u) < dist[v] + 1). Рассмотрим предпоследнюю вершину (w) на кратчайшем пути от (s) до (u). Тогда по лемме 2: (d(w) + 1 = d(u)). Следовательно, (d(w) + 1 < dist[v] + 1) и (d(w) < dist[v]). Но тогда по предположению индукции (w) была извлечена раньше (v), следовательно, при релаксации из неё в очередь должна была быть добавлена вершина (u) с уже корректным расстоянием. Противоречие.
Теперь докажем вторую часть. По предположению индукции в очереди лежали некоторые вершины (u_1, u_2, dots u_k), для которых выполнялось следующее: (dist[u_1] leq dist[u_2] leq dots leq dist[u_k]) и (dist[u_k] – dist[u_1] leq 1). Мы извлекли вершину (v = u_1) и могли добавить в конец очереди какие-то вершины с расстоянием (dist[v] + 1). Если (k = 1), то утверждение очевидно. В противном случае имеем (dist[u_k] – dist[u_1] leq 1 leftrightarrow dist[u_k] – dist[v] leq 1 leftrightarrow dist[u_k] leq dist[v] + 1), то есть упорядоченность сохранилась. Осталось показать, что ((dist[v] + 1) – dist[u_2] leq 1), но это равносильно (dist[v] leq dist[u_2]), что, как мы знаем, верно.
Время работы
Из доказанного следует, что каждая достижимая из (s) вершина будет добавлена в очередь ровно (1) раз, недостижимые вершины добавлены не будут. Каждое ребро, соединяющее достижимые вершины, будет рассмотрено ровно (2) раза. Таким образом, алгоритм работает за (O(V+ E)) времени, при условии, что граф хранится в виде списка смежности.
Неориентированные графы
Если дан неориентированный граф, его можно рассматривать как ориентированный граф с двумя обратными друг другу ориентированными рёбрами.
Восстановление пути
Пусть теперь заданы 2 вершины (s) и (t), и необходимо не только найти длину кратчайшего пути из (s) в (t), но и восстановить какой-нибудь из кратчайших путей между ними. Всё ещё можно воспользоваться алгоритмом BFS, но необходимо ещё и поддерживать массив предков (p), в котором для каждой вершины будет храниться предыдущая вершина на кратчайшем пути.
Поддерживать этот массив просто: при релаксации нужно просто запоминать, из какой вершины мы прорелаксировали в данную. Также будем считать, что (p[s] = -1): у стартовой вершины предок — некоторая несуществующая вершина.
Восстановление пути делается с конца. Мы знаем последнюю вершину пути — это (t). Далее, мы сводим задачу к меньшей, переходя к нахождению пути из (s) в (p[t]).
Реализация BFS с восстановлением пути
// теперь bfs принимает 2 вершины, между которыми ищется пути
// bfs возвращает кратчайший путь из s в t, или же пустой vector, если пути нет
vector<int> bfs(int s, int t) {
vector<int> dist(n, n);
vector<int> p(n, -1);
dist[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (dist[u] > dist[v] + 1) {
p[u] = v;
dist[u] = dist[v] + 1;
q.push(u);
}
}
}
// если пути не существует, возвращаем пустой vector
if (dist[t] == n) {
return {};
}
vector<int> path;
while (t != -1) {
path.push_back(t);
t = p[t];
}
// путь был рассмотрен в обратном порядке, поэтому его нужно перевернуть
reverse(path.begin(), path.end());
return path;
}Проверка принадлежности вершины кратчайшему пути
Дан ориентированный граф (G), найти все вершины, которые принадлежат хотя бы одному кратчайшему пути из (s) в (t).
Запустим из вершины (s) в графе (G) BFS — найдём расстояния (d_1). Построим транспонированный граф (G^T) — граф, в котором каждое ребро заменено на противоположное. Запустим из вершины (t) в графе (G^T) BFS — найдём расстояния (d_2).
Теперь очевидно, что (v) принадлежит хотя бы одному кратчайшему пути из (s) в (t) тогда и только тогда, когда (d_1(v) + d_2(v) = d_1(t)) — это значит, что есть путь из (s) в (v) длины (d_1(v)), а затем есть путь из (v) в (t) длины (d_2(v)), и их суммарная длина совпадает с длиной кратчайшего пути из (s) в (t).
Кратчайший цикл в ориентированном графе
Найти цикл минимальной длины в ориентированном графе.
Попытаемся из каждой вершины найти кратчайший цикл, проходящий через неё, с помощью BFS. Это делается аналогично обычному BFS: мы должны найти расстояний от вершины до самой себя, при этом не считая, что оно равно (0).
Итого, у нас (|V|) запусков BFS, и каждый запуск работает за (O(|V| + |E|)). Тогда общее время работы составляет (O(|V|^2 + |V| |E|)). Если инициализировать массив (dist) единожды, а после каждого запуска BFS возвращать исходные значения только для достижимых вершин, решение будет работать за (O(|V||E|)).
Задача
Дан взвешенный ориентированный граф (G = (V, E)), а также вершина (s). Длина ребра ((u, v)) равна (w(u, v)). Длины всех рёбер неотрицательные.
Найти длину кратчайшего пути от (s) до каждой из вершин графа. Длина пути — сумма длин рёбер в нём.
Алгоритм Дейкстры
Алгоритм Дейкстры решает приведённую выше задачу. Он работает следующим образом.
- Создать массив (dist) расстояний. Изначально (dist[s] = 0) и (dist[v] = infty) для (v neq s).
- Создать булёв массив (used), (used[v] = 0) для всех вершин (v) — в нём мы будем отмечать, совершалась ли релаксация из вершины.
- Пока существует вершина (v) такая, что (used[v] = 0) и (dist[v] neq infty), притом, если таких вершин несколько, то (v) — вершина с минимальным (dist[v]), делать следующее:
- Пометить, что мы совершали релаксацию из вершины (v), то есть присвоить (used[v] = 1).
- Рассматриваем все рёбра ((v, u) in E). Для каждого ребра пытаемся сделать релаксацию: если (dist[v] + w(v, u) < dist[u]), присвоить (dist[u] = dist[v] + w(v, u)).
Иными словами, алгоритм на каждом шаге находит вершину, до которой расстояние сейчас минимально и из которой ещё не была произведена релаксация, и делает её.
Посчитаем, за сколько работает алгоритм. Мы (V) раз ищем вершину минимальным (dist), поиск минимума у нас линейный за (O(V)), отсюда (O(V^2)). Обработка ребер у нас происходит суммарно за (O(E)), потому что на каждое ребро мы тратим (O(1)) действий. Так мы находим финальную асимптотику: (O(V^2 + E)).
Реализация на C++
Рёбра будем хранить как pair<int, int>, где первое число пары — куда оно ведёт; а второе — длина ребра.
// INF - infinity - бесконечность
const long long INF = (long long) 1e18 + 1;
vector<long long> dijkstra(int s) {
vector<long long> dist(n, INF);
dist[s] = 0;
vector<bool> used(n);
while (true) {
// находим вершину, из которой будем релаксировать
int v = -1;
for (int i = 0; i < n; i++) {
if (!used[i] && (v == -1 || dist[i] < dist[v])) {
v = i;
}
}
// если не нашли подходящую вершину, прекращаем работу алгоритма
if (v == -1) {
break;
}
for (auto &e : adj[v]) {
int u = e.first;
int len = e.second;
if (dist[u] > dist[v] + len) {
dist[u] = dist[v] + len;
}
}
}
return dist;
}Восстановление пути
Восстановление пути в алгоритме Дейкстры делается аналогично восстановлению пути в BFS (и любой динамике).
Дейкстра на сете
Искать вершину с минимальным (dist) можно гораздо быстрее, используя такую структуру данных как очередь с приоритетом. Нам нужно хранить пары ((dist, index)) и уметь делать такие операции: * Извлечь минимум (чтобы обработать новую вершину) * Удалить вершину по индексу (чтобы уменьшить (dist) до какого-то соседа) * Добавить новую вершину (чтобы уменьшить (dist) до какого-то соседа)
Для этого используют, например, кучу или сет. Удобно помимо сета хранить сам массив dist, который его дублирует, но хранит элементы по порядку. Тогда, чтобы заменить значение ((dist_1, u)) на ((dist_2, u)), нужно удалить из сета значение ((dist[u], u)), сделать (dist[u] = dist_2;) и добавить в сет ((dist[u], u)).
Данный алгоритм будет работать за (V O(log V)) извлечений минимума и (O(E log V)) операций уменьшения расстояния до вершины (может быть сделано после каждого ребра). Поэтому алгоритм работает за (O(E log V)).
Заметьте, что этот алгоритм не лучше и не хуже, чем без сета, который работает за (O(V^2 + E)). Ведь если (E = O(V^2)) (граф почти полный), то Дейкстра без сета работает быстрее, а если, наример, (E = O(V)), то Дейкстра на сете работает быстрее. Учитывайте это, когда выбираете алгоритм.
Рассмотрим пример нахождение кратчайшего пути. Дана сеть автомобильных дорог, соединяющих области города. Некоторые дороги односторонние. Найти кратчайшие пути от центра города до каждого города области.
Для решения указанной задачи можно использовать алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Работает только для графов без рёбер отрицательного веса.
Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
Кружками обозначены вершины, линиями – пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначен их вес – длина пути. Рядом с каждой вершиной красным обозначена метка – длина кратчайшего пути в эту вершину из вершины 1.

Инициализация
Метка самой вершины 1 полагается равной 0, метки остальных вершин – недостижимо большое число (в идеале — бесконечность). Это отражает то, что расстояния от вершины 1 до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.

Первый шаг
Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Обходим соседей вершины по очереди.
Первый сосед вершины 1 – вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1 (значению её метки) и длины ребра, идущего из 1-й во 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2 (10000), поэтому новая метка 2-й вершины равна 7.

Аналогично находим длины пути для всех других соседей (вершины 3 и 6).
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит. Вершина 1 отмечается как посещенная.
Второй шаг
Шаг 1 алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.
Вершина 1 уже посещена. Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а 9 < 17, поэтому метка не меняется.

Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна 22 (7 + 15 = 22). Поскольку 22<10000, устанавливаем метку вершины 4 равной 22.
Все соседи вершины 2 просмотрены, помечаем её как посещенную.
Третий шаг
Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим следующие результаты.

Четвертый шаг

Пятый шаг

Шестой шаг

Таким образом, кратчайшим путем из вершины 1 в вершину 5 будет путь через вершины 1 — 3 — 6 — 5, поскольку таким путем мы набираем минимальный вес, равный 20.
Займемся выводом кратчайшего пути. Мы знаем длину пути для каждой вершины, и теперь будем рассматривать вершины с конца. Рассматриваем конечную вершину (в данном случае — вершина 5), и для всех вершин, с которой она связана, находим длину пути, вычитая вес соответствующего ребра из длины пути конечной вершины.
Так, вершина 5 имеет длину пути 20. Она связана с вершинами 6 и 4.
Для вершины 6 получим вес 20 — 9 = 11 (совпал).
Для вершины 4 получим вес 20 — 6 = 14 (не совпал).
Если в результате мы получим значение, которое совпадает с длиной пути рассматриваемой вершины (в данном случае — вершина 6), то именно из нее был осуществлен переход в конечную вершину. Отмечаем эту вершину на искомом пути.
Далее определяем ребро, через которое мы попали в вершину 6. И так пока не дойдем до начала.
Если в результате такого обхода у нас на каком-то шаге совпадут значения для нескольких вершин, то можно взять любую из них — несколько путей будут иметь одинаковую длину.
Реализация алгоритма Дейкстры
Для хранения весов графа используется квадратная матрица. В заголовках строк и столбцов находятся вершины графа. А веса дуг графа размещаются во внутренних ячейках таблицы. Граф не содержит петель, поэтому на главной диагонали матрицы содержатся нулевые значения.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 7 | 9 | 0 | 0 | 14 |
| 2 | 7 | 0 | 10 | 15 | 0 | 0 |
| 3 | 9 | 10 | 0 | 11 | 0 | 2 |
| 4 | 0 | 15 | 11 | 0 | 6 | 0 |
| 5 | 0 | 0 | 0 | 6 | 0 | 9 |
| 6 | 14 | 0 | 2 | 0 | 9 | 0 |
Реализация на C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define SIZE 6
int main()
{
int a[SIZE][SIZE]; // матрица связей
int d[SIZE]; // минимальное расстояние
int v[SIZE]; // посещенные вершины
int temp, minindex, min;
int begin_index = 0;
system(“chcp 1251”);
system(“cls”);
// Инициализация матрицы связей
for (int i = 0; i<SIZE; i++)
{
a[i][i] = 0;
for (int j = i + 1; j<SIZE; j++) {
printf(“Введите расстояние %d – %d: “, i + 1, j + 1);
scanf(“%d”, &temp);
a[i][j] = temp;
a[j][i] = temp;
}
}
// Вывод матрицы связей
for (int i = 0; i<SIZE; i++)
{
for (int j = 0; j<SIZE; j++)
printf(“%5d “, a[i][j]);
printf(“n”);
}
//Инициализация вершин и расстояний
for (int i = 0; i<SIZE; i++)
{
d[i] = 10000;
v[i] = 1;
}
d[begin_index] = 0;
// Шаг алгоритма
do {
minindex = 10000;
min = 10000;
for (int i = 0; i<SIZE; i++)
{ // Если вершину ещё не обошли и вес меньше min
if ((v[i] == 1) && (d[i]<min))
{ // Переприсваиваем значения
min = d[i];
minindex = i;
}
}
// Добавляем найденный минимальный вес
// к текущему весу вершины
// и сравниваем с текущим минимальным весом вершины
if (minindex != 10000)
{
for (int i = 0; i<SIZE; i++)
{
if (a[minindex][i] > 0)
{
temp = min + a[minindex][i];
if (temp < d[i])
{
d[i] = temp;
}
}
}
v[minindex] = 0;
}
} while (minindex < 10000);
// Вывод кратчайших расстояний до вершин
printf(“nКратчайшие расстояния до вершин: n”);
for (int i = 0; i<SIZE; i++)
printf(“%5d “, d[i]);
// Восстановление пути
int ver[SIZE]; // массив посещенных вершин
int end = 4; // индекс конечной вершины = 5 – 1
ver[0] = end + 1; // начальный элемент – конечная вершина
int k = 1; // индекс предыдущей вершины
int weight = d[end]; // вес конечной вершины
while (end != begin_index) // пока не дошли до начальной вершины
{
for (int i = 0; i<SIZE; i++) // просматриваем все вершины
if (a[i][end] != 0) // если связь есть
{
int temp = weight – a[i][end]; // определяем вес пути из предыдущей вершины
if (temp == d[i]) // если вес совпал с рассчитанным
{ // значит из этой вершины и был переход
weight = temp; // сохраняем новый вес
end = i; // сохраняем предыдущую вершину
ver[k] = i + 1; // и записываем ее в массив
k++;
}
}
}
// Вывод пути (начальная вершина оказалась в конце массива из k элементов)
printf(“nВывод кратчайшего путиn”);
for (int i = k – 1; i >= 0; i–)
printf(“%3d “, ver[i]);
getchar(); getchar();
return 0;
}
Результат выполнения

Назад: Алгоритмизация
