В данном уроке мы рассмотрим такие понятия как делители и кратные.
Что такое делитель?
Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.
Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:
8 : 2 = 4
Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:
9 : 3 = 3
Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:
10 : 4 = 2 (2 в остатке)
Определение. Делителем числа а называется число, на которое число а делится без остатка.
Данное определение содержит переменную a. Подставим вместо этой переменной любое число, например число 12 и прочитаем определение:
Делителем числа 12 называется число, на которое 12 делится без остатка.
Попробуем перечислить эти числа:
1, 2, 3, 4, 6, 12
Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Кратные числа
Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3
6 : 3 = 2
Определение. Кратным числа а называется число, которое делится без остатка на а.
Данное определение содержит переменную a. Подставим вместо этой переменной любое число, например число 5 и прочитаем определение:
Кратным числа 5 называется число, которое делится без остатка на 5.
У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:
5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Примеры:
10 : 5 = 2
100 : 5 = 20
100 : 2 = 50
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Примеры:
355 : 5 = 71
200 : 5 = 40
475 : 5 = 95
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
27 : 3 = 9
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
18 : 9 = 2
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
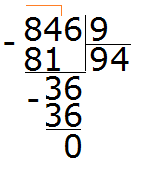
Чётные и нечётные числа
Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:
20 : 2 = 10
Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:
21 : 2 = 10 (1 в остатке)
Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.
Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.
А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
5 : 1 = 5
5 : 5 = 1
Значит, число 5 является простым числом.
Составным же называется число, которое имеет больше двух делителей. Например, число 4 составное, поскольку у него больше двух делителей: 4, 2 и 1
4 : 4 = 1
4 : 2 = 2
4 : 1 = 4
Значит, число 4 является составным числом.
Разложение составного числа на простые множители
Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.
Например, число 6 можно записать в виде суммы 4 + 2 или в виде частного 12 : 2 или в виде произведения 2 × 3. Последнюю запись 2 × 3 можно назвать разложением числа 6 на простые множители.
Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.
Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4
4 = 2 × 2
Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6
6 = 2 × 3
Разложим на множители число 8. Это число можно разложить на множители 2 и 4, при этом множитель 4 можно разложить на два множителя: 2 и 2. Поэтому вместо четвёрки записываем её разложение:
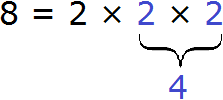
Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10
180 = 18 × 10
Теперь раскладываем множители 18 и 10 на другие множители:
18 = 3 × 6
10 = 5 × 2
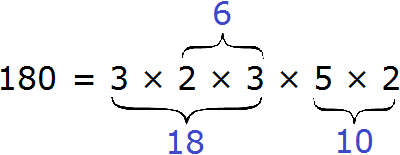
Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:
6 = 2 × 3
Теперь собираем все простые множители вместе:
На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.
Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.
При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.
Например, разложим предыдущее число 180 этим способом.
Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.
180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:
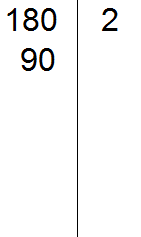
Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.
90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:
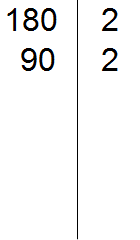
Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:
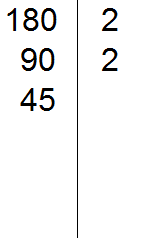
Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.
45 на 2 не делится. Тогда проверяем делится ли 45 на 3.
45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
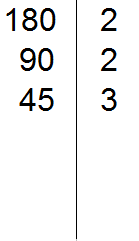
Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:
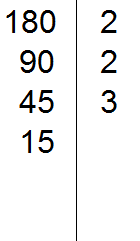
Теперь делим 15. Проверяем делится ли 15 на 2.
15 не делится на 2. Тогда проверяем делится ли 15 на 3.
15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
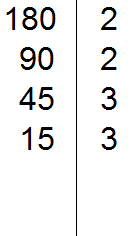
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:
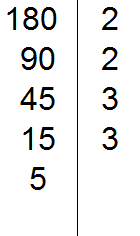
Теперь делим 5. Проверяем делится ли 5 на 2.
5 не делится на 2. Тогда проверяем делится ли 5 на 3.
5 не делится на 3. Тогда проверяем делится ли 5 на 5.
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:
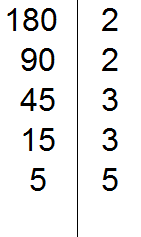
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:
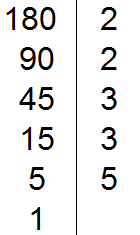
На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.
Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:
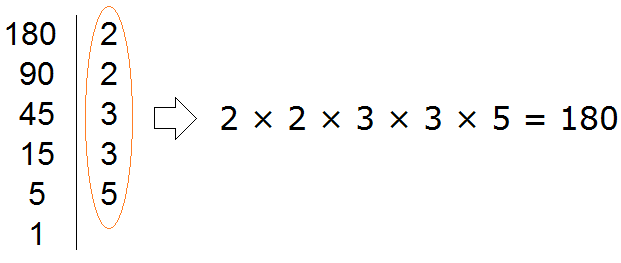
Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.
Нахождение делителей числа
В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.
Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2
6 : 2 = 3
Ещё делителем числа 6 является число 3
6 : 3 = 2
Ещё делителем числа 6 является число 1
6 : 1 = 6
Наконец, делителем числа 6 является само это число
6 : 6 = 1
Перечислим все делители числа 6
1, 2, 3, 6
Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.
Пример 1. Найти делители числа 12
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.
В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:
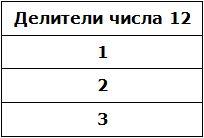
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.
Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4
2 × 2 = 4
Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
На основании приведённого примера можно сформировать правило для нахождения делителей числа:
Чтобы найти делители числа, нужно:
- записать в качестве первого делителя единицу;
- разложить исходное число на простые множители и выписать из полученных простых множителей те множители, которые являются делителями исходного числа (если множитель повторяется, то выписать его нужно только один раз);
- найти все возможные произведения полученных простых множителей между собой. Получаемые в результате ответы будут остальными делителями исходного числа.
Пример 2. Найти делители числа 6
Первым делителем числа 6 запишем единицу:
1
Теперь разложим число 6 на простые множители:
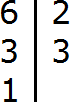
Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:
1, 2, 3
Теперь найдём все возможные произведения простых множителей числа 6. В данном случае имеется только одно произведение, а именно 2 × 3. Это произведение равно 6. Допишем число 6 к нашим делителям:
1, 2, 3, 6
Таким образом, делителями числа 6 являются числа 1, 2, 3, 6.
Задания для самостоятельного решения
Задание 1. Разложите число 256 на простые множители
Решение:
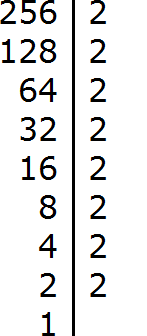
Задание 2. Разложите число 52 на простые множители
Решение:
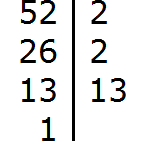
Задание 3. Разложите число 98 на простые множители
Решение:
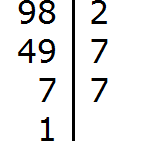
Задание 4. Разложите число 116 на простые множители
Решение:
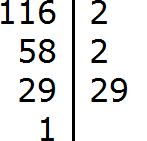
Задание 5. Разложите число 228 на простые множители
Решение:
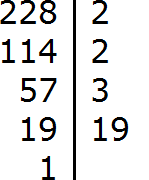
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Кратное и делитель
Если одно натуральное число делится без остатка на другое натуральное число, то первое называется кратным второго, а второе — делителем первого.

Кратное числа — это делимое, которое делится на данный делитель без остатка.
Делитель числа — это делитель, на который делимое делится без остатка.
Пример. Возьмём, например, такое деление:
6 : 3 = 2
Число 6 делится на число 3 без остатка. Следовательно, число 6 — кратное числа 3, а число 3 — делитель числа 6.
Пусть m и n — натуральные числа, если число m является кратным числа n, то говорят: m кратно n
или m делится на n
Пример. 6 кратно 3 (шесть кратно трём) или 6 делится на 3 (шесть делится на три).
Самым маленьким кратным любого натурального числа является само это число, так как любое натуральное число можно разделить само на себя без остатка (в частном всегда будет единица).
Пример. Для числа 7 наименьшим кратным является число 7, для числа 2 — число 2:
7 : 7 = 1 (семь кратно семи);
2 : 2 = 1 (два кратно двум).
Для любого натурального числа существует бесконечно много кратных. Получить кратное для данного числа достаточно легко, можно просто умножить его на любое натуральное число, полученное произведение и будет его кратным.
Пример. Получим кратное числа 5, умножив его, например, на 2:
5 · 2 = 10.
Число 10 — кратное числа 5:
10 : 5 = 2.
Так как на единицу делится любое натуральное число, то число 1 является делителем любого натурального числа.
Пример.
3 : 1 = 3;
4 : 1 = 4;
9 : 1 = 9.
Что такое кратное число
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.
Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.
Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.
Кратное число — это …
Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.
Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).
А у чисел, которые участвуют в делении, есть определенные названия:
- Делимое – то число, которое собираются делить;
- Делитель – число, на которое будут делить делимое. Соответственно, делитель чаще всего меньше делимого. Хотя не исключен и другой вариант. Единственное число, которое не может быть делителем, это ноль.
- Частное – результат деления, то есть число, которое получается в результате выполнения математического действия.
Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.
Одно число называется кратным другому, если его можно на него поделить без остатка.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.
Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.
12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6
Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.
Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:
Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.
Таблицы чисел кратных 2,3,4,5,6,7,9
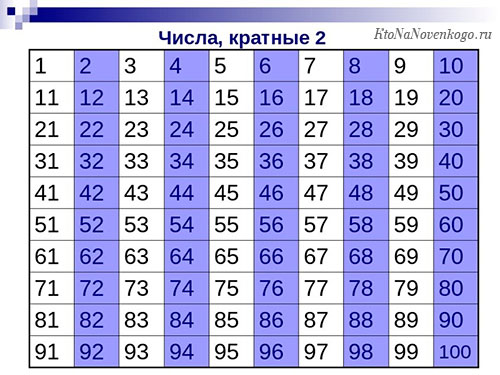
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.
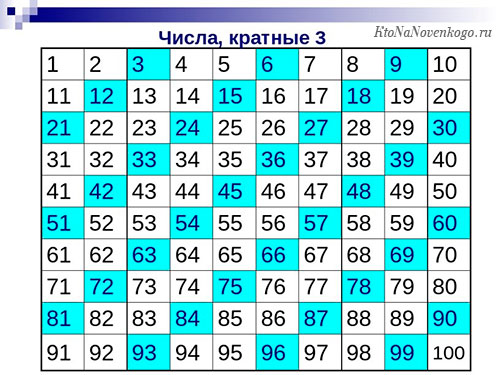
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.
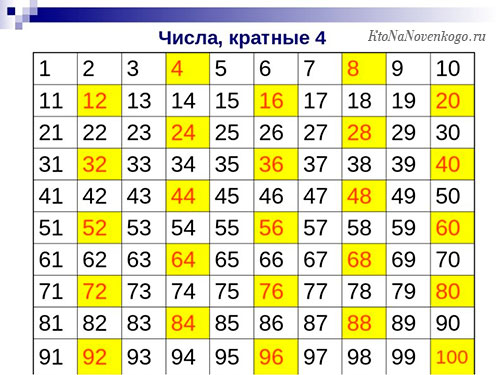
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.
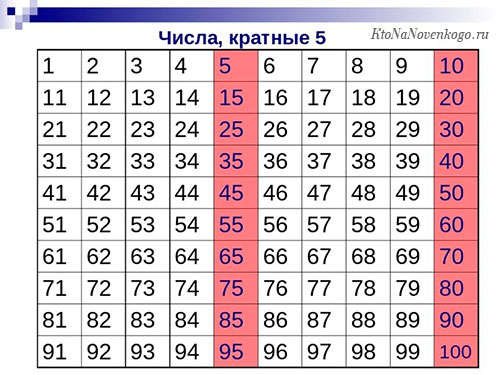
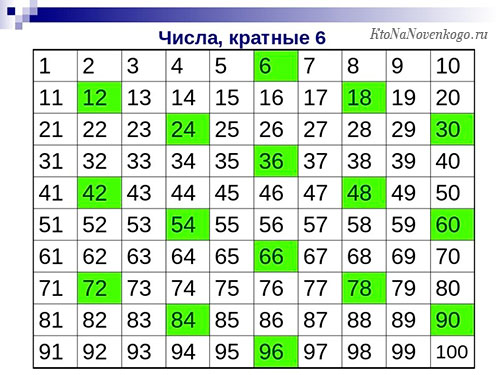
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.
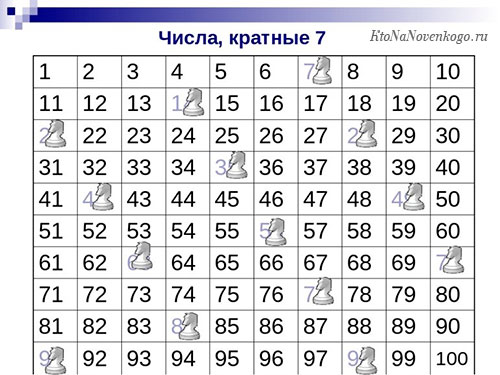
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».
И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.
Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.
| Числа, кратные 9 | 27 | 198 | 5 877 | 3 816 | 117 | 72 |
|---|---|---|---|---|---|---|
| Сумма | 9 | 18 | 27 | 18 | 9 | 9 |
Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.
Вместо заключения
А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.
Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.
В школе даются начальные знания по основным наукам. Огромную роль играет математика. Она используется не только при расчетах, но и в программировании.
В данной статье рассмотрена теория чисел. Она является своеобразной «базой», помогающей более подробно рассматривать математические действия и операции. В ней особую роль играют делители чисел. Зная о них, можно достаточно быстро и точно провести большинство операций. Пример – посчитать дроби и выделить грамотно доли.
Определение
Делители чисел – это такие значения, при делении на которые у «первоначального» числового компонента не будет остатка. Является целым в обязательном порядке. Пример – у 21 два делителя: 3 и 7. Проверить это можно по таблице умножения, которая изучается в начальных классах. Других упомянутых компонентов к 21 нет. В остальных случаях при делении будет получаться остаток.
Кратные
С делителями чисел познакомились. Теперь стоит обратить внимание на еще один момент, изучаемый в младших классах. Речь идет о кратных.
Краткое – это ситуация, при которой какое-нибудь значение удалось поделить без остатка на другое. Кратным a будет называться значение, которое без остатка делится на a.
Каждая «цифра» в математике имеет бесконечно много кратных. Пример – 5. Сюда можно отнести: 5, 10, 15, 20, 25, 100, 1005 и так далее. Все они будут без остатка делиться на пятерку.
Простые и составные
В начальных классах учителя говорят, что в математике есть простые числа и составные. Тут необходимо запомнить:
- Простые – это натуральное число, которое делится только на себя и единицу.
- Единица не включена в ряд простых.
- Составное число – это непростой элемент в математике. Единица сюда тоже не включена. Имеет несколько делителей. Согласно информации, подаваемой в начальных классах – больше двух.
Если интересует, сколько делителей у простого заданного числа, ответ будет очевиден – их всего два. И найти таковые проще простого. Эта информация очевидна из самого определения.
Составные числа могут иметь бесконечное количество делителей. Ответить, сколько именно, невозможно – все зависит от конкретной ситуации. Главное – чтобы их в конечном итоге оказалось больше двух.
В программировании найти «простую цифру» достаточно легко. Операция с легкостью проводится за O(N), где N – это проверяемый элемент. Достаточно проверить, будет ли оно делиться без остатка хотя бы на один элемент среди цепочки: 2, 3, 4, …, N-1. В школьных классах соответствующая информация не изучается. Она пригодится непосредственным программистам.
Вот – пример реализации. Этот код нужно просто обработать компилятором и посмотреть на выданные результаты. N – подставить свое значение.
Делимость – признаки
В разных классах начальной школы (иногда – в среднем звене) активно рассматриваются не только делители числа, но и признаки делимости. Эта информация тоже включена в рассматриваемую теорию. Она помогает найти простые делители заданного числа намного быстрее. А еще – понять, простое оно или сложное. Узнать количество делителей, которые имеют числа, будет намного проще.
На десятку
Если «цифра» заканчивается на 0, она может делиться без остатка на 10. Это – правило, которое нужно запомнить в младших классах. Обычно такие элементы относятся к сложным/составным. Об этом учителя говорят еще в начальных классах. Связано это с тем, что «цифра», которая делится на 10, обычно может быть поделена:
- сама на себя;
- на десятку;
- на пятерку.
Из ранее изученных определений следует достоверность последнего утверждения.
Делимость на 5 и 2
Теперь стоит изучить более сложные варианты. Они тоже рассматриваются в начальных классах и позволяют понять, сколько делителей будет у «цифры», заданной в примере. Среди основных знаний, которые нужно освоить в начальной школе, выделяют признаки делимости на двойку и пятерку.
Тут в начальных классах требуется запомнить, что:
- Любая «цифра», которая заканчивается на 0, делится без остатка на 5 и 2.
- Если в конце стоит 0 или 5, то возможно деление без остатков на «пятерку».
- Когда «цифра» заканчивается на 0, 2, 4, 6, 8 – оно будет делиться на 2. Остаток не предусматривается.
Все это поможет быстрее найти делитель числа в начальных классах. Но есть и иные признаки делимости. Они тоже необходимы для нахождения рассматриваемых элементов.
Согласно установленным правилам, если сумма цифр в заданном элементе делится на 3, то все оно тоже разделяется без остатка на «тройку». Пример – 27. Сумма его составляющих будет равна 9. Оно делится на 3. Отсюда следует, что 27 при делении на «тройку» остатка не образовывается.
Рассматривая делители числа, стоит обратить внимание на еще один признак делимости. Речь идет о 9. Если сумма цифр в заданном компоненте делится на «девятку», то и все оно тоже не образовывает остатка вследствие выполняемых математических манипуляций. Соответствующий принцип тоже изучается в младших классах.
Разложение на множители
Разложение на простые множители – еще одна операция, которая изучается в рассматриваемой теории в начальных классах. Можно провести разложение любого натурального числа, которое входит в заданное выражение им же, но представленном в ином виде. Для этого требуется изучить делители чисел. Они пригодятся в соответствующей операции.
Суть приема заключается в том, что нужно представить «цифру» в виде произведения нескольких простых множителей (делителей заданных чисел). Пример – дана «шестерка». Находим делители этого числа. Справиться с соответствующей задачей сможет ученик младших классов:
- 1;
- 2;
- 3;
- 6.
В поиске натуральных множителей теперь не будет никаких проблем. И в представлении «цифры» соответствующей записью – тоже. Шестерка – это 3*2 и 6*1.
Стоит обратить внимание – согласно правилам, продиктованным математикой в начальных классах, разложить на множители удастся только составную «цифру». У него будет простой делитель натурального заданного числа. Простая заданная «цифра» не подлежит разложению.
Данный вариант разложения – элементарный. Его легко освоить даже в начальных классах, после изучения таблицы умножения. Подходит для небольших «цифр». Когда дело доходит до больших значений, стоит воспользоваться иным методом:
- Провести вертикальную линию.
- Слева написать делимые.
- Справа прописать делители заданного числа.
- Собрать полученные сведения во множители.
Правила, изучаемые в начальных классах, указывают на то, что тут на помощь приходят признаки делимости.
Выше – пример реализации приема с числом 180.
Правило обнаружения делителей
Чтобы найти простые делители числа, в начальных классах необходимо запомнить следующий принцип (правило):
- Записать в качестве первого делителя единицу.
- Исходный элемент разложить на простые множители.
- Выписать из соответствующих делителей те, на которые без остатка делится заданная изначально «цифра». При повторении повторно записывать его не потребуется.
- Отыскать все произведения полученных простых множителей между собой.
Полученные ответы – это остальные искомые компоненты. Если этот принцип усвоить в младших классах школы, удастся достаточно быстро разобраться в математике и счете.
Дроби
Ближе к средним классам школьная программа начинает предлагать дроби. Там рассмотренная тема будет особо актуальна. Одно и то же число можно записать десятично (15 – 3*5) и в виде дроби.
У дробей есть:
- числитель – то, что написано над чертой-разделителем;
- знаменатель – нижняя часть записи.
Чтобы в любом классе без проблем привести дроби к общему знаменателю, потребуется:
- Найти общее кратное знаменателей. Эта запись будет общим знаменателем.
- Разделить общий знаменатель на знаменатель каждой отдельно взятой дроби. Получится дополнительный множитель.
- Умножить числитель каждой дроби на дополнительный множитель.
Лишь после этого можно проводить сложение и вычитание дробей. Соответствующая информация пригодится в любом классе школы и даже во взрослой жизни при разнообразных вычислениях.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!

Нахождение НОК и НОД двух натуральных чисел
Содержание:
- Что такое НОК и НОД двух натуральных чисел
- Особенности вычисления, алгоритм Евклида
- Правило нахождения наибольшего общего делителя (НОД)
- Правило нахождения наименьшего общего кратного (НОК)
Что такое НОК и НОД двух натуральных чисел
Натуральными числами называют числа, которые используются при счете – 1, 2, 3, 16, 25, 101, 2560 и далее до бесконечности. Ноль, отрицательные и дробные или нецелые числа не относятся к натуральным.
Наименьшее общее кратное (НОК) двух натуральных чисел a и b – это наименьшее число, которое делится без остатка на каждое из рассматриваемых чисел.
Наибольший общий делитель (НОД) двух натуральных чисел a и b – это наибольшее число, на которое делится без остатка каждое рассматриваемое число.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свойства НОК и НОД для натуральных чисел a и b
- (НОД (a, b) = НОД (b, a);)
- (НОК (a, b) = НОК (b, a);)
- (НОК;(a,b)=frac{a;times;b}{НОД;(a,b)}.)
Особенности вычисления, алгоритм Евклида
Рассмотрим два способа определения НОД и НОК с помощью алгоритма Евклида:
- Способ деления.
При делении целых чисел с остатком, где a – делимое, b – делитель (b не равно 0) находят целые числа q и r согласно равенству (a=btimes) q+r, в котором q – неполное частное, r – остаток при делении (не отрицательное, по модулю меньше делителя).
Чтобы вычислить НОД, первоначально нужно выбрать наибольшее из двух чисел и поделить его на меньшее. Пока остаток не станет равным нулю, повторяется цикл деления делителя на остаток от деления в соответствии с формулой.
Пример №1
Вычислим НОД для чисел 12 и 20. Делим 20 на 12 и получаем 1 и 8 в остатке. Запишем иначе:
(20=12times1+8), так как остаток не равняется нулю, продолжаем деление. Делим 12 на 8 и получаем 1 и 4 в остатке. Записываем: (12=8times1+4) и по аналогии делим 8 на 4 и получаем 2 и 0 в остатке. НОД равен остатку, предшествующему нулю.
НОД (12;20) = 4
НОК получаем согласно свойству (НОК (a, b) = НОК;(a,b)=frac{a;times;b}{НОД;(a,b)}.) Подставляем числовые значения:
НОК (12; 20) = (12times20div4=60)
НОК (12;20) = 60
- Способ вычитания.
Здесь повторяется цикл вычитания из наибольшего числа меньшего числа до момента, пока разность не станет равна нулю. НОД равен предшествующей нулю разности.
Пример №2
Вычислим НОД для тех же чисел, 12 и 20.
20 – 12 = 8 (разность не равна нулю, продолжаем)
12 – 8 = 4
8 – 4 = 4
4 – 4 = 0
НОД (12;20) = 4
НОК находим также, как и при методе деления.
Правило нахождения наибольшего общего делителя (НОД)
Для нахождения наибольшего общего делителя воспользуемся пошаговым алгоритмом:
- Разложить числа на простые множители.
- Найти общий множитель одного и другого числа.
- Перемножить общие множители, если их несколько, и их произведение будет НОД.
Пример №3
Возьмем натуральные числа 24 и 36.
(24=2times2times2times3)
(36=2times2times3times3)
Правильно записать следующим образом:
(НОД (24;36)=2times3=6)
Примечание
В случае, когда одно или оба числа относятся к простым, т.е. делятся только на единицу и на само себя, то их НОД равняется 1.
Правило нахождения наименьшего общего кратного (НОК)
Для нахождения наименьшего общего кратного воспользуемся подробным алгоритмом:
- Наибольшее из чисел, а затем остальные разложить на простые множители.
- Выделить те множители, которые отсутствуют у наибольшего.
- Перемножить множители п. 2 и множители наибольшего числа, получить НОК.
Пример №4
Возьмем натуральные числа 9 и 12.
(12=2times2times3)
(9=3times3) (видим, что у числа 12 отсутствует одна тройка)
Правильно записать следующим образом:
(НОК (9;12)=2times2times3times3=36)
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
