Как найти кратность деформации

Удобно характеризовать деформацию не относительным удлинением е, а величиной I — отношением текущей и начальной длин образца (кратностью деформации)  [c.11]

Кратность деформации 176 Кривая длительной прочности 4 33  [c.453]

В механике резиноподобных материалов вместо относительной деформации е часто используют величину X = Шц, называемую кратностью. Очевидно,  [c.62]

В теории больших деформаций используются также степени удлинения или кратности >-i,  [c.180]

Ку к Главные степени (кратности) удлинения для деформации 0—>/.  [c.450]

Обозначим А, — кратности удлинения волокон, направленных до деформации вдоль е, — компоненты деформации  [c.277]

Рассматривается цилиндрическое тело, образующие которого параллельны вектору е . Предполагается, что все сечения цилиндра деформируются одинаково, а кратность удлинения волокон осевого направления Лз = Л равна некоторому неизвестному числу. Осевое перемещение V постоянно в поперечном сечении и линейно зависит от осевой координаты. Перемещения / и Н от осевой координаты 1ге зависят. При этих предположениях получим, что деформации 21 = зз = О, 22 — постоянная величина, ц, 33 и 13 — функции точки сечения.  [c.287]

Плоская деформация. При плоской деформации предполагается, что продольные волокна цилиндрического тела не деформируются, кратность их удлинений А равна единице. Перемещение V и деформация 33 равны нулю.  [c.290]

Общие соотношения. Многие формулы осесимметричной деформации аналогичны по структуре формулам обобщенной плоской деформации, но в них параметр А есть кратность удлинения волокон окружного направления, являющегося функцией точки меридионального сечения, причем А = Ао = (1 -Ь егг) — главная кратность удлинения.  [c.291]

Наряду с тензором кратностей удлинений широко используются тензор деформации Коши — Лагранжа  [c.61]

Пусть Xs(=Xi), >10(= Яг)—главные кратности удлинений вдоль меридионального и окружного направлений, являющихся главными линиями деформации. Из рис. 5.8.1, 5.8.2 следует  [c.121]

Такая форма записи подчеркивает то обстоятельство, что накапливаемая телом энергия деформации зависит не только от значения деформации (определяемой главными кратностями удлинений Хху Х2, Я.3), но и от направления деформации. Такую зависимость от направления называют анизотропией механических свойств материала, а сам материал — анизотропным. Анизотропны многие как естественные, так и искусственные материалы (кристаллы, текстуры, древесина и т. п.).  [c.36]

Для кратности ниже приводятся уравнения для скорости накопленной неупругой деформации и для скоростей компонент тензоров напряжений и деформации, при неизотермическом нагружении, без учёта воздействия ионизирующего излучения.  [c.133]

Число зубьев волновой передачи определяют в зависимости от передаточного отношения, числа волн и коэффициента кратности к из формулы (7.2). Чем больше коэффициент кратности, тем больше разность между максимальной и минимальной деформацией гибкого колеса и выше уровень напряжений в нем. Для снижения напряжений в гибком колесе при его деформации принимают коэффициент кратности к = 1. При увеличении числа волн растут неравномерность распределения нагрузки между зонами зацепления и напр ения в гибком колесе. Обычно конструируют передачи с двумя волнами деформации п = 2.  [c.141]

Таким образом, компоненты тензора кратности удлинений выражаются через радиальные деформации Xr=X и константу с  [c.562]

Важным подтверждением феноменологического соответствия механической модели вязкоупругого тела самому телу является функциональное обоснование соотношений (1.1)—(1.4) [204]. Из функционального анализа и очень общих предположений о зависимостях, возникающих в теле в момент 1 для напряжений а,у ( ) от процесса деформаций 1) в интервале времени О < С т прямо вытекают соотношения (1.1)—(1.4), как первые приближения разложения функционалов в виде суммы интегралов возрастающей кратности. Это представление вполне эквивалентно применяемому в теории упругости разложению напряжения по деформации в ряд Тейлора, причем первое приближение этого разложения представляет собой закон Гука.  [c.20]

Контролируемая прокатка — это высокотемпературная обработка низколегированной стали, технология которой основана на определенном сочетании основных параметров горячей деформации температуры нагрева и конца прокатки суммарной степени, кратности деформации и ее величины при раз.пичных температурах, скорости охлаждения между про.ходами 1 н т. д. В процессе прокатки с контролируемым режимом деформации структурные измеиення в деформируемом  [c.15]

Следствие. Пусть v — росток гладкого векторного поля в особой точке с собственным значением О и одномерным центральным многообразием. Пусть кратность этой особой точки равна j,+ l, и вещественные части ее ненулевых собственных значений образует нерезонансный набор. Росток с такими свойствами встречается в типичном семействе, зависящем не менее чем от р, параметров. Деформация такого ростка в типичном гладком ( j,+1)-параметрическом семействе конечногладко эквивалентна главной  [c.75]

Указатель-корректор шкалы, фиксирующей величину перемещения активного захвата, связан с маятником силоизмерителя, что позволяет путем автоматического вычитания хода пассивного захвата фиксировать расстояние, пройденное только активным захватом, т. е. деформацию образца. Машина РТ-250М-2 предназначена для испытания на растяжение образцов из различных тканей. Машина комплектуется захватами одного типа, для текстильных материалов. Тиристорный привод регулирует угловую скорость двигателя с кратностью  [c.40]

Разрывные машины с электронными силоизмерителями. В разрывной машине 2001Р-05 сменные электрические силонзмернтели измеряют нагрузку 2Н—5 кН. Три дополнительные стрелки на шкале нагрузок автоматически фиксируют нагрузки при двух заданных значениях деформации рабочего участка образца и нагрузки при разрыве образца. Специальный реечный механизм позволяет испытывать кольцевые образцы. По конструкции машина 2001 Р-05 аналогична машинам Р-5 и Р-05. Привод машины состоит из электродвигателя постоянного тока, червячного редуктора и зубчатой передачи для привода ходовых винтов. Угловую скорость с кратностью 1 100 плавно регулирует тиристорный электропривод.  [c.42]

Информация о действительной нагруженности и несущей способности — важный элемент при решении вопросов расчета конструкций, совершенствования их схем и форм, применения поверхностного упрочнения и других способов повышения эксплуатационной надежности и ресурса. Далее рассматриваются некоторые вопросы оценки вероятности неразруше-ния (надежности) в связи с условиями нагружения и несущей способностью элементов конструкций. Отказы по прочности, оцениваемые как возникновение разрушения, повреждение опасными трещинами или недопускаемые деформации, могут возникать в результате однократных или кратных перегрузок как статических, так и динамических или же вследствие наличия дефектов, достаточных для разрушения элементов конструкций при свойственном им уровне эксплуатационной нагруженности. Разрушения такого типа рассматриваются как статические, их вероятностная оценка осуществляется с учетом кратности статического нагружения, статистики возможных статических нагрузок и дисперсии статической прочности во внересурсной постановке. Это, например, уже давно делается в области оценки надежности строительных конструкций, гидротехнических сооружений и ряда других, нагруженных в основном статической нагрузкой.  [c.137]

Поэтому наиболее перспективны и точны устройства третьей группы, т. е. устройства с замкнутой цепью воздействия автоматического контроля размеров в процессе обработки. Эти устройства изменяют или прекращают процесс обработки в момент достижения параметров качества (размером) необходимого значения и осуществляют контроль только в процессе обработки. Назовем их для кратности управляющими автотолераторами . Эти устройства по своей природе позволяют вести обработку детали с наивысшей точностью, так как управляют размерной точностью данной конкретной обрабатываемой детали, компенсируя не только систематические погрешности (износ режущего инструмента, силовые и температурные деформации деталей станка, определяющие главную размерную цепочку), но и многие случайные составляющие. При этом автотолераторы конструктивно проще подналадчиков, так как для них отпадает необходимость в дополнительных средствах ориентации, базирования, крепления и транспортирования.  [c.109]

С увеличением коэффициента кратности увеличиваются числа зубьев колес и уменьшается модуль зацепления т при неизменном делительном диаметре колеса = mz и неизмен юй максимальной радиальной деформации Wq =К т.  [c.313]

Блоки могут быть установлены единично (см. блок 3 на рис. 6.4, а) или группами на единой оси (блоки 4, 5), называемыми блочными обоймами. Ради наглядности изображения блоки в каждой из указанных групп показаны раздвинутыми. Единичные блоки, называемые отклоняющими, служат для изменения направления каната, а блоки, объединенные в обоймы, вместе с канатом образуют полиспаст, кратно преобразующий входной параметр – скорость навивки каната на барабан в выходной параметр -скорость подъема груза (v < v ). Отношение i = Vk / v,. называют кратностью полиспаста. В таком же отношении, с учетом потерь энергии на трение каната о боковые стенки ручьев блоков, в подшипниках блоков и деформации проволок в канате при перегибах на блоках, учитываемых КПД полиспаста т), преобразуется сила тяжести груза вместе с грузозахватными приспособлениями mg в усилие в навиваемой на барабан ветви каната  [c.145]

Диаграммы условных и истинных напряжений и деформаций. Протяженность первичных диаграмм растяжения вдоль осей координат Р и А/ зависит от абсолютных размеров образцов. При постоянной 1фатности образца чем больше его длина и площадь поперечного сечения, тем выше и протяженнее первичная диаграмма растяжения. Однако если эту диаграмму представить в относительных координатах, то диаграммы для образцов одной кратности, но разных размеров будут одинаковы. Так, если по оси ординат откладывать условные напряжения ст, равные отношению нагрузки Р к начальной площади поперечного сечения Ро, а по оси абсцисс — условные удлинения 8, равные отношению абсолютного приращения длины образца А/ к его начальной длине о, то диаграмму называют диаграммой условных напряжений и деформаций (или просто условной диаграммой). На рис. 2.9, а схематически представлена условная диаграмма а—5. На этой диаграмме отмечены условный предел текучести Ст(,2, временное сопротивление а,,  [c.35]

Термины прашый и левый условны, так как, например, если вместо F базовым несимметричным тензором деформаций был бы принят тензор градиента места то термины правый и левый пришлось бы поменять местами. Для тензоров деформаций, являющихся функциями правого тензора кратностей удлинений U, часто используются термины материальный или лагранжев , а для тензоров деформаций, являющихся функциями левого тензора кратностей удлинений V, — пространственный или эйлеров . Эти термины искажают механический смысл тензоров деформаций, так как все они по своей сути материальные [63].  [c.35]

Кроме введенных выше тензоров деформадий можно рассмотреть еще ряд объективных тензоров деформаций, содержащих положительные, отрицательные, смешанные степени и натуральный логарифм тензоров кратностей удлинений U и V [3, 35, 36, 38, 46, 63, 74]. Формулировки уравнений механики с любым из этих тензоров теоретически эквивалентны. Предпочтительность использования того или иного тензора зависит в основном от определяющих соотношений материала тела, числа операций при определении компонент тензоров в численных расчетах и от степени нелинейности, учитываемой в формулировках уравнений.  [c.40]

В (5.5) а, у5, 7 углы, определяющие направления главных осей тензоров деформации (например, углы Эйлера). Такая форма записи отражает то обстоятельство, что накапливаемая телом энергия деформации зависит не только от величины деформации (определяемой главными кратностями удлинений Ai, Аг, Аз), но и от направления деформации материальных частиц. Тажую зависимость  [c.59]

Таким образом, рассматривается одномерная, не зависящая от Х2, деформация цилиндрической пластины, испытывающей вместе с тем равномерное продольное растяжение с кратностью удлинения А = Аг = onst. Так как напряженно-деформированное состояние не зависит от хг, можно считать, что исследуется цилиндрическая пластина единичной (по хг) длины. Этим, собственно, и объясняется использование термина арка-полоска.  [c.131]

Отсюда следует, что в отличие от случая плоского резонатора накопление аберращш происходат здесь только на протяжении нескольких обходов. Число обходов, дающих заметный вклад в деформации фронта установившейся волны, убывает с ростом кратности образованной зеркалами телескопической системы (или, в общем случае, с модулем кратности М ). Если неоднородность среды сводится к наличию медленно меняющегося градиента показателя преломления, конечная величина аберраций установившегося фронта легко может быть найдена простым суммированием.  [c.159]

Случай больших (высокоэластичных) деформаций для гипотетически бесструктурного тела по сутцеству нуждается не во вновь создаваемых критериях, а в выборе (и возможно в их обобтцении) среди известных в применении к конкретно поставленным задачам [249, 272]. Папример, можно мыслить аналог вязкого разрушения в виде возникновения, роста и последуютцего слияния полостей (пор) на продолжении большой оси исходного овального отверстия. Условия возникновения пор можно заимствовать из традиционных критериев прочности — ограниченности эквивалентных напряжений (условных или истинных) или ограниченности деформаций (кратностей) или ограниченности удельной энергии деформации. Перемычки между порами, вытягиваясь, уподобляются растягиваемому образцу и разрываются с образованием шейки. В итоге образуется ямочная поверхность излома, если допустить необратимость процесса после разрушения. Расширение полости с образованием новой ее поверхности может также обосновываться энергетическими критериями или деформационным критерием П.Ф. Морозова о предельных взаимных уг-  [c.12]

Уменьшение значений Fou с 0,8 до 0,447о при обкатывании и с 0,57 до 0,37 7о при виброобкатывании по мере возрастания s объясняется увеличением шага создаваемых неровностей. Уместно отметить, что Fon шлифованной и обточенной поверхностей составляет соответственно 0,1—0,16% и 0,31—0,35%. При дальнейшем увеличении подачи значение опорной поверхности Fon при отработке давлением будет уменьшаться и достигать величин значительно меньших, чем при точении и шлифовании. Такое явление объясняется тем, что пластической деформации будет подвергаться только часть поверхности, а значение опорной поверхности будет определяться недеформированной частью предварительно обработанной поверхности. Более плавное уменьшение значения опорной поверхности при виброобкатывании (см. рис. 16, б) можно объяснить повышенным деформирующим действием инструмента, большей перекрываемой поверхностью и увеличением кратности приложения нагрузки в результате колебательного движения шара.  [c.45]

---

73

ГОСУДАРСТВЕННОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ МЕДИКО-

СТОМАТОЛОГИЧЕСКИЙ
УНИВЕРСИТЕТ

МИНИСТЕРСТВА
ЗДРАВООХРАНЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ»

КАФЕДРА

Медицинской
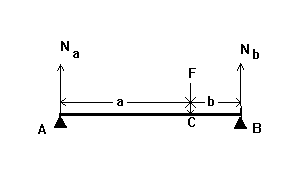
и биологической физики

В.С.
Воеводский А.А. Синицын В.М.Говорун

Вопросы и задачи

к экзамену по
медицинской и биологической

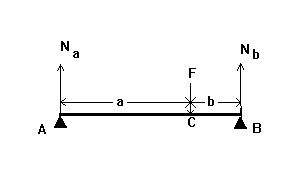
физике
для студентов стоматологического и
лечебного факультетов

3-е издание
переработанное и дополненное

Москва 2008

УДК
330.115(075.8)

С23

ББК
22.3 я 73

Рецензенты:

Н.Н.Фирсов
– профессор кафедры ЭТФ РГМУ доктор мед.
наук.

О.Ф.Беляев
– профессор кафедры общей физики МГТА
доктор физ. – мат. наук

Краткая аннотация

Представленные
вопросы и задачи составляют основу
коллоквиумов и экзаменационных билетов
по курсу медицинской и биологической
физики.
Они охватывают три раздела курса,
читаемого студентам
в первом семестре.

Стр.

1.Биомеханика……………………………… .3 – 24

2.Гемодинамика
и биореология………………25 – 53

3.Биоакустика…………………………………54
– 65

4.Эталоны
ответов…………………………….66 – 68

Разделы
начинается с примерно 20 теоретических
вопросов,
проработка
которых необходима для решения последующих
задач.

В
каждом разделе задачи расположены по
мере возрастания их сложности. При этом
рядом расположенные задачи могут быть
однотипными. Это дает возможность
преподавателю, разобрав одну из них на
занятиях, остальные, однотипные, задать
на дом.

Ответы
на все теоретические вопросы даются в
лекциях, которыми
в первую очередь рекомендуем пользоваться
при подготовке к экзамену.

Издается по решению
Ученого совета МГМСУ (Протокол №8 от25
марта 2008г.)

О
МГМСУ, 2008-01-16

© Кафедра медицинской
и биологической физики МГМСУ

©
Воеводский B.C.
Синицын А. А., Говорун В.М. 20008

Биомеханика

1.Дайте определения:
а) относительной продольной деформации,
б) относительной поперечной
деформации. Приведите соответствующие
математические выражения, раскройте
физический смысл, входящих в них величин.
Укажите единицы измерений.

2.Дайте определения:
а) нормального механического напряжения,
б) касательного (тангенциального)
напряжения. Приведите соответствующие
математические выражения, раскройте
физический смысл, входящих в них величин.
Укажите единицы измерений.

3.Дайте определения:
а) закона упругой деформации
сжатия-растяжения, б) закона упругой
деформации сдвига. Приведите соответствующие
математические выражения, раскройте
физический смысл, входящих в них величин.

4.Дайте определение
модуля упругости Е материала. Раскройте
его физический смысл, укажите единицы
измерения.

5.Перечислите
основные виды деформаций. К каким
простейшим видам их можно свести.

6.В чем отличие
упругой деформации от пластической?

7.В чем особенность
высокоэластической деформации? Каким
телам она присуща?

8.Дайте определение
момента силы, приведите соответствующие
математические выражения, раскройте
физический смысл, входящих в них величин,
укажите единицы измерения.

9.Запишите основное
условие равновесия тела, имеющего ось
вращения.

10.
Дайте определение коэффициента Пуассона.
Приведите соответствующее

математическое
выражение, раскройте физический смысл,
входящих в него величин.

Укажите единицы
измерений.

11.Дайте
определение прочности материала.
Запишите основное условие прочности.

12.
В чем причина различия между технической
и теоретической прочностями? Какая из
них

больше
и почему?

13.Перечислите
основные виды разрушения материалов.
Чем они отличаются?

14.Сформулируйте
с “энергетической точки зрения”
условие прорастания микротрещин.

Пояснения
сделайте с помощью соответствующего
графика.

15.Какие
основные механические характеристики
материалов можно определить из диаграммы

растяжения?

16. Дайте определение
понятия твердости материала. Перечислите
основные методы ее определения, приведите
соответствующие математические
выражения, раскройте физический смысл,
входящих в них величин. Укажите единицы
измерений.

17.Как связаны между
собой основные механические характеристики
материала: модуль Юнга, модуль сдвига
и коэффициент Пуассона. Приведите
соответствующее математическое
выражение, раскройте физический смысл,
входящих в него величин.

18.Что называется
долговечностью материала, в чем она
измеряется? Как зависит долговечность
материала от приложенного механического
напряжения? Приведите соответствующее
математическое выражение, раскройте
физический смысл, входящих в него
величин.

19.Как зависит
долговечность материала от температуры?
Приведите соответствующее

математическое
выражение, раскройте физический смысл,
входящих в него величин.

20.
Каков физический смысл понятия ”
температура хрупкости Т_хр
“

21.
Образец «ортосила – М» – материала для
силиконовых базисных подкладок начальной
длины L₀
= 20 мм
подвергается растяжению до относительной
деформации ε =1,5. Определите получившуюся
при этом длину образца
L .

22.Образец
«ортосила – М» – материала для силиконовых
базисных подкладок начальной длины

L₀
= 20 мм подвергается растяжению до длины
L=
40 мм. Определите величину относительной
деформации образца ε .

23.Образец
«ортосила – М» – материала для силиконовых
базисных подкладок подвергается
растяжению до относительной деформации
ε = 2, получившаяся при этом длина образца

L
= 50мм. Определить начальную длину образца
L₀.

24.Каково
должно быть напряжение σ при сжатии
дентина зуба до относительной деформации

ε
= 2% . Считать дентин зуба упругим материалом
с модулем упругости E = 25000 МПа?

25.
Какова должна быть величина относительной
деформации ε при сжатии дентина зуба
под напряжением σ = 4400 МПа, если считать
дентин зуба упругим материалом с модулем
упругости Юнга E
= 25000 МПа?

26.
Каков модуль упругости Юнга E
дентина зуба, если под напряжением σ =
250 МПа, величина относительной деформации
ε = 2 %

27. Для изготовления
проволочных элементов в ортопедической
стоматологии используют

проволоку из
нержавеющей стали. Отрезок проволоки
длиной L₁ = 200 мм
обладает жесткостью k₁ = 10 МН/м.
определите жесткость k₂
отрезка проволоки длиной L₂
= 75 мм в 1,5 раза большего поперечного
сечения.

28. Для изготовления
проволочных элементов в ортопедической
стоматологии используют

проволоку из
нержавеющей стали. Отрезок проволоки
длиной L₁= 80мм обладает
жесткостью k₁ =5 МН/м. Определите
жесткость k₂ отрезка
проволоки длиной L₂
= 85 мм в 1,5 раза меньшего поперечного
сечения.

29.Для изготовления
проволочных элементов в ортопедической
стоматологии используют проволоку из
нержавеющей стали. Отрезок проволоки
длиной L₁ = 200 мм
обладает жесткостью k₁ = 8 МН/м.
определите жесткость k₂
отрезка проволоки длиной L₂
= 50мм таково же поперечного сечения.

30.Для изготовления
проволочных элементов в ортопедической
стоматологии используют проволоку из
нержавеющей стали. Отрезок проволоки
длиной L₁ = 100 мм
обладает жесткостью k₁ = 10 МН/м.
Определите жесткость k₂
отрезка проволоки длиной L₂
= 300мм таково же поперечного сечения.

31.Для изготовления
проволочных элементов в ортопедической
стоматологии используют проволоку из
нержавеющей стали. Отрезок проволоки
длиной L₁ = 200 мм
обладает жесткостью k₁ = 10 МН/м.
определите жесткость отрезка проволоки
в 2 раза большего поперечного сечения
и 1,5 раза большей длины.

32.Какова будет
жесткость k_об. двух
параллельно соединенных отрезков
проволоки из сплава, применяемого для
изготовления кламмеров зубных протезов?
Оба отрезка проволоки одинаковой длины,
но различного поперечного сечения.
Поперечное сечение первого отрезка в
два раза больше, чем второго. Жесткость
первого из отрезков K₁ = 5 МН/м.?

33.Какова будет
жесткость k_об двух
последовательно соединенных отрезков
проволоки из сплава, применяемого для
изготовления кламмеров зубных протезов?
Оба отрезка проволоки одинакового
поперечного сечения, но различной длины.
Длина первого отрезка в два раза больше,
чем второго. Жесткость первого отрезка
K₁ = 10 МН/м.?

34.Докажите, что
максимальное значение коэффициент
Пуассона µ = 0,5

35.Покажите, что
для несжимаемых материалов коэффициент
Пуассона µ = 0,5

36. Цилиндрический
образец с начальной длиной L₀ =15
мм, изготовленный из сплава золота

подвергался
испытаниям на растяжение. При этом его
длина увеличилась до L =
16,8 мм,

а диаметр
уменьшился с d₀ = 7
мм до d = 6,8 мм. Определите
коэффициент Пуассона µ сплава.

37.Под действием
силы кратность деформации образца в
продольном направлении λ = 2, а в поперечном
направлении 0,625. Найти коэффициент
Пуассона для этого материала.

38.Найти кратность
деформации λ образца в продольном
направлении, если в поперечном направлении
она составила 0,77. Коэффициент Пуассона
равен 0,3.

39.Найти кратность
деформации λ образца в поперечном
направлении, если в продольном направлении
она составила 1,8 . Коэффициент Пуассона
равен 0,32.

40.Под воздействием
механического напряжения σ = 150 МПа,
образец из эластомера

удлинился в три
раза. Чему равен модуль сдвига G
для этого материала?

41.Найти
кратность деформации образец из
эластомера при воздействии растягивающего

механического
напряжения σ = 200 МПа, если модуль сдвига
G = 40 МПа.

42.Определите
модуль сдвига G стали,
если модуль упругости Юнга Е = 300 ГПа, а
коэффициент

Пуассона
μ = 0,3.

43.Определите
модуль упругости Е стали, если модуль
сдвига для нее равен G =
80 ГПа, а

коэффициент
Пуассона μ = 0,33.

44.На рисунке
схематично представлен мостовидный
протез с двумя двусторонними опорами
на

естественные
зубы A и B. Сосредоточенная сила F равная
800 Н приложена в точке C.

Определите силу
реакции опорного зуба А если a = 3
см, а b = 2 см

45.На рисунке
схематично представлен мостовидный
протез с двумя двусторонними опорами
на

естественные
зубы A и B. Сосредоточенная сила F равная
600 Н приложена в точке C.

Определите силу
реакции опорного зуба В если a = 4
см, а b = 2 см

46.На рисунке
схематично представлен мостовидный
протез с двумя двусторонними опорами
на

естественные
зубы A и B. Сосредоточенная сила F равная
900 Н приложена в точке C.

Определите
поперечную силу Q в сечении с координатой
x = 3 см, отсчитанной от точки A,

если a = 4 см, а
b = 2 см

47.На рисунке
схематично представлен мостовидный
протез с двумя двусторонними опорами
на естественные зубы A и B. Сосредоточенная
сила F равная 900 Н приложена в точке C.
Определите поперечную силу Q в сечении
с координатой x = 5 см, отсчитанной от
точки A, если a = 4 см, а b = 2 см

48.На рисунке
схематично представлен мостовидный
протез с двумя двусторонними опорами
на естественные зубы A и B. Сосредоточенная
сила F равная 630 Н приложена в точке C.
Определите изгибающий момент M(x) в
сечении с координатой x = 6 см, отсчитанной
от точки A, если a = 4 см, а b = 3 см.

49.На рисунке
схематично представлен мостовидный
протез с двумя двусторонними опорами
на естественные зубы A и B. Сосредоточенная
сила F равная 980 Н приложена в точке C.
Определите изгибающий момент M(x) в
сечении с координатой x = 3 см, отсчитанной
от точки A, если a = 4 см, а b = 3 см.

50.На рисунке
схематично представлен мостовидный
протез с двумя двусторонними опорами
на естественные зубы A и B. Сосредоточенная
сила F равная 900 Н приложена в точке C.
Определите расстояние от опорного зуба
А, на котором изгибающий момент принимает
максимальное значение, если a = 4 см, а
b = 3 см.

51.На рисунке
схематично представлен мостовидный
протез с двумя двусторонними опорами
на естественные зубы A и B. Сосредоточенная
сила F, равная 980 Н, приложена в точке C.
Определите расстояния от опорного зуба
А, на которых изгибающий момент принимает
значение М = 9Н^. м, если, а = 3 см, а
b = 4 см.

52.На
рисунке даны зависимости пределов
хрупкой прочности и текучести от
температуры

Какое
разрушение хрупкое или пластическое
будет у образца при температуре 200 K?

53.На
рисунке даны зависимости пределов
хрупкой прочности и текучести от
температуры

Какое
разрушение хрупкое или пластическое
будет у образца при температуре 100 K?

54.На
рисунке даны зависимости пределов
хрупкой прочности и текучести от
температуры для

некоторого
материала

Определить
предел текучести при температуре 260 К

55.На
рисунке даны зависимости пределов
хрупкой прочности и текучести от
температур

Определить
предел хрупкой прочности при температуре
80 К

56.На
рисунке даны зависимости пределов
хрупкой прочности и текучести от
температуры

Определить
предел хрупкой прочности при температуре
40 К

57.На
рисунке даны зависимости пределов
хрупкой прочности и текучести от
температуры

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Макеты страниц