Кратные корни многочленов
Пусть p(x) – многочлен степени n , а q(x) – многочлен степени n – k , где n и k – натуральные числа, удовлетворяющие неравенству  .
.
Определение . Число α называют корнем кратности k многочлена p(x) , если справедливо равенство
| p(x) = (x – α) k q (x) , | (1) |
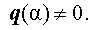
Утверждение 1 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда оно является корнем производной этого многочлена кратности k – 1 .
Доказательство . Взяв производную от обеих частей формулы (1), получаем

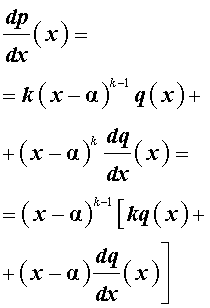
Поскольку выражение, стоящее в квадратных скобках, при x = α не обращается в нуль, то утверждение 1 доказано.
Из утверждения 1 вытекает следующее
Утверждение 2 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда выполнены равенства:
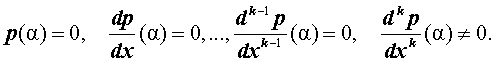
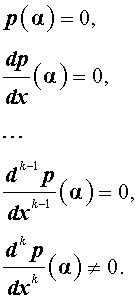
Задача . Найти все значения параметра m , при которых многочлен
имеет корень кратности 2 .
Решение . Воспользовавшись утверждением 2, получаем
Кратные корни многочлена
При рассмотрении вопроса о корнях многочлена, особо выделяют понятие кратных корней.
Определение. Пусть задан многочлен $fleft(xright) in Pleft[xright]$ ($Pleft[xright]$ — множество всех многочленов от буквы $x$ над полем $P$) и $alpha$, где $alpha$ — корень многочлена $fleft(xright)$. Элемент $alpha$ назовем $k$-кратным ($k in mathbb $, $k>1$) корнем многочлена, если имеет место следующее представление: $$fleft(xright)=left(x-alpharight)^k f_<1>left(xright),, f_<1>left(alpharight) ne 0.$$
Принято рассматривать понятие кратного корня для $k>1$. Если же $fleft(xright)$ можно представить следующим образом: $$fleft(xright)=left(x-alpharight) f_<1>left(xright),, f_<1>left(alpharight) ne 0,$$ то $alpha$ называется простым (однократным) корнем многочлена$fleft(xright)$. Если для $fleft(xright)$ имеет место следующее равенство: $$fleft(xright)=left(x-alpharight)^2 f_<1>left(xright),, f_<1>left(alpharight) ne 0,$$ то $alpha$ называется двукратным корнем многочлена $fleft(xright)$. Аналогично, существуют корни трехкратные, четырехкратные и так далее.
Часто условие $f_<1>left(alpharight) ne 0$ заменяют на $f_<1>left(xright),barvdots,(x-alpha)$. Эквивалентность этих условий вытекает из следствий теоремы Безу. Тогда, набор условий, что $f(x),vdots,left(x-alpharight)^k$, но $f(x),barvdots,left(x-alpharight)^$ эквивалентен тому, что $alpha$ — $k$-кратный корень многочлена $f(x)$.
Процесс нахождения кратности корня
Пусть задан многочлен $fleft(xright) in Pleft[xright]$ и его корень $alpha$ ( $deg fleft(xright) > 0$). Рассмотрим задачу о нахождении кратности корня $alpha$.
Так как $alpha$ — корень $fleft(xright)$, то имеет место следующее представление: $$fleft(xright)=left(x-alpharight)f_<1>left(xright).$$ Тогда, если $alpha$ не является корнем $f_<1>left(xright)$ ($f_<1>left(alpharight) ne 0$), то, по определению, $alpha$ — простой корень многочлена $fleft(xright)$. В противном случае, $alpha$ — $k$-кратный ($k in mathbb $, $k > 1 $) корень $fleft(xright)$. Задача сводится к нахождению $k-1$, то есть к нахождению кратности корня $f_<1>left(xright)$, где $deg f_<1>left(xright) = deg fleft(xright) — 1$. Учитывая, что $deg fleft(xright) > 0$, то повторение такого алгоритма решает задачу. Для этого используется алгоритм Горнера.
Стоит упомянуть, что иногда удобней пользоваться критерием кратности корня.
Примеры решения задач
- Пусть задан многочлен $fleft(xright)=x^3-3x^2+4$. Определить, является ли $2$ корнем многочлена $f(x)$. В случае положительного ответа найти его кратность.
Для решении задачи воспользуемся алгоритмом Горнера. Стоит обратить внимание на то, что хоть и слагаемое вида $a_<1>x^1$ отсутствует в записи, но нулевой коэффициент необходимо не забыть занести в таблицу.
| $1$ | $-3$ | $0$ | $4$ | |
| $2$ | $1$ | $-1$ | $-2$ | $0$ |
| $2$ | $1$ | $1$ | $0$ | |
| $2$ | $1$ | $3$ |
Из таблицы видно, что многочлен $f(x)$ поделился на $left(x-2right)^2$ без остатка, а на $left(x-2right)^3$ — нет. Получаем, что $2$ — двукратный корень многочлена $f(x)$.
Так как $alpha$ — двукратный корень многочлена $f(x)$, то $f(x)$ представим в следующем виде: $$fleft(xright)=left(x-alpharight)^2 f_<1>left(xright),$$где $f_<1>(alpha) ne 0$. Аналогично, $g(x)$ можно представить следующим образом: $$gleft(xright)=left(x-alpharight) g_<1>left(xright),$$где $g_<1>(alpha) ne 0$. Тогда, $$f(x)g(x)=left(x-alpharight)^2f_<1>(x)(x-alpha)g_<1>(x)=left(x-alpharight)^3f_<1>(x)g_<1>(x).$$Так как $f_<1>(alpha) ne 0$ и $g_<1>(alpha) ne 0$, то $f_<1>(alpha)g_<1>(alpha)ne0$. Обозначим $f(x)g(x)=h(x)$, $f_<1>(x)g_<1>(x)=h_<1>(x)$, тогда перепишем выражение многочлена $f(x)g(x)$ следующим образом: $$h(x)=left(x-alpharight)^3h_<1>(x),$$ где $h_<1>(alpha)ne0$. Тогда по определению $alpha$ — корень $f(x)g(x)$ третьей кратности.
Для решении задачи воспользуемся алгоритмом Горнера.
| $1$ | $5$ | $10$ | $10$ | $5$ | $1$ | |
| $-1$ | $1$ | $4$ | $6$ | $4$ | $1$ | $0$ |
| $-1$ | $1$ | $3$ | $3$ | $1$ | $0$ | |
| $-1$ | $1$ | $2$ | $1$ | $0$ | ||
| $-1$ | $1$ | $1$ | $0$ | |||
| $-1$ | $1$ | $0$ |
Из таблицы видно, что многочлен пятой степени $f(x)$ поделился на $left(x+1right)^5$ без остатка. Получаем, что $-1$ — корень пятой кратности.
По определению, для того, что бы $2$ была корнем второй кратности, необходимо что бы имело место следующее представление: $$f(x)=left(x-2right)^2f_<1>(x),, f_<1>(2) ne 0.$$С другой стороны, в нашем случае: $$f_<1>(x)=x^2+x-6=(x-2)(x+3),, f_<1>(2)=0.$$ Получаем, что $2$ не корень второй кратности. Тогда найдем его кратность. Выразим $f(x)$ подставив $f_<1>(x)=(x-2)(x+3)$:$$f(x)=left(x-2right)^3(x+3)=left(x-2right)^3f_<2>(x),$$ $f_<2>(2)=(2+3)=5ne0$. Значит, по определению, $2$ — корень многочлена $f(x)$ третьей кратности.
Представим исходный многочлен следующим образом: $$f(x)=x^4(x^4-8x^3+10x^2-1).$$
Обозначим $f_<1>(x)=x^4-8x^3+10x^2-1$. Легко убедиться, что $f_<1>(0)=-1ne0$. Получаем, что, по определению кратного корня, $0$ — корень многочлена $f(x)$ четвертой кратности.
Как определить кратность корня для уравнения
Разделы 
Дополнительно

Алгебраическим уравнением степени $n$ с одной неизвестной $x$ называется уравнение вида
$P_n(x) = a_0 x^n + a_1 x^ + cdots + a_n = 0 (a_0 neq 0)$ (1)
(т. е. уравнение $f(x) = 0$, в левой части которого стоит ц. р. ф степени $n$ от $х$).
Для алгебраических уравнений принято ставить задачу отыскания всех (вообще говоря, комплексных) корней уравнения. Так как корнями уравнения (1) являются нули (корни) многочлена в его левой части, то можно использовать сведения о целых рациональных функциях и их корнях. Утверждение формулируются применительно к уравнению (1) следующим образом:
1) Каждое уравнение степени $n$ имеет по меньшей мере один корень в комплексной области. Если каждый корень учитывать с его кратностью, т. е. считать за столько корней, какова его кратность, то число корней уравнения равно его степени $n$. При этом говорят, что $x = alpha$ — корень кратности $k$, если левая часть уравнения делится на $(x — alpha)^k$ нацело, но не делится нацело на $(x — alpha)^$.
2) Если уравнение (1) имеет комплексный (мнимый) корень $x = sigma + i tau$, то и комплексно сопряженное число $bar <х>= sigma — i tau$ является корнем уравнения (кратности обоих сопряженных корней одинаковы).
На протяжении столетий главной задачей алгебры было указание правил решения алгебраических уравнений. С древности известны формулы для решения уравнений первой и второй степени. Итальянскими математиками эпохи Возрождения (Кардано, Тарталья, Феррари) были найдены формулы для решения уравнений третьей и четвертой степени (они громоздки и не имеют большого практического значения). Попытки решения «в радикалах» (т. е. с применением действия извлечения корня) уравнений степени выше четвертой были в общем случае безуспешны. Уже в XIX веке в работах Руффини, Абеля и Галуа было установлено, что не только для корней общего уравнения степени выше четвертой не может быть дано формул, выражающих их в радикалах, но и что корни многих конкретных уравнений с числовыми (например, целыми) коэффициентами не могут быть выражены через радикалы из рациональных чисел.
источники:
http://ib.mazurok.com/2020/06/06/multiple-roots-of-polynomials/
http://earthz.ru/science/Chislo-i-kratnost-kornej
Кратный
Корень в Энциклопедическом словаре:
Кратный
Корень – алгебраического уравнения
– такое число b,
что f(х) делитсябез остатка на 2-ю
или более высокую степень m
двучлена (х – b); число m
-кратность корня b.
Любой
многочлен n-й степени имеет ровно n
корней.
Если
найти все корни многочлена n-й степени,
то его можно преобразовать к виду:
(x
– x1)*(x-x2)*(x – x3)^k*(x – x4)^l
При
этом корни х3 и х4 (т.е. корни в тех скобках,
которые возведены в степень) являются
кратными, и k – это кратность корня х3, а
l – кратность корня х4. По-другому, если
число х0 является k-кратным корнем
многочлена степени n, то этот многочлен
можно разделить нацело на (x – x0)^k, а если
х0 является простым корнем многочлена
степени n, то этот многочлен можно
назделить нацело на (х – х0).
Простой
пример: многочлен x^2 + 2x + 1 имеет 2 корня:
x1 = -1 и х2 = -1, т.е. фактически он имеет один
кратный корень, то есть:
x^2
+ 2x + 1 = (x + 1)^2.
А
вот многочлен х^2 – 2x + 1 имеет 2 простых
корня: х1 = 1 и х2 = -1, то есть:
x^2
– 2x + 1 = (x + 1)*(x – 1)
Соседние файлы в папке 26
- #
- #
Алгебраическим уравнением степени $n$ с одной неизвестной $x$ называется уравнение вида
$P_n(x) = a_0 x^n + a_1 x^{n-1} + cdots + a_n = 0 (a_0 neq 0)$ (1)
(т. е. уравнение $f(x) = 0$, в левой части которого стоит ц. р. ф степени $n$ от $х$).
Для алгебраических уравнений принято ставить задачу отыскания всех (вообще говоря, комплексных) корней уравнения. Так как корнями уравнения (1) являются нули (корни) многочлена в его левой части, то можно использовать сведения о целых рациональных функциях и их корнях. Утверждение формулируются применительно к уравнению (1) следующим образом:
1) Каждое уравнение степени $n$ имеет по меньшей мере один корень в комплексной области. Если каждый корень учитывать с его кратностью, т. е. считать за столько корней, какова его кратность, то число корней уравнения равно его степени $n$. При этом говорят, что $x = alpha$ – корень кратности $k$, если левая часть уравнения делится на $(x – alpha)^k$ нацело, но не делится нацело на $(x – alpha)^{k+1}$.
2) Если уравнение (1) имеет комплексный (мнимый) корень $x = sigma + i tau$, то и комплексно сопряженное число $bar {х} = sigma – i tau$ является корнем уравнения (кратности обоих сопряженных корней одинаковы).
На протяжении столетий главной задачей алгебры было указание правил решения алгебраических уравнений. С древности известны формулы для решения уравнений первой и второй степени. Итальянскими математиками эпохи Возрождения (Кардано, Тарталья, Феррари) были найдены формулы для решения уравнений третьей и четвертой степени (они громоздки и не имеют большого практического значения). Попытки решения «в радикалах» (т. е. с применением действия извлечения корня) уравнений степени выше четвертой были в общем случае безуспешны. Уже в XIX веке в работах Руффини, Абеля и Галуа было установлено, что не только для корней общего уравнения степени выше четвертой не может быть дано формул, выражающих их в радикалах, но и что корни многих конкретных уравнений с числовыми (например, целыми) коэффициентами не могут быть выражены через радикалы из рациональных чисел.
|
58 / 40 / 41 Регистрация: 26.09.2013 Сообщений: 341 Записей в блоге: 1 |
|
|
1 |
|
Метод неопределенных коэффициентов. Что такое кратность корня и как ее определить?06.05.2014, 18:50. Показов 3112. Ответов 6
В учебнике написано так: k—число, равное кратности корня
0 |
|
4652 / 3404 / 361 Регистрация: 11.11.2010 Сообщений: 6,205 Записей в блоге: 2 |
|
|
06.05.2014, 19:06 |
2 |
|
Например,
1 |
|
58 / 40 / 41 Регистрация: 26.09.2013 Сообщений: 341 Записей в блоге: 1 |
|
|
06.05.2014, 19:11 [ТС] |
3 |
|
Получается, чтобы определить кратность корня нужно характеристическое уравнение разложить на множители?
0 |
|
4652 / 3404 / 361 Регистрация: 11.11.2010 Сообщений: 6,205 Записей в блоге: 2 |
|
|
06.05.2014, 19:16 |
4 |
|
Nickolay0512, нну да.
1 |
|
2525 / 1751 / 152 Регистрация: 11.08.2012 Сообщений: 3,349 |
|
|
07.05.2014, 10:34 |
5 |
|
Получается, чтобы определить кратность корня нужно характеристическое уравнение разложить на множители? Необязательно. Иногда, к тому же, это проблематично (например, для полиномов 10-ой степени с иррациональными коэффициентами).
2 |
|
4652 / 3404 / 361 Регистрация: 11.11.2010 Сообщений: 6,205 Записей в блоге: 2 |
|
|
07.05.2014, 19:41 |
6 |
|
cmath, ну да, согласен.
1 |
|
1891 / 1472 / 173 Регистрация: 16.06.2012 Сообщений: 3,342 |
|
|
07.05.2014, 20:36 |
7 |
|
А почитать об этом можно в книге Винберга “Алгебра многочленов”.
1 |
Макеты страниц
§. 2. Алгебраические уравнения с одной неизвестной
57. Число и кратность корней.
Алгебраическим уравнением степени  с одной неизвестной
с одной неизвестной  называется уравнение вида
называется уравнение вида

(т. е. уравнение f{x) = 0, в левой части которого стоит  степени
степени  от х).).
от х).).
Для алгебраических уравнений принято ставить задачу отыскания всех (вообще говоря, комплексных) корней уравнения. Так как корнями уравнения (57.1) являются нули (корни) многочлена в его левой части, то можно использовать сведения о целых рациональных функциях и их корнях (п. 52). Утверждения, приведенные в п. 52, формулируются применительно к уравнению (57.1) следующим образом:
1) Каждое уравнение степени  имеет по меньшей мере один корень в комплексной области. Если каждый корень учитывать с его кратностью, т. е. считать за столько корней, какова его кратность, то число корней уравнения равно его степени
имеет по меньшей мере один корень в комплексной области. Если каждый корень учитывать с его кратностью, т. е. считать за столько корней, какова его кратность, то число корней уравнения равно его степени  . При этом говорят, что
. При этом говорят, что  а — корень кратности k, если левая часть уравнения делится на
а — корень кратности k, если левая часть уравнения делится на  нацело, но не делится нацело на
нацело, но не делится нацело на 
Если уравнение (57.1) имеет комплексный (мнимый) корень  , то и комплексно сопряженное число
, то и комплексно сопряженное число  является корнем уравнения (кратности обоих сопряженных корней одинаковы).
является корнем уравнения (кратности обоих сопряженных корней одинаковы).
На протяжении столетий главной задачей алгебры было указание правил решения алгебраических уравнений. С древности известны формулы для решения уравнений первой и второй степени. Итальянскими математиками эпохи Возрождения {Кардано, Тарталья, Феррари) были найдены формулы для решения уравнений третьей и четвертой степени (они громоздки и не имеют большого практического значения). Попытки решения «в радикалах» (т. е. с применением действия извлечения корня) уравнений степени выше четвертой были в общем случае безуспешны. Уже в XIX веке в работах Руффини, Абеля и Галуа было установлено, что не только для корней общего уравнения степени выше четвертой не может быть дано формул, выражающих их в радикалах, но и что корни многих конкретных уравнений с числовыми (например, целыми) коэффициентами не могут быть выражены через радикалы из рациональных чисел.
Мы изучаем ниже уравнения первой и второй степени и некоторые частные виды уравнений степени выше второй.



