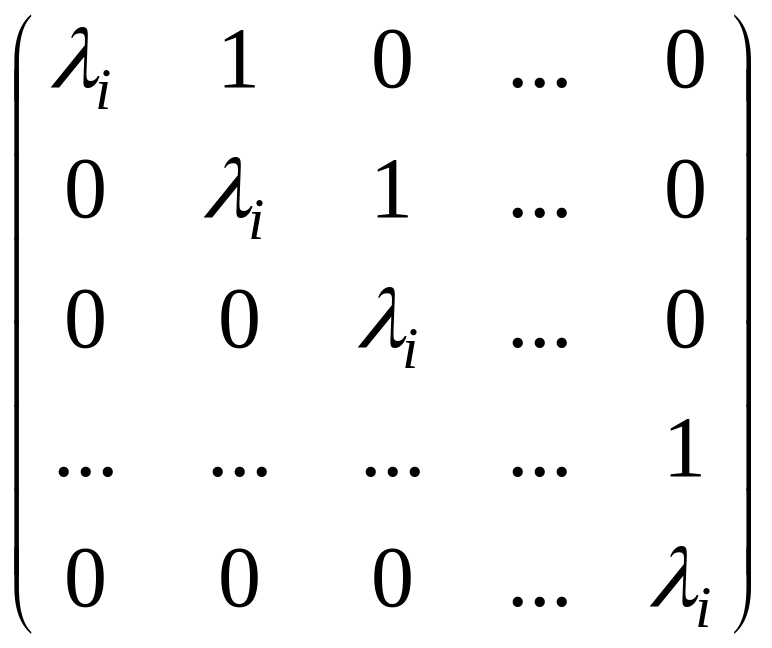Как найти кратность в алгебре - Сайт, где вы сможете решить свои вопросы

Что такое нок в математике? Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы узнаем, как найти наименьшее общее кратное, какие есть для этого способы для трех чисел и более, разберем вопрос о том, как находить НОК отрицательного числа. Также разберемся, что такое нок и нод, как найти нок и нод.

Вычисление наименьшего общего кратного (НОК) через НОД

Мы уже узнали, что такое нок, а также установили связь наименьшего общего кратного с наибольшим общим делителем (кратность показывает в расчетах во сколько раз один показатель больше другого). Теперь как настоящие математики научимся определять НОК через НОД (нок и нод чисел натуральных). Сначала разберемся, как найти нок для положительных чисел. Сделать это можно и онлайн или на калькуляторе, но лучше научиться самостоятельно.

Определение 1

Поиск наименьшего общего кратного через наибольший общий делитель можно по формуле НОК(a, b)=a·b:НОД(a, b).

Пример 1

Необходимо найти НОК чисел 126 и 70.

Решение

Начнем решать. Примем a=126, b=70. Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК(a, b)=a·b:НОД(a, b).

Найдем НОД чисел 70 и 126. Для этого нам понадобится алгоритм Евклида: 126=70·1+56, 70=56·1+14, 56=14·4, следовательно, NOD(126, 70)=14.

Вычислим НОК: НОК(126, 70)=126·70:НОД(126, 70)=126·70:14=630.

Ответ: NOC(126, 70)=630.

Пример 2

Найдите нок чисел 68 и 34.

Решение

Как находить нод? НОД в данном случае нейти несложно, так как 68 делится на 34. Вычислим самое маленькое общее кратное по формуле: НОК(68, 34)=68·34:НОД(68, 34)=68·34:34=68.

Ответ: НОК(68, 34)=68.

В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.

Нахождение НОК с помощью разложения чисел на простые множители

Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители. Перед тем, как это узнавать, дадим небольшое определение.

Определение 2

Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:

составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
исключаем их полученных произведений все простые множители;
полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК(a, b)=a·b:НОД(a, b). Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.

Пример 3

У нас есть два числа 75 и 210. Мы можем разложить их на множители следующим образом: 75=3·5·5 и 210=2·3·5·7. Если составить произведение всех множителей двух исходных чисел, то получится: 2·3·3·5·5·5·7.

Если исключить общие для обоих чисел множители 3 и 5, мы получим произведение следующего вида: 2·3·5·5·7=1050. Это произведение и будет нашим НОК для чисел 75 и 210.

Пример 4

Найдите НОК чисел 441 и 700, разложив оба числа на простые множители.

Решение

Найдем все простые множители чисел, данных в условии:

44114749713377

700350175357122557

Получаем две цепочки чисел: 441=3·3·7·7 и 700=2·2·5·5·7.

Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2·2·3·3·5·5·7·7·7. Найдем общие множители. Это число 7. Исключим его из общего произведения: 2·2·3·3·5·5·7·7. Получается, что НОК(441, 700)=2·2·3·3·5·5·7·7=44 100.

Ответ: НОК(441, 700)= 44 100.

Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.

Определение 3

Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:

разложим оба числа на простые множители:
добавим к произведению простых множителей первого числа недостающие множители второго числа;
получим произведение, которое и будет искомым НОК двух чисел.

Пример 5

Вернемся к числам 75 и 210, для которых мы уже пробовали искать НОК в одном из прошлых примеров. Разложим их на простые множители: 75=3·5·5 и 210=2·3·5·7. К произведению множителей 3, 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210. Получаем: 2·3·5·5·7. Это и есть НОК чисел 75 и 210.

Пример 6

Необходимо вычислить НОК чисел 84 и 648.

Решение

Разложим числа из условия на простые множители: 84=2·2·3·7 и 648=2·2·2·3·3·3·3. Добавим к произведению множителей 2, 2, 3 и 7 числа 84 недостающие множители 2, 3, 3 и
3 числа 648. Получаем произведение 2·2·2·3·3·3·3·7=4536. Это и есть наименьшее общее кратное чисел 84 и 648 .

Ответ: НОК(84, 648)=4 536.

Нахождение НОК трех и большего количества чисел

Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.

Теорема 1

Предположим, что у нас есть целые числа a1, a2, …, ak. НОК mk этих чисел находится при последовательном вычислении m2=НОК(a1, a2), m3=НОК(m2, a3), …, mk=НОК(mk−1, ak).

Теперь рассмотрим, как можно применять теорему для решения конкретных задач.

Пример 7

Необходимо вычислить наименьшее общее кратное четырех чисел 140, 9, 54 и 250.

Решение задания

Введем обозначения: a1=140, a2=9, a3=54, a4=250.

Начнем с того, что вычислим m2=НОК(a1, a2)=НОК(140, 9). Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140=9·15+5, 9=5·1+4, 5=4·1+1, 4=1·4. Получаем: НОД(140, 9)=1, НОК(140, 9)=140·9:НОД(140, 9)=140·9:1=1 260. Следовательно, m2=1 260.

Теперь вычислим по тому е алгоритму m3=НОК(m2, a3)=НОК(1 260, 54). В ходе вычислений получаем m3=3 780.

Нам осталось вычислить m4=НОК(m3, a4)=НОК(3 780, 250). Действуем по тому же алгоритму. Получаем m4=94 500.

НОК четырех чисел из условия примера равно 94500.

Ответ: НОК(140, 9, 54, 250)=94 500.

Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.

Определение 4

Предлагаем вам следующий алгоритм действий:

раскладываем все числа на простые множители;
к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
полученное произведение будет наименьшим общим кратным всех чисел из условия.

Пример 8

Необходимо найти НОК пяти чисел 84, 6, 48, 7, 143.

Решение

Разложим все пять чисел на простые множители: 84=2·2·3·7, 6=2·3, 48=2·2·2·2·3, 7, 143=11·13. Простые числа, которым является число 7, на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.

Теперь возьмем произведение простых множителей 2, 2, 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3. Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.

Продолжаем добавлять недостающие множители. Переходим к числу 48, из произведения простых множителей которого берем 2 и 2. Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2·2·2·2·3·7·11·13=48 048. Это и есть наименьшее общее кратное пяти исходных чисел.

Ответ: НОК(84, 6, 48, 7, 143)=48 048.

Нахождение наименьшего общего кратного отрицательных чисел

Для того чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.

Пример 9

НОК(54, −34)=НОК(54, 34), а НОК(−622, −46, −54, −888)=НОК(622, 46, 54, 888).

Такие действия допустимы в связи с тем, что если принять, что a и −a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа −a.

Пример 10

Необходимо вычислить НОК отрицательных чисел −145 и −45.

Решение

Произведем замену чисел −145 и −45 на противоположные им числа 145 и 45. Теперь по алгоритму вычислим НОК(145, 45)=145·45:НОД(145, 45)=145·45:5=1 305, предварительно определив НОД по алгоритму Евклида.

Получим, что НОК чисел −145 и −45 равно 1 305.

Ответ: НОК(−145, −45)=1 305.

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Линейная алгебра. Как найти алгебраическую кратность собственного значения?

Ученик

(68),
закрыт

1 год назад

0x1е78 = 7800

Гений

(96126)

1 год назад

Если геометрическая кратность собст. значения суть К, то в жордановой формн матрицы А-lambda*E будет РОВНО К нулевых столбцов, правда? А стало быть ранг таеой матрицы суть n-K. Вот этот ранг и нужно найти.
Ну а алгебраическая кратность это просто сумма размеров жордановых клеток с даной лямбдой.

Noname AnonУченик (68)

1 год назад

А для чего мы находим эти кратности? Точнее, для чего нужна каждая из них? Запутался

Источник

ВОРОНЕЖСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Руководство к решению задач по алгебре

Часть II Жорданова форма матрицы и жорданов базис

Практическое
пособие по курсу “Алгебра и геометрия”

для
студентов по специальности

Воронеж

2003

§1. Собственные векторы и собственные значения оператора.

Жорданова
форма матрицы и жорданов базис

Рассмотрим линейный оператор в пространстве и пусть – матрица этого оператора в некотором базисе .

Определение
1.

называется характеристическим
многочленом
матрицы

(
–
единичная матрица порядка

).

Определение
2. Вектор

называется собственным вектором
оператора

,
если

,
а

– собственным значением оператора

,
соответствующим собственному вектору

Алгоритм

нахождения собственного значения и
собственного вектора оператора

1)
Найдем все корни характеристического
многочлена

,
получим

– спектр оператора (множество всех
собственных значений);

2)
подставим

в систему

решим
ее и найдем все собственные векторы,
отвечающие собственному значению

,
затем подставим

и т.д.

1.2. Алгебраическая и геометрическая кратности собственного значения

Определение
3. Кратность
корня

в характеристическом многочлене

называется алгебраической
кратностью собственного значения

Определение
4. Геометрической
кратностью

собственного значения

называется размерность собственного
подпространства оператора

Утверждение.

,
где

– порядок матрицы оператора

Теорема.
Оператор

в базисе

имеет диагональную матрицу

в том и только том случае, когда базисные
векторы

– собственные, то есть

для всех

.

Жорданова форма матрицы и жорданов базис

Определение
5. Жордановой
клеткой
называется клетка вида

.
(1.1)

Теорема.
Для произвольного оператора

существует базис пространства

,
в котором матрица оператора имеет
клеточно-диагональный вид, причем на
главной диагонали стоят жордановы
клетки вида (1.1).

Этот
базис называется жордановым,
а данный канонический вид матрицы
называется жордановой
формой.

Замечание.
Жорданова форма определяется однозначно
с точностью до порядка клеток (каждой
клетке с

соответствует один собственный вектор).

Алгоритм нахождения жорданова базиса для одной жордановой клетки

Рассмотрим
жорданову клетку вида (1.1). По определению
матрицы оператора в 1-м столбце стоит
вектор

,
разложенный по базису

:

поэтому

Во
2-м столбце матрицы находится вектор

,
разложенный по этому же базису и т.д.

Таким
образом, собственный вектор

находим как решение системы

,
присоединенный вектор

– как решение системы

.
Очевидно, что

Продолжая
аналогичные рассуждения, для вектора

получим

.

Определение
6. Вектор

называется присоединенным
вектором высоты

Жорданов базис
состоит из собственных и присоединенных
к ним векторов.

Утверждение.
Алгебраическая кратность собственного
значения

равна сумме размеров жордановых клеток
с этим собственным значением.

Утверждение.
Геометрическая кратность

собственного значения

равна числу клеток в жордановой форме
с собственным значением

или числу линейно независимых собственных
векторов, соответствующих собственному
значению

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Наиме́ньшее о́бщее кра́тное () двух целых чисел и есть наименьшее натуральное число, которое делится на и без остатка, то есть кратно им обоим. Обозначается одним из следующих способов:

Пример: .

Наименьшее общее кратное для нескольких чисел — это наименьшее натуральное число, которое делится на каждое из этих чисел.

Одно из наиболее частых применений — приведение дробей к общему знаменателю.

Свойства[править | править код]

Нахождение НОК[править | править код]

можно вычислить несколькими способами.

1. Если известен наибольший общий делитель, можно использовать его связь с :

$operatorname {lcm}(a,b)={frac {|acdot b|}{operatorname {gcd}(a,b)}}$

2. Пусть известно каноническое разложение обоих чисел на простые множители:

$a=p_{1}^{{d_{1}}}cdot dots cdot p_{k}^{{d_{k}}},$

$b=p_{1}^{{e_{1}}}cdot dots cdot p_{k}^{{e_{k}}},$

где $p_{1},dots ,p_{k}$ — различные простые числа, а $d_{1},dots ,d_{k}$ и $e_{1},dots ,e_{k}$ — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда вычисляется по формуле:

${displaystyle operatorname {lcm} (a,b)=p_{1}^{max(d_{1},e_{1})}cdot dots cdot p_{k}^{max(d_{k},e_{k})}.}$

Другими словами, разложение содержит все простые множители, входящие хотя бы в одно из разложений чисел a,b , причём из показателей степени этого множителя берётся наибольший. Пример для бóльшего количества чисел:

${displaystyle 56;,;,=2^{3}cdot 3^{0}cdot 7^{1}}$

${displaystyle 9;,;,=2^{0}cdot 3^{2}cdot 7^{0}}$

${displaystyle 21;,=2^{0}cdot 3^{1}cdot 7^{1}.}$

${displaystyle operatorname {lcm} (56,9,21)=2^{3}cdot 3^{2}cdot 7^{1}=8cdot 9cdot 7=504.}$

Вычисление наименьшего общего кратного нескольких чисел может быть также сведено к нескольким последовательным вычислениям от двух чисел:

$operatorname {lcm}(a_{1},a_{2},ldots ,a_{n})=operatorname {lcm}(operatorname {lcm}(a_{1},a_{2},ldots ,a_{{n-1}}),a_{n}).$

См. также[править | править код]

Наибольший общий делитель

Литература[править | править код]

Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — 180 с.

Ссылки[править | править код]

Weisstein, Eric W. Least Common Multiple (англ.) на сайте Wolfram MathWorld.

Источник

Свойства собственных векторов линейных операторов (преобразований)

1. Собственные векторы линейного преобразования, принадлежащие различным собственным значениям, линейно независимы.

Аналогичное утверждение было доказано для собственных векторов матрицы (см. свойство 1).

2. Все собственные векторы линейного преобразования mathcal{A}colon Vto V , принадлежащие одному собственному значению, совместно с нулевым вектором образуют линейное подпространство, инвариантное относительно преобразования mathcal{A} . Такое линейное подпространство называется собственным для преобразования .

В самом деле, условие (9.5) можно записать в виде (mathcal{A}- lambdamathcal{E}) (boldsymbol{s})=boldsymbol{o} , где mathcal{E}colon Vto V — тождественное преобразование. Множество векторов , удовлетворяющих последнему равенству, составляет ядро линейного преобразования (mathcal{A}-lambda mathcal{E}) , т.е. является линейным подпространством ker (mathcal{A}-lambda mathcal{E})triangleleft V (собственное подпространство, отвечающее собственному значению lambda ). Покажем, что это подпространство инвариантно относительно преобразования mathcal{A} . Действительно, любой вектор boldsymbol{s}in ker (mathcal{A}-lambdamathcal{E}) в силу равенств (mathcal{A}-lambda mathcal{E})(boldsymbol{s})=boldsymbol{o}~ Leftrightarrow~ mathcal{A} (boldsymbol{s})=lambda boldsymbol{s} отображается в коллинеарный ему вектор lambdacdot boldsymbol{s} , также принадлежащий ker (mathcal{A}-lambdamathcal{E}) .

3. Для собственного значения lambda линейного преобразования mathcal{A}colon Vto V существует цепочка инвариантных подпространств

${boldsymbol{o}}triangleleft boldsymbol{K}_{lambda}^1triangleleft boldsymbol{K}_{lambda}^2triangleleft ldotstriangleleft boldsymbol{K}_{lambda}^mtriangleleft V,$

(9.8)

где $boldsymbol{K}_{lambda}^1= ker (mathcal{A}-lambdamathcal{E}),~ boldsymbol{K}_{lambda}^2= ker (mathcal{A}-lambdamathcal{E})^2,~ldots,~ boldsymbol{K}_{lambda}^m= ker (mathcal{A}-lambdamathcal{E})^m$ ; — некоторое натуральное число (mleqslant n=dim{V}) .

Все перечисленные в цепочке (9.8) множества $boldsymbol{K}_{lambda}^k,~ k=1,ldots,m$ , являются линейными подпространствами по свойству ядра линейного преобразования. Каждое из подпространств $boldsymbol{K}_{lambda}^k$ инвариантно относительно преобразования mathcal{A} , поскольку для любого вектора $boldsymbol{v}in boldsymbol{K}_{lambda}^k$ его образ $boldsymbol{w}= mathcal{A} (boldsymbol{v})in boldsymbol{K}_{lambda}^k$ , так как в силу перестановочности многочленов от одного и того же линейного преобразования (см. пункт 2 замечаний 9.3)

$(mathcal{A}-lambdacdotmathcal{E})^k(boldsymbol{w})= (mathcal{A}-lambdacdot mathcal{E})^k mathcal{A}(boldsymbol{v})= mathcal{A}(mathcal{A}-lambdacdot mathcal{E})^k(boldsymbol{v})= mathcal{A}(boldsymbol{o})=boldsymbol{o},$

так как $(mathcal{A}-lambda mathcal{E})^k(boldsymbol{v})=boldsymbol{o}~ forall boldsymbol{v}in boldsymbol{K}_{lambda}^k$ согласно определения ядра оператора.

Докажем включение $boldsymbol{K}_{lambda}^1triangleleft boldsymbol{K}_{lambda}^2$ . Если $boldsymbol{v}in boldsymbol{K}_{lambda}^1$ , то (mathcal{A}-lambda mathcal{E}) (boldsymbol{v})=boldsymbol{o} , при этом очевидно, что

(mathcal{A}-lambdacdot mathcal{E})cdot (mathcal{A}- lambdacdot mathcal{E})(boldsymbol{v})= (mathcal{A}-lambdacdotmathcal{E}) (mathcal{o})= boldsymbol{0}, то есть $boldsymbol{v}in boldsymbol{K}_{lambda}^2.$

Остальные включения доказываются аналогично.

Из цепочки (9.8) “расширяющихся” подпространств следует, что их размерности не убывают

$0leqslant dim boldsymbol{K}_{lambda}^1leqslant dim boldsymbol{K}_{lambda}^2 leqslant ldotsleqslant dim boldsymbol{K}_{lambda}^mleqslantdim{V},$

поэтому в силу конечномерности пространства существует такое , что $dim boldsymbol{K}_{lambda}^m=dim boldsymbol{K}_{lambda}^{m+1}$ , т.е. $boldsymbol{K}_{lambda}^m= boldsymbol{K}_{lambda}^{m+1}$ . Покажем, что дальнейшего “увеличения” подпространств нет, т.е. $boldsymbol{K}_{lambda}^m= boldsymbol{K}_{lambda}^{m+1}=ldots= boldsymbol{K}_{lambda}^{m+k}$ для любого натурального . Предположим противное. Пусть $boldsymbol{K}_{lambda}^m= boldsymbol{K}_{lambda}^{m+1}$ и для некоторого k>1 пространства не совпадают: $boldsymbol{K}_{lambda}^{m+k}ne boldsymbol{K}_{lambda}^{m+k+1}$ , то есть существует вектор $boldsymbol{v}in boldsymbol{K}_{lambda}^{m+k+1}$ , который не принадлежит пространству $boldsymbol{K}_{lambda}^{m+k}$ . Обозначим $boldsymbol{w}= (mathcal{A}-lambda mathcal{E})^k(boldsymbol{v})$ . Тогда, с одной стороны, $boldsymbol{w}in boldsymbol{K}_{lambda}^{m+1}$ , так как $(mathcal{A}- lambda mathcal{E})^{m+1}(boldsymbol{w})=(mathcal{A}-lambda mathcal{E})^{m+k+1}(boldsymbol{v})=boldsymbol{o}$ , поскольку $boldsymbol{v}in boldsymbol{K}_{lambda}^{m+k+1}$ . С другой стороны, $boldsymbol{w}notin boldsymbol{K}_{lambda}^m$ , так как $(mathcal{A}- lambda mathcal{E})^m(boldsymbol{w})= (mathcal{A}- lambda mathcal{E})^{m+k} (boldsymbol{v})ne boldsymbol{o}$ , поскольку $boldsymbol{v}notin boldsymbol{K}_{lambda}^{m+k}$ . Следовательно, и $boldsymbol{w}in boldsymbol{K}_{lambda}^{m+1}$ и $boldsymbol{w}notin boldsymbol{K}_{lambda}^m$ одновременно, что противоречит предположению $boldsymbol{K}_{lambda}^m= boldsymbol{K}_{lambda}^{m+1}$ .

Таким образом, в цепочке (9.8) размерности пространств $boldsymbol{K}_{lambda}^k,~ k=1,ldots,m$ , возрастают. Поэтому mleqslant n=dim{V} .

Корневым подпространством линейного преобразования mathcal{A} для собственного значения lambda называется линейное подпространство $boldsymbol{K}_{lambda}^m= ker (mathcal{A}-lambda mathcal{E})^m$ с наименьшим натуральным показателем , для которого $boldsymbol{K}_{lambda}^m= boldsymbol{K}_{lambda}^{m+1}$ .

4. Если lambda — собственное значение линейного преобразования mathcal{A}colon Vto V , то пространство можно представить в виде прямой суммы $V= boldsymbol{K}_{lambda}^moplus L$ , где $boldsymbol{K}_{lambda}^m$ — корневое подпространство, а $L=operatorname{Lin} (mathcal{A}-lambdamathcal{E})^m$ — инвариантное относительно подпространство, в котором нет собственных векторов, принадлежащих собственному значению lambda .

В самом деле, покажем, что пересечение этих подпространств есть нулевой вектор: $boldsymbol{K}_{lambda}^m cap L={boldsymbol{o}}$ . Выберем вектор $boldsymbol{e}in boldsymbol{K}_{lambda}^mcap L$ . Так как вектор boldsymbol{w}in L , то существует такой вектор boldsymbol{v}in V , что $boldsymbol{w}=(mathcal{A}- lambdamathcal{E})^m (boldsymbol{v})$ . Поскольку $boldsymbol{w}in boldsymbol{K}_{lambda}^m$ , то $(mathcal{A}- lambda mathcal{E})^m (boldsymbol{w})= boldsymbol{o}$ . Тогда $(mathcal{A}- lambdamathcal{E})^{2m}(boldsymbol{v})= (mathcal{A}- lambda mathcal{E})^m (boldsymbol{w})= boldsymbol{o}$ . Следовательно, вектор $boldsymbol{v}in boldsymbol{K}_{lambda}^{2m}$ , но $boldsymbol{K}_{lambda}^{2m}= boldsymbol{K}_{lambda}^m$ , так как $boldsymbol{K}_{lambda}^m$ — корневое подпространство. Значит,

$boldsymbol{v}in boldsymbol{K}_{lambda}^m~~Rightarrow~~ boldsymbol{w}= (mathcal{A}- lambda mathcal{E})^m (boldsymbol{v})= boldsymbol{o}$ то есть $boldsymbol{K}_{lambda}^mcap L={boldsymbol{o}}$

По теореме 9.1 о размерности ядра и образа получаем, что $dim boldsymbol{K}_{lambda}^m+ dim{L}= dim{V}$ . Следовательно, пространство можно представить в виде прямой суммы подпространств $Vin boldsymbol{K}_{lambda}^m oplus L$ (см. признаки прямых сумм подпространств).

Докажем, что в нет собственных векторов, принадлежащих собственному значению lambda . Действительно, пусть boldsymbol{s} — собственный вектор, соответствующий собственному значению lambda . Тогда $boldsymbol{s}in boldsymbol{K}_{lambda}^1$ и в силу (9.8) $boldsymbol{}in boldsymbol{K}_{lambda}^m$ . Подпространство имеет с $boldsymbol{K}_{lambda}^m$ только один общий вектор (нулевой). Поэтому boldsymbol{s}notin L , так как boldsymbol{s}ne boldsymbol{o} . Инвариантность подпространства следует из перестановочности операторов mathcal{A} и $(mathcal{A}- lambda mathcal{E})^m$ (см. пункт 2 замечаний 9.3). В самом деле, для любого вектора boldsymbol{w}in L существует прообраз boldsymbol{v}in Vcolon $boldsymbol{w}=(mathcal{A}- lambda mathcal{E})^m (boldsymbol{v})$ . Поэтому в силу перестановочности операторов

$mathcal{A}(boldsymbol{w})= mathcal{A}(mathcal{A}- lambdacdot mathcal{E})^m (boldsymbol{v})= (mathcal{A}-lambdacdot mathcal{E})^m mathcal{A} (boldsymbol{v})in L,$

поскольку mathcal{A}(boldsymbol{v})in V и $L=operatorname{Lin} (mathcal{A}-lambda mathcal{E})^m$ . Таким образом, инвариантность подпространства доказана, так как mathcal{A}(boldsymbol{w})in L~ forall boldsymbol{w}in L .

Теорема (9.5) о разложении пространства в сумму корневых подпространств

Если все различные корни lambda_1,ldots,lambda_2,lambda_k характеристического уравнения линейного преобразования mathcal{A}colon Vto V являются его собственными значениями, то пространство можно разложить в прямую сумму инвариантных (корневых) подпространств:

$V= boldsymbol{K}_{lambda_1}^{m_1}oplus boldsymbol{K}_{lambda_2}^{k_2} oplus ldotsoplus boldsymbol{K}_{lambda_k}^{m_k},$

(9.9)

где $boldsymbol{K}_{lambda_i}^{m_i}= ker (mathcal{A}- lambda_i mathcal{E})^{m_1}$ — корневое подпространство, соответствующее собственному значению lambda_1,~ i=1,2,ldots,k .

В самом деле, по свойству 4 можно “отщепить” корневое подпространство $boldsymbol{K}_{lambda_1}^{m_1}$ , т.е. представить пространство в виде прямой суммы инвариантных подпространств $V= boldsymbol{K}_{lambda_1}^{m_1} oplus L_1$ , причем в L_1 нет собственных векторов, принадлежащих собственному значению . В пространстве L_1 определено сужение $mathcal{A}_{L_1}colon L_1to L_1$ преобразования . Применяя свойство 4 к сужению $mathcal{A}_{L_1}colon L_1to L_1$ , аналогичным образом можно “отщепить” корневое подпространство $boldsymbol{K}_{lambda_2}^{m_2}$ , т.е. представить пространство L_1 в виде прямой суммы инвариантных подпространств: $L_1= boldsymbol{K}_{lambda_2}^{m_2} oplus L_2$ . Этот процесс следует продолжить до тех пор, пока не исчерпаются все корни характеристического уравнения.

Следствие. Если все различные корни lambda_1,lambda_2,ldots,lambda_k характеристического уравнения линейного преобразования mathcal{A}colon Vto V являются его собственными значениями, то существует базис пространства , в котором матрица линейного преобразования имеет блочно-диагональный вид

$A= operatorname{diag}(A_1,A_2,ldots,A_k),$

где A_1,A_2,ldots,A_k — матрицы сужений $mathcal{A}_{boldsymbol{k}_i}colon boldsymbol{k}_i to boldsymbol{k}_i~ (boldsymbol{k}_i=boldsymbol{K}_{lambda_i}^{m_i},~ i=1,ldots,k)$ , преобразования на корневые подпространства.

Согласно следствию из теоремы 9.2, такой базис можно получить, записывая последовательно базисы корневых подпространств (9.9).

Алгебраическая и геометрическая кратности собственных значений

Алгебраической кратностью собственного значения lambda_1 линейного оператора (преобразования) mathcal{A}colon Vto V называется кратность корня lambda=lambda_1 характеристического многочлена $Delta_{mathcal{A}} (lambda)$ (или, что то же самое, кратность корня характеристического уравнения $Delta_{mathcal{A}}(lambda)$ ).

Геометрической кратностью собственного значения lambda_1 линейного оператора (преобразования) mathcal{A}colon Vto V называется размерность собственного подпространства $boldsymbol{K}_{lambda_1}^1= ker (mathcal{A}-lambda_1 mathcal{E})$ , соответствующего этому собственному значению.

Теорема 9.6 о кратностях собственных значений оператора. Геометрическая кратность собственного значения не превосходит его алгебраической кратности.

Представим пространство в виде прямой суммы $V=boldsymbol{K}_{lambda_1}^{m_1}oplus L$ (см. свойство 4) и обозначим $r=dimboldsymbol{K}_{lambda_1}^{m_1}$ . Выбрав базис пространства $boldsymbol{K}_{lambda_1}^{m_1}$ , дополним его до базиса всего пространства. В этом базисе, согласно следствию теоремы 9.5, матрица преобразования mathcal{A} будет иметь блочно-диагональный вид $A=operatorname{diag} (A_1,A_2)$ , где квадратная матрица A_1 порядка является матрицей сужения $mathcal{A}_{boldsymbol{K}_{lambda_1}^{m_1}}$ преобразования на подпространство $boldsymbol{K}_{lambda_1}^{m_1}$ , а матрица A_2 является матрицей сужения $mathcal{A}_L$ . Характеристический многочлен матрицы имеет вид (см. определитель блочно-диагональной матрицы)

det(A-lambda E)= det(A_1-lambda E)cdot det(A_2-lambda E)= p_1(lambda)cdot p_2(lambda),

где p_1(lambda),,p_2(lambda) — многочлены степеней и (n-r) соответственно. Так как сужение $mathcal{A}_{boldsymbol{K}_{lambda_1}^{m_1}}$ не имеет собственных значений, отличных от , то p_1(lambda)= (-r)^r(lambda-lambda_1)^r , в силу того, что p_1(lambda_1)=0 и основной теоремы алгебры. Поскольку сужение $mathcal{A}_L$ не имеет собственных векторов, принадлежащих собственному значению , то p_2(lambda_1)ne0 . Следовательно, -алгебраическая кратность собственного значения . Тогда утверждение теоремы следует из включения (9.8): $dim boldsymbol{K}_{lambda_1}^{1} leqslant dimboldsymbol{K}_{lambda_1}^{m_1}$ , так как $boldsymbol{K}_{lambda_1}^{1}triangleleft boldsymbol{K}_{lambda_1}^{m_1}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Вычисление наименьшего общего кратного (НОК) через НОД

Нахождение НОК с помощью разложения чисел на простые множители

Нахождение НОК трех и большего количества чисел

Нахождение наименьшего общего кратного отрицательных чисел

Линейная алгебра. Как найти алгебраическую кратность собственного значения?

Руководство к решению задач по алгебре

Часть II Жорданова форма матрицы и жорданов базис

§1. Собственные векторы и собственные значения оператора.

Рассмотрим линейный оператор в пространстве и пусть – матрица этого оператора в некотором базисе .

1.2. Алгебраическая и геометрическая кратности собственного значения

Жорданова форма матрицы и жорданов базис

Алгоритм нахождения жорданова базиса для одной жордановой клетки

Свойства[править | править код]

Нахождение НОК[править | править код]

См. также[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Свойства собственных векторов линейных операторов (преобразований)

Теорема (9.5) о разложении пространства в сумму корневых подпространств

Алгебраическая и геометрическая кратности собственных значений

Вам также может понравиться

Как найти радиус окружности описанной около фигуры

Как найти журнал музыка

Как найти фонетическую фразу

Добавить комментарий Отменить ответ