Содержание:
В теории определенного интеграла для нахождения площади криволинейной трапеции вводится понятие интегральной суммы, пределом которой является определенный интеграл. Определенный интеграл существует для трех типов функций: непрерывных, кусочно-непрерывных и монотонных. Задача интегрирования может быть также сформулирована и для функции n переменных, заданной в ограниченной области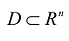 
Интегрирование функций многих переменных
Понятие двумерной интегральной суммы, пределом которой является двойной интеграл, можно ввести на основе задачи об объеме тела.
Задача: Найти объем тела, ограниченного сверху непрерывной поверхностью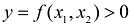 
Для этого разобьем основание S на конечное число элементарных ячеек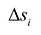 
и в каждой из этих ячеек выберем точку 
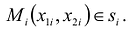Объем такого элемента равен 
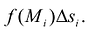Объем всей фигуры можно приближенно найти как сумму 
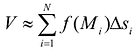с любой степенью точности в зависимости от числа ячеек 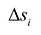и, соответственно, их размера. Если предположить, что число элементарных ячеек 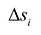бесконечно возрастает, а их диаметр при этом является величиной бесконечно малой, то можно получить точное выражение для объема всей фигуры: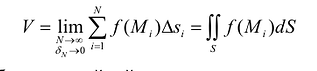 
Таким образом, двойной интеграл имеет простой геометрический смысл, он выражает объем криволинейного цилиндрического бруса, ограниченного сверху непрерывной поверхностью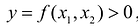 
, снизу – конечной замкнутой областью S плоскости 
и с боков – прямой цилиндрической поверхностью, построенной на границе объекта S и имеющей образующие, перпендикулярные плоскости .
Двумерной интегральной суммой от данной функции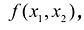 
определенной на области S называется сумма парных произведений площадей элементарных ячеек 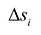области S на значения функции 
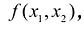в точке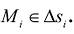 
Двойным интегралом от функции 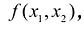определенной на области S называется предел соответствующей двумерной интегральной суммы при неограниченном возрастании числа N элементарных ячеек 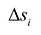и стремлении к нулю их наибольшего диаметра 
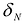при условии, что этот предел существует и не зависит от способа разбиения области S на элементарные ячейки 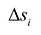и выбора точек 
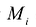в них.
Теорема. Если область S с кусочно-непрерывной границей I ограничена и замкнута, а функция 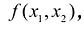непрерывна в области S, то двойной интеграл
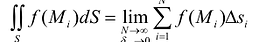, т.е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа разбиения области S на элементарные ячейки 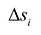и выбора точек 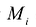в них.
Так как значение двойного интеграла не зависит от вида элементарных ячеек, то в дальнейшем целесообразно пользоваться наиболее удобным для декартовой системы координат разбиением на прямоугольную сетку, образованную пересечением двух систем прямых, параллельных соответственно координатным осям Ох и Оу. В этом случае элементарными ячейками являются прямоугольники, со сторонами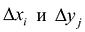 
. Таким образом, в обозначении интеграла можно учесть что
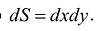Тогда: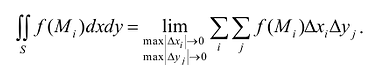 
Для вычисления двойного интеграла применяется процедура повторного интегрирования.
Предположим для определенности, что область интегрирования S представляет собой криволинейную трапецию: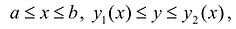 
где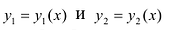 
– однозначные непрерывные функции на отрезке [а,b]. Важно отметить, что вертикаль, проходящая через любую точку х па отрезке [а,b) оси Ох, пересекает границу области интегрирования S только в двух точках: в точке входа 
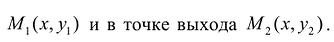Такая область называется стандартной относительно оси Оу.
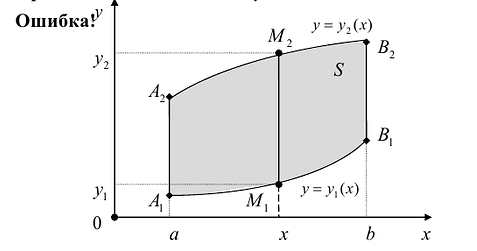
Теорема. Если для функции f(x,y) определенной в области S (стандартной относительно оси Оу), существует двойной интеграл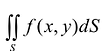 
и существует интеграл 
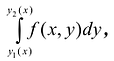то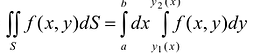 
.
При этом, интеграл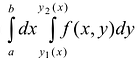 
называется повторным.
Таким образом, вычисление двойного интеграла сводится к вычислению двух интегралов: вначале находится внутренний интеграл по переменной у (при этом переменная х рассматривается как постоянная величина); после этого полученное выражение повторно интегрируется по переменной х.
Задача вычисления кратного интеграла может быть обобщена на n-мерный случай и аналогично решена путем сведения кратного интеграла к повторному. Пусть функция у = f(M) определена и ограничена в замкнутой области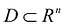 
. Область D разбивается на N элементарных частей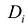 
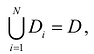пересечением любой пары элементарных частей будет множество точек, размерность которого не превышает n -1.
В каждой элементарной части выбирается точка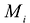 
и составляется интегральная сумма: 
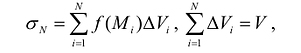где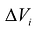 
– объемная мера области 
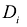; V-объемная мера области D.
Для того чтобы вычислить интегральную сумму, необходимо, чтобы элементарные части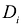 
допускали исчисление объемной меры в достаточно простой и редуктируемой форме.
n-кратным интегралом функции у = f(M) по области D называется предел интегральной суммы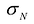 
при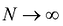 
и, соответственно, 
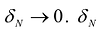– наибольшая протяженность элементарной области 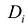для данного разбиения.
Этот предел не должен зависеть от способов разбиения D на части и от выбора точек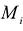 
в каждой из них. Указанный интеграл можно представить в следующим образом:
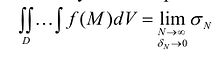
По форме этот интеграл сходен с определенным интегралом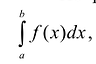 
, который также является пределом интегральной суммы:
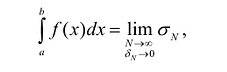
где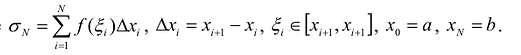 
Очевидно, что в n-кратном интеграле, как и в случае определенного интеграла, интегральные суммы ограничены снизу и сверху значениями сумм Дарбу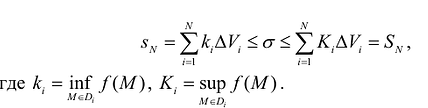 
Свойствами одномерных сумм Дарбу обладают и n -мерные суммы. При этом для любой ограниченной функции: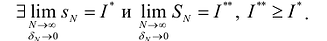 
Необходимым и достаточным условием интегрируемости функции является условие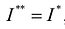 
, что эквивалентно выражению:
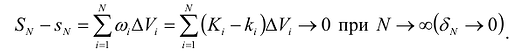
Величина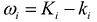 
, называется колебанием функции в элементарной области 
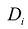и является величиной положительной при любом i.
В результате можно установить, что к числу интегрируемых функций будут относиться функции, непрерывные на замкнутой области D. При вычислении n-кратный интеграл сводится к повторному интегралу, т.е. вычислению обычного интеграла от внутреннего интеграла кратности n -1.
Свойства n-кратного интеграла
- Интеграл по области, имеющей нулевую «объемную» меру в
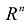, равен нулю. При этом к областям с нулевой «объемной» мерой в 
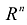, относятся разнообразные множества, которые заданы в пространстве 
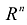, (m
- Если две функции f(M) и g(M) интегрируемы в D, то сумма этих функций также интегрируема в D и
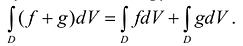
- Если функция f(M) интегрируема в D, а С – постоянная величина, то функция С f(M) также интегрируема в D и
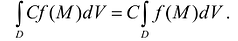
- Пусть область D является объединением областе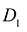й
и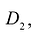 
, а пересечение этих областей есть множество S, размерность которого меньше N. Если функция f(M) интегрируема в D, то она интегрируема в 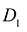и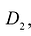 
и при этом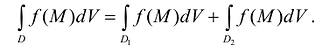
- Если функция f(M) определена и интегрируема в D, и при этом
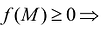(за исключением, быть может, некоторой части D с размерностью меньше n), то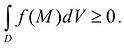 
- Если две функции /fМ) и g(M) определены и интегрируемы в D, причем
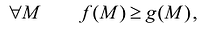то 
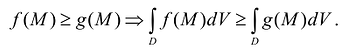
- Если функция f(M) определена и интегрируема в D, то
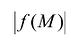также интегрируема в D, причем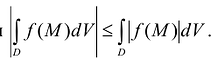 
- Если функция f(M) = С является постоянной
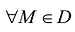, то 
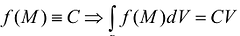. - Если функция f(M) определена и интегрируема в D и ограничена снизу и сверху значениями к к К, соответственно
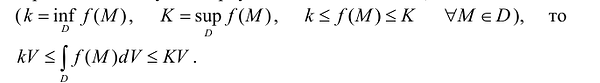
Понятие о двойном интеграле
Мы рассматривали определенный интеграл, как предел суммы для случая, когда функция f(x) определена на отрезке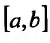 
, который называется отрезком интегрирования. В настоящем параграфе мы обобщим понятие интеграла на случай, когда областью интегрирования является некоторая область на плоскости, или некоторая область в пространстве, при этом мы будем пользоваться интуитивным представлением площади и объема.
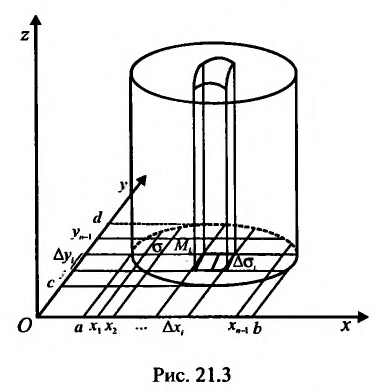
Пусть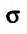 
– ограниченная плоская область (см. рис. 21.3). Рассмотрим функцию z = f{x,y), определенную и непрерывную в области 
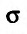, ограниченной замкнутой линией L. Разобьем область о на элементарные области 
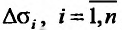, произвольной формы, при-чем через 
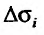, обозначим сами элементарные области и их площади. В каждой из элементарных областей 
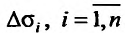произвольно выберем точки 
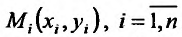, и вычислим значения функции в этих точках: 
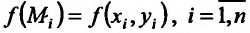. Составим сумму произведений значений функции 
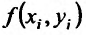на площади 
:
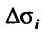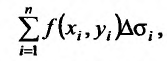которая называется интегральной суммой.
Предел этой интегральной суммы при неограниченном увеличении числа делений и неограниченном уменьшении каждой из элементарных областей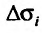 
, если он существует, называется двукратным (двойным) интегралом от функции f(x,y) и обозначается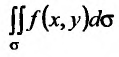 
Если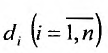 
– максимальное расстояние между двумя точками элементарной области 
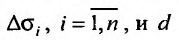– наибольшее из этих чисел: 
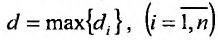то неограниченное уменьшение каждой из элементарных областей равносильно тому, что 
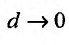. Тогда можно записать:
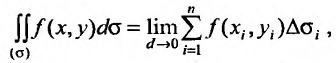
где f(х,у) – подынтегральная функция, а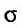 
– область интегрирования.
Если отнести область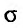 
к прямоугольной системе координат (см. рис. 21.3), то 
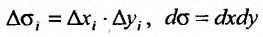(элемент площади) и тогда справедливо равенство:
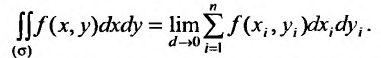
Геометрический смысл двойного интеграла состоит в том, что он равен объему цилиндра с основанием о и ограниченного сверху поверхностью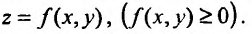 
Вычисление двойного интеграла сводится к вычислению двух определенных интегралов; при вычислении “внутреннего интеграла” (записанного в скобках) х (у) считается постоянным (рис. 21.4):
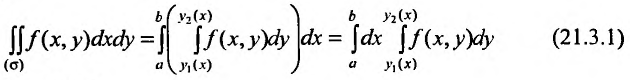
или (рис. 21.5)
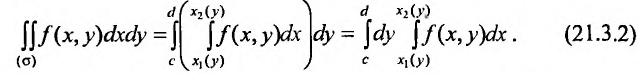
Если область интегрирования о отлична от областей, указанных на рисунках 21.4 и 21.5, то ее разбиваем на части прямыми, параллельными оси Ох и оси Оу, чтобы каждая из полученных частей имела соответствующий вид.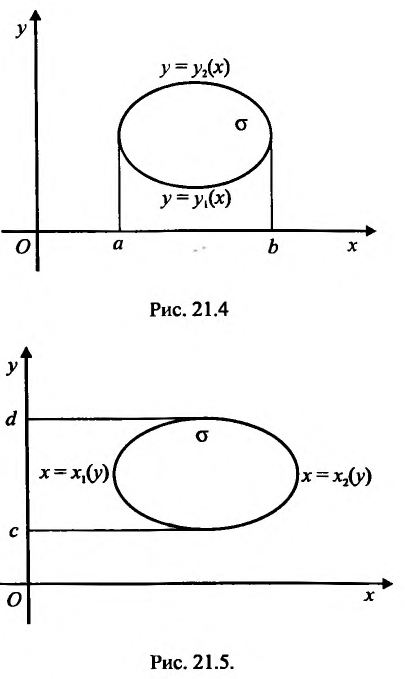 
Пример №1
Вычислить двойной интеграл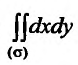
по области
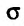, ограниченной линиями: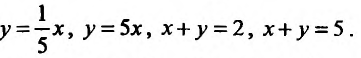 
Решение:
Построим на плоскости хОу область а (см. рис. 21.6).
Из рисунка 21.6 мы видим, что область 
отлична от областей, указанных на рисунках 21.5 и 21.6, так как ни одну из границ в направлении оси Ох или оси Оу нельзя записать одним уравнением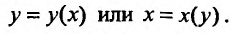
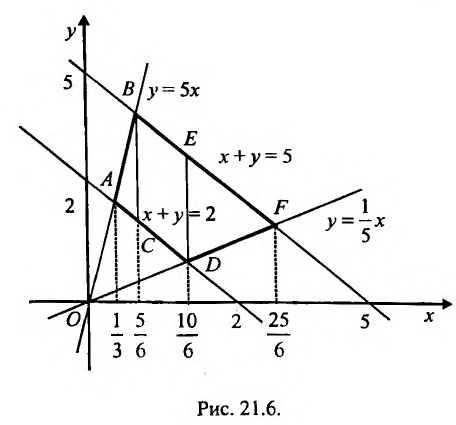
Поэтому разобьем заданную область на части прямыми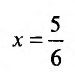 
(абсцисса точки пересечения прямых _у = 5х и х + у = 5) и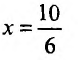 
(абсцисса точки пересечения прямых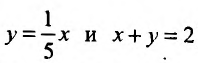 
). Тогда заданный интеграл будет равен сумме трех интегралов по областям: ABC, CBED, DEF: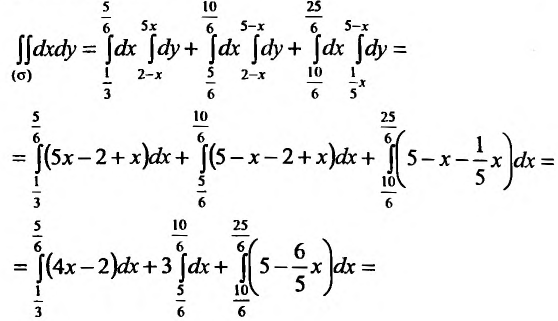 
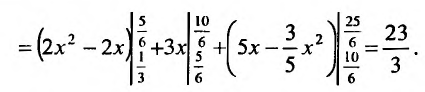
- Заказать решение задач по высшей математике
Понятие о тройном интеграле
По аналогии с двойным интегралом вводится понятие тройного интеграла. Пусть задана замкнутая пространственная область V, в которой задана непрерывная функция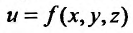 
. Разобьем область V на и элементарных пространственных областей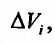
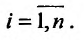. Составим сумму произведений значений функции на объемы элементарных областей:
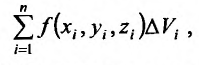
которая называется интегральной суммой.
Обозначим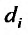 
– максимальное расстояние между двумя точками элементарной пространственной области 
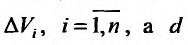-наибольшее из этих чисел: 
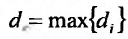. Предел этой интегральной суммы, при неограниченном увеличении числа делений n и неограниченном уменьшении (при 
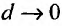) каждой из элементарных областей
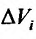, если он существует, называется трехкратным (тройным) интегралом от функции f (х, у, z) и обозначается
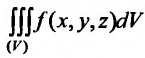. Итак, по определению:
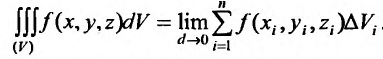
Если ввести в пространстве прямоугольные координаты, то будет справедливо равенство:
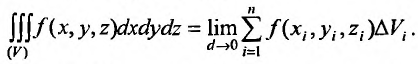
При вычислении тройного интеграла, он сводится к двойному интегралу, путем проектирования поверхности, ограничивающий объем V , на плоскость хОу в виде области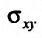 
и определение координат 
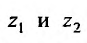точек входа и выхода прямой, параллельной оси Oz и проведенной через точку (х, у) области
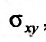и вычисления интеграла 
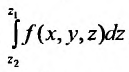, считая х и у постоянными, а затем вычисляется двойной интеграл:
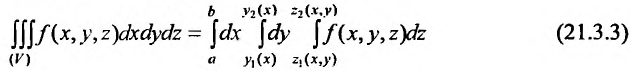
или
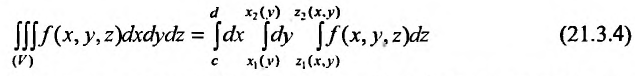
Кратные интегралы (двойные и тройные) удовлетворяют следующим основным свойствам:
- Постоянный множитель можно выносить за знак кратного интеграла.
- Кратный интеграл от алгебраической суммы интегрируемых функций равен алгебраической сумме кратных интегралов от отдельных слагаемых.
- Если подынтегральная функция интегрируема в области, а эта область разбита на две непересекающиеся части, то кратный интеграл по области равен сумме кратных интегралов по непересекающимся частям.
Пример №2
Вычислить тройной интеграл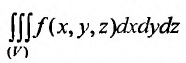 
по пространственной области V, ограниченной плоскостями: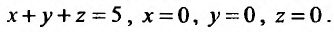 
Решение:
Область V является треугольной пирамидой (см. рис. 21.7), ограниченной плоскостью х + у + z = 5 . Спроектируем поверхность, ограничивающую объем V, на плоскость хОу, получим греугольник ЛОВ, при этом z будет изменяться от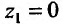 
до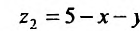 
. Двойной интеграл 
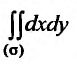вычислим, используя формулу (21.3.1).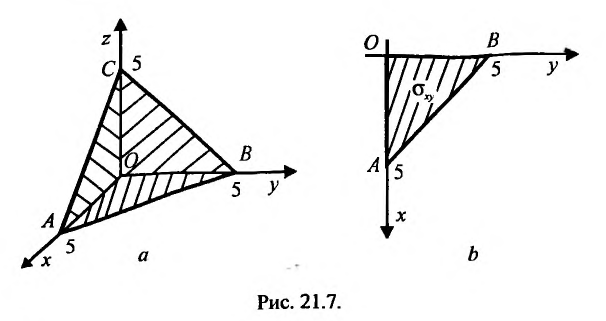 
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица – определение и нахождение
- Ранг матрицы – определение и вычисление
- Пространство R”
- Неопределённый интеграл
- Методы интегрирования неопределенного интеграла
- Определённый интеграл
В математическом анализе кратным или многократным интегралом называют множество интегралов, взятых от 
Замечание: кратный интеграл — это определённый интеграл, при его вычислении всегда получается число.
Определение кратного интеграла[править | править код]
Пусть 
Разбиение 
Мелкость разбиения 
Разбиение называется конечным, если является конечным множеством, и измеримым, если все его элементы — измеримые (в данном случае — по Жордану) множества.
Кратным (n-кратным) интегралом функции 
:
:
Здесь 
Это определение можно сформулировать в другой форме с использованием интегральных сумм. А именно, для данного разбиения 
Кратным интегралом функции
если он существует. Предел берётся по множеству всех последовательностей разбиений, с мелкостью стремящейся к 0. Разумеется, это определение отличается от предыдущего, по сути, лишь используемым языком.
Интеграл обозначается следующим образом:
- В векторном виде[2]
-
,
В современных математических и физических статьях многократное использование знака интеграла не применяется.
Такой кратный интеграл называется интегралом в собственном смысле.
В случае 
Существование кратного интеграла[править | править код]
- Достаточные условия
- Если функция непрерывна на измеримом по Жордану компакте, то она интегрируема на нем.
- Если функция определена на измеримом по Жордану множестве, у которого существуют сколь угодно мелкие разбиения, для которых данная функция неограничена на объединении всех их элементов положительной меры, то эта функция неинтегрируема на этом множестве.
- Критерий Дарбу
Пусть существуют верхний 
- Критерий Лебега
Пусть
Функция интегрируема на
Свойства кратных интегралов[править | править код]
-
.
-
.
-
.
- Интегральное неравенство треугольника. Следствие предыдущего свойства.
-
.
- Как следствие,
.
Вычисление кратных интегралов[править | править код]
Сведение кратного интеграла к повторным[править | править код]
Пусть 
- называемый повторным интегралом от функции
по множеству
.
Любой d-мерный интеграл можно свести к d одномерным.
Замена переменных в кратном интеграле[править | править код]
Пусть задано биективное отображение 
,
где 
Пусть далее функции, задающие отображение, имеют в области
.
Тогда при условии существования интеграла
справедлива формула замены переменных:
Использование симметрии[править | править код]
Если область интегрирования симметрична относительно начала координат по крайней мере для одной из переменных интегрирования и подынтегральная функция нечётна по этой переменной, интеграл равен нулю, поскольку интегралы по двум половинкам области интегрирования имеют одно и то же абсолютное значение, но противоположные знаки. Если подынтегральная функция чётна по этой переменной, интеграл равен удвоенному интегралу по одной из половинок области интегрирования, поскольку интегралы по каждой из половинок равны.
Пример 1. Пусть функция
интегрируется по области
кругу радиуса 1 с центром в начале координат.
Используя свойство линейности, интеграл можно разложить на три части:
2sin(x) и 3y3 являются нечётными функциями и, кроме того, очевидно, что диск T симметричен как относительно оси x, так и по оси y. Таким образом, вклад в конечный результат даёт только константа 5.
Пример 2. Пусть функция f(x, y, z) = x exp(y2 + z2) интегрируется по сфере радиуса 2 с центром в начале координат,
“Шар” симметричен по всем трём осям, но достаточно проинтегрировать по оси x, чтобы показать, что интеграл равен 0, поскольку по этой переменной функция нечётна.
Двойной интеграл[править | править код]
Геометрический смысл двойного интеграла
Двойным интегралом называют кратный интеграл с 
. Здесь
— элемент площади в рассматриваемых координатах.
В прямоугольных координатах: 
Геометрический смысл двойного интеграла[править | править код]
Пусть функция 
Выражение двойного интеграла через полярные координаты[править | править код]
Переход из прямоугольных координат в полярные.
Переход из прямоугольных координат в полярные.
В некоторых случаях двойной интеграл проще считать не в прямоугольных, а в полярных координатах, так как при этом может произойти существенное упрощение вида области интегрирования и всего процесса интегрирования в целом.
Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
Модуль якобиана отображения равен 
где
.
Здесь 
Пример перехода в произвольную систему координат[править | править код]
Посчитаем площадь области 
Переход в полярную систему координат не сделает область проще:
.
Множитель перед синусом «мешает». В этом случае переход можно немного скорректировать:
.
Это преобразование переведет исходную область в следующую:
.
Якобиан отображения:
.
Модуль якобиана также равен 
Отсюда
.
Результат верный, так как область 
Приложения двойных интегралов[править | править код]
| Наименование величины | Общее выражение | Прямоугольные координаты | Полярные координаты |
|---|---|---|---|
| Площадь плоской фигуры | 
|
|
|
| Масса тонкой плоской пластинки
плотностью |
|
|
|
Площадь куска поверхности
|
|
|
|
| Объем цилиндрического тела,
стоящего на плоскости |
|
|
|
Момент инерции плоской фигуры
относительно оси |
|
|
|
| Момент инерции плоской фигуры
относительно оси |
|
|
|
| Координаты центра масс
однородной пластинки |
|
|
|
| Примечания |
1) Область
2) Совмещенной с плоскостью 3) Или, что то же, относительно центра О. |
Тройной интеграл[править | править код]
Тройным интегралом называют кратный интеграл с 
где 
Выражение тройного интеграла через прямоугольные координаты[править | править код]
В прямоугольных координатах тройной интеграл имеет следующий вид:
где 
Выражение тройного интеграла через цилиндрические координаты[править | править код]
Объем в цилиндрических координатах
Аналогично в некоторых случаях тройной интеграл проще считать не в прямоугольных, а в цилиндрических координатах. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
Модуль якобиана отображения равен
где 
Выражение тройного интеграла через сферические координаты[править | править код]
Объем в сферических координатах
Кроме цилиндрических можно также переходить и в сферические координаты. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
Модуль якобиана отображения равен 
где 
Приложения тройных интегралов[править | править код]
| Наименование величины | Общее выражение | Прямоугольные координаты | Цилиндрические координаты | Сферические координаты |
|---|---|---|---|---|
| Объем тела | 
|
|
|
|
| Момент инерции геометрического
тела относительно оси |
|
|
|
|
Масса физического тела с плотностью 
|
|
|
|
|
| Координаты центра масс
однородного тела |
|
|
— | — |
См. также[править | править код]
- Дискретная теорема Грина
- Интеграл
- Мера множества
- Теорема Тонелли — Фубини
- Механические приложения интегралов
Примечания[править | править код]
Литература[править | править код]
- Выгодский, М. Я. Дифференцирование и интегрирование функций нескольких аргументов // Справочник по высшей математике. — М.: Астрель, АСТ, 2005. — 991 с. — 10 000 экз. — ISBN 5-17-012238-1, 5-271-03651-0.
- Ильин, В. А., Позняк, Э. Г. Глава 2. Двойные и n-кратные интегралы // Основы математического анализа. — 4. — М.: ФИЗМАТЛИТ, 2001. — Т. 2. — 464 с. — (Курс высшей математики и математической физики). — 5000 экз. — ISBN 5-9221-0131-5.
- Кудрявцев, Л. Д. Глава 6. Интегральное исчисление функций многих переменных // Курс математического анализа. — М.: Высшая школа, 1981. — Т. 2. — 584 с.
- Будак, Б. М., Фомин С. В. Кратные интегралы и ряды. — М.: Наука, 1967. — 608 с.
При изучении темы «Кратные интегралы» вы научитесь записывать области (на плоскости и в пространстве) с помощью неравенств в декартовых, полярных, цилиндрических и сферических координатах, расставлять пределы интегрирования и сводить кратные
интегралы к повторным. Вы научитесь также решать задачи геометрии и механики с использованием двойных и тройных интегралов (в декартовых, полярных, обобщенных полярных, цилиндрических и сферических координатах).
Изменение порядка интегрирования
Постановка задачи. Изменить порядок интегрирования
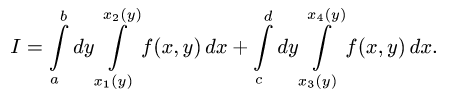
План решения.
1.Область интегрирования состоит из двух областей 
и 
Зададим их неравенствами
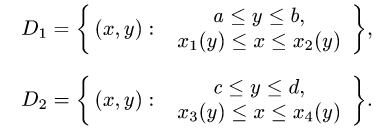
2.Решаем системы неравенств, определяющих област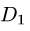и и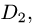 
относительно у и получаем
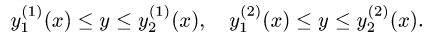
3.Определяем границы изменения х, решая неравенства
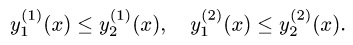
Получаем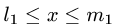 
и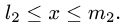 
4.Области и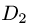 
можно представить в виде
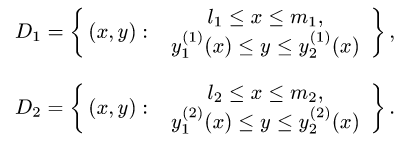
5.Записываем интегралы I с измененным порядком интегрирования:
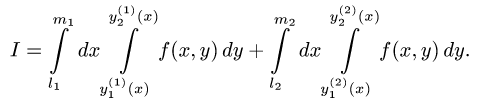
6.Если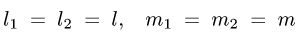 
и 
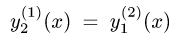или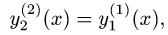 
то I можно представить одним интегралом
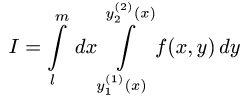или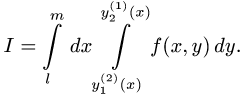 
Записываем ответ.
Пример:
Изменить порядок интегрирования
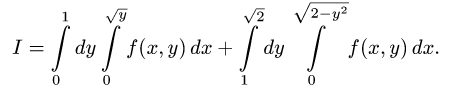
Решение:
1.Область интегрирования состоит из двух областей и
Зададим их неравенствами
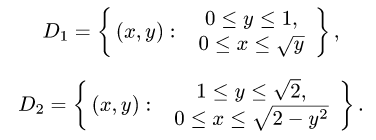
2.Решаем системы неравенств, определяющих област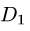и и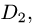
относительно у и получаем
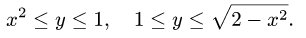
3.Определяем границы изменения х, решая неравенства
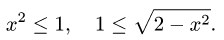
Учитывая, что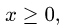 
в обоих случаях получаем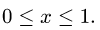 
4.Област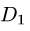и и 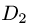можно представить в виде
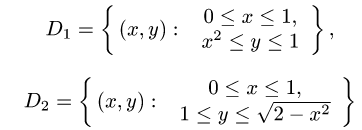
5.Записываем интегралы I с измененным порядком интегрирования:
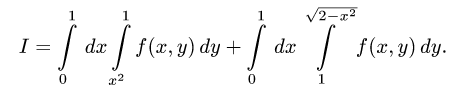
6.Пользуясь линейностью и аддитивностью интегралов, получаем
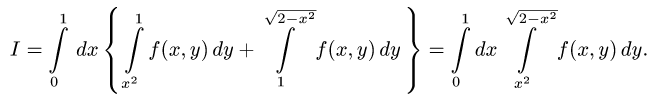
Ответ.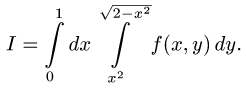 
Двойной интеграл в декартовых координатах
Постановка задачи. Вычислить двойной интеграл
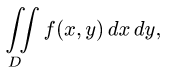
где область D ограничена линиями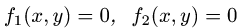 
(и, возможно, прямыми х = а и х = b или у = с и у = d).
План решения.
1.Зададим область D неравенствами. Для этого выясним, каким
из неравенств
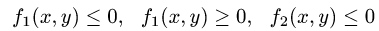или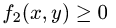 
удовлетворяют координаты точек области D.
Пусть, например, такими неравенствами оказались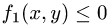 
и 
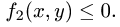Тогда
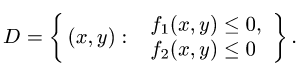
Решаем неравенства, определяющие D, относительно х и у. Получаем
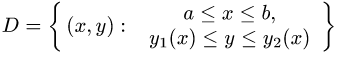
или
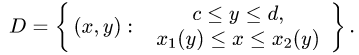
2.Переходим от двойного интеграла к повторному:
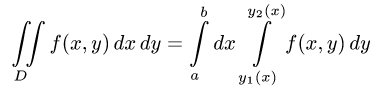
или
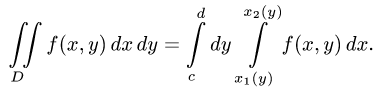
3.Последовательно интегрируем, используя свойства определенного интеграла.
Записываем ответ.
Замечание:
Если необходимо, разбиваем область на части и используем свойство аддитивности интеграла.
Пример:
Вычислить двойной интеграл
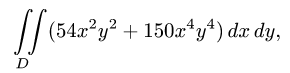
где область D ограничена линиями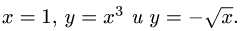 
Решение:
1.Зададим область D неравенствами. Очевидно, что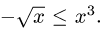 
Поэтому 
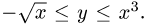Поскольку ж фигурирует под знаком квадратного корня, 
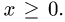Для х возможны неравенства 
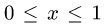или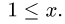 
Во втором случае область неограничена, что неприемлемо.
Итак,
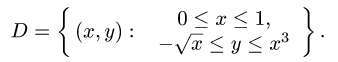
2.Переходим от двойного интеграла к повторному:
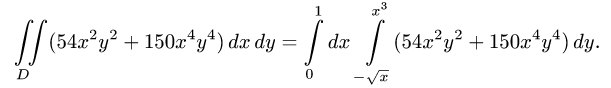
3.Используя свойства определенного интеграла, последовательно
интегрируем сначала по у (считая х постоянной), затем по х:
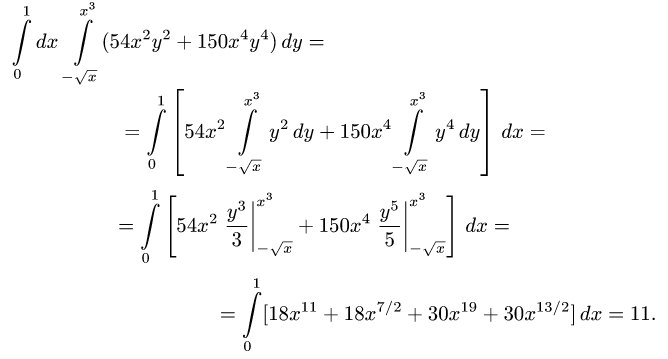
Ответ.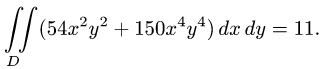 
Двойной интеграл в полярных координатах
Постановка задачи. Вычислить двойной интеграл
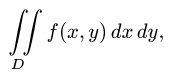
где область D ограничена двумя окружностями
или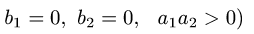 
и двумя прямыми
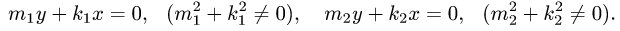
План решения.
1.Зададим область D неравенствами в декартовой системе координат.
Для этого заметим, что окружност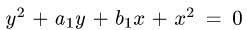и 
и
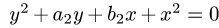проходят через начало координат и их центры
расположены на оси ОХ (при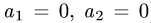 
) или на оси OY (при
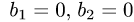) по одну сторону от начала координат (так как 
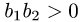или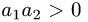 
). Поэтому та из окружностей, которая имеет меньший радиус, расположена внутри другой. Пусть, например, это окружность 
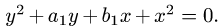Область D находится между окружностями, поэтому координаты точек области D удовлетворяют неравенствам
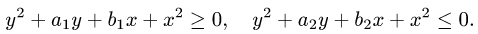
Прямые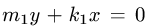 
и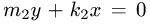 
проходят через начало
координат. Область D расположена между ними. Учитывая, в какой полуплоскости находятся окружности и, следовательно, область
D, определяем, каким из следующих пар неравенств удовлетворяют
координаты точек области D:
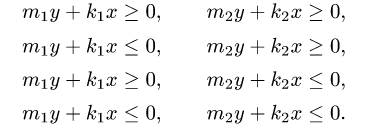
2.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать в полярных координатах
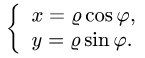
При этом 
а искомый интеграл определяется формулой
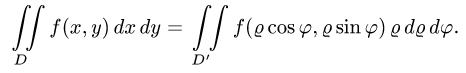
3.Чтобы найти область D’, заменяем в неравенствах, определяющих область D, х на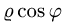 
и y на 
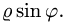Затем разрешаем полученные неравенства относительно 
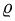и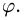 
Таким образом получим
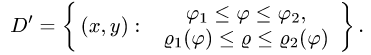
4.Переходим от двойного интеграла к повторному:
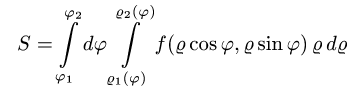
и последовательно интегрируем, используя свойства определенного
интеграла.
Записываем ответ.
Пример:
Вычислить двойной интеграл
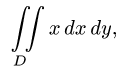
где область D ограничена линиями
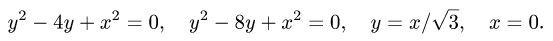
Решение:
1.Зададим область D неравенствами в декартовой системе координат. Для этого заметим, что, выделяя полные квадраты в уравнениях окружносте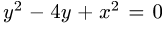й 
и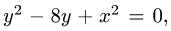 
их можно
привести к виду
Очевидно, что обе окружности проходят через начало координат
и их центры расположены на оси OY в точках (0,2) и (0,4). Окружность (1) имеет радиус 2 и, следовательно, лежит внутри окружности (2), имеющей радиус 4. Поскольку область D находится между окружностями, координаты ее точек удовлетворяют неравенствам
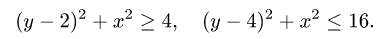
Прямые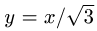 
и х = 0 проходят через начало координат. Область D расположена между ними. Учитывая, что окружности, а следовательно, и область D находятся в верхней полуплоскости, заключаем, что область D находится над прямой 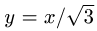и справа от прямой х = 0. Поэтому координаты точек области D удовлетворяют неравенствам
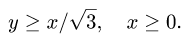
Итак,
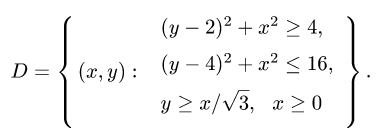
2.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать в полярных координатах
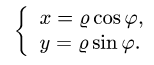
При этом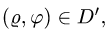 
а искомый интеграл определяется формулой
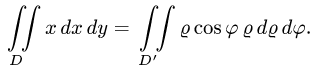
3.Чтобы найти область D’, заменяем в неравенствах, определяющих область D, х на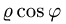 
и y на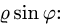 
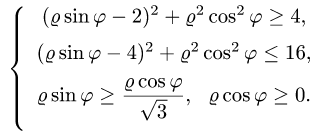
Решая эти неравенства относительно 
и 
получаем
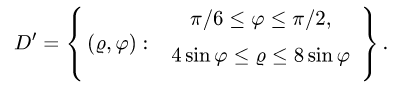
4.Переходим от двойного интеграла к повторному:
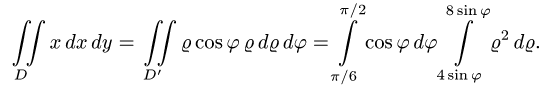
Последовательно интегрируя, получаем
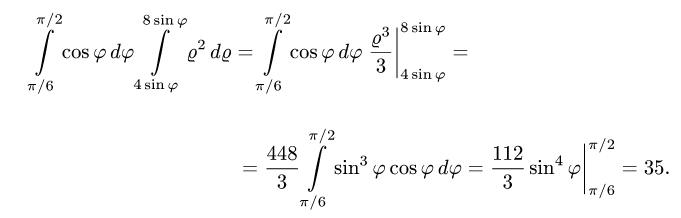
Ответ.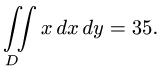 
Двойной интеграл в обобщенных полярных координатах
Постановка задачи. Вычислить двойной интеграл
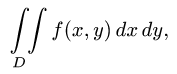
где область D задана неравенствами
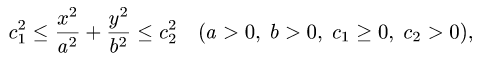
План решения.
1.Область D задана неравенствами в декартовой системе координат, т.е.
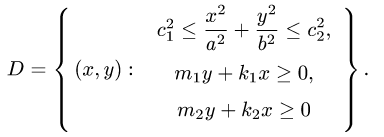
2.Так как область D ограничена эллипсами и прямыми, проходящими через начало координат, поставленную задачу проще решать в
обобщенных полярных координатах
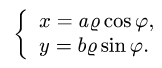
При этом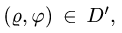 
а искомый интеграл определяется формулой
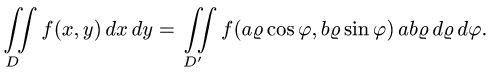
3.Чтобы найти область D’, заменяем в неравенствах, определяющих область D, х на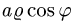 
и у на 
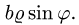Затем разрешаем полученные неравенства относительно 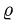и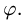 
Таким образом, получаем
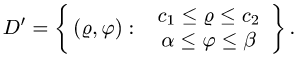
4.Переходим от двойного интеграла к повторному:
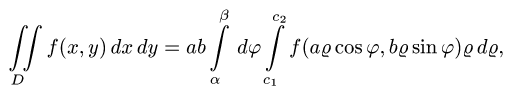
и последовательно интегрируем, используя свойства определенного
интеграла.
Записываем ответ.
Пример:
Вычислить двойной интеграл
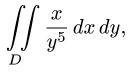
где область D задана неравенствами
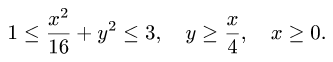
Решение:
1.Область D задана неравенствами в декартовой системе координат:
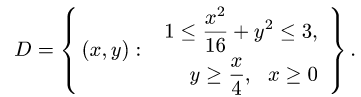
2.Так как область D ограничена эллипсами и прямыми, проходящими через начало координат, поставленную задачу проще решать в
обобщенных полярных координатах
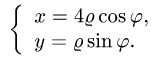
При этом 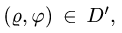а искомый интеграл определяется формулой
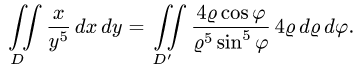
3.Чтобы найти область D’, заменяем в неравенствах, определяющих область D, х на 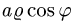и у на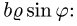 
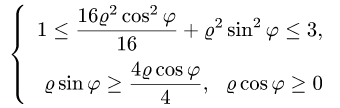
Решая эти неравенства относительно 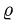и 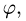получаем
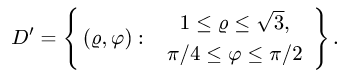
4.Переходя от двойного интеграла к повторному и последовательно интегрируя, получаем
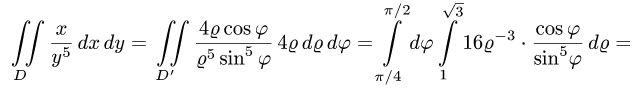
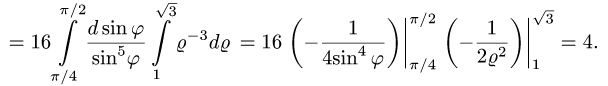
Ответ.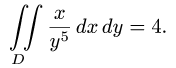 
Вычисление объемов с помощью двойного интеграла
Постановка задачи. Найти объем тела, ограниченного поверхностями
План решения.
1.Объем цилиндрического бруса, ограниченного заданными поверхностями, определяется формулой
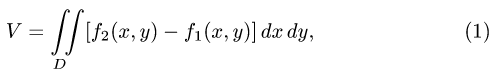
где D — проекция тела на плоскость XOY.
2.Чтобы найти D, задаем тело с помощью неравенств и исключаем из них z.
Допустим, например, что координаты точек тела удовлетворяют
неравенствам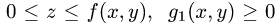 
и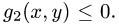 
Тогда тело определяется системой неравенств
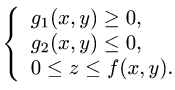
Исключая z, получим
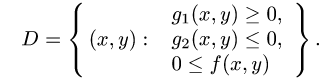
3.Вычисляем двойной интеграл по формуле (1) пр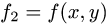и 
и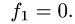 
Записываем ответ, не забывая о размерности.
Пример:
Найти объем тела, ограниченного поверхностями
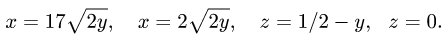
Решение:
1.По формуле (1) с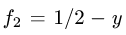 
и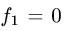 
искомый объем равен
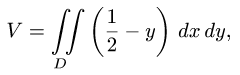
где D — проекция тела на плоскость XOY.
2.Чтобы найти D, задаем тело с помощью неравенств и исключаем из них z. В данном случае тело определяется системой неравенств
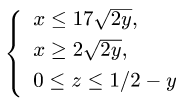
Поэтому
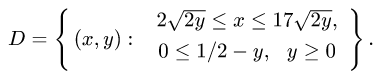
Здесь неравенство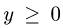 
необходимо, так как у стоит под знаком
квадратного корня.
3.Вычисляем двойной интеграл:
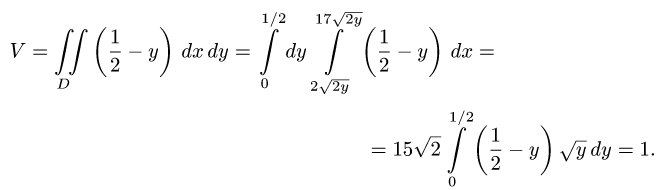
Ответ. V = 1 ед. объема.
Пример:
Найти объем тела, ограниченного поверхностями
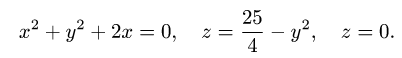
Решение:
1.По формуле (1) с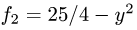 
и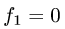 
искомый объем равен
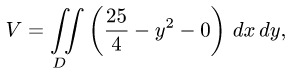
где D — проекция тела на плоскость XOY.
2.Чтобы найти D, задаем тело с помощью неравенств и исключаем из них z. В данном случае тело определяется неравенствами
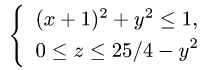
Из первого неравенства очевидно, что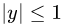 
и, следовательно, второе неравенство выполняется автоматически (геометрически это означает, что проекция поверхности 
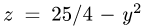на плоскость XOY охватывает круг 
Поэтому
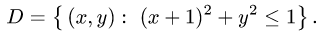
3.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать в полярных координатах
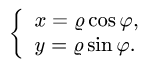
При этом 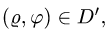а искомый объем определяется формулой
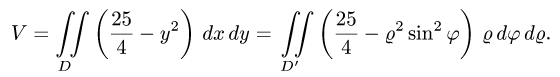
4.Чтобы найти область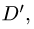 
заменяем в неравенстве, определяющем область D, х на 
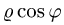и у на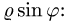 
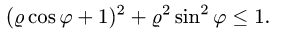
Получаем
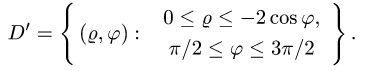
Заметим, что из неравенств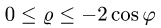 
следует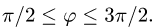 
5.Переходим от двойного интеграла к повторному:
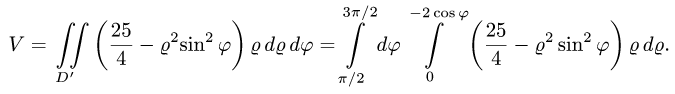
Последовательно интегрируя, получаем
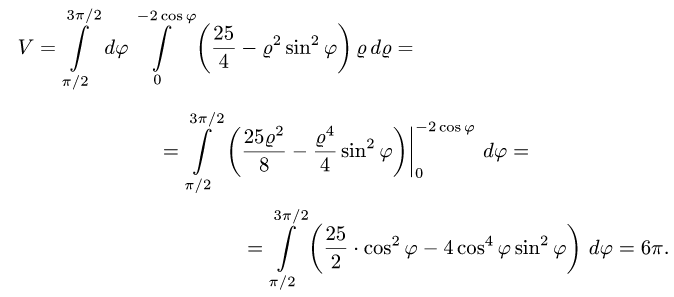
Ответ.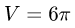 
ед. объема.
Вычисление площадей в декартовых координатах
Постановка задачи. Найти площадь области D, ограниченной
линиями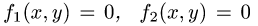 
(и, возможно, прямыми х = а и
х = b или у = с и у = d).
План решения.
Из определения двойного интеграла следует, что искомая площадь
S численно равна
1.Зададим область D неравенствами. Для этого выясним, какие
из неравенств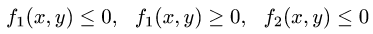 
или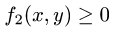 
выполняются для координат точек области D.
Пусть, например, такими неравенствами оказались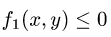 
и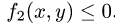 
. Тогда
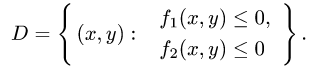
Решаем неравенства, определяющие D, относительно х и у. Получаем
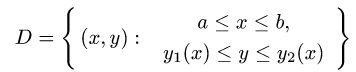
или
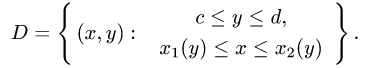
2.Переходим от двойного интеграла к повторному:
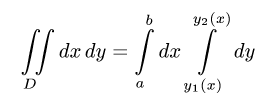
или
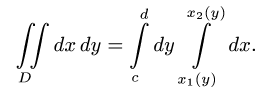
3.Последовательно интегрируем, используя свойства определенного интеграла.
Записываем ответ, не забывая о размерности.
Замечание:
Если необходимо, разбиваем область на части и используем свойство аддитивности интеграла.
Пример:
Найти площадь области D, ограниченной линиями
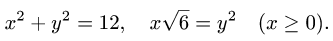
Решение:
1.Зададим область D неравенствами. Область не может находиться вне круга, так как тогда она неограничена. Область не может
находиться слева от параболы, так как в этом случае ее точки могут
иметь отрицательные абсциссы, что исключено условием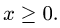 
Следовательно,
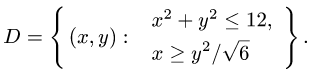
Решаем неравенства, определяющие D, относительно х и у. Получаем
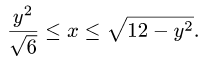
Следовательно,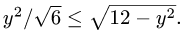 
Отсюда 
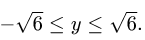Итак,
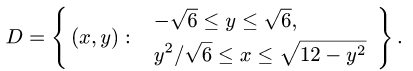
2.Вычисляем площадь области D по формуле (1). Переходя от
двойного интеграла к повторному, получим
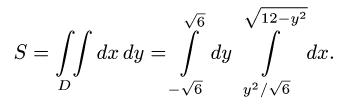
3.Используя свойства определенного интеграла, последовательно
интегрируем:
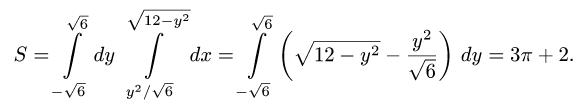
Ответ.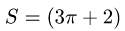 
(ед. длины
Вычисление площадей в полярных координатах
Постановка задачи. Найти площадь области D, ограниченной
двумя окружностями
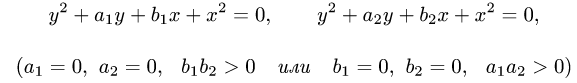
и двумя прямыми
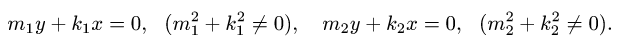
План решения. Из определения двойного интеграла следует, что
искомая площадь S численно равна
1.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать, переходя к полярным координатам
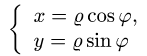
и записывая уравнения границ в полярных координатах.
При этом область D перейдет в область D’, а искомая площадь
будет равна
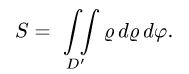
2.Зададим неравенствами область D’ в полярных координатах:
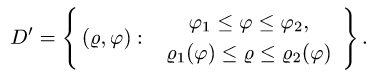
3.Переходим от двойного интеграла к повторному:
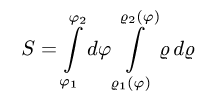
и вычисляем его, пользуясь свойствами определенного интеграла.
Записываем ответ, не забывая о размерности.
Пример:
Найти площадь фигуры, ограниченной данными линиями
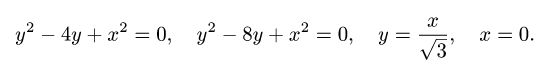
Решение:
1.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать, переходя к полярным координатам
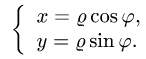
При этом область D перейдет в область D’, ограниченную линиями
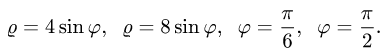
А искомая площадь будет равна
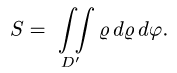
2.Зададим неравенствами область D’ в полярных координатах:
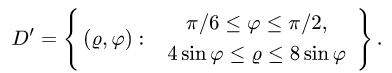
3.Переходим от двойного интеграла к повторному:
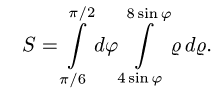
Последовательно интегрируя, получим
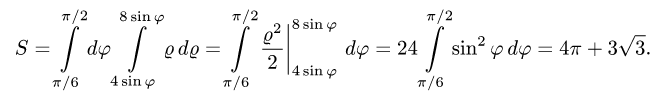
Ответ.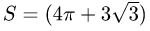 
(ед. длины
Вычисление массы плоской пластины
Постановка задачи. Найти массу плоской пластины D с поверхностной плотностью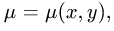 
ограниченной заданными кривыми.
План решения.
1.Масса пластины D с поверхностной плотностью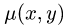 
определяется формулой
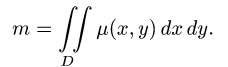
2.Вычисляем полученный двойной интеграл. Записываем ответ,
не забывая о размерности.
Пример:
Найти массу пластины D с поверхностной плотностью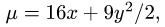 
ограниченной кривыми
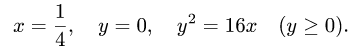
Решение:
1. Масса пластины D с поверхностной плотностью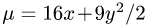 
определяется формулой
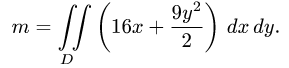
2.Вычисляем полученный двойной интеграл в декартовых координатах:
а) зададим область D системой неравенств:
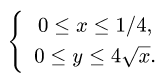
Неравенство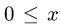 
следует из того, что 
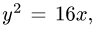т.е. х неотрицательно;
б) перейдем от двойного интеграла к повторному:
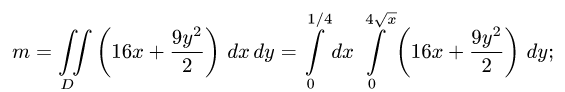
в) последовательно интегрируем, используя свойства определенного интеграла:
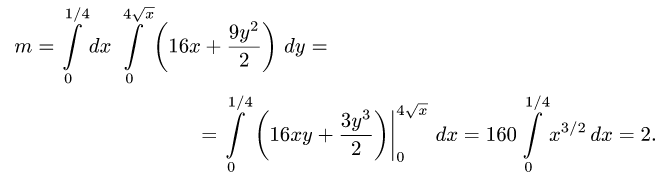
Ответ. m = 2 ед. массы.
Пример:Найти массу пластины D с поверхностной плотностью
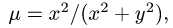ограниченной кривыми
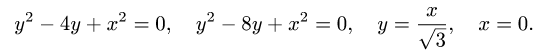
Решение:
1.Масса пластины D с поверхностной плотностью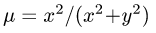 
определяется формулой
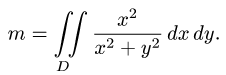
2.Вычисляем полученный двойной интеграл:
а) так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать в полярных координатах
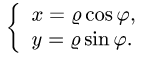
При этом область D перейдет в область D’, ограниченную линиями
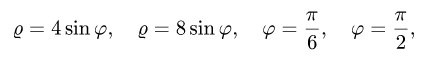
а искомая масса определяется формулой
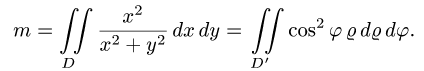
Зададим неравенствами область D’ в полярных координатах:
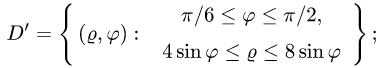
б) перейдем от двойного интеграла к повторному
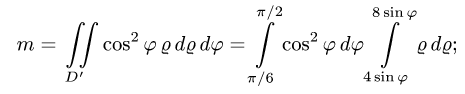
последовательно интегрируя, получим
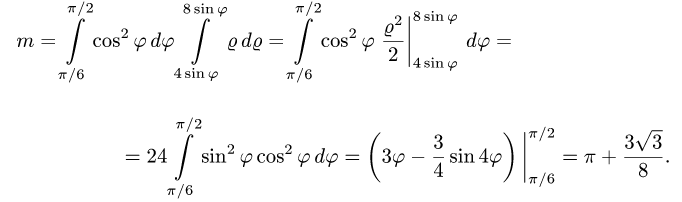
Ответ.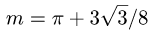 
ед. массы.
Пример:
Найти массу пластины D с поверхностной плотностью
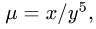ограниченной кривыми
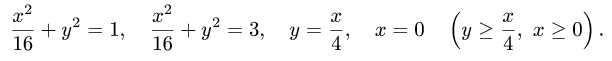
Решение:
1.Масса пластины D с поверхностной плотностью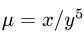 
определяется формулой
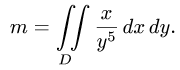
2.Вычисляем полученный двойной интеграл:
а) зададим область D неравенствами в декартовой системе координат
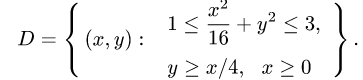
Так как область D ограничена эллипсами и прямыми, проходящими
через начало координат, поставленную задачу проще решать в обобщенных полярных координатах
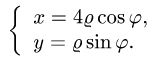
При этом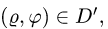 
а искомая масса определяется формулой
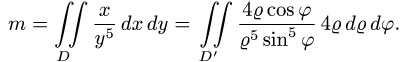
Чтобы найти область D’, заменяем в неравенствах, определяющих
область D, х на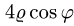 
и у на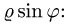 
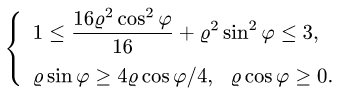
Решая эти неравенства относительно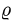 
и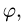 
получаем
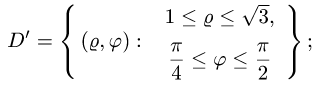
б) переходим от двойного интеграла к повторному:
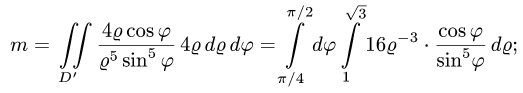
в) последовательно интегрируя, получаем
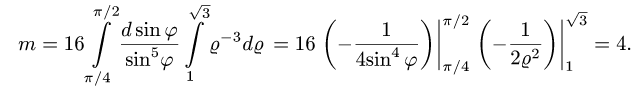
Ответ. m = 4 ед. массы.
Тройной интеграл в декартовых координатах
Постановка задачи. Вычислить тройной интеграл
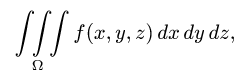
где область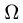 
ограничена некоторыми поверхностями.
План решения.
1.Зададим область 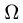системой неравенств, например,
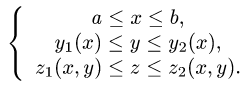
2.Перейдем от тройного интеграла к повторному:
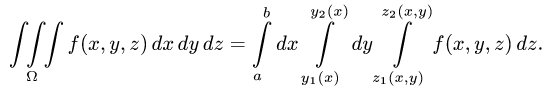
Используя свойства определенного интеграла, последовательно
интегрируем сначала по z (считая хну постоянными), затем по у
(считая х постоянной), затем по х.
Записываем ответ.
Пример:
Вычислить тройной интеграл
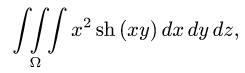
где 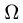ограничена плоскостями
Решение:
1.Зададим область 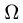неравенствами. Очевидно, что 
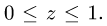Для у возможны неравенства 
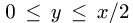или 
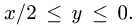Если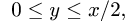 
то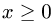 
и для х имеем 
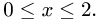Если же 
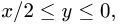то 
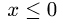и область не примыкает к плоскости х = 2. Значит, мы должны принять, что 
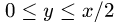и определить 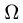системой неравенств
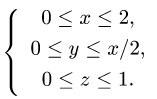
2.Перейдем от тройного интеграла к повторному:
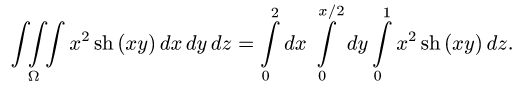
3.Используя свойства определенного интеграла, последовательно
интегрируем сначала по z (считая хну постоянными), затем по у
(считая х постоянной), затем по х:
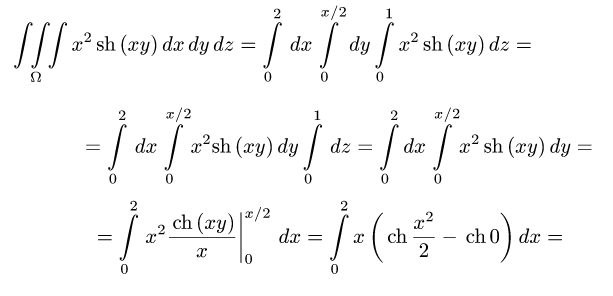
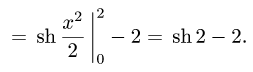
Ответ.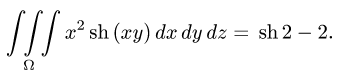 
Тройной интеграл в цилиндрических координатах
Постановка задачи. Вычислить тройной интеграл
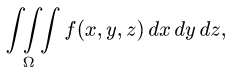
где область 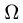ограничена поверхностями
План решения.
1.Поскольку 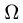— тело вращения вокруг оси OZ, удобно перейти
к цилиндрическим координатам
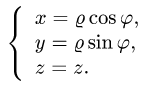
При этом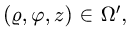 
а искомый интеграл определяется формулой
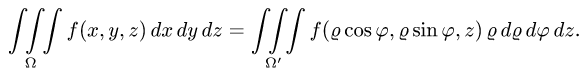
2.Зададим область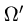 
неравенствами. Для этого сначала заменим в уравнениях поверхностей х на 
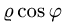и у на 
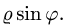Тогда
определяется неравенствам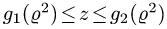и 
или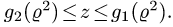 
Чтобы выбрать правильные неравенства, решаем уравнение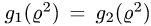 
относительно 
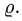Если оно имеет два решения 
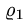и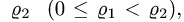 
то исследуем какая из функций 
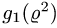или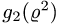 
больше другой на промежутке 
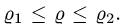Предположим для определенности, что 
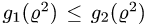при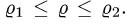 
Тогда область 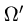определяется системой неравенств
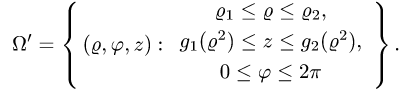
Если уравнение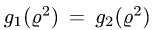 
имеет единственное положительное решение 
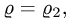то неравенства для 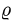имеют вид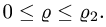 
3.Переходим от тройного интеграла к повторному:
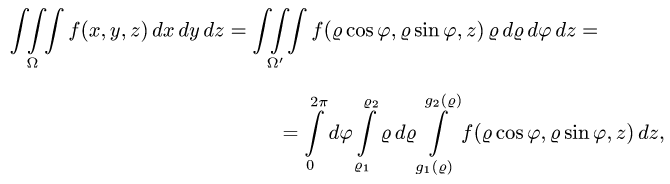
и последовательно интегрируем, используя свойства определенного
интеграла.
Записываем ответ.
Пример:
Вычислить тройной интеграл
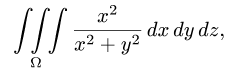
где область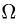 
ограничена поверхностями
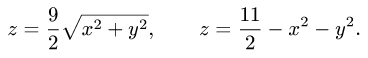
Решение:
1.Поскольку — тело вращения вокруг оси OZ, удобно перейти
к цилиндрическим координатам
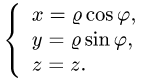
При этом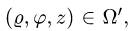 
а искомый интеграл определяется формулой
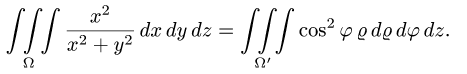
2.Зададим область 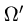неравенствами. Для этого сначала заменим
в уравнениях поверхностей х на 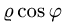и у н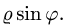а Тогда 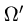определяется неравенствами 
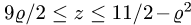или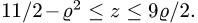 
Чтобы выбрать правильные неравенства, решаем уравнение
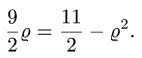
Это уравнение имеет единственное положительное решение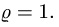 
Следовательно,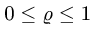 
. При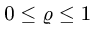 
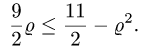
Таким образом, область 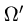определяется системой неравенств:
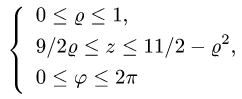
3.Переходим от тройного интеграла к повторному:
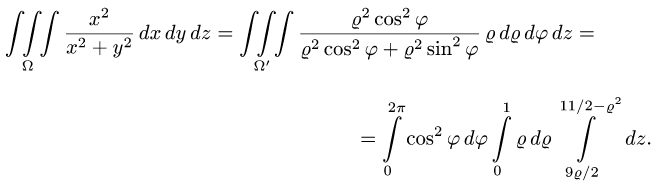
Последовательно интегрируя, получаем
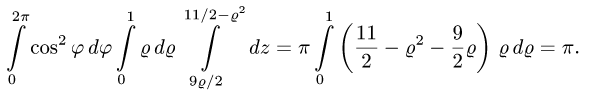
Ответ.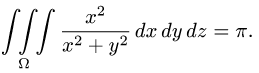 
Тройной интеграл в сферических координатах
Постановка задачи. Вычислить тройной интеграл
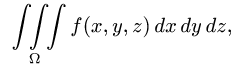
где область ограничена поверхностями
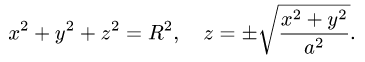
План решения.
1.Поскольку 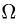ограничена сферой и круглым конусом, удобно
перейти к сферическим координатам
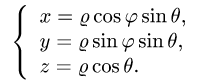
Возможные границы изменения сферических координат суть
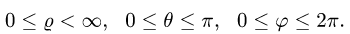
При этом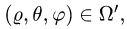 
а искомый интеграл определяется формулой
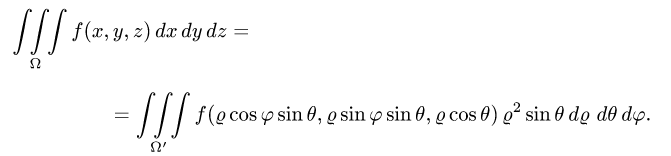
2.Заменяем в уравнениях поверхностей х 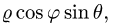на 
у на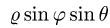 
и z на 
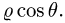Получаем
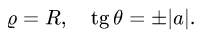
3.Зададим область 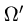с помощью системы неравенств:
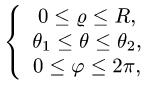
где границы изменения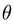 
находим, решая уравнение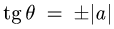 
учитывая, что 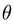может изменяться только от 0 до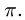 
Замечание. Если 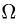ограничена также плоскостями 
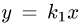и 
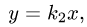проходящими через ось OZ, уравнения которых в сферических координатах имеют вид 
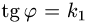и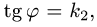 
находим границы изменения 
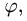решая эти уравнения.
4.Переходим от тройного интеграла к повторному:
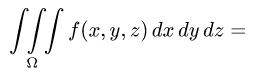
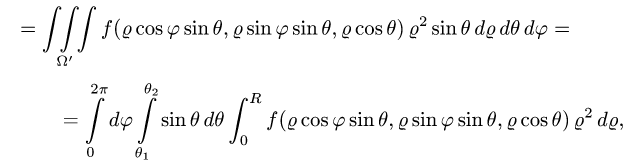
и последовательно интегрируем, используя свойства определенного
интеграла.
Записываем ответ.
Пример:
Вычислить тройной интеграл
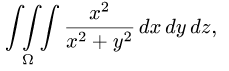
где область 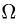ограничена поверхностями
Решение:
1.Поскольку — область, ограниченная верхней полусферой и
верхним полуконусом, удобно перейти к сферическим координатам
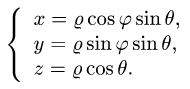
При этом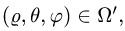 
а искомый интеграл определяется формулой
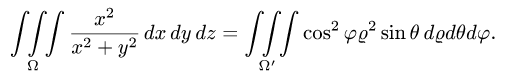
2.Заменяем в уравнениях поверхностей x на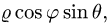 
у на 
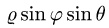и z на 
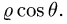Получаем
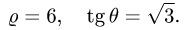
3.Зададим область 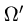с помощью системы неравенств:
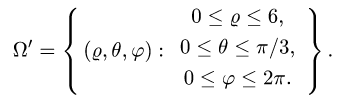
4.Переходя от тройного интеграла к повторному и последовательно интегрируя, получаем
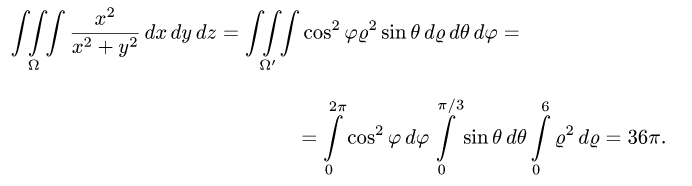
Ответ.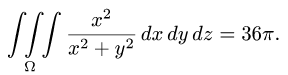
Вычисление объемов с помощью тройного интеграла
Постановка задачи. Найти объем тела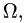 
ограниченного заданными поверхностями.
План решения. Искомый объем равен
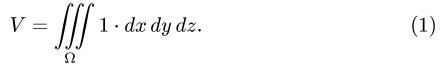
1.Зададим область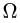 
неравенствами.
2.Вычисляем тройной интеграл, сводя его к повторному, и записываем ответ, не забывая о размерности.
Пример:
Найти объем тела 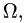ограниченного поверхностями
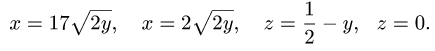
Решение:
1.Зададим область 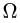неравенствами. Поскольку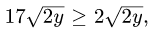 
для х имеем неравенства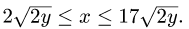 
Поскольку у фигурирует под знаком квадратного корня, 
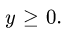Для z возможны неравенства
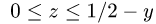или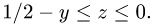 
В первом случае 
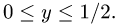Во втором случае 
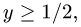т.е. область неограничена, что неприемлемо.
Итак,
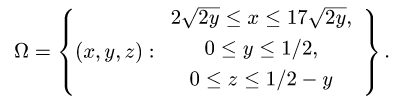
2.Вычисляем объем по формуле (1), сводя тройной интеграл к
повторному:
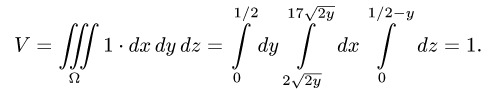
Ответ. V = 1 ед. объема.
Пример:
Найти объем тела 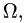ограниченного поверхностями
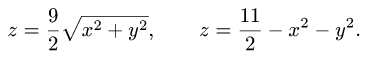
Решение:
1.Поскольку 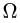— тело вращения вокруг оси OZ, удобно использовать цилиндрические координаты
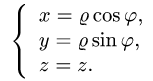
При этом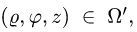 
а искомый объем определяется формулой
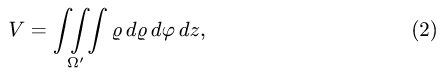
где область 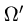ограничена поверхностями
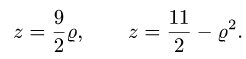
2.Зададим область 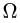неравенствами. Возможны два случая: л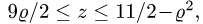ибо 
либо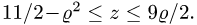 
В первом случае 
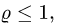во втором случае 
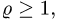т.е. область неограничена, что неприемлемо.
Итак,
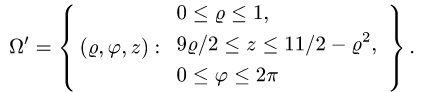
3.Вычисляем объем по формуле (2), сводя тройной интеграл к
повторному:
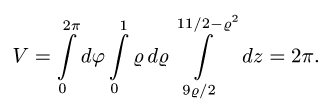
Ответ.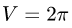 
ед. объема.
Пример:
Найти объем тела 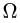, ограниченного поверхностями
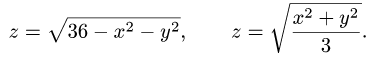
Решение:
1.Поскольку 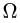— область, ограниченная верхней полусферой и
верхним полуконусом, удобно перейти к сферическим координатам
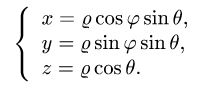
При этом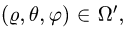 
а искомый объем определяется формулой
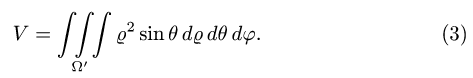
Заменяем в уравнениях поверхностей х 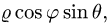на у на 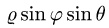и z на 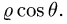После преобразований получаем
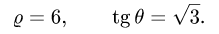
Область ограничена этими поверхностями.
2.Зададим область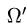 
системой неравенств
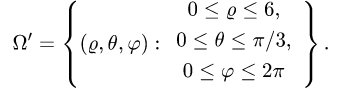
3.Вычисляем объем по формуле (3), сводя тройной интеграл к
повторному:
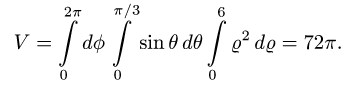
Ответ.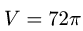 
ед. объема.
Вычисление массы тела
Постановка задачи. Найти массу тела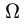 
с плотностью 
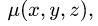ограниченного заданными поверхностями.
План решения.
1.Масса тела 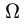с плотностью 
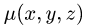определяется формулой
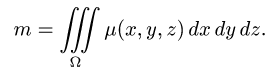
2.Зададим область 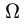неравенствами.
3.Вычисляем тройной интеграл, сводя его к повторному, и записываем ответ, не забывая о размерности.
Пример:
Найти массу тела 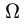с плотностью 
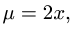ограниченного поверхностями
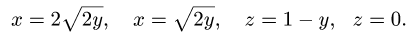
Решение:
1.Масса тела 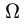с плотностью 
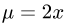определяется формулой
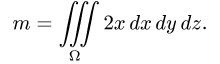
2.Зададим область 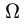неравенствами. Поскольку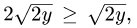 
для х имеем неравенства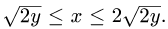 
Поскольку у фигурирует под знаком квадратного корня, 
Для z возможны неравенства
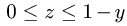или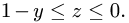 
В первом случае 
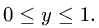Во втором случае 
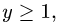т.е. область неограничена, что неприемлемо.
Итак,
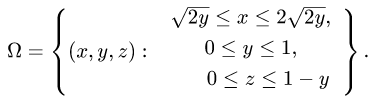
3.Вычисляем m, сводя тройной интеграл к повторному:
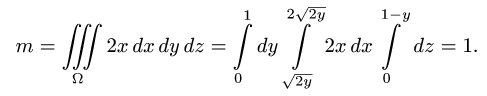
Ответ. m = 1 ед. массы.
Пример:
Найти массу тела с плотностью 
ограниченного поверхностями
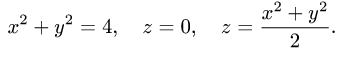
Решение:
1.Масса тела 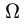с плотностью 
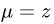определяется формулой
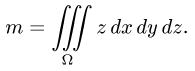
Поскольку 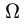— тело вращения вокруг оси OZ, удобно перейти к
цилиндрическим координатам
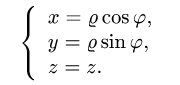
При этом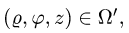 
а искомая масса определяется формулой
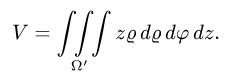
Заменяем в уравнениях поверхностей х на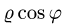 
и у на 
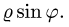Получим
2.Зададим область 
системой неравенств
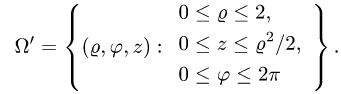
3.Вычисляем m, сводя тройной интеграл к повторному:
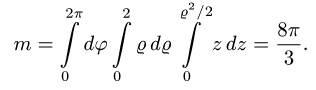
Ответ.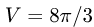 
ед. массы.
Пример:
Найти массу тела с плотностью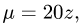 
ограниченного поверхностями
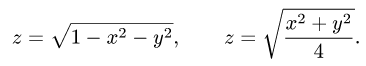
Решение:
1.Масса тела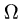 
с плотностью 
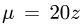определяется формулой
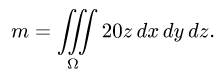
Поскольку 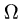— область, ограниченная верхней полусферой и верхним полуконусом, удобно перейти к сферическим координатам:
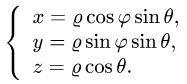
При этом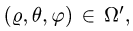 
а искомая масса определяется формулой
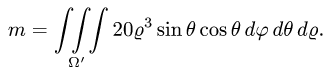
Заменяем в уравнениях поверхностей х 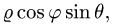на 
у на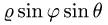 
и z на 
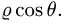Получаем
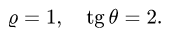
Область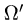 
ограничена этими поверхностями.
2.Зададим область 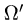системой неравенств
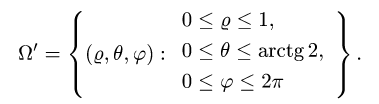
3.Вычисляем m, сводя тройной интеграл к повторному:
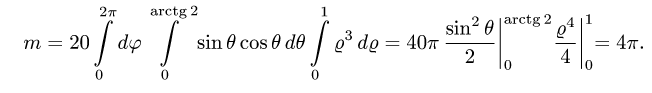
Здесь мы воспользовались формулой
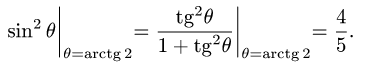
Ответ.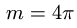 
Определение кратного интеграла
Смотрите также:
Решение задач по математическому анализу
Глава 26
Решение кратных интегралов
Задача, приводящая к понятию двойноrо интеграла. Определение двойного интеграла
К понятию двойного интеграла мы приходим, решая конкретную задачу вычисления объема цилиндрического тела.
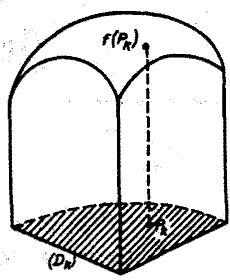
Цилиндрическим телом называется тело, ограниченное плоскостью 
, некоторой поверхностью 
, 
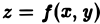, и цилиндрической поверхностью, образующие которой параллельны оси (см. рис.l).
Область 
изменения переменных 
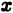и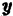 
называется основанием цилиндрического тела.
При определении объема тела будем исходить из двух принципов:
1)если разбить тело на части, то его объем, равен сумме объемов всех частей (свойство аддитивности);
2) объем прямого цилиндра, ограниченного плоскостью 
, параллельной плоскости , равен площади основания, умноженной на высоту.
В дальнейшем мы будем предполагать, что область D является связной (состоящей из одного куска), квадрируемой (т. е. имеющей площадь) и ограниченной (т. е. расположенной внутри некоторого круга с центром в начале координат) .
Пусть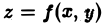 
— непрерывная функция точки 
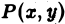в област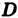и 
и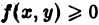 
всюду в области 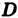, т. е. что рассматриваемая цилиндрическая поверхность целиком лежит над плоскостью 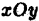. Обозначим объём цилиндрического тела через 
.
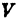Разобъём область 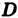— основание цилиндрического тела на некоторое число 
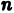непересекающихся квадрируемых областей произвольной формы; будем называть их частичными областями. Пронумеровав частичные области в каком-нибудь порядке, обозначим их через 
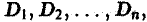а их площади — через 
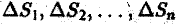соответственно. Назовем диаметром частичной области 
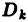величину 
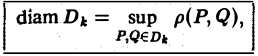где символ 
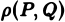означает расстояние между точками 
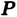и 
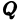. Обозначим через 
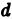наибольший из диаметров частичных областей 
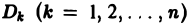. Проведем через границу каждой частичной области цилиндрическую поверхность с образующими, параллельными оси 
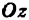. В результате цилиндрическое тело окажется разбитым на 
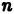частичных цилиндрических тел. Заменим 
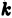-oe частичное тело прямым цилиндром с тем же основанием и высотой, равной аппликате какой-нибудь точки заменяемой поверхности (рис. 2). Объем такого цилиндра равен 
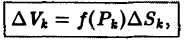где точка 
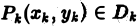— площадь 
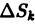области 
.
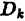Проделав описанные построения для каждого частичного цилиндрического тела:, получим -cтyпенчaтoe тело, объем которого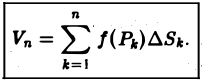 
(1)
Интуитивно ясно,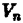 
тем точнее выражает искомый объем 
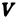, чем меньше размеры частичных областей 
.
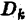Принимаем объем 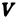цилиндрического тела равным пределу, к которому стремится объем (1) 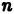-ступенчатоrо тела nри 
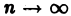и стремлении к нулю наибольшего диаметра 
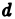частичных областей 
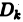. Естественно, предел не должен зависеть от вида разбиения области 
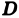на частичные области 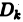: и от выбора точек 
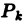в частичных областях.
Пусть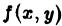 
— произвольная функция, заданная в области 
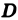. Сумма 
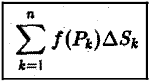(1) называется интегральной суммой для функции 
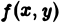по области 
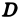, соответствующей данному разбиению этой области на 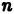частичных областей и данному выбору точек 
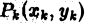на частичных областях 
.
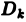Определение:
Если nри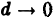 
существует предел интегральных сумм 
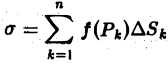, не зависящий ни от способа разбиения области 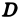на частичные области, ни от выбора точек 
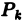в частичных областях, то он называется двойным интегралом от функции 
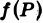( или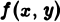 
) по области 
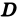и обозначается символом: 
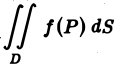или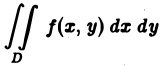 
.
Итак,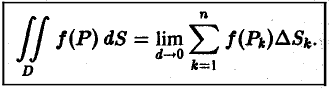 
(2)
Сама функция 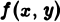при этом называется интегрируемой в области 
( 
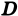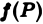— подынтегральная функция, 
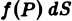— подынтегральное выражение, 
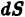— дифференциал (или элемент) площади, область 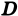— область интегрирования, точка 
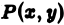— переменная точка интегрирования)
Возвращаясь к цилиндрическому телу, заключаем: объем цилиндрического тела, ограниченного плоскостью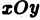 
, поверхностью 
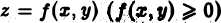, и цилиндрической поверхностью с образующими, параллельными оси 
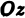, равен двойному интегралу от функции 
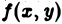по области 
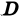, являющейся основанием цилиндрического тела 
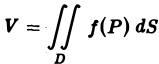или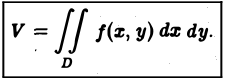 
Здесь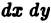 
— элемент площади в декартовых координатах. Таков геометрический смысл двойного интеграла от неотрицательной функции.
Если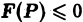 
в 
, то объем 
.
Если в области 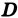функции 
принимает как положительные, так и отрицательные значения, то интеграл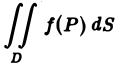 
представляет алгебраическую сумму объемов тех частей тела, которые расположены над плоскостью 
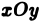(берутся со знаком 
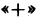), и тех частей тела, которые расположены под плоскостью 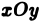(берутся со знаком 
).
К составлению сумм вида (l) для функции двух независимых переменных и к последующему переходу приводят самые разнообразные задачи, а не только задача об объеме цилиндрического тела.
Сформулируем достаточные условия интегрируемости.
Теорема:
Всякая функция 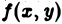, непрерывная в ограниченной замкнутой области 
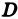, интегрируема в этой области.
Требование непрерывности подынтегральной функции часто оказывается слишком стеснительным. Для приложений важна следующая теорема, гарантирующая существование двойного интеграла для некоторого класса разрывных функций.
Будем говорить, что некоторое множество точек плоскости, имеет площадь нуль, если ero можно заключить в многоугольную фигуру сколь угодно малой площади.
Теорема:
Если функция 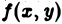ограничена в замкнутой ограниченной области и непрерывна повсюду в , кроме некоторого множества точек площади нуль, то эта функция интегрируема в области .
Основные свойства двойного интеграла
Двойные интегралы обладают рядом свойств, аналогичных свойствам определенного интеграла для функций одной независимой переменной.
Линейное свойство
Если функции f(P) и φ(Р) интегрируемы в области D, а а и β — любые вещественные числа, то функция af(P) + βφ(Р) также интегрируема в области D, причем
(1)
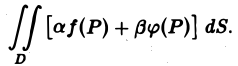
Интегрирование неравенств
Если функции f(P) и φ(Р) интегрируемы в области D и всюду в этой области
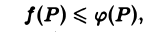
то
(2)
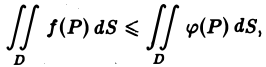
т. е. неравенства можно интегрировать. В частности, интегрируя очевидные неравенства
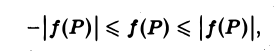
получим
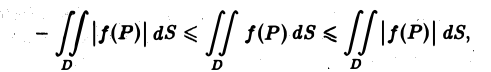
или, что то же,
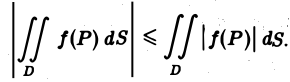
Площадь плоской области
Площадь плоской области D равна двойному интегралу по этой области от функции, тождественно равной единице. Действительно, интегральная сумма для функции f(P) = 1 в области D имеет вид
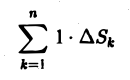
и при любом разбиении области D на частичные области Dk равна ее площади S. Но тогда и предел этой суммы, т. е. двойной интеграл, равен площади S области D:
(3)
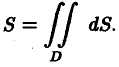
Оценка интеграла
Пусть функция f(Р) непрерывна в ограниченной замкнутой области D, пусть М и т — наибольшее и наименьшее значения f(Р) в области D и S — ее площадь. Тогда
(4)
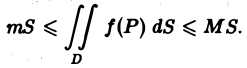
Аддитивность
Если функция f(P) интегрируема в области D и область D разбита на две области D1 и D2 без общих внутренних точек, то f{Р) интегрируема на каждой из областей D1 и D2, причем
(5)
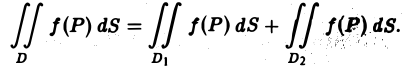
Теорема о среднем значении
Теорема:
Если функция f(P) непрерывна в замкнутой ограниченной области D, то найдется по крайней мере одна тонка Ре области D такая, что будет справедлива формула
(6)
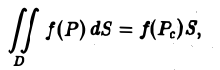
где S — площадь области D.
В самом деле, так как f(P) непрерывна в замкнутой ограниченной области D, то она принимает в D свое наибольшее значение М и свое наименьшее значение т. По свойству 4 об оценке интеграла имеем
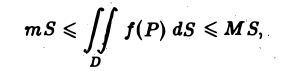
откуда
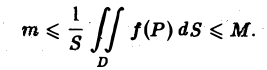
Таким образом, число
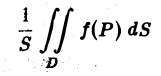
заключено между наибольшим и наименьшим значениями функции f(P) в области D. В силу непрерывности функции f(P) в области D она принимает в некоторой точке Рe ∈ D значение, равное этому числу,
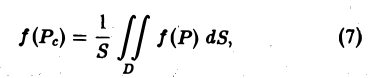
откуда
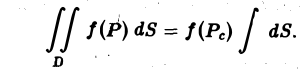
Значение f (Pe), определяемое по формуле (7), называется средним значением функции f(Р) в области D.
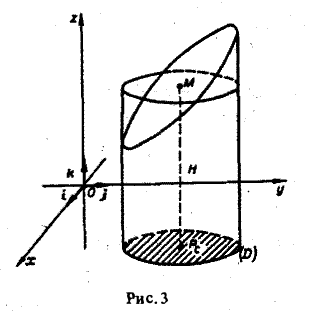
Геометрический смысл теоремы о среднем значении
Если в области D функция f(Р) ≥ 0, то формула (6) означает, что существует прямой цилиндр с основанием D (площадь которого равна S) и высотой H = f(Pe), объем которого равен объему цилиндрического тела (рис. 3).
Сведение двойного интеграла к повторному
Одним из эффективных способов вычисления двойного интеграла является сведение его к повторному.
Случай прямоугольника
Пусть область D — замкнутый прямоугольник П со сторонами, параллельными осям координат
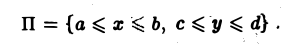
Пусть функция f(x, у) непрерывна в прямоугольнике П. Двойной интеграл
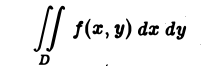
можно интерпретировать как (алгебраический) объем цилиндрического тела с основанием П, ограниченного поверхностью
z = f(х, y).
Рассмотрим соответствующее цилиндрическое тело. Проведем плоскость
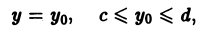
перпендикулярную оси Оу (рис. 4). Эта плоскость рассечет цилиндрическое тело по криволинейной трапеции АВВ1А1, ограниченной сверху плоской линией z, описываемой уравнениями
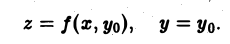
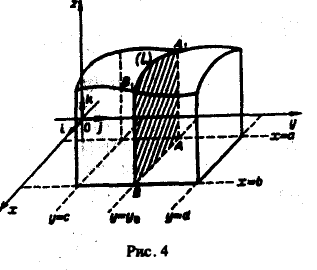
Площадь трапеции АВВ1А1 выражается интегралом
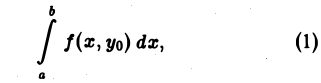
где интегрирование производится по х, а уо — второй аргумент подынтегральной функции — рассматривается при этом как постоянный (с ≤ уо ≤ d). Величина интеграла (1) зависит от выбора значения уо. Положим
(2)
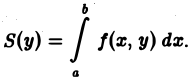
Выражение (2) дает площадь поперечного сечения цилиндрического тела как функции от у. Поэтому объем цилиндрического тела можно вычислить по формуле
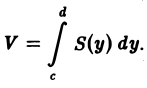
С другой стороны, этот объем выражается двойным интегралом от функции f(х, у) по прямоугольнику П. Значит,
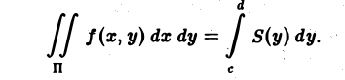
Заменяя S(y) его выражением (2), получим
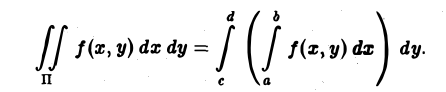
Последнее соотношение обычно записывается так
(3)
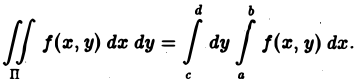
Объем цилиндрического тела можно отыскать также по площадям сечений плоскостями х = х0. Это приводит к формуле
(4)
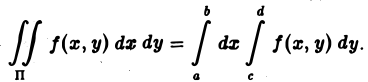
Каждое из выражений, стоящих в правых частях формул (3) и (4), содержит две последовательные операции обыкновенного интегрирования функции f(x, у). Они называются повторными интегралами от функции f(х, у) по области П.
Если f(x, у) непрерывна в замкнутом прямоугольнике П, то переход к повторным интегралам всегда возможен и
(5)
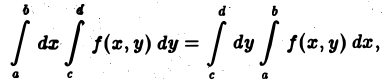
т. е. значения повторных интегралов от непрерывной функции f(х, у) не зависят от порядка интегрирования.
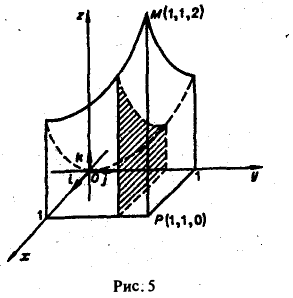
Пример:
Найти двойной интеграл от функции
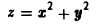
по области
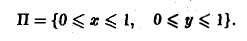
4 Имеем (см. рис. 5):
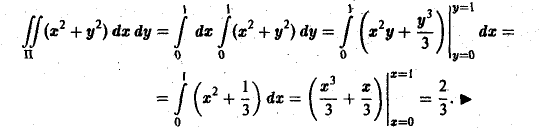
Случай произвольной области
Предположим теперь, что областью интегрирования является произвольная ограниченная квадрируемая замкнутая область D на плоскости хОу, удовлетворяющая следующему условию: любая прямая, параллельная оси Оу, пересекает границу области D не более чем в двух точках или по целому отрезку (рис. 6 а). Заключим область D внутрь прямоугольника
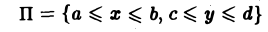
так, как показано на рис. 66. Отрезок [а, b] является ортогональной проекцией области D на ось Ох, а отрезок [с, d] — ортогональной проекцией области D на ось Оу. Точками А и С граница области D разбивается на две кривые ABC и АЕС. Каждая из этих кривых пересекается с произвольной прямой, параллельной оси Оу, не более чем в одной точке. Поэтому их уравнения можно записать в форме, разрешенной относительно у:
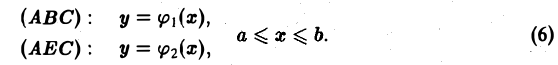
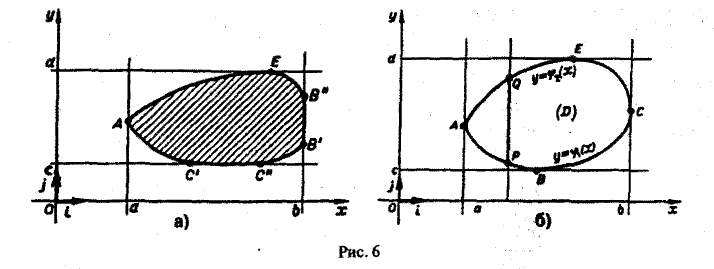
Пусть f(x, у) — некоторая функция, непрерывная в области D. Рассечем рассматриваемое цилиндрическое тело плоскостью
х = const (а < х < b).
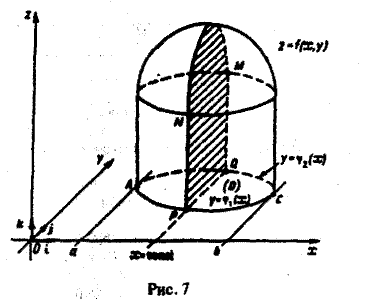
В сечении получим криволинейную трапецию PQMN (рис.7), площадь которой выражается обыкновенным интегралом от функции f(x, у),рассматриваемой как функция одной переменной у. При этом переменная у изменяется от ординаты φ1(x) точки Р до ординаты φ2(х) точки Q; точка Р есть точка «входа» прямой х = const (в плоскости хОу) в область D, a Q — точка ее «выхода» из этой области. Так как уравнение кривой ABC есть у = φ(x), а кривой АЕС — у = φ2(х), то эти ординаты при взятом х соответственно равны φ1(x) и φ2(х). Следовательно, интеграл
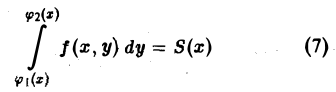
дает нам выражение для площади плоского сечения цилиндрического тела как функции положения секущей плоскости x = const.
Объем всего тела будет равен интегралу от этого выражения по х в промежутке изменения х (a ≤ х ≤ b). Таким образом,
(8)
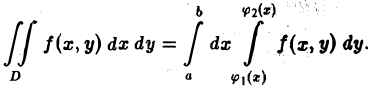
В частности, для площади S области D получим (9)
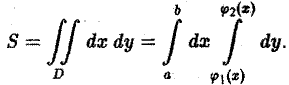
Предположим теперь, что каждая прямая
у = const (с ≤ у ≤ d)
пересекает границу области D не более чем в двух точках Р и Q, абсциссы которых равны ψ1(у) и ψ2{y) соответственно (или по целому отрезку) (рис. 8). Проводя аналогичные рассуждения, приходим к формуле
(10)
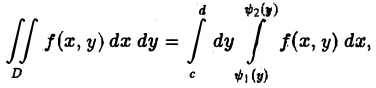
также сводящей вычисление двойного интеграла к повторному.
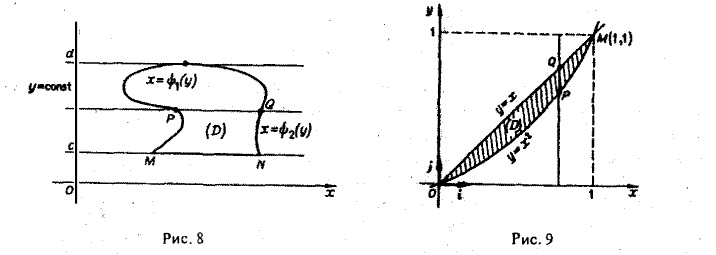
Пример:
Вычислить двойной интеграл от функции
f(x, у) = 2х — у + 3
по области D, ограниченной линиями у = х и у = х2 (рис.9).
Первый способ. Изобразим область интегрирования D. Прямая у = х и парабола у = х2 пересекаются в точках O(0,0) и M(l,1). Значит, х изменяется в пределах от 0 до I, a ψ1(x) = х2 и ψ2(х) = х. Любая прямая х = const (0 ≤ х ≤ 1) пересекает границу области не более чем в двух точках. Поэтому применима формула (8):
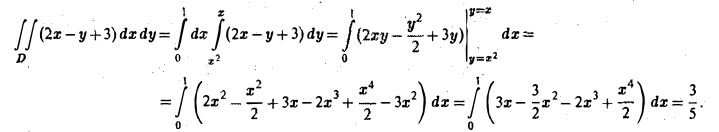
Второй способ (рис. 10). Применяя формулу (10), получим тот же результат:
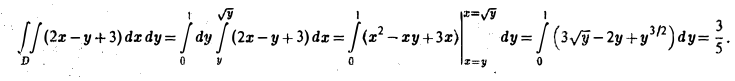
Пример:
Вычислить обьем тела, ограниченного поверхностью
и плоскостью хОу.
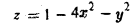
Эллиптический параболоид
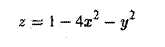
пересекается с плоскостью хОу по линии
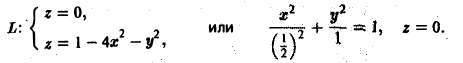
Это — эллипс с полуосями а = 1/2 и b = 1 (рис. 11).
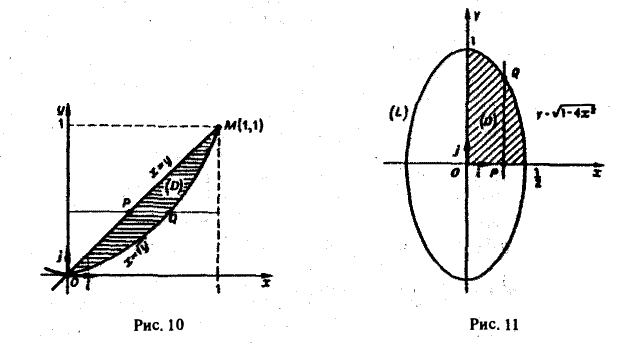
В силу симметрии данного тела относительно координатных плоскостей xОz и уOz получаем:
Замечание:
Если область D такова, что некоторые прямые (вертикальные или горизонтальные) пересекают ее границу более чем в двух точках, то для вычисления двойного интеграла по области D следует разбить ее подходящим образом на части, свести к повторному каждый из интегралов по этим частям и полученные результаты сложить.
Пример:
Вычислить двойной интеграл
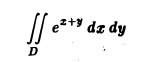
по области D, заключенной между двумя квадратами с центрами в начале координат и сторонами, параллельными осям координат, если сторона внутреннего квадрата равна 2, а внешнего — 4.
Функция
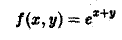
непрерывна как в большом квадрате Q, сторона которого равна 4, так и в малом квадрате Р, сторона которого равна 2 (рис. 12).
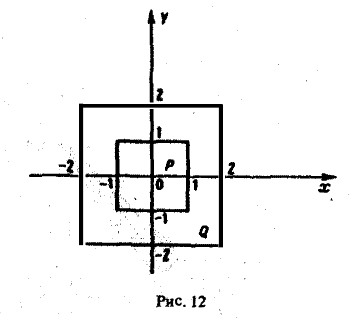
Согласно теореме 1, интегралы от функции еz+y по указанным квадратам существуют, так что величина искомого интеграла
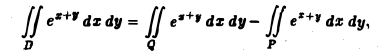
так как
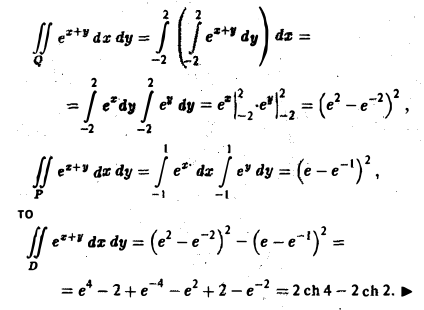
Замена переменных в двойном интеграле
Понятие криволинейных координат точки:
Пусть в области D* плоскости uOv задана пара функций
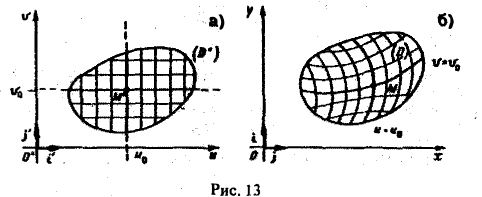
которые мы будем считать непрерывными в этой области и имеющими непрерывные частные производные. В силу уравнения (1) каждой точке М*(и, v) области D* отвечает одна определенная точка М(х, у) в плоскости хОу и тем самым точкам области D* отвечает некоторое множество D точек (x, у) в плоскости хОу (рис. 13). При этом говорят, что функции (1) осуществляют отображение области D на множество D.
Предположим, что различным точкам (и, v) отвечают различные точки (х,у). Это равносильно однозначной разрешимости уравнений (1) относительно и, v:
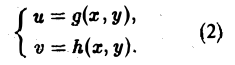
В этом случае отображение называется взаимно однозначным отображением области D* на область D. При таком преобразовании любая непрерывная кривая L*, лежащая в области D*, перейдет в непрерывную кривую L, лежащую в области D. Если функции g(х, у) и h(x,y) также непрерывны, то любая непрерывная линия L ⊂ D с помощью преобразования (2) перейдете непрерывную линию L* ⊂ D*.
По заданной паре uо, vo значений переменных и, v из области D* можно однозначно определить не только положение точки М*(и0, vo) в самой области D*, ной положение соответствующей точки М(хо, уо) в области D, xо = φ(uo, vo), уо = ψ(uо. vо). Это дает основание рассматривать числа u, v как некоторые новые координаты точки D области М на плоскости хОу. Их называют криволинейными координатами точки М.
Множество точек области D, у которых одна из координат сохраняет постоянное значение, называют координатной линией. Полагая в формуле (1) и = vo, получим параметрические уравнения координатной линии,
Здесь роль параметра играет переменная и. Придавая координате v различные (возможные для нее) постоянные значения, получим семейство координатных линий (v = const) на плоскости хОу. Аналогично получаем и другое семейство координатных линий (u = const).
При наличии взаимно однозначного соответствия между областями D* и D различные координатные линии одного и того же семейства Hie пересекаются между собой, и через любую точку области D проходит по одной линии из каждого семейства. Сетка криволинейных координатных линий на плоскости хОу является образом прямоугольной сетки на плоскости uOv (см. рис. 13).
Элемент площади в криволинейных координатах. Якобиан и его геометрический смысл
Выделим в области D* на плоскости Uo*V малый прямоугольник P’pj Р3Р4 со сторонами, параллельными осям координат О*и и О* v и длинами сторон ∆u и ∆v (для определенности считаем, что ∆u > О, ∆v > 0) соответственно (рис. 14а). Его площадь
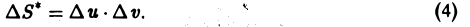
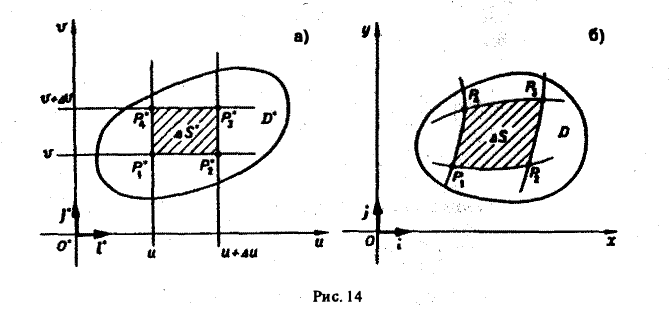
Прямоугольник P*1P*2P*3P*4 переходит в криволинейный четырехугольник Р1Р2Р3Р4 в области D (рис. 146). Если вершины Р*i(i = 1, 2, 3,4) имеют координаты
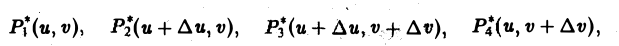
то, согласно формулам (1), соответствующие им вершины Рi имеют координаты
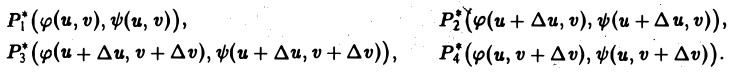
Пользуясь формулой Тейлора для функции двух переменных и ограничиваясь членами первого порядка относительно ∆и и ∆v, получим следующие приближенные значения координат для вершин четырехугольника Р1Р2Р3Р4:
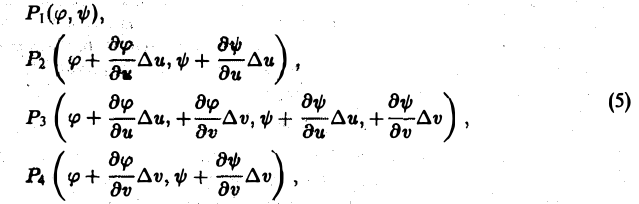
где функции φ, ψ и все их производные вычислены в точке (и, v). Найденные выражения для координат точек показывают, что с точностью до малых высшего порядка четырехугольник Р1Р2Р3Р4 есть параллелограмм. Это следует из того, что
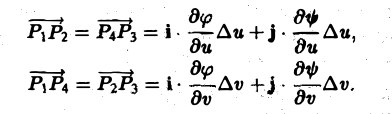
Тогда площадь ∆S четырехугольника Р1Р2Р3Р4 можно приближенно выразить через длину векторного произведения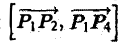 
,
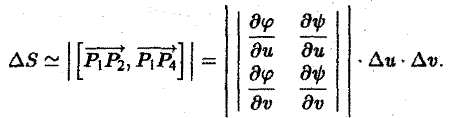
Определитель
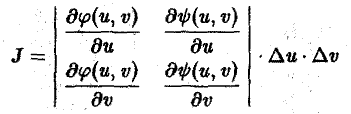
называется функциональным определителем функций φ{и, v), ψ (u, v), или якобианом. Итак, (6)
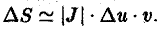
Выражение в правой части (6) называется элементом площади в криволинейных координатах. Так как ∆и ⋅ ∆v,to из формулы (6) получаем, что
Равенство (7) является приближенным. Однако в пределе, когда диаметры площадок ∆S* и ∆S стремятся к нулю, оно переходит в точное:
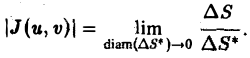
Из формул (7) и (8) видано, что абсолютная величина якобиана играет роль локального коэффициента растяжения области D* (в данной точке (u, v)) при отображении ее на область D при помощи формул преобразования (1).
Формула замены переменных в двойном интеграле
Пусть непрерывныефункции
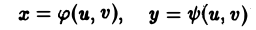
осуществляют взаимнооднозначное отображение области D* на D и имеют непрерывные частные производные первого порядка. Пусть в области D на плоскости хОу задана непрерывная функция
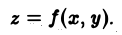
Каждому значению функции z = f(x, у) в области D соответствует равное значение функции z = F(u, v) в области D*, где
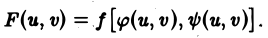
Разобьем область D* на частичные области и построим соответствующее разбиение области D. Выберем в соответствующих частичных областях точки (u, v) и (х, у) так, чтобы значения функций F(u, v) и f(x, у) в них совпадали, и составим интегральные суммы для функций z = f(x, у) и F(u,v) по областям D и D*. Получим
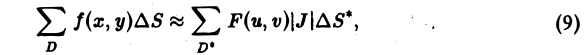
где
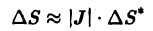
и J(и, v) — якобиан функций φ(и, v) и ψ =(u, v). Переходя в равенстве (9) к пределу при стремлении к нулю наибольшего диаметра d* частичных областей D*k (в силу непрерывности отображения (1) будет стремиться к нулю и наибольший из диаметров d частичных областей в D), будем иметь
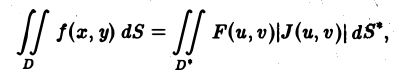
или (10)
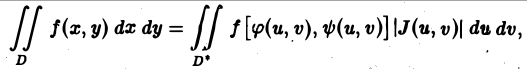
где
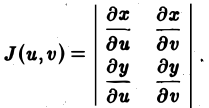
Условие J ≠ 0 является условием локальной взаимноoднозначности отображения, осуществляемого функциями φ(и, v) и ψ =(u, v).
Теорема:
Для того чтобы преобразовать двойной интеграл, заданный в декартовых координатах, в двойной интеграл в криволинейных координатах, нужно заменить в подынтегральной функции f(x, у) переменные х и у соответственно через φ(и, v) и ψ =(u, v), а элемент площади dx dy — его выражением в криволинейных координатах:
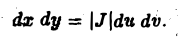
Пример:
Найти площадь фигуры, ограниченной гиперболами
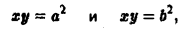
где х > 0, у > 0, 0 < а < b, и прямыми
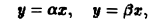
где 0 < а < β (рис. 15 а).
Отыскание площади указанной фигуры сводится к вычислению двойного интеграла
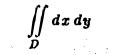
по области D. Введем новые, криволинейные координаты и и v формулами
Из условия задачи ясно, что a2 ≤ u ≤ b2. а ≤ v ≤ β. Значит, в плоскости uOv мы получили прямоугольник (рис. 15b)
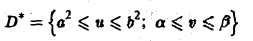
— фигуру Солее простую, чем заданная фигура D.
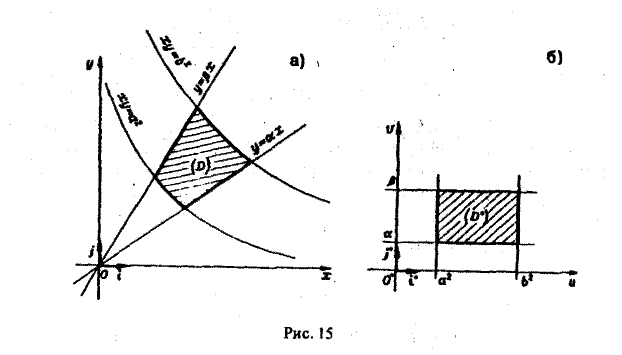
Выразим х и у из соотношений (11) через u и v:
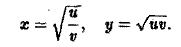
Тогда
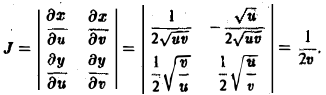
По формуле (10) при f(x,y) = 1 получим
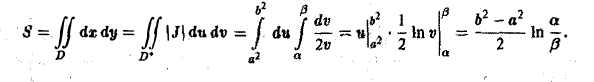
Двойной интеграл в полярных координатах
Вычисление двойного интеграла часто упрощается заменой прямоугольных координат х и у полярными координатами р и φ по формулам
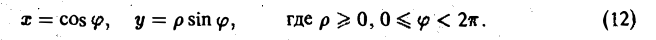
В этом случае
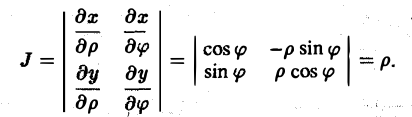
Элемент площади в полярных координатах имеет вид
(13)
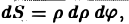
и формулу перехода от интеграла в декартовых координатах к интегралу в полярных координатах можно записать так:
(14)
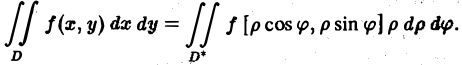
Элемент площади в полярных координатах можно подучить и из геометрических соображений (см. рис. 16).
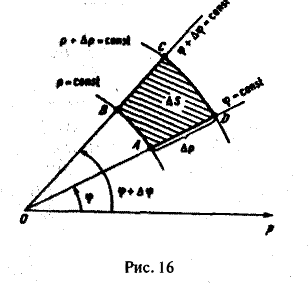
Площадь заштрихованной на рисунке области
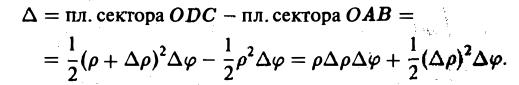
Отбрасывая бесконечно малую величину высшего порядка, получаем
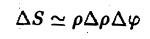
и принимаем
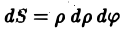
за элемент площади в полярных координатах.
Итак, чтобы преобразовать двойной интеграл в декартовых координатах в двойной интеграл в полярных координатах, нужно х к у в подынтегральной функции заменить соответственно через р cos φ и р sin φ, а элемент площади в декартовых координатах dx dy заменить элементом площади в полярных координатах р dp dφ.
Займемся теперь вычислением двойного интеграла в полярных координатах. Как и в случае прямоугольных декартовых координат, вычисление интеграла в полярных координатах осуществляется путем сведения его к повторному интегралу.
Рассмотрим сначала случай, когда полюс О лежит вне заданной области D. Пусть область D обладает тем свойством, что любой луч, исходящий из полюса (координатная линия φ = const) пересекает ее границу не более чем в двух точках или по целому отрезку (рис. 17). Отметим крайние значения φ1 и φ2 полярного угла φ, φ1 ≤ φ ≤ φ2-Числа φ1 и φ2 являются пределами внешнего интегрирования.
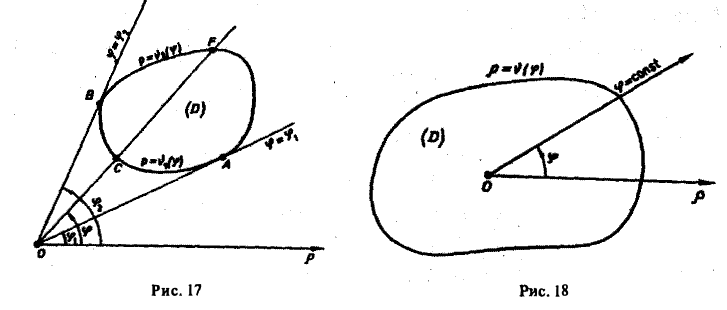
Луч φ = φ1 проходит через точку А контура области D, а луч φ = φ2 — через точку В. Точки А и В разбивают контур области D на две части: АС В и AFB. Пусть р = v1( φ ) и р = v2( φ ) — их полярные уравнения, причем v1( φ ) и v2( φ ) — однозначные непрерывные функции φ, удовлетворяющие условию
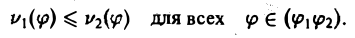
Функции v1( φ ) и v2( φ ) являются пределами внутреннего интегрирования. Переходя к повторным интегралам, получаем следующую формулу
(15)
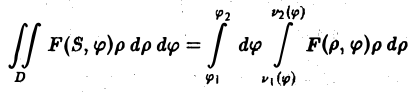
В частности, для площади S области D при F(p, φ) = 1 получаем
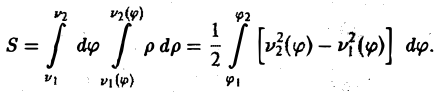
Пусть теперь полюс О расположен внутри области D. Предположим, что область D является звездной относительно полюса, т. е. любой луч φ = const пересекает границу области только в одной точке или по целoму отрезку (рис. 18). Пусть р = v( φ ) — уравнение границы области в полярных координатах. Тогда
(16)
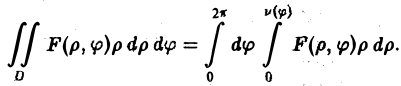
Пример:
Вычислить интеграл
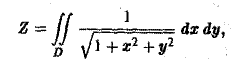
где область
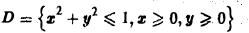
— четверть единичного круга, расположенная в первом квадранте.
Перейдем к полярным координатам
х ~ = р cos φ, у = р sin φ.
Тогда областью интегрирования будет прямоугольник
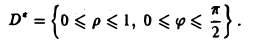
Преобразованный интеграл I легко вычисляется:
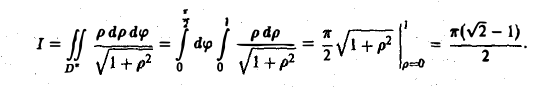
Замечание:
Если якобиан отличен от нуля в области D, то отображение в некоторой окрестности каждой точки этой области является взаимнооднозначным. При этом может, однако, случиться, что отображение всей области не будет взаимнооднозначным. Рассмотрим отображение, определяемое функциями
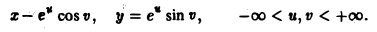
Якобиан этих функций равен
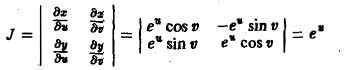
и, следовательно, везде отличен от нуля. Несмотря на это, для u = 0, v = 0 и дня и = 0, v = 2π мы получим х = 1, у = 0, так что это отображение не является взаимнооднозначным.
С другой стороны, если якобиан отображения обращается в нуль в какой-нибудь точке, то, тем не менее, отображение в окрестности этой точки может оказаться взаимно однозначным. Например, для отображения, определяемого функциями
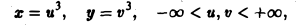
якобиан
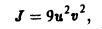
равен нулю и при и = 0, и при v = 0, но отображение является взаимнооднозначным. Обратное отображение определяется функциями
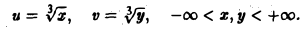
Площадь поверхности
Интеграл по площади поверхности. Вычисление площади поверхности
Пусть задана поверхность π, однозначно проектирующаяся на область D плоскости хОу. Это означает, что данная поверхность задается уравнением
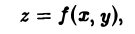
где Р(х, у) ∈ D.
Будем считать поверхность гладкой; это означает, что в области D функция f(x, у) непрерывна и имеет непрерывные частные производные f’x(x, у) и f’y(x, у). Разобьем область D на квадрируемые подобласти
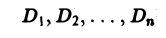
без общих внутренних точек, площади которых обозначим соответственно через
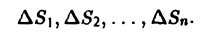
Пусть d — наибольший из диаметров частичных областей Dk (k = 1,2,…, п). В каждой подобласти Dk выберем произвольную точку Pk( ξk, ηk)- На поверхности π точке Рk будет соответствовать точка Mk( ξk, ηk, ζk), где ζk= f( ξk, ηk) (рис. 19). Проведем в точке Мk касательную плоскость к поверхности π. Ее уравнение имеет следующий вид __(1)
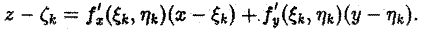
Построим на границе частичной области dk, как на направляющей, цилиндрическую поверхность с образующими, параллельными оси Oz. Эта цилиндрическая поверхность вырежет из касательной плоскости, проведенной через точку Мk, область πk площади ∆qк. Площадка Пk проектируется на элементарную область Dk плоскости хОу взаимнооднозначно.
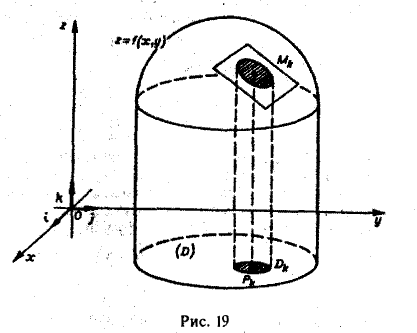
Рассмотрим сумму
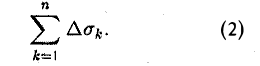
Определение:
Если при d→0 сумма (2) имеет конечный предел S,
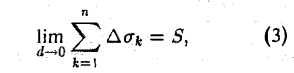
то число S называется площадью поверхности π.
Таким образом, мы заменяем данную поверхность «чешуйчатой», затем подсчитываем плошадь этой «чешуйчатой» поверхности и переходим к пределу при стремлении диаметра «чешуек» к нулю (диаметры чешуек стремятся к нулю при d —> 0).
Перейдем теперь к выводу формулы, по которой вычисляют площадь поверхности. Известно, что площадь проекции плоской фигуры на какую-нибудь плоскость равна произведению площади проектируемой фигуры на косинус острого угла между плоскостью проекции и плоскостью, в которой лежит проектируемая фигура.
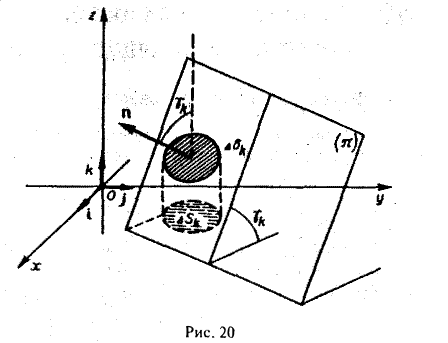
Обозначим через γk угол между касательной плоскостью к поверхности π в точке Мk и плоскостью хОу (рис. 20). Тогда
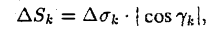
откуда
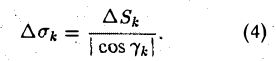
Но угол γk есть в то же время угол между осью Oz и нормалью касательной плоскости к поверхности (1). Обозначим вектор нормали к касательной плоскости к поверхности в точке Мk через
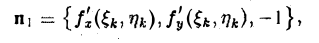
а через п2 = {0, 0,1} — единичный вектор оси Оz. Тогда получим
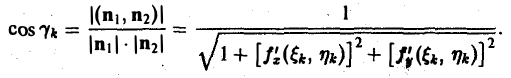
Таким образом,
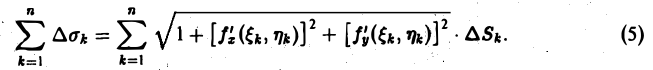
По условию функции f’z(x,y) и f’у(х, у) непрерывны в области D. Следовательно, функция
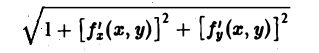
непрерывна, а, значит, и интегрируема в области D. Поэтому при d → 0 сумма (5) имеет конечный предел,
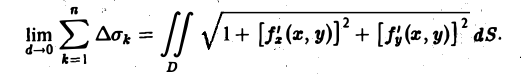
Учитывая равенство (3), определяющее площадь S поверхности заключаем, что
(6)
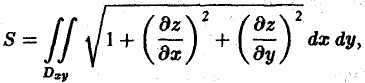
где Dxy — проекция поверхности я- на плоскость хОу. Выражение
(7)
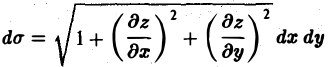
называется элементом площади поверхности.
Если спроектировать участок поверхности π на плоскость хОу, то получим
(8)
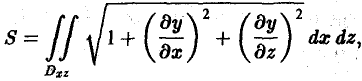
где Dyz — проекция участка поверхности на плоскость хОу. Соответственно, при проектировании на плоскость yOz имеем
(9)
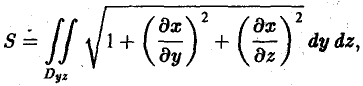
где Dyz — проекция участка поверхности на плоскость yOz.
Пример:
Найти площадь сферы радиуса R с центром в начале координат
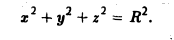
Уравнение верхней полусферы —
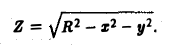
Поэтому
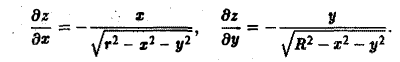
Следовательно,
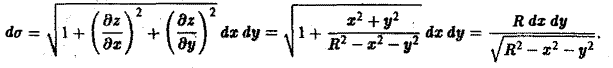
Область интегрирования
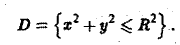
Искомая площадь S
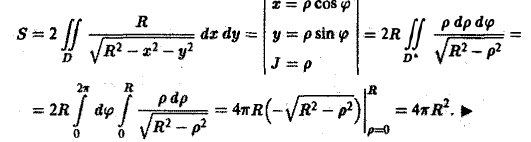
Отметим следующие полезные формулы:
1) для элемента площади цилиндрической поверхности радиуса R
(10)
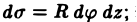
2) для элемента площади сферической поверхности радиуса R
(11)
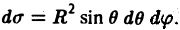
Используя формулу (11) для элемента площади сферической поверхности получим площадь сферы:
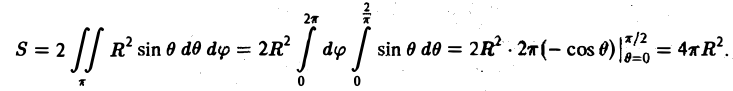
Интеграл по площади поверхности (интеграл по поверхности 1-го рода)
Пусть на гладкой поверхности π задана непрерывная функция f(М). Разобьем поверхность π на части
с площадями
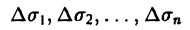
соответственно, выделим на каждой из частичных поверхностей по произвольной точке Mi, Мг,… , Мп и составим сумму
которую будем называть интегральной суммой для функции f{М) по площади поверхности π.
Определение:
Если при стремлении к нулю наибольшего из диаметров частичных поверхностей πk интегральная сумма (12) имеет конечный предел, не зависящий ни от способа разбиения поверхности т на части, ни от выбора точек Mk, то этот предел называется интегралом от функции f(M) по площади поверхности π (интегралом по поверхности 1-го рода) и обозначается символом
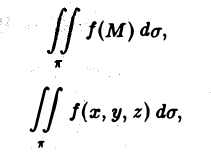
где dσ — элемент площади поверхности.
Общие свойства двойных интегралов легко переносятся на интегралы по площади поверхности. В частности, если поверхность π разбита на неперекрывающиеся части π1, π2,…, πn, то
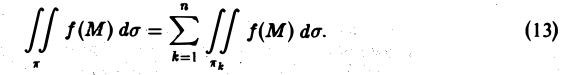
Теорема:
Пусть -к — гладкая поверхность, заданная уравнением z = φ(x, у), где (х,у) ∈ D, причем функция φ(х, у) имеет непрерывные частные производные в некоторой области D1, D ⊂ D1. Пусть, далее, f(x, у, z) — непрерывная функция, определенная на поверхности π. Тогда справедливо равенство
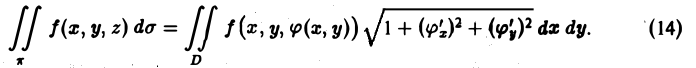
Интеграл
где μ(Р) ≥ 0 на π, можно истолковать как массу π оболочки, представляющей собой поверхностью, на которой масса распределена с поверхностной плотностью μ = μ(Р).
Пример:
Найти массу параболической оболочки
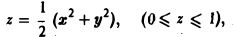
плотность которой меняется по закону μ = z (рис. 21).
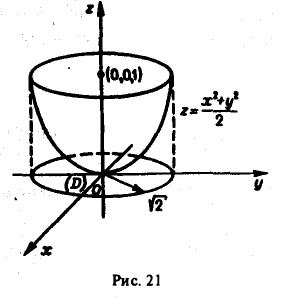
Имеем Рис.21
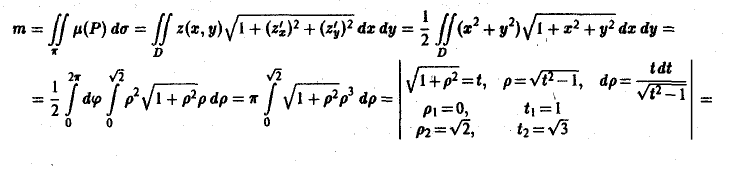
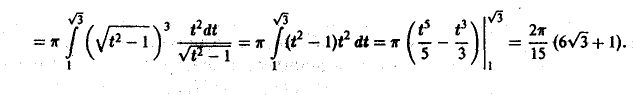
Тройной интеграл
Задача, приводящая к тройному интегралу
Пусть дано материальное тело, представляющее собой пространственную область Ω, заполненную массой. Требуется найти массу то этого тела при условии, что в каждой точке Р ∈ Ω известна плотность
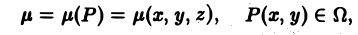
распределения масс.
Разобьем область Ω на неперекрывающиеся кубируемые (т. е. имеющие объем) части
с объемами
соответственно. В каждой из частичных областей Ωk выберем произвольную точку Рk. Примем приближенно, что в пределах частичной области Ωk плотность постоянна и равна μ(Рk)- Тогда масса ∆тk этой части тела выразится приближенным равенством
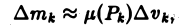
а масса всего тела будет приближенно равна
Пусть d — наибольший из диаметров частичных областей Ωk(k = 1,2,…, п). Если при d —> О сумма (1) имеет конечный предел, не зависящий ни от способа разбиения области Ω на частичные подобласти, ни от выбора точек Рk ∈ Ωk, то этот предел принимается за массу т заданного тела,
Пусть в замкнутой кубируемой области Ω определена ограниченная функция
f(Р), Р ∈ Ω.
Разобьем Ω на п непересекающихся кубируемых частей
а их объемы обозначим через
соответственно. В каждой частичной подобласти Ωk произвольным образом выбираем точку Рk(хk, yk, zk) и составляем интегральную сумму
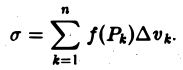
Пусть d — наибольший из диаметров частичных областей Ωk(k = 1, 2,…, п).
Определение:
Если при d → 0 интегральные суммы а имеют предел, не зависящий ни от способа разбиения области Ω на частичные подобласти Ωk, ни от выбора точек Рk ∈ Ωk, то этот предел называется тройным интегралом от функции f(x, у, z) по области Ω и обозначается символом
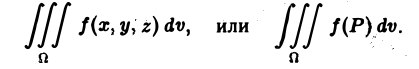
При этом функция f(х, у, z) называется интегрируемой в области Ω.
Таким образом, по определению имеем
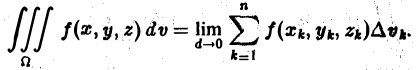
Возвращаясь к задаче о вычислении массы тела, замечаем, что предел (2) есть тройной интеграл от функции μ(Р) по области Ω. Значит,
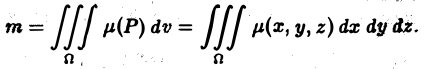
Здесь dx dy dz — элемент объема dv в прямоугольных координатах.
Теорема 6. Если функция f(x, у, z) непрерывна в замкнутой кубируемой области Ω, то она интегрируема в этой области.
Свойства тройных интегралов
Свойства тройных интегралов аналогичны свойствам двойных интегралов. Перечислим основные из них.
Пусть функции f(Р) и φ(Р) интегрируемы в кубируемой области Ω.
1, Линейность.
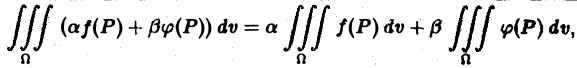
где а и β — произвольные вещественные постоянные.
2. f(Р) ≤ φ(P) всюду в области Ω, то
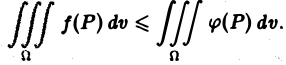
3. Если f(P) ≡ 1 в области Ω, то
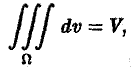
где V — объем области Ω.
4. Если функция f(P) непрерывна в замкнутой кубируемой области Ω и М и т — ее наибольшее и наименьшее значения в Ω, то
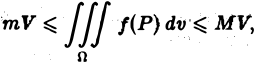
где V — объем области Ω.
5. Аддиктивность. Если область Ω разбита на кубируемые области Ω1 и Ω2 без общих внутренних точек и f(Р) интегрируема в области Ω,то f(P) интегрируема на каждой из областей Ω1 и Ω2, причем
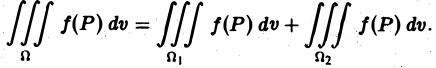
Теорема о среднем значении
Теоремa:
Если функция f(P) непрерывна в замкнутой кубируемой области Ω, то найдется точка Рс ∈ Ω , такая, что будет справедлива формула
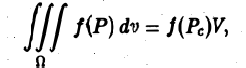
где V — объем области Ω (напомним, что область — связное множество).
Вычисление тройного интеграла в декартовых координатах
Как и при вычислении двойных интегралов, дело сводится к вычислению повторных интегралов. Предположим, что функция f(х, у, z) непрерывна в некоторой области Ω.
1-й случай. Область Ω представляет собой прямоугольный параллелепипед
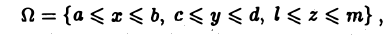
проектирующийся на плоскость yOz в прямоугольник R;
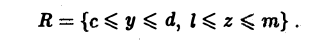
Тогда получим
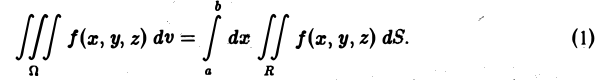
Заменяя двойной интеграл через повторный, окончательно получим
(2)
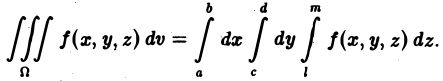
Таким образом, в случае, когда область Ω — прямоугольный параллелепипед, мы свели вычисление тройного интеграла к последовательному вычислению трех обыкновенных интегралов.
Формулу (2) можно переписать в виде
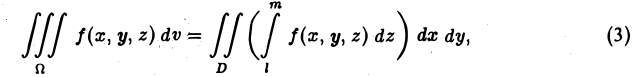
где прямоугольник
есть ортогональная проекция параллелепипеда Ω на плоскость хОу.
2-й случай. Рассмотрим теперь область Ω такую, что ограничивающая ее поверхность S пересекается любой прямой, параллельной оси Oz, не более чем в двух точках или по целому отрезку (рис.22).
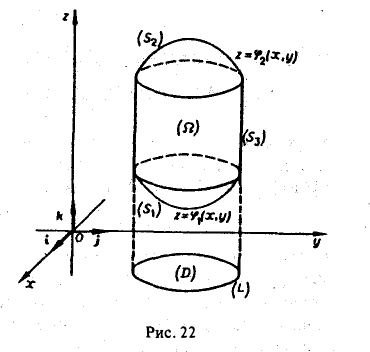
Пусть z = φ1(x,y) уравнение поверхности S1, ограничивающей область Ω снизу, а поверхность S2, ограничивающая область Ω сверху, имеет уравнение z = φ2(x,y).
Пусть обе поверхности S1 и S2 проектируются на одну и ту же область плоскости хОу. Обозначим ее через D, а ограничивающую ее кривую через L. Остальная часть границы S тела Ω лежит на цилиндрической поверхности с образующими, параллельными оси Oz, и с кривой L в роли направляющей. Тогда по аналогии с формулой (3) получим
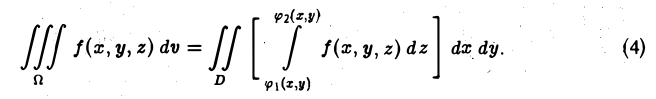
Если область D плоскости хОу представляет собой криволинейную трапецию, ограниченную двумя кривыми у = ψ1(х) И y = ψ2(х) (а ≤ х ≤ b), то двойной интеграл в формуле (4) можно свести к повторному, и мы получим окончательно
(4)
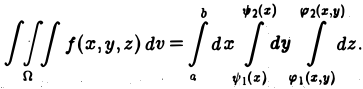
Эта формула является обобщением формулы (2).
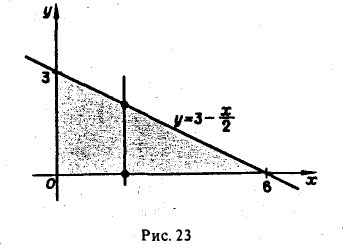
Пример:
Вычислить объем тетраэдра, ограниченного плоскостями
x = 0, у = 0, z = 0 и х + 2у + z- 6 = 0.
Проекцией тетраэдра на плоскость хОу служит треугольник, образованный прямыми
x = 0, у = 0 и х + 2у = 6,
так что х изменяется от 0 до 6, а при фиксированном х (0 ≤ х ≤ 6) у изменяется от 0 до 3 — π/2 (рис. 23). Если же фиксированы и х, и у, то точка может перемещаться по вертикали от плоскости z=0 до плоскости x + 2y + z- 6 = 0, т. е. г меняется в пределах от 0 до 6 — х — 2у. По формуле (5) при f{x, у, z) = 1 получаем
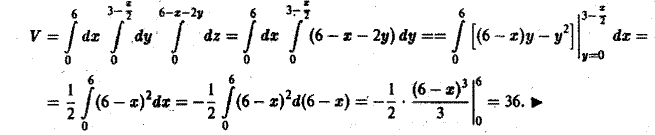
Вычисление тройного интеграла в цилиндрических и сферических координатах
Вопрос о замене переменных в тройном интеграле решается таким же путем, как и в случае двойного интеграла. Пусть функция f(x,y, z) непрерывна в замкнутой кубируемой области Ω, а функции
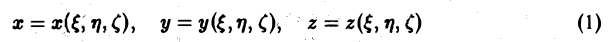
непрерывны вместе со своими частными производными первого порядка в замкнутой кубируемой области Ω*. Предположим, что функции (1) устанавливают взаимнооднозначное соответствие между всеми точками ( ξ, η, ζ) области Ω*, с одной стороны, и всеми точками (х, у, z) области Ω — с другой. Тогда справедлива формула замены переменных в тройном интеграле —
(2)
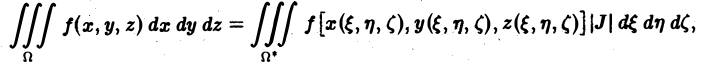
где
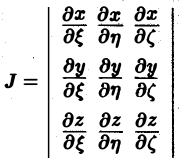
— якобиан системы функций (1).
На практике при вычислении тройных интеграловчасто пользуются заменой прямоугольных координат цилиндрическими и сферическими координатами.
Тройной интеграл в цилиндрических координатах
В цилиндрической системе координат положение точки Р в пространстве определяется тремя числами р, φ, z, где р и φ — полярные координаты проекции Р» точки Р на плоскость хОу, a z — аппликата точки Р (рис. 24). Числа р, φ, z называются цилиндрическими координатами точки Р.
Ясно, что
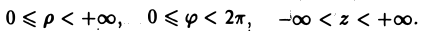
В системе цилиндрических координат координатные поверхности
р = const, φ = const, z = const
соответственно описывают: круговой цилиндр, ось которого совпадает с осью Oz, полуплоскость, примыкающую к оси Oz, и плоскость, параллельную плоскости хОу.
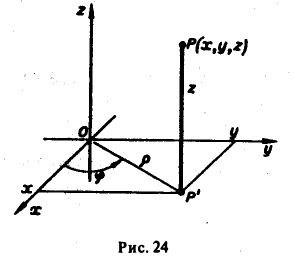
Цилиндрические координаты связаны с декартовыми следующими формулами
x = p cost φ, y = p sin φ, Z = Z (3)
(см. рис. 24). Для системы (3), отображающей область Ω на область Ω*, имеем
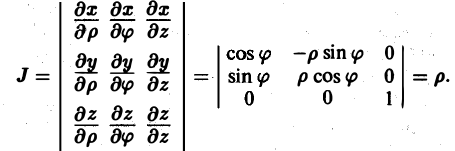
Так как p ≥ 0, то
|J|= p
и формула (2) перехода от тройного интеграла в прямоугольных координатах к интегралу в цилиндрических координатах принимает вид
(4)
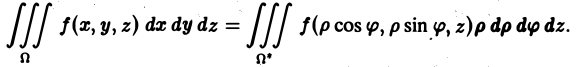
Выражение
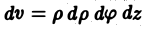
называется элементом объема в цилиндрических координатах.
Это выражение для элемента объема может быть получено и из геометрических соображений. Разобьем область Ω на элементарные подобласти координатными поверхностями
р = const, φ = const, z = const
и вычислим объемы полученных криволинейных призм (рис. 25).
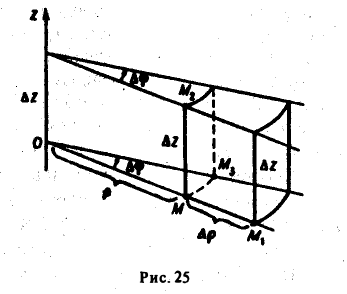
Видно, что
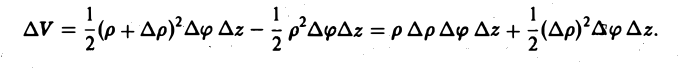
Отбрасывая бесконечно малую величину более высокого порядка, получаем
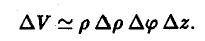
Это позволяет принять за элемент объема в цилиндрических координатах следующую величину
dv = p dp dφ dz.
Пример:
Найти объем тела, ограниченного поверхностями
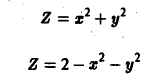
(рис.26).
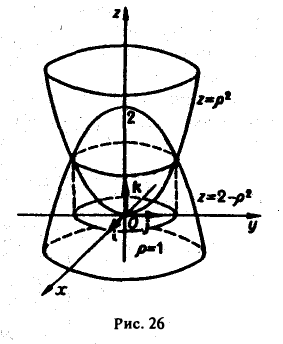
В цилиндрических координатах заданные поверхности будут иметь уравнения
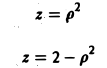
(см. формулы (3)). Эти поверхности пересекаются по линии г, которая описывается системой уравнений
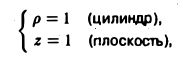
а ее проекция на плоскость хОу системой
р = 1, z = 0.
Таким образом.
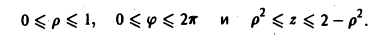
Искомый объем вычисляется по формуле (4), в которой f ≡ 1.
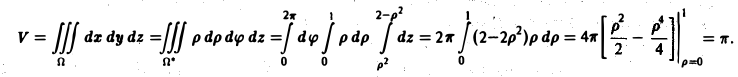
Тройной интеграл в сферических координатах
В сферической системе координат положение точки Р(х, у, z) в пространстве определяется тремя числами r, φ, θ, где r — расстояние от начала координат до точки Р, φ — угол между осью Ох и проекцией радиуса-вектора ОР точки Р на плоскость хОу, а θ — угол между осью Oz и радиусом-вектором ОР точки Р, отсчитываемый от оси Oz (рис. 27).
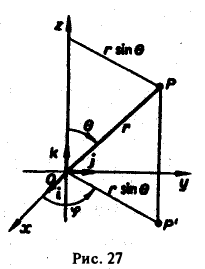
Ясно, что 0 ≤ r < + ∞, 0 ≤ φ < 2 π, 0 ≤ θ ≤ π. Координатные поверхности в этой системе координат:
r = const — сферы с центром в начале координат; φ = const полуплоскости, исходящие из оси Oz; θ = const — круговые конусы с осью Oz.
Из рисунка видно, что сферические и декартовы координаты связаны следующими соотношениями
(5)
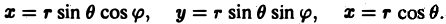
Вычислим якобиан функций (5). Имеем
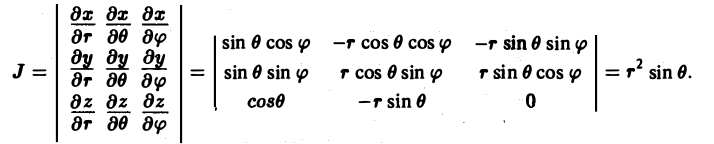
Следовательно,
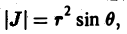
и формула (2) принимает вид
(6)
Элемент объема в сферических координатах —
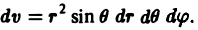
Выражение для элемента объема можно получить и из геометрических соображений. Рассмотрим элементарную область в пространстве, ограниченную сферами радиусов г и г + dr, конусами в и в + d$ и полуплоскостями <р и <р + d(p. Приближенно эту область можно считать прямоугольным параллелепипедом с измерениями DB = dr, DC = г sin 0 dp, AD = rd6 (рис.28). Тогда
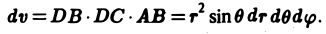
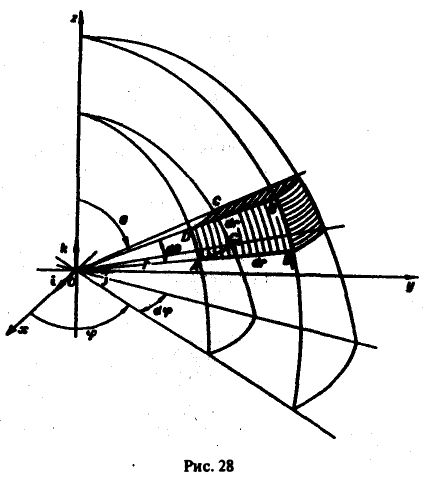
Пример:
Найти объем выпуклого тела П, вырезаемого из конуса
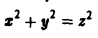
концентрическими сферами
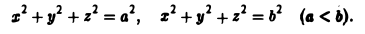
Переходим к сферической системе координат
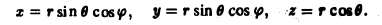
Из первых двух уравнений видно, что а ^ г ^ 6. Из третьего уравнения находим пределы изменения угла в:
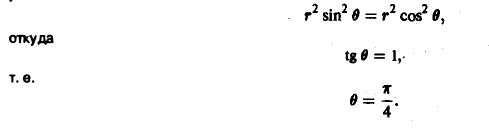
Тем самым, 0 ≤ θ ≤ π/4. Полагая в формуле (6) f(x, у, z) ≡ 1, получим
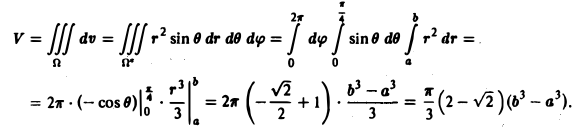
Приложения двойных и тройных интегралов
Масса плоской фигуры
Пусть задана плоская ограниченная фигура D, по которой непрерывным образом распределена масса с поверхностной плотностью μ(Р) = μ(х, у) ≥ 0, где μ(х, у) — функция, непрерывная в D. Разобьем фигуру D на п частей
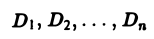
без общих внутренних точек, площади которых соответственно равны
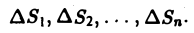
В каждой части (к = 1,2,…, п) произвольно выберем точку Рk(хk, уk) и вычислим в ней плотность μ(xk, yk). В силу непрерывности μ(х, у) можно считать, что масса mk части Dk фигуры D приближенно равна μ(хk, yk) ∆Sk, a масса всей фигуры — сумме
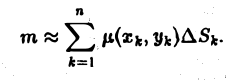
Последняя является интегральной суммой для непрерывной функции μ(x, у) в области D. Переходя к пределу при d → 0 (здесь d — наибольший из диаметров частичных областей Dk(k = 1,…, п)), получим точное равенство
(1)
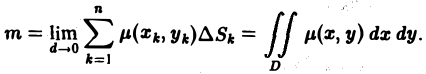
Если масса распределена равномерно по всей фигуре, μ = const, то формула (1) принимает вид
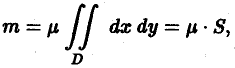
где S — площадь фигуры D.
Пример:
Найти массу кольца, ограниченного двумя концентрическими окружностями радиусов r и R, где r < R, если плотность кольца в каждой точке обратно пропорциональна расстоянию от этой точки до центра окружности и равна 1 на окружности внутреннего круга. Фигура D задается условиями
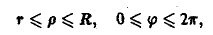
а плотность
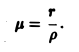
Значит, масса кольца
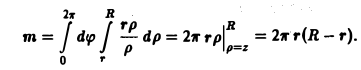
Статические моменты плоской фигуры относительно осей координат. Координаты центра тяжести
Статическим моментом Мх материальной точки массы m относительно оси Ох называется произведение ту, где у — ордината материальной точки, т. е.
Мх = ту.
Здесь у может быть как положительным, так и отрицательным числом.
Разбивая фигуру D на части D1,…, Dn, выбирая в каждой части Dk произвольно точку Pk(xk, yk) и считая, что масса этой k-й части приближенно равна μ(хk, yk) ∆Sk и сосредоточена в точке Pk(xk,yk), запишем приближенно величину статического момента фигуры D относительно оси Ох. Имеем
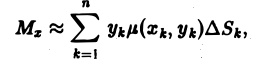
где ∆Sk — площадь части Dk, а μ(х, у) — поверхностная плотность. Переходя к пределу при d —» 0, получаем
(3)
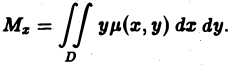
Статический момент фигуры D относительно оси Оу находится по аналогичной формуле
(4)
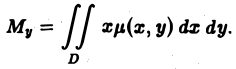
Если известны статические моменты Мх и Му и масса m плоской фигуры, то координаты центра тяжести этой фигуры находятся по следующим формулам
(5)
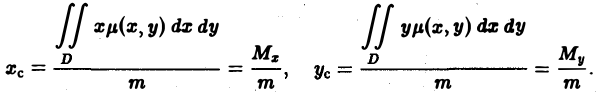
Если μ = const, т = μS, где S — площадь фигуры D, и формулы (5) принимают вид:
(6)
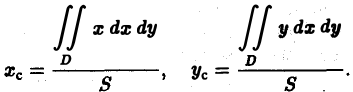
Пример:
Hайти центр тяжести однородной плоской фигуры, ограниченной косинусоидой
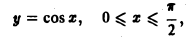
осью Ох и осью Оу.
Так как фигура — однородная, то координаты центра тяжести будем искать по формулам (б). Найдем сначала площадь 5 заданной фигуры. Имеем
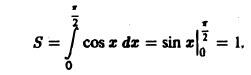
Затем найдем статические моменты Mz и Му
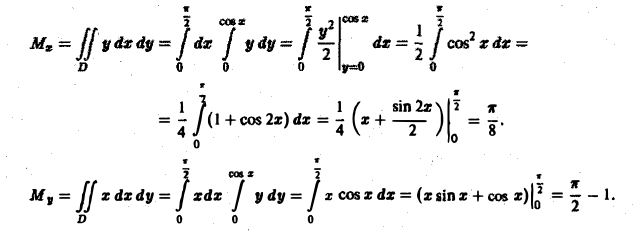
Теперь no формулам (6) получаем
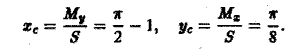
Моменты инерции плоской фигуры относительно осей координат
Рассуждая аналогично изложенному выше, легко установить, что элементарные моменты инерции относительно осей Ох и Оу будут соответстве нно равны
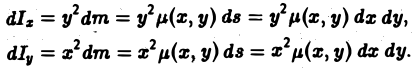
Интегрируя по плоской фигуре D, получим формулы для самих моментов инерции (7), (8)
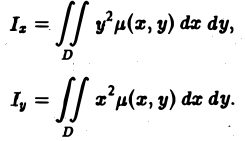
где, как и ранее, μ(x, у) — поверхностная плотность распределения масс.
Вычисление массы тела
Рассматривая задачу, приводящую к тройному интегралу, мы показали, что если известна плотность распределения масс ц(х, у, z) в каждой точке некоторого тела Ω, то масса этого тела вычисляется по формуле
(9)
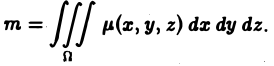
Мы предполагаем, что функция μ(х, у, z) непрерывна в области Ω.
Пример:
Вычислить массу m тела, ограниченного полусферами
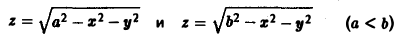
и плоскостью хОу, если плотность в каждой точке пропорциональна расстоянию от этой точм до начала координат.
По условию задачи плотность μ в точке (x,y,z) выражается формулой
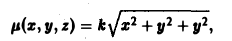
где к > 0 — коэффициент пропорциональности. Тогда
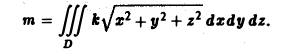
Переходя к сферическим координатам, получим, что
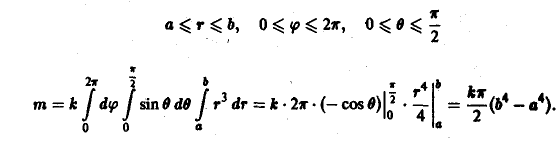
Статические моменты тела относительно координатных плоскостей. Центр тяжести
Напомним, что задача о вычислении статических моментов и центра тяжести плоской фигуры решалась при помощи двойных интегралов (см. формулы (3), (4) и (5)). Задачи о вычислении статических моментов тела Ω относительно координатных плоскостей и отыскания центра тяжести тела Ω решаются аналогичным способом при помощи тройных интегралов. Например, элементарный статический момент относительно плоскости хОу равен
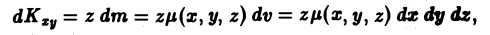
где μ(x, у, z) — плотность. Отсюда статический момент
(10)
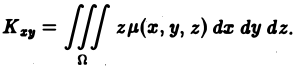
Аналогично выписываются статические моменты относительно плоскостей хОу и Y
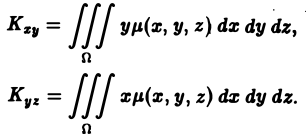
Вычислив массу m тела Ω и его статические моменты, легко найти координаты центра тяжести тела: (11)
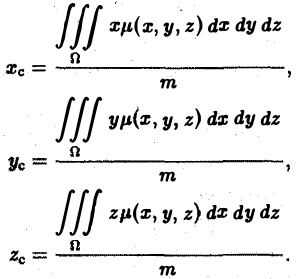
Если тело однородно, то плотность μ = const и формулы (11) упрощаются — постоянный множитель μ в числителе можно вынести за знак интеграла и сократить на него числитель и знаменатель (ибо т = μy). Тогда получим (12)
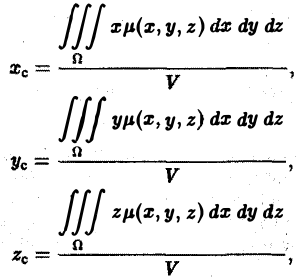
где V — объем тела Ω.
Пример:
Найти координаты центра тяжести однородного полушара радиуса R.
Считаем, что центр шара находится в начале координат, а рассматриваемая фигура — полушар — расположена над плоскостью хОу. Тогда в силу симметрии имеем
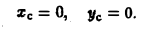
Объем полушара равен
Найдем статический момент относительно плоскости хОу :
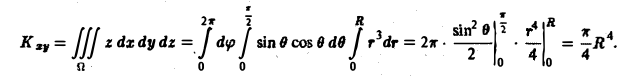
Значит,
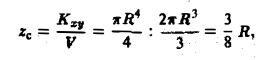
и 
— центр тяжести.
Понятие о несобственном кратном интеграле по неограниченной области
При необходимости интегрирования функций нескольких переменных по неограниченной области D поступают так. Выбирают последовательность ограниченных областей интегрирования
монотонно исчерпывающих область D, т. е.
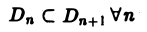
и
Dn —> D при п —> ∞.
Например, если область интегрирования {Dn} совпадает со всей плоскостью хОу, то за последовательность {Dn} можно принять совокупность концентрических кругов
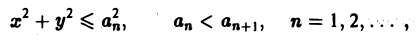
где
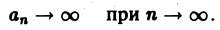
Определение:
Несобственным интегралом от функции f(х, у) по неограниченной области интегрирования D называется предел последовательности интегралов
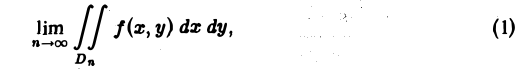
не зависящий от выбора последовательности Db.
Итак, по определению
(2)
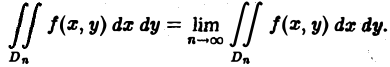
Если предел (1) существует и конечен, то несобственный интеграл по неограниченной области называется сходящимся, в противном случае — расходящимся.
Пример:
Вычислить интеграл
где область интегрирования
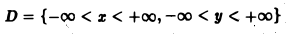
— вся плоскость.
В качестве областей интегрирования {Dn} выберем круги
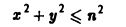
радиуса п (n = 1,2,… ). Переходя к полярным координатам, получим
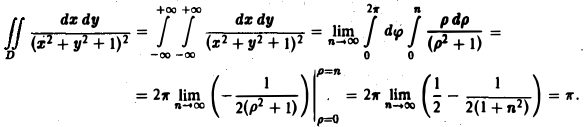
Итак, интеграл (3) сходится и равен π.
Для интеграла по неограниченной области D справедлив следующий Признак сравнения. Если 0 ≤ f(x, у) ≤ g(х, у) ∀(x, у) ∈ D,u интеграл
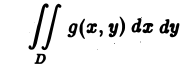
сходится, то сходится и интеграл
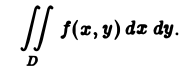
Если же интеграл
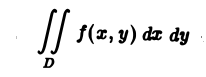
расходится, то расходится и интеграл
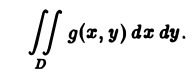
Интегралы, сходящиеся на всей плоскости, можно вычислять с помощью повторного интегрирования:
(4)
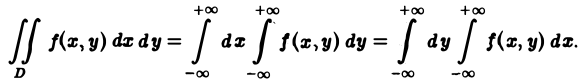
Пример:
Вычислить интеграл
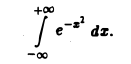
Так как
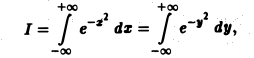
то, согласно соотношению (4),
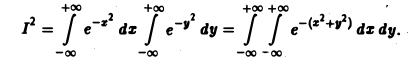
Переходя в двойном интеграле к полярным координатам, получим новую область интегрирования
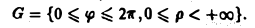
Следовательно,
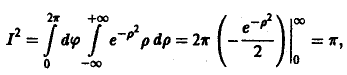
откуда
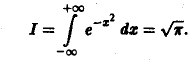
Несобственные интегралы от функции трех, четырех и большего числа переменных по неограниченным областям определяются аналогично.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Integral as area between two curves.
Double integral as volume under a surface z = 10 − (x2 − y2/8). The rectangular region at the bottom of the body is the domain of integration, while the surface is the graph of the two-variable function to be integrated.
In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in 
Introduction[edit]
Just as the definite integral of a positive function of one variable represents the area of the region between the graph of the function and the x-axis, the double integral of a positive function of two variables represents the volume of the region between the surface defined by the function (on the three-dimensional Cartesian plane where z = f(x, y)) and the plane which contains its domain.[1] If there are more variables, a multiple integral will yield hypervolumes of multidimensional functions.
Multiple integration of a function in n variables: f(x1, x2, …, xn) over a domain D is most commonly represented by nested integral signs in the reverse order of execution (the leftmost integral sign is computed last), followed by the function and integrand arguments in proper order (the integral with respect to the rightmost argument is computed last). The domain of integration is either represented symbolically for every argument over each integral sign, or is abbreviated by a variable at the rightmost integral sign:[2]
Since the concept of an antiderivative is only defined for functions of a single real variable, the usual definition of the indefinite integral does not immediately extend to the multiple integral.
Mathematical definition[edit]
For n > 1, consider a so-called “half-open” n-dimensional hyperrectangular domain T, defined as:
Partition each interval [aj, bj) into a finite family Ij of non-overlapping subintervals ijα, with each subinterval closed at the left end, and open at the right end.
Then the finite family of subrectangles C given by
is a partition of T; that is, the subrectangles Ck are non-overlapping and their union is T.
Let f : T → R be a function defined on T. Consider a partition C of T as defined above, such that C is a family of m subrectangles Cm and
We can approximate the total (n + 1)-dimensional volume bounded below by the n-dimensional hyperrectangle T and above by the n-dimensional graph of f with the following Riemann sum:
where Pk is a point in Ck and m(Ck) is the product of the lengths of the intervals whose Cartesian product is Ck, also known as the measure of Ck.
The diameter of a subrectangle Ck is the largest of the lengths of the intervals whose Cartesian product is Ck. The diameter of a given partition of T is defined as the largest of the diameters of the subrectangles in the partition. Intuitively, as the diameter of the partition C is restricted smaller and smaller, the number of subrectangles m gets larger, and the measure m(Ck) of each subrectangle grows smaller. The function f is said to be Riemann integrable if the limit
exists, where the limit is taken over all possible partitions of T of diameter at most δ.[3]
If f is Riemann integrable, S is called the Riemann integral of f over T and is denoted
Frequently this notation is abbreviated as
where x represents the n-tuple (x1, …, xn) and dnx is the n-dimensional volume differential.
The Riemann integral of a function defined over an arbitrary bounded n-dimensional set can be defined by extending that function to a function defined over a half-open rectangle whose values are zero outside the domain of the original function. Then the integral of the original function over the original domain is defined to be the integral of the extended function over its rectangular domain, if it exists.
In what follows the Riemann integral in n dimensions will be called the multiple integral.
Properties[edit]
Multiple integrals have many properties common to those of integrals of functions of one variable (linearity, commutativity, monotonicity, and so on). One important property of multiple integrals is that the value of an integral is independent of the order of integrands under certain conditions. This property is popularly known as Fubini’s theorem.[4]
Particular cases[edit]
In the case of 
is the double integral of f on T, and if 
is the triple integral of f on T.
Notice that, by convention, the double integral has two integral signs, and the triple integral has three; this is a notational convention which is convenient when computing a multiple integral as an iterated integral, as shown later in this article.
Methods of integration[edit]
The resolution of problems with multiple integrals consists, in most cases, of finding a way to reduce the multiple integral to an iterated integral, a series of integrals of one variable, each being directly solvable. For continuous functions, this is justified by Fubini’s theorem. Sometimes, it is possible to obtain the result of the integration by direct examination without any calculations.
The following are some simple methods of integration:[1]
Integrating constant functions[edit]
When the integrand is a constant function c, the integral is equal to the product of c and the measure of the domain of integration. If c = 1 and the domain is a subregion of R2, the integral gives the area of the region, while if the domain is a subregion of R3, the integral gives the volume of the region.
Example. Let f(x, y) = 2 and
in which case
since by definition we have:
Use of symmetry[edit]
When the domain of integration is symmetric about the origin with respect to at least one of the variables of integration and the integrand is odd with respect to this variable, the integral is equal to zero, as the integrals over the two halves of the domain have the same absolute value but opposite signs. When the integrand is even with respect to this variable, the integral is equal to twice the integral over one half of the domain, as the integrals over the two halves of the domain are equal.
Example 1. Consider the function f(x,y) = 2 sin(x) − 3y3 + 5 integrated over the domain
a disc with radius 1 centered at the origin with the boundary included.
Using the linearity property, the integral can be decomposed into three pieces:
The function 2 sin(x) is an odd function in the variable x and the disc T is symmetric with respect to the y-axis, so the value of the first integral is 0. Similarly, the function 3y3 is an odd function of y, and T is symmetric with respect to the x-axis, and so the only contribution to the final result is that of the third integral. Therefore the original integral is equal to the area of the disk times 5, or 5π.
Example 2. Consider the function f(x, y, z) = x exp(y2 + z2) and as integration region the ball with radius 2 centered at the origin,
The “ball” is symmetric about all three axes, but it is sufficient to integrate with respect to x-axis to show that the integral is 0, because the function is an odd function of that variable.
Normal domains on R2[edit]
This method is applicable to any domain D for which:
- the projection of D onto either the x-axis or the y-axis is bounded by the two values, a and b
- any line perpendicular to this axis that passes between these two values intersects the domain in an interval whose endpoints are given by the graphs of two functions, α and β.
Such a domain will be here called a normal domain. Elsewhere in the literature, normal domains are sometimes called type I or type II domains, depending on which axis the domain is fibred over. In all cases, the function to be integrated must be Riemann integrable on the domain, which is true (for instance) if the function is continuous.
x-axis[edit]
If the domain D is normal with respect to the x-axis, and f : D → R is a continuous function; then α(x) and β(x) (both of which are defined on the interval [a, b]) are the two functions that determine D. Then, by Fubini’s theorem:[5]
y-axis[edit]
If D is normal with respect to the y-axis and f : D → R is a continuous function; then α(y) and β(y) (both of which are defined on the interval [a, b]) are the two functions that determine D. Again, by Fubini’s theorem:
Normal domains on R3[edit]
If T is a domain that is normal with respect to the xy-plane and determined by the functions α(x, y) and β(x, y), then
This definition is the same for the other five normality cases on R3. It can be generalized in a straightforward way to domains in Rn.
Change of variables[edit]
The limits of integration are often not easily interchangeable (without normality or with complex formulae to integrate). One makes a change of variables to rewrite the integral in a more “comfortable” region, which can be described in simpler formulae. To do so, the function must be adapted to the new coordinates.
Example 1a. The function is f(x, y) = (x − 1)2 + √y; if one adopts the substitution u = x − 1, v = y therefore x = u + 1, y = v one obtains the new function f2(u, v) = (u)2 + √v.
- Similarly for the domain because it is delimited by the original variables that were transformed before (x and y in example).
- the differentials dx and dy transform via the absolute value of the determinant of the Jacobian matrix containing the partial derivatives of the transformations regarding the new variable (consider, as an example, the differential transformation in polar coordinates).
There exist three main “kinds” of changes of variable (one in R2, two in R3); however, more general substitutions can be made using the same principle.
Polar coordinates[edit]
Transformation from cartesian to polar coordinates.
In R2 if the domain has a circular symmetry and the function has some particular characteristics one can apply the transformation to polar coordinates (see the example in the picture) which means that the generic points P(x, y) in Cartesian coordinates switch to their respective points in polar coordinates. That allows one to change the shape of the domain and simplify the operations.
The fundamental relation to make the transformation is the following:
Example 2a. The function is f(x, y) = x + y and applying the transformation one obtains
Example 2b. The function is f(x, y) = x2 + y2, in this case one has:
using the Pythagorean trigonometric identity (very useful to simplify this operation).
The transformation of the domain is made by defining the radius’ crown length and the amplitude of the described angle to define the ρ, φ intervals starting from x, y.
Example of a domain transformation from cartesian to polar.
Example 2c. The domain is D = {x2 + y2 ≤ 4}, that is a circumference of radius 2; it’s evident that the covered angle is the circle angle, so φ varies from 0 to 2π, while the crown radius varies from 0 to 2 (the crown with the inside radius null is just a circle).
Example 2d. The domain is D = {x2 + y2 ≤ 9, x2 + y2 ≥ 4, y ≥ 0}, that is the circular crown in the positive y half-plane (please see the picture in the example); φ describes a plane angle while ρ varies from 2 to 3. Therefore the transformed domain will be the following rectangle:
The Jacobian determinant of that transformation is the following:
which has been obtained by inserting the partial derivatives of x = ρ cos(φ), y = ρ sin(φ) in the first column respect to ρ and in the second respect to φ, so the dx dy differentials in this transformation become ρ dρ dφ.
Once the function is transformed and the domain evaluated, it is possible to define the formula for the change of variables in polar coordinates:
φ is valid in the [0, 2π] interval while ρ, which is a measure of a length, can only have positive values.
Example 2e. The function is f(x, y) = x and the domain is the same as in Example 2d. From the previous analysis of D we know the intervals of ρ (from 2 to 3) and of φ (from 0 to π). Now we change the function:
finally let’s apply the integration formula:
Once the intervals are known, you have
![{displaystyle int _{0}^{pi }int _{2}^{3}rho ^{2}cos varphi ,drho ,dvarphi =int _{0}^{pi }cos varphi dvarphi left[{frac {rho ^{3}}{3}}right]_{2}^{3}={Big [}sin varphi {Big ]}_{0}^{pi } left(9-{frac {8}{3}}right)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c24af37a02677e30af2c5a9651a5f0b21702db9)
Cylindrical coordinates[edit]
In R3 the integration on domains with a circular base can be made by the passage to cylindrical coordinates; the transformation of the function is made by the following relation:
The domain transformation can be graphically attained, because only the shape of the base varies, while the height follows the shape of the starting region.
Example 3a. The region is D = {x2 + y2 ≤ 9, x2 + y2 ≥ 4, 0 ≤ z ≤ 5} (that is the “tube” whose base is the circular crown of Example 2d and whose height is 5); if the transformation is applied, this region is obtained:
(that is, the parallelepiped whose base is similar to the rectangle in Example 2d and whose height is 5).
Because the z component is unvaried during the transformation, the dx dy dz differentials vary as in the passage to polar coordinates: therefore, they become ρ dρ dφ dz.
Finally, it is possible to apply the final formula to cylindrical coordinates:
This method is convenient in case of cylindrical or conical domains or in regions where it is easy to individuate the z interval and even transform the circular base and the function.
Example 3b. The function is f(x, y, z) = x2 + y2 + z and as integration domain this cylinder: D = {x2 + y2 ≤ 9, −5 ≤ z ≤ 5}. The transformation of D in cylindrical coordinates is the following:
while the function becomes
Finally one can apply the integration formula:
developing the formula you have
![{displaystyle int _{-5}^{5}dzint _{0}^{2pi }dvarphi int _{0}^{3}left(rho ^{3}+rho zright),drho =2pi int _{-5}^{5}left[{frac {rho ^{4}}{4}}+{frac {rho ^{2}z}{2}}right]_{0}^{3},dz=2pi int _{-5}^{5}left({frac {81}{4}}+{frac {9}{2}}zright),dz=cdots =405pi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/561ce31823c00933f3b238c5e77d711c59b22619)
Spherical coordinates[edit]
In R3 some domains have a spherical symmetry, so it’s possible to specify the coordinates of every point of the integration region by two angles and one distance. It’s possible to use therefore the passage to spherical coordinates; the function is transformed by this relation:
Points on the z-axis do not have a precise characterization in spherical coordinates, so θ can vary between 0 and 2π.
The better integration domain for this passage is the sphere.
Example 4a. The domain is D = x2 + y2 + z2 ≤ 16 (sphere with radius 4 and center at the origin); applying the transformation you get the region
The Jacobian determinant of this transformation is the following:
The dx dy dz differentials therefore are transformed to ρ2 sin(φ) dρ dθ dφ.
This yields the final integration formula:
It is better to use this method in case of spherical domains and in case of functions that can be easily simplified by the first fundamental relation of trigonometry extended to R3 (see Example 4b); in other cases it can be better to use cylindrical coordinates (see Example 4c).
The extra ρ2 and sin φ come from the Jacobian.
In the following examples the roles of φ and θ have been reversed.
Example 4b. D is the same region as in Example 4a and f(x, y, z) = x2 + y2 + z2 is the function to integrate. Its transformation is very easy:
while we know the intervals of the transformed region T from D:
We therefore apply the integration formula:
and, developing, we get
![{displaystyle iiint _{T}rho ^{4}sin theta ,drho ,dtheta ,dvarphi =int _{0}^{pi }sin varphi ,dvarphi int _{0}^{4}rho ^{4}drho int _{0}^{2pi }dtheta =2pi int _{0}^{pi }sin varphi left[{frac {rho ^{5}}{5}}right]_{0}^{4},dvarphi =2pi left[{frac {rho ^{5}}{5}}right]_{0}^{4}{Big [}-cos varphi {Big ]}_{0}^{pi }={frac {4096pi }{5}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a516016630752bd88bc15b50f1c56bc3e28e612)
Example 4c. The domain D is the ball with center at the origin and radius 3a,
and f(x, y, z) = x2 + y2 is the function to integrate.
Looking at the domain, it seems convenient to adopt the passage to spherical coordinates, in fact, the intervals of the variables that delimit the new T region are obviously:
However, applying the transformation, we get
Applying the formula for integration we obtain:
which can be solved by turning it into an iterated integral.
.
,
,
.
Collecting all parts,
.
Alternatively, this problem can be solved by using the passage to cylindrical coordinates. The new T intervals are
the z interval has been obtained by dividing the ball into two hemispheres simply by solving the inequality from the formula of D (and then directly transforming x2 + y2 into ρ2). The new function is simply ρ2. Applying the integration formula
Then we get
Thanks to the passage to cylindrical coordinates it was possible to reduce the triple integral to an easier one-variable integral.
![{displaystyle {begin{aligned}int _{0}^{2pi }dvarphi int _{0}^{3a}rho ^{3}drho int _{-{sqrt {9a^{2}-rho ^{2}}}}^{sqrt {9a^{2}-rho ^{2}}},dz&=2pi int _{0}^{3a}2rho ^{3}{sqrt {9a^{2}-rho ^{2}}},drho \&=-2pi int _{9a^{2}}^{0}(9a^{2}-t){sqrt {t}},dt&&t=9a^{2}-rho ^{2}\&=2pi int _{0}^{9a^{2}}left(9a^{2}{sqrt {t}}-t{sqrt {t}}right),dt\&=2pi left(int _{0}^{9a^{2}}9a^{2}{sqrt {t}},dt-int _{0}^{9a^{2}}t{sqrt {t}},dtright)\&=2pi left[9a^{2}{frac {2}{3}}t^{frac {3}{2}}-{frac {2}{5}}t^{frac {5}{2}}right]_{0}^{9a^{2}}\&=2cdot 27pi a^{5}left(6-{frac {18}{5}}right)\&={frac {648pi }{5}}a^{5}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af098069c3b8ff1087445391685cf4cd031b2fda)
See also the differential volume entry in nabla in cylindrical and spherical coordinates.
Examples[edit]
Double integral over a rectangle[edit]
Let us assume that we wish to integrate a multivariable function f over a region A:
From this we formulate the iterated integral
The inner integral is performed first, integrating with respect to x and taking y as a constant, as it is not the variable of integration. The result of this integral, which is a function depending only on y, is then integrated with respect to y.
![{displaystyle {begin{aligned}int _{11}^{14}left(x^{2}+4yright),dx&=left[{frac {1}{3}}x^{3}+4yxright]_{x=11}^{x=14}\&={frac {1}{3}}(14)^{3}+4y(14)-{frac {1}{3}}(11)^{3}-4y(11)\&=471+12yend{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e379a90e5e09f77929215570fd91403ed6369fc)
We then integrate the result with respect to y.
![{displaystyle {begin{aligned}int _{7}^{10}(471+12y) dy&={Big [}471y+6y^{2}{Big ]}_{y=7}^{y=10}\&=471(10)+6(10)^{2}-471(7)-6(7)^{2}\&=1719end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0be5e82a2ea1d74e5c4855cda9e3cc1a983a64c)
In cases where the double integral of the absolute value of the function is finite, the order of integration is interchangeable, that is, integrating with respect to x first and integrating with respect to y first produce the same result. That is Fubini’s theorem. For example, doing the previous calculation with order reversed gives the same result:
![{displaystyle {begin{aligned}int _{11}^{14}int _{7}^{10},left(x^{2}+4yright),dy,dx&=int _{11}^{14}{Big [}x^{2}y+2y^{2}{Big ]}_{y=7}^{y=10},dx\&=int _{11}^{14},(3x^{2}+102),dx\&={Big [}x^{3}+102x{Big ]}_{x=11}^{x=14}\&=1719.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6902d512bb9ffd641e8f845affaa6a7cfdf34b58)
Double integral over a normal domain[edit]
Example: double integral over the normal region D
Consider the region (please see the graphic in the example):
Calculate
This domain is normal with respect to both the x– and y-axes. To apply the formulae it is required to find the functions that determine D and the intervals over which these functions are defined. In this case the two functions are:
while the interval is given by the intersections of the functions with x = 0, so the interval is [a, b] = [0, 1] (normality has been chosen with respect to the x-axis for a better visual understanding).
It is now possible to apply the formula:
![iint _{D}(x+y),dx,dy=int _{0}^{1}dxint _{x^{2}}^{1}(x+y),dy=int _{0}^{1}dx left[xy+{frac {y^{2}}{2}}right]_{x^{2}}^{1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb7167bdf5af04201ecc485005f1a4d2d3a1be0f)
(at first the second integral is calculated considering x as a constant). The remaining operations consist of applying the basic techniques of integration:
![int _{0}^{1}left[xy+{frac {y^{2}}{2}}right]_{x^{2}}^{1},dx=int _{0}^{1}left(x+{frac {1}{2}}-x^{3}-{frac {x^{4}}{2}}right)dx=cdots ={frac {13}{20}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/4744ee01be3a22946754f8b05e22b277ad7cae1c)
If we choose normality with respect to the y-axis we could calculate
and obtain the same value.
Example of domain in R3 that is normal with respect to the xy-plane.
Calculating volume[edit]
Using the methods previously described, it is possible to calculate the volumes of some common solids.
- Cylinder: The volume of a cylinder with height h and circular base of radius R can be calculated by integrating the constant function h over the circular base, using polar coordinates.
![{displaystyle mathrm {Volume} =int _{0}^{2pi }dvarphi ,int _{0}^{R}hrho ,drho =2pi hleft[{frac {rho ^{2}}{2}}right]_{0}^{R}=pi R^{2}h}](https://wikimedia.org/api/rest_v1/media/math/render/svg/175b2407b091e6319ed5f8d9b7b3165d611f2114)
This is in agreement with the formula for the volume of a prism
- Sphere: The volume of a sphere with radius R can be calculated by integrating the constant function 1 over the sphere, using spherical coordinates.
![{displaystyle {begin{aligned}{text{Volume}}&=iiint _{D}f(x,y,z),dx,dy,dz\&=iiint _{D}1,dV\&=iiint _{S}rho ^{2}sin varphi ,drho ,dtheta ,dvarphi \&=int _{0}^{2pi },dtheta int _{0}^{pi }sin varphi ,dvarphi int _{0}^{R}rho ^{2},drho \&=2pi int _{0}^{pi }sin varphi ,dvarphi int _{0}^{R}rho ^{2},drho \&=2pi int _{0}^{pi }sin varphi {frac {R^{3}}{3}},dvarphi \&={frac {2}{3}}pi R^{3}{Big [}-cos varphi {Big ]}_{0}^{pi }={frac {4}{3}}pi R^{3}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be398a13123b1ce86d7c6c2c95b4eca73d8fadf1)
- Tetrahedron (triangular pyramid or 3-simplex): The volume of a tetrahedron with its apex at the origin and edges of length ℓ along the x-, y– and z-axes can be calculated by integrating the constant function 1 over the tetrahedron.
![{displaystyle {begin{aligned}{text{Volume}}&=int _{0}^{ell }dxint _{0}^{ell -x},dyint _{0}^{ell -x-y},dz\&=int _{0}^{ell }dxint _{0}^{ell -x}(ell -x-y),dy\&=int _{0}^{ell }left(l^{2}-2ell x+x^{2}-{frac {(ell -x)^{2}}{2}}right),dx\&=ell ^{3}-ell ell ^{2}+{frac {ell ^{3}}{3}}-left[{frac {ell ^{2}x}{2}}-{frac {ell x^{2}}{2}}+{frac {x^{3}}{6}}right]_{0}^{ell }\&={frac {ell ^{3}}{3}}-{frac {ell ^{3}}{6}}={frac {ell ^{3}}{6}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27d9273e17f4a9be07068ddd2c1e782008c3f0dc)
- This is in agreement with the formula for the volume of a pyramid
Example of an improper domain.
Multiple improper integral[edit]
In case of unbounded domains or functions not bounded near the boundary of the domain, we have to introduce the double improper integral or the triple improper integral.
Multiple integrals and iterated integrals[edit]
Fubini’s theorem states that if[4]
that is, if the integral is absolutely convergent, then the multiple integral will give the same result as either of the two iterated integrals:
In particular this will occur if |f(x, y)| is a bounded function and A and B are bounded sets.
If the integral is not absolutely convergent, care is needed not to confuse the concepts of multiple integral and iterated integral, especially since the same notation is often used for either concept. The notation
means, in some cases, an iterated integral rather than a true double integral. In an iterated integral, the outer integral
is the integral with respect to x of the following function of x:
A double integral, on the other hand, is defined with respect to area in the xy-plane. If the double integral exists, then it is equal to each of the two iterated integrals (either “dy dx” or “dx dy“) and one often computes it by computing either of the iterated integrals. But sometimes the two iterated integrals exist when the double integral does not, and in some such cases the two iterated integrals are different numbers, i.e., one has
This is an instance of rearrangement of a conditionally convergent integral.
On the other hand, some conditions ensure that the two iterated integrals are equal even though the double integral need not exist. By the Fichtenholz–Lichtenstein theorem, if f is bounded on [0, 1] × [0, 1] and both iterated integrals exist, then they are equal. Moreover, existence of the inner integrals ensures existence of the outer integrals.[6][7][8] The double integral need not exist in this case even as Lebesgue integral, according to Sierpiński.[9]
The notation
![int _{[0,1]times [0,1]}f(x,y),dx,dy](https://wikimedia.org/api/rest_v1/media/math/render/svg/0951af4caeac621f11d9b15d72e9b4c6c866d88c)
may be used if one wishes to be emphatic about intending a double integral rather than an iterated integral.
Triple integral[edit]
Triple integral was demonstrated by Fubini’s theorem.[10][11] Drichlet theorem and Liouville ‘s extension theorem on Triple integral.
Some practical applications[edit]
Quite generally, just as in one variable, one can use the multiple integral to find the average of a function over a given set. Given a set D ⊆ Rn and an integrable function f over D, the average value of f over its domain is given by
where m(D) is the measure of D.
Additionally, multiple integrals are used in many applications in physics. The examples below also show some variations in the notation.
In mechanics, the moment of inertia is calculated as the volume integral (triple integral) of the density weighed with the square of the distance from the axis:
The gravitational potential associated with a mass distribution given by a mass measure dm on three-dimensional Euclidean space R3 is[12]
If there is a continuous function ρ(x) representing the density of the distribution at x, so that dm(x) = ρ(x)d3x, where d3x is the Euclidean volume element, then the gravitational potential is
In electromagnetism, Maxwell’s equations can be written using multiple integrals to calculate the total magnetic and electric fields.[13] In the following example, the electric field produced by a distribution of charges given by the volume charge density ρ( r→ ) is obtained by a triple integral of a vector function:
This can also be written as an integral with respect to a signed measure representing the charge distribution.
See also[edit]
- Main analysis theorems that relate multiple integrals:
- Divergence theorem
- Stokes’ theorem
- Green’s theorem
References[edit]
- ^ a b c Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks Cole Cengage Learning. ISBN 978-0-495-01166-8.
- ^ Larson; Edwards (2014). Multivariable Calculus (10th ed.). Cengage Learning. ISBN 978-1-285-08575-3.
- ^ Rudin, Walter (1976). Principles of Mathematical Analysis. Walter Rudin Student Series in Advanced Mathematics (3rd ed.). McGraw–Hill. ISBN 978-0-07-054235-8.
- ^ a b Jones, Frank (2001). Lebesgue Integration on Euclidean Space. Jones and Bartlett. pp. 527–529. ISBN 9780763717087.[ISBN missing]
- ^ Stewart, James (2015-05-07). Calculus, 8th Edition. Cengage Learning. ISBN 978-1285740621.
- ^ Lewin, Jonathan (2003). An Interactive Introduction to Mathematical Analysis. Cambridge. Sect. 16.6. ISBN 978-1107694040.
- ^ Lewin, Jonathan (1987). “Some applications of the bounded convergence theorem for an introductory course in analysis”. The American Mathematical Monthly. AMS. 94 (10): 988–993. doi:10.2307/2322609. JSTOR 2322609.
- ^ Sinclair, George Edward (1974). “A finitely additive generalization of the Fichtenholz–Lichtenstein theorem”. Transactions of the American Mathematical Society. AMS. 193: 359–374. doi:10.2307/1996919. JSTOR 1996919.
- ^ Bogachev, Vladimir I. (2006). Measure Theory. Vol. 1. Springer. Item 3.10.49.[ISBN missing]
- ^ Rai University (2015-03-17). “Btech_II_ engineering mathematics_unit2”.
- ^ “5.4 Triple Integrals – Calculus Volume 3 | OpenStax”. openstax.org. Retrieved 2022-08-25.
- ^ Kibble, Tom W. B.; Berkshire, Frank H. (2004). Classical Mechanics (5th ed.). Imperial College Press. ISBN 978-1-86094-424-6.
- ^ Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X.
Further reading[edit]
- Adams, Robert A. (2003). Calculus: A Complete Course (5th ed.). ISBN 0-201-79131-5.
- Jain, R. K.; Iyengar, S. R. K. (2009). Advanced Engineering Mathematics (3rd ed.). Narosa Publishing House. ISBN 978-81-7319-730-7.
- Herman, Edwin “Jed” & Strang, Gilbert (2016): Calculus : Volume 3 : OpenStax, Rice University, Houston, Texas, USA. ISBN 978-1-50669-805-2. (PDF)
External links[edit]
- Weisstein, Eric W. “Multiple Integral”. MathWorld.
- L.D. Kudryavtsev (2001) [1994], “Multiple integral”, Encyclopedia of Mathematics, EMS Press
- Mathematical Assistant on Web online evaluation of double integrals in Cartesian coordinates and polar coordinates (includes intermediate steps in the solution, powered by Maxima (software))
- Online Double Integral Calculator by WolframAlpha
- Online Triple Integral Calculator by WolframAlpha
