Как найти критерий архимеда

Механика сплошных сред

Сплошная среда
Классическая механика Закон сохранения массы · Закон сохранения импульса
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука
См. также: Портал:Физика

Число Архимеда () — безразмерная величина, названная в честь древнегреческого учёного Архимеда. Она применяется при расчётах, связанных с движением тел во внешней среде (жидкость или газ), возникающим вследствие неоднородности плотности в системе «тело — внешняя среда»

${displaystyle mathrm {Ar} ,={frac {gL^{3}rho _{ell }(rho -rho _{ell })}{eta ^{2}}},={frac {gL^{3}(rho -rho _{ell })}{rho _{ell }nu ^{2}}},}$

где — ускорение свободного падения (9,81 м/с²);

${displaystyle rho _{ell }}$ — плотность среды, кг/м³;

rho — плотность тела, кг/м³;

eta — динамическая вязкость среды, Па·с;

— кинематическая вязкость среды, м²/с;

— характерный линейный размер тела, м.

Число Архимеда представляет собой критерий подобия, характеризующий соотношение между архимедовой силой, обусловленной различием плотностей в отдельных областях рассматриваемой системы, и вязкими силами в основном потоке.

Применение[править | править код]

В химической технологии число Архимеда используется при расчёте аппаратов для отстаивания жидкостей, реакторов с кипящим слоем катализатора, систем с пневмотранспортом.
В нефтегазовой отрасли, при расчете эффективности горизонтальных сепараторов гравитационного типа.

Литература[править | править код]

Справочник химика. Том 5. 2-е изд. — М. — Л.: Химия, 1968. — Раздел III. Гидродинамика зернистых материалов. — с. 426-467.

Примечания[править | править код]

Источник

Число Архимеда

${displaystyle mathrm {Ar} ,={frac {gL^{3}rho _{ell }(rho -rho _{ell })}{eta ^{2}}},={frac {gL^{3}(rho -rho _{ell })}{rho _{ell }nu ^{2}}},}$

где — ускорение свободного падения (9,81 м/с²);

${displaystyle rho _{ell }}$ — плотность среды, кг/м³;

rho — плотность тела, кг/м³;

eta — динамическая вязкость среды, Па·с;

— кинематическая вязкость среды, м²/с;

— характерный линейный размер тела, м.

Применение

Литература

Справочник химика. Том 5. 2-е изд. — М. — Л.: Химия, 1968. — Раздел III. Гидродинамика зернистых материалов. — с. 426-467.

Примечания

Источник

1. Цель работы –
определение опытных значений скорости
осаждения и сравнение с расчетными.

2.Теоретические сведения.

Для правильного
проектирования пылеулавливающих
аппаратов (и пылеотборных устройств)
необходимо знать, как движутся частицы
под действием внешних сил.

Пылевая частица,
осаждаясь под действием гравитационной
силы, испытывает сопротивление
газообразной среды. Вектор этой силы
направлен в сторону, обратную движению
частицы. Режим движения среды может
быть вязким и турбулентным, что
характеризуется соответствующей
величиной числа Рейнольдса – Re. Принято
весь диапазон чисел Re от 0 до 
делить на три области. В каждой такой
области сопротивление движению частицы
F_c
имеет определенную закономерность:
область закона Стокса, область закона
Ньютона, промежуточная область. Скорость
осаждения частиц также зависит от
величины Re и рассчитывается по
соответствующим формулам.

Сопротивление
среды в зависимости от числа Рейнольдса
-Re

При медленном
движении частицы увлекаемые ею слои
среды имеют строго ламинарный, слоистый
характер движения. Сопротивление среды
при этом складывается из суммы сил
внутреннего трения между этими слоями
и выражается законом Стокса. Для
сферической частицы сила сопротивления
по Стоксу равна

,
( 1 )

где

– диаметр частицы, м;

– вязкость среды,
Па;

– скорость движения
частиц, м/с.

Формула Стокса
справедлива для Re < 1.

Увеличение скорости
движения частицы вызывает турбулизацию
среды. Силы инерции становятся значительно
больше сил вязкости.

Среда приближается
по своим свойствам к идеальной жидкости.
Для больших скоростей (Re > 500) сопротивление
среды будет обусловлено только инерцией
ее перехода из спокойного состояния в
движение под действием движущейся
частицы. Это сопротивление среды можно
определить по закону Ньютона для
идеальной, не имеющей вязкости жидкости.
В общем виде для частицы диаметром

,
расположенной в потоке, сила сопротивления
среды плотностью

,
Н, равна

;………………………………………………………………………
.(2)

где

– коэффициент сопротивления, зависящий
от режима движения и формы тела.

В области Re > 500
опыт показывает, что для диска,
расположенного перпендикулярно потоку,

= 1,12; для шара –

= 0,44. Следовательно, для сферической
частицы турбулентное сопротивление
среды (по Ньютону), Н, можно записать
следующим образом:

;…………………………………………………………………
.(3)

В опытах также
установлено, что формула Ньютона
справедлива для относительно крупных
частиц.

По многочисленным
экспериментальным данным построена
зависимость

для сферических тел (рис.4.) (т.н. стандартная
кривая). Для области действия закона
Стокса, т.е. для области ламинарного
сопротивления, пропорционального
скорости движения частицы в первой
степени, коэффициент сопротивления
можно выразить так:

…………………………………………………….(4)

Формула (41) верна,
если Re < 1 и размеры частиц

мкм. В промежуточной области значений
Re от 1 до 500 нельзя пренебречь турбулентным
сопротивлением среды. Здесь коэффициент
сопротивления изменяется пропорционально

.
С увеличением числа Re значение

непрерывно возрастает от единицы до
двух. Хорошие результаты дает формула

,
где А = 24…5,8

= 1…0,37. При Re > 500 можно полностью
пренебречь вязким сопротивлением. В
этой области для шарообразных тел

= 0.44.

При дальнейшем
увеличении числа Re до 10⁵
коэффициент сопротивления

остается примерно постоянной величиной
(рис.4).

Применимость
закона Стокса имеет и нижний предел,
определяемый такими мелкими частицами
(d << 1 мкм), что они становятся
чувствительными к ударам молекул и
находятся в броуновском движении. Здесь
вводится поправка Канингема.

Скорость осаждения
частиц

Знание законов
сопротивления среды при осаждении
частиц, как было сказано выше, необходимо
для определения скорости их осаждения.
Известно, что под действием любой силы
тело движется ускоренно. Так как с
увеличением скорости движения
увеличивается и сопротивление среды,
то в ходе осаждения неизбежно должен
наступать такой момент, когда сопротивление
среды F станет равным движущей силе Р,
т.е. когда вся движущая сила расходуется
только на преодоление сопротивления
среды, и движение становится установившимся,
а ускорение равным нулю. С этого момента
частица осаждается с постоянной
установившейся скоростью.

Рис.4. Зависимость

для сферических частиц

Из сказанного
следует, что скорость осаждения
определяется путем приравнивания силы
сопротивления среды движущей силе F=P.

При осаждении
сферических частиц под действием тяжести
в условиях применимости закона Стокса
возникает равенство:

(5)

откуда

(6)

где

– постоянная времени или время релаксации.

Это выражение
справедливо, когда число

.

При осаждении
сферических частиц под действием силы
тяжести в условиях применимости закона
Ньютона (Re < 500) запишем аналогично

(7)

Выражение справедливо
только тогда, когда Re >500.

Скорость осаждения
частиц в промежуточной области 1 < Re <
500 можно определять по формуле

(8)

где

– критерий Архимеда,

,
(46)

Порядок расчета
скорости таков: определив значение
числа

,
по формуле (8) находят число Re и далее
искомую скорость осаждения

(9)

Влияние формы
частицы на процесс осаждения.

Все приведенные
выражения для сопротивления среды, а
следовательно, и скорости осаждения
справедливы, как указывалось выше, для
шарообразных частиц. В технике, как
правило, частицы пыли неправильной
формы. Коэффициент сопротивления среды

является функцией не только числа Re, но
и формы частицы. В то же время влияние
формы на коэффициент сопротивления
также зависит от режима движения среды,
вызванного движением частицы, т.е. от
числа Re. Из-за влияния формы расчет
скорости осаждения частиц в технологических
аппаратах является приближенным, т.к.
вводится эквивалентный их диаметр.

В большинстве
случаев скорость осаждения частиц
несферической формы меньше, чем
сферической при равных эквивалентных
диаметрах. Эквивалентный диаметр частицы
определяется по ее массе

(10)

Если влиянием
формы можно пренебречь, то скорость
осаждения таких частиц рассчитывают
по формуле (6) или (9) с учетом (10). Для учета
влияния формы на скорость осаждения
можно применять следующие теоретические
формулы:

,
(11)

для диска радиусом

,
падающего

плашмя

,

(12)

ребром

,

(13)

Влияние стесненности
движения осаждающейся частицы на
скорость осаждения

Стесненность
движения осаждающейся частицы возникает
при прохождении ее траектории вблизи
вертикальной стенки. Величину поправки
(
)
на скорость осаждения (
)
можно определить по одной из формул:
при прохождении частицы

на расстоянии

от плоской стенки

;
при осаждении частицы между двумя
плоскими стенками, находящимися на
расстоянии

друг от друга,

,
или при осаждении частицы

по оси трубки диаметром

В данной лабораторной
работе определяется опытная и расчетная
скорость осаждения в глицерине стальных
шариков разных диаметров и частиц
сложной формы типа тонких цилиндров и
дисков.

3. Описание установки

Лабораторная
установка для определения скорости
осаждения частиц состоит из стеклянного
цилиндра с нанесенными на нем метками
(ниже участка установления равномерной
скорости), расстояние между которыми
равно 0,1 м. Цилиндр заполнен глицерином
до уровня примерно 1 м от его дна.

В комплект
оборудования входит микрометр для
определения диаметра шариков, ареометр
для определения плотности глицерина,
секундомер для замера времени осаждения
частиц, весы для определения массы
частиц несферической формы.

4. Порядок проведения
работы

1. Перед началом
работы на установке получить допуск у
преподавателя по знанию техники
безопасности.

2. Микрометром
измерить диаметры всех шариков, выданных
преподавателем или лаборантом.

3. Каждый шарик
поочередно осторожно опустить на
поверхность глицерина ближе к центру
цилиндра. При прохождении шариком
верхней метки включить секундомер и
следить за движением шарика. При
достижении нижней метки выключить
секундомер и таким образом засечь
продолжительность t
прохождения шариком пути h
= 0,7…0,8 м (расстояние уточнить).

4. Ареометром
измерить плотность глицерина.

5. На весах определить
массу несферических частиц.

6. Определить время
осаждения двух одинаковых шариков на
расстоянии

и 2

от стенки цилиндра.

7. Результаты всех
замеров внести в табл. 2 и приступить к
обработке результатов.

5. Обработка
результатов опыта.

1. Опытную скорость
осаждения всех шариков определить так
же, как и скорость осаждения самого
маленького шарика:

м/с. Результаты вычисления внести в
табл. 3.

2. По опытному
значению скорости осаждения самого
маленького шарика

,
используя уравнение (6), определить
вязкость глицерина

Па.с.

Полученное значение
занести в табл. 2

Таблица 2

Результат опытов
по осаждению частиц

№ п/п	Размер частиц, , м	Путь осаждения, , м	Время осаждения, , с	Наименование измеряемых величин	Единица измерения	Величина
1 2				Плотность частиц,	кг/м³	7800
3 4				Плотность глицерина,	кг/м³	1250
5 6				Вязкость глицерина,	кг/м³	Опред-ся в опыте

Таблица 3

Расчетная скорость
осаждения частиц

№ п/п

Размер частиц,

или

,
м

Опытная скорость
осаждения

,
м/с

Теоретическая
скорость осаждения

,
м/с

,
%

3. Проверить
справедливость закона Стокса для данного
шарика путем вычисления числа

,
которое должно быть меньше единицы.

4. Определить
теоретическую скорость осаждения других
шариков и частиц. Очевидно, что
теоретическая скорость осаждения самого
маленького шарика должна совпадать с
опытной величиной, поскольку последняя
была использована для определения
вязкости ц на основании применимости
закона Стокса. Для определения
теоретической скорости осаждения
остальных частиц необходимо найти
значение критерия Архимеда

По численному
значению критерия

по формуле (8) определить число

и отсюда искомую скорость осаждения

м/с.

5. Далее находят
величину отклонения теоретической
скорости осаждения от скорости,
определенной в опыте:

Результаты
вычислений внести в табл. 3.

6. Требования к
отчету. Отчет должен содержать:

6.1. Краткое изложение
теории и цель работы.

6.2. Заполненные
табл. 107 и 108.

6.3. Расчет вязкости
для табл. 107 и расчет одной-двух строк
из табл. 108.

6.4. Анализ полученных
результатов и выводы.

7. Контрольные
вопросы

7.1. Какова область
применимости закона Стокса и закона
Ньютона для определения силы сопротивления
при осаждении частицы?

7.2. Каков вид
обобщенного закона сопротивления среды?

7.3. Чему равен
коэффициент сопротивления для шара при
Re
;
при Re>500 и 1 < Re <500 ?

7.4. Чему равна
скорость осаждения сферической частицы
при Re

(закон Стокса); при Re>500 (закон Ньютона)?

7.5. Как определяется
скорость осаждения для промежуточной
области Re(l<Re<500)r>

7.6. Какова цель
работы?

7.7. Расскажите
порядок проведения экспериментальной
части работы?

7.8. Как рассчитать
теоретическую скорость осаждения
частицы?

7.9. В чем заключается
метод определения вязкости жидкости,
основанный на законе Стокса?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Таблицы, расчетные номограммы и диаграммы по курсу «Процессы и аппараты химической технологии»: Справочно-методическое пособие

Страницы работы

Фрагмент текста работы

Таблица 21 – Значение поправочного
множителя k, при расчете расхода через нормальную диафрагму

Диаметр трубопровода, м	m = 0,1	m = 0,2	m = 0,3	m = 0,4	m = 0,5	m = 0,6	m = 0,7
0,05	1,0037	1,0063	1,0082	1,0118	1,0144	1,0172	1,02
0,10	1,0024	1,0045	1,0064	1,0065	1,0108	1,013	1,0148
0,20	1,0017	1,0023	1,0034	1,004	1,0052	1,006	1,007
0,30	1,0005	1,001	1,001	1,001	1,001	1,001	1,001
m = (d₀/d)².

Таблица 22 – Характеристика
скрубберных насадок из колец и кускового материала

Вид насадки	Размеры элемента насадки, мм	Число элементов в 1 м³ объема, заполненного насадкой	Свободный объем, м³/м³	Удельная поверх ность, м²/м³	Масса 1 м³ насадки, кг
Кольца фарфоровые	8×8×1,5	1 465 000	0,64	570	600
» керамические	15×15×2	250 000	0,70	330	690
» »	25×25×3	53 200	0,74	204	532
» »	35×35×4	20 200	0,78	140	505
» »	50×50×5	6 000	0,785	87,5	530
» стальные	35×35×2,5	19 000	0,83	147	—
» »	50×50×1	6 000	0,95	110	430
Гравий круглый	42	14 400	0,388	80,5	—
Андезит кусковой	43,2	12 600	0,565	68	1200
Кокс кусковой	42,6	14 000	0,56	77	455
» »	40,8	15 250	0,545	86	585
» »	28,6	27 700	0,535	110	660
» »	24,4	64 800	0,532	120	600
Катализатор синтеза аммиака в кусочках	6,1	5 200 000	0,465	960	2420
Катализатор конверсии СО в таблетках	d = 11,5; h = 6	1 085 000	0,38	460	1100
Катализатор сернокислотный (ванадиевый) в таблетках	d = 11; h = 6,5	1 000 000	0,43	415	614

Таблица 23 – Характеристика
хордовых насадок (деревянные рейки)

Сечение рейки	Размеры сечения, мм	Расстояние между рейками, мм	Расстояние между рядами реек, мм	Удельная поверхность м²/м³
Прямоугольное	12,5×100	25,0	20	50
12,5×100	12,5	20	75
12,5×100	10,0	20	89
Треугольное	30×30×30	30	12,5	78

Таблица 24 – Зависимость
атмосферного давления от высоты над уровнем моря
Пересчет в СИ: 1 м вод. ст. = 9810 Па.

Высота над уровнем моря, м	–600	0	+100	200	300	400	500	600	700	800	900	1000	1500
Атмосферное давление А, м вод. ст	11,3	10,3	10,2	10,1	10	9,8	9,7	9,6	9,5	9,4	9,3	9,2	8,6

Таблица 25 – Допустимая высота
всасывания (в м) при перекачивании воды поршневыми насосами

Частота вращения насоса, об/мин	Температура воды, °С
0	20	30	40	50	60	70
50	7	6,5	6	5,5	4	2,5	0
60	6,5	6	5,5	5	3,5	2	0
90	5,5	5	4,5	4	2,5	1	0
120	4,5	4	3,5	3	1,5	0,5	0
150	3,5	3	2,5	2	0,5	0	0
180	2,5	2	1,5	1	0	0	0

Таблица 26 – Значения постоянных c
и m для различных типов мешалок.

Тип мешалки	Геометрическая характеристика	Значения постоянных	Примечание
H₀/d	D/d	h/d	с	m
Двухлопастная	2	2	0,36	111,0 14,35	1,0 0,31	Re < 20 Re = 10045×10⁴
» »	3	3	0,33	6,8	0,2
Двухлопастная с лопастями под углом 45°	3	3	0,33	4,05	0,2
Четырехлопастная	3	3	0,33	8,52	0,2
Четырехлопастная с лопастями, наклонными вверх под углом 45°	3	3	0,33	5,05	0,2
Четырехлопастная с лопастями, наклонными вверх под углом 60°	3	3	0,33	6,30	0,18
Якорная двухлопастная	1,11	1,11	0,11	6,2	0,25
Якорная четырехлопастная	1,11	1,11	0,11	6,0	0,25	Форма лопасти круглая
Пропеллерная двухлопастная с углом наклона 25,5°	3	3	0,33	0,985	0,15
Пропеллерная трехлопастная	3,5	3,8	1	230 4,63 1,19	1,67 0,35 0,15	Re < 30 Re < 3×10³ Re > 3×10³
Турбинная трехлопастная с входным отверстием 37 мм	3	3	0,33	3,90	0,2
Турбинная шестилопастная с направляющим аппаратом	1,78	2,4	0,25	5,98	0,15

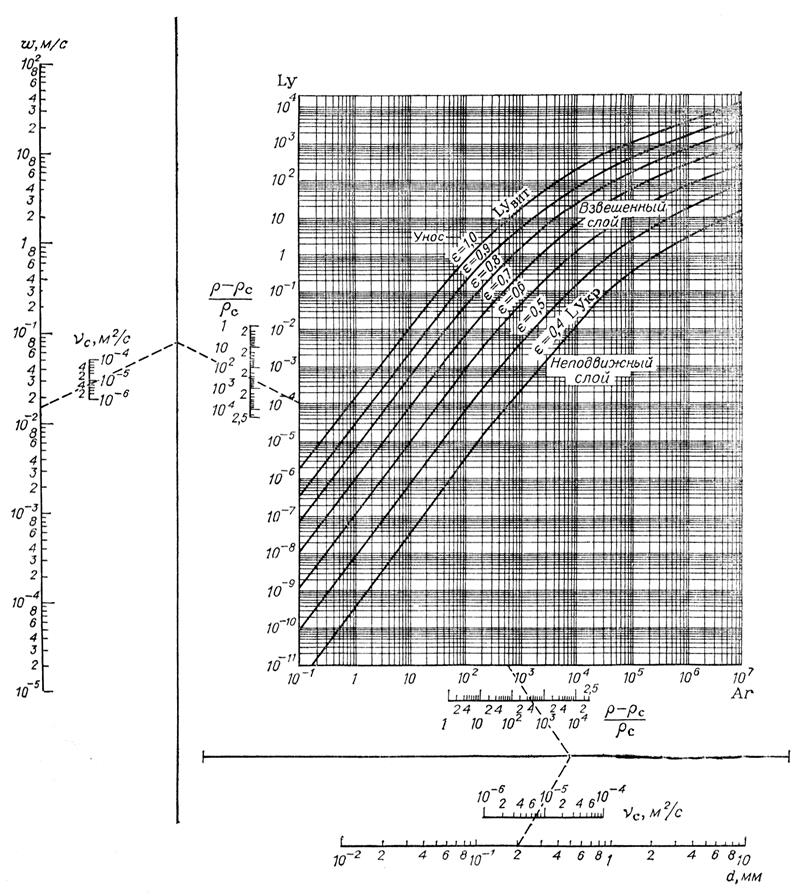
13. Диаграмма зависимости критерия
Лященко от критерия Архимеда.

Диаграмма составлена на основе приближенной эмпирической
формулы:

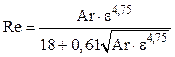Критерий Лященко: .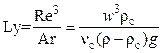

Критерий Архимеда: .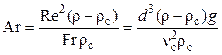

Здесь w – скорость среды (для однородного взвешенного
слоя) или скорость витания частиц (по верхней кривой), м/с; r и r_c–
плотность частиц и среды, соответственно, кг/м³; d – диаметр
частиц, м; m_c – динамический
коэффициент вязкости среды, Па×с; v_c=μ_c/ρ – кинематический коэффициент вязкости среды, м²/с;
g – ускорение свободного падения, м/с²; e – порозность слоя (в долях единиц).

На диаграмме дана зависимость критерия Лященко Ly от
критерия Архимеда Ar при различной порозности слоя (e = 0,4¸1).

Диаграмма позволяет определить диаметр сферических частиц,
скорость среды и порозность взвешенного слоя, а также скорость осаждения частиц
в неподвижной среде (по верхней кривой). Для приближенных расчетов у осей
координат построены номографические шкалы для w, d, v_c
и (ρ–ρ_c)/ρ_c.

Схема пользования показана пунктиром. Например, дано: d =
0,2мм, v_c= 7×10^–6
м²/с, и (ρ–ρ_c)/ρ_c=4×10²;
находим Ar = 6×10², Ly_кр
= 10^–4и w_кр= 1,5 ×10^–2м/с.

14. Зависимость критериев Re и Ly
от критерия Ar для осаждения одиночной частицы в неподвижной среде

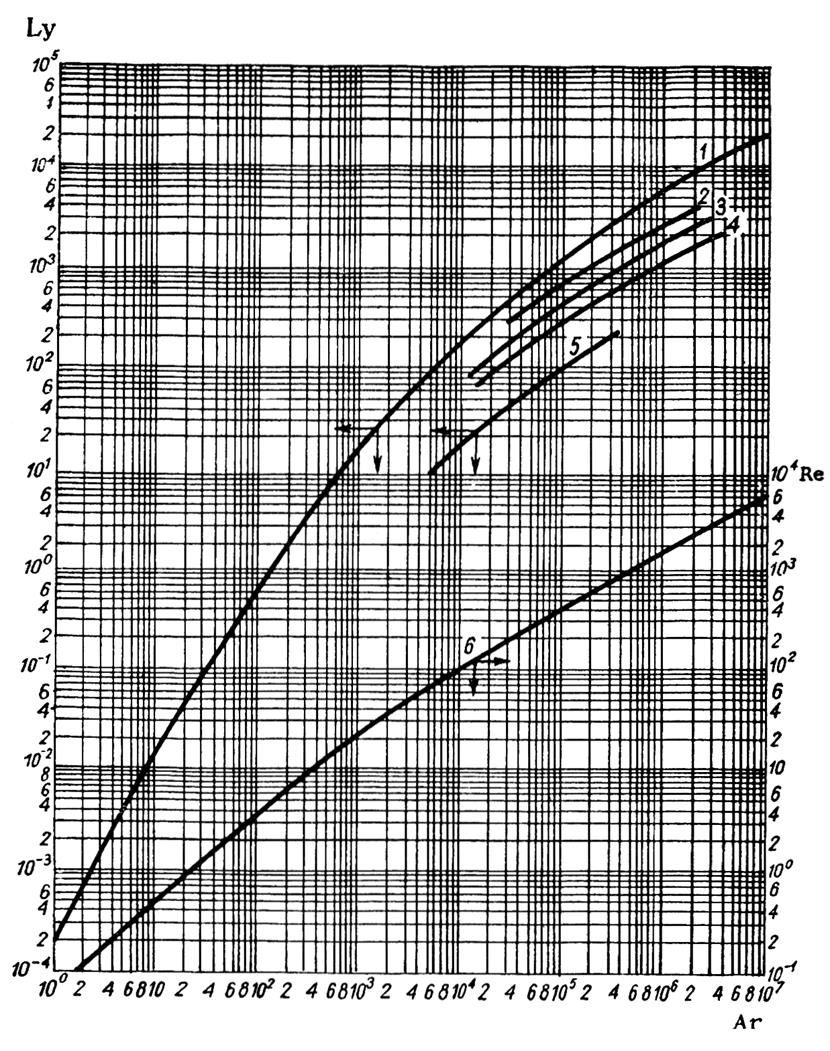
1 и 6 – шарообразные частицы; 2 –
округленные; 3 – угловатые; 4 – продолговатые; 5 – пластинчатые.

15. Зависимость критерия мощности
от критерия Рейнольдса

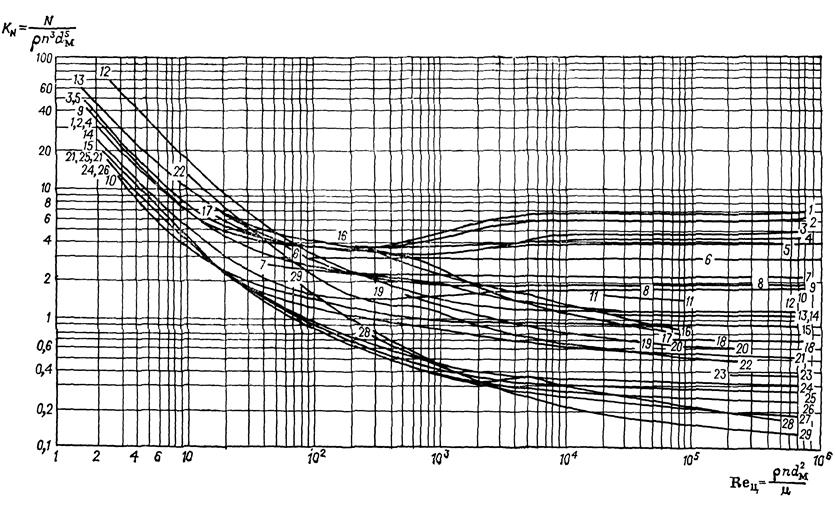
1 – открытая турбинная мешалка с шестью прямыми вертикальными
лопатками (b=0,2d_м; l=0,25d_м) при D/d_м=3 в сосуде с четырьмя перегородками (B/d_м=0,17); 2 –
турбинная мешалка типа 1 при B/d_м=0,1;3 – открытая турбинная мешалка с шестью
изогнутыми вертикальными лопатками (b=0,2d_м;
l=0,25d_м) при D/d_м=3 в сосуде
с четырьмя перегородками (B/d_м=0,1);
4 – турбинная мешалка типа 1 при B/d_м=0,04; 5 – открытая турбинная мешалка с
шестью стреловидными лопатками (b=0,2d_м;
l=0,25d_м) при D/d_м=3 в сосуде
с четырьмя перегородками (B/d_м=0,1);
6 – односторонняя радиально–дисковая мешалка с
шестью прямыми вертикальными лопатками (b=0,1d_м;
l=0,35d_м) снизу диска при D/d_м=2,5 в
сосуде с четырьмя перегородками (B/d_м=0,25); 7 – радиальная турбинная мешалка с
шестнадцатью лопатками со статором в сосуде без перегородок; 8 – двухлопастная
мешалка с прямыми вертикальными лопастями (b=0,25d_м)
при D/d_м=4,35
в сосуде с тремя перегородками (B/d_м=0,11); 9 –
восьмилопастная мешалка с прямыми лопастями (b=0,25d_м)
под углом 45° при D/d_м=3
в сосуде с четырьмя перегородками (B/d_м=0,1); 10 – двухлопастная мешалка типа 8 при
D/d_м=3
в сосуде с четырьмя перегородками (B/d_м=0,1); 11 – закрытая турбинная мешалка с шестью
лопатками при D/d_м=2,4
в сосуде без перегородок; 12 – турбинная мешалка,
сходная с типом 11 при D/d_м=3
в сосуде

Информация о работе

Тип:

Методические указания и пособия

Источник

Применение[править | править код]

Литература[править | править код]

Примечания[править | править код]

Число Архимеда

Применение

Литература

Примечания

2.Теоретические сведения.