Как найти критические точки 10 класс

Содержание:

1. Критические точки и экстремумы функции
2. Теорема Ферма (Необходимое условие существовании экстремумов)
3. Достаточное условие существования экстремума
4. Задача пример №117
5. Задача пример №118
6. Задача пример №119
7. Задача пример №120
8. Задача пример №121

Критические точки и экстремумы функции

В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.

1. Для значений равных угловой коэффициент касательной к графику равен 0. Т.e. . Эти точки являются критическими точками функции.

2. В точках функция не имеет производной. Эти тоже критические точки функции.

3. Для рассматриваемой нами функции критические точки делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки – критические точки, которые не изменяют возрастание и убывание (или наоборот).

По графику видно, что в точках внутреннего экстремума производная функции равна нулю, а в точке производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.

Теорема Ферма (Необходимое условие существовании экстремумов)

Во внутренних точках экстремума производная либо равна нулю, либо не существует.

Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке производная функции равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.

На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т.е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.

Достаточное условие существования экстремума

Пусть функция непрерывна на промежутке и . Если является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:

1 ) слева от точки положительна, а справа – отрицательна, то точка является точкой максимума.

2) слева от отрицательна, а справа – положительна, то точка является точкой минимума

3) с каждой стороны от точки имеет одинаковые знаки, то точка не является точкой экстремума.

Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.

Соответствующие наибольшее и наименьшее значения функции на отрезке записываются как и .

Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.

Задача пример №117

Для функции определите максимумы и минимумы и схематично изобразите график.

Решение:

Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.

1. Производная функции:

2. Критические точки функции:

3. Точки и разбивают область определения функции на три промежутка.

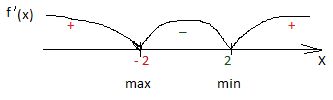
Проверим знак на интервалах, выбрав пробные точки:

для интервала

для интервала

для интервала

Интервал Пробные точки

Знак Возрастание и убывание

При имеем . (-1;3) – максимум

При имеем (1;-1) – минимум

4. Используя полученные для функции данные и найдя координаты нескольких дополнительных точек, построим график функции.

Задача пример №118

Найдите наибольшее и наименьшее значение функции на отрезке [-1;2].

Решение:

Сначала найдем критические точки. Так как , то критические точки можно найти из уравнения . Критическая точка не принадлежит данному отрезку [-1; 2], и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке и на концах отрезка.

Из этих значений наименьшее – 4, наибольшее 12. Таким образом:

Задача пример №119

Найдите экстремумы функции .

Решение:

1. Производная функции:

2. Критические точки: ,

3. Интервалы, на которые критические точки делят область определения функции:

Проверим знак на интервалах, выбрав пробные точки.

Для промежутка возьмем

Для промежутка (0; 1,5) возьмем

Для промежутка возьмем

Интервал

Пробные точки

Знак Возрастание-убывание

Используя полученную для функции информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами и касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.

• Функция на промежутке возрастает.

• Точка критическая точка функции , но не является экстремумом.

• Функция на промежутке [0; 1,5] возрастает.

• Функция на промежутке убывает.

•

Задача пример №120

Найдите экстремумы функции

Решение:

1. Производная

2. Критические точки: для этого надо решить уравнение или найти точки, в которых производная не существует. В точке функция не имеет конечной производной. Однако точка принадлежит области определения. Значит, точка является критической точкой функции.

3. Промежутки, на которые критическая точка делит область определения функции: и

Определим знак , выбрав пробные точки для каждого промежутка:

Для возьмем Для возьмем

Интервал Пробные точки

Знак

Возрастание-убывание

• Функция на промежутке убывает.

• Функция на промежутке возрастает.

•

Задача пример №121

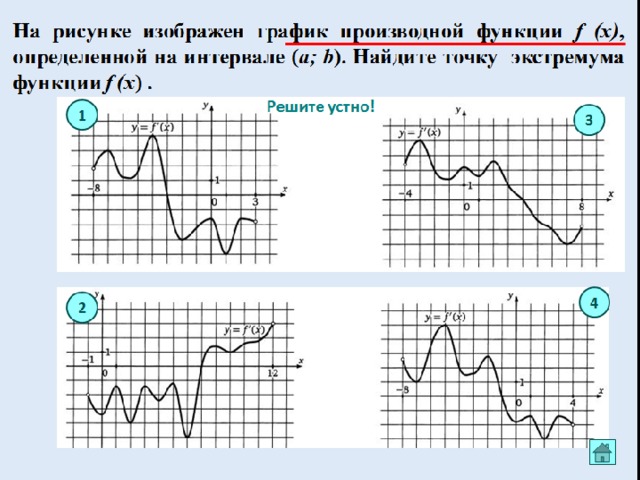
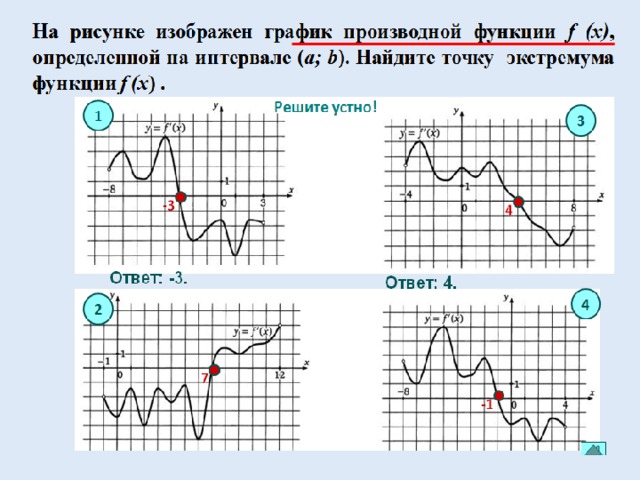
По графику функции производной схематично изобразите график самой функции.

Решение:

Производная в точке равна нулю, а при отрицательна, значит, на интервале функция убывающая. При производная положительна, а это говорит о том, что функция на промежутке возрастает. Точкой перехода от возрастания к убыванию функции является точка . Соответствующий график представлен на рисунке.

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Другие темы которые вам помогут понять математику:

Объемы подобных фигур

Нахождение промежутков возрастания и убывания функции

Построение графиков функции с помощью производной

Задачи на экстремумы. Оптимизации

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Критические точки и
  точки экстремума
  функции
  10 класс
  Алгебра и начала анализа
  Специализированная гимназия № 8 с обучением на трех языках имени М.Х. Дулати
  Шымкент-2020
  учитель математики
  Харченко Татьяна Викторовна

• 

  2 слайд

  – знать определения критических точек и точек экстремума функции, условие существования экстремума функции.
  Цель урока:
  10.4.1.28
  Критерии оценивания
  – Использует определение находит критические (стационарные) точки, используя определение;
  – применяет необходимое и достаточное условие для определение точек экстремума функции.
  Учащийся:

• 

  3 слайд

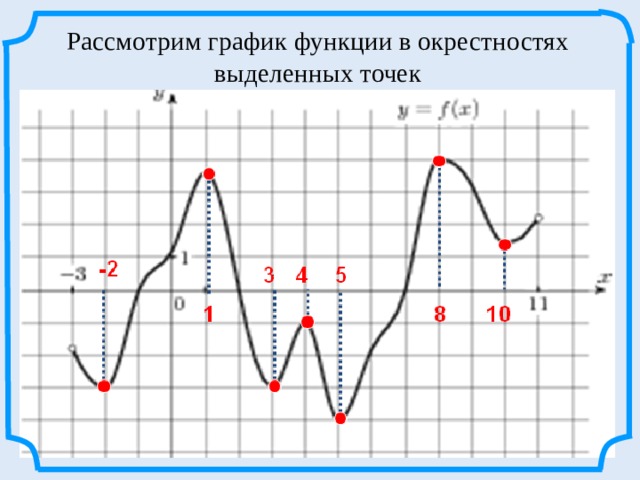
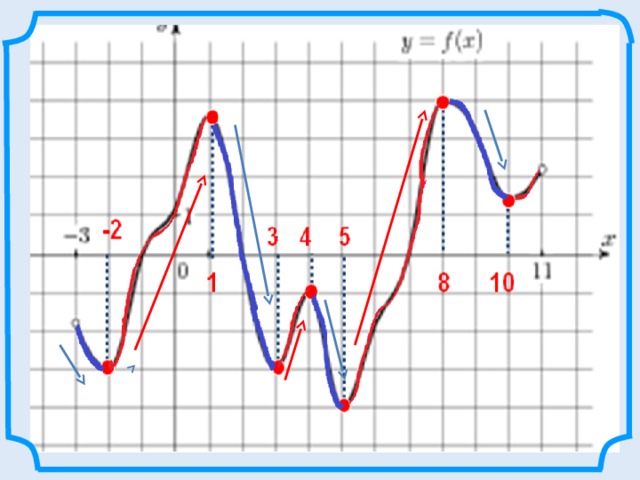
  Рассмотрим график функции в окрестностях выделенных точек

• 

• 

  5 слайд

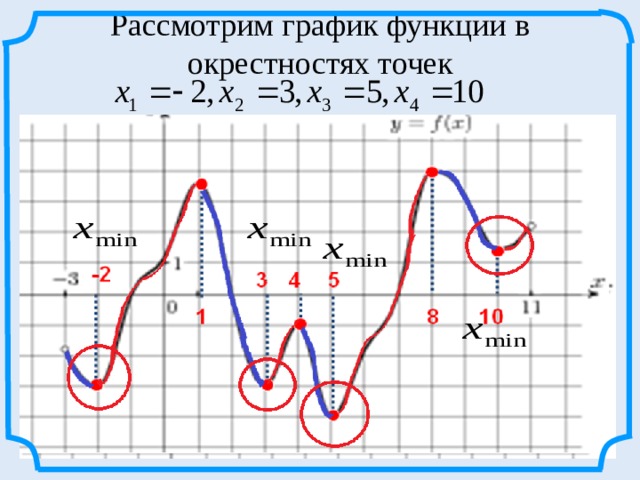
  Рассмотрим график функции в окрестностях точек

• 

  6 слайд

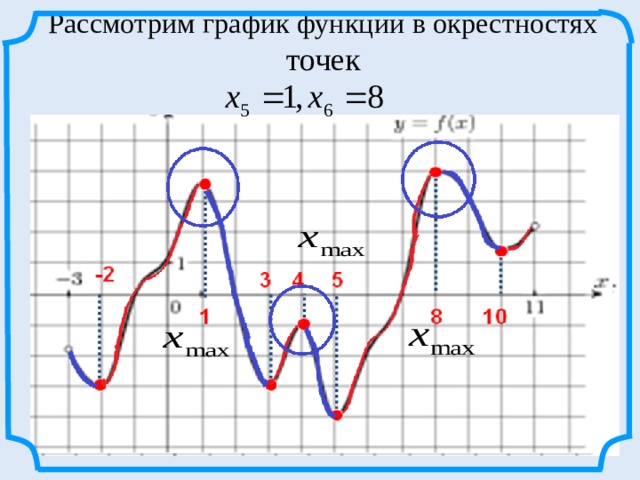
  Рассмотрим график функции в окрестностях точек

• 

  7 слайд

  Точки экстремума
  экстремумы

• 

  8 слайд

  Критические точки
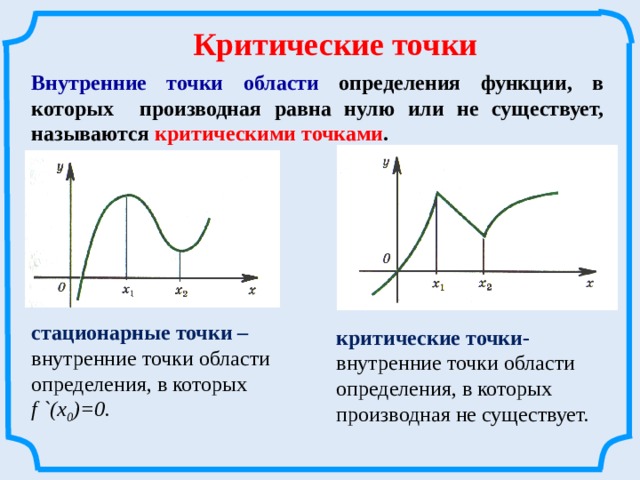
  Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками.
  стационарные точки –
  внутренние точки области
  определения, в которых f `(х0)=0.
  критические точки- внутренние точки области
  определения, в которых производная не существует.

• 

  9 слайд

  x
  y
  O
  1
  1
  4
  7
  9
  12
  15
  19
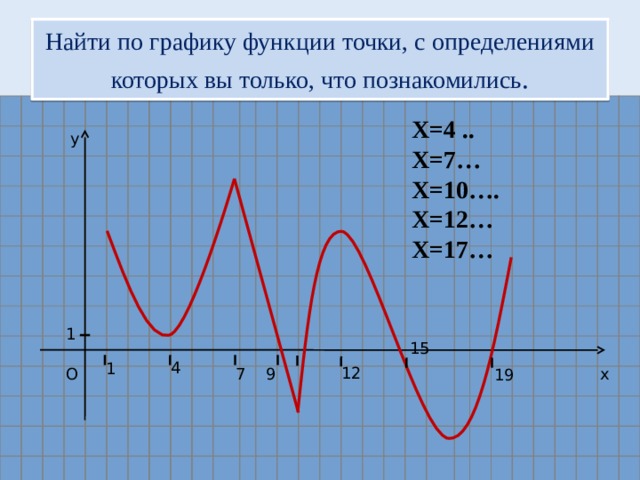
  Найти по графику функции точки, с определениями которых вы только, что познакомились.
  Х=4 ..
  Х=7…
  Х=10….
  Х=12…
  Х=17…

• 

  10 слайд

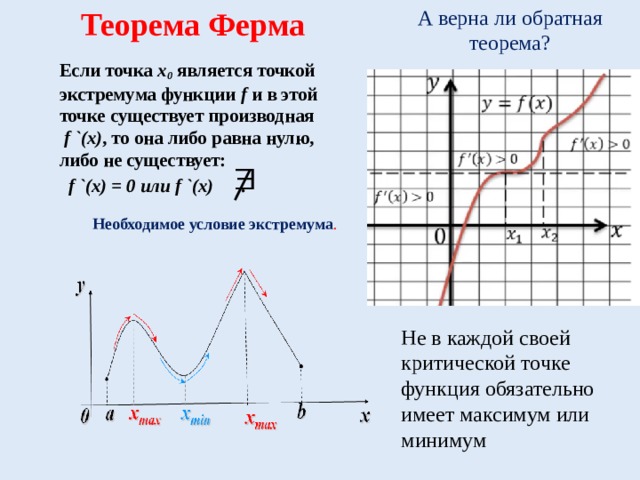
  Если точка х0 является точкой экстремума функции f и в этой точке существует производная f `(x), то она либо равна нулю, либо не существует:
  f `(x) = 0 или f `(x) .
  Теорема Ферма
  Не в каждой своей критической точке функция обязательно имеет максимум или минимум
  А верна ли обратная теорема?
  Необходимое условие экстремума.

• 

  11 слайд

  Достаточные условия существования экстремума в точке
  Признак минимума функции.
  Если функция у=f((х) непрерывна в точке х0, f `(x) < 0 на интервале (а; х0) и f `(x) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f

  Признак максимума функции.
  Если функция у= f(х) непрерывна в точке х0, а f `(x) > 0 на интервале (а; х0), и f `(x) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f.

• 

• 

• 

  14 слайд

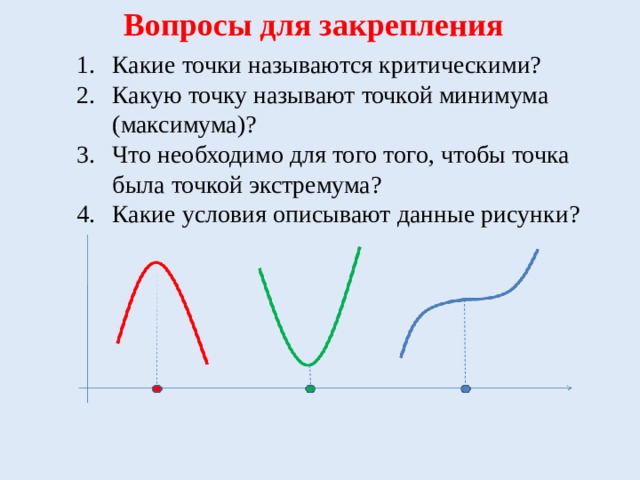
  Вопросы для закрепления
  Какие точки называются критическими?
  Какую точку называют точкой минимума (максимума)?
  Что необходимо для того того, чтобы точка была точкой экстремума?
  Какие условия описывают данные рисунки?

• 

• 

  16 слайд

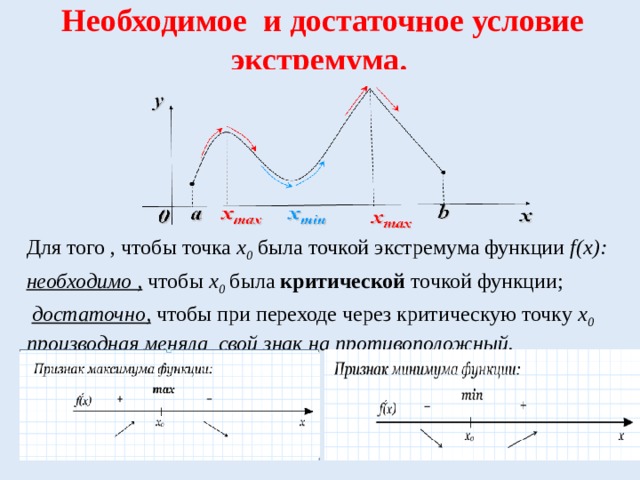
  Необходимое и достаточное условие экстремума.
  Для того , чтобы точка х0 была точкой экстремума функции f(х):
  необходимо , чтобы х0 была критической точкой функции;
  достаточно, чтобы при переходе через критическую точку х0 производная меняла свой знак на противоположный.

• 

• 

• 

  19 слайд

  Задания для самостоятельного решения
  1А. (5б) Найдите критические точки функции. Выясните, какие из этих точек являются:
  а) точками минимума; б) точками максимума.

• 

  20 слайд

  Задания для самостоятельного решения
  2Б. (6б) Найдите экстремумы функции:

• 

  21 слайд

  Задания для самостоятельного решения
  3С.(7б)Найдите промежутки возрастания и убывания, точки экстремума функции:

• 

  22 слайд

  https://videouroki.net/video/45-primienieniie-proizvodnoi-dlia-otyskaniia-tochiek ekstriemuma.html
  https://infourok.ru/videouroki/1215
  Дополнительные цифровые ресурсы

• 

  23 слайд

  https://bilimland.kz/ru/subject/algebra/10-klass/kriticheskie-tochki-dostatochnoe-uslovie-sushestvovaniya-ehkstremuma?mid=%info%
  https://www.yaklass.ru/p/algebra/10-klass/proizvodnaia-9147/primenenie-proizvodnoi-dlia-issledovaniia-funktcii-na-monotonnost-i-ekstr_-11226
  bilimland.kz
  www.yaklass.ru
  Ссылки на дополнительные ресурсы для самообразования

• 

  24 слайд

  Рефлексия содержания учебного материала
  Продолжи фразу:
  Теперь я могу…
  Было трудно…
  Сегодня я узнал…

• 

  25 слайд

  Дорогие дети!
  Вы получили самое основное содержание по новой теме, другие материалы вы получите от своего учителя!
  Если у вас есть вопросы, вы их можете задать учителю!
  Удачи в освоении нового материала, наши юные друзья!

Краткое описание документа:

Презентация содержит понятийный аппарат по теме ” Критические точки. Точки экстремума функции”, алгоритм нахождения точек экстремума с образцами решения для рациональной функции, дробно-рациональной и иррациональной, а также задания для самостоятельной работы, которые можно оценить по предложенным дескрипторам

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 261 953 материала в базе

• Выберите категорию:
• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»

• Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»

• Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Основы менеджмента в туризме»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»

• Курс повышения квалификации «Мировая экономика и международные экономические отношения»

• Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»

• Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»

• Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»

Специализированная гимназия № 8 с обучением на трех языках имени М.Х. Дулати

10 класс

Алгебра и начала анализа

Критические точки и

точки экстремума

функции

Л.С. Атанасян. Геометрия 10-11

учитель математики

Харченко Татьяна Викторовна

Шымкент-2020

Цель урока:

10.4.1.28

– знать определения критических точек и точек экстремума функции, условие существования экстремума функции.

Критерии оценивания

Учащийся:

Л.С. Атанасян. Геометрия 10-11

– Использует определение находит критические (стационарные) точки, используя определение;

– применяет необходимое и достаточное условие для определение точек экстремума функции.

Рассмотрим график функции в окрестностях выделенных точек

Рассмотрим график функции в окрестностях точек

Рассмотрим график функции в окрестностях точек

f( х 0 ) ” width=”640″

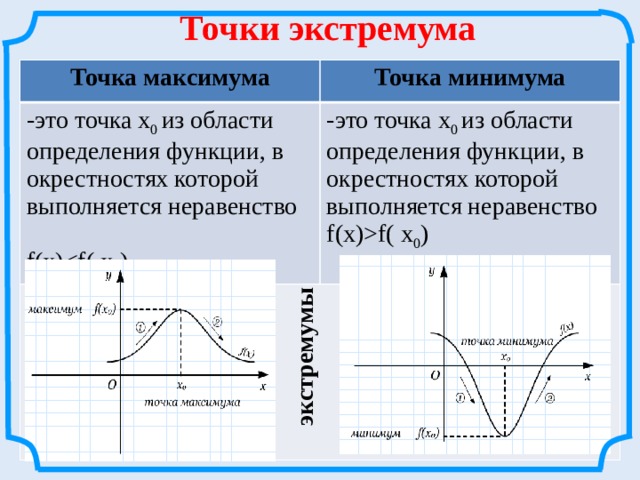
Точки экстремума

экстремумы

Точка максимума

-это точка х 0 из области определения функции, в окрестностях которой выполняется неравенство

Точка минимума

f(x)

-это точка х 0 из области определения функции, в окрестностях которой выполняется неравенство f(x)f( х 0 )

Критические точки

Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками .

стационарные точки –

внутренние точки области

определения, в которых f `(х 0 )=0.

критические точки- внутренние точки области

определения, в которых производная не существует.

Найти по графику функции точки, с определениями которых вы только, что познакомились .

Х=4 ..

Х=7…

Х=10….

Х=12…

Х=17…

y

1

15

4

1

12

9

7

x

O

19

Теорема Ферма

А верна ли обратная теорема?

Если точка х 0 является точкой экстремума функции f и в этой точке существует производная f `(x) , то она либо равна нулю, либо не существует:

f `(x) = 0 или f `(x) .

Необходимое условие экстремума .

Не в каждой своей критической точке функция обязательно имеет максимум или минимум

0 на интервале (а; х 0 ), и f `(x) на интервале (х 0 ; b), то точка х 0 является точкой максимума функции f. Признак минимума функции. Если функция у= f((х) непрерывна в точке х 0 , f `(x) на интервале (а; х 0 ) и f `(x) 0 на интервале (х 0 ; b) , то точка х 0 является точкой минимума функции f ” width=”640″

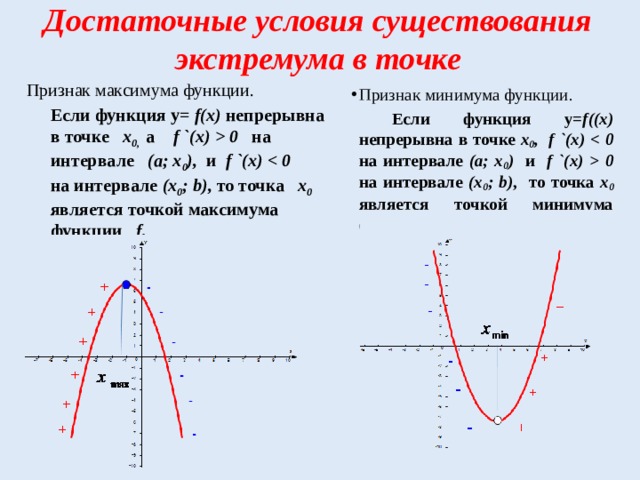
Достаточные условия существования экстремума в точке

Признак максимума функции.

Если функция у= f(х) непрерывна в точке х 0 , а f `(x) 0 на интервале (а; х 0 ), и f `(x) на интервале (х 0 ; b), то точка х 0 является точкой максимума функции f.

• Признак минимума функции.

Если функция у= f((х) непрерывна в точке х 0 , f `(x) на интервале (а; х 0 ) и f `(x) 0 на интервале (х 0 ; b) , то точка х 0 является точкой минимума функции f

Вопросы для закрепления

• Какие точки называются критическими?
• Какую точку называют точкой минимума (максимума)?
• Что необходимо для того того, чтобы точка была точкой экстремума?
• Какие условия описывают данные рисунки?

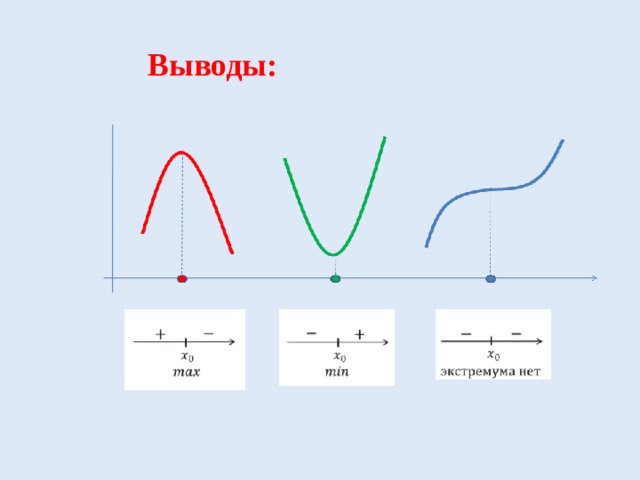
Выводы:

Необходимое и достаточное условие экстремума.

Для того , чтобы точка х 0 была точкой экстремума функции f(х):

необходимо , чтобы х 0 была критической точкой функции;

достаточно, чтобы при переходе через критическую точку х 0 производная меняла свой знак на противоположный.

Найдите точку минимума функции

Найдите точку максимума функции

Задания для самостоятельного решения

1А. (5б) Найдите критические точки функции. Выясните, какие из этих точек являются:

а) точками минимума; б) точками максимума.

№ п/п

1.

дескрипторы

балл

Находит правильно производную

2.

1

3.

Находит критические точки

4.

1

Расставляет верно знаки производной

5.

Определяет точки минимума

1

1

Определяет точки максимума

1

минимума

Задания для самостоятельного решения

2Б. (6б) Найдите экстремумы функции:

№ п/п

дескрипторы

1.

балл

Находит область определения

2.

Находит правильно производную

3.

1

1

Находит критические точки

4.

Расставляет верно знаки производной

5.

1

1

Определяет точки экстремума

6.

Находит экстремумы функции

1

1

Задания для самостоятельного решения

3С.(7б)Найдите промежутки возрастания и убывания, точки экстремума функции:

№ п/п

дескрипторы

1.

балл

Находит область определения

2.

Находит производную

1

3.

1

Находит критические точки

4.

Расставляет знаки производной

1

5.

Исследует поведение функции

6.

1

Находит промежутки монотонности

1

7.

1

Определяет точки экстремума

1

Дополнительные цифровые ресурсы

Ссылки на дополнительные ресурсы для самообразования

https:// bilimland.kz /ru/subject/algebra/10-klass/kriticheskie-tochki-dostatochnoe-uslovie-sushestvovaniya-ehkstremuma?mid=%info%

https:// www.yaklass.ru/ p/algebra/10-klass/proizvodnaia-9147/primenenie-proizvodnoi-dlia-issledovaniia-funktcii-na-monotonnost-i-ekstr_-11226

Продолжи фразу:

Рефлексия содержания учебного материала

Теперь я могу…

Было трудно…

Сегодня я узнал…

Дорогие дети! Вы получили самое основное содержание по новой теме, другие материалы вы получите от своего учителя! Если у вас есть вопросы, вы их можете задать учителю! Удачи в освоении нового материала, наши юные друзья!

Применение
производной.

Нахождение экстремумов (
максимумов и минимумов) функции.

Краткая теория. (Разобрать, записать в тетрадь основные понятия, ответить на
вопросы по теоретической части) .

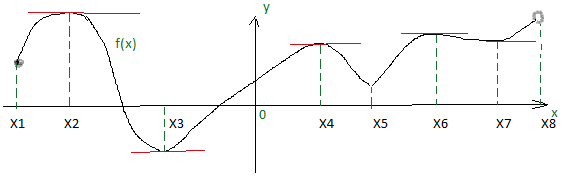
 Рисунок 1.  Рассмотрим внутренние точки области определения функции,
изображенной на рис.1, в которых производная равна нулю или не существует. В точках,
где производная равна 0, касательная параллельна оси ОХ. Это точки Х₂,
Х₃, Х₄, Х₆ и Х₇.  В точке Х₅
касательную провести нельзя, т.к. острый график, поэтому в этой точке
производная не существует.  На концах промежутка в точках Х₁ и Х₈
тоже касательные провести нельзя, так как нужна окрестность точки. На концах
промежутка экстремумов не бывает.

Определение.  Точки,
в которых производная функции равна 0 или не существует называются критическими.

На
нашем  рисунке это точки Х₂, Х₃,
Х₄, Х_5, Х₆ и Х₇.  Среди этих точек
могут быть точки максимума ( max ) и  минимума ( min ), которые называются точками экстремума       ( X_max и X_min ).  Значения функции в
этих точках называют экстремумами функции   и обозначают f_max (X_max)  и  f_min (X_min). 

Необходимым условием существования экстремумов является
равенство нулю производной или если производная не существует, то есть необходимое
условие – это наличие критических точек. (Это теорема Ферма), но этого условия
еще не достаточно. Чтобы функция имела экстремум в некоторой точке, надо, чтобы
при переходе через эту точку производная меняла свой знак, то есть надо, чтобы
возрастание менялось на убывание, или убывание на возрастание. Если такой смены
нет, то в этой критической точке не будет экстремума.

Если
знак производной меняется с  (+ ) на (- ) – это точка max, если знак производной меняется с  (- )
на (+ ) – это точка min.

На
рис.1:  Точка Х₂ является точкой max, т.к. при переходе через
эту точку возрастание сменилось убыванием ( f ´(x) поменяла знак с  (+ ) на (- )). Такими же будут
точки  Х₄   и Х_6.             В
точках Х₃   и  Х₅   при переходе  f ´(x) поменяла знак с  (- ) на (+ ). Это точки min.

В  критической точке Х₇  не произошло
смены знака производной (функция возрастала до этой точке и возрастает после
этой точки). Здесь никакого экстремума нет. Это  точка перегиба. Не будет существовать экстремумов и в точках, в которых график функции
будут разрываться. На нашем рисунке такого случая нет.

Вывод. Для существования
экстремумов необходимо выполнение двух условий:

1.       Существование критических точек.

2.       Смена знака производной при переходе через критическую точку.

Ответить на
вопросы.

Нахождение экстремумов
функции осуществляют по следующему плану:

1.      Найти
область определения функции.

2.      Найти
производную.

3.      Найти
критические точки ( приравнять производную к нулю).

4.      На
числовой прямой отметить найденные критические точки, выделить           
полученные числовые промежутки и проверить знак производной в каждом из них.

5.      Записать,
где получились точки максимума или минимума, (а может быть и перегиба, если
знак производной не менялся при переходе через точку, или разрыва).

6.      Вычислить
значение  экстремумов функции (значение самой функции в точках экстремума.

7.      Для
наглядности или когда надо построить график заданной функции, заносятся все
полученные данные в таблицу.

Рассмотрим примеры.

Пример 1. Найти
критические точки функции f(x)
=x³
-7x²
-5x +6 (в
ответ записать большее значение).          Решение.

(В данном примере надо выполнить
только три первых пункта плана.)

1.      D(
f ) = (- ∞; + ∞).

2.      Найдем
производную f ´(x)
=(x³ -7x²
-5x +6)´ =3х² – 14х -5

3.      3х²
– 14х -5= 0      D= (-14)² – 4·3·(-5) = 196
+ 60 = 256 = 16²

X₁
= (14+16)/(2·3) = 5      X₂
= (14 – 16)/(2·3) = – 1/3     Ответ: 5

Пример 2. Исследовать
функцию f(x)
=2x³  –
24x на
экстремумы ( сделать таблицу, в ответ записать а) точку минимума; б) максимум
функции).  

 Решение.

(В этом задании надо
выполнить все пункты плана.)

1.      D(
f ) = (- ∞; + ∞).

2.      Найдем
производную f ´(x)
=(2x³ – 24x)´=
6х² – 24

3.      
6х²
– 24=0 Здесь неполное
квадратное уравнение, вынесем за скобки общий множитель  6 (х²
– 4)=0;    х² – 4=0;     х² = 4;     х₁ =2 и х₂=
– 2  это критические
точки.   

4.      
 Знаки в
промежутках определяют,  выбирая любые числа из каждого промежутка и подставляя
в производную. Например, из промежутка ( -∞; -2)
можно взять число         х= – 3.        6· (-3)² -24 = 6· 9 -24=30
> 0  (если квадратичная функция, знаки чередуются).       

5.      
     Xmax
= -2     Xmin = 2

   6. f_max
(-2)
=2·(-2)³  – 24·(-2)=32  

    
 f_min
(2)
=2·(2)³  – 24·(2)= – 32

7.

X	( -∞; -2)	-2	(-2; 2)	2	(2 ; +∞)
f ´ (x)	+	0	–	0	+
f (x)	↑	32	↓	-32	↑
	max		min

Ответ:  
а)  2               б)  32.

Пример 3. Исследовать
функцию f(x)
= Х +(1/х) на экстремумы ( сделать таблицу, в ответ
записать  а) критические точки; б)  точку максимума; в) минимум функции).

Решение.

(В этом задании надо
выполнить все пункты плана.)

1.     
D( f
) = (- ∞; 0)  U (0; + ∞).      ( так
как  в выражении 1/х   х≠0)

2.     
Найдем
производную f ´(x)
=( Х +(1/х))´= 1 – (1 / х²) = (х² -1) / х²   

3.       (х²
-1) = 0     х² =1      x₁
= -1   x₂
=1  при х=0 производная не существует.  
Критических точек 3.
Это  -1;
0; 1.                               

4.          

Здесь функция не квадратичная
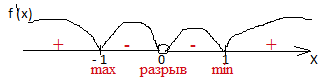
функция и знаки надо проверять в каждом  промежутке.  Например, из промежутке  
( -1; 0) можно взять х= – 0,5.    1 – (1 / х²) =
1 – (1 /( – 0,5)²) = 1 –( 1/0,25)= 
1 – 16 =-15 <0 ( поставили на рисунке знак минус.). Так проверяем знак в
каждом промежутке в этом задании.

5. В этом примере две
точки экстремума   Xmax = -1     Xmin
= 1

6.
f_max
(-1)
=  -1
+(1/-1)= -2

    
 f_min
(1)
= 1 +(1/1) = 2

7.

X	( -∞; -1)	-1	(-1; 0)	0	(0 ; 1)	1	(1 ; +∞)
f ´ (x)	+	0	—	Не существует	–	0	+
f (x)	↑	– 2	↓		↓	2	↑
	max		разрыв		min

Ответ:  а)  -1;  0;  1.          б)  –
1.         в)  2.

Решить самостоятельно.

1.     Найти
критические точки функции f(x)
= -2x³
+6x²
+ 48x – 16 (в
ответ записать меньшее значение).  

2.     Исследовать
функцию f(x)
=x³
– 27x + 20 на
экстремумы ( без таблицы, в ответ записать а) точку минимума; б) минимум
функции).  

3.      Исследовать
функцию f(x)
=3x⁴ –
4x³
+ 5 на
экстремумы ( сделать таблицу, в ответ записать  а) наименьшую критическую
точку; б) точку экстремума; в) экстремум функции; г) что происходит с функцией
в критической точке х=0 ?).  

Ответы на вопросы.

1.    Производная
равна нулю или не существует.

2.    Точки
минимума и максимума.

3.    Значение
функции в точках экстремума.

4.    Максимум
функции и минимум функции.

5.    Существование
критических точек.

6.    Смена
знака производной в этой точке.

7.    Максимум,
если знак меняется с ( + ) на ( – ).

8.    Минимум,
если знак меняется с ( – ) на ( + ).

Ответы на задачи.

1.    Критические
точки   х= -2 и х=4;      меньшее  -2

2.      а)
Точка минимума х=  3

б) 
минимум функции f(x)
=  -34

3.    а)
наименьшая критическая точка х = 0

б) 
точка экстремума    х=1

в) экстремум
функции    f(1) = -1

г)
что происходит с функцией в т. х=0?   Перегиб графика.

Значит, производная меняет знак только в точках (x=0) и (x=2).

В точке (x=0) она меняет знак с положительного на отрицательный, значит, это точка локального максимума со значением функции (f(0)=0).

В точке (x=2) она меняет знак с отрицательного на положительный, значит, это точка локального минимума со значением функции (f(2)=4).