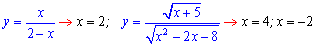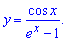Как найти критические точки функции алгоритм - Сайт, где вы сможете решить свои вопросы

Цель урока: проверка умений и навыков исследования
функций и построения графиков с помощью
производной.

Теоретическая часть зачета.

Вопросы

Определение точки минимума и точки максимума.
Определение критической точки.
Необходимое условие, чтобы точка х₀ была
точкой экстремума.
Алгоритм нахождения критических точек функции.
Определение стационарных точек.
Теорема Ферма (необходимое условие экстремума
функции).
Достаточные условия существования экстремума
функции .
Достаточный признак возрастания, убывания
функции.
Точки экстремума ,экстремум функции.
Алгоритм нахождения экстремумов функции.
Алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке.

Теоретическая часть зачета

Ответы

1) Определение точки минимума.

Если функция определена в некоторой
окрестности точки Х₀ , то точка Х₀
называется точкой минимума функции
f(х), если существует такая окрестность точки Х₀
,что для всех хх₀
из этой окрестности выполняется неравенство
f(х)>f(х₀).

Определение точки максимума.

Если функция определена в некоторой
окрестности точки Х₀ , то точка Х₀называется
точкой максимума функции f(х),если
существует такая окрестность точки Х₀ , что
для всех х?х₀ из этой окрестности
выполняется неравенство f(х)<f(х₀).

2) Определение критических точек.

Критические точки – это внутренние точки
области определения функции в которых
производная не существует или равна нулю.

3) Необходимое условие, чтобы Х₀была
точкой экстремума: эта точка должна
быть критической.

4) Алгоритм нахождения критических точек.

1. Найти область определения функции.

2. Найти производную функции.

3. Найти область определения производной данной
функции.(Чтобы определить есть ли точки в которых
производная не существует. Если такие точки есть,
то проверить являются ли они внутренними точками
области определения функции.

4. Найти точки, в которых производная равна нулю,
решив уравнение: f ‘(х)=0.

Проверить являются ли найденные точки
внутренними точками области определения
функции.

5) Стационарные точки – точки, в которых
производная функции равна нулю.

6) Теорема Ферма. (Необходимое условие экстремума
функции.)

у=f(х)-функция, которая определена в некоторой
окрестности точки Х₀, и имеет производную в
этой точке.

Теорема: если Х₀-точка экстремума
дифференцируемой функции f(х), то f ‘(х)=0.

7) Достаточные условия существования
экстремума функции в точке.

y=f(х) определена на (а;в). Х₀-критическая
точка.

Если функция f непрерывна в точке Х₀, а f
‘(х)>0 на интервале (а;х₀) и f ‘(х)<0 на
интервале (х₀;в), то точка х₀ является точкой
максимума функции f.

(Упрощенная формулировка: если в точке Х₀
производная меняет знак с “+” на “ ^_”, то Х₀
есть точка максимума.)

Если функция f непрерывна в точке Х₀, а f
‘(х)<0 на интервале (а;X₀) и f ‘(х)>0 на
интервале (X₀;в), то точка х₀ является точкой
минимума функции f.

(Упрощенная формулировка: если в точке Х₀
производная меняет знак с “^_” на “+”, то Х₀
есть точка минимума.)

8) Достаточный признак возрастания, убывания
функции.

Если f ‘(х)>0 для всех х из промежутка (а; в), то
функция возрастает на промежутке (а; в).

Если f ‘(х)<0 для всех х из промежутка (а; в), то
функция убывает на промежутке (а; в).

(Если функция непрерывна на конце промежутка,
то его можно присоединить к промежутку
возрастания (убывания) функции.)

9) Точки экстремума, экстремум функции.

Х₀ – точка максимума, Х₀ –точка
минимума называются точками экстремума.

f(х₀) – максимум функции,

f(х₀) – минимум функции называются экстремумами
функции.

10) Алгоритм нахождения экстремумов функции.

1. Находим область определения функции.

2. Находим производную функции.

3. Находим критические точки.

4. Определим знак производной на каждом из
интервалов, на которые критические точки
разбивают область определения.

5. Найдем точки экстремума, учитывая характер
изменения знака производной.

6. Найдем экстремумы функций.

11) Алгоритм нахождения наибольшего и наименьшего
значений функции на отрезке.

1. Найти значения функции на концах отрезка [а;
в].

2. Найти значения функции в тех критических
точках, которые принадлежат интервалу (а; в).

3. Из найденных значений выбрать наибольшее и
наименьшее.

Практическая часть зачета

“Исследование функций с помощью
производной.

Наибольшее и наименьшее значения
функций на отрезке”

Найти:

а) критические точки функций,

б) экстремумы функций

в) наибольшее и наименьшее значения функций на
указанном промежутке

г) построить график.

1. у=(х-3)²(х-2).	[1;4]	11. у=2х⁴-х.	[-1;1]
2. у=1/3х³+х²	[-4;1]	12. у=х²-2/х.	[-3;-0,5]
3. у=1/3х³-х²-3х	[-2;6]	13. у=1/(х²+1).	[-1;2]
4. у=-1/4х⁴+2х²+1.	[-3;3]	14. у=3х-х³.	[-1,5;1,5]
5. у=х⁴-8х²-9.	[-3;3]	15. у=2х²-х⁴.	[-2;1,5]
6. у=(х-2)(х+1)².	[-1,5;1,5]	16. у=3х^2/3-х².	[-8;8]
7. у=-2/3х³+2х-4/3.	[-1,5;1,5]	17. у=3х^1/3-х.	[-8;8]
8. у=3х⁵-5х⁴+4.	[-1;1]	18. у=х³-1,5х²-6х+4.	[-2;3]
9. у=9х²-9х³.	[-0,5;1]	19. у=(1-х)/(х²+3).	[-2;5]
10. у=1/3х³-4х.	[-3;3]	20. у= -х⁴+2х²+3.	[-0,5;2]

Ответы к практической части зачета (Приложение1)

Источник

Критические точки – это точки в которых производная функции равна нулю или не существует. Если производная равна 0 то функция в этой точке принимает локальный минимум или максимум. На графике в таких точках функция имеет горизонтальную асимптоту, то есть касательная параллельна оси Ох.

Такие точки называют стационарными. Если видите на графике непрерывной функции «горб» или «яму» помните, что максимум или минимум достигается в критической точке. Рассмотрим для примера следующее задание.

Пример 1. Найти критические точки функции y=2x^3-3x^2+5 .
Решение. Алгоритм нахождения критических точек следующий:

Итак функция имеет две критические точки.

Далее, если нужно провести исследование функции то определяем знак производной слева и справа от критической точки. Если производная при переходе через критическую точку меняет знак с «-» на «+», то функция принимает локальный минимум. Если с «+» на «-» должны локальный максимум.

Второй тип критических точек это нули знаменателя дробных и иррациональных функций

Функции с логарифмами и тригонометрические, которые не определены в этих точках

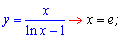
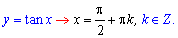
Третий тип критических точек имеют кусочно-непрерывные функции и модули.
Например любая модуль-функция имеет минимум или максимум в точке излома.

Например модуль y = | x -5 | в точке x = 5 имеет минимум (критическую точку).
Производная в ней не существует, а справа и слева принимает значение 1 и -1 соответственно.

Попробуйте определить критические точки функций

1)
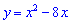
2)
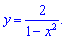
3)
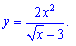
4)
5)

Если в ответе у Вы получите значение
1) x=4;
2) x=-1;x=1;
3) x=9;
4) x=Pi*k;
5) x=1.
то Вы уже знаете как найти критические точки и сможете справиться с простой контрольной или тестами.

Источник

Теоремы о дифференцируемых функциях

Рассмотрим функции и , которые непрерывны на отрезке и дифференцируемы на интервале .
Теорема Ферма
: если функция в точке $LaTeX formula: x_{0}in (a;b)$ имеет локальный экстремум, то $LaTeX formula: f'(x_{0})=0$ .
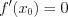
Геометрический смысл теоремы: касательная к графику функции в точке $LaTeX formula: x_{0}$ параллельна оси абсцисс.

Теорема Лагранжа: 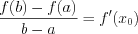$LaTeX formula: frac{f(b)-f(a)}{b-a}=f'(x_{0})$ , где $LaTeX formula: x_{0}in (a;b)$ .

Геометрический смысл теоремы: касательная к графику функции в точке $LaTeX formula: x_{0}in (a;b)$ параллельна секущей, соединяющей концы графика этой функции.

Теорема Ролля: если 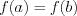и $LaTeX formula: x_{0}in (a;b)$ , то $LaTeX formula: f'(x_{0})=0$ .

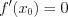
Геометрический смысл теоремы: у графика функции существует точка, в которой касательная параллельна оси абсцисс.

Теорема Коши: если $LaTeX formula: x_{0}in (a;b)$ , то $LaTeX formula: frac{f(b)-f(a)}{g(b)-g(a)}=frac{f'(x_{0})}{g'(x_{0})}$ .

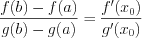
Исследование функции с помощью первой производной

С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.

Достаточное условие возрастания (убывания) функции:

а) если на заданном промежутке , то функция возрастает на этом промежутке;

б) если , то функция убывает на этом промежутке.

Экстремум
функции

Максимумом (минимумом)
функции называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.

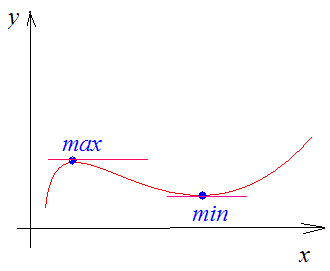
Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 6.4).

Максимум и минимум функции называются
экстремумом функции
. Значение аргумента, при котором достигается экстремум, называется
точкой экстремума
. На рисунке 6.4 значения $LaTeX formula: x_{1}$ , $LaTeX formula: x_{2}$ , $LaTeX formula: x_{3}$ , $LaTeX formula: x_{4}$ и $LaTeX formula: x_{5}$ являются точками экстремума рассматриваемой функции.

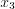
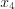
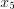
Критическими точками
функции называют те значения аргумента, при которых производная функции равна нулю или не существует. Критические точки функции находят, решая уравнение: .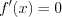

Алгоритм нахождения точек экстремума функции:

1) находим область определения функции ;
2) находим ;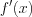

3) находим критические точки функции, решая уравнение ;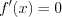

4) наносим критические точки на область определения функции;

5) определяем знак производной функции на полученных промежутках;

6) определяем точки экстремума функции по правилу:
если при переходе через критическую точку производная меняет знак c «+» на «–», то имеем точку максимума, а если с «–» на «+», то имеем точку минимума.

Рассмотрим функцию на отрезке . Свое наибольшее и наименьшее значение она может принимать либо на концах отрезка, либо в точках экстремума.

Алгоритм нахождения наибольшего и наименьшего
значений
функции на заданном отрезке:

1) находим ;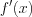

2) находим критические точки функции, решая уравнение ;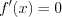

3) находим значение функции на концах отрезка и в критических точках, принадлежащих данному отрезку;

4) определяем наибольшее и наименьшее значение из полученных.

Исследование
функции с помощью второй производной

Критическими точками второго рода
функции называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.

Критические точки второго рода функции находят, решая уравнение .

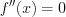
Если при переходе через критическую точку второго рода вторая производная функции меняет знак, то имеем точку перегиба
графика функции.

Если на некотором промежутке выполняется неравенство , то функция вогнута
на этом промежутке, а если 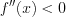, то функция
выпукла
на этом промежутке.

Пример 1.
Найдите промежутки монотонности и точки экстремума функции $LaTeX formula: y=frac{x^{3}}{3}-2x^{2}-5x+1$ .
Решение . Используя таблицу производных найдем производную функции: $LaTeX formula: y'=x^{2}-4x-5$ . Найдем критические точки: $LaTeX formula: x^{2}-4x-5=0$ , $LaTeX formula: x_{1}=-1$ , $LaTeX formula: x_{2}=5$ . Нанесем числа и на координатную прямую и установим знаки производной на полученных промежутках:

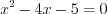
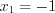
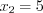
Ответ
: На промежутках и функция возрастает. На промежутке функция убывает. Точки экстремума: $LaTeX formula: x_{max}=-1$ , $LaTeX formula: x_{min}=5$ .
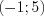
Пример 2.
Найдите точки перегиба и промежутки выпуклости и вогнутости графика функции $LaTeX formula: y=frac{x^{3}}{3}-2x^{2}-5x-23$ .
Решение
. 1. Используя таблицу производных найдем первую производную функции: $LaTeX formula: y'=x^{2}-4x-5$ .
2. Используя таблицу производных найдем вторую производную функции: .
3. Найдем критические точки второго рода: , .
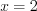
4. Нанесем точку 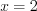на область определения данной функции и установим знаки ее второй производной на полученных промежутках:

Ответ
: На промежутке функция выпукла вверх; на промежутке функция выпукла вниз; – точка перегиба графика функции.
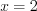
Пример 3.
Найдите наибольшее и наименьшее значение функции на отрезке .
Решение
. 1. По формуле найдем производную данной функции: .
2. Найдем критические точки функции, решая уравнение , откуда , $LaTeX formula: x=e^{-1}$ .
3. Найдем значение функции на концах отрезка и в критической точке $LaTeX formula: x=e^{-1}$ , поскольку она принадлежит данному отрезку: , $LaTeX formula: f(e^{-1})=e^{-1}ln e^{-1}=-e^{-1}$ , .

Ответ
: $LaTeX formula: y_{min}=$ $LaTeX formula: f(e^{-1})=-e^{-1}$ , $LaTeX formula: y_{max}=f(e)=e$ .

Приведем схему полного исследования функции .
1. Находим область определения функции.
2. Определяем, является ли функция четной или нечетной.
3. Выясняем, является ли функция периодической.
4. Находим точки пересечения графика функции с осью ординат.
5. Находим нули функции (точки пересечения графика функции с осью абсцисс).
6. Проводим исследование функции с помощью первой производной:
а) находим критические точки первого рода;
б) находим промежутки возрастания и убывания функции;
в) находим точки экстремума функции и значение функции в точках экстремума.
7. Проводим исследование функции с помощью второй производной:
а) находим критические точки второго рода;
б) находим промежутки выпуклости и вогнутости функции;
в) находим точки перегиба графика функции.
8. Находим асимптоты графика функции.
9. Строим график функции.
10. Находим промежутки знакопостоянства функции: промежутки, на которых функция положительна и промежутки, на которых функция отрицательна.
11. Находим область значений функции.

Источник

Содержание:

Критические точки и экстремумы функции
Теорема Ферма (Необходимое условие существовании экстремумов)
Достаточное условие существования экстремума
Задача пример №117
Задача пример №118
Задача пример №119
Задача пример №120
Задача пример №121

Критические точки и экстремумы функции

В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.

1. Для значений равных угловой коэффициент касательной к графику равен 0. Т.e. . Эти точки являются критическими точками функции.

2. В точках функция не имеет производной. Эти тоже критические точки функции.

3. Для рассматриваемой нами функции критические точки делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки – критические точки, которые не изменяют возрастание и убывание (или наоборот).

По графику видно, что в точках внутреннего экстремума производная функции равна нулю, а в точке производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.

Теорема Ферма (Необходимое условие существовании экстремумов)

Во внутренних точках экстремума производная либо равна нулю, либо не существует.

Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке производная функции равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.

На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т.е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.

Достаточное условие существования экстремума

Пусть функция непрерывна на промежутке и . Если является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:

1 ) слева от точки положительна, а справа – отрицательна, то точка является точкой максимума.

2) слева от отрицательна, а справа – положительна, то точка является точкой минимума

3) с каждой стороны от точки имеет одинаковые знаки, то точка не является точкой экстремума.

Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.

Соответствующие наибольшее и наименьшее значения функции на отрезке записываются как и .

Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.

Задача пример №117

Для функции определите максимумы и минимумы и схематично изобразите график.

Решение:

Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.

1. Производная функции:

2. Критические точки функции:

3. Точки и разбивают область определения функции на три промежутка.

Проверим знак на интервалах, выбрав пробные точки:

для интервала

Интервал Пробные точки

Знак Возрастание и убывание

При имеем . (-1;3) – максимум

При имеем (1;-1) – минимум

4. Используя полученные для функции данные и найдя координаты нескольких дополнительных точек, построим график функции.

Задача пример №118

Найдите наибольшее и наименьшее значение функции на отрезке [-1;2].

Решение:

Сначала найдем критические точки. Так как , то критические точки можно найти из уравнения . Критическая точка не принадлежит данному отрезку [-1; 2], и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке и на концах отрезка.

Из этих значений наименьшее – 4, наибольшее 12. Таким образом:

Задача пример №119

Найдите экстремумы функции .

Решение:

1. Производная функции:

2. Критические точки: ,

3. Интервалы, на которые критические точки делят область определения функции:

Проверим знак на интервалах, выбрав пробные точки.

Для промежутка возьмем

Для промежутка (0; 1,5) возьмем

Для промежутка возьмем

Интервал

Пробные точки

Знак Возрастание-убывание

Используя полученную для функции информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами и касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.

• Функция на промежутке возрастает.

• Точка критическая точка функции , но не является экстремумом.

• Функция на промежутке [0; 1,5] возрастает.

• Функция на промежутке убывает.

•

Задача пример №120

Найдите экстремумы функции

Решение:

1. Производная

2. Критические точки: для этого надо решить уравнение или найти точки, в которых производная не существует. В точке функция не имеет конечной производной. Однако точка принадлежит области определения. Значит, точка является критической точкой функции.

3. Промежутки, на которые критическая точка делит область определения функции: и

Определим знак , выбрав пробные точки для каждого промежутка:

Для возьмем Для возьмем

Интервал Пробные точки

Знак

Возрастание-убывание

• Функция на промежутке убывает.

• Функция на промежутке возрастает.

•

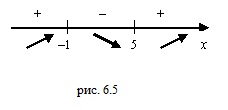
Задача пример №121

По графику функции производной схематично изобразите график самой функции.

Решение:

Производная в точке равна нулю, а при отрицательна, значит, на интервале функция убывающая. При производная положительна, а это говорит о том, что функция на промежутке возрастает. Точкой перехода от возрастания к убыванию функции является точка . Соответствующий график представлен на рисунке.

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Другие темы которые вам помогут понять математику:

Объемы подобных фигур

Нахождение промежутков возрастания и убывания функции

Построение графиков функции с помощью производной

Задачи на экстремумы. Оптимизации

Лекции:

Экстремумы функции двух переменных. Производная по направлению
Доказательство неравенств
Системы уравнений
Максимальные и минимальные значения функции
Действия с корнями
Отрицательное биномиальное распределение
Длина дуги кривой
Вычислить несобственный интеграл
Градиент функции: пример решения
Интеграл натурального логарифма

Источник

Алгоритмы решения задач с применением производной

В 11 классе с помощью производной мы находим мгновенную скорость и ускорение точки; строим касательную к графику функции; находим критические точки; промежутки возрастания, убывания и постоянства функции; точки экстремума; экстремумы функции; используем производную для исследования функции и построения ее графика; для решения «экстремальных задач»; для нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке.

Почти все типы задач решаю с учащимися с помощью алгоритмов.

Критические точки

Определение. Критические точки – это внутренние точки области определения, в которых производная равна нулю или не существует.

Алгоритм нахождения критических точек функции.

Найти область определения функции.
Найти производную функции.
Решить уравнение f ‘(х) = 0.
Выяснить, являются ли корни уравнения f ‘(х) = 0 внутренними точками определения функции.
Сделать вывод.

Учащиеся очень часто не обращают внимания на слова «внутренние точки области определения», поэтому при изучении данной темы, на уроке рассматриваю три функции, для которых находим критические точки.

Найти критические точки функций.

а) б) в) .

а)

Решение.

Область определения функции

x ≠ 0 D (y) = (-∞; 0) ⋃ (0; ∞).

.
Решим уравнение у'(х) = 0.

4 ∊D(у) и -4 ∊D(у) и являются внутренними точками области определения, значит являются критическими.у'(х) не существует при х = 0, но 0 ∉ D(у), значит х = 0 не является критической точкой.

Ответ: ± 4.

б)

Решение.

Найдем область определения функции

100 – х²≥ 0

х²-100 ≤ 0

(х – 10)(х + 10) ≤ 0

D (y)=[-10; 10]

0∊D(у)и является внутренней точкой области определения.у'(х) не существует при х = ±10, -10 D(у),и 10 D(у), но они не являються внутренними точками области определения,значит не являются критическими.

Ответ: 0.

в)

Решение.

Область определения функции

D (y) =R.

Точек, в которых производная равна нулю, не существует.

Производная не существует при , х + 8 = 0; х = -8.

-8∊D(у)и является внутренней точкой области определения, значит является критической.

Ответ: -8.

При построении графиков функций, очень важно находить промежутки возрастания, убывания функции (промежутки монотонности, а также точки экстремума и экстремумы функции.

Алгоритм нахождения промежутков возрастания и убывания функции.

Найти область определения функции и интервалы, на которых функция непрерывна.
Найти производную функции.
Найти критические точки: f ‘(х) = 0.
Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов. (Если на рассматриваемом интервале
f ‘(х)> 0, то функция возрастает, а если f ‘(х)< 0, то функция убывает).

Найти промежутки возрастания и убывания функции

Решение.

Область определения

D (y) =R. Функция непрерывна в каждой точке своей области определения.

Найдем критические точки у'(х) = 0.

x₁ = 3; x₂ = -2.

Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов.

у'(х) = х³ – х² – 6х

у’ (-3) = (-3)³– (-3)² – 6(-3) = -27 – 9 + 18 = -18 < 0.

у’ (-1) = (-1)³– (-1)² – 6(-1) = -1 – 1 + 6 = 4 > 0.

у’ (1) = 1³– 1² – 6 · 1 = -6 < 0.

у’ (4) = 4³– 4² – 6 · 4 = 64 – 16 – 24 = 24 > 0.

Функция возрастает при х∊ (- ∞; -2] ∪ [0; 3].

Ответ; Функция возрастает при х∊ (- 2; 0] ∪ [3; ∞] и убывает при х∊ (-∞;-2] ∪ [0;3].

Найти промежутки монотонности функции

Решение.

Область определения

х + 2 ≠ 0

х ≠ -2

D (y) = (-∞; -2) ∪ (-2; ∞).

Функция непрерывна в каждой точке своей области определения.

Найдем критические точки у'(х) = 0.

2 ∊ D (y) и -6 ∊ D (y) и являются внутренними точками области определения, значит являются критическими,у’ (х) не существует при х = -2, но -2 ∉D (y), значит не является критической.

Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов.

Функция возрастает при х∊ [-6; -2) ∪ (-2; 2 ].

Ответ: функция возрастает при х ∊ (-∞; -6] ∪ [2; ∞) и убывает при
х∊ [-6; -2) ∪ (-2; 2 ].

Необходимое условие экстремума

В точках экстремума, производная функции равна нулю или не существует. Но не в каждой точке х₀, где f ‘(х₀) = 0 или f ‘(х₀) не существует. Но не в каждой точке х₀, где f ‘(х₀) =0 или f ‘(х₀) не существует, будет экстремум.

Достаточное условие экстремума

Если функция f (х) непрерывна в точке х₀ и производная f ‘(х) = меняет знак в точке х_0,то х₀ – точка экстремума функции f ‘(х).

Если в точке х₀ знак f ‘(х) меняется с «+» на «-», то х₀ – точка максимума.

Если в точке х₀ знак f ‘(х) меняется с «-» на «+», то х₀ – точка минимума.

Точки максимума и минимума называются точками экстремума. А значения функции в точках экстремума называются экстремумами функции.

Алгоритм нахождения точек экстремума и экстремумов функций

Найти область определения.
Найти производную функции
Найти критические точки
Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов.
Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума.

точки максимума

=>точки экстремума

точки минимума

Найти значения функции в точках экстремума – это экстремумы функции.
Записать требуемый результат исследования функции.

Найти точки экстремума функции.

Решение

Область определения

х²≠ 0

х ≠ 0.

D (y) = (-∞; 0) ∪ (0; ∞).

Найдем критические точки f ‘(х) = 0

Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов.

х = 2 – точка min, т.к. при переходе через точку х = 2, производная поменяла знак с «-» на «+»

Ответ: 2.

Найти точки экстремума функции f(x) = x² · e^x. Если их несколько, найти их сумму.

Решение.

D(f) = R.
f ‘(х) = (х²)’·е^х + х²· (е^х)’ = 2х · е^х + х²е^х = х· е^х(2 + х).
Найдем критические точки f ‘(х) = 0.

х · е^х (2 + х) = 0, е^х ≠ 0.

х = 0 или 2 + х = 0

х = -2.

0 ∊D(f)и -2 ∊D(f)и являются внутренними точками области определения, значит являются критическими

Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов.

f ‘(х) = х· е^х (2 + х)

x = -2 –точка мах

точки экстремума

х = 0 – точка min

-2 + 0 = -2.

Ответ: -2.

Найти точки экстремума функции . Если их несколько, найти их сумму.

Решение.

Найдем область определения.

х ≠ 0

D(f) = (-∞; 0) ∪ (0; ∞).

Найдем критические точки f ‘(х) = 0.

Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов.

х = -1 – точка min – точка экстремума.
– экстремум функции.

Ответ: 3.

Уравнение касательной к графику функции

у = kx + b – прямая.

k = f‘(х₀) = tgα

Уравнение касательной имеет вид

y = f (x₀) + f‘ (x₀) · (x – x₀), где х₀– абсцисса точки касания.

f (x₀)
f ‘ (x)
f‘ (x₀)

Уравнение привести к виду y = kx + b

Составить уравнение касательной к графику функции у = х² – 2х в точке с абсциссой х₀ = 3.

Решение.

Уравнение касательной имеет вид:

y = f (x₀) + f ‘ (x₀) · (x – x₀).

f (x₀) = f(3) = 3² – 2 · 3 = 9 – 6 = 3.

f ‘(x) = 2х – 2; f ‘(x₀) = f ‘(3) = 2 · 3 – 2 = 4.

у = 3 + 4 (х – 3)

у = 3 + 4х – 12.

у = 4х – 9.

Ответ:у = 4х – 9.

Дана кривая у = -х² + 1. Найти точку ее графика, в которой касательная параллельна прямой у = 2х + 3.

Решение.

Так как касательная параллельная прямой у = 2х + 3, то их угловые коэффициенты равны, т.е.k = y‘(х₀) = 2.

y‘(х) = -2 х.

Пусть х₀ – абсцисса точки касания, тогда y‘(х₀) = -2 х₀, поэтому -2 х₀ = 2, х₀ = -1,

аy₀ = f(-1) = -(-1)² + 1= 0.

Итак, (-1; 0) – искомая точка.

Ответ: (-1; 0).

На параболе у = х² – 2х – 8 найти точку М, в которой касательная к ней параллельна прямой 4х + у + 4 = 0.

Решение.

Определим угловой коэффициент касательной к параболе у = х² – 2х – 8:у’ = 2х – 2.

Найдем угловой коэффициент прямой 4х + у + 4 = 0: у = -4х – 4, k = -4.

Касательная к параболе и данная прямая по условию параллельны, следовательно, их угловые коэффициенты равны 2х – 2 = -4, 2х = -2, х = -1.

Найдем ординату точки М:у (-1) = (-1)² – 2 · (-1) -8 = 1 + 2 – 8 = -5.

М (-1; -5)

Ответ: М (-1; -5).

Найти координаты точки, в которой касательная к параболе у = х² – х – 12, образует с осью ОХ угол 45°.

Решение.

Найдем тангенс угла наклона касательной, проведенной в искомой точке, к оси ОХ:
tgα = y‘ (x) = 2x – 1, т.к. α = 45°, то tg 45° = 2x – 1,

1 = 2х – 1

2х = 2

х = 1.

Определим ординату искомой точки: у (1) = 1² – 1 – 12 = -12.

Искомая точка (1; -12).

Ответ: (1; -12).

В какой точке кривой, касательная наклонена к оси абсцисс под углом 60°?

Решение.

Находим у'(х).

Т.к. по условию у'(х) = k = tg 60°, то

Возведем обе части уравнения в степень , тогда

Найдем ординату точки касания:

. Итак, искомая точка .

Ответ:.

Найти угол между прямой х = 3 и параболой у = х².

Решение.

Углом между прямой и кривой называется угол между этой прямой и касательной к кривой в точке их пересечения.

ΔАВС прямоугольный (), тогда , значит φ = 90° – α или . Найдем у’ (х) = 2х. Т.к. tgα = y‘ (3) = 2 · 3 = 6, то α = arctg 6. Следовательно,

Ответ:

Найти, под каким углом ось ОХ пересекает параболу у = х² + х.

Решение.

Найдем точки пересечения параболы у = х² + х сосью ОХ. Для этого следует решить систему уравнений

x² + x= 0

x (x + 1) = 0

x = 0 или x + 1 = 0, x= -1.

Значит парабола пересекает ось ОХ в точках
(-1; 0) и (0; 0).

у‘ = (х² + х)’ = 2х + 1

k₁ = y‘ (-1) = 2 ·(-1) + 1 = -1 k₂ = y‘ (0) = 2 · 0 + 1 = 1

k = tgα, tgα₁ = -1 tgα₂ = 1

α₁ = 135° α₂ = 45°

Ответ: 135°, 45°.

Составить уравнение касательной к графику y = cosx в точке абсцисс

Решение.

Уравнение касательной имеет вид

y = у(x₀) + у ‘(x₀) · (x – x₀).

а)

– уравнение касательной в точке .

б)

– уравнение касательной в точке .

Ответ: ; у = 1

Найти координаты точки пересечения касательных к графику функции f(x) = sin 3x в точках с абсциссами .

Решение.

Напишем уравнение касательной к графику функции в точке с абсциссой

y = f (x₁) + f ‘(x₁) · (x – x₁).

– уравнение касательной в точке с абсциссой .

Напишем уравнение касательной в точке с абсциссой .

y = f (x₂) + f ‘(x₂) · (x – x₂).

– уравнение касательной в точке с абсциссой .

Чтобы найти координаты точки пересечения касательных, решим систему уравнений

– точка пересечения касательных.

Найти площадь треугольника, ограниченного координатными осями и касательной к графику функции в точке с абсциссой х₀ = 1.

Решение.

Напишем уравнение касательной к графику функции в точке с абсциссой х₀ = 1.

y = f (x₀) + f ‘(x₀) · (x – x₀).

y = -2 – 5 ∙ (x – 1)

y = -2 – 5x + 5

y = -5x + 3 – уравнение касательной.

Найдем координаты точек пересечения касательной с осями координат

На оси ОХ у = 0

0 = -5х + 3

5х = 3

На оси ОYx = 0

y = -5∙0 + 3

y = 3 (0; 3)

АО = 3; ОВ =

Ответ: 0,9.

Найти уравнения касательных к графику функции f(x)=6x – x² в точках с абсциссами х₁ = 1 и х₂ = 4 и площадь треугольника, ограниченного этими касательными и осью ОУ.

Решение.

Графиком функции f(x)=6x–x² является парабола, ветви которой направлены вниз.

Нули функции

6х – х² = 0

х (6 – х) =0

х = 0 х = 6

Напишем уравнение касательной к графику функции f(x)=6x–x² в точке с абсциссой х₁ = 1

y = f (x₁) + f ‘(x₁) · (x – x₁).

y = 5 + 4(x – 1)

y = 5 + 4x – 4

y = 4x + 1

Данная касательная пересекает ось OY в точке А

х = 0, у = 4∙ 0 + 1 = 1, А (0; 1).

Напишем уравнение касательной к графику функции в точке с абсциссой х₂ = 4.

y = f (x₂) + f ‘(x₂) · (x – x₂).

у = 8 – 2 (х – 4)

у = 8 – 2х + 8

у = -2х + 16.

Данная касательная пересекает ось OYв точке В

х = 0, у = 16, В (0; 16).

ТочкаС – точка пересечения касательных.

СК ⊥ АВ, СК – высота ΔАВС.

Найдем абсциссу точки пересечения касательных

4x + 1 = -2x + 16

4x + 2x = 16 – 1

6x = 15

Ответ: 18,75

Решение экстремальных задач

Алгоритм решения текстовых задач на определение наименьшего и наибольшего значения с помощью производной

Ввести переменную х.
Определить промежуток изменения х, исходя из реального условия задачи.
Составить формулу для функции от х, наименьшее или наибольшее значение которой требуется определить.
Найти производную функции.
Вычислить критические точки функции.
Выбрать те критические точки, которые принадлежат промежутку для х.
Вычислить значения функции в критических точках, лежащих внутри промежутка и на его концах.
Установить вид экстремума в критических точках внутри промежутка с помощью достаточного условия экстремума.
Из всех полученных чисел выбрать наибольшее или наименьшее.
Записать ответ.

Задача 1. Вычислить длину сторон прямоугольника, периметр которого 48 см., имеющего наибольшую площадь.

Решение.

В С

Р = 2 (АВ + АD)

48 = 2(AB + AD)

AB + AD = 24

А D

Пусть АВ = х см, тогда АD = (24 – х) см.

Исходя из условия задачи х ϵ (0; 24).

Составим функцию площади прямоугольника, наибольшее значение которой необходимо найти.

S (x) = x∙(24 – x)

S (x) = 24x – x²

Найдем критические точки функции S (x) = 24x – x²

S΄ (x) = (24x – x²)΄ = 24 – 2х

S΄ (x) = 0

24 – 2х = 0

2х = 24

х = 12 ϵ (0; 24)

Определим вид экстремума в критической точке х = 12

S΄ (x) = 24 – 2х

S΄ (1) = 24 – 2 ∙1 = 22 > 0

S΄ (13) = 24 – 2 ∙ 13 = 24 – 26 = -2 < 0.

х = 12 – точка мах

S (0) = 0 ∙(24 – 0) = 0

S (24) = 24 ∙(24 – 24) = 0

S (12) = 12 ∙(24 – 12) = 12 ∙12 = 144.

Наибольшее значение площади прямоугольника при х = 12 см., значит

АВ = CD = 12 (см), а

AD = BC = 24 – 12 = 12 (см)

т.е. АВСD – квадрат со стороной 12 см.

Ответ: квадрат со стороной 12 см.

Задача 2. Забором длиной ℓ требуется огородить наибольшую по площади прямоугольную площадку, примыкающую к реке. Каковы должны быть размеры прямоугольника, если со стороны реки забор не установлен.

Решение.

АВ + AD + CD = ℓ.

Пусть АВ = CD = х см, тогда АD = ℓ – 2х.

Исходя из условия задачи хϵ (0; ℓ).

Составим формулу площади прямоугольника, наибольшее значение которой нужно найти.

S (x) = x∙ (ℓ – 2х).

S (x) = ℓx– 2х².

S΄(x) = (ℓx– 2х²)΄=ℓ – 4х.

Найдем критические точки функции S΄(x) = 0.

ℓ – 4х = 0

4х = ℓ

Установим вид экстремума в критической точке

S΄(x) = ℓ – 4х

– точка мах.

S (0) = 0 (

S (ℓ) = ℓ∙(ℓ – 2ℓ) = –ℓ².

Наибольшую площадь прямоугольная площадка имеет при , значит АВ = СD = , а .

Ответ:

Нахождение наибольшего и наименьшего значения функции, непрерывной на отрезке

Если функция f (x) непрерывна на отрезке и имеет на нем конечное число критических точек, то она принимает свое наибольшее и наименьшее значение на этом отрезке или в критических точках, принадлежащих этому отрезку, или на концах отрезка.

Алгоритм нахождения наибольшего и наименьшего значения функции,

непрерывной на отрезке

Найти область определения функции и проверить принадлежит ли отрезок области определения.
Найти производную f΄(x).
Найти критические точки.
Выбрать критические точки, принадлежащие заданному отрезку.
Вычислить значения функции в этих критических точках и на концах отрезка.
Сравнить полученные значения и выбрать из них наименьшее и наибольшее.

Найти наибольшее и наименьшее значение функции на отрезке.

Решение.

Область определения

Найдем критические точки y΄(x) = 0.

Вычислим значения функции в критической точке х = -2 и на концах отрезка [-3;0]

max y(x) = y (-2) = -4

[-3; 0 ]

miny(x) = y (0) = -8

[-3; 0 ]

Ответ: -4; -8.

Применение производной при решении уравнений,

неравенств, доказательстве тождеств.

При этом будем использовать следующие свойства функций:

Если непрерывная функция f(x) возрастает или убывает на некотором промежутке, то на этом промежутке уравнение f(x) = 0 имеет не более одного корня.
Если f΄(x) = 0 на некотором промежутке, то f(x) =const на этом промежутке.