Как найти критический путь для сетевого графика

Как найти критический путь для сетевого графика

Определение критического пути

Будем
предполагать, что время выполнения
каждой работы точно известно. Введем
следующие определения.

Путь— последовательность взаимосвязанных
работ, ведущая из одной вершины проекта
в другую вершину. Например (см. Рисунок 48),
{A, D, G} и {C, F} – два различных пути.

Рисунок
48. Различные пути на сетевом графике

Длина
пути— суммарная продолжительность
выполнения всех работ пути.

Полный
путь— это путь от исходного к
завершающему событию.

Критический
путь— полный путь, суммарная
продолжительность выполнения всех
работ которого является наибольшей.

Очевидно,
что минимальное время, необходимое для
выполнения любого проекта равно длине
критического пути. Именно на работы,
принадлежащие критическому пути, следует
обращать особое внимание. Если такая
работа будет отложена на некоторое
время, то время окончания проекта будет
отложено на то же время. Если необходимо
сократить время выполнения проекта, то
в первую очередь нужно сократить время
выполнения хотя бы одной работы на
критическом пути.

Для
того, чтобы найти критический путь,
достаточно перебрать все пути и выбрать
тот, или те из них, которые имеют наибольшую
суммарную продолжительность выполнения
работ. Однако для больших проектов
реализация такого подхода связана с
вычислительными трудностями. Метод
критического пути (метод CPM — Critical Path
Method) позволяет получить критический
путь намного проще.

Расчет
сетевой модели начинают с временных
параметров событий, которые вписывают
непосредственно в вершины сетевого
графика (Рисунок 49):

  • –ранний
    срок наступления события i, минимально
    необходимый для выполнения всех работ,
    которые предшествуют событию i;

  • –поздний
    срок наступления события i, превышение
    которого вызовет аналогичную задержку
    наступления завершающего события сети;

  • –резерв
    события i, т.е. время, на которое может
    быть отсрочено наступление события i
    без нарушения сроков завершения.

Рисунок
49. Параметры событий

Ранние
сроки наступления событий рассчитываются
от исходного (S) к завершающему (F) событию
следующим образом:

  1. для
    исходного события S:
    ;

  2. для
    всех остальных событий i:
    ,

где
максимум берется по всем работам (k,i),
входящим в событие i;
— длительность работы (k,i) (см. Рисунок 50).

Рисунок
50. Ранние сроки наступления событий

Поздние
сроки наступления событий
рассчитываются от завершающего к
исходному событию:

  1. для
    завершающего события F:
    ;

  2. для
    всех остальных событий i:
    ,

где
минимум берется по всем работам (i,j),
выходящим из события i;
— длительность работы (i,j) (см. Рисунок 51).

Рисунок
51. Поздние сроки наступления событий

Условия
критичности пути:

  • необходимое
    условие: нулевые резервы событий,
    лежащих на критическом пути
    ;

  • достаточное
    условие: нулевые полные резервы работ,
    лежащих на критическом пути
    .—
    показывает максимальное время, на
    которое можно увеличить длительность
    работы (i,j) или отсрочить ее начало,
    чтобы не нарушился срок завершения
    проекта в целом.

Пример

Рассмотрим
пример. Компания разрабатывает
строительный проект. Исходные данные
по основным операциям проекта представлены
в таблице. Нужно построить сетевую
модель проекта, определить критические
пути и проанализировать, как влияет на
ход выполнения проекта задержка работы
D на 4 недели.

Работа

Непосредственно
предшествующая работа

Длительность,
недели

A

–

4

B

–

6

C

A,
B

7

D

B

3

E

C

4

F

D

5

G

E,F

3

Сетевой
график проекта показан на рисунке ниже
(см. Рисунок 52).

Рисунок
52. Пример. Сетевой график проекта

Согласно
необходимому условию два полных пути
сетевой модели (см. Рисунок 52)
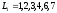
имогут быть критическими. Проверим
достаточное условие критичности для
работ (1,2) и (1,3)

,

.

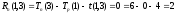
Путь
,
начинающийся с работы (1,3) не является
критическим, т.к. поскольку как минимум
одна из его работ не является критической.
Работа (1,3) имеет ненулевой полный резерв,
а значит может быть задержана с
выполнением, что недопустимо для
критических работ.

Таким
образом, сетевая модель имеет единственный
критический путь
длительностью 20 недель. За выполнением
работ этого пути необходим особый
контроль, т.к. любое увеличение их
длительности нарушит срок выполнения
проекта в целом.

Работа
D или (2,5) не является критической, ее
полный резерв равен 3-м неделям. Это
означает, что при задержке работы в
пределах 3-х недель срок выполнения
проекта не будет нарушен. Поэтому если
согласно условию работа D задержится
на 4 недели, то весь проект закончится
на 1 неделю позже.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Критический путь

Критический путь

Критический путь (англ. Critical Path Method — СРМ) является основным методом управления проектами, наравне с системой оценки и пересмотра планов проектов и программ (англ. Program Evaluation and Review Technique – PERT). В советской практике оба метода, а также их более сложные модификации объединяются понятием «методы сетевого планирования и управления«.

Критический путь сетевой модели – это самая длинная по срокам последовательная цепочка работ. Как в методе критического пути, так и в методе PERT проекты рассматриваются как сети отдельных событий и работ. Работа в этих системах представляет собой любой элемент проекта, на выполнение которого требуется время, и который может задержать начало выполнения других работ.

Основное различие между методом критического пути и методом PERT заключается в различном подходе к длительности операций. Метод критического пути исходит из того, что длительность операций можно оценить с достаточно высокой степенью точности и определенности.

Метод PERT допускает неопределенность продолжительности операций и анализирует влияние этой неопределенности на продолжительность работ по проекту в целом. Большее распространение получил метод критического пути, а не метод оценки и пересмотра планов. Системы управления работами по реализации проектов, в основе которых лежит метод критического пути, в настоящее время применяются во всем мире.

Планирование работ по методу критического пути

Применение метода критического пути для разработки календарного графика реализации работ по проекту предусматривает в основном выполнение четырех этапов анализа. Их может быть намного больше, если проект более масштабный. В качестве примера для анализа возьмем пример проекта по строительству гаража.

Рисунок 1. Работы проекта по строительству гаража.

1 этап планирования по методу критического пути

Цели и ограничения

Чтобы установить цели и ограничения в рамках планирования по методу критического пути, необходимо рассмотреть проект в следующих аспектах:

  • продолжительность;
  • стоимость;
  • качество;
  • наличие производственных ресурсов (рабочая сила и оборудование);
  • другие важные аспекты.

В нашем примере строительства гаража целью будет являться скорейшее завершение строительства при следующих ограничениях:

  • Стоимость проекта не должна превышать 150 тыс. руб.
  • Обязательное соблюдение технических условий проекта и всех строительных норм.
  • Для строительства гаража имеется только двое рабочих.
  • Некоторые виды работ нельзя выполнять в ненастную работу.

2 этап планирования по методу критического пути

Продолжительность работ

Второй этап планирования по методу критического пути представляет собой определение работ, входящий в проект, и расчете длительности каждой работы. В нашем примере ожидание того, пока бетонная плита затвердеет, считается операцией, поскольку на это требуется время и начать выполнение других работ до затвердения плиты невозможно. Перечень работ по строительству гаража и их продолжительность показаны на рисунке 1.

3 этап планирования по методу критического пути

Сетевой график работ

Третий этап планирования по методу критического пути включает в себя анализ установки очередности работ и составление графика, отражающего последовательность работ. Некоторые работы должны производиться в определенной последовательности, некоторые можно выполнять параллельно. Очередность работ в основном определяется техническими причинами.

Например, технически невозможно уложить кровлю крыши до тех пор, пока не будет произведена ее обшивка. Но в некоторых случаях очередность определяется по принципу предпочтительности с учетом качества, эффективности или требованиями техники безопасности. Например, электрическую проводку в гараже можно установить сразу после возведения каркаса, но чтобы избежать попадания дождя на арматуру, лучше подождать с электропроводкой до установки боковых стен и крыши. В нашем примере очередность работ выглядит следующим образом:

Критический путь
Рисунок 2. Очередность работ и критический путь.

4 этап планирования по методу критического пути

Линейная диаграмма Ганта и сетевой график

Четвертый этап планирования по методу критического пути предусматривает построение диаграммы Ганта и календарного сетевого графика на основе оценок продолжительности работ (рисунок 1) и полученной сети расписания (рисунок 2). Линейная диаграмма Ганта и сетевого график на данном рисунке построены в программе Microsoft Project по данным проекта по строительству гаража.

Диаграмма Ганта
Рисунок 3. Линейная диаграмма Ганта.
Сетевой график
Рисунок 4. Фрагмент сетевого графика.

Критический путь

Критический путь в проекте — это самая продолжительная последовательная цепочка операций. Критическим путем на диаграмме Ганта, является непрерывная последовательность работ, проходящая через центр графика (Рисунок 2).

Длина критического пути определяет продолжительность работ по выполнению проекта. Любые задержки на критическом пути ведут к увеличению сроков работ. Кроме того, необходимо подчеркнуть, что для сокращения продолжительности работ по проекту необходимо сокращать длину критического пути. Резерв или запас времени – это разность между самым ранним возможным сроком завершения работы и самым поздним допустимым временем ее выполнения.

Резерв времени имеется только в тех работах, которые не лежат на критическом пути, и дает некоторую степень гибкости при календарном планировании таких работ. Линейная диаграмма Ганта и сетевой график дают наглядную и понятную картину последовательности работ по реализации проекта помимо того, что такие графики показывают начало и окончание работы. Они четко указывают на очередность выполнения работ. На линейной диаграмме Ганта и сетевом графике наглядно видны последствия запаздывания любой работы с точки зрения времени реализации всего проекта.

Алексей Голубицкий, компания Alawar

Просмотры: 108 930

Источник

Анализ сетевого графика

С помощью данной программы можно онлайн определить параметры сетевого графика (рассчитать сроки свершения событий, резервы времени и критический путь), найти коэффициенты напряженности. Оптимизация сетевого графика проводится по следующим критериям: число исполнителей, резервы-затраты, сокращение сроков (см. вкладку Параметры сетевого графика).

Сетевой график можно нарисовать, а также задать в виде матрицы или таблицы (меню Действия).

  • Ввод данных
  • Параметры сетевого графика
  • Решение
  • Видеоинструкция
  • Оформление Word

Нумерация вершин с №1

Выберите нужный тип вершины и нажмите левой кнопкой мыши на графическом полотне

Размеры графического полотна

Ширина
Высота

Созданный сетевой график можно сохранить в форматах docx и png (меню Действия).

Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).

Для сформированного графа можно выполнить следующие действия:

Здесь будет показано решение

Инструкция к сервису

Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить. Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с 0, для этого нужно снять отметку с пункта Нумерация вершин с №1.

1234
1103015

Нумерация вершин с 0

0123
1103015



Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить.

Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции.

Построенный граф можно сохранить в формате docx или png.

Если в качестве формы вершин используется прямоугольник, то при построении секторальной диаграммы применяется методология Microsoft Visio с отображением параметров duration, ES, EF, LS, LF, and slack.

Основные определения

Ориентированный граф, в котором существует лишь одна вершина, не имеющая входящих дуг, и лишь одна вершина, не имеющая выходящих дуг, называется сетью. Сеть, моделирующая комплекс работ, называется его сетевой моделью или сетевым графиком. Дуги, соединяющие вершины графа, ориентированы в направлении достижения результата при осуществлении комплекса работ.

Наиболее распространен способ представления моделируемого комплекса работ в понятиях работ и событий.

Понятие «работа» имеет следующие значения:

  • «действительная работа» – процесс, требующий затрат времени и ресурсов;
  • «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.

Работа на графике изображается стрелкой, над которой указывается затрачиваемое на нее время. Длина стрелки и ее ориентация на графике не имеют значения. Желательно только выдерживать направление стрелок так, чтобы начальное событие для работы (обозначается i) располагалось слева в сетевом графике, а конечное (обозначается j) – справа. Для отображения фиктивных работ используют пунктирные стрелки, над которыми время не указывается или проставляется ноль.

На сетевой модели событиям соответствуют вершины графа.

Правила построения сетевой модели

Правило 1. Каждая операция в сети представляется одной и только одной дугой (стрелкой). Ни одна из операций не должна появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на части; тогда каждая часть изображается отдельной дугой.

Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.

Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:

а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?

б) Какие операции должны непосредственно следовать после завершения данной операции?

в) Какие операции могут выполняться одновременно с рассматриваемой?

При построении сетевого графика следует соблюдать следующие правила:

  • в сети не должно быть “тупиков”, т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
  • В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
  • в сети не должно быть замкнутых контуров (рис.1);
  • Любые два события должны быть непосредственно связаны не более чем одной работой.
  • В сети рекомендуется иметь одно исходное и одно завершающее событие.
  • Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелка

завершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.

Методы оптимизации сетевого графика

Логико-математическое описание, формирование планов и управляющих воздействий осуществляется на базе использования особого класса моделей, называемых сетевыми моделями.

После построения и расчета сетевого графика (определения его параметров), выполнения анализа графика, заключающегося в оценке его целесообразности и структуры, оценке загрузки исполнителей, оценке вероятности наступления завершающего события в заданный срок, следует приступать к оптимизации сетевого графика. Процедура оптимизации заключается в приведение графика в соответствие с заданными сроками выполнения работ, возможностями подрядных организаций и т.д. В общем случае под оптимизацией следует понимать процесс улучшения организации выполнения работ.

Для возможности оптимизации сетевой модели, все исходные данные вводятся в виде таблицы (Операции/Добавить в виде таблицы).

  • Оптимизация сетевой модели по критерию “число исполнителей”. Заполняется столбец Количество исполнителей Ч
  • Оптимизация сетевой модели по критерию “время – стоимость” (время – затраты). В случае известных коэффициентов затрат на ускорение работ заполняется только этот столбец h(i,j). Иначе, заполняются столбцы tопт (Нормальный режим), Минимальное время работ, tmin (Ускоренный режим), Нормальная стоимость, Cн и Срочная стоимость, Cc.

Графики привязки (а) и загрузки (b) до оптимизации

1,261,311,452,532,613,684,644,725,866,817,83 1122 3194175 6 7 8189 10 11 12 13 141315 16 17 181019 20 21 22423 24 25 26127

Графики привязки (а) и загрузки (b) после оптимизации

1,261,311,452,532,613,684,644,725,866,817,83 1122 3114145 6 7158 9 10 111812 13 14 151016 17 18419 20 21 221023 24 25 26727

Диаграмма Ганта

1,241,331,452,5112,6143,64,6174,75,8196,8277,825

Чтобы построить диаграмму Ганта по графику работ, необходимо выделить пункт Строить диаграмму Ганта. Также можно создать график на основе введенных данных. Для этого следует указать количество работ (мероприятий) и даты их проведения.

Количество работ

Примеры сетевых моделей

Рассмотрим варианты сетевых графиков из кулинарной области на примере варки борща из курицы.

а) Варка в обычной посуде

12345
11030157

Работы:

1,2: чистка овощей (капуста, морковь, картофель, свекла, лук), 10 мин.

1,3: варить курицу, 30 мин.

2,3: положить капусту и варить 10 мин.

3,4: положить 1/2 свеклы, морковь и картофель. Варить 15 мин.

4,5: доложить остатки свеклы, лук, зелень. Варить 7 мин.

б) Варка в посуде с эффектом русской печи (трехслойное дно, крышка без отверстий)

12345
1010203060

Работы:

1,2: чистка овощей (капуста, морковь, картофель, свекла, лук), 10 мин.

1,4: варить курицу в обычной посуде, 30 мин.

2,3: положить овощи в спецпосуду, добавить 3 ложки воды, нагреть до T=70 C и выключить, 10 мин.

3,4: приготовление овощей в собственном соку, 20 мин.

4,5: добавить к курице приготовленные овощи. Настаивается 60 мин.

Список литературы

  1. Мушик Э., Мюллер П. Методы принятия технических решений. Пер. с нем. –М.: Мир, 1990.
  2. Таха Х. Введение в исследование операций. В 2-х книгах. Кн. 2. Пер. с англ. –М.: мир, 1985.
  3. Управление в системах РАВ: Учебник. –Л.: Воениздат, 1980.

Текст

РазмерЦвет

Линия

ТолщинаЦвет

пунктирная – – – –
Размеры в px и фон

wh

Текст (вес)

РазмерЦвет

Линия

ТолщинаЦвет

пунктирная – – –
концевой маркер →

Тип

Число строк

Минимальное время работ, tmin

Максимальное время работ, tmax

Количество исполнителей, чел., Ч

Коэффициент затрат на ускорение работ, руб./сут., h(i,j)

Нормальная стоимость, Cн

Срочная стоимость, Cc

По умолчанию минимальное количество заполняемых столбцов равно трем: i, j, tопт. Чтобы иметь возможность ввести и другие данные, выделите соответствующий пункт.

В каждой строке укажите вершины в формате:v1-v2:n, например
1-2:4
1-3:8
2-4:12
4-1:6

Выберите номер критического пути.

Источник

Добавить комментарий