Виктор Матвеевич Скоков
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Переход вещества через критическое состояние характерен тем, что при этом исчезает различие между жидкой и газообразной фазами вещества. Критическое состояние характеризуется определенными для конкретного вещества параметрами: критическими температурой ($T_{kr})$, давлением ($p_{kr}$), объемом ($V_{kr}$). Если вещество, имеющее критическую температуру будет находиться в объеме не равном критическому, то состояние этого вещества критическим не будет. Различие между фазами в этом случае не исчезнет. Все вещество постепенно перейдет в одну фазу, при V${ > V}_{kr}$ вся жидкость испарится. При V${
Состояние реального газа
Рассмотрим реальный газ. Состояние такого газа опишем уравнением Ван-дер-Ваальса в виде:
Уравнение (1) является кубическим уравнением по отношению к объему, которое имеет переменные коэффициенты, зависящие от давления и температуры и свободный член. Такое уравнение может иметь Это уравнение имеет три корня. По отношению к решениям уравнения возможны следующие варианты в зависимости от соотношения коэффициентов: три вещественных корня, или один корень — вещественный, два комплексных. Так как объем может быть только вещественным, то комплексные решения смысла не имеют. Начиная с температуры, которая называется критической, при любом давлении, вещественным является только один корень уравнения. Критическая температура каждая своя для вещества.
Изотерма для газа Ван-дер-Ваальса
Опыт показывает, что изотерма для газа Ван-дер-Ваальса имеет вид рис.1, то есть существуют области, в которых при изменении объема давление неизменно. В некоторых отрезках график изотермы параллелен оси V(рис 1). Это область фазового перехода, где жидкость и газ существую одновременно.
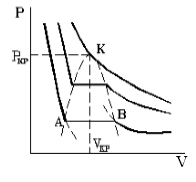
Рис. 1
По мере увеличения температуры участок отражающий состояние нахождения газа одновременно в двух фазах на графиках p(V) сужается, и превращается в точку (рис. 1). Это особая точка К, в которой пропадает различие между жидкостью и паром. Это так называемая критическая точка.
Касательная к критической точке К параллельна оси V. Следовательно, производная $frac{dp}{dV}=0$ в точке К. Кроме того точка К является точкой перегиба, поэтому в ней равняется нулю и вторая производная: $frac{d^2p}{dV^2}=0$.
«Критические параметры газа» 👇
Пример 1
Задание: Найдите критические параметры газа описываемого уравнением Ван-дер-Ваальса.
Решение:
В качестве основания для решения задачи запишем уравнение Ван-дер-Ваальса (для одного моля газа, соответственно в уравнении V=$V_{mu }$):
[left(p+frac{a}{V^2}right)left(V-bright)=RTleft(1.1right).]
Выразим из уравнения (1.1) давление, получим:
[p=frac{RT}{V-b}-frac{a}{V^2} left(1.2right).]
Продифференцируем давление по объему ($frac{dp}{dV})$:
[frac{dp}{dV}=-frac{RT}{{left(V-bright)}^2}-frac{2a}{V^3} left(1.3right).]
Найдем вторую производную:
[frac{d^2p}{dV^2}=frac{2RT}{{left(V-bright)}^3}-frac{6a}{V^4} left(1.4right).]
В критической точке первая и вторая производные раны нулю. Запишем:
[frac{dp}{dV}=-frac{RT_{kr}}{{left(V_{kr}-bright)}^2}-frac{2a}{{V_{kr}}^3}=0 left(1.5right).]
[frac{d^2p}{dV^2}=frac{2RT_{kr}}{{left(V_{kr}-bright)}^3}-frac{6a}{{V_{kr}}^4}=0 left(1.6right).]
И из (1.2) для критического давления имеем:
[p_{kr}=frac{RT_{kr}}{V_{kr}-b}-frac{a}{{V_{kr}}^2} left(1.7right).]
Уравнения (1.5)-(1.7) образуют систему из трех уравнений с тремя неизвестными: $p_{kr}, T_{kr},V_{kr}.$ Решая эту систему, получим:
[V_{kr}=3b,]
[p_{kr}=frac{a}{27b^2},]
[T_{kr}=frac{8a}{27bR}.]
Так, зная постоянные Ван-дер-Ваальса a и b можно найти соответствующие критические параметры газа. И наоборот, по критическим параметрам газа можно вычислить константы уравнения Ван-дер-Ваальса.
Ответ: Критические параметры газа описываемого уравнением Ван-дер-Ваальса равны $V_{kr}=3b,p_{kr}=frac{a}{27b^2},T_{kr}=frac{8a}{27bR}.$
Пример 2
Задание: Какую часть объема сосуда должен занимать жидкий эфир при комнатной температуре, чтобы при достижении критической температуры он оказался в критическом состоянии? Для эфира $p_{kr}=35,5атм .,T_{kr}=467К, mu =74frac{г}{моль}, rho =714frac{кг}{м^3}$
Решение:
Для решения задачи используем результаты, полученные в предыдущем примере, а именно:
[V_{mu kr}=3b,p_{kr}=frac{a}{27b^2},T_{kr}=frac{8a}{27bR}(2.1)]
Найдем из (2.1) $frac{T_{kr}}{p_{kr}}$:
[frac{T_{kr}}{p_{kr}}=frac{8a}{27bR}frac{27b^2}{a}=frac{8b}{R}to b=frac{T_{kr}}{p_{kr}}frac{R}{8}left(2.2right)]
[V_{mu kr}=3b=frac{{3T}_{kr}}{p_{kr}}frac{R}{8}(2.3)]
Для того, чтобы наблюдался переход вещества через критическое состояние, необходимо, чтобы при достижении критической температуры занимаемый им объем был равен критическому объему. Плотность жидкой фазы:
[rho =frac{m}{V_g}left(2.4right),]
где $V_g- $объем жидкости.
[frac{V_g}{V_{kr}}=frac{V_gmu }{mV_{mu kr}}=frac{mu }{rho V_{mu kr}} left(2.5right),]
где $V_{mu kr}$- критический молярный объем.
Используем (2.3) подставим $V_{mu kr}$- в (2.5), получим:
[frac{V_g}{V_{kr}}=frac{8mu }{rho R}frac{p_{kr}}{{3T}_{kr}}left(2.6right).]
Прежде чем провести вычисления, переведём данные в СИ:
[p_{kr}=35,5атм=35,5cdot {10}^5Па,T_{kr}=467К, mu =74frac{г}{моль}=74cdot {10}^{-3}frac{кг}{моль}]
Подставим данные в (2.6), получим:
[frac{V_g}{V_{kr}}=frac{8cdot 74cdot {10}^{-3}}{714cdot 8,31}frac{35,5cdot {10}^5}{3cdot 467}=0,25 left(2.7right)]
Ответ: 0,25 часть объема сосуда должен занимать жидкий эфир.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Из
уравнения Ван-дер-Ваальса кроме факта
сосуществования двух фаз вещества –
жидкого и газообразного, следует и
наличие у веществ критической температуры,
критического состояния.
Д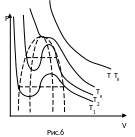
ля
этого рассмотрим, как изменяются изотермы
с изменением температуры (рис.6). С
повышением температуры изотермы
располагаются выше, причем расстоянием
между максимумами и минимумами
уменьшаются. Наконец, при вполне
определенной температуре максимумы и
минимумы изотермы сливаются, вырождаясь
в точку перегиба. При дальнейшем повышении
температуры, изотермы становятся схожими
с изотермами идеального газа. Таким
образом, при определенной температуре
Тк
все три значения объема сливаются, т.е.
корни уравнения становятся кратными.
Следовательно, при этой температуре
исчезает различие между различными
состояниями вещества. Эту температуру
называют критической. Воспользуясь
уравнением Ван-дер-Ваальса, вычислим
критическую температуру, а также значения
двух других критических параметров –
критического объема
![]()
и
критического давления
![]()
.
Действительно, при Т=Тк,
Р=Рк,
V=Vк
левая часть уравнения Ван-дер-Ваальса
(5.7) должна быть точным кубом и может
быть представлена в виде:
![]()
.
Это
равенство тождественно выполняется,
если коэффициенты при одинаковых
степенях
в
обеих частях равны между собой:
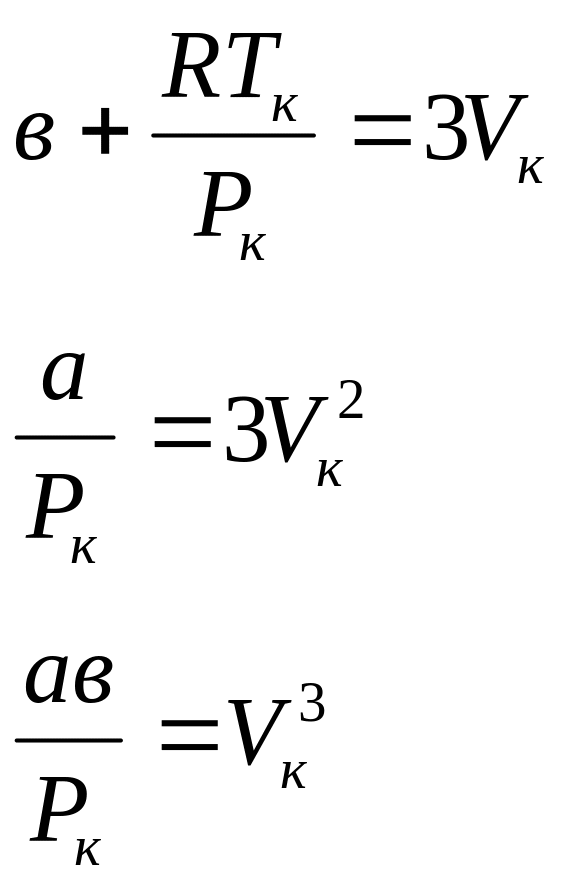
.
Решив
эту систему уравнений, получим значения
критических параметров, выраженных
через константы
![]()
и
![]()
:
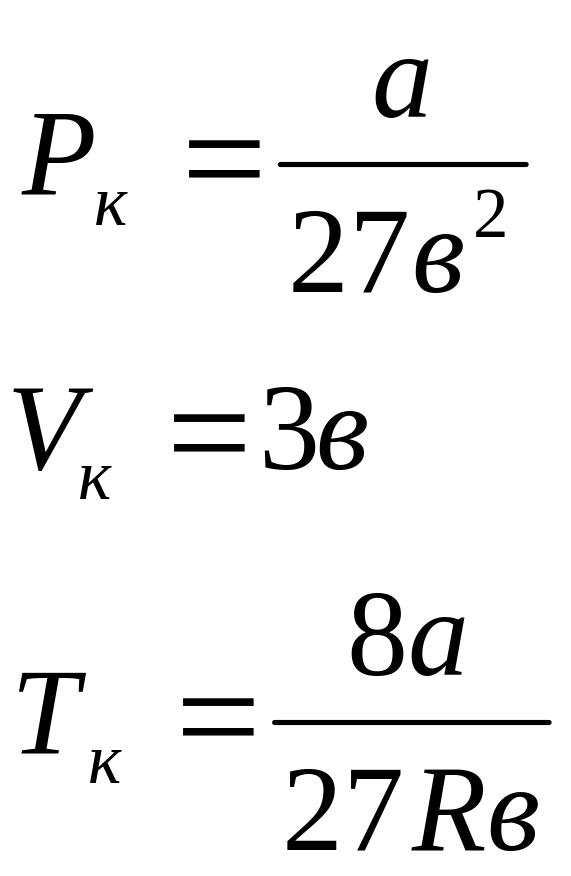
.
(5.8)
Значение
критических параметров можно также
получить из следующей системы уравнений:
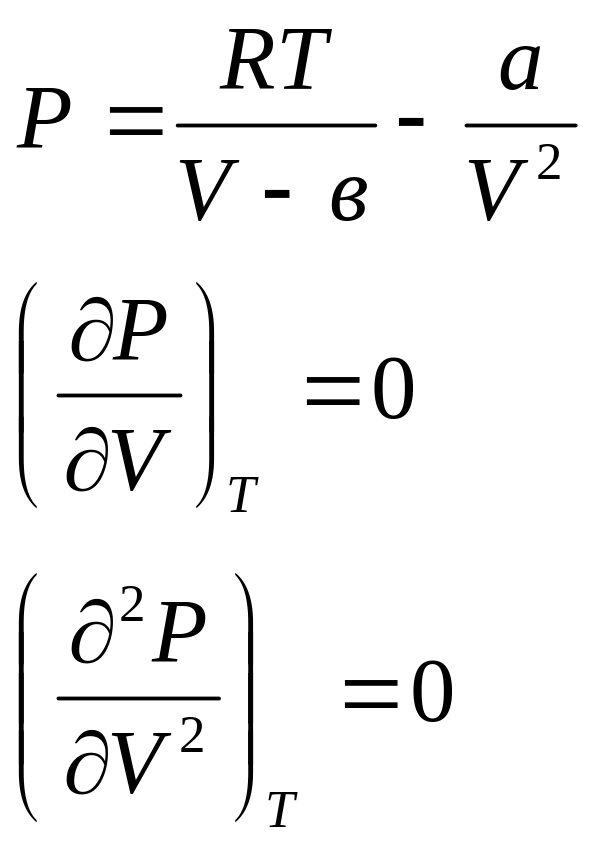
.
Второе
уравнение этой системы связано с тем,
что в критической точке совпадают
максимумы и минимумы изотермы, т.е.
критическая точка является точкой
экстремума. Третье уравнение этой
системы связана тем, что критическая
точка является точкой перегиба.
Состояние
веществ при критических значениях
температуры, объема и давления называется
критическим состоянием. В критическом
состоянии жидкость проявляет очень
интересные свойства:
-
Происходит
резкое возрастание коэффициента
изотермической сжимаемости; -
Наблюдается
скачок теплоемкости; -
Наблюдается
аномальный рост рассеяния света, т.е.
происходит опалесценция света.
33. Приведенное уравнение Ван-дер-Ваальса. Закон соответственных состояний
Изотермы, построенные
при одной и той же температуре для разных
газов, выглядят по-разному, потому что
и
и связанные
с ними критические величины
![]()
различные
для разных газов. Можно, однако, и для
неидеальных газов написать уравнение
изотермы, чтобы оно не зависело от
природы газа, т.е. было бы универсальным.
Для этого оказывается достаточно, чтобы
параметры состояния газа находились в
одинаковых отношениях к соответствующим
критическим параметрам. Для этого введем
безразмерные параметры, обезразмеренные
с помощью критических величин, т.е.
![]()
.
Параметры
![]()
называют
приведенными параметрами. Поставим в
уравнение Ван-дер-Ваальса значения
параметров
![]()
,
вырожденные через приведенные параметры.
Получим:
![]()
.
(5.12)
В (5.12) подставим
значения
![]()
.
Тогда получим:
![]()
.
(5.13)
С учетом известных
соотношений
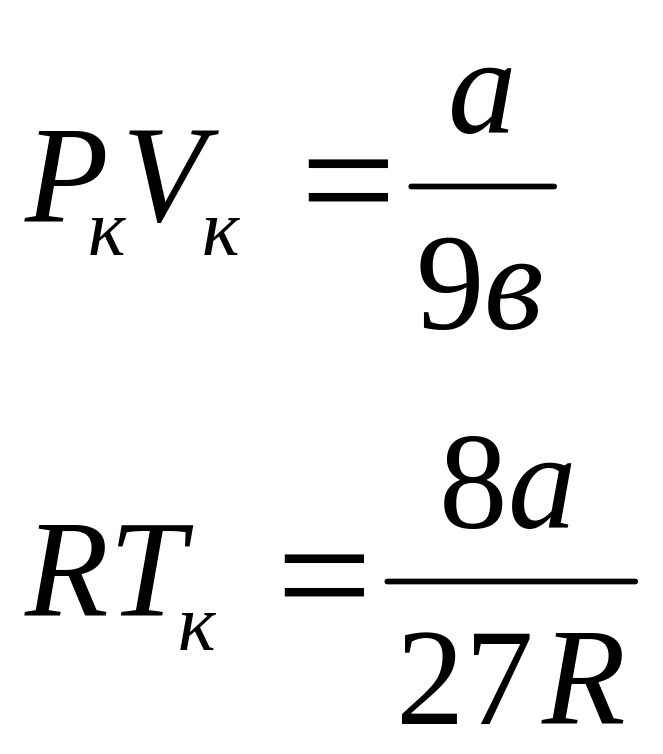
имеем:
![]()
.
(5.14)
Уравнение (5.14)
является приведенным уравнением
состояния. В этом уравнении не содержатся
константы, характерные для конкретного
вещества. Из него следует, что если
вещества обладают двумя одинаковыми
приведенными параметрами из трех, то и
третий параметр тоже одинаков для этих
веществ. Этот закон носит название
закона соответственных состояний. Он
выражает тот факт, что изменяя масштаб,
которым измеряются две из трех величин,
характеризующих состояние веществ,
т.е. используя приведенные параметры,
можно совместить изотермы всех веществ.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Критические температура и давление. Газы могут быть превращены в жидкость сжатием при условии, что температура не превышает определенного для каждого газа значения.
Температура, при которой и выше которой данный газ не может быть сжижен никаким повышением давления, называется критической Ткр. Давление, при котором и выше которого повышением температуры нельзя испарить жидкость, называется критическим ркр. Объем газа, соответствующий критической температуре, называется критическим Vкр, а состояние газа, отвечающее критической температуре, критическому давлению и критическому объему, —критическим состоянием газа. При критическом состоянии плотность пара становится равной плотности жидкости. Критические температура и давление для газов приведены в табл. 2.4.(Глава 2.5)
Приведенные критические параметры и закон соответственных состояний. Отношения параметров газа р, Т и V, характеризующих его состояние, к их критическим значениям, называются приведенными. Под приведенной температурой понимается отношение абсолютной температуры газа к его критической температуре:
Тпр = Т/Ткр
Приведенным давлением называется отношение абсолютного давления газа к его абсолютному критическому давлению:
pпр = pабс/pкр
Если параметры газа выразить в безразмерных приведенных величинах, можно установить, что для газов существует так называемое общее уравнение состояния, лишенное величин, характеризующих данный газ:
f (pпр, Тпр, Vпр) = 0
Состояние, отвечающее этому условию, называется законом соответственных состояний, по которому два газа будут иметь один и тот же приведенный объем, если у них равны приведенные давление и температура. Значение закона соответственных состояний заключается в том, что он позволяет с достаточной точностью определять коэффициенты сжимаемости газов и другие параметры по графикам для других газов, построенным в приведенных параметрах.
