Определенные интегралы в случаях когда интегрирование проводится не вдоль отрезка, а некоторой кривой (на плоскости или в пространстве) называются криволинейными. Различают криволинейные интегралы І и ІІ рода.
Формулы криволинейного интегралу первого рода
Пусть в пространстве (на плоскости) задано параметрическое уравнение гладкой кривой f (x, y, z)
x=x(t), y=y(t), z=z(t).
tє[a, b].
Каждая из функций непрерывна на промежутке интегрирования.
Функция f(x, y, z)=0 описывает кривую в пространстве.
В таком случае криволинейный интеграл первого рода равен интегралу за параметром от функции умноженной на корень квадратный из суммы квадратов производных координат за параметром
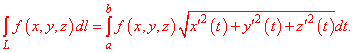
Для случая кривой на плоскости формула неопределенного интегралу I роду упрощается
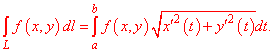
Когда кривая интегрирования задана явно y=y(x), формула перехода к определенному интегралу имеет вид
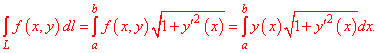
Пусть функция задана полярными координатами rho=rho(phi), phi1<phi<phi2. Тогда криволинейный интеграл первого рода вдоль кривой вычисляется по формуле
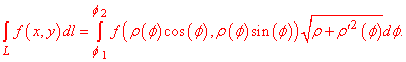
На этом все формулы, что Вам нужны для вычисления интегралов, однако без готовых ответов трудно представить их приложение, поєтому перейдем к практической части.
Примеры подобрано из учебной программы для студентов ЛНУ им. И. Франко. Они охватывают широкий класс заданий, которые непременно встретите на контрольной работе и экзаменах. Поэтому внимательно разберите ответы к примерам и выучите приведенные наверху формулы вічисления криволинейных интегралов.
Пример 1.7 Вычислить криволинейный интеграл 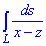 вдоль дуги L – отрезок прямой z=x/2-2, что соединяет точки A(0;- 2) и B(4;0) в плоскости xOz.
вдоль дуги L – отрезок прямой z=x/2-2, что соединяет точки A(0;- 2) и B(4;0) в плоскости xOz.
Решение: Построим графически прямую и нанесем на нее точки ограничивающие дугу
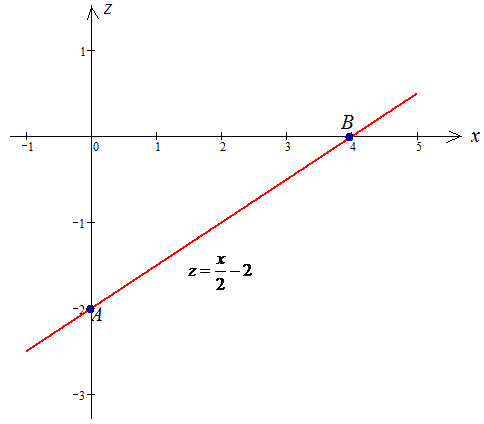
За видом видим, что необходимо вычислить криволинейный интеграл I рода.
z=x/2-2, z’=1/2.
Подынтегральная функция примет значение
1/(x-z)=1/(x -(x/2-2))=1/(0,5x+2).
Найдем дифференциал дуги заданной кривой по формуле
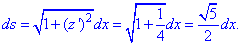
Подставляем и находим криволинейный интеграл
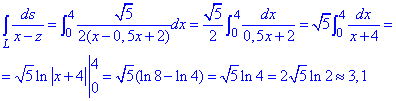
Неопределенный интеграл сводится к логарифму, который не имеет особенностей (гладкая функция) на промежутке интегрирования.
Пример 1.10 Вычислить криволинейный интеграл вдоль дуги L:
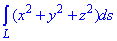 , где L – дуга кривой x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi].
, где L – дуга кривой x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi].
Решение: Параметрическая кривая x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi] описывает часть винтовой линии.
Ее график на цилиндрической поверхности имеет вид.
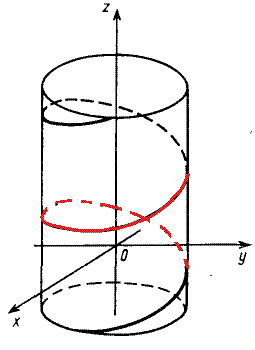
Часть винтовой линии, которая отвечает промежутку [0;2pi] изображена красным цветом.
Подынтегральная функция равна x2+y2+z2.
Нужно вычислить криволинейный интеграл I рода.
Находим производные координат по параметру
x’t=a*sin(t), y’t=a*sin(t), z’t=b.
Дальше вычисляем дифференциал дуги параметрически заданной кривой согласно формуле:
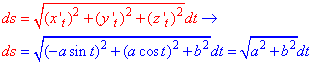
Формулы дифференциалу дуги в декартовой, полярной и пространственной системах координат приведены в теоретическом материале и поэтому здесь на них задерживаться не будем.
Интегрированием вычисляем криволинейный интеграл
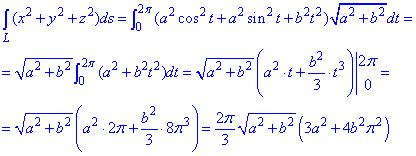
Интеграл не сложен в плане расчетов.
Пример 1.12 Вычислить криволинейный интеграл 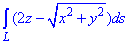 вдоль дуги L, где L – дуга кривой x=cos(t), y=sin(t), z=t [0;2pi].
вдоль дуги L, где L – дуга кривой x=cos(t), y=sin(t), z=t [0;2pi].
Решение: Имеем идентичное уравнение x=cos(t), y=sin(t), z=t – винтовой линии.

Для вычисления криволинейного интеграла I рода находим производные координат
x’t=-sin(t), y’t=cos(t), z’t=1.
Подставляем их в дифференциал дуги винтовой линии:
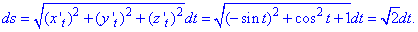
Превращаем подінтегральную функцию и находим криволинейный интеграл
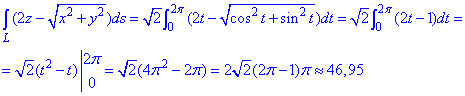
Пример 1.14 Вычислить криволинейный интеграл int(x+y, dS)
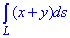 вдоль дуги L – дуга кривой x=t,
вдоль дуги L – дуга кривой x=t, 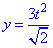 , z=t3, [0;1].
, z=t3, [0;1].
Решение: Прежде чем вычислить криволинейный интеграл I рода находим производные за параметром.
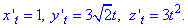
Подставляем их в формулу дифференциала дуги:
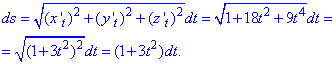
Определенный интеграл вычисляем в указанных пределах
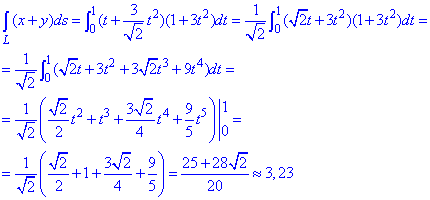
Под интегралом раскрыли скобки и применили простые формулы интегрирования.
Пример 1.18 Вычислить криволинейный интеграл int (1/x2+y2+z2,ds)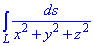 вдоль дуги кривой L:
вдоль дуги кривой L:
x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi].
Решение: Интегрировать опять придется вдоль винтовой линии.

Производные за параметром имеют вид
x’t=-a*sin(t), y’t=a*sin(t), z’t=b.
Вычисляем дифференциал дуги кривой:

Дальше превращаем криволинейный интеграл к определенному и находим его значение
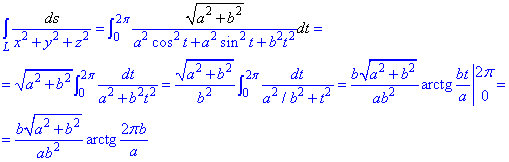
При интегрировании будем иметь арктангенс.
В результате вычислений получили компактную формулу через параметры формы цилиндра.
Пример 1.20 Вычислить криволинейный интеграл int(x4/3+y4/3,ds) вдоль дуги L:
дуга астроиды x2/3+y2/3=a2/3.
Решение: Запишем параметрическое уравнение астроиды:
x=a*cos3(t), y=a*sin3(t), где t[0;2pi].
График астроиды в декартовой системе координат имеет вид
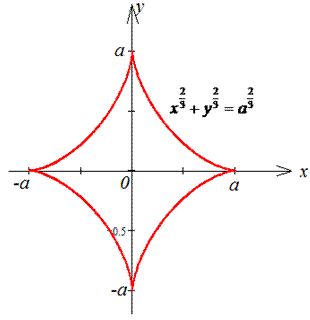
Для вычисления криволинейного интеграла I рода вычисляем производные за параметром
x’t=-3a*cos2(t)*sin(t), y’t=3a*cos(t)*sin2(t).
и подставляем в дифференциал дуги астроиды: 
Криволинейный интеграл 1 рода находим методом замены переменной
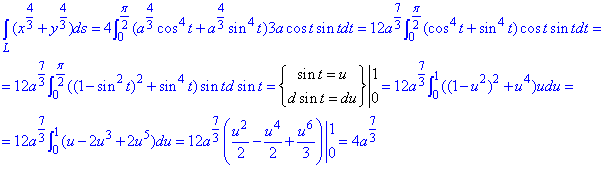
Это позволяет перейти к простому понятному виду подынтегральной функции.
Пример 1.21 Вычислить криволинейный интеграл 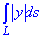 вдоль дуги лемнискаты (x2+y2)2=a2(x2-y2).
вдоль дуги лемнискаты (x2+y2)2=a2(x2-y2).
Решение: Для лемнискаты раньше рассматривали интегралы на нахождение площади.
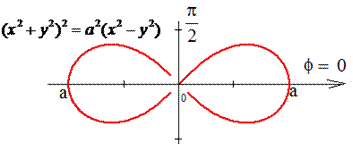
Запишем уравнение лемнискаты в полярной системе координат, используя превращение координат:
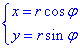
Тогда из уравнения дуги
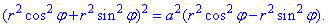
выражаем радиус-вектор и вычисляем производную за углом
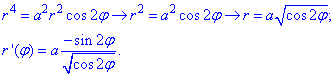
Найдем дифференциал дуги по формуле:
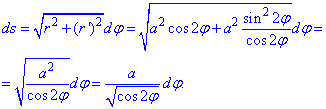
Запишем подынтегральную функцию:
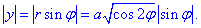
Вычисляем криволинейный интеграл первого роду как 4 интеграла по 1 четверти
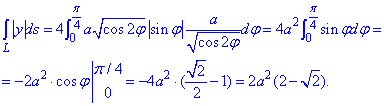
Синус в первой четверти положителен, поэтому модуль опускаем.
Пример 1.25 Вычислить криволинейный интеграл вдоль дуги L:
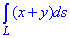 , где L – четверть круга x2+y2+z2=R2, y=x что лежит в первом октанте.
, где L – четверть круга x2+y2+z2=R2, y=x что лежит в первом октанте.
Решение: Имеем сферу x2+y2+z2=R2 и плоскость y=x, которая ее пересекает.
График дуги в пространстве имеет вид как на рисунку
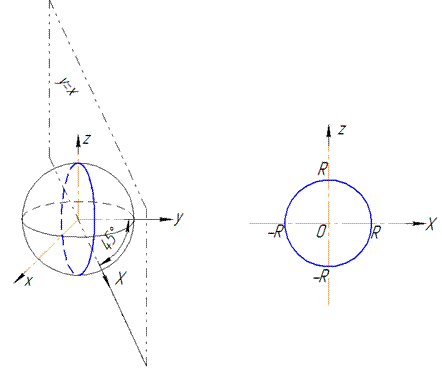
В сечении получим круг, который проектируется на плоскость y=x уравнением X2+z2=R2, где 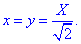
Такие манипуляции необходимы, чтобы параметризовать круг
Параметрическое уравнение круга:
x=R*cos(t), z=R*sin(t) и t[0;Pi/2] (I октант).
Тогда переменные выражаются зависимостью
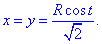
Вычисляем производные
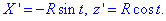
затем находим дифференциал дуги:
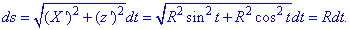
Подставляем все в интеграл и выполняем вычисление
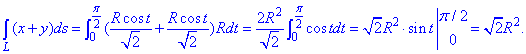
Как Вы могли убедиться, ничего сложного в нахождении криволинейных интегралов первого рода нет. В теории известны формулы как переходить от криволинейных к определенным интегралам, ими и воспользовались. Сами же интегралы не сложны, да и кривые на практике подбираются таким образом, чтобы Вы с ними долго не возились на практических занятиях.
Все сводится к умению интегрировать, что в свою очередь требует знания таблицы основных интегралов.
Определение: Пусть в каждой точки гладкой кривой L = AB в плоскости Oxy задана непрерывная функция двух переменных f(x,y). Произвольно разобьем кривую L на n частей точками A = М0, М1, М2, … Мn = B. Затем на каждой из полученных частей ![]() выберем любую точку
выберем любую точку ![]() и составим сумму
и составим сумму
![]()
где ![]() — дуга дуги
— дуга дуги ![]() . Полученная сумма называется интегральной суммой первого рода для функции f(x,y), заданой на кривой L.
. Полученная сумма называется интегральной суммой первого рода для функции f(x,y), заданой на кривой L.
Обозначим через d наибольшую из длин дуг ![]() (таким образом, d =
(таким образом, d = ![]() ). Если при d ? 0 существует предел интегральных сумм Sn (не зависящих от способа разбиения кривой L на части и выбора точек
). Если при d ? 0 существует предел интегральных сумм Sn (не зависящих от способа разбиения кривой L на части и выбора точек ![]() ), то этот предел называется криволинейным интегралом первого порядка от функции f(x,y) по кривой L и обозначается
), то этот предел называется криволинейным интегралом первого порядка от функции f(x,y) по кривой L и обозначается
![]()
Можно доказать, что если функция f(x,y)непрерывна, то криволинейный интеграл ![]() существует.
существует.
Криволинейный интеграл первого рода обладает свойствами, аналогичными соответствующим свойства определеннного интеграла:
- аддитивность,
- линейность,
- оценка модуля,
- теорема о среднем.
Однако есть отличие:
![]()
т.е. криволинейный интеграл первого рода не зависит от направления интегрирования.
Вычисление криволинейных интегралов первого рода
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла. А именно:
- Если кривая L задана непрерывно дифференцируемой функцией y=y(x), x
 [a,b], то
[a,b], то
![Rendered by QuickLaTeX.com [{intlimits_L {fleft( {x,y} right)dl} } = {intlimits_a^b {fleft( {x,yleft( x right)} right)sqrt {1 + {{left( {y'left( x right)} right)}^2}} dx} ;}]](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_356,h_64/https://shkolnaiapora.ru/wp-content/ql-cache/quicklatex.com-364ab818d2700a5b997ad6215eaab084_l3.png)
при этом выражение
 называется дифференциалом длины дуги.
называется дифференциалом длины дуги. - Если крива L задана параметрически, т.е. в виде x=x(t), y=y(t), где x(t), y(t) — непрерывно дифференцируемые функции на некотором отрезке
![Rendered by QuickLaTeX.com left [ alpha ,beta right ]](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_36,h_18/https://shkolnaiapora.ru/wp-content/ql-cache/quicklatex.com-28c477da92c93164e8f63b80569d3c13_l3.png) , то
, то
![Rendered by QuickLaTeX.com [{intlimits_L {fleft( {x,y} right)dl} } = {intlimits_alpha ^beta {fleft ( {xleft( t right),yleft( t right)} right )sqrt {{{left( {x'left( t right)} right)}^2} + {{left( {y'left( t right)} right)}^2}} dt}}]](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_417,h_65/https://shkolnaiapora.ru/wp-content/ql-cache/quicklatex.com-b4e92c431aef426a00f121daf242b15c_l3.png)
Это равенство распространяется на случай пространственной кривой L, заданной параметрически: x=x(t), y=y(t), z=z(t),
![Rendered by QuickLaTeX.com tin left [ alpha ,beta right ]](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_66,h_18/https://shkolnaiapora.ru/wp-content/ql-cache/quicklatex.com-2510140b81ed30c7d91fd2bf07d3761e_l3.png) . В этом случае, если f(x,y,z) — непрерывная функция вдоль кривой L, то
. В этом случае, если f(x,y,z) — непрерывная функция вдоль кривой L, то![Rendered by QuickLaTeX.com [{intlimits_L {fleft( {x,y,z} right)dl} } = {intlimits_alpha ^beta {fleft [ {xleft( t right),yleft( t right),zleft( t right)} right ]sqrt {{{left( {x'left( t right)} right)}^2} + {{left( {y'left( t right)} right)}^2} + {{left( {z'left( t right)} right)}^2}} dt}}]](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_553,h_65/https://shkolnaiapora.ru/wp-content/ql-cache/quicklatex.com-356035f336017fdd48bbb24635450edd_l3.png)
- Если плоская кривая L задана полярным уравнением r=r(
![Rendered by QuickLaTeX.com varphi inleft [ alpha ,beta right ]](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_71,h_18/https://shkolnaiapora.ru/wp-content/ql-cache/quicklatex.com-1b41cf72f7da9e0e53d23cf314ced13a_l3.png) ),
), ![Rendered by QuickLaTeX.com varphi inleft [ alpha ,beta right ]](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_71,h_18/https://shkolnaiapora.ru/wp-content/ql-cache/quicklatex.com-1b41cf72f7da9e0e53d23cf314ced13a_l3.png) , то
, то
![Rendered by QuickLaTeX.com [{intlimits_L {fleft( {x,y} right)dl} } = {intlimits_alpha ^beta {fleft( {rcos varphi ,rsin varphi } right)sqrt {{r^2} + {{{r}'}^2}} dvarphi}}]](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_369,h_65/https://shkolnaiapora.ru/wp-content/ql-cache/quicklatex.com-8584268c1eca821ea92d4f64ca9deb22_l3.png)
Криволинейные интегралы 1 рода — примеры
Пример 1
Вычислить криволинейный интеграл первого рода
![]()
где L дуга параболы y2=2x, заключенная между точками (2,2) и (8,4).
Решение: Найдем дифференциал дуги dl для кривой ![]() . Имеем:
. Имеем:
![]()
![]()
Следовательно данный интеграл равен:
![]()
![]()
Пример 2
Вычислить криволинейный интеграл первого рода ![]() , где L — окружность x2+y2=ax (a>0).
, где L — окружность x2+y2=ax (a>0).
Решение: Введем полярные координаты: ![]() ,
, ![]() . Тогда поскольку x2+y2=r2, уравнение окружности имеет вид:
. Тогда поскольку x2+y2=r2, уравнение окружности имеет вид: ![]() , то есть
, то есть ![]() , а дифференциал дуги
, а дифференциал дуги
![]()
![]()
.
При этом ![]() . Следовательно,
. Следовательно,
![]()
Содержание:
Криволинейные интегралы
Криволинейный интеграл первого рода
Пусть К — некоторая гладкая (или кусочно-гладкая) плоская кривая
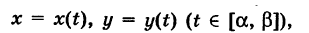
где t — параметр, а
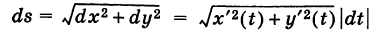
— ее дифференциал дуги. Здесь если 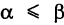 , то dt > 0 и
, то dt > 0 и 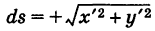 ; если же
; если же 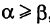 , то dt < 0 и
, то dt < 0 и 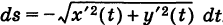 . Если
. Если 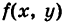 — функция, непрерывная на кривой К, то под ее криволинейным интегралом первого рода, взятым по кривой понимается интеграл
— функция, непрерывная на кривой К, то под ее криволинейным интегралом первого рода, взятым по кривой понимается интеграл
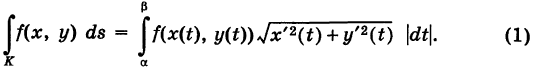
Если кривая 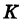 задана уравнением
задана уравнением
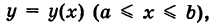
то, рассматривая х как параметр, получим
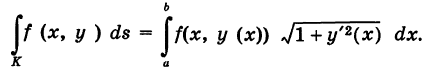
Допустим, что кривая К — материальная, т. е. имеет массу. Пусть  — некоторая дуга кривой К, содержащая точку М, а
— некоторая дуга кривой К, содержащая точку М, а  — масса этой дуги. Тогда отношение
— масса этой дуги. Тогда отношение 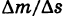 носит название средней плотности дуги
носит название средней плотности дуги 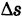 , а
, а
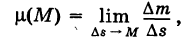
т. е предел средней плотности дуги при условии, что дуга 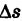 стягивается в точку М, называется линейной плотностью дуги в точке М.
стягивается в точку М, называется линейной плотностью дуги в точке М.
Если 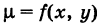 рассматривать как линейную плотность дуги в текущей ее точке М (х, у), то
рассматривать как линейную плотность дуги в текущей ее точке М (х, у), то
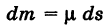
есть масса бесконечно малой дуги ds (элементарная масса) и интеграл

представляет собой массу линии (физический смысл криволинейного интеграла первого рода).
Криволинейный интеграл первого рода обладает следующими очевидными свойствами.
1) При изменении направления интегрирования криволинейный интеграл первого рода не изменяет своего значения (рис. 238), т. е.
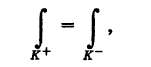
где К+ — кривая К, пробегаемая в заданном направлении (например, при возрастании параметра t), а К-— кривая К, пробегаемая в противоположном направлении (соответственно при убывании t).
2) Если кривая интегрирования К с помощью некоторой точки разбита на части: 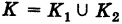 (рис. 238), то
(рис. 238), то
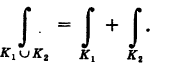
Пример:
Найти массу полуокружности 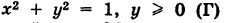 (рис. 239), если линейная плотность ее в текущей точке М (х, у) пропорциональна ординате у.
(рис. 239), если линейная плотность ее в текущей точке М (х, у) пропорциональна ординате у.
Решение:
Беря в качестве параметра t полярный угол (рис. 239), получаем параметрические уравнения полуокружности
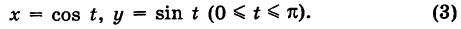
Элементарная масса
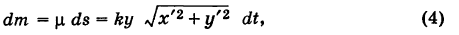
где k — коэффициент пропорциональности. Так как
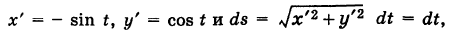
то из (4) имеем
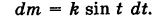
Отсюда масса линии Г будет равна
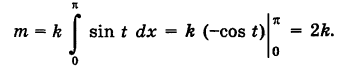
Аналогично определяется криволинейный интеграл первого рода от функции f(x, у, z), взятый по кусочно-гладкой пространственной кривой К:
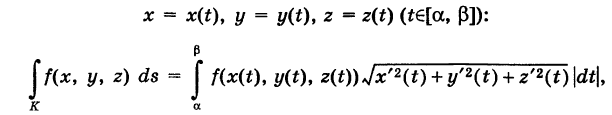
где
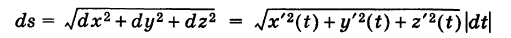
— дифференциал дуги пространственной кривой -К.
Криволинейный интеграл второго рода
Пусть
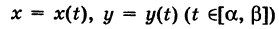
— гладкая (или кусочно-гладкая) кривая К с выбранным направлением (такую линию, для краткости, будем называть путем) и Х(х, у), Y (х, у) — пара функций, непрерывных на кривой К. Учитывая, что дифференциалы текущих координат х и у кривой К имеют вид
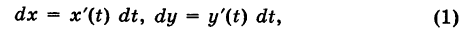
под криволинейным интегралом второго рода от пары функций X и Y, взятым по кривой К, понимается интеграл
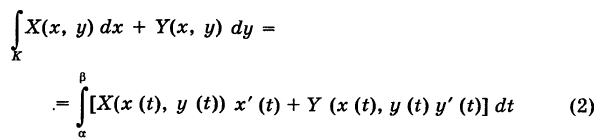
(по традиции для выражения, стоящего слева, скобки не пишутся и предполагается, что интеграл  относится ко всей сумме).
относится ко всей сумме).
Если путь К задается уравнением 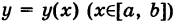 , то формула (2) принимает вид
, то формула (2) принимает вид
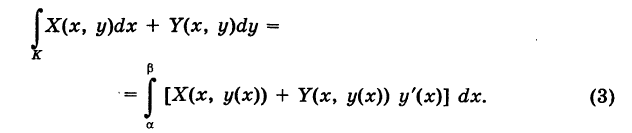
Аналогично, если K, задается уравнением 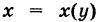
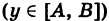 , то
, то
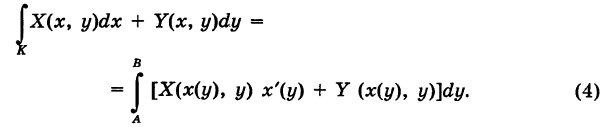
Криволинейный интеграл второго рода обладает следующими свойствами.
1) При изменении направления пути интегрирования криволинейный интеграл второго рода изменяет свой знак на обратный, т. е

Действительно, изменение направления пути интегрирования равносильно перестановке пределов интегрирования  в определенном интеграле (2); а это влечет изменение знака определенного интеграла.
в определенном интеграле (2); а это влечет изменение знака определенного интеграла.
2) Если путь интегрирования К состоит из двух частей К = 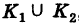 , то
, то

Пример:
Найти значения интеграла 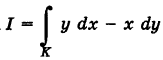 вдоль указанных путей: 1) OA — прямая; 2)
вдоль указанных путей: 1) OA — прямая; 2) 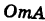 — парабола с вершиной О и осью Оу; 3) ОВА — ломаная, 4) ОСА — ломаная (рис. 240).
— парабола с вершиной О и осью Оу; 3) ОВА — ломаная, 4) ОСА — ломаная (рис. 240).
Решение:
1) Уравнение прямой OA есть у = 2х 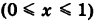 . Отсюда dy = 2 dx и, следовательно,
. Отсюда dy = 2 dx и, следовательно,
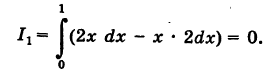
2) Уравнение параболы 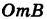 имеет вид у = kx2. Так как парабола проходит через точку
имеет вид у = kx2. Так как парабола проходит через точку 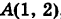 , то 2 = k – 12 и, значит, k = 2, т. е. у = 2х2. Отсюда dу = 4х dx и
, то 2 = k – 12 и, значит, k = 2, т. е. у = 2х2. Отсюда dу = 4х dx и
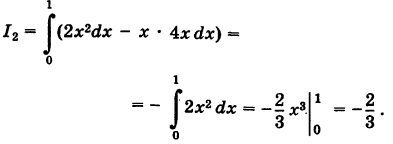
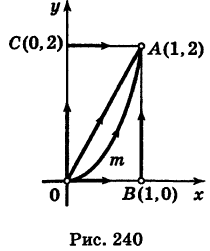
3) На основании свойства 2 имеем
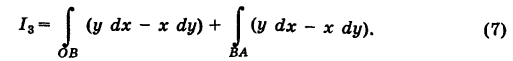
Так как уравнение ОВ есть у = 0  , то
, то  = 0. Далее, уравнение ВА записывается так: х = 1
= 0. Далее, уравнение ВА записывается так: х = 1 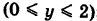 ; поэтому х'(у) = 0. Из формулы (7) получаем
; поэтому х'(у) = 0. Из формулы (7) получаем
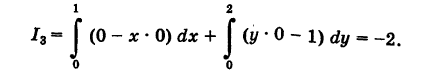
4) Аналогично,
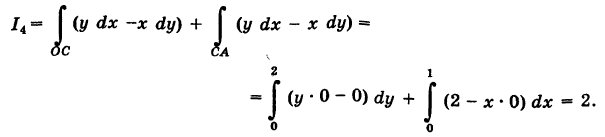
Заметим, что здесь интеграл I при фиксированных концах пути интегрирования К зависит от вида этого пути.
Пример:
Найти
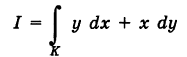
вдоль линий К, указанных в примере 1.
Воспользовавшись приведенными выше уравнениями линии К, последовательно имеем:
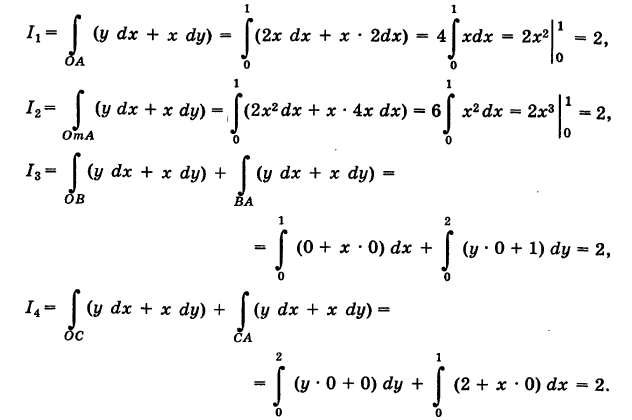
Таким образом, здесь интеграл I имеет одно и то же значение для различных путей, соединяющих точки О и А. Принципиальное различие примеров 1 и 2 будет разъяснено. Если
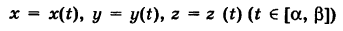
есть кусочно-гладкая пространственная кривая 
 — тройка функций, непрерывных на кривой К, то под соответствующим криволинейным интегралом второго рода понимается интеграл
— тройка функций, непрерывных на кривой К, то под соответствующим криволинейным интегралом второго рода понимается интеграл
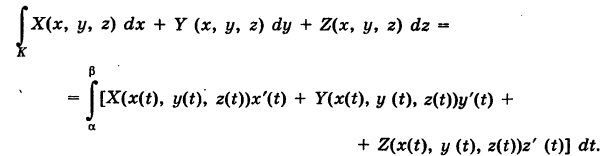
Физический смысл криволинейного интеграла второго рода
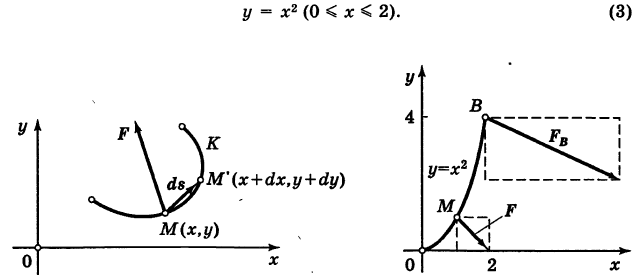
Пусть 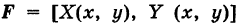 — непрерывно меняющаяся переменная сила и
— непрерывно меняющаяся переменная сила и
— путь К, пробегаемый точкой ее приложения (рис. 241); обозначим через 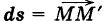 бесконечно малый вектор перемещения из текущей точки М (х, у) кривой К в бесконечно близкую точку
бесконечно малый вектор перемещения из текущей точки М (х, у) кривой К в бесконечно близкую точку 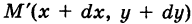 (мы здесь пренебрегаем бесконечно малыми высшего порядка по сравнению с ds). Имеем ds = {dx, dy}. Так как на бесконечно малом пути ds непрерывную силу F можно считать постоянной, то элементарная работа силы равна
(мы здесь пренебрегаем бесконечно малыми высшего порядка по сравнению с ds). Имеем ds = {dx, dy}. Так как на бесконечно малом пути ds непрерывную силу F можно считать постоянной, то элементарная работа силы равна
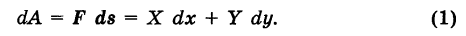
Интегрируя выражение (1) вдоль кривой К, получим работу силы
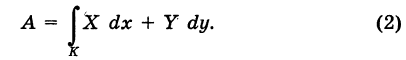
Выражение (2), очевидно, есть соответствующий криволинейный интеграл второго рода.
Итак, криволинейный интеграл второго рода представляет собой работу переменной силы вдоль пути интегрирования, проекциями которой на координатные оси являются соответствующие коэффициенты при дифференциалах переменных.
Пример:
Найти работу А переменной силы 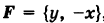 , точка приложения которой описывает параболу ОВ (рис. 242)
, точка приложения которой описывает параболу ОВ (рис. 242)
Решение:
Согласно формуле (2) имеем
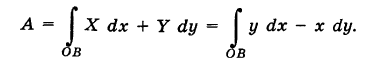
Из уравнения (3) получаем dy = 2х dx, поэтому
Аналогично, работа пространственной силы
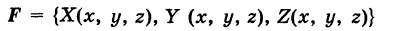
вдоль пути К: 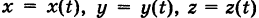 выражается криволинейным интегралом второго рода
выражается криволинейным интегралом второго рода
- Заказать решение задач по высшей математике
Условие независимости криволинейного интеграла второго рода от вида пути интегрирования
Пусть 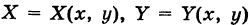 — непрерывные функции в области G (рис. 243). Рассмотрим две произвольные точки
— непрерывные функции в области G (рис. 243). Рассмотрим две произвольные точки 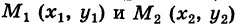 области и всевозможные пути
области и всевозможные пути 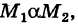
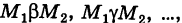 соединяющие эти точки (М1 — начало пути, М2 — конец пути) и не выходящие за пределы области G. Может случиться, что
соединяющие эти точки (М1 — начало пути, М2 — конец пути) и не выходящие за пределы области G. Может случиться, что
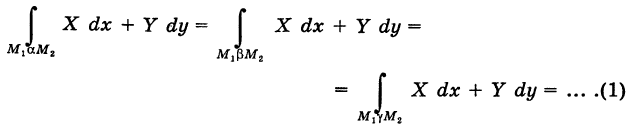
В таком случае говорят, что криволинейный интеграл второго рода
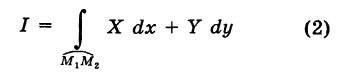
не зависит от вида пути интегрирования в данной области G.
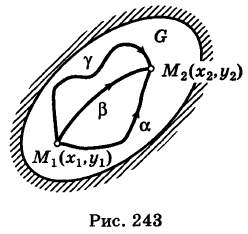
Если выполняются условия (1), то для интеграла (2) нет необходимости указывать путь интегрирования, а достаточно отметить лишь его начальную точку  и его конечную точку М2
и его конечную точку М2 пути. Поэтому здесь употребляется обозначение
пути. Поэтому здесь употребляется обозначение
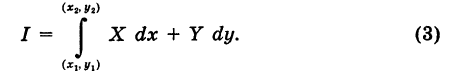
Справедлива следующая теорема:
Теорема: Если в области G подынтегральное выражение X dx + Y dy является полным дифференциалом некоторой функции U = U (х, у), т. е.
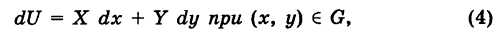
то криволинейный интеграл (2) не зависит от пути интегрирования в области G.
Доказательство: Пусть
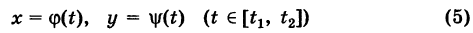
— произвольный путь К в области G, соединяющий точки 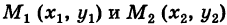 , причем
, причем
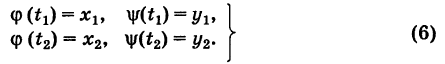
Из формулы (4) имеем
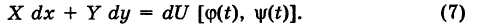
Отсюда получаем
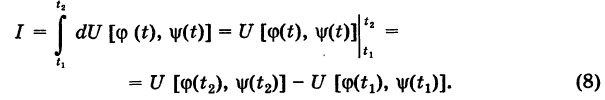
Далее, используя соотношения (6), будем иметь
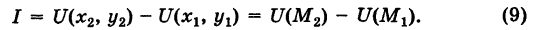
Таким образом, значение интеграла I одно и то же при любом выборе функций 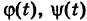 , и, следовательно, интеграл I не зависит от вида пути, соединяющего точки
, и, следовательно, интеграл I не зависит от вида пути, соединяющего точки 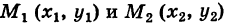
Следствие 1. Если выполнено соотношение (4), то в силу (9) имеем
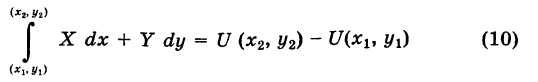
(обобщенная формула Ньютона — Лейбница).
Следствие 2. Если подынтегральное выражение X dx + Y dy есть полный дифференциал и путь интегрирования К замкнутый, то
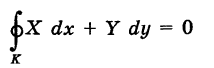
(кружок при интеграле обозначает интегрирование вдоль замкнутого пути).
Пример:
Найти
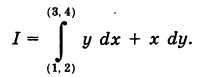
Решение:
Так как у dx + х dy = d (ху), то, независимо от вида пути, соединяющего точки 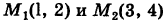 , имеем
, имеем
Работа потенциальной силы
Теорема предыдущего параграфа имеет физическое содержание. Пусть в области G определено силовое поле
Примером силового поля может служить поле силы тяжести у поверхности Земли, где на любую материальную точку массы т действует сила mg (g — ускорение свободного падения). Более общим примером силового поля является гравитационное поле, создаваемое массой М. Здесь на материальную точку массы  находящуюся на расстоянии г от притягивающего центра, согласно закону Ньютона действует сила
находящуюся на расстоянии г от притягивающего центра, согласно закону Ньютона действует сила 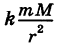 (k — гравитационная постоянная), направленная к притягивающему центру. Другим примером силового поля служит электрическое поле Кулона.
(k — гравитационная постоянная), направленная к притягивающему центру. Другим примером силового поля служит электрическое поле Кулона.
Если существует функция 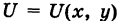 такая, что
такая, что
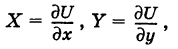
то говорят, что поле потенциальное (иначе, F — потенциальная сила), а функцию U называют потенциалом поля. В этом случае, очевидно,
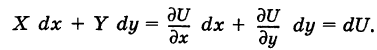
Отсюда для работы А потенциальной силы F вдоль пути, соединяющего точки 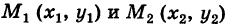 , имеем
, имеем
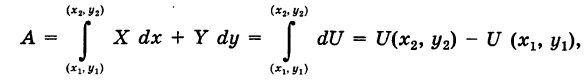
т. е. работа потенциальной силы не зависит от вида пути и равна разности потенциалов силы для конечной и начальной точек пути.
В частности, если путь замкнут, то работа А = 0.
Пример:
Найти работу А силы тяжести при перемещении в вертикальной плоскости Оху (вблизи поверхности Земли) точки массы т из положения 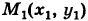 в положение
в положение 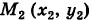 (рис. 244).
(рис. 244).
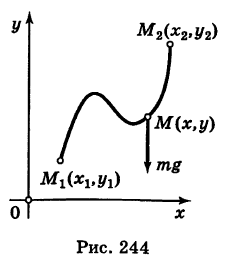
Решение:
Если ось Ох горизонтальна, а ось Оу вертикальна, то проекции силы тяжести, действующей на материальную точку массы т, равны X = 0, У = -mg. Имеем
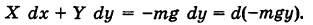
Поэтому за потенциал поля силы тяжести можно принять
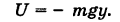
Отсюда работа силы тяжести, независимо от пути  , равна
, равна
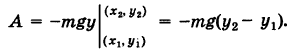
Замечание. Аналогичные результаты справедливы для криволинейного интеграла, взятого по пространственной кривой. В частности, если
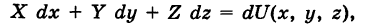
то
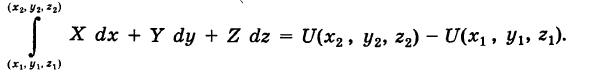
- Двойные и тройные интегралы
- Делимость чисел в математике
- Обыкновенные дроби
- Отношения и пропорции
- Уравнения поверхности и линии в пространстве
- Общее уравнение плоскости
- Угол между плоскостями
- Понятие о производной вектор-функции
Краткая теория
Пусть
функция
непрерывна в каждой точке
гладкой кривой
. Разобьем кривую
произвольным образом на
частей длиной
. Обозначим
. В каждой части возьмем
произвольную точку
, тогда предел
последовательности интегральных сумм
при
и
называется криволинейным интегралом I рода:
Основные свойства криволинейных интегралов I рода
1.
Криволинейный интеграл не зависит от направления пути интегрирования:
2. Если
кривая
разбита на части
и
, то
3. Если
и
– непрерывные функции на
и
– постоянные числа, то
Вычисление криволинейного интеграла I рода
Вычисление криволинейного интеграла I рода зависит от того, каким
образом задана кривая интегрирования.
1. Если
пространственная кривая
задана параметрическими уравнениями
то
2. В
частности для плоской кривой
:
Получаем:
3. Если
плоская кривая
определена уравнением
,
, то
4. Если
кривая
задана полярным уравнением
, то
Примеры решения задач
Задача 1
Вычислить
криволинейный интеграл 1-го рода
По замкнутому
контуру
, образованному сторонами
треугольника
с вершинами
.
Решение
Искомый криволинейный интеграл будет
равен:
Для отрезка
:
Для отрезка ВС:
Найдем уравнение прямой BC:
Для отрезка СА:
Найдем уравнение прямой СА:
Искомый интеграл:
Ответ:
Задача 2
Вычислить
криволинейный интеграл по указанной кривой.
– дуга кривой
от
до
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Криволинейный
интеграл 1-го рода можно вычислить по формуле:
Производная:
Получаем:
Ответ:
Задача 3
В задаче
вычислить криволинейные интегралы по кривой
:
Решение
Криволинейный
интеграл 1-го рода можно вычислить по формуле:
Ответ:
3.1.1. Как вычислить криволинейный интеграл первого рода?
Пусть точки ![]() являются концами
являются концами
линии ![]() , а сама она задана
, а сама она задана
функцией одной переменной ![]() (в плоскости
(в плоскости ![]() ). Тогда криволинейный
). Тогда криволинейный
интеграл первого рода можно свести к определённому интегралу по следующей
формуле:
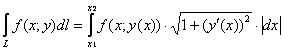
Формулу можно расписать подробно, без модуля при «дэ икс»:
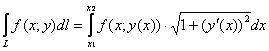 , если
, если ![]() (стандартный случай) или
(стандартный случай) или
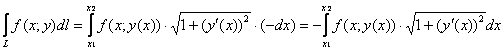 , если
, если ![]() .
.
В частности, при ![]() получается хорошо знакомая формула длины дуги кривой
получается хорошо знакомая формула длины дуги кривой 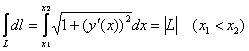 . …Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже
. …Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже
решали! И теперь вам совсем не нужно решимости:)
Пример 53
Вычислить интеграл ![]() от точки
от точки ![]() до точки
до точки ![]() , если кривая
, если кривая ![]() задана уравнением
задана уравнением ![]()
Решение: перед нами каноническое уравнение параболы, и коль скоро в условии дана точка ![]() , то речь идёт о её верхней ветке:
, то речь идёт о её верхней ветке: ![]() . И вы можете даже не знать, как выглядит
. И вы можете даже не знать, как выглядит
эта кривая. Здесь важно, что интегрирование проводится от точки ![]() до точки
до точки ![]() , а посему
, а посему ![]() . Таким образом, у нас наиболее распространённый случай
. Таким образом, у нас наиболее распространённый случай ![]() , следовательно, нужно использовать формулу:
, следовательно, нужно использовать формулу:
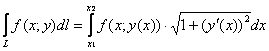 .
.
Сначала удобно найти производную: ![]() и сразу же упростить корень:
и сразу же упростить корень: 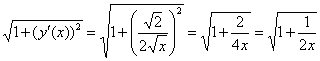 .
.
Так как ![]() и
и ![]() , то
, то ![]() – грубо говоря, на данном шаге мы избавляемся от «игреков».
– грубо говоря, на данном шаге мы избавляемся от «игреков».
Предварительная подготовка завершена, пользуемся формулой:
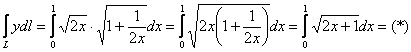
здесь можно провести замену переменной, но гораздо сподручнее подвести подкоренное выражение под знак
дифференциала и обойтись без перехода к новым пределам интегрирования:
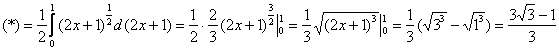
Ответ: ![]()
Если вычислить тот же самый интеграл в противоположном направлении – от точки ![]() до точки
до точки ![]() , то результат не изменится. В этом случае пределы интегрирования
, то результат не изменится. В этом случае пределы интегрирования
поменяются местами ![]() , и коль скоро
, и коль скоро
![]() , то мы пользуемся второй
, то мы пользуемся второй
формулой: 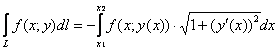 , в нашем случае:
, в нашем случае:
![]()
По существу, тут работает свойство 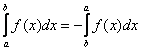 определённого интеграла.
определённого интеграла.
Таким образом, криволинейный интеграл 1-го рода не зависит от направления интегрирования: ![]() .
.
В этой связи типовая задача, как правило, формулируется «нейтрально»: вычислить интеграл ![]() вдоль дуги параболы
вдоль дуги параболы ![]() , расположенной между точками
, расположенной между точками ![]() . Иными словами, совершенно не важно, какая из точек является началом,
. Иными словами, совершенно не важно, какая из точек является началом,
а какая – концом кривой.
Следует отметить, что криволинейный интеграл можно вычислить и другим способом. Поскольку буква «игрек» ничем не хуже
«икса», то для вычисления криволинейного интеграла 1-го рода справедлива «зеркальная» формула (тривиальный вариант
![]() ):
):
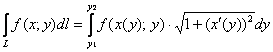 , где
, где ![]() – обратная функция, выражающая линию
– обратная функция, выражающая линию ![]() .
.
С параболой никаких проблем ![]() ,
,
и производной – тем более: 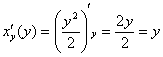
При переходе от ![]() к
к ![]() мы должны избавиться от всех «иксов»,
мы должны избавиться от всех «иксов»,
однако функция ![]() от них не
от них не
зависит, а значит, делать ничего не нужно.
И, учитывая, что для «игрековых» координат точек ![]() справедливо неравенство
справедливо неравенство ![]() , доводим решение до того же самого результата:
, доводим решение до того же самого результата:

В чём состоит геометрический смысл разобранной задачи? На плоскости ![]() между точками
между точками ![]() и
и ![]() находится кусок параболы
находится кусок параболы ![]() , через который проходит «одноимённый» параболический
, через который проходит «одноимённый» параболический
цилиндр ![]() параллельно оси
параллельно оси
![]() .
.
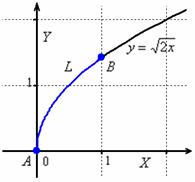
Этот цилиндр «высекает» из плоскости ![]() пространственную «ниточку» (выше плоскости
пространственную «ниточку» (выше плоскости ![]() ).
).
Криволинейный интеграл ![]() численно равен площади
численно равен площади ![]() фрагмента параболического цилиндра, который расположен между
фрагмента параболического цилиндра, который расположен между
куском параболы и этой «ниткой». …Вроде всё понятно….
Как я уже отмечал, криволинейный интеграл может получиться отрицательным – это означает, что фрагмент полностью или бОльшей
частью лежит ниже плоскости ![]() .
.
Не удивляйтесь и нулю (в каких случаях?). То есть, «всё как у нормальных интегралов» 🙂
Аналогичный пример для самостоятельного решения:
Пример 54
Вычислить интеграл ![]() по дуге
по дуге
окружности ![]() от точки
от точки ![]() до точки
до точки ![]() . Пояснить геометрический смысл полученного результата.
. Пояснить геометрический смысл полученного результата.
Краткое решение с комментариями в конце книги – тот, кто правильно во всём разобрался, может считать себя «самоваром»
интегралов =)
Но этим практика не исчерпывается, ситуации бывают разные:
 3.1.2. Если линия задана параметрически
3.1.2. Если линия задана параметрически
 3.1. Криволинейные интегралы первого рода
3.1. Криволинейные интегралы первого рода
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
