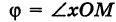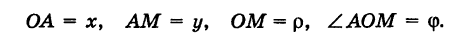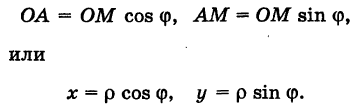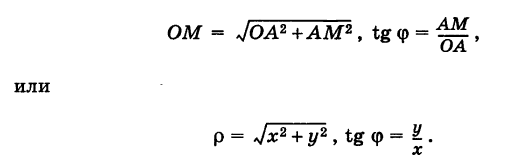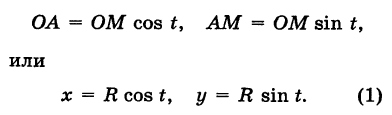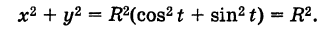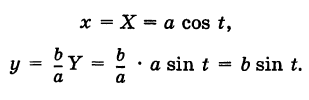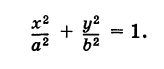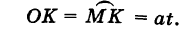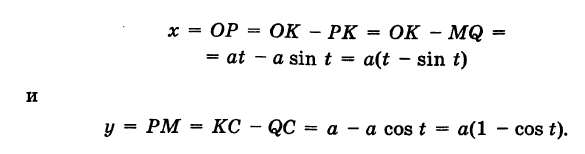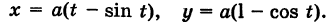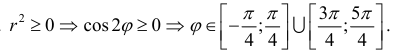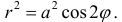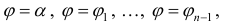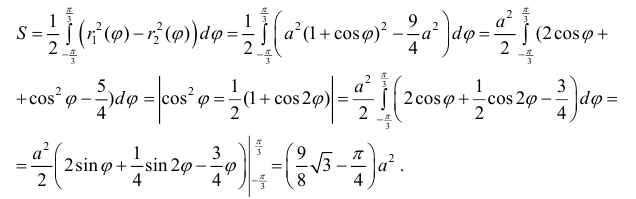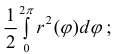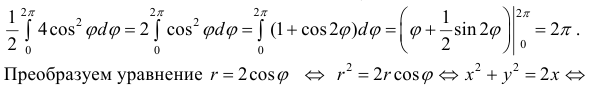Полярная сетка, на которой отложено несколько углов с пометками в градусах
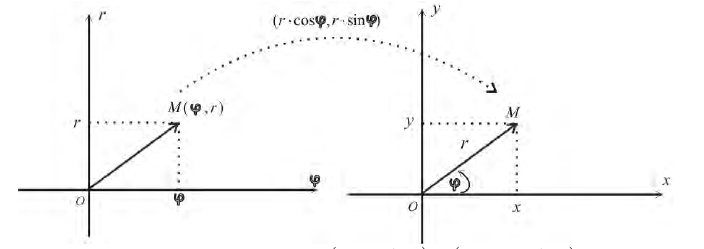
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой декартовой, или прямоугольной, системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся лучом, который называют нулевым лучом, или полярной осью.
Точка, из которой выходит этот луч, называется началом координат, или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой.
Радиальная координата (обычно обозначается 

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
История[править | править код]
Понятие угла и радиуса были известны ещё в первом тысячелетии до нашей эры. Греческий астроном Гиппарх (190—120 до н. э.) создал таблицу, в которой для разных углов приводились длины хорд. Существуют свидетельства применения им полярных координат для определения положения небесных тел[2]. Архимед в своём сочинении «Спирали» описывает так называемую спираль Архимеда, функцию, радиус которой зависит от угла. Работы греческих исследователей, однако, не развились в целостное определение системы координат.
В IX веке персидский математик Хаббаш аль-Хасиб (аль-Марвази́) применял методы картографических проекций и сферической тригонометрии для преобразования полярных координат в другую систему координат с центром в некоторой точке на сфере, в этом случае, для определения Киблы — направления на Мекку[3]. Персидский астроном Абу Райхан Бируни (973—1048) выдвинул идеи, которые выглядят как описание полярной системы координат. Он был первым, кто, примерно в 1025 году, описал полярную экви-азимутальную равнопромежуточную проекцию небесной сферы[4].
Существуют разные версии о введении полярных координат в качестве формальной системы координат. Полная история возникновения и исследования описана в работе профессора из Гарварда Джулиан Лоувел Кулидж «Происхождение полярных координат»[5]. Грегуар де Сен-Венсан и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625 году, напечатав свои труды в 1647; а Кавальери напечатал свои труды в 1635 году, и исправленную версию в 1653 году. Кавальери применял полярные координаты для вычисления площади, ограниченной спиралью Архимеда. Блез Паскаль впоследствии использовал полярные координаты для вычисления длин параболических дуг.
В книге «Метод флюксий» (англ. Method of Fluxions, написана в 1671 году, напечатана в 1736 году) сэр Исаак Ньютон исследовал преобразование между полярными координатами, которые он обозначал как «Седьмой способ; Для спиралей» («англ. Seventh Manner; For Spirals»), и девятью другими системами координат[6]. В статье, опубликованной в 1691 году в журнале Acta eruditorum, Якоб Бернулли использовал систему с точкой на прямой, которые он назвал полюсом и полярной осью соответственно. Координаты задавались как расстояние от полюса и угол от полярной оси. Работа Бернулли была посвящена проблеме нахождения радиуса кривизны кривых, определённых в этой системе координат.
Введение термина «полярные координаты» приписывают Грегорио Фонтана. В XVIII веке он входил в лексикон итальянских авторов. В английский язык термин попал через перевод трактата Сильвестра Лакруа «Дифференциальное и интегральное исчисление», выполненного в 1816 году Джорджем Пикоком[7][8] Для трёхмерного пространства полярные координаты впервые предложил Алекси Клеро, а Леонард Эйлер был первым, кто разработал соответствующую систему[5].
Графическое представление[править | править код]
Точка в полярной системе координат
Каждая точка в полярной системе координат может быть определена двумя полярными координатами, что обычно называются 






Полярный радиус определен для любой точки плоскости и всегда принимает неотрицательные значения 



- в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
- в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Например, точка с координатами 

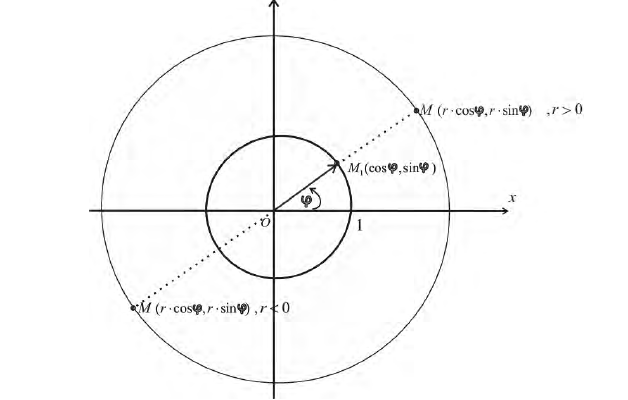
Одной из важных особенностей полярной системы координат является то, что одна и та же точка может быть представлена бесконечным количеством способов. Это происходит потому, что для определения азимута точки нужно повернуть полярную ось так, чтобы она указывала на точку. Но направление на точку не изменится, если осуществить произвольное число дополнительных полных оборотов. В общем случае точка 



Для обозначения полюса используют координаты 




![(-180^{circ },;180^{circ }]](https://wikimedia.org/api/rest_v1/media/math/render/svg/535196b36d3271ec1d81408cf666971e69c412a8)

![(-pi ,;pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d42d585d0cc7e452cd100efa4127cc28bedceb)
Углы в полярных координатах задаются либо в градусах, либо в радианах, при этом 
Связь между декартовыми и полярными координатами[править | править код]
Пару полярных координат 




в то время как две декартовы координаты 


(по теореме Пифагора).
Для определения угловой координаты 
Для вычисления 


.
Для вычисления 
![(-pi ,;pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d42d585d0cc7e452cd100efa4127cc28bedceb)
.
Учитывая, что для вычисления полярного угла недостаточно знать отношение 

atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты 


Уравнение кривых в полярных координатах[править | править код]
Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат было бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.
Окружность[править | править код]
Окружность, заданная уравнением
Общее уравнение окружности с центром в (

Это уравнение может быть упрощено для частных случаев, например
является уравнением, определяющим окружность с центром в полюсе и радиусом 
Прямая[править | править код]
Радиальные прямые (те, которые проходят через полюс) определяются уравнением
,
где 




Полярная роза[править | править код]
Полярная роза задана уравнением
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:
для произвольной постоянной 








Если считать, что радиус не может быть отрицательным, то при любом натуральном 

будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.
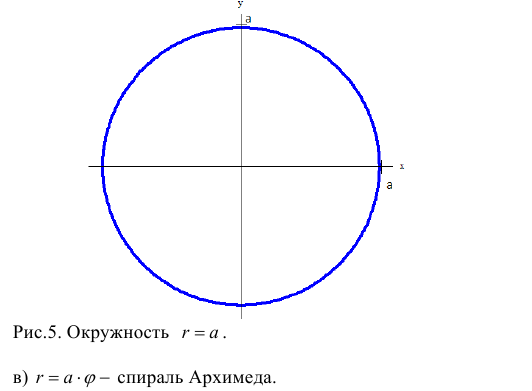
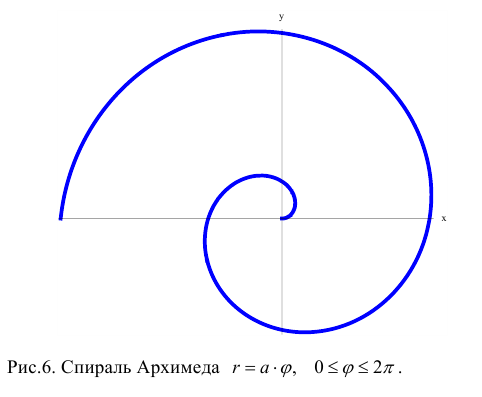
Спираль Архимеда[править | править код]
Одна из ветвей спирали Архимеда, задаваемая уравнением 
Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:
Изменения параметра 



Конические сечения[править | править код]
Коническое сечение, один из фокусов которого находится в полюсе, а другой где-то на полярной оси (так, что большая полуось лежит вдоль полярной оси) задаётся уравнением:
,
где 






Комплексные числа[править | править код]
Пример комплексного числа 
Пример комплексного числа, нанесённого на график, с использованием формулы Эйлера
Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число 
,
где 
и отсюда:
,
где 

Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.
Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:
- Умножение:
- Деление:
- Возведение в степень (формула Муавра):
В математическом анализе[править | править код]
Операции математического анализа тоже можно сформулировать, используя полярные координаты[16][17].
Дифференциальное исчисление[править | править код]
Справедливы следующие формулы:
Чтобы найти тангенс угла наклона касательной к любой данной точке полярной кривой 
Дифференцируя оба уравнения по 
Разделив эти уравнения (второе на первое), получим искомый тангенс угла наклона касательной в декартовой системе координат в точке 
Интегральное исчисление[править | править код]
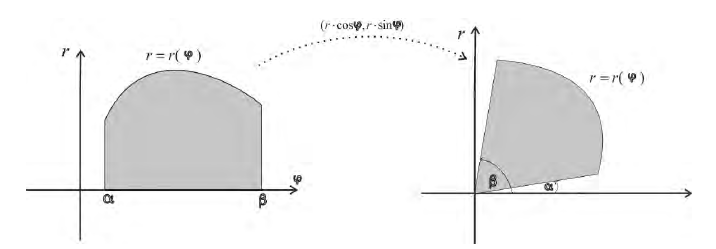
Область 


Пусть 




Область 


Такой результат можно получить следующим образом. Сначала разобьём интервал ![[a,;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e682a8a7d3222e237401e57d673fd362523662cd)










Если число подынтервалов 


Обобщение[править | править код]
Используя декартовы координаты, площадь бесконечно малого элемента может быть вычислена как 
Для полярной системы координат, определитель матрицы Якоби равен 
Следовательно, площадь элемента в полярных координатах можно записать так:
Теперь, функция, записанная в полярных координатах, может быть интегрирована следующим образом:
Здесь область 



Формула для вычисления площади, описанная в предыдущем разделе, получена в случае 
Векторный анализ[править | править код]
Для полярных координат можно применить элементы векторного анализа. Любое векторное поле 
в направлении 
Связь между декартовыми компонентами поля 

Соответствующим образом в полярной системе координат определяются операторы векторного анализа. Например, градиент скалярного поля 
Всё это работает за исключением одной особой точки — полюса, для которой 
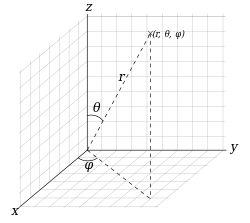
Трёхмерное расширение[править | править код]
Полярная система координат распространяется в третье измерение двумя системами: цилиндрической и сферической, обе содержат двумерную полярную систему координат как подмножество. По сути, цилиндрическая система расширяет полярную добавлением ещё одной координаты расстояния, а сферическая — ещё одной угловой координаты.
Цилиндрические координаты[править | править код]
Точка 
Цилиндрическая система координат, грубо говоря, расширяет плоскую полярную систему добавлением третьей линейной координаты, называемой «высотой» и равной высоте точки над нулевой плоскостью подобно тому, как декартова система расширяется на случай трёх измерений. Третья координата обычно обозначается как 

Тройку цилиндрических координат можно перевести в декартову систему следующими преобразованиями:
Сферические координаты[править | править код]
Точка начертана в сферической системе координат
Также полярные координаты можно расширить на случай трёх измерений путём добавления угловой координаты 











Тройку сферических координат можно перевести в декартову систему следующими преобразованиями:
Обобщение на n измерений[править | править код]
Полярную систему координат можно расширить на случай 






Для перевода обобщённых 
Как можно показать, случай 

Якобиан преобразования полярных координат в декартовы даётся формулой:
,
где 
Применение[править | править код]
Полярная система координат двумерная и поэтому может применяться только в тех случаях, когда местонахождение точки определяется на плоскости, или для случая однородности свойств системы в третьем измерении, например, при рассмотрении течения в круглой трубе. Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра. Например, в приведённых выше примерах видно, что простых уравнений в полярных координатах достаточно для определения таких кривых как спираль Архимеда, уравнения которых в прямоугольной системе координат гораздо сложнее. Кроме того, многие физические системы — такие, которые содержат тела, движущиеся вокруг центра, либо явления, распространяющиеся из некоторого центра — гораздо проще моделировать в полярных координатах. Поводом создания полярной системы координат было исследование орбитального и движения по кругу, впоследствии оказалось, что она крайне удобна иногда и для исследования некругового движения (см. Кеплерова задача).
Позиционирование и навигация[править | править код]
Полярную систему координат часто применяют в навигации, поскольку пункт назначения можно задать как расстояние и направление движения от отправной точки. Например, в авиации, для навигации применяют несколько изменённую версию полярных координат. В этой системе, обычно используемой для навигации, луч 0° называют направлением 360, а углы отсчитываются в направлении по часовой стрелке. Направление 360 соответствует магнитному северу, а направления 90, 180, и 270 соответствуют магнитным востоку, югу и западу[19]. Так, самолёт, летящий 5 морских миль на восток можно описать как самолёт, летящий 5 единиц в направлении 90 (центр управления полётами назовёт его найн-зиро)[20].
Применение в физике[править | править код]
Cечение комптоновского рассеяния от угла рассеяния (для разной энергии фотона)
Системы с радиальной симметрией очень хорошо подходят для описания в радиальных координатах, где полюс системы координат совпадает с центром симметрии. В качестве примера можно привести уравнение тока грунтовых вод в случае радиально симметричных колодцев. Системы с центральными силами также подходят для моделирования в полярных координатах. К таким системам относятся гравитационные поля, подчиняющиеся закону обратно-квадратичной зависимости, и вообще центральные силы. Также существенное удобство полярные координаты предоставляют при работе с системами, имеющими точечные (или приближенно точечные) источники энергии, такие как радиоантенны — при исследовании их излучения на сравнительно больших расстояниях от антенны, распространение звука или света — в особенности (но не обязательно) сферически- или цилиндрически-симметричное.
В определенных задачах, в том числе из числа упомянутых выше, использование сферических или цилиндрических координат (являющихся для этих задач естественными) по сути сводится к использованию просто двумерных полярных координат.
Полярные координаты как для вычислений, так и для наглядного изображения их результатов, бывают достаточно полезны не только в случаях, когда симметрия задачи близка в целом к осевой или сферической, но и в случаях, когда симметрия явно далека от таковой, например, для вычисления поля диполя. В этом случае применение полярных координат имеет мотивировку в малом размере источника поля (заряды диполя расположены очень близко друг к другу), к тому же поле каждого такого заряда просто выражается в полярных координатах, особенно если поместить полюс в один из этих зарядов (поле второго будет отличаться, кроме знака, лишь на малую поправку).
В квантовой механике и химии полярные координаты (наряду со сферическими для более сложных случаев) используются для изображения угловой зависимости волновой функции электрона в атоме, в том числе в целях качественного анализа и наглядности при преподавании.
Применение в прикладных целях, диаграммы направленности[править | править код]
Диаграмма направленности (азимутальная) типичной направленной антенны
Фронт мощности звуковой волны промышленного громкоговорителя показан в сферических координатах при шести частотах
В разных прикладных областях, полярные координаты применяются как способами, близкими к применяемым в соответствующих областям фундаментальной физики, так и самостоятельным образом.
Трёхмерное моделирование звука динамиков может использоваться для прогнозирования их эффективности. Необходимо сделать несколько диаграмм в полярных координатах для широкого диапазона частот, поскольку фронт существенно меняется в зависимости от частоты звука. Полярные диаграммы помогают увидеть, что многие громкоговорители с понижением частоты звука теряют направленность. В случае излучателя, имеющего строгую осевую симметрию или слабо от нее отклоняющегося, достаточно использовать не сферические, а обычные (двумерные) полярные координаты, так как во всех плоскостях, проходящих через ось симметрии, зависимость будет одинаковой или почти одинаковой. Если такой симметрии нет, то какое-то представление о звуковом потоке в разных направлениях может дать пара (для каждой частоты) полярных диаграмм в перпендикулярных плоскостях, для эллиптического или прямоугольного излучателя — связанного с его главными осями.
В полярных координатах также принято представлять характеристику направленности микрофонов, определяемую отношением чувствительности при падении звуковой волны под углом относительно акустической оси микрофона к его осевой чувствительности.
В принципе, полярные диаграммы могут использоваться для представления практически любых зависимостей. Но на практике обычно этот вид представления выбирается в случаях, когда речь идет от зависимости от реального геометрического направления (см. например Роза ветров, Диаграмма рассеяния, зависимость отраженного светового потока от угла в фотометрии, диаграмма направленности антенн, светодиодов и других светоизлучателей, фотодатчиков, акустических систем итп). Также довольно нередко можно встретиться с применением полярных координат в случаях, когда одна из переменных имеет циклический характер (в полярных координатах ее довольно естественно представлять углом).
Могут применяться и областях, не связанных прямо с физикой (хотя иногда можно проследить более или менее прямую аналогию в этом плане), например, можно использовать полярные диаграммы, аналогичные розе ветров, например, для изучения направлений миграций животных. Такое использование достаточно удобно и наглядно.
См. также[править | править код]
- Системы координат в элементарной математике
Примечания[править | править код]
- ↑ 1 2 Brown, Richard G. Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis (англ.) / Andrew M. Gleason. — Evanston, Illinois: McDougal Littell (англ.) (рус., 1997. — ISBN 0-395-77114-5.
- ↑ Friendly, Michael Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization. Дата обращения: 10 сентября 2006. Архивировано из оригинала 26 апреля 2001 года.
- ↑ T. Koetsier, L. Bergmans (2005), Mathematics and the Divine, Elsevier, с. 169, ISBN 0444503285
- ↑ David A. King (1996), «Astronomy and Islamic society: Qibla, gnomics and timekeeping», in Roshdi Rashed (ed.), Encyclopedia of the History of Arabic Science, Vol. 1, pp. 128—184 [153], Routledge, London and New York
- ↑ 1 2 Coolidge, Julian (англ.) (рус.. The Origin of Polar Coordinates (англ.) // American Mathematical Monthly : journal. — 1952. — Vol. 59. — P. 78—85. — doi:10.2307/2307104.
- ↑ Boyer, C. B. Newton as an Originator of Polar Coordinates (англ.) // American Mathematical Monthly : journal. — 1949. — Vol. 56. — P. 73—78. — doi:10.2307/2306162.
- ↑ Miller, Jeff Earliest Known Uses of Some of the Words of Mathematics. Дата обращения: 10 сентября 2006. Архивировано 15 февраля 2012 года.
- ↑ Smith, David Eugene. History of Mathematics, Vol II (неопр.). — Boston: Ginn and Co., 1925. — С. 324.
- ↑ Polar Coordinates and Graphing (PDF) (недоступная ссылка — история) (13 апреля 2006). Дата обращения: 22 сентября 2006. Архивировано 15 февраля 2012 года.
- ↑ Lee, Theodore; David Cohen, David Sklar. Precalculus: With Unit-Circle Trigonometry (англ.). — Fourth Edition. — Thomson Brooks/Cole, 2005. — ISBN 0534402305.
- ↑ Stewart, Ian; David Tall. Complex Analysis (the Hitchhiker’s Guide to the Plane) (англ.). — Cambridge University Press, 1983. — ISBN 0521287634.
- ↑ Serway, Raymond A.; Jewett, Jr., John W. Principles of Physics (неопр.). — Brooks/Cole—Thomson Learning, 2005. — ISBN 0-534-49143-X.
- ↑ Torrence, Bruce Follett; Eve Torrence. The Student’s Introduction to Mathematica® (англ.). — Cambridge University Press, 1999. — ISBN 0521594618.
- ↑ Claeys, Johan Polar coordinates (недоступная ссылка — история). Дата обращения: 25 мая 2006. Архивировано 15 февраля 2012 года.
- ↑
Smith, Julius O. Euler’s Identity // Mathematics of the Discrete Fourier Transform (DFT) (англ.). — W3K Publishing, 2003. — ISBN 0-9745607-0-7. - ↑ Husch, Lawrence S. Areas Bounded by Polar Curves. Дата обращения: 25 ноября 2006. Архивировано из оригинала 11 октября 2014 года.
- ↑ Lawrence S. Husch. Tangent Lines to Polar Graphs. Дата обращения: 25 ноября 2006. Архивировано из оригинала 2 июля 2015 года.
- ↑ Wattenberg, Frank Spherical Coordinates (недоступная ссылка — история) (1997). Дата обращения: 16 сентября 2006. Архивировано 15 февраля 2012 года.
- ↑ Santhi, Sumrit Aircraft Navigation System (недоступная ссылка — история). Дата обращения: 26 ноября 2006. Архивировано 15 февраля 2012 года.
- ↑ Emergency Procedures (PDF). Дата обращения: 15 января 2007. Архивировано 15 февраля 2012 года.
Литература[править | править код]
- Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. (недоступная ссылка) Издание пятое, стереотипное. Серия: Библиотечка физико-математической школы. Математика. Выпуск 1. М.: Наука, 1973, стр. 47-50.
Ссылки[править | править код]
- Программы для рисования графиков в каталоге ссылок Curlie (dmoz)
Содержание:
Полярные координаты. параметрические уравнения линии
Полярные координаты
Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.
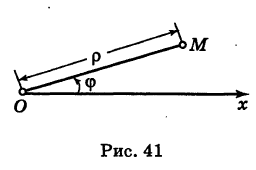
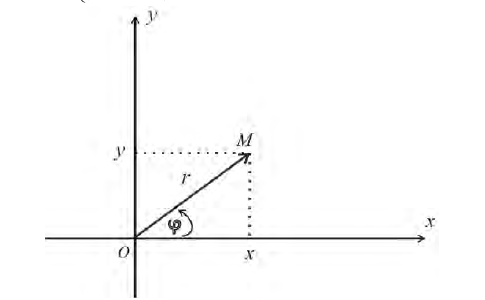
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол
Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до 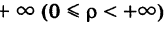
Связь между прямоугольными и полярными координатами
Рассмотрим переход от полярных координат к прямоугольным и обратно.
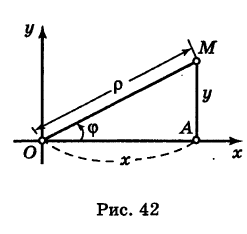
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).
Тогда для произвольной точки М имеем
Считая угол ф острым, из прямоугольного треугольника АОМ находим
Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем
Так выражаются полярные координаты точки через ее прямоугольные координаты.
Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.
Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.
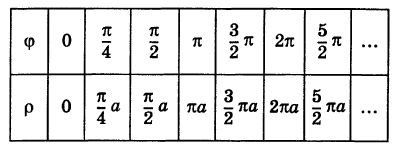
Пример:
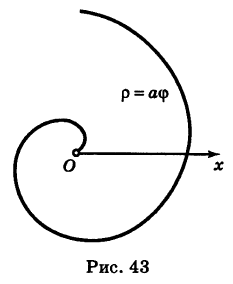
Рассмотрим кривую 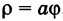
По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).
Параметрические уравнения линии
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 
Пример:
Выведем параметрические уравнения окружности.
Пусть М
Это и есть параметрические уравнения окружности.
Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:
Пример:
Выведем параметрические уравнения эллипса.
Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где
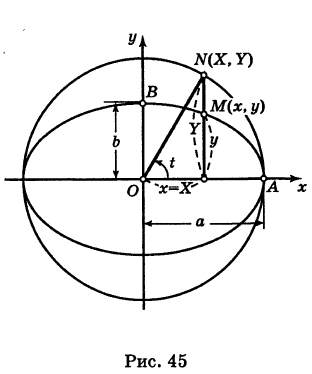
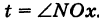
Таким образом, параметрические уравнения эллипса с полуосями а и b есть
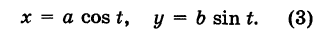
Имея параметрические уравнения линии, можно по точкам построить ее.
Пример:
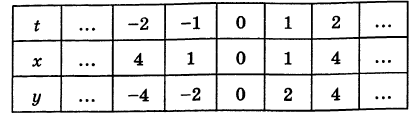
Построить кривую
Решение:
Составляем таблицу значений:
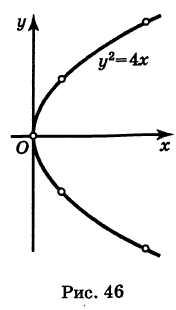
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 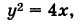
Параметрические уравнения циклоиды
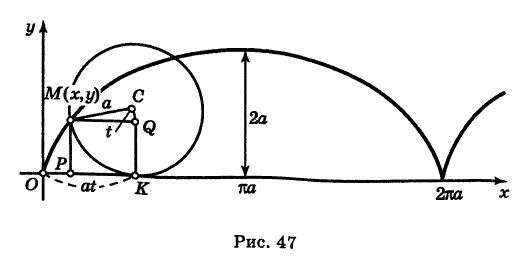
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).
Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем
Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:
Таким образом, параметрические уравнения циклоиды есть
——-
Полярная система координат
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 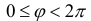
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 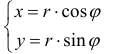
Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:
Пример 1.
Построим на плоскости линию, заданную уравнением:
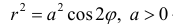
Решение.
Вычислим значения r при различных значениях ϕ :
Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :
Рис.3. Лемниската
- Заказать решение задач по высшей математике
Пример 2.
а) Построим кривую 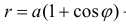
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ < 2π и не требовать r > 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).
При этом, если r > 0, то векторы 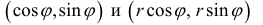
Тогда, с учетом (1), кривую r= r(ϕ) можно рассматривать как заданную параметрически в виде:
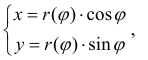
В этом случае на кривой 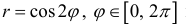
лепестка, когда 
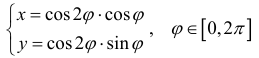
На кривой 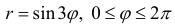
задается параметрически формулами:
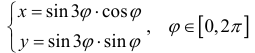
Пусть r = r(ϕ) – кривая в полярной системе координат, r (ϕ) – непрерывна при 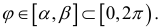
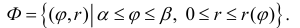
соответствует обычная криволинейная трапеция на плоскости (O, r, ϕ)
Разобьем фигуру Ф на n частичных фигур лучами 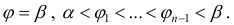
трапеции:
Рассмотрим, например, нижние суммы Дарбу:
Каждое слагаемое в нижней сумме 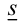
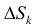
сектора радиуса 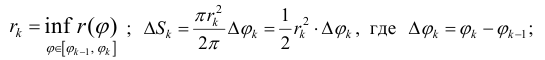
таким образом,
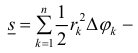
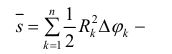
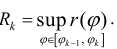
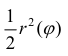
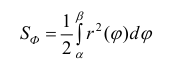
Пример 3.
Найти площадь ограниченную лемнискатой 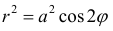
Решение.
По формуле (4):
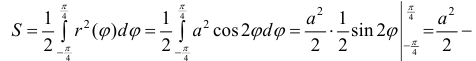
Поэтому
Пример 4.
Найти площадь фигуры ограниченной линиями: 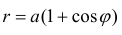
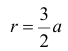
Решение. Найдем точки пересечения кривых: 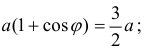
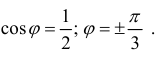
Пример 3.
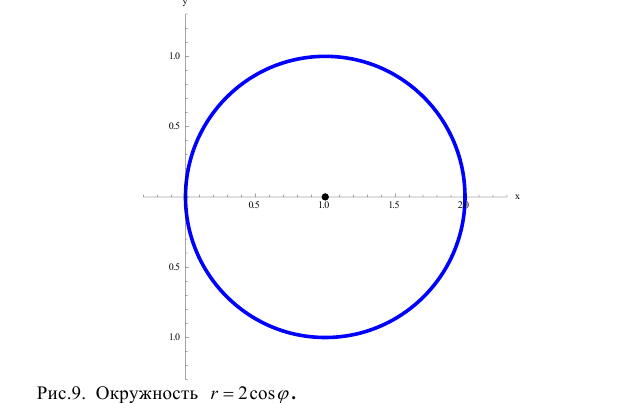
r=2cosϕ. Вычислим
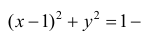
При изменении ϕ от 0 до 2 π окружность проходится дважды и оба раза против
часовой стрелки, поэтому (см. § 30) найденное значение интеграла задает
удвоенную площадь круга.
- Непрерывность функции
- Уравнения поверхности и линии в пространстве
- Общее уравнение плоскости
- Угол между плоскостями
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
П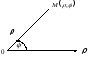
системакоординат задается на
плоскости точкой–
полюсом и лучом– полярной осью.
Положение точки
относительно полярной системы координат
определяют ее полярные координаты:– полярный радиус, равный расстоянию
точкиот полюса
,
т.е.,
и– полярный угол, который образует
полярный радиус с полярной осью. Пишут:,
где,
.
С
между декартовыми и полярными координатами
точки.Если полюс полярной системы координат
совместить с началом координат декартовой
системы, а полярную ось направить по
оси,
то между декартовыми и полярными
координатами одной и той же точкилегко обнаружить следующую зависимость,
которую иллюстрирует рисунок:
Замечание:Чтобы правильно
выбрать угол, имеющий тангенс, равный,
следует
иметь в виду положение точки
относительно декартовой системы
координат.
Приведем примеры некоторых кривых на
плоскости, заданных в полярной системе
координат.
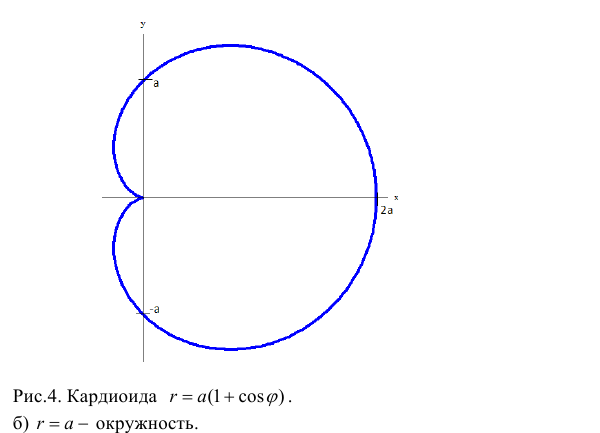
1. Окружность
или
.
или. или
.
2
СпиральАрхимеда . 3.
Лемниската Бернулли .
4. Кардиоида

; б)
;
в)
; г)
.
5. Розы
трехлепестковые четырехлепестковые
3.4 Параметрический способ задания кривых
на плоскости
Некоторые кривые на плоскости удобно
задавать уравнениями вида
,
где зависимость между функциейи аргументом
устанавливается через посредство
параметра (промежуточной переменной),
причем.
1. Параметрические уравнения прямой
l:

где;
– направляющий вектор прямой
,
– параметр.
2. Окружность:;
.
3. Эллипс: ;
.
3. Циклоида:– это
линия, которую описывает неподвижная
точка на окружности, в то время, как
окружность без скольжения катится по
оси.
4
Астроида:
3.5 Плоскость в пространстве
Задачи по теме «Плоскость в пространстве»
Задача1.Составить уравнение
плоскости,
параллельной плоскостии проходящей через точку
.
Р
7
ешение.Искомая плоскостьпараллельна координатной плоскости
,
значит, параллельна осями
.
Следовательно, в общем уравнении,
, т.е. оно имеет вид
,
где,
.
Найдеми
.
Так как точка,
то ее координаты должны удовлетворять
уравнение:
,
подставивв уравнение
и сократив на
,
получимили
.
Ответ:.
Задача
2. Составить уравнение плоскости,
проходящей через осьи через точку
.
Р
3
7
ешение.Плоскость,
проходящая через ось,
проходит через начало координат
параллельно оси,
значит, в общем уравнении,
,
т.е. оно имеет вид,
где,
и . Так как точка
,
то ее координаты должны удовлетворять
уравнение:
.
Подставимв уравнение
и сократим на
:
,
получим– уравнение
.
Ответ:.
З
3.Найти объем пирамиды, отсекаемой
плоскостьюот координатного угла.
Решение. Приведем уравнение данной
плоскости к виду «уравнение в отрезках
н
5
а осях» :
или
.
Откуда,
,
–
отрезки, отсекаемые плоскостью от осей
координат, совпадающие с
ребрами пирамиды
.
Так как они взаимно перпендикулярны,
то
.
Ответ:куб.ед.
Задача 4. Составить уравнение
плоскости,
проходящей через точкупараллельно плоскости
.
Р
11
6
ешение.Если две плоскости
параллельны, то их нормали тоже параллельны
,.
Поэтому в качестве нормали к искомой
плоскости можно взять нормаль к данной
плоскости.
Уравнение плоскости, проходящей через
данную точкуперпендикулярно данному вектору
:
, следовательно, искомая плоскость:
или
.
Ответ:.
Задача 5. Даны две точки:и
.
Через точкупровести плоскость, перпендикулярную
отрезку.
Найти направляющие косинусы нормали к
плоскости.
Р
6
ешение.Воспользуемся уравнением
плоскости, проходящей через данную
точку перпендикулярно данному вектору. Примем за нормаль
:
вектор.
Тогда уравнение плоскости:или
.
Чтобы найти направляющие косинусы
вектора,
найдем его орт:;
.
Следовательно:
или
;
;
.
Ответ: ;
;
;
.
Задача 6. Найти объем куба, если
грани его лежат на плоскостяхи
.
9
Решение. Объем куба,
где–
длина ребер куба. Ребро куба равно
расстоянию между данными плоскостями,
т. к. эти плоскости параллельны
(коэффициенты при переменных
пропорциональны), значит, на этих
плоскостях лежат противоположные грани
куба. Чтобы найти расстояние между двумя
плоскостями, воспользуемся формулой. Для этого на одной из плоскостей
выберем произвольную точку, например,
и найдем расстояние от нее до второй
плоскости:

Итак,
.
Ответ:.
Задача 7. Найти точку пересечения
данных плоскостей:,
,
.
Решение. Чтобы найти точку пересечения
трех плоскостей, т. е. общую точку этих
трех плоскостей, достаточно решить
систему их уравнений:
Используем метод Гаусса:


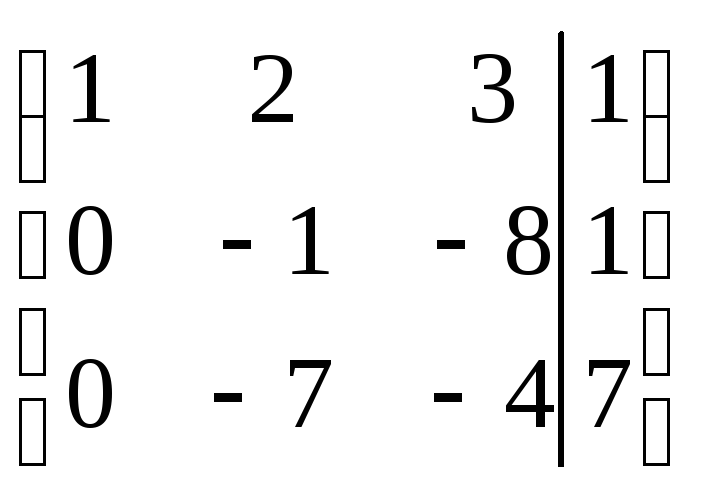
Ответ:.
Задача 8. Найти угол между
плоскостьюи плоскостью
.
9
Решение. Угол между двумя
плоскостями можно найти по формуле; нормаль к первой плоскости
;
уравнение второй плоскости.
Вычислим

т. е..
Ответ:.
Задача 9. Найти длину высоты
пирамиды,
опущенной из вершинына грань
,
если,
,
,
.
10
Р
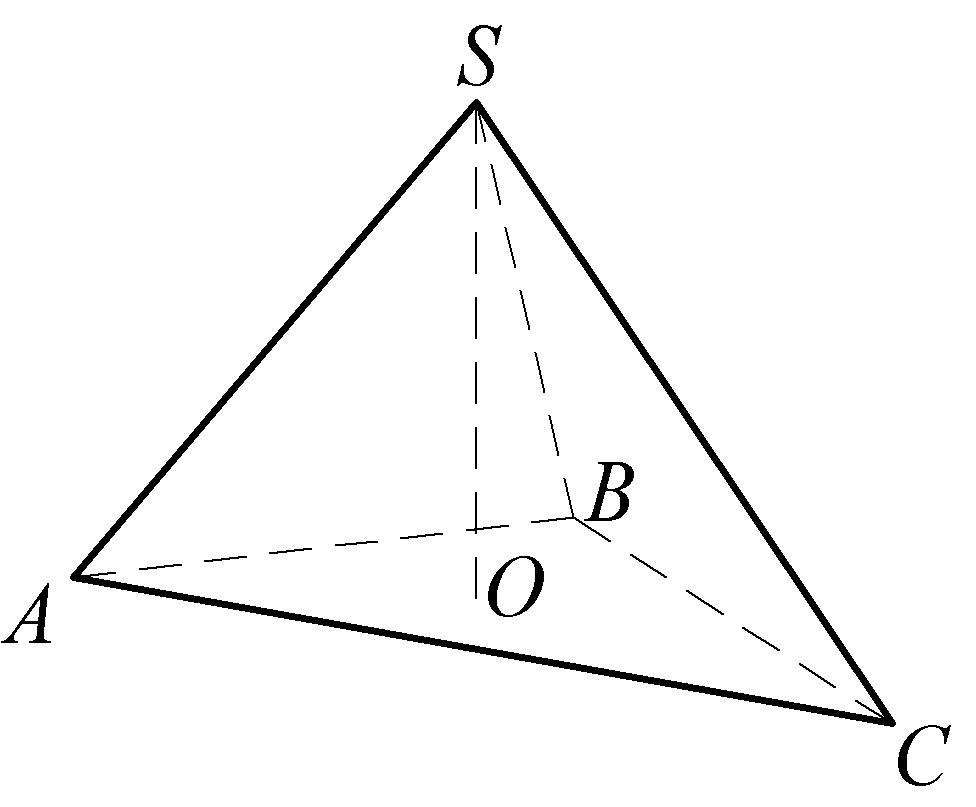
–
это длина перпендикуляра, опущенного
из вершиныпирамиды на плоскость ее основания, с
помощью которого измеряется расстояние
от точкидо плоскости основания
.
Составим уравнение плоскости,
проходящей через три данные точки,
и
,
для этого воспользуемся уравнением
:



или
–
9
уравнение плоскости основания
пирамиды. Расстояние
(высота
)
можно найти по формуле расстояния от
точки до плоскости :
.
Ответ:.
Задача 10. Найти уравнение
плоскости,
проходящей через точкупараллельно векторам
и
.
11
Р

данную точку перпендикулярно данному
вектору:
, точказадана в условии задачи; в качестве
нормального вектораможно
взять векторное произведение векторови
,
которые параллельны плоскости,
т. к.будет
перпендикулярен искомой плоскости.
9
Уравнение:
,
сократив на 8, получим
.
Ответ:.
3.6 Прямая в пространстве
З
по теме «Прямая и плоскость в пространстве»
Задача 1. Составить уравнение
прямой,
проходящей через точку
параллельно
оси.
3
Решение. В канонических уравнениях
прямойточка
,
а вектор–
направляющий вектор прямой. По условию
задачи прямая параллельна оси,
следовательно, направляющим вектором
прямой может служить орт осивектор
.
Итак, канонические уравнения прямой.
Приравнивая попарно отношения, получим
общие уравнения ее
.
Ответ:
Задача 2. Даны координаты вершин
треугольника;
;
.
Составить уравнения медианыи найти ее длину.
Решение.
а) Найдем координаты точки
–
середины отрезкапо
формулам:

;
,
т.е..
Через точки
и
проведем
прямую,
используя уравнения
или
.
б) Длину медианы
можно найти по формуле расстояния между
двумя точками:
.
Ответ: 1):
:
2)
.
Задача
3. Через точкупровести
прямую,
параллельную прямой:
.
Решение. Так как прямыеи
параллельны, то за направляющий вектор
искомой прямойможно принять направляющий вектор
данной прямой,
который можно найти как векторное
произведение нормалей к плоскостям,
при пересечении которых образуется
данная прямая:
и
.
5
Итак,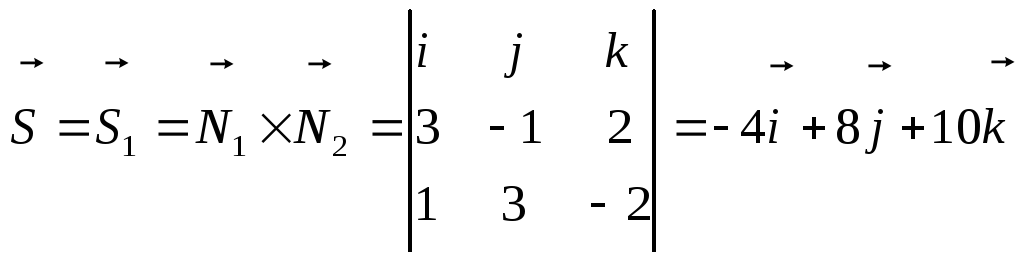
Канонические уравнения прямой
:
или
.
Ответ::
.
Задача 4.Доказать, что прямые:
и
:
:
перпендикулярны.
7
5
Решение.Если прямые перпендикулярны,
то перпендикулярны их направляющие
векторыи
. Из условий задачи ясно, что
,
а направляющий вектор второй прямойможно найти как векторное произведение
нормалей плоскостей, заданных в общих
уравнениях прямой,
т. е.и
.
Таким образом,
Скалярное произведение взаимно
перпендикулярных векторов равно нулю:
.
Что и требовалось доказать.
Задача 5.Найти угол между прямой,
проходящей через точкии
и плоскостью
:
.
8
Решение. Угол между прямой и
плоскостью можно найти по формуле, где
– нормаль к плоскости, а
–
направляющий вектор прямой.
8
По условию задачи.
Составим канонические уравнения прямой,
используя уравнения прямой, проходящей
через две данные точки:или
,
откуда.
Используем формулу.
Ответ:.
Задача 6.Привести общие уравнения
прямой:
к
каноническому виду.
5
Решение.Канонические уравнения
прямой имеют вид,
где точка,
а вектор–
направляющий вектор прямой.
Точкувыберем абсолютно произвольно на прямой
,
т. е. найдем одно из бесчисленного
множества решений системы уравнений.
Положим
,
тогда из первого уравнения,
а из второго,
т. е..
Направляющий вектор прямой,
как и ранее, найдем с помощью векторного
произведения векторови
:

5
Подставим координаты точкии
векторав
уравнения .
Ответ:.
Задача 7. Найти точку,
симметричную точкеотносительно
плоскости:
.
10
Решение. Точка– симметрична точке
относительно плоскости
,
если лежит на прямойи на одинаковом расстоянии от плоскости
, т. е.
.
Проведем через точкупрямую
,
приняв за ее
н
векторвектор
– нормаль к плоскости
:
.
или

уравнения прямой
.
Решив совместно уравнения плоскостии прямой
,
найдем точку.
Подставим,
,
,
выраженные через параметрв уравнениях
,
в уравнение,
получим.
–
это значение параметра,
соответствующее точке,
подставим его в параметрические уравнения
прямой , получим–середину
отрезка.
По формулам координат середины отрезка
получим
,
где,
откуда,
,
где,
откуда,
,
где,
откуда,
Ответ:.
Замечание:точкаявляется ортогональной проекцией точки
на плоскость
.
Задача 8. Найти проекцию точкина
прямую:
.
Р
на
прямуюв пространстве, проведем плоскость
через точку
перпендикулярно прямой
:
,
приняв за нормаль к плоскости– направляющий вектор прямой
:
или
:
.
6
Искомая точка–
точка пересечения прямойи плоскости
.
Решим систему их уравнений:
,
:
или
:

6
Подставим,
,
из уравнений прямой в уравнение
плоскости:,
откуда,
или,
или,
или,
.
Ответ:.
Задача 9. Найти проекцию прямой:
на плоскость
:
.
Р
на плоскость
называется линия пересечения плоскости
и плоскости
,
проходящей через прямуюперпендикулярно плоскости
,
т.е. прямая.
Приведем канонические уравнения прямой
к общему виду:(приравняв попарно отношения) .
2
Теперь составим уравнение пучка
плоскостей , проходящих через прямую:
,
и выделим из этого пучка плоскость,
перпендикулярную плоскости.
Воспользуемся условием перпендикулярности
двух плоскостей:,
подчинив ему уравнение плоскости:
и
плоскости:
.
Получим.
Подставим найденное значениев уравнение пучка плоскостей, получим
:
.
Проекция прямойна плоскость
– линия пересечения плоскостей
и
,
т.е.–
это
ответ.
3.7 Криволинейные поверхности
1оЦилиндрические поверхности
Цилиндром (цилиндрической поверхностью)
называют поверхность, которую описывает
прямая (образующая цилиндра), перемещающаяся
в пространстве параллельно некоторой
прямой, пересекая по пути некоторую
плоскую линию (направляющую цилиндра).
З
образующие которых параллельны
осям координат.
Если направляющая цилиндра
расположена в плоскости
,
ее уравнение,
а
образующие параллельны оси
,
то уравнение цилиндрической поверхности
совпадает с
уравнением направляющей:
.
Вообще, уравнение цилиндрической
поверхности
содержит только две переменные, оно
полностью совпадает с уравнением
направляющей
цилиндра, которая определяет его
фору. При этом образующие этого цилиндра,
параллельные
координатной оси, одноименной
координате, отсутствующей в уравнении.
Примеры
а
–
параболический цилиндр, образующие
которого параллельны оси.
б
–
«синусоидальный» цилиндр, образующие
которого параллельны оси
Теория
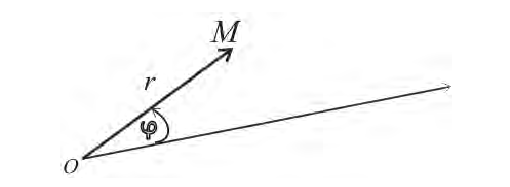
Полярная система координат на плоскости — координаты объекта, выраженные через направление и расстояние. Эта система включает в себя точку отсчета — полюс и луч , начинающийся в этой точке, — полярную ось. Положительным направлением отсчета углов считается направление «против часовой стрелки». Полярная система координат используется в астрономии, военном деле, геодезии, медицине.
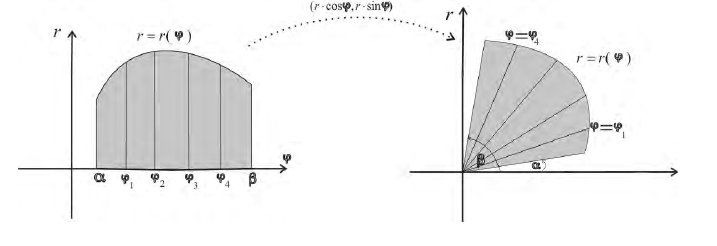
Выразим площадь S криволинейного сектора, то есть плоской фигуры, ограниченной непрерывной линией r = r(φ) и двумя лучами φ = α и φ = β , где r и φ – полярные координаты.
1. Будем считать часть искомой площади S как функцию угла φ, т.е. S = S(φ), где α < φ < β ( если φ = α, то S(α) = 0, если φ = β, то S(β) = S).
2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади ΔS равно площади “элементарного криволинейного сектора” OAB. Дифференциал dS представляет собой главную часть приращения ΔS при dφ → 0 и равен площади кругового сектора OAC (смотри рисунок) радиуса r с центральным углом dφ.
Поэтому dS = (1/2)⋅ r² ⋅ dφ.
3. Интегрируя полученное равенство в пределах от φ = α до φ = β, получим искомую площадь
Задача 1. Найти площадь, ограниченную кривыми, заданными в полярной системе координат: r = 1 – cos(φ) ; r = 1; r ⩾ 1
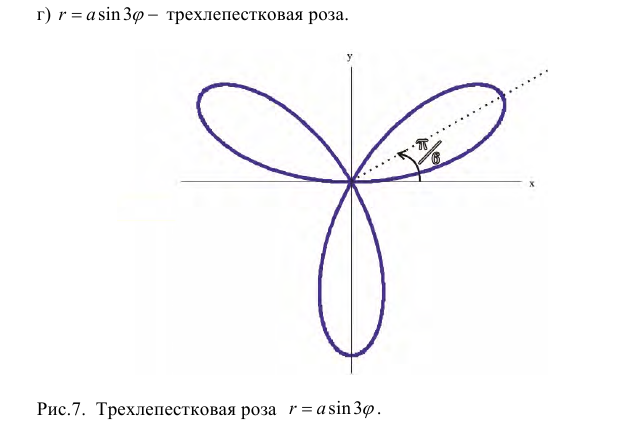
Задача 2. Найти площадь фигуры, ограниченной “трехлепестковой розой” r = a ⋅ cos(3φ).
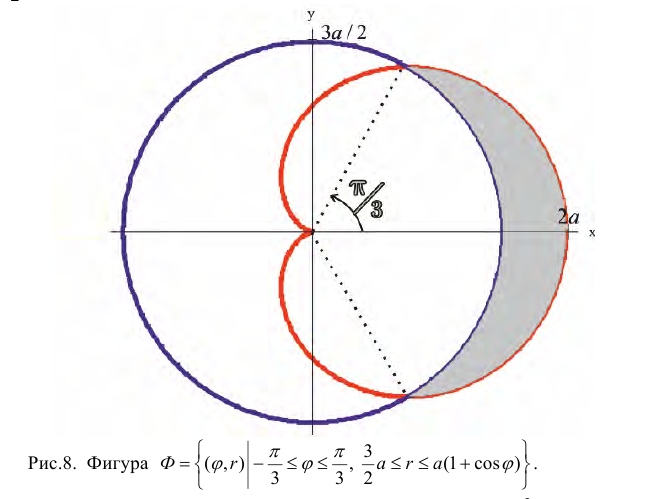
Задача 3. Если плоская фигура имеет “сложную” форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке ниже, имеем:
Задача 4. Вычислить площадь фигуры, ограниченной линией r = 2 cos²(φ)
Задача 5. Вычислить площадь фигуры, ограниченной линиями r = -2⋅sin(3φ) и r = 2⋅sin(φ) в полярной системе координат.
Задача 6. Вычислить площадь фигуры, ограниченной r = √3⋅cos(φ) и r = sin(φ) в полярной системе координат.
Важные заметки
1. Интегралы лучше всего считать раздельно. Когда площадь вы хотите сразу посчитать одним интегралом, то велика вероятность допустим ошибку из-за невнимательности. Да, здесь все интегралы оказываются положительными, поэтому один не сможет обнулить другой. Но вот большое количество упрощений, подстановок, коэффициентов в результате понижения степени могут вас запутать. Поэтому разбиваем фигуру на более простые части, затем ищем площади всех частей отдельно, потом складываем.
2. Некоторые сложные функции легче всего исследовать в полярной системе координат. Вы можете самостоятельно убедиться в этом, если попробуйте перейти в декартовую систему координат с помощью формул перехода: x = r⋅cos(φ) и y = r⋅sin(φ).
Переход от декартовой системы координат к полярной
r = √(x² + y²) ; cos(φ) = x / √(x² + y²) ; sin(φ) = y / √(x² + y²) ; φ = arctan(y/x)
Применение полярных координат
Полярные координаты оказываются удобнее декартовых, для задания кривых на плоскости, особенно для задания различных спиралей, например, спирали Архимеда, логарифмической спирали, трилистника.
- В астрономических наблюдениях.
- В фотографии используют фильтр, переводящий координаты точек из прямоугольной системы в полярную, создавая сферический эффект снимка.
- Необычный формат биржевых графиков на основе полярных координат предложил в 1990-е годы российский математик Владимир Иванович Елисеев. Используя такую систему координат, относительно просто связать градусы и время (в году 365 дней, в окружности – 360 градусов)
- В военном деле на радиолокационных станциях. Координаты цели могут выдаваться в полярной системе координат (азимут, дальность), прямоугольной (X, Y), геодезической (широта, долгота).
- В медицине. Компьютерная томография сердца изображается в системе полярных координат.
- В системах безопасности при идентификации по радужной оболочке глаза.
- В геодезии в лазерном сканере получают координаты точек объекта с помощью измерения полярных углов и расстояний до объекта.
- В приборах измерительных лабораторий на предприятиях точного приборостроения, машиностроения, микроэлектроники, в инструментальном производстве, в лабораториях институтов.
- В компьютерных играх.
Если Вам нужна помощь или репетитор по физике, математике или информатике/программированию, Вы можете написать в группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Линия в полярной системе координат
Краткая теория
В полярной системе координат точка задается полярным углом φ и полярным радиусом r.
φ – угол, отсчитываемый от полярной оси в положительном направлении (против часовой стрелки)
r – расстояние от заданной точки до полюса
Если совместить начало декартовых координат с полюсом, а ось абсцисс с полярной осью, то между полярной и декартовой системой координат может быть установлена однозначная связь.
Пример решения задачи
Задача
Линия задана
уравнением
в полярной
системе координат. Требуется:
Решение
Построение линии по точкам
Построим линию по
точкам, предварительно заполнив таблицу значений r и j:
|
|
|
|
|
|
| 1 | 0 | 1 | 9 | 0,556 |
| 2 |
|
0,924 | 8,772 | 0,570 |
| 3 |
|
0,707 | 8,121 | 0,616 |
| 4 |
|
0,383 | 7,148 | 0,699 |
| 5 |
|
0,000 | 6,000 | 0,833 |
| 6 |
|
-0,383 | 4,852 | 1,031 |
| 7 |
|
-0,707 | 3,879 | 1,289 |
| 8 |
|
-0,924 | 3,228 | 1,549 |
| 9 |
|
-1 | 3 | 1,667 |
| 10 |
|
-0,924 | 3,228 | 1,549 |
| 11 |
|
-0,707 | 3,879 | 1,289 |
| 12 |
|
-0,383 | 4,852 | 1,031 |
| 13 |
|
0,000 | 6,000 | 0,833 |
| 14 |
|
0,383 | 7,148 | 0,699 |
| 15 |
|
0,707 | 8,121 | 0,616 |
| 16 |
|
0,924 | 8,772 | 0,570 |
| 17 |
|
1 | 9 | 0,556 |
Используя данные
таблицы, строим линию.
- Отмечаем полюс и указываем масштаб.
- С помощью транспортира прочерчиваем
угловые направления - Циркулем и линейкой отмечаем найденные
точки - Отложенные точки соединяем линией
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
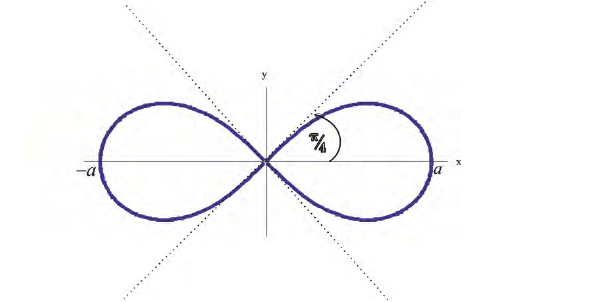
График в полярной
системе координат имеет вид:
Уравнение линии в декартовой прямоугольной системе координат
Найдем уравнение
данной линии в декартовой системе координат:
Подставляя в исходное
уравнение в полярных координатах, получаем:
Полученная линия
-эллипс






































![{frac {1}{2}}int limits _{a}^{b}[r(varphi )]^{2},dvarphi .](https://wikimedia.org/api/rest_v1/media/math/render/svg/266e820a4d162bf3999f98de23e8237ad757c5ee)


![lim _{{Delta varphi to 0}}sum _{{i=1}}^{infty }{frac {1}{2}}r(varphi _{i})^{2},Delta varphi ={frac {1}{2}}int limits _{a}^{b}[r(varphi )]^{2},dvarphi .](https://wikimedia.org/api/rest_v1/media/math/render/svg/9889d1586d04c6f806776f20f2e9e4f0407d694c)