Как найти круг сходимости степенного ряда - Сайт, где вы сможете решить свои вопросы

Степенные ряды с комплексными членами и их свойства

Круг сходимости степенного ряда

Степенным рядом называется функциональный ряд (3.1), члены которого образованы степенями z^n или (z-z_0)^n , то есть ряд вида

$sum_{n=0}^{infty}c_n(z-z_0)^n= c_0+ c_1(z-z_0)+ ldots+ c_n(z-z_0)^n+ldots~~(3.9)$

или

$sum_{n=0}^{infty}c_nz^n= c_0+c_1z+c_2z^2+ ldots+ c_nz_n+ldots~~~~~~~~(3.10)$

Ряд (3.9) называется рядом по степеням разности (z-z_0) ; ряд (3.10) — рядом по степеням . Очевидно, один ряд к другому можно преобразовать простой заменой.

Особенностью степенного ряда, как частного вида ряда (3.1), является аналитичность его членов во всей комплексной плоскости. Другая особенность связана с видом его области сходимости. В общем случае функционального ряда, областью сходимости может быть множество произвольного вида (см. примеры 3.1-3.5). Это и вся плоскость, и плоскость с выколотой точкой, и круг, и внешность круга, и полуплоскость, и кольцо, и пустое множество (ряд расходится всюду). В случае степенного ряда последнего случая быть не может — ряд имеет хотя бы одну точку сходимости. Так, ряд (3.9), очевидно, сходится в точке z_0 , а ряд (3.10) — в точке z=0 .

В примере 3.1 определялась область сходимости степенных рядов вида (3.10). Кроме двух тривиальных случаев области сходимости — вся плоскость и только одна точка, в двух других областью сходимости оказывается круг, как и для ряда вида (3.9) из примера 3.4, п.”а”. Полученный результат не является случайным. Действительно, областью сходимости степенного ряда является круг. При этом область сходимости, состоящую из одной точки, можно рассматривать как круг радиуса R=0 , а в случае сходимости ряда во всей комплексной плоскости как круг радиуса R=infty . Доказательство этого утверждения получается из основной теоремы теории степенных рядов — теоремы Абеля, которая формулируется и доказывается так же, как и в действительной области.

Теорема Абеля о сходимости ряда

Теорема 3.3 (теорема Абеля). Если степенной ряд (3.10) сходится в точке z_0ne0 , то он сходится, и притом абсолютно, для любого , удовлетворяющего неравенству |z|<|z_0| .

Как следствие этой теоремы устанавливается существование положительного числа , такого, что ряд (3.10) при |z|<R сходится, а при |z|>R расходится, т.е. окружность |z|=R разделяет плоскость на две части: внутри окружности ряд сходится, вне — расходится. Радиус этой окружности — число — называется радиусом сходимости, круг |z|<R — кругом сходимости ряда.

Формула Коши-Адамара

Радиус сходимости степенного ряда определяется по формуле Коши-Адамара

$R=dfrac{1}{varlimsuplimits_{ntoinfty}sqrt[LARGE{n}]{|c_n|}},.$

(3.11)

Здесь $varlimsuplimits_{ntoinfty}sqrt[LARGE{n}]{|c_n|}=ell$ — верхний предел последовательности $a_n=sqrt[LARGE{n}]{|c_n|}$ . Он всегда существует (конечный или бесконечный), и притом единственный. В случае ell=+infty полагают R=0 , а в случае ell=0 полагают R=infty .

Замечания 3.1

1. Для ряда (3.9) имеем такое же утверждение: он сходится в круге |z-z_0|<R , где радиус сходимости определяется по формуле (3.11).

2. Радиус сходимости ряда можно определить иначе. Например, найти область сходимости ряда, используя формулы (3.8), а затем — радиус. Так, в примере 3.1 рассматриваются степенные ряды. Для первого из этих рядов найдена область сходимости |z|<1 , поэтому R=1 , для второго из |z|<2 получаем R=2 . Для двух других рядов имеем соответственно R=0 и R=infty .

Пример 3.8. Доказать, что для ряда $sum_{n=0}^{infty}c_nz^n$ , где c_nne0 для любого , радиус сходимости можно определить по формулам:

$R=frac{1}{limlimits_{ntoinfty}sqrt[LARGE{n}]{|c_n|}},qquad R=lim_{ntoinfty} left|frac{c_n}{c_{n+1}}right|.$

(3.12)

Решение

Найдем область сходимости ряда, используя формулы (3.8):

$|f(z)= lim_{ntoinfty}sqrt[LARGE{n}]{|u_n(z)|}= lim_{ntoinfty}sqrt[LARGE{n}]{|c_nz^n|}= |z|cdot lim_{ntoinfty}sqrt[LARGE{n}]{|c_n|},.$

Если $lim_{ntoinfty}sqrt[LARGE{n}]{|c_n|}=0$ , то неравенство |f(z)|<1 выполняется при любом , т.е. ряд сходится всюду и R=infty . Если $lim_{ntoinfty}sqrt[LARGE{n}]{|c_n|}=infty$ , то неравенство не выполняется ни для какого значения zne0 и ряд сходится только в одной точке z=0 , то есть R=0 .

В случае, когда предел является конечным и не равен нулю, обозначим его ell , то есть $lim_{ntoinfty}sqrt[LARGE{n}]{|c_n|}=ell$ . Тогда неравенство |f(z)|<1 , то есть |z|cdotell<1 , выполняется для , удовлетворяющих условию $|z|<frac{1}{ell}$ , а это есть круг сходимости, следовательно, $R= frac{1}{ell}$ . Первая из формул (3.12) доказана. Аналогично доказывается вторая.

Пример 3.9. Найти области сходимости комплексных рядов $sum_{n=1}^{infty} frac{z^n}{n^2},~ sum_{n=1}^{infty}frac{z^n}{n},~ sum_{n=1}^{infty}z^n$ .

Решение

Радиус сходимости каждого из рядов R=1 , так как для первого ряда $c_n=frac{1}{n^2}$ и согласно (3.12) $R=lim_{ntoinfty} left|frac{(n+1)^2}{n^2}right|=1$ ; для второго ряда имеем $c_n=frac{1}{n}$ и $R=lim_{ntoinfty} left|frac{n+1}{n}right|=1$ ; для третьего из c_n=1 получаем $R=lim_{ntoinfty}frac{1}{sqrt[LARGE{n}]{n}}=1$ . Поэтому областью сходимости каждого из этих рядов является круг |z|<1 .

Исследуем сходимость рядов на границе круга сходимости — на окружности |z|=1 , или, что то же, $z=e^{ivarphi}$ .

Для первого ряда в точках границы, т.е. при |z|=1 , получаем абсолютно сходящиеся ряды, так как $sum_{n=1}^{infty}frac{|z|^n}{n^2}= sum_{n=1}^{infty}frac{1}{n^2}$ , а ряд $sum_{n=1}^{infty}frac{1}{n^2}$ сходится. Следовательно, ряд $sum_{n=1}^{infty}frac{z^n}{n^2}$ сходится во всех граничных точках. Поэтому он сходится абсолютно — круге |z|leqslant1 .

Ряд $sum_{n=1}^{infty}z^n$ на границе расходится (см. пример 3.1, п.”а”).

Ряд $sum_{n=1}^{infty}frac{z^n}{n}$ , очевидно, расходится в точке z=1 (точке границы $z=e^{ivarphi}$ при varphi=0 ) как гармонический ряд $sum_{n=1}^{infty}frac{1}{n}$ и сходится в точке z=-1 (точке $z=e^{ivarphi}$ при varphi=pi ) как знакочередующийся ряд $sum_{n=1}^{infty}frac{(-1)^n}{n}$ . Заметим, что сходимость последнего ряда неабсолютная. Можно показать, что ряд расходится на границе $z=e^{ivarphi}$ только при varphi=0 , то есть , а во всех других точках границы, т.е. при varphine0 , он сходится.

Заметим, что данные в примере ряды могут быть получены один из другого с помощью дифференцирования или интегрирования. Так, из ряда $sum_{n=1}^{infty} frac{z^n}{n^2}$ получаем дифференцированием ряд $sum_{n=1}^{infty} frac{z^{n-1}}{n}$ или $frac{1}{z}sum_{n=1}^{infty} frac{z^n}{n}$ , а из ряда $sum_{n=1}^{infty} frac{z^n}{n}$ также дифференцированием — ряд $sum_{n=1}^{infty}z^{n-1}$ или $frac{1}{z}sum_{n=1}^{infty}z^n$ .

Пример 3.10. Найти радиус сходимости рядов: а) $sum_{n=0}^{infty} 3^n(z-1)^n$ ; б) $sum_{n=0}^{infty} frac{z^{2n}}{3^n}$ .

Решение

Свойства степенных рядов

1. Если Rne0 , т.е. ряд (3.10) сходится в круге |z|<R , то, используя признак Вейерштрасса, нетрудно установить, что ряд сходится равномерно в круге |z|leqslant r , где — любое положительное, меньшее число, 0<r< R . Это означает, что степенной ряд сходится равномерно внутри круга сходимости.

2. В силу аналитичности членов степенного ряда и свойств равномерно сходящихся рядов получаем (см. теорему 3.2), что внутри круга сходимости сумма степенного ряда есть функция аналитическая.

3. Степенной ряд можно почленно интегрировать и дифференцировать любое число раз внутри круга сходимости.

Последнее свойство означает, что ряд, полученный из ряда $sum_{n=0}^{infty}c_nz^n$ дифференцированием, т.е. ряд $sum_{n=0}^{infty}(c_nz^n)'= sum_{n=1}^{infty}nc_nz^{n-1}$ или, что удобнее, $sum_{n=0}^{infty}(n+1)c_{n+1}z^n$ , и ряд, полученный интегрированием, т.е. ряд $sum_{n=0}^{infty}int c_nz^{n}dz= sum_{n=0}^{infty} frac{c_nz^{n+1}}{n+1}$ , сходятся внутри круга сходимости исходного ряда, а потому их радиусы сходимости не меньше радиуса сходимости исходного ряда.

Покажем, что радиус сходимости при дифференцировании и интегрировании не меняется. Обозначим радиус сходимости данного степенного ряда $sum_{n=0}^{infty}c_nz^n$ через $R=frac{1}{ell}$ , где $ell= varlimsuplimits_{ntoinfty} sqrt[LARGE{n}]{|c_n|}$ . Рассмотрим ряд, членами которого являются производные от членов данного ряда, т.е. ряд, полученный почленным дифференцированием: $sum_{n=0}^{infty} (n+1)c_{n+1}z^n$ . Общий член этого ряда $(n+1)c_{n+1}z^n$ запишем в виде a_nz^n , где $a_n=(n+1)c_{n+1}$ , а $c_{n+1}$ — коэффициент исходного ряда. Радиус сходимости полученного ряда определим по формуле Коши-Адамара, т.е. $R_1= frac{1}{ell_1}$ , где

$ell_1=varlimsuplimits_{ntoinfty} sqrt[LARGE{n}]{|c_{n+1}|(n+1)}= varlimsuplimits_{ntoinfty} left(sqrt[LARGE{n}]{|c_{n+1}|}cdot sqrt[LARGE{n}]{n+1}right)= varlimsuplimits_{ntoinfty} sqrt[LARGE{n}]{|c_{n+1}|}= varlimsuplimits_{ntoinfty} sqrt[LARGE{n}]{|c_{n}|}=ell,.$

Следовательно, R_1=R . Здесь использован известный предел $lim_{ntoinfty} sqrt[LARGE{n}]{an+b}=1$ , частный случай которого $lim_{ntoinfty} sqrt[LARGE{n}]{n}=1$ был использован при решении примера 3.3. Так как ряд $sum_{n=0}^{infty}c_nz^n$ получается из ряда $sum_{n=0}^{infty}(n+1)c_{n+1}z^n$ интегрированием, то из доказанного следует, что при интегрировании ряда радиус сходимости не изменяется.

Пример 3.11. Найти суммы следующих рядов с комплексными членами:

а) $sum_{n=0}^{infty}z^n$ ; б) $sum_{n=0}^{infty} frac{z^n}{2^{n+1}}$ ; в) $sum_{n=1}^{infty}nz^n$ ; г) $sum_{n=1}^{infty}z^n$ .

Решение

Действия над степенными рядами

Кроме упомянутых выше свойств дифференцирования и интегрирования степенных рядов внутри круга сходимости как рядов, равномерно сходящихся, они обладают в круге сходимости общими свойствами сходящихся, в частности абсолютно сходящихся, рядов: ряды можно складывать и перемножать, т.е. рассматривать сумму и произведение рядов; можно также рассматривать их отношение — деление рядов.

Рассмотрим подробнее арифметические действия над степенными рядами. Обозначим R_1 и R_2 — радиусы сходимости двух рядов $sum_{n=0}^{infty} a_nz^n$ и $sum_{n=0}^{infty}b_nz^n$ .

1. В общей области сходимости, т.е. в круге |z|<r , где r= min(R_1,R_2) , можно рассматривать сумму (разность) рядов: ряд $sum_{n=1}^{infty} c_nz^n,~ c_n=a_npm b_n$ . Радиус сходимости полученного ряда не меньше rcolon, Rgeqslant r . Сумма нового ряда равна S_1pm S_2 , где S_1 и S_2 — суммы рядов — слагаемых.

2. В круге |z|<r можно рассматривать произведение рядов:

$begin{aligned}sum_{n=0}^{infty} a_nz^ncdot sum_{n=0}^{infty} b_nz^n&= bigl(a_0+a_1z+a_2z^2+ldots+ a_nz^n+ldotsbigr)cdot bigl(b_0+b_1z+b_2z^2+ldots+ b_nz^n+ldots bigr)=\ &=a_0b_0+ z(a_0b_1+a_1b_0)+ z^2(a_0b_2+a_1b_1+a_2b_0)+ ldots+ c_nz^n+ldots end{aligned}$

Получаем ряд $sum_{n=1}^{infty}c_nz^n$ , где $c_n=a_0b_n+a_1b_{n-1}+ ldots+ a_kb_{n-k}+ ldots+a_nb_0$ . или $c_n=sum_{k=0}^{n}a_kb_{n-k}$ . Радиус сходимости полученного ряда не меньше r,~ Rgeqslant r , его сумма равна S_1cdot S_2 , где S_1 n S_2 — суммы рядов — сомножителей.

3. В некоторой окрестности точки z_0=0 можно рассматривать отношение рядов $sum_{n=0}^{infty}a_nz^n$ (делимое) и $sum_{n=0}^{infty}b_nz^n$ (делитель) при условии b_0ne0 . Частным этих рядов будет ряд $sum_{n=0}^{infty}c_nz^n$ , такой, что выполняется равенство $sum_{n=0}^{infty} a_nz^n= sum_{n=0}^{infty}b_nz^ncdot sum_{n=0}^{infty}c_nz^n$ Коэффициенты c_n определяются, как и в случае многочленов, методом неопределенных коэффициентов или делением “углом”.

Замечание 3.2. При сложении и умножении рядов, как отмечено выше, может получиться ряд, сходящийся в большей области, чем общая часть кругов сходимости двух исходных рядов: Rgeqslant r,~ r=min(R_1,R_2) .

Приведем пример, подтверждающий это свойство. При сложении рядов $sum_{n=0}^{infty}! left(frac{(-1)^{n+1}}{3^n}-1right)!z^n$ и $sum_{n=1}^{infty}! left(frac{(-1)^n}{2^n}+ 1right)!z^n$ , для которых, как нетрудно проверить, имеем R_1=R_2=1 , получим ряд $sum_{n=0}^{infty}! left(frac{(-1)^{n}}{2^n}-frac{(-1)^{n}}{3^n}right)!z^n$ . Радиус сходимости этого ряда R=2 .

Рассмотренные арифметические операции- над рядами используются при решения задач разложения функции в степенные ряды: функций вида

$f(z)= f_1(z)+ f_2(z),qquad f(z)=f_1(z)cdot f_2(z),qquad f(z)=frac{f_1(z)}{f_2(z)},.$

Подстановка ряда в ряд

4. Еще одно действие — подстановка ряда в ряд связано с разложением в ряд сложной функции. Пусть ряд $sum_{n=0}^{infty}c_nu^n$ сходится в круге |u|<R , его сумма равна S_1=f(u) ; а ряд $sum_{n=0}^{infty}b_nz^n$ в круге |z|<r и его сумма в этом круге равна S_2=varphi(z) . Тогда в некоторой окрестности точки z_0=0 , т.е. в круге |z|<rho , можно рассматривать ряд $sum_{n=0}^{infty}c_n left(sum_{n=0}^{infty} b_nz^nright)^n$ . Заметим, что для возможности выполнения этого действия требуется, чтобы имело место условие varphi(0)= 0 , то есть b_0=0 ,в противном случае, как правило, не удается привести подобные члены. Поэтому записываем ряд в виде

$sum_{n=0}^{infty}c_n left(sum_{n=0}^{infty} b_nz^nright)^n= c_0+ c_1 bigl(b_1z+ b_2z^2+ldotsbigr)+ c_2 bigl(b_1z+b_2z^2+ldotsbigr)^2+ ldots+c_n bigl(b_1z+ b_2z^2+ ldotsbigr)^n+ldots$

Произведя действия возведения в степень (как умножение ряда на ряд) и приведение подобных членов, можно записать любое число членов ряда:

c_0+c_1b_1z+ z^2 bigl(c_1b_2+c_2b_1^2bigr)+ z^3 bigl(c_1b_3+2c_1b_1b_2+ c_3b_1^3bigr)+ldots

Суммой нового ряда будет функция f(varphi(z)) .

Обобщение свойств степенных рядов

Обобщим свойства степенных рядов и действия над ними в виде утверждения.

Утверждение 3.1

1. Степенной ряд $sum_{n=0}^{infty}c_nz^n$ сходится в круге |z|<R ; ряд $sum_{n=0}^{infty}c_n(z-z_0)^n$ сходится в круге |z-z_0|<R .

2. Радиус сходимости ряда определяется по формулам (3.11) и (3.12).

3. На границах круга сходимости могут быть как точки сходимости, так и точки расходимости ряда.

4. Внутри круга сходимости ряд сходится равномерно; для ряда (3.10) это круг |z|leqslant r , для (3.9): |z-z_0|leqslant r , где — любое число, 0<r<R .

5. Сумма степенного ряда внутри круга сходимости — функция аналитическая.

6. Внутри круга сходимости ряд можно интегрировать почленно и дифференцировать почленно любое число раз. Радиус сходимости ряда при этом не меняется. Сходимость в отдельных точках границы может измениться.

Ряды с комплексными членами по целым степеням

Рассмотрим два ряда $sum_{n=0}^{infty}a_n(z-z_0)^n$ и $sum_{n=1}^{infty} frac{b_n}{(z-z_0)^n}$ . Первый ряд — степенной и, если он сходится не только в одной точке z_0 , но и не всюду, то сходится в круге |z-z_0|<r . Второй ряд — не степенной, но, после замены $frac{1}{z-z_0}=w$ , получим степенной ряд $sum_{n=1}^{infty}b_nw^n$ , область сходимости которого: |w|<r_1ne0 . Поэтому для ряда $sum_{n=1}^{infty} frac{b_n}{(z-z_0)^n}$ имеем $left|frac{1}{z-z_0}right|<r_1$ , или $|z-z_0|>frac{1}{r_1}=R$ .

Если r<R , то исходные ряды имеют общую область сходимости — кольцо r<|z-z_0|<R . Для каждого , принадлежащего этому кольцу, получаем два сходящихся числовых ряда, которые, по свойству сходящихся числовых рядов, можно складывать. Следовательно, в области r<|z-z_0|<R можно рассматривать ряд вида

$sum_{n=0}^{infty}a_n(z-z_0)^n+sum_{n=1}^{infty} frac{b_n}{(z-z_0)^n}= sum_{n=-infty}^{infty} c_n(z-z_0)^n.$

(3.14)

Ряд (3.14) — ряд по целым степеням, он состоит из двух частей: первое слагаемое $sum_{n=0}^{infty} a_n(z-z_0)^n$ составляют члены ряда с положительными степенями; второе слагаемое $sum_{n=1}^{infty} frac{b_n}{(z-z_0)^n}$ — с отрицательными. Вторую часть можно записать в виде $sum_{n=-infty}^{-1} b_{-n}(z-z_0)^n$ , после чего становится понятней возможность записи суммы двух рядов в виде одного ряда, а именно по формуле (3.14), где полагаем c_n=a_n для ngeqslant0 и $c_n=b_{-n}$ для n<0 .

Используя для составляющих ряда (3.14) — рядов $sum_{n=0}^{infty}a_n(z-z_0)^n$ и $sum_{n=1}^{infty} b_nw^n$ свойства степенных рядов (см. утверждение 3.1), можно сформулировать следующее утверждение для рядов по целым степеням.

Утверждение 3.2

1. Ряд $sum_{n=-infty}^{infty}c_n(z-z_0)^n$ сходится в кольце r<|z-z_0|<R .
2. В кольце r_1leqslant |z-z_0|leqslant R_1 , где r_1>r,~ R_1<R , ряд сходится равномерно.
3. В кольце сумма ряда (3.14) — функция аналитическая и ряд можно почленно интегрировать и дифференцировать любое число раз.

Пример 3.12. Найти кольцо сходимости и сумму ряда $sum_{n=1}^{infty} frac{z^n}{3^n}+ sum_{n=-infty}^{-1}frac{z^n}{2^n}$ .

Решение

Запишем ряд в виде $sum_{n=1}^{infty} !left(frac{z^n}{3^n}+ frac{2^n}{z^n}right)$ и, повторяя решение примера 3.4, находим кольцо сходимости ряда 2<|z|<3 . Сумму ряда S(z) можно записать в виде S(z)= S_1(z)+ S_2(z) , где S_1 -сумма ряда $sum_{n=1}^{infty} !left(frac{z}{3} right)^n$ , S_2 — ряда $sum_{n=1}^{infty}!left(frac{2}{z}right)^n$ . Для нахождения суммы этих рядов применим формулу суммы членов бесконечно убывающей геометрической прогрессии. Получаем $S_1=frac{frac{z}{3}}{1-frac{z}{3}}$ для |z|<3 и $S_2=frac{frac{2}{z}}{1-frac{2}{z}}$ для |z|>2 . Окончательный ответ:

$S(z)= frac{z}{3-z}+frac{2}{z-2}= frac{z^2-4z+6}{(z-2)(3-z)},.$

Заметим, что функция S(z) является аналитической всюду, кроме точек z=2 и z=3 , суммой данного ряда она является только в кольце 2<|z|<z .

Отметим также, что в данном ряде отсутствует свободный член. Ряд $sum_{n=0}^{infty} frac{z^n}{3^n}+ sum_{n=-infty}^{-1}frac{z^n}{2^n}$ , где свободный член равен 1 (при n=0 ), очевидно, сходится в том же кольце, а сумма его равна

$S(z)=S_1(z)+S_2(z)= frac{1}{1-frac{z}{3}}+frac{2}{z-2}= frac{z}{(3-z)(z-2)},.$

Она действительно отличается только на величину свободного члена, т.е. на единицу от найденной выше.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Круг сходимости^[1] степенного ряда $sum_{n=0}^infty a_n(z-z_0)^n$ — это круг вида

$D={z: |z-z_0| <R }$

в котором ряд абсолютно сходится, а вне его, при , расходится. Иными словами, круг сходимости степенного ряда есть внутренность множества точек сходимости ряда. Круг сходимости может вырождаться в пустое множество, когда R = 0 , и может совпадать со всей плоскостью переменного , когда .

Радиус сходимости[править | править код]

Радиус круга сходимости называется радиусом сходимости^[1] ряда.

Радиус сходимости ряда Тейлора аналитической функции равен расстоянию от центра ряда до множества особых точек функции, и может быть вычислен по формуле Коши — Адамара:

${1over R} = {varlimsuplimits_{nrightarrow infty}} , |a_n|^{1/n}$

Эта формула выводится на основе признака Коши.

Теорема Островского — Адамара[править | править код]

Для степенного ряда

$f(z)=sum_{k=0}^infty alpha_k (z-z_0)^k$

у которого почти все коэффициенты равны нулю, в том смысле, что последовательность ненулевых коэффициентов $a_{k(i)}$ удовлетворяет

${displaystyle {frac {k(i+1)}{k(i)}}>1+delta }$

для некоторого фиксированного , круг с центром $z_{0}$ и радиусом, равным радиусу сходимости, является естественной границей — аналитическое продолжение функции, определяемой таким рядом, невозможно за пределы круга.

Литература[править | править код]

↑ ¹ ² Фихтенгольц Григорий Михайлович. Курс дифференциального и интегрального исчисления — 2 том. — 8. — Москва: Физматлит, 2001-. — С. 557. — 864 с. — ISBN 5-9221-0157-9.

См. также[править | править код]

Аналитическое продолжение

Источник

Степенные ряды

3 раздела

от теории до практики

2 примера

Примеры решения задач

видео

Примеры решения задач

Радиус и круг сходимости степенного ряда.

Начать изучение
Регулярные функции.

Начать изучение
Свойства степенных рядов.

Начать изучение

Радиус и круг сходимости степенного ряда.

Функциональные ряды вида
$$
sum_{n=0}^{infty}c_{n}(zeta — a)^{n},label{ref1}
$$
где (c_{n} (n = 1, 2, ldots)) и (a) — заданные комплексные числа, (zeta) — комплексное переменное, называют степенными рядами, а числа (c_{n}) — коэффициентами степенного ряда eqref{ref1}.

Полагая в eqref{ref1} (z = zeta — a), получим ряд
$$
sum_{n=0}^{infty}c_{n}z^{n},label{ref2}
$$
исследование сходимости которого эквивалентно исследованию сходимости ряда eqref{ref1}.

Теорема 1 (Абеля).

Если степенной ряд eqref{ref2} сходится при (z = z_{0} neq 0), то он сходится, и притом абсолютно, при любом (z) таком, что (|z| < |z_{0}|); а если этот ряд расходится при (z = z_{1} neq 0), то он расходится при всяком (z), для которого (|z| > |z_{1}|).

Доказательство.

(circ) Пусть (K_{0} = {z: |z| < |z_{0}|}) — круг на комплексной плоскости с центром в точке (O) (рис. 43.1) радиуса (|z_{0}|), и пусть (z) — произвольная точка круга (K_{0}), то есть (|z| < |z_{0}|), и поэтому
$$
q = left|frac{z}{z_{0}}right| < 1,label{ref3}
$$

Рис. 43.1
Так как ряд eqref{ref2} сходится в точке (z_{0}), то должно выполняться условие
$$
lim_{n rightarrow infty}c_{n}z_{0}^{n} = 0,nonumber
$$
откуда следует ограниченность последовательности ({c_{n}z_{0}^{n}}), то есть
$$
exists M > 0: forall n in mathbb{N} rightarrow |c_{n}z_{0}^{n}| leq M.label{ref4}
$$
Используя неравенства eqref{ref3} и eqref{ref4}, получаем
$$
|c_{n}z^{n}| = |c_{n}z_{0}^{n}|left|frac{z}{z_{0}}right|^{n} leq M q^{n}, mbox{где} 0 leq q < 1.label{ref5}
$$
Так как ряд (displaystylesum_{n=0}^{infty}M q^{n}), где (0 leq q < 1), сходится, то по признаку сравнения сходится ряд (displaystylesum_{n=0}^{infty}|c_{n}z^{n}|), то есть ряд eqref{ref2} сходится абсолютно в каждой точке круга (K_{0}).
Пусть ряд eqref{ref2} расходится в точке (z_{1} neq 0). Тогда он должен расходиться в любой точке (tilde{z}) такой, что (|z_{1}| < |tilde{z}|), так как в противном случае по доказанному выше ряд eqref{ref2} сходился бы в точке (z_{1}). (bullet)

Следствие 1.

Если ряд eqref{ref2} сходится в точке (z_{0} neq 0), то в круге (K_{1} = {z: |z| < p}), где (p < |z_{0}|), этот ряд сходится абсолютно и равномерно.

(circ) Если (z in K_{1}), то (|c_{n}z^{n}| leq M q_{1}^{n}), где (q_{1} = displaystylefrac{p}{|z_{0}|}) и поэтому (0 leq q_{1} < 1), причем (q_{1}) не зависит от (z). По признаку Вейерштрасса ряд eqref{ref2} сходится абсолютно и равномерно в круге (K_{1}). (bullet)

Следствие 2.

Если ряд eqref{ref2} сходится в точке (z_{0} neq 0), то ряды
$$
sum_{n = m}^{infty}c_{n}z^{n — m},quad m in mathbb{N},label{ref6}
$$
$$
sum_{n = 1}^{infty}nc_{n}z^{n — 1}label{ref7}
$$
сходятся абсолютно в круге (K_{0}), а в круге (K_{1}) — абсолютно и равномерно.

(circ) Для ряда eqref{ref6} в круге (K_{0}) выполняется неравенство
$$
|c_{n}z^{n — m}| leq frac{M}{|z_{0}|^{m}}q^{n — m}, 0 leq q < 1,nonumber
$$
в круге (K_{1}) — неравенство
$$
|c_{n}z^{n — m}| leq frac{M}{|z_{0}|^{m}}q_{1}^{n — m}, 0 leq q < 1,nonumber
$$
и (q_{1} = displaystylefrac{p}{|z_{0}|}) не зависит от (z). Для ряда eqref{ref7} в кругах (K_{0}) и (K_{1}) справедливы соответственно неравенства
$$
|nc_{n}z^{n — 1}| leq frac{M}{|z_{0}|}nq^{n — 1} qquad mbox{и}qquad |nc_{n}z^{n — 1}| leq frac{M}{|z_{0}|}nq_{1}^{n — 1}.nonumber
$$
Далее следует использовать сходимость рядов (displaystylesum_{n = 1}^{infty}Aq^{n}) и (displaystylesum_{n = 1}^{infty}Bnq^{n-1}), где (A > 0), (B > 0), (0 leq q < 1). (bullet)

Теорема 2.

Для всякого степенного ряда eqref{ref2} существует (R) ((R geq 0) — число или (+infty)) такое, что:

если (R neq 0) и (R neq +infty), то ряд eqref{ref2} абсолютно сходится в круге (K = {z: |z| < R}) и расходится вне круга (K); этот круг называют кругом сходимости ряда eqref{ref2}, а (R) — радиусом сходимости ряда;
если (R = 0), то ряд eqref{ref2} сходится в одной точке (z = 0);
если (R = +infty), то этот ряд сходится во всей комплексной плоскости.

Доказательство.

(circ) Пусть (D) — множество всех точек сходимости ряда eqref{ref2}. Это непустое множество, так как в точке (z = 0) ряд eqref{ref2} сходится.

Если (D) — неограниченное множество, то ряд eqref{ref2} сходится в произвольной точке (tilde{z}) комплексной плоскости. В самом деле, возьмем точку (z_{0} in D) такую, что (|tilde{z}| < |z_{0}|). Тогда по теореме Абеля ряд eqref{ref2} будет сходиться в точке (tilde{z}).

Пусть (D) — ограниченное множество. Если (D) состоит из одной точки (z = 0), то ряд eqref{ref2} сходится при (z = 0) и расходится при (z neq 0). В этом случае (R = 0). Если (D) содержит хотя бы одну точку, отличную от (z = 0), то, обозначив (R = sup_{z in D} |z|), докажем, что ряд eqref{ref2} сходится в круге (K = {z: |z| < R}) и расходится в каждой точке, лежащей вне этого круга. Пусть (tilde{z}) — произвольная точка круга (K), тогда (|tilde{z}| < R). По определению точной верхней грани
$$
exists z_{1} in D: |tilde{z}| < |z_{1}| < R.nonumber
$$

Так как ряд eqref{ref2} сходится в точке (z_{1}), то по теореме Абеля он абсолютно сходится в точке (tilde{z}). Итак, в каждой точке, лежащей внутри круга (K), ряд eqref{ref2} абсолютно сходится.

Пусть точка (z’) лежит вне круга (K), то есть (|z’| > R). Тогда (z’ in D) (по определению точной верхней грани), и поэтому ряд eqref{ref2} расходится в точке (z’). (bullet)

Замечание 1.

На границе круга (K) ряд eqref{ref2} может как сходиться, так и расходиться. В любом меньшем круге (K_{1} = {z: |z| leq p < R}) ряд eqref{ref2} сходится абсолютно и равномерно.

Теорема 3 (Абеля).

Если (R) — радиус сходимости степенного ряда eqref{ref2}, причем (0 < R < +infty), и если этот ряд сходится при (z = R), то он сходится равномерно на отрезке ([0, R]), а его сумма непрерывна на этом отрезке.

Доказательство.

(circ) Теорема приводится без доказательства. (bullet)

Теорема 4.

Если существует конечный или бесконечный (displaystylelim_{n rightarrow infty} sqrt[n]{|c_{n}|}), то для радиуса (R) сходимости ряда eqref{ref2} справедлива формула
$$
frac{1}{R} = lim_{n rightarrow infty} sqrt[n]{|c_{n}|},label{ref8}
$$
а если существует конечный или бесконечный (displaystylelim_{n rightarrow infty} left|frac{c_{n}}{c_{n + 1}}right|), то
$$
R = lim_{n rightarrow infty} left|frac{c_{n}}{c_{n + 1}}right|,label{ref9}
$$

Доказательство.

(circ) Докажем формулу eqref{ref8}. Обозначим (rho = displaystylelim_{n rightarrow infty} sqrt[n]{|c_{n}|}).

Пусть (0 < rho < +infty) и пусть (z_{0}) — произвольная точка круга (K = {z: |z| < 1/rho}), тогда (|z_{0}| < 1/rho) и
$$
lim_{n rightarrow infty} sqrt[n]{|c_{n}z_{0}^{n}|} = |z_{0}| lim_{n rightarrow infty} sqrt[n]{|c_{n}|} = |z_{0}| rho < 1.nonumber
$$
По признаку Коши ряд (displaystylesum_{n=0}^{infty}c_{n}z_{0}^{n}) абсолютно сходится. Так как (z_{0}) — произвольная точка крута (K), то ряд eqref{ref2} абсолютно сходится в этом круге.Пусть точка (tilde{z}) лежит вне круга (K). Тогда (|tilde{z}| > 1/rho), и поэтому (displaystylelim_{n rightarrow infty} sqrt[n]{|c_{n}tilde{z}^{n}|}). Следовательно, ряд (displaystylesum_{n=0}^{infty}c_{n}tilde{z}^{n}) расходится при (|tilde{z}| > 1/rho).Таким образом, если правая часть равенства eqref{ref8} — положительное число, то ряд eqref{ref2} сходится в круге (K) и расходится вне этого круга. Следовательно, (1/rho) — радиус сходимости ряда eqref{ref2}.
Если (rho = 0), то (displaystylelim_{n rightarrow infty} sqrt[n]{|c_{n}z^{n}|} = |z|rho = 0) для любой точки (z) комплексной плоскости, и поэтому ряд eqref{ref2} сходится при любом (z). Это означает, что радиус сходимости ряда (R = +infty) . И в этом случае формула eqref{ref8} верна, если считать, что (1/rho = 0).
Если (rho = +infty), то для любой точки (z neq 0) имеем (displaystylelim_{n rightarrow infty} sqrt[n]{|c_{n}z^{n}|} = |z| lim_{n rightarrow infty} sqrt[n]{|c_{n}|} = +infty), и поэтому ряд eqref{ref2} при (z neq 0) расходится. Это означает, что (R = 0).Аналогично можно доказать формулу eqref{ref9}, используя признак Д’Аламбера сходимости рядов. (bullet)

Замечание 2.

Пределы eqref{ref8} и eqref{ref9} могут не существовать. Однако имеется универсальная формула для вычисления радиуса сходимости (R) степенного ряда eqref{ref2}, а именно формула
$$
frac{1}{R} = overline{lim_{n rightarrow infty}} sqrt[n]{|c_{n}|},label{ref10}
$$
которую называют формулой Коши-Адамара.

Напомним, что символом (displaystyleoverline{lim_{n rightarrow infty}} x_{n}) обозначается точная верхняя грань множества всех частичных пределов последовательности ({x_{n}}).

Например, если (x_{n} = 1 + (-1)^{n}), то (displaystyleoverline{lim_{n rightarrow infty}}x_{n} = 2).

Пример 1.

Найти радиус сходимости (R) степенного ряда (displaystylesum_{n=0}^{infty}c_{n}z^{n}),

(c_{n} = displaystylefrac{a^{n}}{n!}, a > 0;)
(c_{n} = displaystylefrac{(1 + i)^{n}}{n3^{n}};)
(c_{n} = displaystylefrac{n^{n}}{e^{n}n!}.)

Решение.

(vartriangle) Так как (displaystylefrac{c_{n}}{c_{n + 1}} = frac{n + 1}{a} rightarrow +infty), тo при (n rightarrow infty), то по формуле eqref{ref9} находим (R = +infty).
В этом случае (c_{n} = displaystylefrac{(sqrt{2})^{n}}{n3^{n}}), и поэтому (displaystylesqrt[n]{|c_{n}|} rightarrow frac{sqrt{2}}{3}) при (n rightarrow infty), так как (sqrt[n]{n} rightarrow 1) при (n rightarrow infty). По формуле eqref{ref8} находим (R = displaystylefrac{3}{sqrt{2}}).
Так как (c_{n + 1} = displaystyle c_{n}left(frac{n + 1}{n}right)^{n}frac{1}{e}), то (displaystylefrac{c_{n}}{c_{n + 1}} = frac{e}{displaystyleleft(1 + frac{1}{n}right)^{n}} rightarrow 1) при (n rightarrow infty), и по формуле eqref{ref9} находим (R = 1). (blacktriangle)

Пример 2.

Найти радиус сходимости (R) степенного ряда (displaystylesum_{n=0}^{infty}2^{n}z^{5n}).

Решение.

(vartriangle) Обозначим (2z^{5} = t). Тогда (displaystylesum_{n=0}^{infty}2^{n}z^{5n} = sum_{n=0}^{infty}t^{n}), причем ряд (sum_{n=0}^{infty}t^{n}) сходится, если (|t| < 1), и расходится, если (|t| > 1). Поэтому ряд (displaystylesum_{n=0}^{infty}2^{n}z^{5n}) сходится, если (2|z|^{5} < 1), то есть при (|z| < displaystylefrac{1}{sqrt[5]{2}}), и расходится при (|z| > displaystylefrac{1}{sqrt[5]{2}}). Итак, радиус сходимости (R = displaystylefrac{1}{sqrt[5]{2}}). Тот же результат следует из формулы eqref{ref10}, так как
$$
overline{lim_{n rightarrow infty}} sqrt[n]{|c_{n}|} = lim_{n rightarrow infty} sqrt[5n]{2^{n}} = sqrt[5]{2}. blacktrianglenonumber
$$

Для степенного ряда (displaystylesum_{n=0}^{infty}c_{n}(z — a)^{n}) круг сходимости (K) имеет вид (K = {z: |z — a| < R}). Например, степенной ряд (displaystylesum_{n=0}^{infty}n_{2}(z — 1)^{n}) сходится в круге (K = {z: |z — 1| < 1}) и расходится вне этого круга.

Для степенного ряда вида
$$
sum_{n=0}^{infty}a_{n}(x — x_{0})^{n},label{ref11}
$$
где (a_{n} (n = 0, 1, 2, …)), (x_{0}) — заданные действительные числа, (x) — действительное переменное, существует, согласно теореме 2, такое (R) ((R geq 0) — число или (+infty)), что при (R neq 0, +infty) ряд eqref{ref11} сходится, если (|x — x_{0}| < R), и расходится, если (|x — x_{0}| > R). Интервал ((x_{0} — R, x_{0} + R)) называют интервалом сходимости, a (R) — радиусом сходимости ряда eqref{ref11}. Радиус сходимости ряда eqref{ref11} совпадает с радиусом сходимости ряда (displaystylesum_{n=0}^{infty}a_{n}(z — x_{0})^{n}), где (z) — комплексное переменное. При (R = 0) ряд eqref{ref11} сходится лишь в точке (x = x_{0}), а при (R = +infty) — на всей числовой прямой.

Регулярные функции.

Введем понятие функции комплексного переменного. Пусть каждой точке (z in E), где (E) — множество точек комплексной плоскости, поставлено в соответствие комплексное число (w). Тогда говорят, что на множестве (E) определена функция комплексного переменного, и пишут (w = f(z)), где символом (f) обозначено правило (закон), определяющее это соответствие.

Понятия предела, непрерывности, производной для функции комплексного переменного вводятся по аналогии с соответствующими понятиями для функции действительного переменного. Если
$$
forall varepsilon > 0 exists delta = delta_{varepsilon} > 0: forall z: |z — a| < delta_{varepsilon} rightarrow |f(z) — f(a)| < varepsilon,nonumber
$$
то функцию (f(z)) называют непрерывной в точке (a).

Отметим еще, что понятие равномерной сходимости ряда (displaystylesum_{n=0}^{infty}u_{n}(z)) с комплексными членами формально вводится так же, как и для рядов с действительными членами, а сумма равномерно сходящегося ряда, составленного из непрерывных функций комплексного переменного, есть непрерывная функция.

Введем важное для функций комплексного переменного понятие регулярности.

Определение.

Функция комплексного переменного (f(z)) называется регулярной (однозначной аналитической, голоморфной) в точке (a), если она определена в некоторой окрестности точки (a) и представима в некотором круге (|z — a| < rho), (rho > 0), сходящимся к (f(z)) степенным рядом
$$
f(z) = sum_{n=0}^{infty}c_{n}(z — a)^{n}.label{ref12}
$$

Отметим, что любой многочлен, то есть функция вида (P(z) = displaystylesum_{k = 0}^{infty}a_{k}z^{k}), является регулярной функцией в каждой точке комплексной плоскости.

Рациональная функция (f(z) = displaystylefrac{P_{n}(z)}{Q_{m}(z)}), где (P_{n}) и (Q_{m}) — многочлены степени (n) и (m) соответственно, регулярна в каждой точке (a), в которой (Q_{m} neq 0). Если многочлены (P_{n}) и (Q_{m}) не имеют общих корней и если (z = z_{0}) — корень многочлена (Q_{m}(z)), то (displaystylelim_{z rightarrow z_{0}}f(z) = infty), а точку (z_{0}) называют полюсом функции (f(z)). Полюсы — один из типов особых точек функций комплексного переменного.

В теории функций комплексного переменного доказывается, что на границе круга сходимости степенного ряда (displaystylesum_{n=0}^{infty}c_{n}(z — a)^{n}) лежит хотя бы одна особая точка его суммы (f(z)) и что радиус сходимости этого ряда равен расстоянию от точки (a) до ближайшей к (a) особой точки функции (f(z)).

В частности, если (f(z) = displaystylefrac{P_{n}(z)}{Q_{m}(z)}), причем многочлены (P_{n}) и (Q_{m}) не имеют общих корней, то радиус сходимости (R) степенного ряда (displaystylesum_{n=0}^{infty}c_{n}(z — a)^{n}) равен расстоянию от точки (a) до ближайшего к этой точке корня многочлена (Q_{m}(z)), то есть
$$
R = min_{1 leq k leq m} |z_{k} — a|,nonumber
$$
где (z_{k} (k = overline{1, m})) — корни многочлена (Q_{m}(z)) (предполагается, что (a neq z_{k}), (k = overline{1, m})).

Например, если (f(z) = displaystylefrac{2z}{(z-3)(z^{2} + 1)}), то корнями многочлена ((z-3)(z^{2} + 1)) являются числа (z_{1} = 3), (z_{2} = i), (z_{3} = -i). Поэтому радиус сходимости (R) степенного ряда (displaystylesum_{n=0}^{infty}c_{n}(z-1)^{2}) равен наименьшему из чисел (|3-1|, |i-1|, |i+1|), то есть равен (sqrt{2}).

Теорема 5.

Функция (f(z)), регулярная в точке (a), единственным образом представляется рядом eqref{ref12}.

Доказательство.

(circ) Пусть функция (f(z)) имеет два представления в виде степенного ряда eqref{ref12} в круге (K = {z: |z — a| < rho}), где (rho > 0), то есть
$$
f(z) = sum_{n=0}^{infty}c_{n}(z — a)^{n} = sum_{n=0}^{infty}tilde{c}_{n}(z — a)^{n}.label{ref13}
$$
Докажем, что (c_{n} = tilde{c}_{n}) для (n = 0, 1, 2, …)

По условию ряды (displaystylesum_{n=0}^{infty}c_{n}(z — a)^{n}) и (displaystylesum_{n=0}^{infty}tilde{c}_{n}(z — a)^{n}) сходятся в круге (K), и поэтому (см. следствие 1 из теоремы 1) эти ряды сходятся равномерно в круге (K_{1} = {z: |z — a| leq rho_{1} < rho}), а их общая сумма -непрерывная в круге (K_{1}) функция. В частности, функция (f(z)) непрерывна в точке (a). Подходя к пределу при (z rightarrow a) в равенстве eqref{ref13}, получаем (c_{0} = tilde{c}_{0}). Отбрасывая одинаковые слагаемые (c_{0}) и (tilde{c}_{0}) в равенстве eqref{ref13}, получаем после деления на (z — a) равенство
$$
c_{1} + c_{2}(z — a) + c_{3}(z — a)^{2} + ldots = tilde{c}_{1} + tilde{c}_{2}(z — a) + tilde{c}_{3}(z — a)^{2} + ldots,label{ref14}
$$
которое справедливо в круге (K) с выколотой точкой (а). Ряды в левой и правой частях eqref{ref14} сходятся равномерно в круге (K_{1}) (следствие 2 из теоремы 1), а их общая сумма непрерывна в круге (K_{1}). Переходя в равенстве eqref{ref14} к пределу при (z rightarrow a), получаем (c_{1} = tilde{c}_{1}). Справедливость равенства (c_{n} = tilde{c}_{n}) при любом (n) устанавливается с помощью индукции. (bullet)

Свойства степенных рядов.

Теорема 6.

Степенные ряды
$$
sum_{n=0}^{infty}c_{n}z^{n},label{ref15}
$$
$$
sum_{n=0}^{infty}frac{c_{n}}{n + 1}z^{n + 1},label{ref16}
$$
$$
sum_{n=0}^{infty}nc_{n}z^{n — 1}label{ref17}
$$
имеют один и тот же радиус сходимости.

Доказательство.

(circ) Пусть (R), (R_{1}) и (R_{2}) — радиусы сходимости рядов eqref{ref15}, eqref{ref16} и eqref{ref17} соответственно, (K), (K_{1}) и (K_{2}) — круги сходимости этих рядов. Докажем, что
$$
R_{1} = R = R_{2}.label{ref18}
$$

Так как (displaystylefrac{1}{n + 1} leq 1 leq n) для любого (n in mathbb{N}), то
$$
left|frac{c_{n}}{n + 1}z^{n + 1}right| leq |z| cdot |c_{n}z^{n}| leq |z|^{2} cdot |nc_{n}z^{n — 1}|.label{ref19}
$$
Неравенства eqref{ref19} справедливы при любом (n in mathbb{N}) и при любом (z).

Пусть (z = z_{0} in K_{2}) и (z_{0} neq 0). Тогда по теореме 2 ряд eqref{ref17} сходится абсолютно в точке (z_{0}), а из правого неравенства eqref{ref19} в силу теоремы сравнения следует абсолютная сходимость ряда eqref{ref15} в точке (z_{0}). Итак, если (z_{0} in K_{2}), то (z_{0} in K_{1}), и поэтому
$$
R_{2} leq R.label{ref20}
$$
Аналогично, если (z = z_{0} neq 0) и (z_{0} in K), то из левого неравенства eqref{ref19} следует, что ряд eqref{ref16} абсолютно сходится в точке (z_{0}). Таким образом, если (z_{0} in K), то (z_{0} in K_{1}) и поэтому
$$
R leq R_{1}.label{ref21}
$$
Из eqref{ref20} и eqref{ref21} получаем двойное неравенство
$$
R_{1} leq R leq R_{2}.label{ref22}
$$
Докажем, что
$$
R_{1} leq R_{2}.label{ref23}
$$
Пусть (z_{0} in K_{1}) и (z_{0} neq 0). Тогда (|z_{0}| < R_{1}), и ряд eqref{ref16} абсолютно сходится в точке (z_{0}) (теорема 2). Выберем (rho) так, чтобы выполнялись неравенства
$$
|z_{0}| < rho < R_{1}.label{ref24}
$$
Запишем следующее равенство:
$$
|nc_{n}z_{0}^{n — 1}| = left|frac{c_{n}rho^{n + 1}}{n + 1}right|left(frac{|z_{0}|}{rho}right)^{n + 1} frac{n(n + 1)}{|z_{0}|^{2}}.label{ref25}
$$
Так как (rho in K) в силу условия eqref{ref24}, то ряд eqref{ref16} сходится при (z = rho), и поэтому
$$
exists m > 0: forall n in mathbb{N} rightarrow left|frac{c_{n}rho^{n + 1}}{n + 1}right| leq M.label{ref26}
$$
Обозначим (displaystylefrac{|z_{0}|}{rho} = q). Тогда (0 < q < 1), так как (z_{0} neq 0), и выполняется условие eqref{ref24}. Из равенства eqref{ref25} в силу условия eqref{ref26} следует, что
$$
|nc_{n}z_{0}^{n — 1}| leq frac{M}{|z_{0}|^{2}}n(n + 1)q^{n + 1}, 0 < q < 1.label{ref27}
$$
Так как ряд (displaystylesum_{n = 1}^{infty}frac{M}{|z_{0}|^{2}}n(n + 1)q^{n + 1}), где (0 < q < 1), сходится по признаку Д’Аламбера, то из eqref{ref27} следует абсолютная сходимость ряда eqref{ref17} в точке (z_{0}). Итак, если (z_{0} in K_{1}), то (z_{0} in K_{2}), откуда получаем
$$
R_{1} leq R_{2}.label{ref28}
$$
Из неравенств eqref{ref22} и eqref{ref28} следует равенство eqref{ref18}. (bullet)

Обратимся теперь к степенным рядам вида eqref{ref11}, где коэффициенты ряда — действительные числа, а переменное (x) принимает действительные значения.

Теорема 7.

Если ряд
$$
sum_{substack{k = 0} }^{infty}a_{k}(x — x_{0})^{k} = f(x)label{ref29}
$$
имеет радиус сходимости (R > 0), то:

в интервале сходимости ((x_{0} — R, x_{0} + R)) функция (f) имеет производные любого порядка, получаемые почленным дифференцированием ряда eqref{ref29};
внутри интервала сходимости этот ряд можно почленно интегрировать, то есть для любого (x in (x_{0} — R, x_{0} + R)) справедливо равенство
$$
intlimits_{x_{0}}^x f(t) dt = sum_{substack{k = 0} }^{infty}a_{k}frac{(x — x_{0})^{k + 1}}{k + 1}.label{ref30}
$$

Доказательство.

(circ) Рассмотрим ряд
$$
sum_{k = 1}^{infty} k a_{k} (x — x_{0})^{k — 1}.label{ref31}
$$
составленный из производных членов ряда eqref{ref29}. По теореме 6 ряд eqref{ref31} имеет тот же радиус сходимости, что и ряд eqref{ref29}, а по следствию 1 из теоремы 1 ряд eqref{ref31} сходится равномерно на отрезке (Delta_{rho} = [x_{0} — rho, x_{0} + rho]), где (rho) — произвольное число такое, что (0 < rho < R).

В силу теоремы о почленном дифференцировании рядов ряд eqref{ref29} можно почленно дифференцировать на (Delta_{rho}), а значит, и в любой точке (x in (x_{0} — R, x_{0} + R)), то есть справедливо равенство
$$
f'(x) = sum_{k = 1}^{infty} k a_{k} (x — x_{0})^{k — 1},quad x in (x_{0} — R, x_{0} + R).label{ref32}
$$
По индукции доказывается, что
$$
f^{(n)}(x) = sum_{k = n}^{infty} a_{k} k(k — 1)ldots(k — (n -1))(x — x_{0})^{k — n}.label{ref33}
$$
где (n in mathbb{N}), (x in (x_{0} — R, x_{0} + R)), то есть ряд eqref{ref29} можно почленно дифференцировать любое число раз.

Справедливость равенства eqref{ref30} следует из теоремы о почленном интегрировании функциональных рядов. (bullet)

Следствие.

Коэффициенты ряда eqref{ref29}, имеющего радиус сходимости (R > 0), выражаются формулами
$$
a_{0} = f(x_{0}),quad a_{n} = frac{f^{(n)}(x_{0})}{n!},quad n in mathbb{N}.label{ref34}
$$

(circ) Формулы eqref{ref34} получаются из равенств eqref{ref29} и eqref{ref33} при (x = x_{0}). (bullet)

Замечание 3.

Из формул eqref{ref34} следует единственность разложения функции (f(x)) в степенной ряд вида eqref{ref29}.

Источник

Степенные ряды.

Степенные
ряды – это частный случай функциональных
рядов, в котором члены ряда представляют
собой степени отклонения переменнойот некоторой фиксированной точки
плоскости(центра сходимости ряда). Степенные ряды
действительной переменной сходятся в
интервале,
где
–
радиус сходимости ряда. Точно так же
степенной ряд комплексной переменной
сходится на множестве,
только в комплексных числах это множество
представляет собой круг без границы.
Сходимость ряда на границе исследуется
отдельно.

Теорема Абеля.Если степенной рядсходится в точке,
то он абсолютно сходится в круге.
Если степенной рядрасходится в точке,
то он расходится во внешности круга.

Доказательство(аналогично случаю действительной
переменной).

Пусть ряд сходится в точке
и.

Так как ряд
сходится в точке
,
то по необходимому признаку сходимости
ряда.

Тогда
.

Исследуем
степенной ряд на абсолютную сходимость.
Рассмотрим ряд из модулей членов ряда.
Оценим
общий член ряда из модулей.

Ряд из модулей исходного ряда
сходится по первому признаку сравнения
числовых рядов (ряд сравнения – сходящаяся
бесконечно убывающая геометрическая
прогрессия
).
Следовательно, исходный ряд в областисходится абсолютно.

Замечание.Казалось бы, что из признака Вейерштрасса
в областиследует равномерная сходимость исходного
ряда, но здесь,
а в признаке Вейерштрасса требуется
указать один мажорирующий ряд для всех
точекрассматриваемой
области, то естьне
должно зависеть от.
Поэтому равномерную сходимость ряда в
областиутверждать нельзя. Однако если взять(не зависит от),
то в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса.

Пусть ряд расходится в
точке
и.

Если ряд сходится
в точке
,
то по доказанному в пункте 1), он должен
абсолютно сходиться в точке,
следовательно, сходиться в точке.
Это противоречит тому, что исходный ряд
расходится в точке,
следовательно исходный ряд расходится
в области.

Определение радиуса сходимости и исследование сходимости ряда на границе круга сходимости.

Рассмотрим
монотонноубывающуюпоследовательность,
такую, что в точкестепенной
рядрасходится.
Если выбрать,
то степенной ряд будет сходиться (ряд
из нулей), поэтому рассматриваемая
последовательность ограничена снизу
нулем. По теореме Вейерштрасса монотонно
убывающая, ограниченная снизу числовая
последовательность имеет предел. То
есть.

Такое число
называетсярадиусом сходимости
степенного ряда.Следовательно,степенной ряд абсолютно сходится в
круге сходимости степенного ряда.

Теорема.
Степенной ряд равномерно сходится
внутри круга сходимости.

Доказательство.
Пусть.
Выберем,
например.
На окружностистепенной ряд сходится абсолютно, так
как эта окружность лежит внутри круга
сходимости. Тогда(не зависит от),
тогда в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса (замечание в
доказательстве теоремы Абеля).

Следствие.
Внутри круга сходимости справедливы
теоремы о непрерывности суммы ряда, о
почленном интегрировании (по любой
кусочно-гладкой дуге, принадлежащей
кругу сходимости) и дифференцировании
ряда.

Теорема. При
почленном дифференцировании и
интегрировании степенного ряда его
радиус сходимости не меняется.

Доказательство.
Рассмотрим ряд из модулей членов
степенного ряда (это – знакоположительный
числовой ряд в конкретной точке) и
определим радиус сходимости по признаку
Даламбера.

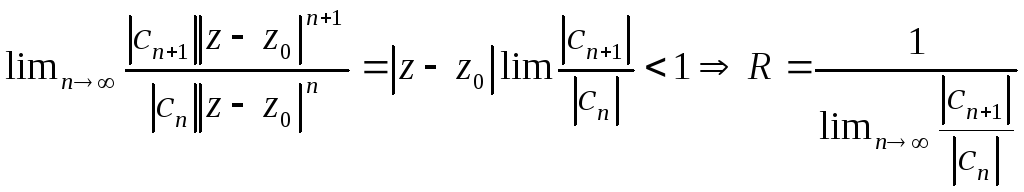
Продифференцируем
почленно степенной ряд
,
перейдем к ряду из модулей и найдем
радиус сходимости по признаку Даламбера.

Таким образом,
при почленном дифференцировании радиус
сходимости степенного ряда не меняется.
Он не меняется и при почленном
интегрировании, иначе он изменился бы
при почленном дифференцировании.

Исследуем
сходимость степенного ряда на границе
круга сходимости.

Рассмотрим ряд
из модулей на границе круга сходимости
.

Если ряд из модулей на
границе круга сходимости сходится, то
исходный степенной ряд абсолютно
сходится на всей границе.

В самом деле
этот ряд является мажорантным для
степенного ряда в любой точке границы.

Если
,
то исходный степенной ряд расходится
на всей границе.

В этом случае
,
и не выполняется необходимый признак
сходимости для исходного степенного
ряда на всей границе круга сходимости.
Поэтомуисходный степенной ряд
расходится на всей границе.

Если ряд из модулей на
границе круга сходимости расходится,
но
,то исходный степенной ряд сходится в
одних точках границе и расходится в
других. В этом случае для того, чтобы
исследовать сходимость в точке границы,
надо подставить ее в качествев степенной ряд и исследовать сходимость
полученного числового ряда.

Приведенные
выше примеры 3, 4, 5 (после критерия Коши):
ряд
,
ряд,
рядиллюстрируют все три случая. Первый ряд
расходится на всей границе,
так как на ней не выполняется необходимый
признак сходимости ряда. Второй ряд
сходится на всей границе, третий ряд
сходится в одних точках границы и
расходится в других.

Теорема. Сумма
степенного ряда является аналитической
функцией в его круге сходимости (без
доказательства).

Ряд
Тейлора.

Рядом Тейлораназывается степенной ряд вида(предполагается,
что функцияявляется бесконечно дифференцируемой).

Рядом Маклорена
называется ряд Тейлора при,
то есть ряд.

Теорема.
Степенной ряд является рядом Тейлора
для своей суммы.

Доказательство.Пустьи
степенной ряд сходится в круге.
Подставим в разложение,
получим.

Так как сумма
степенного ряда – функция аналитическая,
мы можем дифференцировать функцию, а
так как степенной ряд сходится равномерно
внутри круга сходимости, мы можем его
дифференцировать почленно. Полученный
ряд будет сходиться в том же круге, так
как радиус сходимости при дифференцировании
не меняется. Поэтому сумма этого ряда
будет
фунцией аналитической в том же круге.
Ее вновь можно дифференцировать,
дифференцируя почленно степенной ряд
и т.д. Отсюда следует, что если
аналитическая функция является суммой
степенного ряда (это будет показано
позже), то она является бесконечно
дифференцируемой функцией. Вычислим
коэффициенты в степенных рядах, полученных
почленным дифференцированием.=,

,,,

Продолжая этот
процесс, получим
.
Это – коэффициенты ряда Тейлора.

Запишем разложения
в ряд Маклорена основных элементарных
функций.

Так как эти
формулы справедливы на всей действительной
оси, то по теореме Абеля они справедливы
и на всей комплексной плоскости (в круге
с началом координат бесконечного
радиуса).

,
.

(
интегрируя предыдущую формулу)

Источник

Содержание:

Радиус сходимости и круг сходимости степенного ряда

Степенным рядом называется ряд

где — коэффициенты степенного ряда.

Областью сходимости степенного ряда называется совокупность тех значений х, при которых степенной ряд (14.1) сходится.

Число R — такое, что при ряд (14.1) сходится, а при — расходится, называется радиусом сходимости степенного ряда.

Интервал называется интервалом сходимости степенного ряда. При ряд может как сходиться, так и расходиться.

Радиус сходимости степенного ряда может быть найден по формуле:

Формула (14.2) применима, если, начиная с некоторого номера , все

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Для степенного ряда вида

радиус сходимости находится по формуле (14.2), а интервал сходимости из условия , т.е. имеет вид:

Пример с решением 1:

Найти области сходимости степенных рядов:

Решение:

а) Найдем радиус сходимости ряда по формуле (14.2): т.е. интервал сходимости ряда

Теперь выясним поведение ряда на концах интервала сходимости.

Возможно вам будут полезны данные страницы:

На левом конце при — данный степенной ряд принимает вид этот ряд сходится по признаку Лейбница (см. §13.3, п. 4). На правом конце при

нический ряд (§ 13.2, п. 3) при у которого все члены с четными номерами равны нулю. Так как , то этот ряд сходится.

Следует отметить, что сходимость ряда на левом конце интервала сходимости при — могла быть установлена с помощью достаточного признака сходимости знакопеременного ряда, так как ряд, составленный из абсолютных величин его членов, т.е. ряд сходится. Итак, область сходимости данного ряда

Обращаем внимание на то, что при исследовании сходимости степенного ряда на концах интервала сходимости в ситуации, когда получаемый ряд — с положительными членами, применять признак Даламбера не имеет смысла, так как при этом всегда будем получать с нерешенным вопросом о сходимости ряда: в этом случае рекомендуется рассматривать другие признаки сходимости (например, признак сравнения, интегральный, необходимый признаки и т.д.)

б) Найдем радиус сходимости по формуле (14.2):

т.е область сходимости ряда

в) Задачу можно решать аналогично предыдущим. Решение упрощается, если заметить, что при

т.е. необходимый признак сходимости не выполняется, и ряд расходится.

Итак, область сходимости ряда состоит из одной точки х = 0.

г) Найдем радиус сходимости по формуле (14.2)

Для нахождения предела заменим бесконечно малые величины

при им эквивалентными

получим В соответствии с п. 4 интервал сходимости находится из условия , или (1; 3).

Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при х = 1 данный ряд принимает вид

при любом натуральном ).

Так как при любом есть сходящийся обобщенный гармонический ряд при , то по признаку сравнения данный ряд сходится.

На правом конце при степенной ряд принимает вид , т.е. является знакочередующимся рядом и по достаточному признаку сходимости знакопеременного (а значит, и знакочередующегося) ряда сходится, так как сходится ряд, составленный из абсолютных величин его членов, т.е. ряд . Итак, область сходимости данного ряда [I; 3].

д) Выпишем несколько первых членов ряда:

Очевидно, что находить радиус сходимости по формуле (14.2) в данном случае не представляется возможным, так как коэффициенты ряда (14.1) и т.д. равны нулю. Поэтому применим непосредственно признак Даламбера. Данный ряд будет абсолютно сходиться, если и расходиться, если Поэтому найдем Следовательно, ряд сходится при или на интервале Исследуем сходимость на концах интервала сходимости.

При ряд принимает вид п~ -I (-1/ = 1 f (-1Г = _lf 1 _ 1+1

„=1 п 3″-’ п з1 2 3

Этот ряд сходится по признаку Лейбница (§ 13.3).

При ряд принимает вид расходящийся

гармонический ряд. Итак, область сходимости ряда [-1/3; 1/3).

е) Так как члены ряда, стоящие на нечетных местах, отсутствуют, т.е. коэффициенты ряда и т.д., то формулу (14.2) для нахождения радиуса сходимости использовать нельзя. Можно применить непосредственно признак Даламбера, как это делалось в примере в п. д). Но в данном случае удобнее сделать замену Тогда ряд примет вид Область сходимости этого ряда получена в п. а): Возвращаясь к переменной х, получим откуда т.е. область сходимости ряда

Радиус сходимости и круг сходимости степенного ряда

Определение 1. Функциональные ряды вида

где — заданные комплексные числа, — комплексное переменное, называются степенными рядами. Числа называются коэффициентами степенного ряда (33.1).

Предполагая, что коэффициенты ряда и число фиксированы, будем исследовать поведение ряда (33.1) при различных .

Если в ряде (33.1) выполнить замену переменного, положив , то получим ряд

Очевидно, что исследование сходимости ряда (33.1) эквивалентно исследованию сходимости ряда (33.2), поэтому в дальнейшем будем рассматривать ряды вида (33.2), используя, как правило, для обозначения переменной букву , а не

ТЕОРЕМА 1 (первая теорема Абеля). Если степенной ряд сходится при , то он сходится, и притом абсолютно, при любом , для которого

Доказательство. Пусть ряд

сходится. Тогда его n-й член стремится к нулю при

(см. п. 30.1), поэтому последовательность ограничена, т. е. существует такая постоянная , что

В силу этого, для n-го члена ряда (33.3) имеет место оценка Если (рис. 9), то ряд являясь суммой геометрической прогрессии со знаменателем сходится. Поэтому, согласно признаку сравнения (см. п. 30.5), сходится и ряд а это означает абсолютную сходимость ряда (33.3) при

СЛЕДСТВИЕ. Если степенной ряд (33.3) расходится при , то он расходится и при всяком , для которого

Действительно, если и ряд (33.4) расходится, то расходится и ряд (33.3), так как если бы он сходился, то, в силу доказанного, сходился бы и ряд (33.4).

Неравенство задает на комплексной плоскости С замкнутый круг радиуса R с центром в точке

Определение 2. Пусть задан ряд . Если R — неотрицателъное число или обладает тем свойством, что при всех z, для которых ряд (33.3) сходится, а при всех z, для которых , ряд (33.3) расходится, то R называется радиусом сходимости степенного ряда (33.3).

Множество точек , для которых , называется кругом сходимости ряда (33.3).

Если , то круг сходимости вырождается в точку, а если , то круг сходимости совпадает со всей комплексной плоскостью С.

ТЕОРЕМА 2. У всякого степенного ряда (33.3) существует радиус сходимости R. Внутри круга сходимости, т. е. при любом , для которого ряд (33.3) сходится абсолютно. На любом круге , где г фиксировано и , ряд (33.3) сходится равномерно.

Доказательство. Обозначим через А множество всех неотрицательных чисел х, в которых ряд сходится. При х = 0 этот ряд заведомо сходится, поэтому множество А не пусто и, следовательно, имеет конечную или бесконечную верхнюю грань. Пусть sup А = R. Покажем, что R — радиус сходимости ряда (33.3). Действительно, пусть и Согласно определению верхней грани, существует такое , что (см. определение 4′ в п. 3.4). В силу определения множества А, для указанного х ряд (33.5) сходится, поэтому, согласно первой теореме Абеля, в выбранной точке г сходится абсолютно ряд Если , то выберем такое действительное число х, что ; тогда снова, в силу определения множества А, ряд (33.5) в такой точке х расходится — она лежит на действительной оси правее всех точек, в которых ряд (33.5) сходится. Поэтому, согласно следствию из первой теоремы Абеля, для выбранного z расходится и ряд

Итак, действительно, R является радиусом сходимости ряда (33.3).

Если теперь , то, по доказанному, ряд (33.3) при z = г абсолютно сходится, т. е. сходится числовой ряд А так как для любой точки круга (рис. 10)

то, согласно признаку Вейерштрасса (см. п. 32.3), на этом круге ряд (33.3) сходится равномерно. □

Таким образом, областью сходимости всякого степенного ряда является всегда «круг», т. е. обычный круг, исключая, быть может, некоторое множество точек ограничивающей его окружности (будем для краткости называть ее границей круга сходимости), в которых он может расходиться.

Пример с решением 2:

Подчеркнем, что радиус сходимости степенного ряда (33.3) обладает следующим свойством: для каждого числа z такого, что , указанный ряд абсолютно сходится, а для каждого z такого, что , он просто, а следовательно, и подавно абсолютно расходится (расходится ряд, составленный из абсолютных величин членов данного ряда). Это следует, очевидно, из определения радиуса сходимости и теоремы 2.

Члены степенного ряда являются непрерывными функциями и, как было показано, на всяком круге, лежащем вместе со своей границей внутри круга сходимости, степенной ряд сходится равномерно, поэтому его сумма непрерывна на всяком указанном круге. Очевидно, что для любой точки z круга сходимости, |z| < R, можно подобрать круг, содержащий эту точку и лежащий вместе с границей в круге сходимости (достаточно взять его радиус г таким, что |z| < г < R), поэтому степенной ряд непрерывен в каждой точке г, лежащей внутри его круга сходимости: |z| < R. Рассмотрим теперь случай, когда степенной ряд сходится в точке , лежащей на границе его круга сходимости. Отметим, что случай может быть сведен к случаю z = R простой заменой переменного

ТЕОРЕМА 3 (вторая теорема Абеля). Если R — радиус сходимости ряда и этот ряд сходится при то он сходится равномерно на отрезке [0, R] действительной оси.

СЛЕДСТВИЕ. Если степенной ряд (33.3) сходится при z = R, то его сумма непрерывна на отрезке [0, /?] действительной оси.

Доказательство. Пусть Представим ряд Члены ряда

не зависят от х, поэтому его сходимость означает и его равномерную сходимость. Последовательность же ограничена

на отрезке , ее члены неотрицательны: и она убывает в каждой точке (при она не строго убывает, точнее, является стационарной). Поэтому, в силу признака Абеля равномерной сходимости рядов (см. теорему 7 в п. 32.3), ряд (33.3) равномерно сходится на отрезке .

Следствие вытекает из того, что сумма равномерно сходящегося ряда непрерывных функций является также непрерывной функцией.

Все сказанное с помощью преобразования типа , (— новая переменная, фиксировано) переносится и на общие степенные ряды вида (33.1). В частности, областью сходимости такого степенного ряда всегда является круг вида , конечно, как и выше, с точностью до точек ограничивающей его окружности. Этот круг называется кругом сходимости (ряда (33.1)), aR — его радиусом сходимости.

Пример с решением 3:

Радиус сходимости равен нулю, т. е. этот ряд сходится только при

Действительно, исследуя абсолютную сходимость этого ряда по признаку Даламбера, при любом получим

Таким образом, рассматриваемый ряд не сходится абсолютно при любом ; отсюда, в силу следствия из первой теоремы Абеля, он расходится при любом .

Пример с решением 4:

Радиус сходимости ряда равен , так как было показано (см. п. 32.1), что этот ряд сходится при любом .

Пример с решением 5:

Сумма бесконечной геометрической прогрессии

сходится при и расходится при . Поэтому ее радиус сходимости R = 1. Отметим, что во всех точках границы круга сходимости, т. е. во всех точках окружности , ряд (33.6) расходится, так как для общего члена ряда имеем следовательно, он не стремится к нулю при .

Пример с решением 6:

Ряд

сходится при , так как при выполнении этого условия

При ряд (33.7) расходится, поскольку в этом случае т. е. не выполняется необходимое условие сходимости ряда. Радиус сходимости ряда (33.7), как и ряда (33.6), равен единице, однако в каждой точке границы круга сходимости ряд (33.7), в отличие от ряда (33.6), сходится.

Пример с решением 7:

Ряд имеет радиус сходимости R = 1.

Действительно, применив признак Даламбера для определения z, при которых ряд абсолютно сходится (расходится), получим

и, следовательно, при данный ряд сходится, причем абсолютно, а при он расходится. При получается расходящийся гармонический ряд , а при z = -1 — сходящийся ряд (см. и. 30.3 и 30.9). Таким образом, в этом п = О П

примере на границе круга сходимости есть точки, в которых ряд сходится, и точки, в которых он расходится.

Таким образом, область сходимости степенного ряда не совпадает, вообще говоря, с его кругом сходимости, а состоит из внутренности этого круга, т. е. множества , и, быть может, еще из некоторого множества точек, лежащих на его границе.

Из рассмотренных примеров видно, что иногда радиус сходимости R степенного ряда находится с помощью признака Даламбера сходимости рядов с положительными членами .

Действительно, справедливо следующее утверждение: если существует предел

В самом деле, если число R определено этой формулой и то

поэтому ряд (33.3) для такого z сходится (и притом абсолютно).

Если же и, следовательно, ряд (33.3) абсолютно расходится. Таким образом, R действительно является радиусом сходимости ряда (33.3).

Аналогично можно найти величину радиуса сходимости R и с помощью признака Коши (см. теорему 9 в п. 30.6), если только существует предел (конечный или бесконечный) . В этом случае

Действительно, если число R задается этой формулой и если , то

и поэтому ряд (33.3) сходится. Если же , то и, следовательно, ряд (33.3) абсолютно не сходится.

Таким образом, R является радиусом сходимости ряда (33.3).

Затруднения при использовании таких методов определения радиуса сходимости степенного ряда могут возникнуть, например, уже в том случае, когда в рассматриваемом ряде имеются коэффициенты со сколь угодно большими номерами, равные нулю. Тогда можно попробовать применить один из этих методов, предварительно перенумеровав подряд все члены ряда с отличными от нуля коэффициентами (отчего его сходимость и сумма в случае, если он сходится, не изменяются).

Поясним сказанное на примере. Пусть требуется определить радиус сходимости ряда Признак Даламбера неприменим для определения сходимости этого ряда, так как отношение не имеет смысла

для четных номеров п. Не дает ответа здесь и признак Коши, поскольку нетрудно проверить, что здесь предел не существует.

Однако если положить , и записать данный ряд в виде

то, исследовав абсолютную сходимость этого ряда с помощью признака Даламбера, получим

Отсюда следует, что рассматриваемый ряд абсолютно сходится, когда , т. е. когда , и абсолютно расходится, когда . Таким образом, радиус сходимости этого степенного ряда равен 1.

Подчеркнем, что с помощью признака Даламбера и признака Коши можно найти радиус сходимости не для произвольного степенного ряда, а лишь для такого, у которого существуют указанные выше пределы (быть может, после новой нумерации членов).

Лекции:

Матрица перехода
Дифференциальные уравнения второго порядка
Сюръекция, инъекция и биекция.
Множество
Область сходимости функционального ряда
Что такое производная
Криволинейный интеграл 1 рода
Исследовать ряд на сходимость: пример решения
Площадь фигуры ограниченной линиями
Объем цилиндра

Источник

Степенные ряды с комплексными членами и их свойства

Круг сходимости степенного ряда

Теорема Абеля о сходимости ряда

Формула Коши-Адамара

Свойства степенных рядов

Действия над степенными рядами

Подстановка ряда в ряд

Обобщение свойств степенных рядов

Ряды с комплексными членами по целым степеням

Радиус сходимости[править | править код]

Теорема Островского — Адамара[править | править код]

Литература[править | править код]

См. также[править | править код]

Степенные ряды

Радиус и круг сходимости степенного ряда.

Регулярные функции.

Свойства степенных рядов.

Степенные ряды.

Определение радиуса сходимости и исследование сходимости ряда на границе круга сходимости.

Пример с решением 1:

Радиус сходимости и круг сходимости степенного ряда

Пример с решением 2:

Пример с решением 3:

Пример с решением 4:

Пример с решением 5:

Пример с решением 6:

Пример с решением 7:

Вам также может понравиться

Как в bios найти power

Как найти дешевые двери

Как найти доход за квартал

Добавить комментарий Отменить ответ