Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое диаметр круга?
Диаметр круга – это отрезок, соединяющий две точки на окружности и проходящий через центр круга.
Если же говорить, про другие фигуры, то диаметром называется максимальное расстояние между точками этой фигуры. Диаметр круга – не исключение, так как это самый длинный отрезок, который можно провести в границах окружности.
Если нарисовать диаметр, то он будет выглядеть следующим образом (выделен красным на рисунке ниже).
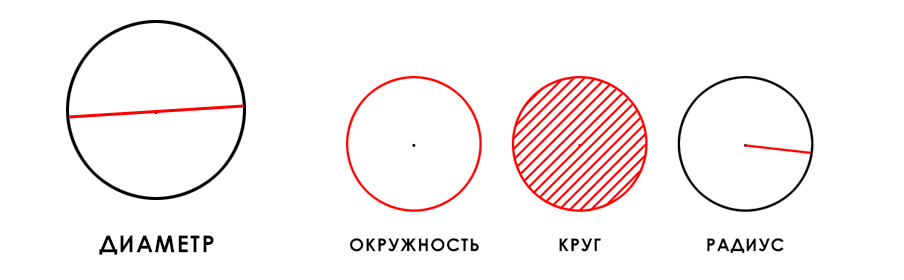
Теперь давайте рассмотрим, как можно найти диаметр и какие для этого существуют формулы.
Формулы определения диаметра круга
Для определения диаметра существует несколько разных способов в зависимости от известных частей круга.
По радиусу
Самая простая формула определения диаметра может быть использована, если известен радиус круга. Радиус — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности. Диаметр равен двум радиусам.
d = r × 2
Где d – это диаметр, а r – радиус.
По длине окружности
Второй способ нахождения диаметра можно использовать тогда, когда известна длина окружности. Окружность — это замкнутая плоская кривая, все точки которой равноудалены от центра. Тако вот, диаметр равен длине окружности, делённой на число Пи.
d = L / π
Где d – это диаметр, а L – длина окружности, а π – константа, равная 3,14.
Эта формула, основывает на том, что отношение длины окружности к её диаметру всегда является постоянным числом, которое равняется примерно 3,14 и называется π (пи).
Через площадь круга
Чуть более изощренной и сложной является формула вычисления диаметра через площадь круга. Чаще всего требуется, наоборот, посчитать площадь круга, если известен диметр. Но если задача стоит обратная, то формула расчёта будет выглядеть следующим образом:
d = 2 × (S/π)1/2
Где d – диаметр, S – площадь круга, а π – константа, которая примерно равна 3,14.
То есть диаметр равен удвоенному корню частного площади круга к числу пи. Стоит отметить, что корень и степень ½ – это одно и то же.
Примеры вычисления диаметра
Давайте для закрепления рассмотрим несколько примеров.
Пример 1. Диаметр по длине окружности трубы 🚿
Предположим, у вас под рукой не оказалось штангенциркуля (устройства для измерения ширины изделий).

А вам требуется рассчитать диаметр действующей трубы, конца которой не видно. Для этого с помощью рулетки или сантиметра, вы можете измерить длину окружности, просто обернув рулетку вокруг трубы. А потом эту длину нужно будет разделить на 3,14. Если длина окружности трубы оказалась 31,4 сантиметра, тогда диаметр будет равен частному этой длинны к числу Пи, то есть:
d = 31,4 / 3,14 = 10 см.
Это и есть правильный ответ – 10 сантиметров.
Пример 2. Диаметр по колеса радиусу 🚲
Тут всё гораздо проще. Предположим, что вы знаете радиус колеса велосипеда – 10 дюймов. Какой будет диаметр?
Диаметру будет равен двум радиусам, то есть 20 дюймов.
Кстати, для справки, 1 дюйм = 2,54 сантиметра. То есть 10 дюймов = 25,4 сантиметра. В итоге диаметр колеса равен: 2 × 25,4 = 50,8 см.
❓Вопросы и ответы
И конечно же обратите внимание на ответы на часто задаваемые вопросы относительно расчёта длины диаметра круга.
Как работает ваш онлайн-калькулятор?
Просто. Вы выбираете, что известно: радиус, длина окружности или площадь круга (1), затем вписываете известное значение (2), выбираете размерность из мм, см, м, км (3) и нажимаете кнопку «рассчитать»?
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть различные калькуляторы, в частности калькуляторы: площади круга, длины окружности и диаметра. Для последнего калькулятор находится на данной странице.
Достаточно ли у меня данных для расчёта?
Для вычисления диаметра круга нужно что-то одно: радиус, длина окружности или площадь круга. Остальное вычислит наш калькулятор по специальным формулам, которые описаны выше.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Если у автомобильного колеса параметр R16, то какой у него диаметр?
16 дюймов, а радиус 8 дюймов. Как ни странно, диаметр такого колеса (точнее диска колеса) составляет 16 дюймов, то есть 40,64 см. Очень часто люди называют радиус в качестве единицы измерения: мол, радиус 16 дюймов. Но тогда представьте, для какого трактора диаметр диска будет более 80 сантиметров.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
При помощи нашего калькулятора вы легко сможете узнать диаметр круга или окружности.
Для того что бы вычислить диаметр круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить диаметр круга.
Диаметр круга рассчитывается по следующим формулам:
- Если нам известна длина:
Формула для расчета диаметра круга через его длину:
D=P/π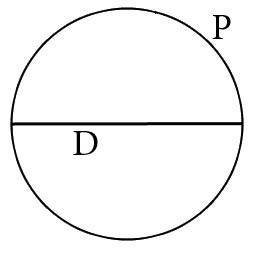
- Если нам известна площадь:
Формула для расчета диаметр круга через площадь:
D=2√
S/π
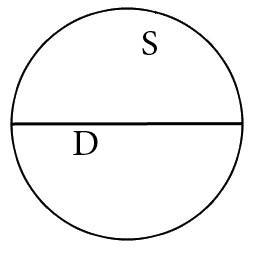
- Если нам известен диаметр:
Формула для расчета диаметр круга через радиус:
D=2R
Где D – диаметр круга, S – площадь круга, P – длина круга, R – радиус, π – число Пи которое всегда примерно равно 3,14.
Как посчитать диаметр окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать диаметр окружности
Чтобы посчитать диаметр окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
 Для того чтобы вычислить диаметр окружности вам необходимо знать её радиус, либо длину окружности, либо её площадь. Если вы знаете хотя бы один из этих параметров, введите его в соответствующие поле и узнаете, чему равен диаметр окружности.
Для того чтобы вычислить диаметр окружности вам необходимо знать её радиус, либо длину окружности, либо её площадь. Если вы знаете хотя бы один из этих параметров, введите его в соответствующие поле и узнаете, чему равен диаметр окружности.
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Ответ:
0
Каков диаметр (d) если длина окружности C?
Формула
d = C/π, где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
её радиус ?
Ответ:
0
Каков диаметр окружности (d) если её радиус r?
Формула
d = 2⋅r
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
её площадь ?
Ответ:
0
Каков диаметр окружности (d) если её площадь S?
Формула
d = √4S/π, где π ≈ 3.14
Пример
Если площадь круга равна 5 см2, то его диаметр примерно равен 2.52 см.
См. также
Загрузить PDF
Загрузить PDF
Вычислить диаметр окружности не составит труда, если вы знаете какие-либо другие ее размеры: радиус, длину окружности или площадь ограничиваемого ею круга. Диаметр можно вычислить, даже не зная этих размеров – при наличии начерченной окружности. Если вы хотите узнать, как вычислить диаметр окружности, следуйте указанным ниже шагам.
-

1
Если вам известен радиус окружности, то, для того чтобы узнать диаметр, удвойте его. Радиус – это расстояние от центра окружности до любой точки, лежащей на ней. Например, если радиус окружности равен 4 см, то диаметр окружности составляет 4 см x 2, или 8 см.
-

2
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π. Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
-

3
Если вам известна площадь круга, то для нахождения диаметра разделите ее на π и извлеките из результата квадратный корень, чтобы получить радиус; затем умножьте на 2 для получения диаметра. Данное вычисление вытекает из формулы площади круга, A = πr2, преобразованной для нахождения диаметра. Например, если площадь круга равна 25 см2, разделите ее на число π и извлеките квадратный корень: √(25/3,14) = √7,96 = 2,82 см. Это радиус окружности. Умножьте его на 2, и вы получите диаметр: 2,82 х 2 = 5,64 см.
Реклама
-

1
Внутри окружности начертите горизонтальную прямую, проходящую от одной точки окружности к другой. Для этого воспользуйтесь линейкой или угольником. Прямая может проходить в верхней части круга, в нижней, или где-нибудь посередине.
-

2
Пометьте точки, в которых прямая пересекает окружность, буквами “A” и “B.”
-

3
Начертите две пересекающиеся окружности, одну – с центром в точке A, а другую – с центром в точке B. Убедитесь, что две окружности пересекаются так, будто образуют диаграмму Венна.
-

4
Через две точки, в которых окружности пересеклись, проведите прямую. Отрезок этой прямой между двумя точками и будет равен диаметру окружности.
-

5
Измерьте диаметр. Измерьте его с помощью линейки, а если нужна большая точность – штангенциркулем с цифровой индикацией. Готово!
Реклама
Советы
- Научитесь пользоваться циркулем. Это очень полезный инструмент, который предназначен для многих целей, включая определение диаметра окружности описанным выше графическим способом. Для этого можно также использовать измерительный циркуль.
- Работа с геометрическими формулами и уравнениями станет легче при условии постоянной практики. Попросите кого-то, кто работал с окружностями или другими геометрическими фигурами, помочь вам. Когда вы наберетесь немного опыта, вы скорее всего почувствуете, что задачи по геометрии будут казаться легче.
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Циркуль
- Линейка
- Штангенциркуль с цифровой индикацией (при необходимости)
Об этой статье
Эту страницу просматривали 1 261 095 раз.
Была ли эта статья полезной?
Как найти диаметр окружности

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Формулы для вычисления диаметра конуса. Пример решения геометрической задачи

Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.
Круглый прямой конус
В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая – директрисой, или направляющей.
Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.
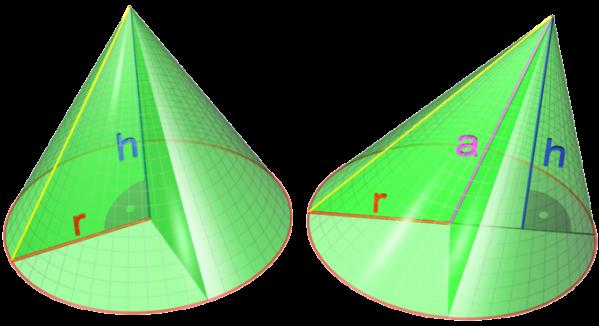
Здесь r – радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.
Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая – это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.
Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.
Вычисление диаметра фигуры через линейные параметры и угол при основании
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
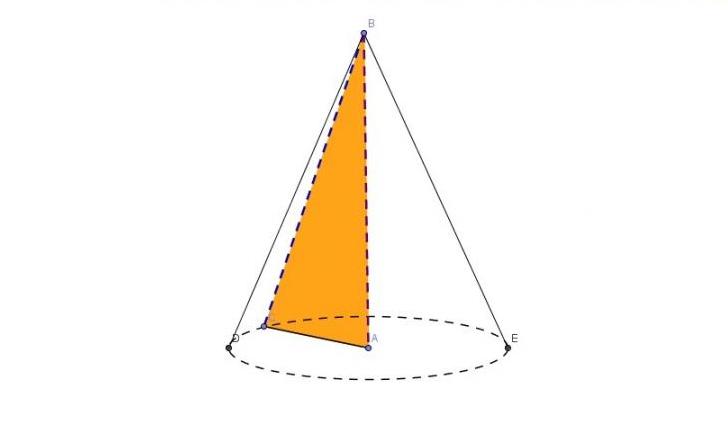
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g – это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Вычисление диаметра через площадь поверхности и генератрису
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
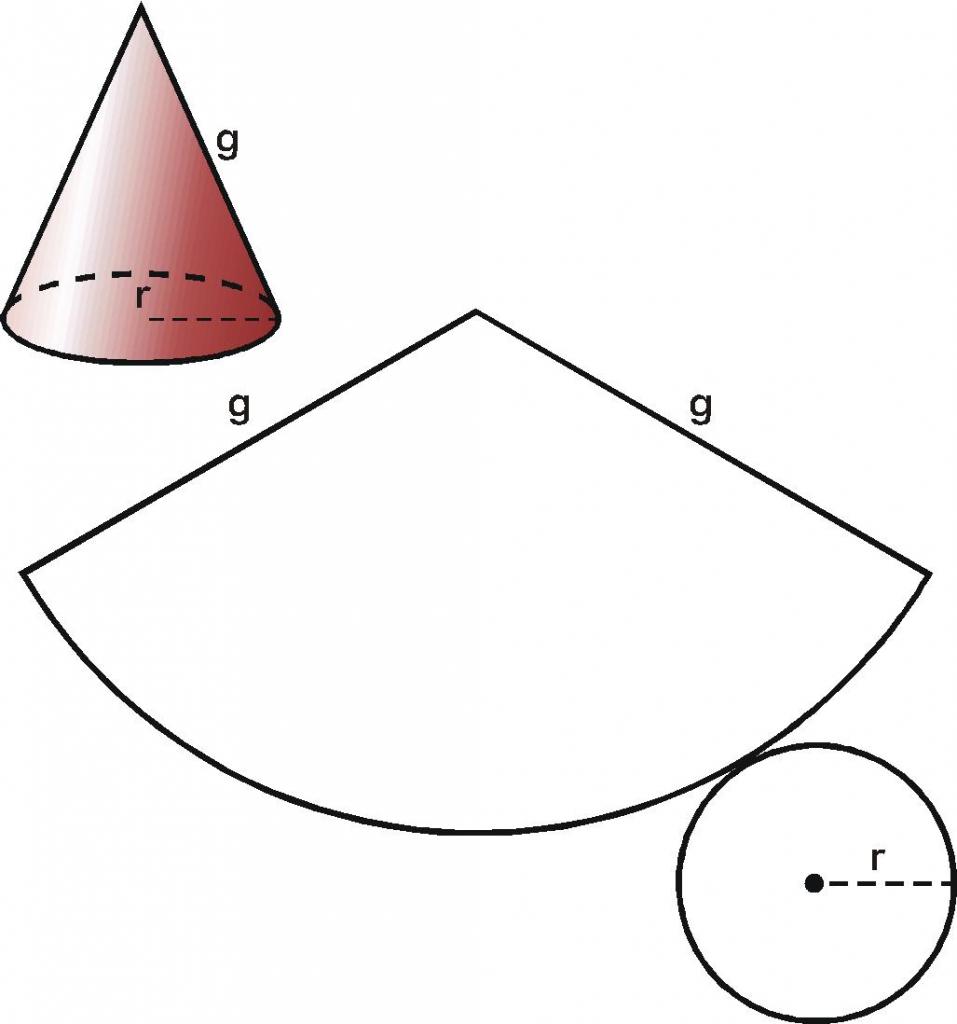
Общая площадь развертки определяется по следующей формуле:
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Определение диаметра через объем и высоту

Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
Здесь S – площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Задача на определение диаметра через известную площадь конуса и его образующую
Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?
Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:
r 2 + 14*r – 150/3,14 = 0
При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:
Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:
Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:
Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.
В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.
Как найти диаметр основания окружности
Как найти диаметр окружности

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Радиус и диаметр окружности

Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).
Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.
Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.

На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.
Формула радиуса окружности через диаметр:
Формула диаметра окружности через радиус:
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.
Существует радиус вписанной окружности
и радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.
Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.
Как посчитать диаметр окружности
Онлайн калькулятор
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Каков диаметр (d) если длина окружности C?
Формула
d = C /π , где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её радиус r?
Формула
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её площадь S?
Формула
d = √ 4S /π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.
[spoiler title=”источники:”]
http://fb.ru/article/446998/formulyi-dlya-vyichisleniya-diametra-konusa-primer-resheniya-geometricheskoy-zadachi
http://b4.cooksy.ru/articles/kak-nayti-diametr-osnovaniya-okruzhnosti
[/spoiler]
