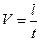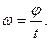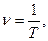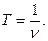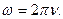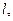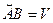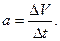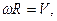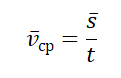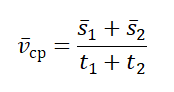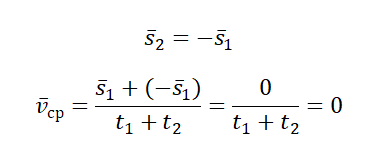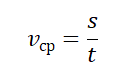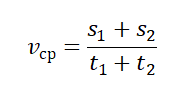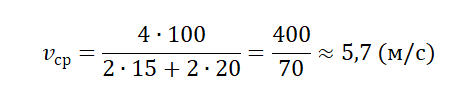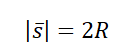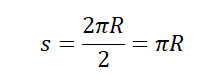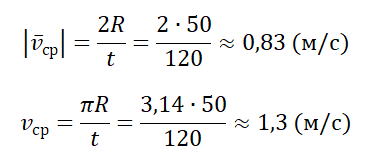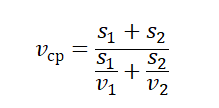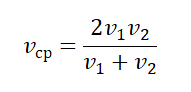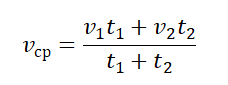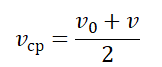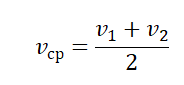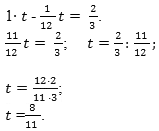Человек регулярно сталкивается с разными видами движения. Перемещение тела по окружности позволяет понять многие физические процессы. На основе закономерностей такого явления работают разнообразные механизмы. Рассчитать характеристики движения по окружности достаточно просто, если знать и уметь применять несколько основных формул.
Движение тела по окружности — какими законами описывается
Движением по окружности в теории называют вращение какой-либо материальной точки или тела относительно оси, неподвижной в выбранной системе отсчета и не проходящей через центр тела.
Тело может двигаться по окружности двумя способами:
- равномерно;
- неравномерно.
Равномерное движение тела характеризуется постоянной угловой скоростью. Для описания такого перемещения применяют следующие формулы:
- угловая скорость: (omega =frac{2pi }{T})
- скорость движения: (V =frac{2pi R}{T}=omega R)
- угол поворота: (phi =2pi frac{t}{T}=omega t)
- ускорение: (frac{2pi v}{T}=omega ^{2}R)
Неравномерное движение возможно при переменной угловой скорости тела. В данном случае применимы формулы:
- тангенциальное ускорение: (a_{t}=frac{dv}{dt})
- центростремительное ускорение: (a_{n}=frac{v^{2}}{R}=omega ^{2}R)
В представленных уравнениях используются такие параметры, как:
- Т — период вращения;
- t — время;
- ω — угловая скорость;
- R — радиус;
- at — тангенциальное ускорение;
- an — центростремительное или полное ускорение.
При отсутствии специальных оговорок, в процессе решения задач движение тела по окружности принимают за равномерное. Для расчета пройденного пути используют формулу:
(S=frac{v}{t})
где:
- S является расстоянием, которое преодолело тело;
- v представляет собой скорость движения тела;
- t определяет время движения.
Таким образом, справедливы выражения:
(v=frac{S}{t})
(t =frac{v}{S})
Величины, которые применяют для решения задач, характеризуются положительными значениями:
S > 0, v > 0, t > 0
При решении задач принято все величины переводить в единицы измерения, согласно системе СИ.
Секретом заданий на движение тела по окружности является то, что обгоняющий будет преодолевать на 1 круг больше при первом обгоне. Данное расстояние считается на n кругов больше, если первый объект обогнал другого в n-ый раз.
Задачи на движение по окружности от простых до сложных
Задачи на движение тела по окружности отличаются по степени сложности. Можно рассмотреть примеры простых заданий.
Задача 1
Длина круговой трассы составляет 8 километров. Из ее точки в один момент времени в одинаковом направлении выехали два автомобиля. Первый автомобиль развил скорость 114 км/ч и, спустя 20 минут после начала движения, обогнал второй автомобиль на один круг. Требуется определить скорость, с которой двигался второй автомобиль. Ответ необходимо представить в км/ч.
Решение
Известно, что старт произошел одновременно для обоих автомобилей. Через 20 минут после начала движения первое транспортное средство опережало второе на один круг. Таким образом, в течение 20 минут или 1/3 часа первый автомобиль преодолел на 1 круг больше, то есть на 8 км больше. За час первый автомобиль проехал на 8*3=24 км больше, чем второй. Скорость второго транспортного средства на 24 км/ч меньше по сравнению с первым, и равна 114-24=90 км/ч.
Ответ: второй автомобиль двигался со скоростью 90 км/ч.
Задача 2
Из пункта А круговой трассы выехал велосипедист, а спустя полчаса стартовал мотоциклист. Через 10 минут после начала пути водитель мотоцикла догнал велосипедиста в первый раз. Спустя еще 30 минут мотоциклист догнал велосипедиста повторно. Требуется определить, какова скорость мотоциклиста, в том случае, когда длина трассы составляет 30 км. Ответ необходимо представить в км/ч.
Решение
В первую очередь требуется перевести минуты в часы. Скорости мотоциклиста и велосипедиста можно обозначить х и у. В первый раз водитель мотоцикла обогнал велосипедиста, спустя 10 минут или 1/6 часа после начала движения. До этого момента велосипедист находился в движении 40 минут или 2/3 часа.
Можно упростить запись условий задачи:
велосипедист: v = х, t = 2/3, S = 2/3*х;
мотоциклист: v = у, t = 1/6, S = 1/6*у.
Велосипедист и мотоциклист преодолели одинаковый путь:
(frac{1}{6}y=frac{2}{3}x)
Спустя 30 минут или 1/2 часа после первого обгона мотоциклист выполнил второй обгон велосипедиста.
Таким образом:
велосипедист: v = х, t = 1/2, S = 1/2*х;
мотоциклист: v = у, t = 1/2, S = 1/2*у.
Требуется определить расстояния, которые преодолели гонщики. Мотоциклист обогнал велосипедиста, то есть проехал больше на один круг. Это является ключевым моментом в данной задаче. Один круг составляет 30 километров. Второе уравнение будет иметь вид:
(frac{1}{2}y-frac{1}{2}x=30)
Далее необходимо решить полученную систему:
у = 4х
у – х = 60
Таким образом, х = 20, у = 80.
Ответ: скорость мотоциклиста равна 80 км/ч.
Бывают задания на движение тела по окружности с повышенной степенью сложности. Как правило, подобные примеры при невозможности проведения экспериментов требуют сложных вычислений.
Задача 3
На часах со стрелками время 8 часов 00 минут. Требуется определить, через сколько минут минутная стрелка в четвертый раз догонит часовую стрелку.
Решение
Спустя один час минутная стрелка преодолевает один круг, а часовая проходит лишь 1/12 циферблата. Допустим, что скорости равны 1 круг в час и 1/12 круга в час соответственно. Начало движения приходится на 8.00. Необходимо определить время, в течение которого минутной стрелке в первый раз удастся догнать часовую.
Минутная стрелка преодолеет на 2/3 круга больше. Исходя из этого, можно записать уравнение:
(1*t-frac{1}{12}t=frac{2}{3})
Таким образом, спустя 8/11 часа стрелки совпадут. Предположим, что через время z стрелки совпадут повторно. Минутная стрелка преодолеет расстояние 1*z, а часовая 1/12*z. При этом минутной стрелкой будет пройдено на один круг больше. Можно записать уравнение:
(1*z-frac{1}{12}z=1)
Решение данного уравнения будет таким:
(z=frac{12}{11})
Таким образом, через 12/11 часа стрелки совпадут повторно. Спустя еще 12/11 часа они встретятся вновь и так далее. Поэтому при старте в 8.00 в четвертый раз минутная стрелка догонит часовую через:
(frac{8}{11}+3frac{12}{11}) часа
Ответ: минутная и часовая стрелки совпадут в четвертый раз через (frac{8}{11}+3frac{12}{11})часа.
Нередко при решении задач на движение по окружности требуется рассчитать среднюю скорость тела. Важно, что данная величина не совпадает со средним арифметическим скоростей. Средняя скорость определяется с помощью формулы:
(v=frac{S_{0}}{t_{0}})
где v является средней скоростью;
S0 представляет собой общий путь;
t0 определяет общее время.
При наличии двух участков пути средняя скорость рассчитывается по формуле:
(v=frac{S_{1}+S_{2}}{t_{1}+t_{2}})
Наиболее сложными задачами считаются примеры с пятизначными дискриминантами. Рассмотрим алгоритм действий в таком случае.
Задача 4
Пара гонщиков участвует в соревновании. Путь, который требуется преодолеть, равен 60 кругам кольцевой трассы в 3 км. После одновременного старта первый гонщик пересек финиш раньше, чем второй на 10 минут. Требуется рассчитать среднюю скорость второго гонщика. Известно, что впервые первый участник обогнал второго на круг, спустя 15 минут после начала движения. Ответ требуется записать в км/ч.
Решение
Первый участник гонки, находясь в движении 15 минут, догнал второго гонщика на первом круге. Таким образом, в течение 15 минут он преодолел на 1 круг или на 3 км больше, чем второй. За час первый гонщик проехал 3*4=12 километров больше. При этом скорость его движения на 12 км/ч превышает скорость второго гонщика. 10 минут соответствует ¼ часа. Можно записать уравнение:
(frac{180}{x}-frac{180}{x+12}=frac{1}{6})
Далее необходимо преобразовать выражение к квадратному уравнению:
(x^{2}+12x-12960=0)
Таким образом, получен пятизначный дискриминант. Есть более простой вариант решения задачи. Можно записать уравнение:
(frac{180}{x}-frac{180}{x+12}=frac{1}{6})
В нем 180 можно поделить на 12. Заменим х=12z:
(frac{180}{12z}-frac{180}{12z+12}=frac{1}{6})
(frac{15}{z}-frac{15}{z+1}=frac{1}{6})
(frac{90}{z}-frac{90}{z+1}=1)
Данное равенство можно преобразить в квадратное уравнение. Целый положительный корень такого выражения z=9. Тогда получим:
(х=12z=108)
Ответ: средняя скорость второго гонщика равна 108 км/ч.
Нахождение линейной скорости при движении по окружности
Любая точка, находящаяся на окружности, перемещается с некоторой скоростью. Данная величина называется линейной скоростью. Вектор линейной скорости всегда совпадает по направлению с касательной к окружности. К примеру, стружка из точильного станка движется, повторяя направление мгновенной скорости.
Можно рассмотреть какую-то точку на окружности, совершившую один оборот. При этом было затрачено время равное периоду Т. Расстояние или путь, пройденный точкой, представляет собой длину рассматриваемой окружности.
Задачи на тему равномерное движение по окружности
Задача 1
Радиус выпуклого моста равен 90 м. Требуется определить скорость, с которой автомобиль должен пройти его середину, чтобы пассажир на мгновение ощутил невесомость.
Решение
Согласно условиям задачи:
R = 90 м
N = 0
Сила реакции опоры обладает нулевым значением, так как пассажир в состоянии невесомости не оказывает давление на сиденье автомобиля.
Решение задачи необходимо представить в системе отсчета, которая связана с Землей. Человек совершает движение вместе с автомобилем. Ускорение при этом направлено вниз. На пассажира действует сила притяжения Земли, которая будет центростремительной:
(mg=mfrac{v^{2}}{R})
Таким образом:
(v=sqrt{frac{Rmg}{m}}=sqrt{Rg}=sqrt{90*10}=30) м/с
Ответ: скорость автомобиля составляет 30 м/с.
Задача 2
Масса девочки 40 кг. Она качается на качелях, длина подвеса которых составляет 4 м. Требуется определить силу, с которой девочка давит на сиденье при прохождении среднего положения со скоростью 5 м/с.
Решение
На девочку действует сила тяжести (mvec{g}) и сила реакции опоры (vec{N}).
Качели находятся под действием силы давления (vec{F_{g}}), которая направлена вниз. Согласно третьему закону Ньютона, данная сила соответствует взятой со знаком минус силе реакции опоры:
(vec{F_{g}}=-vec{N})
Таким образом, решением задачи является определение силы реакции опоры. Исходя из закона динамики:
(mvec{g}+vec{N}= mvec{a})
В проекции на ось Х:
(N-mg=mfrac{v^{2}}{R})
Из чего следует вывод:
(F_{g}=left|N right|=m(g+frac{v^{2}}{R}))
(F_{g}=40(10+frac{5^{2}}{4})=650) Н
Ответ: сила равна 650 Н.
Задача 3
Шарик привязали с помощью нити к подвесу. Он описывает в горизонтальной плоскости окружность, совершая движение с постоянной скоростью. Нить обладает длиной 0,6 м и составляет с вертикалью угол в 60 градусов. Необходимо рассчитать, какова скорость шарика.
Решение
Сумма сил (mvec{g}) и натяжения (vec{F_{n}}), исходя из правила параллелограмма, соответствует результирующей силе, направленной в центр вращения (sum_{i}^{}{vec{F}_{i}}):
(sum_{i}^{}{vec{F}_{i}}= mvec{g}+vec{F_{n}}= mvec{a})
Силы в сумме определяются из прямоугольного треугольника с углом α равным 60 градусам. Исходя из того, что (vec{F_{n}}) является противолежащим катетом, получим:
(vec{F_{n}}=mg*tg α)
Таким образом:
(mg*tg α= mvec{a}= mfrac{v^{2}}{R})
(v^{2}=frac{mg*tan alpha *R}{m}=gR*tan alpha)
R включен в прямоугольный треугольник, в котором длина нити представляет собой гипотенузу. R является катетом, противолежащий углу α в 60 градусов.
(R=l*sin alpha)
Преобразив формулу квадрата скорости шарика с помощью подстановки выражения для радиуса, получим:
(v^{2}=gl*sin alpha *tan alpha )
(v=sqrt{gl*sin alpha *tan alpha }=sqrt{10*0.6*frac{sqrt{3}}{2}*sqrt{3}}=3) м/с
Ответ: скорость шарика составляет 3 м/с.
Задача 4
Необходимо определить максимальную скорость мотоцикла по горизонтальной плоскости, который описывает при этом дугу окружности с радиусом 100 м. Коэффициент трения резины о плоскость составляет 0,4.
Решение
Во время поворота мотоцикл наклоняется к центру поворота. На транспортное средство оказывают действие:
- сила тяжести (mvec{g});
- сила реакции опоры (vec{N});
- сила трения (vec{F_{tr}});
- сила тяги (vec{F_{t}});
- сила сопротивления (vec{F_{c}}).
Данные силы в сумме составляют:
(mvec{g}+vec{N}+vec{F_{tr}}+vec{F_{t}}+vec{F_{c}}= mvec{a})
Согласно выражениям:
(mvec{g}+vec{N}=0)
(vec{F_{t}}+vec{F_{c}}=0)
Получим:
(vec{F_{tr}}= mvec{a})
Сила трения составляет:
(F_{tr}= mu mg)
Таким образом:
(mu mg=ma= mfrac{v^{2}}{R})
(v=sqrt{frac{mu mgR}{m}}=sqrt{mu gR}=sqrt{0.4*10*100}=20) м/с
Ответ: максимальная скорость равна 20 м/с.
Задачи разной сложности по теме движения тела по кружности часто встречаются не только в школьной программе, но и во время обучения в вузе. Знание основных закономерностей позволит быстро найти решение примера любой сложности. Если в процессе расчетов возникают трудности, всегда можно обратиться за помощью к сервису Феникс.Хелп.
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Как найти среднюю скорость по окружности
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Движение по окружности.
1.Равномерное движение по окружности
2.Угловая скорость вращательного движения.
5.Связь линейной скорости с угловой.
7.Равнопеременное движение по окружности.
8.Угловое ускорение в равнопеременном движении по окружности.
10.Закон равноускоренного движения по окружности.
11. Средняя угловая скорость в равноускоренном движении по окружности.
12.Формулы, устанавливающие связь между угловой скоростью, угловым ускорением и углом поворота в равноускоренном движении по окружности.
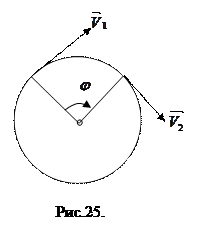
и называется линейной скоростью движения по окружности.
Как и в криволинейном движении вектор скорости направлен по касательной к окружности в направлении движения (Рис.25).
2. Угловая скорость в равномерном движении по окружности – отношение угла поворота радиуса ко времени поворота:
В равномерном движении по окружности угловая скорость постоянна. В системе СИ угловая скорость измеряется в(рад/c). Один радиан – рад это центральный угол, стягивающий дугу окружности длиной равной радиусу. Полный угол содержит 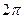
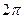
3. Период вращения – интервал времени Т, в течении которого материальная точка совершает один полный оборот. В системе СИ период измеряется в секундах.
4. Частота вращения – число оборотов 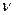
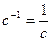
Если за время t точка совершает n оборотов по окружности то 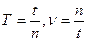
Зная период и частоту вращения, угловую скорость можно вычислять по формуле:
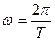
5 Связь линейной скорости с угловой. Длина дуги окружности равна 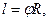
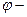
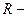
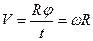
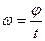
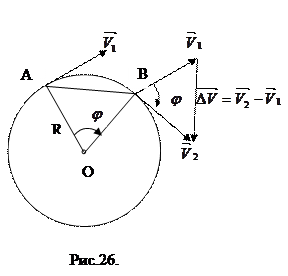
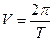
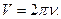
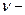
6. Центростремительное ускорение. В равномерном движении по окружности модуль скорости остаётся неизменным 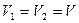
Пусть за промежуток времени 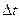
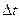
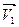
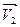
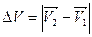
На Рис.26 треугольники АОВ и ДВС равнобедренные и углы при вершинах О и В равны, как углы с взаимно перпендикулярными сторонами АО 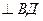
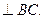
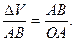
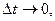
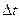
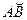
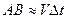
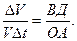
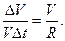
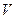
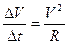
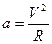

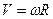
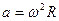
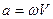
Итак, в равномерном движении по окружности центростремительное ускорение постоянно по модулю.
Легко сообразить, что в пределе при 
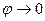
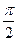
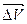
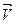
7. Равнопеременное движение по окружности – движение по окружности, при котором за равные интервалы времени угловая скорость изменяется на одну и ту же величину.
8. Угловое ускорение в равнопеременном движении по окружности – отношение изменения угловой скорости к интервалу времени 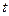
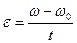
где 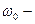
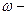
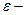
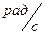
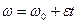
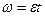
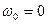
Умножая обе части этих равенств на 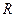
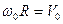
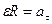
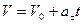
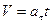
9. Тангенциальное ускорение численно равно изменению скорости в единицу времени и направлено вдоль касательной к окружности. Если 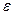
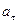
Дата добавления: 2015-08-08 ; просмотров: 17263 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
- vср= v ср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
- vср>v ср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
- Если известны скорости на первой и второй половине пути (s1=s2), средняя скорость равна:
- Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:
- Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:
- Если известны скорости тела за равные промежутки времени, его средняя скорость равна:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/kak-nayti-srednyuyu-skorost-po-okruzhnosti
[/spoiler]
Download Article
Download Article
Velocity is an object’s speed in a particular direction. Mathematically, velocity is often described as the change in position over the change in time.[1]
[2]
This fundamental concept shows up in many basic physics problems. Which formula you use depends on what you know about the object, so read carefully to make sure you’ve chosen the right one.
Quick Formulas
-
1
-
2
Set up an equation with position and time instead. You can also find the velocity from the object’s change in position and time. This works for any problem. Note that, unless the object is moving at a constant velocity, your answer will be the average velocity during the movement, not the specific velocity at a certain time.[4]
Advertisement
-
3
Find the distance between the start and end points. When measuring velocity, the only positions that matter are where the object started, and where the object ended up. This, along with which direction the object traveled, tells you the displacement, or change in position.[5]
The path the object took between these two points does not matter.-
Example 1: A car traveling due east starts at position x = 5 meters. After 8 seconds, the car is at position x = 41 meters. What was the car’s displacement?
- The car was displaced by (41m – 5m) = 36 meters east.
-
Example 2: A diver leaps 1 meter straight up off a diving board, then falls downward for 5 meters before hitting the water. What is the diver’s displacement?
- The diver ended up 4 meters below the starting point, so her displacement is 4 meters downward, or -4 meters. (0 + 1 – 5 = -4). Even though the diver traveled six meters (one up, then five down), what matters is that the end point is four meters below the start point.
-
Example 1: A car traveling due east starts at position x = 5 meters. After 8 seconds, the car is at position x = 41 meters. What was the car’s displacement?
-
4
Calculate the change in time. How long did the object take to reach the end point? Many problems will tell you this directly. If it does not, subtract the start time from the end time to find out.[6]
- Example 1 (cont.): The problem tells us that the car took 8 seconds to go from the start point to the end point, so this is the change in time.
- Example 2 (cont.): If the diver jumped at t = 7 seconds and hits the water at t = 8 seconds, the change in time = 8s – 7s = 1 second.
-
5
Divide the total displacement by the total time. In order to find the velocity of the moving object, you will need to divide the change in position by the change in time. Specify the direction moved, and you have the average velocity.[7]
-
6
Solve problems in two dimensions. Not all word problems involve movement back along one line. If the object turns at some point, you may need to draw a diagram and solve a geometry problem to find the distance.
-
Example 3: A man jogs for 3 meters east, then make a 90º turn and travels 4 meters north. What is his displacement?
- Draw a diagram and connect the start point and end point with a straight line. This is the hypotenuse of a triangle, so solve for its length of this line using properties of right triangles. In this case, the displacement is 5 meters northeast.
- At some point, your math teacher may require you to find the exact direction traveled (the angle above the horizontal). You can do this by using geometry or by adding vectors.
-
Example 3: A man jogs for 3 meters east, then make a 90º turn and travels 4 meters north. What is his displacement?
Advertisement
-
1
Understand the velocity formula for an accelerating object. Acceleration is the change in velocity. If the acceleration is constant, the velocity continues to change at the same rate.[8]
We can describe this by multiplying acceleration and time, and adding the result to the initial velocity: -
2
Multiply the acceleration by the change in time. This will tell you how much the velocity increased (or decreased) over this time period.[9]
-
Example: A ship sailing north at 2 m/s accelerates north at a rate of 10 m/s2. How much did the ship’s velocity increase in the next 5 seconds?
- a = 10 m/s2
- t = 5 s
- (a * t) = (10 m/s2 * 5 s) = 50 m/s increase in velocity.
-
Example: A ship sailing north at 2 m/s accelerates north at a rate of 10 m/s2. How much did the ship’s velocity increase in the next 5 seconds?
-
3
Add the initial velocity. Now you know the total change in the velocity. Add this to the initial velocity of the object, and you have your answer.[10]
-
4
Specify the direction of movement. Unlike speed, velocity always includes the direction of movement. Make sure to include this in your answer.
- In our example, since the ship started going north and did not change direction, its final velocity is 52 m/s north.
-
5
Solve related problems. As long as you know the acceleration, and the velocity at any one point in time, you can use this formula to find the velocity at any other time. Here’s an example solving for the initial velocity:
- “A train accelerates at 7 m/s2 for 4 seconds, and ends up traveling forward at a velocity of 35 m/s. What was its initial velocity?”
Advertisement
-
1
Learn the formula for circular velocity. Circular velocity refers to the velocity that one object must travel in order to maintain its circular orbit around another object, usually a planet or other gravitating mass.[11]
- The circular velocity of an object is calculated by dividing the circumference of the circular path by the time period over which the object travels.
- When written as a formula, the equation is:
- v = (2πr) / T
- Note that 2πr equals the circumference of the circular path.
- r stands for “radius”
- T stands for “time period”
-
2
Multiply the circular radius by 2π. The first stage of the problem is calculating the circumference. To do this, multiply the radius by 2π. If you are calculating this by hand, you can use 3.14 as an approximation for π.[12]
- Example: Find the circular velocity of an object traveling a circular path with a radius of 8 m over a full time interval of 45 seconds.
- r = 8 m
- T = 45 s
- Circumference = 2πr = ~ (2)(3.14)(8 m) = 50.24 m
- Example: Find the circular velocity of an object traveling a circular path with a radius of 8 m over a full time interval of 45 seconds.
-
3
Divide this product by the time period. In order to find the circular velocity of the object in question, you need to divide the calculated circumference by the time period over which the object traveled.[13]
- Example: v = (2πr) / T = 50.24 m / 45 s = 1.12 m/s
- The circular velocity of the object is 1.12 m/s.
- Example: v = (2πr) / T = 50.24 m / 45 s = 1.12 m/s
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
When do we have deceleration?
Benjamin Walker
Community Answer
As the object loses energy passing through a medium. The medium an object is passing through will determine the deceleration.
-
Question
How do I calculate the velocity of something given its time traveled and distance covered?
Divide distance traveled by the time taken to get the average speed.
Velocity is the term used for speed when the object travels in a uniform direction (i.e. straight line or circle). -
Question
How does velocity change if the distance decreases and the time increases?
Velocity decreases. Think about it: It takes a longer time to cover a shorter distance.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Meters per second (m/s) is the standard scientific unit for velocity.[14]
Make sure your units match by measuring distance in meters (m), time in seconds (s), and acceleration in meters per second per second (m/s2).[15]
-
Average velocity measures the average velocity an object travels over the full course of its path. Instantaneous velocity measures the velocity of an object at a specific moment along its path.
Advertisement
References
About This Article
Article SummaryX
Velocity is defined as the speed at which an object travels in a given direction. The right formula to use for calculating velocity depends on a few different factors, such as whether the object is accelerating at a constant rate, or whether it is moving in a circle as opposed to a line. The most basic formula for calculating velocity is velocity (v) = distance (d)/time (t). If you don’t already know the time and distance, you’ll need to calculate them first. Subtract the initial position from the final position to find distance, and subtract the start time from the end time to find the time. For instance, if a runner began sprinting due east at the 22-meter mark along a track and ended up at the 52-meter mark, you’d subtract 22 from 52 to find the distance, or displacement, of 30 meters. Similarly, if they began their sprint at 5:35:01 pm and ended it at 5:35:06 pm, you can find the time by subtracting 1 from 6, giving you 5 seconds. This will tell you that they ran 30 meters in 5 seconds, which means that they maintained an average velocity of 6 m/s east. If you’re finding the velocity of an object that’s accelerating instead of moving at a constant rate, things get a little more complicated. If you know the acceleration rate of the object, you can find the final velocity using the formula vf (final velocity) = vi (initial velocity) + a(t) (acceleration x time). For example, if an object accelerated north at a rate of 5m/s2 over 5 seconds and had a starting velocity of 6 m/s, its final velocity would be 6m/s + (5m/s2 x 5s), or 31m/s north. Once you know both the final and initial velocity, you can calculate the average velocity of an accelerating object. To do this, add initial velocity to final velocity and divide the result by 2. In this case, 6m/s + 30m/s divided by 2 = 18 m/s north. The method for finding the velocity of an object around a circle is a little different. To do this, use the formula v (velocity) = 2πr (the circumference of the circle)/t (time). For example, an object that moves around a circle with a radius of 50 meters in 13 seconds would have a velocity of 2π(50)m/13s, or approximately 24.17 m/s. To learn more, such as how to calculate average or circular velocity, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,427,409 times.
Reader Success Stories
-
Tommie Depew
May 27, 2017
“Taking college physics, and I know nothing because I dropped out of high school without taking any science or…” more
Did this article help you?
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Или:
Отсюда:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 21.6k
В статье рассмотрены задачи в помощь учащимся:
для отработки навыков решения текстовых задач
при подготовке к ЕГЭ, при обучении решению задач
на составление математической модели реальных
ситуаций во всех параллелях основной и старшей
школы. В ней представлены задачи: на движение по
окружности; на нахождение длины движущегося
объекта; на нахождение средней скорости.
I. Задачи на движение по окружности.
Задачи на движение по окружности оказались
сложными для многих школьников. Решаются они
почти так же, как и обычные задачи на движение. В
них также применяется формула . Но есть момент, на
который обратим внимание.
Задача 1. Из пункта А круговой трассы выехал
велосипедист, а через 30 мин следом за ним
отправился мотоциклист. Через 10 мин после
отправления он догнал велосипедиста в первый
раз, а еще через 30 мин после этого догнал его во
второй раз. Найдите скорость мотоциклиста, если
длина трассы равна 30 км. Ответ дайте в км/ч.
Решение. Скорости участников примем за х
км/ч и у км/ч. В первый раз мотоциклист обогнал
велосипедиста через 10 мин, то есть через ч после
старта. До этого момента велосипедист был в пути
40 мин, то есть ч. Участники движения проехали
одинаковые расстояния, то есть y =
x. Внесем данные в таблицу.
Таблица 1
Мотоциклист затем второй раз обогнал
велосипедиста. Произошло это через 30 мин, то есть
через ч
после первого обгона. Какие расстояния они
проехали? Мотоциклист обогнал велосипедиста. А
это значит, он проехал на один круг больше. Вот
тот момент,
на который надо обратить внимание. Один круг –
это длина трассы, Она равна 30 км. Составим другую
таблицу.
Таблица 2
Получим второе уравнение: y –
x = 30. Имеем систему
уравнений: 
В ответе укажем скорость мотоциклиста.
Ответ: 80 км/ч.
Задачи (самостоятельно).
I.1.1. Из пункта “А” круговой трассы выехал
велосипедист, а через 40 мин следом за ним
отправился мотоциклист. Через 10 мин после
отправления он догнал велосипедиста в первый
раз, а еще через 36 мин после этого догнал его во
второй раз. Найдите скорость мотоциклиста, если
длина трассы равна 36 км. Ответ дайте в км/ч.
I.1. 2. Из пункта “А” круговой трассы выехал
велосипедист, а через 30 мин следом за ним
отправился мотоциклист. Через 8 мин после
отправления он догнал велосипедиста в первый
раз, а еще через 12 мин после этого догнал его во
второй раз. Найдите скорость мотоциклиста, если
длина трассы равна 15 км. Ответ дайте в км/ч.
I.1. 3. Из пункта “А” круговой трассы выехал
велосипедист, а через 50 мин следом за ним
отправился мотоциклист. Через 10 мин после
отправления он догнал велосипедиста в первый
раз, а еще через 18 мин после этого догнал его во
второй раз. Найдите скорость мотоциклиста, если
длина трассы равна 15 км. Ответ дайте в км/ч.
Задача 2.
Два мотоциклиста стартуют одновременно в одном
направлении из двух диаметрально
противоположных точек круговой трассы, длина
которой 20 км. Через сколько минут мотоциклисты
поравняются в первый раз, если скорость одного из
них на 15 км/ч больше скорости другого?
Решение.
Рисунок 1
При одновременном старте мотоциклист,
стартовавший из “А”, проехал на полкруга больше,
стартовавший из “В”. То есть на 10 км. При
движении двух мотоциклистов в одном направлении
скорость удаления v = –
. По условию задачи v= 15 км/ч =
км/мин =
км/мин –
скорость удаления. Находим время, через которое
мотоциклисты поравняются в первый раз.
10:=
40(мин).
Ответ: 40 мин.
Задачи (самостоятельно).
I.2.1. Два мотоциклиста стартуют одновременно в
одном направлении из двух диаметрально
противоположных точек круговой трассы, длина
которой 27 км. Через сколько минут мотоциклисты
поравняются в первый раз, если скорость одного из
них на 27 км/ч больше скорости другого?
I.2.2. Два мотоциклиста стартуют одновременно в
одном направлении из двух диаметрально
противоположных точек круговой трассы, длина
которой 6 км. Через сколько минут мотоциклисты
поравняются в первый раз, если скорость одного из
них на 9 км/ч больше скорости другого?
Задача 3.
Из одной точки круговой трассы, длина которой
равна 8 км, одновременно в одном направлении
стартовали два автомобиля. Скорость первого
автомобиля равна 89 км/ч, и через 16 мин после
старта он опережал второй автомобиль на один
круг. Найдите скорость второго автомобиля. Ответ
дайте в км/ч.
Решение.
16 мин ==
.
х км/ч – скорость второго автомобиля.
(89 – х) км/ч – скорость удаления.
8 км – длина круговой трассы.
Уравнение.
(89 – х)
= 8,89 – х = 2· 15,
89 – х = 30,
х = 59.
Ответ: 59 км/ч.
Задачи (самостоятельно).
I.3.1. Из одной точки круговой трассы, длина
которой равна 12 км, одновременно в одном
направлении стартовали два автомобиля. Скорость
первого автомобиля равна 103 км/ч, и через 48 мин
после старта он опережал второй автомобиль на
один круг. Найдите скорость второго автомобиля.
Ответ дайте в км/ч.
I.3.2 . Из одной точки круговой трассы, длина
которой равна 6 км, одновременно в одном
направлении стартовали два автомобиля. Скорость
первого автомобиля равна 114 км/ч, и через 9 мин
после старта он опережал второй автомобиль на
один круг. Найдите скорость второго автомобиля.
Ответ дайте в км/ч.
I.3.3. Из одной точки круговой трассы, длина
которой равна 20 км, одновременно в одном
направлении стартовали два автомобиля. Скорость
первого автомобиля равна 105 км/ч, и через 48 мин
после старта он опережал второй автомобиль на
один круг. Найдите скорость второго автомобиля.
Ответ дайте в км/ч.
I.3.4. Из одной точки круговой трассы, длина
которой равна 9 км, одновременно в одном
направлении стартовали два автомобиля. Скорость
первого автомобиля равна 93 км/ч, и через 15 мин
после старта он опережал второй автомобиль на
один круг. Найдите скорость второго автомобиля.
Ответ дайте в км/ч.
Задача 4.
Часы со стрелками показывают 8 ч 00 мин. Через
сколько минут минутная стрелка в четвертый раз
поравняется с часовой?
Решение. Предполагаем, что экспериментально
не решаем задачу.
За один час минутная стрелка проходит один
круг, а часовая часть круга. Пусть их скорости равны 1
(круг в час) и Старт – в 8.00. Найдем время, за которое
минутная стрелка в первый раз догонит часовую.
Минутная стрелка пройдет на больше, поэтому получим
уравнение
1 –
.
Значит, в первый раз стрелки поравняются через
Пусть во второй раз стрелки поравняются через
время z. Минутная стрелка пройдет расстояние 1·z, а
часовая причем минутная стрелка пройдет на
один круг больше. Запишем уравнение:
1· z –
= 1.
Решив его, получим, что .
Итак, через стрелки поравняются во второй раз, еще
через – в третий, и ещё через
– в четвертый раз.
Следовательно, если старт был в 8.00., то в
четвертый раз стрелки поравняются через
4ч = 60 * 4 мин = 240 мин.
Ответ: 240 минут.
Задачи (самостоятельно).
I.4.1.Часы со стрелками показывают 4 ч 45 мин. Через
сколько минут минутная стрелка в седьмой раз
поравняется с часовой?
I.4.2.Часы со стрелками показывают 2 ч ровно. Через
сколько минут минутная стрелка в десятый раз
поравняется с часовой?
I.4.3. Часы со стрелками показывают 8 ч 20 мин. Через
сколько минут минутная стрелка в четвертый раз
поравняется с часовой? четвертый
II. Задачи на нахождение длины движущегося
объекта.
Задача 1.
Поезд, двигаясь равномерно со скоростью 80км/ч,
проезжает мимо придорожного столба за 36 с.
Найдите длину состава поезда в метрах.
Решение. Так как скорость поезда указана в
часах, то переведем секунды в часы.
1) 36 сек =
2) найдем длину состава поезда в километрах.
80·
Ответ: 800м.
Задачи (самостоятельно).
II. 2.Поезд, двигаясь равномерно со скоростью
60км/ч, проезжает мимо придорожного столба за 69 с.
Найдите длину поезда в метрах. Ответ: 1150м.
II. 3. Поезд, двигаясь равномерно со скоростью
60км/ч, проезжает мимо лесополосы, длина которой 200
м, за 1мин 21 с. Найдите длину поезда в метрах.
Ответ: 1150м.
III. Задачи на среднюю скорость.
На экзамене по математике может встретиться
задача о нахождении средней скорости. Надо
запомнить, что средняя скорость не равна
среднему арифметическому скоростей. Средняя
скорость находится по специальной формуле:
=
.
Если участков пути было два, то.
Задача 1.
Расстояние между двумя селами 18 км.
Велосипедист ехал из одного села в другое 2ч, а
возвращался по той же дороге 3ч. Какова средняя
скорость движения велосипедиста на всем участке
пути?
Решение:
2 ч+3 ч = 5 ч – затратил на всё движение,
.
Ответ: .
Задача 2.
Турист шел со скоростью 4км/ч, потом точно такое
же время со скоростью 5 км/ч. Какова средняя
скорость движения туриста на всем участке пути?
Решение:
Пусть турист шел t ч со скоростью 4 км/ч и t ч со
скоростью 5 км/ч. Тогда за 2t ч он прошел 4t + 5t = 9t (км).
Средняя скорость движения туриста равна = 4,5 (км/ч).
Ответ: 4,5 км/ч.
Замечаем, средняя скорость движения туриста
оказалась равной среднему арифметическому двух
данных скоростей. Можно убедиться в том, что если
время движения на двух участках пути одинаково,
то средняя скорость движения равна среднему
арифметическому двух данных скоростей. Для этого
решим эту же задачу в общем виде.
Задача 3.
Турист шел со скоростью км/ч, потом точно такое же
время со скоростью км/ч. Какова средняя скорость
движения туриста на всем участке пути?
Решение:
Пусть турист шел t ч со скоростью км/ч и t ч со скоростью
км/ч. Тогда за 2t ч он
прошел t +
t =
t (км). Средняя скорость
движения туриста равна
= (км/ч).
Задача 4.
Некоторое расстояние автомобиль преодолел в
гору со скоростью 42 км/ч, а с горы – со скоростью 56
км/ч.
Какова средняя скорость движения автомобиля на
всем участке пути?
Решение:
Пусть длина участка пути равна s км. Тогда в оба
конца автомобиль проехал 2 s км, затратив на весь
путь .
Средняя скорость движения равна 2 s: (км/ч).
Ответ: 48 км/ч.
Задача 5.
Некоторое расстояние автомобиль преодолел в
гору со скоростью км/ч, а с горы – со скоростью
км/ч.
Какова средняя скорость движения автомобиля на
всем участке пути?
Решение:
Пусть длина участка пути равна s км. Тогда в оба
конца автомобиль проехал 2 s км, затратив на весь
путь .
Средняя скорость движения равна 2 s: (км/ч).
Ответ:км/ч.
Рассмотрим задачу, в которой средняя скорость
задана, а одну из скоростей нужно определить.
Потребуется применение уравнения.
Задача 6.
В гору велосипедист ехал со скоростью 10 км/ч, а с
горы – с некоторой другой постоянной скоростью.
Как он подсчитал, средняя скорость движения
оказалась равной 12 км/ч.
С какой скоростью велосипедист ехал с горы?
Решение:
Пусть в гору и с горы велосипедист проехал по s
км, всего 2s км. Так как средняя скорость равна 12
км/ч, то на путь туда и обратно затрачено Пусть
скорость движения с горы равна, тогда на путь туда и
обратно затрачено Составим уравнение:
.
Разделим обе части уравнения на s (s 0), , получим равносильное уравнение:
Велосипедист ехал с горы со скоростью 15 км/ч.
Ответ: 15 км/ч.
Задачи (самостоятельно).
III. 1. Расстояние между двумя пунктами 45 км.
Мотоциклист проехал это расстояние в одном
направлении (в гору) со скоростью 40 км/ч, а в
другом направлении (с горы) со скоростью 60 км/ч.
Какова средняя скорость движения мотоциклиста
на всем участке пути?.
III. 2. Половину времени, затраченного на
дорогу, автомобиль ехал со скоростью 60 км/ч, а
вторую половину времени – со скоростью 46 км/ч.
Найдите среднюю скорость автомобиля на
протяжении всего пути..
III. 3.На пути из одного поселка в другой
автомобиль некоторое время шел со скоростью 60
км/ч, потом точно такое же время со скоростью
40км/ч, потом точно такое же время со скоростью,
равной средней скорости движения на двух первых
участках пути. Какова средняя скорость движения
на всем пути из одного поселка в другой?
III. 4. Велосипедист едет от дома до места
работы со средней скоростью 10 км/ч, а обратно – со
средней скоростью 15 км/ч, поскольку дорога идет
немного под уклон. Найдите среднюю скорость
движения велосипедиста на всем пути от дома до
места работы и обратно..
III. 5. Автомобиль ехал из пункта А в пункт В
порожняком с постоянной скоростью, а возвращался
по той же дороге с грузом со скоростью 60 км/ч. С
какой скоростью он ехал порожняком, если средняя
скорость движения оказалась равной 70 км/ч?.
III. 6. Первые 100 км автомобиль ехал со
скоростью 50 км/ч, следующие 120 км – со скоростью 90
км/ч, а затем 120 км – со скоростью 100 км/ч. Найдите
среднюю скорость автомобиля на протяжении всего
пути..
III. 7. Первые 100 км автомобиль ехал со
скоростью 50 км/ч, следующие 140 км – со скоростью 80
км/ч, а затем 150 км – со скоростью 120 км/ч. Найдите
среднюю скорость автомобиля на протяжении всего
пути..
III. 8. Первые 150 км автомобиль ехал со
скоростью 50 км/ч, следующие 130 км – со скоростью 60
км/ч, а затем 120 км – со скоростью 80 км/ч. Найдите
среднюю скорость автомобиля на протяжении всего
пути..
III. 9. Первые 140 км автомобиль ехал со
скоростью 70 км/ч, следующие 120 км – со скоростью 80
км/ч, а затем 180 км – со скоростью 120 км/ч. Найдите
среднюю скорость автомобиля на протяжении всего
пути..