Наклон графика – это не что иное, как уклон или крутизна линии. Эта статья дает полное представление о том, как найти наклон графика.
Когда график построен, он определяет отношения между любыми двумя физическими величинами, а наклон определяет некоторую другую третью физическую величину. Чтобы получить подробные сведения о том, как найти наклон графика, давайте прочитаем дальше.
График используется для визуального представления физических концепций для облегчения и лучшего понимания. Например, график движения используется для описания движения движущегося объекта, такого как положение, скорость, расстояние и ускорение. График помогает нам лучше понять взаимосвязь между двумя физическими концепциями. Например, график положения и времени позволяет нам узнать, как положение тела меняется со временем.
Компания декартов граф делится на четыре квадранта положительной и отрицательной осью x и положительной и отрицательной осью y. В первом квадранте x и y оба имеют положительные значения, тогда как в третьем квадранте оба становятся отрицательными. Теперь во втором и четвертом один положительный, а другой отрицательный.
После построения графика полученная линия или кривая называется наклоном. Наклон определяет значение некоторой конкретной физической величины. Например, наклон графика скорости и времени дает значение ускорения объекта.
Наклон графика рассчитывается по формуле:
Подставляя значения, формула становится:
Наклон = (y2-y1)/(Икс2-x1)
Как найти наклон четырех точек на графике
Оцениваем наклон заданных точек по формуле. Четыре точки можно расположить по-разному. Возьмем общий случай, показанный на рисунке выше. Здесь A (3, 5), B (-4, 4), C (-2, -1) и D (5, 1) – это четыре точки графика и, следовательно, четыре угла наклона. Значения наклона могут быть одинаковыми или разными. Итак, здесь мы индивидуально найдем наклон всех этих четырех наклонов, используя формулу:
Наклон = (y2-y1)/(Икс2-x1)
Наклон AB, подставляем значение A (3,5) и B (-4, 4)
Наклон AB=(4-5)/(-4-3)
Уклон АВ=1/7
Точно так же наклон BC становится:
Наклон ВС=(-1-4)/(-2+4)
Уклон ВС=-(5/2)
Наклон CD будет;
Наклон CD = (1+1)/(5+2)
Уклон CD=2/7
Наклон DA рассчитывается как;
Наклон DA=(1-5)/(5-3)
Наклон DA=-2
Как найти наклон графика с одной точкой
Если нам дан только один набор точек, мы не сможем найти наклон графика. Для наклона нужны две точки графика.
Эти два момента важны для описания линии; точно так же, как на рисунке (i), мы получаем определенную линию, построив график. По этим точкам можно оценить уклон. Но один набор точек может быть решением многих линий, и поэтому они могут иметь разные наклоны, как на рисунке (ii). И именно поэтому невозможно найти наклон графика по одной точке.
Мы можем найти наклон по одной точке, если нам также предоставят линию графика. Например, нам предоставлен приведенный выше график и точка A (2,4). Теперь в этом случае мы можем случайным образом взять другую точку B (4,6) на прямой и отследить ее координаты. Наконец, мы подставляем точки A и B в формулу наклона;
Наклон = (y2-y1)/(Икс2-x1)
Наклон = (6-4)/(4-2)
наклон=1
Таким образом, наклон графика равен 1.
Как найти наклон графика без точек
Если нам не дается ни одной точки, мы не можем найти наклон линии. Для расчета наклона должна быть какая-то информация. Таким образом, если точка не указана, то для того, чтобы найти наклон графика, нам необходимо предоставить уравнение прямой.
Прямая линия представлена уравнением в виде
у=мх+с
Здесь y – ордината, а x – абсцисса координаты. m дает значение наклона линии, а c – точка, в которой линия пересекает ось y.
Так что в случае, если нам предоставлено уравнение линии, мы можем найти по нему наклон. Например, уравнение задается как y = 4x + 2. Сравнивая его с вышеупомянутым общим уравнением, мы получаем:
м = 4.
Следовательно, наклон линии равен 4.
Как найти наклон прямой с двумя точками
Если нам не дано ничего, связанного с графиком, кроме двух точек, то мы также можем найти наклон линии. Он рассчитывается по общей формуле наклона. Предположим, нам предоставлены две точки, A (1,3) и B (2,6), и мы должны найти наклон от этих точек. Подставим значения этих точек в формулу наклона;
Наклон = (y2-y1)/(Икс2-x1)
Наклон = (6-3)/(2-1)
наклон=3
Следовательно, наклон линии становится равным 3.
Итак, в этой статье мы рассмотрели все, как найти уклон от одной точки, двух или четырех точек, и даже без какой-либо точки.
Часто задаваемые вопросы (FAQ)
Какую информацию предоставляет склон?
Наклон линии описывает наклон графика.
Глядя только на наклон, мы узнаем, изменяются ли эти две величины прямо или наоборот. Он определяет соотношение между двумя соответствующими физическими переменными. Вычисляя его, мы узнаем ценность некоторой третьей величины.
Как найти наклон графика?
Наклон линии оценивается, когда известны как минимум две точки графика.
Формула, которую мы используем для определения наклона прямой:
Здесь дельта x – это изменение по оси x, а дельта y – это изменение по оси y.
Поэтому формулу можно также сформулировать как:
Наклон = (y2-y1)/(Икс2-x1)
Можно ли найти уклон с помощью одной точки?
Если нам дана только одна точка и больше ничего, мы не сможем найти наклон линии.
С одной точки можно пройти множество линий, и поэтому могут быть разные уклоны. Следовательно, найти конкретный уклон от одной точки становится невозможным. Чтобы найти уклон, необходимо предоставить некоторую необходимую информацию.
Если набор точек не указан, какая еще информация должна быть доступна для определения наклона?
Без точки мы не можем найти наклон линии. Должна быть доступна какая-то другая информация.
Если точка не указана, то, по крайней мере, необходимо знать уравнение прямой, чтобы найти наклон прямой. Общее уравнение прямой: у = мх + с, где m – наклон линии.
Расчет и построение графика заложений
Крутизну ската
(угол наклона ската
)
и уклон линии i
между точками, лежащими на соседних
горизонталях, определяют по формулам:
отсюда
. (15)
Чтобы избежать
расчетов, при решении указанных задач
по карте используют графики заложений,
которые рассчитывают и строят
соответственно высоте сечения рельефа
и масштабу данного плана (карты).
Построение графика заложения выполняют
в следующем порядке:
1. Горизонтальную
линию делят на равные отрезки произвольной
длины; у концов отрезков подписывают
значения углов наклона, начиная с 0°30′.
2. Вычисляют
заложения, соответствующие каждому
значению угла наклона при принятой
высоте сечения рельефа, по формуле
,
м. (16)
Длину каждого
отрезка выражают в масштабе плана
(карты) как
,
см,
где М
– знаменатель численного масштаба
плана.
Результаты
вычислений заносят в табл. 13.
Таблица 13
Расчет элементов
графика заложений
|
|
d, |
|
|
|
0°30′ |
114,60 |
286,5 |
2,86 |
|
1° |
57,29 |
143,2 |
1,43 |
|
2° |
… |
… |
… |
|
3° |
… |
… |
… |
|
4° |
… |
… |
… |
|
5° |
… |
… |
… |
|
… |
… |
… |
… |
3. Полученные
величины заложений
откладывают на перпендикулярах линии
против соответствующих углов наклона.
Через полученные точки проводят плавную
кривую и получают график крутизны (рис.
6).
Если у точек деления
горизонтальной линии вместо углов
наклона подписаны значения уклонов и
на перпендикулярах отложены соответствующие
заложения, то имеем график уклонов.
График заложений вычерчивают на листке
миллиметровой бумаги и вклеивают в
рабочую тетрадь.
Определение уклона и крутизны ската
Заданием предусмотрено
определение уклона и крутизны ската по
линии 1–5 по карте масштаба
1:10 000 с h
= 2,5 м
расчетным и графическим способами.
Для этого на карте
измеряют величину заложения и по
масштабной линейке определяют
соответствующие ему горизонтальное
проложение линии местности d.
Уклон ската рассчитывают по формуле
Рассчитанный уклон
линии выражают в тысячных долях единицы
(промилле) и процентах.
Пример.
По линии 1-5 (см. рис. 5) h
= 2,5 м, d
= 62,0 м.
.
Крутизну ската
определяют по таблицам тригонометрических
функций либо при помощи калькулятора
исходя из выражения
.
Для рассматриваемого
примера
.
При малых (до 5°)
углах наклона скатов крутизну можно
рассчитать по формуле
,
где
– радиан.
Для графического
определения крутизны ската с плана
берут в раствор циркуля заложение 1-5 и
переносят его на график заложений (рис.
7) так, чтобы отрезок 1-5 оказался
параллельным линиям графика, а одна
ножка циркуля располагалась на
горизонтальной линии, другая – на кривой
графика. Значение крутизны определяют
по оцифровке горизонтальной шкалы
графика.
Полученные
различными способами
значения крутизны
ската по линии 1-5 сравнивают между собой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
Нахождение угла наклона прямой – это один из важнейших навыков в геометрии, необходимый для построения графика линейной функции или для определения координат точек пересечения прямой с осями X и Y. Угол наклона прямой определяет скорость ее роста или убывания,[1]
то есть как быстро прямая перемещается по вертикали в зависимости от движения по горизонтали. Угол наклона прямой легко вычисляется по координатам двух точек, лежащих на этой прямой.
-
1
Уясните формулу для вычисления углового коэффициента. Угловой коэффициент равен тангенсу угла наклона прямой, который она образует с осью Х, и вычисляется как отношение вертикального расстояния между двумя точками к горизонтальному расстоянию между двумя точками.
-
2
Выберите две точки и найдите их координаты. Можно выбрать любые две точки, лежащие на прямой.
-
3
Задайте порядок точек (относительно друг друга). Одна точка будет первой точкой, а другая – второй. Не имеет значения, какая точка будет первой, а какая второй – главное не перепутать их порядок в процессе вычисления.[2]
-
4
Запишите формулу для вычисления углового коэффициента. Формула:
, где VR – вертикальное расстояние, определяемое изменением координаты «у», GR – горизонтальное расстояние, определяемое изменением координаты «х».[3]
Реклама
-
1
В формулу для вычисления углового коэффициента подставьте координаты «у». Не перепутайте их с координатами «х» и убедитесь, что подставляете правильные координаты первой и второй точек.
-
2
В формулу для вычисления углового коэффициента подставьте координаты «х». Не перепутайте их с координатами «у» и убедитесь, что подставляете правильные координаты первой и второй точек.
-
3
Вычтите координаты «у». Вы найдете вертикальное расстояние.
-
4
Вычтите координаты «х». Вы найдете горизонтальное расстояние.
-
5
Если возможно, сократите дробь. Вы найдете угловой коэффициент.
-
6
Обращайте внимание на отрицательные числа. Угловой коэффициент может быть положительным или отрицательным. В случае положительного значения прямая возрастает (движется вверх слева направо); в случае отрицательного значения прямая убывает (движется вниз слева направо).
- Помните, что если и в числителе, и в знаменателе стоят отрицательные числа, то результат будет положительным.
- Если в числителе или в знаменателе стоит отрицательное число, то результат будет отрицательным.
-
7
Проверьте ответ. Для этого измерьте или посчитайте (по шкалам осей) вертикальное и горизонтальное расстояния. Если они совпали с вычисленными, то ответ правильный.
- Если измеренные или посчитанные вертикальное и горизонтальное расстояния не совпали с вычисленными, то ответ не правильный.
Реклама
Советы
Похожие статьи
Об этой статье
Эту страницу просматривали 90 284 раза.
Была ли эта статья полезной?
Пользователям электронных таблиц часто требуется вычислить наклон линии, относящейся к данным в их электронной таблице. Если вы новый пользователь или привыкли использовать Microsoft Excel, может быть немного сложно понять, как это сделать самостоятельно. К счастью, поиск наклона в Google Sheets — это простой процесс, который занимает всего минуту или около того, если вы знаете, что делаете.
В этой статье вы научитесь рассчитывать значения уклона в Google Sheets с графиками и без них.
Что такое наклон?
Прежде всего, что такое наклон в Google Таблицах?
Наклон — это понятие в геометрии, которое описывает направление и крутизну линии на декартовой плоскости. (Декартова плоскость — это стандартная координатная сетка, которую вы, возможно, помните из уроков математики, с осью X и осью Y.)
Линия, идущая вверх слева направо на плоскости, имеет положительный наклон; линия, идущая вниз слева направо, имеет отрицательный наклон.
На диаграмме ниже синяя линия имеет положительный наклон, а красная линия имеет отрицательный наклон:
Наклон выражается в виде числа, и это число указывает, насколько линия поднимается или опускается на заданном расстоянии (известном как подъем над пробегом).
Вот пример:
Если линия идет от X=1, Y=0 до X=2, Y=1 (то есть линия поднимается на +1 по оси Y, а также поднимается на +1 по оси X), наклон равен 1. Если бы он увеличился с X = 1, Y = 0 до X = 2, Y = 2, наклон был бы равен 2 и так далее.
Большие числа означают более крутой наклон; наклон +10 означает линию, которая идет вверх на 10 по оси Y для каждой единицы, которую она перемещает по оси X, а наклон -10 означает линию, которая идет вниз на 10 по оси Y для каждой единицы на ось X.
В электронной таблице значения наклона обычно связаны с линейной регрессией, которая представляет собой способ анализа взаимосвязи между двумя или более переменными.
Переменные состоят из зависимых значений Y и независимых значений X, которые в электронных таблицах будут храниться как два отдельных столбца таблицы.
Зависимое значение — это значение, которое изменяется автоматически на количество, а независимое значение — это значение, которое может изменяться свободно. Типичным примером может быть один столбец (зависимая переменная X), который содержит ряд дат, а другой столбец (независимая переменная Y), содержащий числовые данные, например данные о продажах за этот месяц.
Где линии? Где график? Наклон зависит от того, как движется линия, верно?
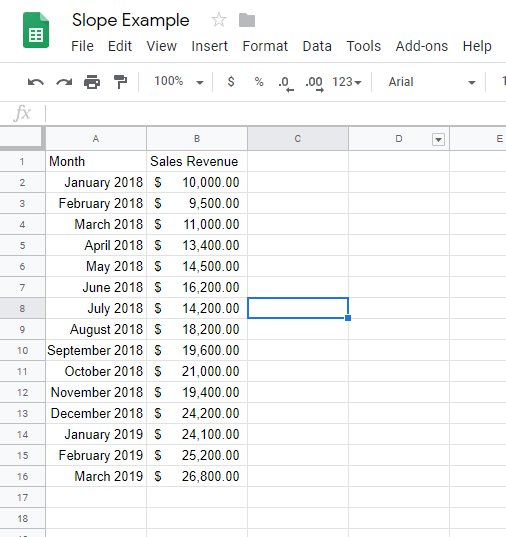
Думайте о данных электронной таблицы как о точках графика. Данные, представленные в этой таблице, можно легко визуализировать с помощью линейного графика.
Google Sheets предоставляет простой, но мощный набор инструментов для создания линейных графиков из табличных данных. В этом примере все, что вам нужно сделать, это выбрать всю таблицу данных (от A1 до B16) и нажать кнопку «Вставить диаграмму». После этого Sheets мгновенно создаст следующую диаграмму:
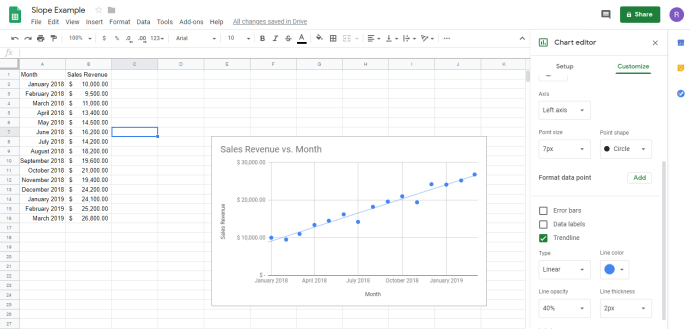
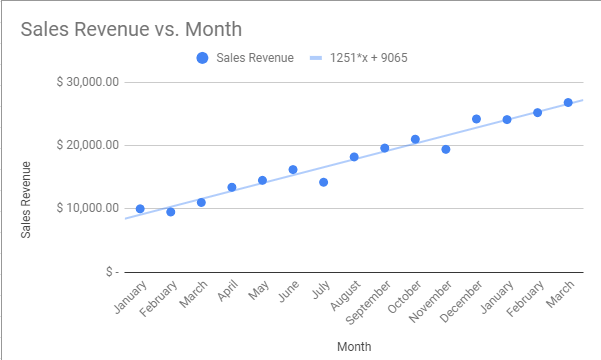
В одних местах падает, а в других поднимается! Как вы должны вычислить наклон такой сумасшедшей линии? Ответ — это то, что называется линией тренда. Линия тренда — это сглаженная версия вашей линии, которая показывает общую тенденцию чисел.
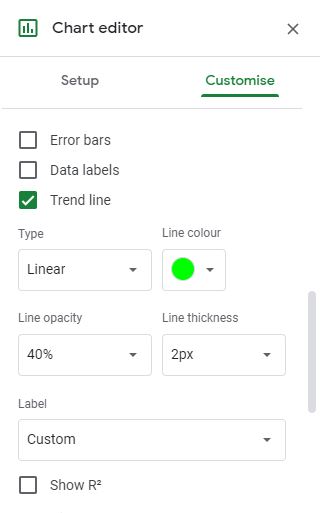
Теперь ваша диаграмма должна выглядеть так:
Голубая линия, которая следует за цепочкой точек на графике, является линией тренда.
Так как же найти наклон этой линии?
Ну, если бы это был урок математики, тебе бы пришлось заняться математикой. К счастью, на дворе 21 век, и уроки математики остались далеко позади. Вместо этого мы можем просто сказать компьютеру сделать это за нас. Спасибо, Гугл.
Как найти наклон графика в Google Таблицах
Мы можем использовать Google Sheets для расчета наклона в редакторе диаграмм. Просто следуйте этим инструкциям, чтобы найти наклон любого линейного графика в Google Таблицах.
3. Интересно, что на самом деле вам не обязательно иметь диаграмму, чтобы вычислить наклон. В Google Таблицах есть функция НАКЛОН, которая вычисляет наклон любой таблицы данных, не утруждая себя сначала отрисовкой ее в виде изображения. Однако рисование картинок очень помогает научиться делать все это, поэтому мы и сделали это именно так.
4. Вместо того, чтобы создавать диаграмму, вы можете просто добавить функцию НАКЛОН в ячейку электронной таблицы. Синтаксис функции НАКЛОН в Google Таблицах: НАКЛОН (данные_y, данные_x). Эта функция вернет то же значение наклона, что и в уравнении графика.
Обратите внимание, что порядок ввода немного отличается от того, как вы, вероятно, отображаете информацию в своей таблице. Это связано с тем, что Таблицы хотят, чтобы независимые данные (доход от продаж) помещались на первое место, а зависимая переменная (месяц) — на второе.
Вы также должны отметить, что функция НАКЛОН не так умна, как создатель диаграммы. Для зависимой переменной нужны чисто числовые данные, поэтому мы изменили эти ячейки на номера от 1 до 15.
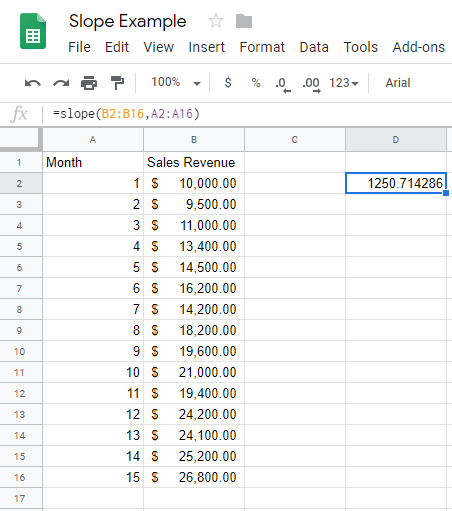
Выберите любую пустую ячейку в электронной таблице, введите «= НАКЛОН (b2: b16, a2: a16)» и нажмите «Return».
А вот и наш наклон с чуть большей точностью, чем на графике.
Последние мысли
Вот как вы можете найти уклон в Google Таблицах. Надеюсь, если у вас возникли проблемы с самостоятельным пониманием этого, эти инструкции смогли вам помочь.
Если вы предпочитаете использовать Excel вместо Таблиц, есть также руководство TechJunkie по поиску значений уклона в Excel.
У вас есть интересные приложения для поиска уклона в Google Sheets? Поделитесь ими с нами ниже!
Видеоурок: График линейной функции
Лекция: Линейная функция, её график
Мы уже умеем характеризовать функции, а также касались некоторых основных из них. Сейчас бы хотелось поговорить о каждой из них более детально. И начнем мы с линейной функции и её графика.
Любая функция, которая имеет вид: y = kx + b, называется линейной.
Коэффициент, находящийся перед переменной, называется коэффициентом угла наклона и определяет крутизну графика функции относительно оси ОХ. Свободный коэффициент показывает смещение графика относительно начала координат по оси ОУ.
Если Вам необходимо построить график данной функции, то Вы должны знать, что это будет прямая.
Как строить график?
Для построения данного графика необходимо выбрать две точки данного графика. Почему нам не достаточно одной точки, но достаточно двух? Потому что из геометрии мы знаем, что через любые две точки можно провести только одну прямую.
А теперь давайте разберемся, как это сделать. Допустим, возьмем функцию вида:
у = х/3 +2.
Итак, для начала нам необходимо взять произвольные два значения “х”, подставить их в уравнение и найти значение “у”. Далее по двум полученным точкам строим прямую.
Возьмем в качестве координаты “х” для первой точки значение 3. Тогда у = 3. В качестве второй точки возьмем х = 0, тогда у = 2.
Получим:
Теперь давайте разберемся, на что влияет коэффициент при переменной. Как уже говорилось ранее, по нему определяется наклон графика относительно ОХ. Если коэффициент больше нуля k > 0, то угол между осью ОХ и графиком прямой получается острый.
Если же коэффициент меньше нуля k < 0, то угол между осью ОХ и построенной прямой будет тупым.
Если коэффициент при переменной равен нулю, то график приобретает вид прямой, параллельной оси ОХ. Если свободный коэффициент больше нуля b > 0, то прямая будет находиться выше оси ОХ, если коэффициент меньше нуля, то прямая ниже оси ОХ.
Свободный коэффициент отвечает за параллельный перенос графика. График заданной функции пересекает ось ОУ в точке (0;b).
То есть, если значение свободного коэффициента больше нуля b > 0, то график смещается относительно начала координат вверх по оси ОУ, а если свободный коэффициент меньше нуля b < 0, то смещение происходит по оси ОУ вниз от начала координат.