Как найти ктг через тг

На этой странице сайта вы найдете ответы на вопрос Как найти син кос и ктг, зная только тг?,
относящийся к категории Алгебра. Сложность вопроса соответствует базовым
знаниям учеников 10 – 11 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.

Основные формулы тригонометрии – это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных тригонометрических формул можно находить и решать практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь все тригонометрические формулы, а не их вывод, которому будут посвящены отдельные статьи.

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую (посредством преобразования).

sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg) и их свойств.

Основные формулы приведения в тригонометрии

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов, то есть, преобразовывать их.

sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα

Формулы приведения являются следствием периодичности тригонометрических функций.

Все формулы сложения в тригонометрии

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ

На основе формул сложения выводятся тригонометрические формулы кратного угла. 

Формулы кратного угла: двойного, тройного и т.д.

sin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы понижения степени

sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8

Часто при расчетах действовать с громоздкими степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно для применения при решении тригонометрических уравнений и упрощении выражений.

sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению или умножению, то формулы произведения (здесь нужно умножать) тригонометрических функций осуществляют обратный переход – от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.

sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции – тангенс, котангенс, синус, косинус – могут быть выражены через тангенс половинного угла. 

sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2

Значения тангенса и котангенса на тригонометрическом круге

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.

Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.

Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.

Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).

Синус (sin) угла поворота

Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y

Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х

Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x

Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Синус и косинус определены для любых углов α .

Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )

Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )

При решении практических примеров не говорят “синус угла поворота α “. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности – точка A c координатами ( 1 , 0 ).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y

Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x

Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс – основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Как найти тангенс и котангенс без тригонометрической таблицы?

В статье мы рассмотрим, как найти значения:

Есть два способа вычислять тангенсы и котангенсы. Первый – через синусы и косинусы , второй – через оси тангенсов и котангенсов. Первый способ проще в освоении, второй – быстрее в применении.

Но в любом случае вам нужно уметь уверенно расставлять числа с пи на тригонометрическом круге и откладывать углы.

Способ 1 – вычисление тангенсов и котангенсов через синусы и косинусы

Конечно, этот способ подразумевает, что вы уже умеете вычислять синус и косинус. Не умеете? Тогда бегом читать эту статью , и эту тоже.

Уже умеете? Тогда ловите два определения:

– тангенс равен отношению синуса к косинусу числа.

– котангенс равен отношению косинуса к синусу числа.

Ищем сначала (frac<π><3>), а после вычисляем (sin,⁡frac<π><3>) и (cos⁡,frac<π><3>).

(0) на тригонометрическом круге совпадает с (1) на оси косинусов, значит (cos⁡,0=1).
Если из точки (0) на тригонометрическом круге провести перпендикуляр (красная пунктирная линия) к оси синусов, то мы попадем в (0), получается (sin,⁡0=0). Следовательно: (tg, 0=) (frac) (=frac<0><1>=0).

С котангенсом интереснее: (ctg, 0=) (frac) (=frac<1><0>=. ). На ноль делить нельзя – это железное правило математики. Поэтому и посчитать такой котангенс не получится. (ctg,⁡0) – не вычислим в принципе.

Способ 2 – вычисление тангенсов и котангенсов с использованием осей

Прямая, проходящая через начало отсчета тригонометрического круга и параллельная оси синусов (ось (y)), называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.

Прямая проходящая через (frac<π><2>) ((90^°)) тригонометрического круга и параллельная оси косинусов (ось (x)) называется осью котангенсов. Направление оси котангенсов и оси косинусов совпадает.

Ось тангенсов – сдвинутая копия оси синусов, ось котангенсов – копия оси косинусов. Единицы на осях котангенсов и тангенсов совпадают.

Чтобы определить тангенс и котангенс с помощью тригонометрического круга, нужно:
1) Начертить тригонометрический круг и оси тангенсов и котангенсов;
2) Отметить аргумент тангенса или котангенса на тригонометрическом круге;
3) Соединить прямой эту точку, соответствующую аргументу и начало координат;
4) Продлить прямую до осей и найти координаты пересечения, как показано на картинке ниже:

О том, как просто запомнить где какое значение стоит на осях, можно прочитать в статье « Как запомнить тригонометрический круг ».

1) Строим круг, оси и отмечаем аргумент на окружности;

2) Соединяем точку, соответствующую аргументу, и начало координат;

3) Продляем до осей;

И на оси тангенсов, и на оси котангенсов мы пришли в единицу, поэтому (tg, frac<π><4>=1) и (ctg, frac<π><4>=1).

Понятно, что во время ЕГЭ такой красивой картинки не будет, но она и не нужна. Если вы будете знать, как правильно расставлять значения на тригонометрическом круге и будете помнить расположение чисел на осях, то вам будет достаточно нарисованного от руки круга.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/trigonometrija/sinus-kosinus-tangens-i-kotangens/

http://cos-cos.ru/ege/zadacha209/358/

[/spoiler]

Содержание:

1. Что такое КТГ?
2. Что показывает КТГ при беременности?
3. О каких патологиях можно судить по результатам КТГ плода при беременности?
4. Как подготовиться к процедуре?
5. Как проводится КТГ плода при беременности?
6. Этапы выполнения КТГ плода при беременности
7. Когда делают КТГ при беременности?

Во время беременности тщательному наблюдению и обследованию подлежит не только будущая мама, но и активно развивающийся в ее утробе малыш. Существует целый комплекс исследований, благодаря которым врачи отслеживают, насколько благополучно протекает рост и развитие плода. Одним из основных методов оценки состояния является КТГ.

Что такое КТГ?

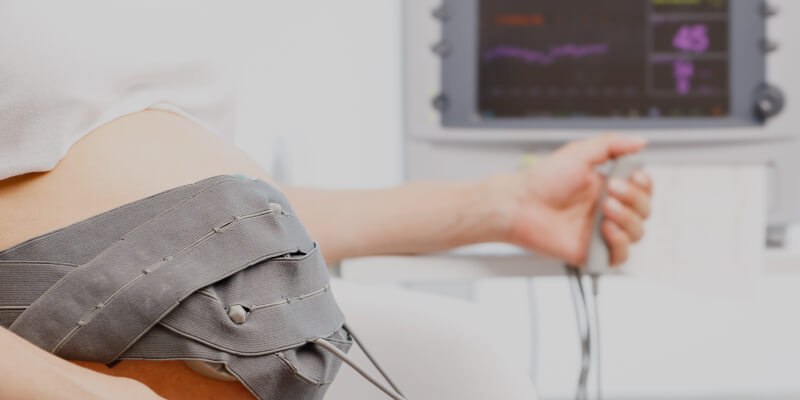
Кардиотокография (КТГ) — это способ функциональной оценки состояния плода во время беременности и родов.

Он получил широкое распространение благодаря:

• простоте проведения;

• безопасности для мамы и малыша;

• безболезненности;

• стабильности получаемых данных;

• высокой информативности.

Что показывает КТГ при беременности?

Процедура проводится с помощью кардиотокографа. Он регистрирует сердцебиение ребенка и реагирует на изменения частоты сердечных сокращений в ответ на активность матки, действие внешних раздражителей и шевеления малыша.

Сердечную деятельность плода фиксируют с помощью ультразвука. Его принцип работы базируется на эффекте Допплера. От специального датчика исходит ультразвуковая волна, которая движется к пульсирующему сердцу малыша, после чего волна отражается, изменяет частоту и направляется обратно. Полученный сигнал улавливается и регистрируется в виде графика на мониторе. Данная запись называется кардиотокограммой.

Расшифровка полученного результата КТГ плода при беременности осуществляется как автоматически, так и вручную. Интерпретируя полученные данные, можно заметить начальные признаки кислородной недостаточности малыша.

Посмотрите эти статьи, чтобы получить важную информацию об анализах и медицинских осмотрах при беременности:

• Какие анализы нужно сдать при подготовке к беременности?

• Что показывает уровень ХГЧ?

• Как измеряют ВДМ и ОЖ и зачем это нужно?

О каких патологиях можно судить по результатам КТГ плода при беременности?

Основным критерием внутриутробного состояния плода является базальная ЧСС. С этого параметра начинается оценка КТГ.

При доношенной беременности и нормальном самочувствии малыша ЧСС равна 110–160 уд./мин.

Если ЧСС в течение 10 минут превышает 160 уд./мин., это называется тахикардией. В случае урежения ЧСС менее 110 уд./мин. говорят о брадикардии.

После подсчета частоты сердечных сокращений можно заподозрить следующие патологические состояния:

• гипоксия плода;

• анемия плода;

• сердечные пороки развития плода;

• лихорадочное состояние беременной;

• гипертиреоз беременной;

• амнионит;

• длительное сдавление пуповины;

• сниженное АД у матери;

• сниженное АД у матери;

Как подготовиться к процедуре?

Особой подготовки это обследование не требует. Однако, учитывая, сколько по времени проводится КТГ при беременности, и специфику процедуры, следует придерживаться нескольких рекомендаций.

1. Перед обследованием нужно сходить в туалет.

2. За 1,5–2 часа показан легкий прием пищи.

3. Избегать курения за 2–3 часа до начала.

4. Выспаться накануне.

5. Расслабиться и не нервничать.

6. Отложить телефон, планшет и другие электронные устройства, так как они могут вызывать помехи.

7. Найти удобное положение сидя, полулежа или на боку.

8. По желанию можно отвлечься на чтение книги или журнала.

9. Если вам знаком секрет, как разбудить свое чадо в животике, воспользуйтесь им.

В случае нежелания малыша бодрствовать, длительность процедуры может несколько увеличиться. Поэтому маме стоит набраться терпения и обеспечить себе максимальное спокойствие и комфорт.

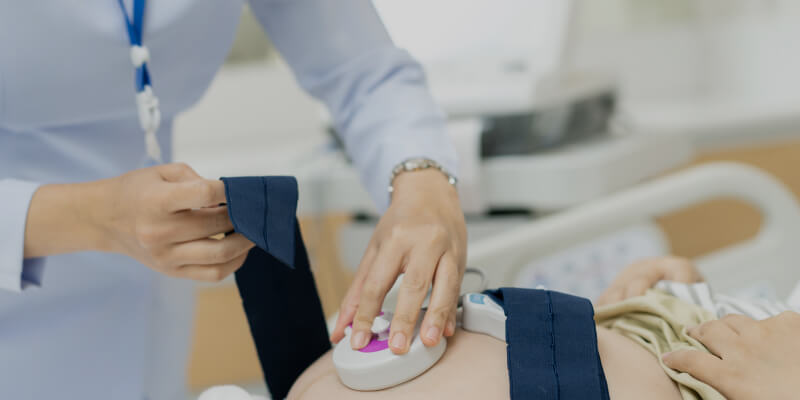
Как проводится КТГ плода при беременности?

Техника выполнения процедуры не представляет сложностей. Выполнять ее может как старший, так и средний медицинский персонал. Но интерпретировать результаты кардиотокограммы будет врач.

Этапы выполнения КТГ плода при беременности

1. Женщина принимает удобное положение на кушетке.

2. На переднюю брюшную стенку наносят гипоаллергенный гель.

3. Ультразвуковой датчик № 1 устанавливают в области наилучшей слышимости сердечных тонов плода.

4. Тензометрический датчик № 2 фиксируют в области дна матки ближе к правому углу.

5. Датчики не должны сползать, поэтому их укрепляют поясами.

6. Пациентка получает специальное устройство и, нажимая на кнопку, отмечает каждое шевеление плода.

7. Аппарат записывает маточные сокращения, сердечную деятельность и шевеления плода.

8. Постепенно распечатывается бумажная лента с графиком (по аналогии с аппаратом ЭКГ), также результат может быть виден на мониторе.

9. Если мама и малыш начинают активно двигаться, то датчики могут потерять контакт. Тогда аппарат начнет издавать громкие звуки, которые привлекут внимание акушерки. Она поправит датчики, и исследование продолжится.

Для регистрации сердечного ритма требуется не менее 20 минут.

В связи с тем, что во время проведения КТГ плода при беременности необходимо поймать как минимум два шевеления малыша длительностью не менее 15 секунд, то чаще всего на это уходит 30–40 минут. Если по окончании этого периода у врача есть сомнения относительно результата, КТГ продолжают до 60–90 минут.

Когда делают КТГ при беременности?

Согласно клиническим рекомендациям МЗ РФ «Нормальная беременность» от 2020 г., процедура проводится с 33 недель беременности.

Кратность исследования должна составлять не менее 1 раза в 2 недели.

Почему нет смысла выполнять КТГ на более ранних сроках?

Потому что только к 32-й неделе внутриутробного развития у малыша формируется цикличность периодов сна и бодрствования. Работа сердца начинает регулироваться вегетативной нервной системой, и частота сердечных сокращений отвечает на шевеления плода.

Данные рекомендации применительны к беременности, протекающей без осложнений. В особых случаях процедуру могут повторять каждые 5–7 дней. А если у плода отмечаются признаки гипоксии, то женщине показана госпитализация, и в условиях стационара контролировать сердечную деятельность будут ежедневно или даже несколько раз в день.

Полезные сервисы для будущих мам:

• Готовы ли вы к родам? Пройдите тест и узнайте

• Что нужно взять в роддом? Вот полный список

• 40 недель: подробный гайд по каждой неделе беременности

Основаниями для проведения внепланового КТГ плода при беременности могут быть:

• жалобы на низкую или высокую активность плода;

• маловодие или многоводие;

• задержка развития плода;

• переношенная беременность;

• преэклампсия;

• аномалии развития плода, выявленные при УЗИ;

• многоплодная беременность;

• чрезмерная обеспокоенность женщины, связанная с проблемами во время предыдущих беременностей и родов.

Изменения сердечной деятельности косвенно свидетельствуют о характере патологических процессов в фетоплацентарном комплексе. Поэтому полноценный диагноз врач ставит, сопоставляя результаты КТГ плода при беременности, клиническое состояние, а также данные дополнительных методов исследования — УЗИ и допплерометрии.

Надеемся, эта статья была вам полезна. Чтобы получать подобные материалы, подпишитесь на нашу рассылку. Она будет снабжать вас полезной и актуальной информацией не только во время беременности, но и в первые, самые сложные месяцы материнства.

Источники:

1. Grivell RM, Alfirevic Z, Gyte GML, Devane D. Antenatal cardiotocography for fetal assessment. Cochrane database Syst Rev. 2015 Sep 12;(9):CD007863.

2. Макаров И.О., Юдина Е.В. Кардиотокография при беременности и в родах: Учебное пособие. — Москва «МЕДпресс-информ», 2016 г.

3. Воскресенский С.Л. Оценка состояния плода. Кардиотокография. Допплерометрия. Биофизический профиль: Учебное пособие. — Мн.: Книжный Дом, 2004г. — 304с.

4. Руководство по безопасному материнству. М.: Издательство «Триада-Х», 2000 г. — 531с.

5. Воскресенский С.Л., Зеленко Е.Н. Учебно-методическое пособие «Кардиотокография в антенатальном периоде», 2010 г.

6. Клинические рекомендации МЗ РФ «Нормальная беременность», 2020 г.