Как найти длину куба, зная ширину и высоту?
Андрей Филимонов
Ученик
(113),
закрыт
14 лет назад
Я склерозник 🙁 Седня в школе это делал, а сечас забыл…
Дополнен 14 лет назад
тьфу… паралелепипеда
Лучший ответ
Екатерина
Мудрец
(12909)
14 лет назад
Высоту поделить на ширину =длина
Источник: Моя дочь (8 класс)
Остальные ответы
Арсений
Профи
(999)
14 лет назад
подели объём на ширину и высоту
Марк Екимов
Искусственный Интеллект
(159312)
14 лет назад
В кубе ширина, длина и высота РАВНЫ!
natalja ivanova
Мудрец
(11513)
14 лет назад
это что, шутка-если это куб то у него все грани равны
Лев Градский
Профи
(779)
14 лет назад
а у куба есть длинна… .
наверно я отстал…)))
wanderer Ергушов
Гуру
(3205)
14 лет назад
на то он и куб. длина, ширина, высота равны 🙂
Татьяна Гладких
Мыслитель
(8901)
14 лет назад
длина=ширине = высоте, т. к. это куб
Ромашка
Мастер
(1026)
14 лет назад
у куба все стороны равны
Конфеточк@
Ученик
(210)
14 лет назад
Наверно ты плохо учился в школе у куба все строны равны!!! а если параелепипеда то обьем : на ширину и высоту
Дмитрий
Гуру
(3432)
14 лет назад
В паралепипеде высота и ширина которого известны длинну можно только задать. Если ты меня понимаешь?
Fiesta
Мастер
(1044)
14 лет назад
Проверь свою тетрадь, там все должно быть, не зря же в школу ходишь, и тебе уже не раз это написали
Найти объём заданной фигуры в принципе не сложно, если изначально есть информация о всех трёх необходимых размерах. То есть о длинне, о ширине и о высоте. Ведь ещё со школы всем известно, что именно перемножив данные размеры, мы и получим объём фигуры. В заданном вопросе присутствуют три различные сложные объёмны фигуры. Сложными их можно назвать потому, что они состоят и некоего количества маленьких кубиков.
Учитывая то, что благодаря заданному условию по объёму каждого маленького кубика,- получается возможным узнать необходимые нам размеры, – получается, что и объём этих трёх сложных фигур найти можно. Причём сделать это можно отталкиваясь от двух принципов. Первый это традиционное умножение размеров длинны, ширины и высоты. А второй это сложение общего количества маленьких кубиков в каждой сложной фигуре.
1) Решение задачи по первому варианту:
а) Длинна фигуры 5 кубиков, ширина 2 кубика, высота 2 кубика. И ходя из известных условий мы знаем, что длинна любого рёбра маленького кубика равна 1-му сантиметру. Умножаем соответственно 5 х 2 х 2. Получаем число 20. Значит объём этой фигуры равен 20 кубическим сантиметрам.
б) В этом примере все три размера одинаковы и составляют по 10 кубиков. Умножая 10 х 10 х 10 получаем число 1000. Ну и подставляя всё тот же один сантиметр получаем 1000 кубических сантиметров или просто один кубометр.
в) В третьем случае можно предположить, что целой сложная фигура будет тогда, когда крановщик закончит работу и уложит сверху последний пласт. В получившейся фигуре длинна и ширина будут равны,- по 10 кубиков, а высота получится 6 кубиков. Умножая 10 х 10 х 6, получаем число 600. Объём этой сложной фигуры равен 600 кубических сантиметров. Ну а если не считать верхний пласт, то конечно 500, поскольку в верхнем пласте маленьких кубиков ровно 100 штук. Ну и соответственно объём верхнего пласта равен 100 кубическим сантиметрам.
Ну а при использовании второго варианта нужно просто складывать общее количество объёмов маленьких кубиков в каждой фигуре. А так как для сложения можно использовать и умножение, то основной принцип никуда не денется. Только вместо линейных размеров длинны, ширины и высоты, будем складывать объёмы. И в итоге всё получится точно так же. В первом случае 20 маленьких кубиков по одному кубическому сантиметру каждый. В итоге сложения получим те же самые 20 кубических сантиметров. Во втором и в третьем случаях всё точно так же. Только учитывая количество маленьких кубиков в каждой сложной фигуре, чтобы узнать их количество будет проще применить умножение, чем сложение!
- Какой котлован нужно вырыть для погреба или фундамента?
- Как узнать вместимость комнаты?
В расчетах поможет калькулятор объема в м3. Он пригодится в расчете объема прямоугольного параллелепипеда или куба, достаточно ввести данные в поля и узнать результат.
Справка. У прямоугольного параллелепипеда все грани являются прямоугольниками.

Формула объема, по которой ведется расчет:
V=a*b*c
Где:
- а – длина;
- b – ширина;
- c – высота.
Указано, что нужно вводить данные в метрах и результат получается в кубометрах (м3), но использовать можно любые системные единицы: мм, см или дм. Для конвертации используйте подсказки:
- 1 мм3 = 0,000000001 м3;
- 1 см3 = 0,000001 м3;
- 1 дм3 = 0,001 м3.
Калькулятор кубических метров — это простой и эффективный инструмент для расчета вместимости любой прямоугольной формы. Этот инструмент поможет вам быстро получить ответ и будет полезен как для практических работ, так и в учебе. Используйте онлайн-калькулятор объема и получайте точные данные.
Как вычислить кубатуру
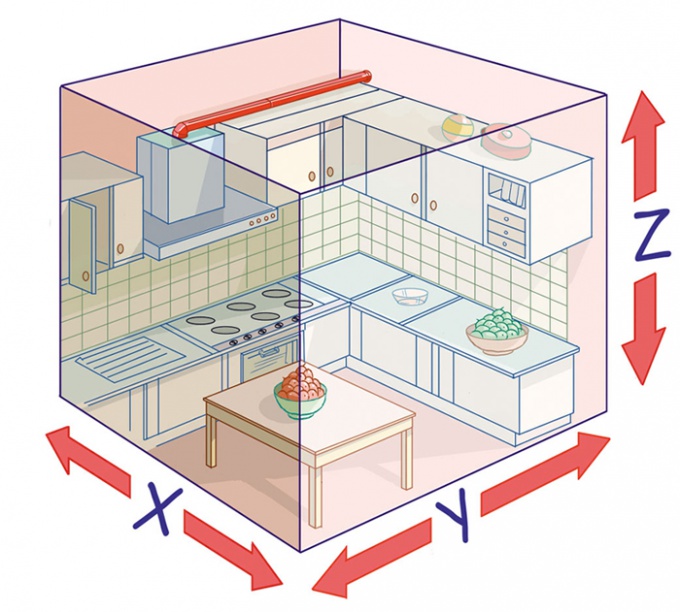
Под кубатурой помещения обычно подразумевается его объем, выраженный в кубических метрах. Если известны основные параметры помещения (длина, ширина и высота), то вычислить его кубатуру очень просто. Однако, если строение имеет сложную форму, то посчитать его объем бывает довольно-таки затруднительно.
Вам понадобится
- калькулятор
Инструкция
Чтобы вычислить кубатуру помещения перемножьте его длину, ширину и высоту. То есть воспользуйтесь формулой:
К = Д х Ш х В, где:
К – кубатура помещения (объем, выраженный в кубических метрах),
Д, Ш и В – длина, ширина и высота помещения, выраженные в метрах, соответственно.
Например, если длина помещения составляет 11 метров, ширина – 5 метров, а высота – 2 метра, то его кубатура будет 11 х 5 х 2 = 110 кубометров.
Если одна или несколько характеристик помещения неизвестны, то измерьте их, воспользовавшись строительной рулеткой или электронным дальномером. При использовании электронного дальномера следите, чтобы он был направлен строго перпендикулярно той стене, расстояние до которой измеряется. Чтобы повысить точность вычислений, высоту и ширину измерьте дважды – у противоположных стен, а затем найдите среднее арифметическое (сложите и разделите на 2).
Пусть, например, измерения длины помещения показали 10,01 м и 10,03 м, измерения ширины – 5,25 м и 5,26 м, а измерение высоты – 2,50 м. В таком случае, кубатура помещения будет равняться:
(10,01+10,03)/2 х (5,25+5,26)/2 х 2,5 = 131,638
(в большинстве случаев трех знаков после запятой вполне достаточно).
Если известка площадь помещения, то для вычисления кубатуры просто умножьте эту площадь на высоту. Т.е., используйте формулу:
К = П х В, где
П – площадь помещения, заданная в квадратных метрах (м²).
Так, например, если площадь помещения равняется 100 квадратных метров, а его высота – 3 метра, то его объем будет:
100х3=300 (метров кубических).
Если помещение имеет сложную форму, то для определения его площади воспользуйтесь соответствующими геометрическими формулами или разделите помещение на более простые участки.
Так, например, арена цирка всегда имеет форму круга радиусом 13 метров. Следовательно, ее площадь будет равна πR²=3,14 х 169 = 531 (метр квадратный).
Если же, например, помещение состоит из трех комнат площадью 30, 20 и 50 м², то общая площадь помещения будет равняться 100 м².
Источники:
- как вычислить кубические метры
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Загрузить PDF
Загрузить PDF
Кубические метры (м3) – это единица измерения объема, равная объему куба, стороны которого равны одному метру. Кубические метры являются предпочтительной единицей измерения при различных работах, например, при заливке бетона. Объем любого прямоугольного пространства длиной “L”, шириной “W” и высотой “Н” вычисляется по формуле: Объем = L × W × H.
-

1
Измерьте все необходимые расстояния в метрах. Объем многих трехмерных фигур легко вычислить по соответствующим формулам. Однако все значения, подставляемые в формулы, должны измеряться в метрах. Таким образом, перед подстановкой значений в формулу убедитесь, что все они измеряются в метрах, или что вы конвертировали другие единицы измерения в метры.
- 1 мм = 0,001 м
- 1 см = 0,01 м
- 1 км = 1000 м
-

2
Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = L × W × H (длину умножить на ширину умножить на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани.
- Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
- 4 × 3 × 2,5
- = 12 × 2,5
- = 30. Объем этой комнаты равен 30 м3.
- Куб – объемная фигура, у котрой все стороны равны. Таким образом, формулу для вычисления объема куба можно записать в виде: объем = L3 (или W3, или H3).
- Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
-

3
Для вычисления объема фигур в виде цилиндра используйте формулу: пи × R2 × H. Вычисление объема цилиндра сводится к умножению площади круглого основания на высоту (или длину) цилиндра. Найдите площадь круглого основания, умножив число пи (3,14) на квадрат радиуса круга (R) (радиус – расстояние от центра окружности до любой точки, лежащей на этой окружности). Затем полученный результат умножьте на высоту цилиндра (H), и вы найдете объем цилиндра. Все значения измеряются в метрах.
- Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
- (3,14) × 0,752 × 10
- = (3,14) × 0,5625 × 10
- = 17,66. Объем колодца равен 17,66 м3.
- Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
-

4
Для вычисления объема шара используйте формулу: 4/3 х пи × R3. То есть вам нужно знать только радиус (R) шара.
- Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
- 4/3 х пи × (5)3
- = 4/3 х (3,14) × 125
- = 4,189 × 125
- = 523,6. Объем воздушного шара равен 523,6 м3.
- Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
-

5
Для вычисления объема фигур в виде конуса используйте формулу: 1/3 х пи × R2 × H. Объем конуса равен 1/3 объема цилиндра, который имеет такую же высоту и радиус.
- Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см. Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
- 1/3 х (3,14) × 0,032 × 0,15
- = 1/3 х (3,14) × 0.0009 × 0,15
- = 1/3 × 0.0004239
- = 0,000141. Объем конуса мороженного равен 0,000141 м3.
- Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см. Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
-

6
Для вычисления объема фигур неправильной формы используйте несколько формул. Для этого попробуйте разбить фигуру на несколько фигур правильной формы. Затем найдите объем каждой такой фигуры и сложите полученные результаты.
- Например, вычислим объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиус 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Вычислив отдельно объем крыши и отдельно объем корпуса, мы можем найти общий объем зернохранилища:
- пи × R2 × H + 1/3 х пи × R2 × H
- (3,14) × 1,52 × 12 + 1/3 х (3,14) × 1,52 × 1
- = (3,14) × 2,25 × 12 + 1/3 х (3,14) × 2,25 × 1
- = (3,14) × 27 + 1/3 х (3,14) × 2,25
- = 84,822 + 2,356
- = 87,178. Объем зернохранилища равен 87,178 м3.
Реклама
- Например, вычислим объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиус 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Вычислив отдельно объем крыши и отдельно объем корпуса, мы можем найти общий объем зернохранилища:
-

1
Найдите площадь заливаемой бетоном поверхности. При заливке бетоном некоторого пространства (например, прямоугольной выемки в земле глубиной до нескольких десятков сантиметров) нет необходимости использовать сложные формулы для вычисления объема бетона, который вам потребуется. Вместо этого воспользуйтесь методом быстрого вычисления объема бетона. Начните с вычисления площади заливаемой поверхности.
- Все значения измеряются в метрах.
- Напомним, что площадь квадрата или прямоугольника вычисляется по формуле: площадь = длина × ширина. Площадь круга с радиусом r равна πr2.
-

2
Определите толщину бетонной заливки. Для этого просто измерьте глубину выемки в земле. Так как выемка относительно неглубокая, используйте значения, измеренные в сантиметрах.
-

3
Разделите площадь на коэффициент, основанный на толщине бетона. Все, что вам нужно сделать, чтобы определить точный объем, это разделить площадь на определенное число – если толщина бетона будет небольшой, эта цифра будет больше. Если толщина бетона будет большой, то это число будет меньше. Ниже даны самые распространенные значения. Если ваша толщина не соответствует ни одной из представленных, перейдите к следующему шагу.
- Если толщина бетона равна 10,16 сантиметрам (0,1016 м), разделите площадь на 205,74, чтобы определить объем.
- Если толщина бетона равна 15,24 сантиметрам (0,1524 м), разделите площадь на 137,16, чтобы определить объем.
- Если толщина бетона равна 20,32 сантиметрам (0,2032 м), разделите площадь на 101,6, чтобы определить объем.
- Если толщина бетона равна 30,48 сантиметрам (0,3048 м), разделите площадь на 68,58, чтобы определить объем.
-

4
Вычислите объем бетона с помощью быстрого метода. Если в вашем случае толщина бетона не соответствует ни одному из приведенных выше примеров, не волнуйтесь – вычислить объем можно достаточно просто. Для этого вычислите площадь заливаемой поверхности, разделите ее на 100, а затем умножьте полученный результат на толщину бетона (в сантиметрах).
- Допустим, выемка в земле имеет размеры 10 м × 15 м и глубину 20 см.
- 10 х 15 = 150
- 150/100 = 1,5
- 1,5 х 20 = 30. Нам понадобится 30 м3 бетона.
- Допустим, выемка в земле имеет размеры 10 м × 15 м и глубину 20 см.
-

5
Купите немного больше бетона, чем нужно. Он пригодится в том случае, если ваши измерения не были точными. В конце концов, сухую бетонную смесь, которая останется, можно сохранить,а затем использовать в другом проекте.
Реклама
Советы
- Метод быстрого вычисления объема бетона работает для заливаемых поверхностей любой правильной формы, но вычисляйте площадь заливаемой поверхности по соответствующей формуле.
Реклама
Об этой статье
Эту страницу просматривали 673 538 раз.
