- Какой котлован нужно вырыть для погреба или фундамента?
- Как узнать вместимость комнаты?
В расчетах поможет калькулятор объема в м3. Он пригодится в расчете объема прямоугольного параллелепипеда или куба, достаточно ввести данные в поля и узнать результат.
Справка. У прямоугольного параллелепипеда все грани являются прямоугольниками.

Формула объема, по которой ведется расчет:
V=a*b*c
Где:
- а – длина;
- b – ширина;
- c – высота.
Указано, что нужно вводить данные в метрах и результат получается в кубометрах (м3), но использовать можно любые системные единицы: мм, см или дм. Для конвертации используйте подсказки:
- 1 мм3 = 0,000000001 м3;
- 1 см3 = 0,000001 м3;
- 1 дм3 = 0,001 м3.
Калькулятор кубических метров — это простой и эффективный инструмент для расчета вместимости любой прямоугольной формы. Этот инструмент поможет вам быстро получить ответ и будет полезен как для практических работ, так и в учебе. Используйте онлайн-калькулятор объема и получайте точные данные.
Введите а — длину прямоугольника в м (метрах):
Введите b — ширину прямоугольника в м (метрах):
Введите h — толщину прямоугольника в м (метрах):
Как рассчитать объем прямоугольника?
Если прямоугольник имеет толщину, то фактически это параллелепипед. Объем параллелепипед в общем случае рассчитывается по формуле:
V = a x b х h
V — объем параллелепипеда . Объем прямоугольника имеющего толщину (высоту).
a — длина прямоугольника основания параллелепипеда
b — ширина прямоугольника основания параллелепипеда
h — высота параллелепипеда. Толщина прямоугольника.
Объем в миллиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vмм3 = aм х bм х hм x 1 000 000 000
Vмм3 — объем в миллиметрах кубических (мм3).
aм — длина прямоугольника в метрах (м).
bм — ширина прямоугольника в метрах (м).
hм — толщина прямоугольника в метрах (м).
Объем в сантиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vсм3 = aм х bм х hм x 1 000 000
Vсм3 — объем в сантиметрах кубических (см3).
aм — длина прямоугольника в метрах (м).
bм — ширина прямоугольника в метрах (м).
hм — толщина прямоугольника в метрах (м).
Объем в метрах кубических прямоугольника имеющего толщину (параллелепипед):
Vм3 = aм х bм х hм
Vм3 — объем в метрах кубических (м3).
aм — длина прямоугольника в метрах (м).
bм — ширина прямоугольника в метрах (м).
hм — толщина прямоугольника в метрах (м).
Объем в литрах прямоугольника имеющего толщину (параллелепипед):
Vл = aм х bм х hм x 1 000
Vл — объем в литрах (л).
aм — длина прямоугольника в метрах (м).
bм — ширина прямоугольника в метрах (м).
hм — толщина прямоугольника в метрах (м).
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
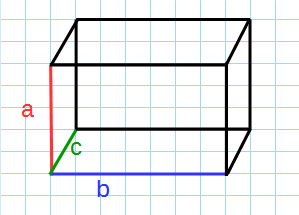
Формула объема параллелепипеда через его ребра:
a,b,c – ребра параллелепипеда.
Через стороны и высоту
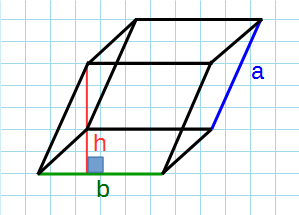
Формула объема параллелепипеда:
a,b – ребра параллелепипеда; h – высота параллелепипеда.

{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
Формула объема прямоугольного параллелепипеда через три стороны
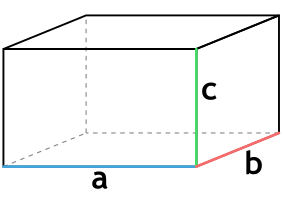
{V= a cdot b cdot c}
a – длина параллелепипеда
b – ширина параллелепипеда
c – высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab – это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
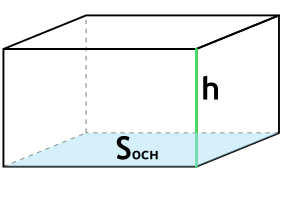
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
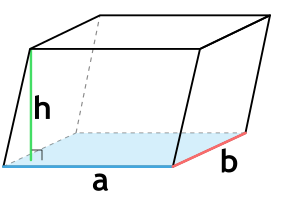
{V= a cdot b cdot h}
a – длина основания параллелепипеда
b – ширина основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через площадь основания и высоту
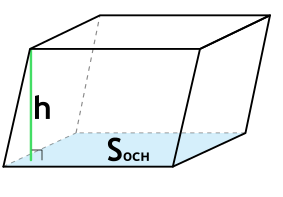
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Форма объекта и его линейные размеры определяют один из важных с геометрической точки зрения параметров — объём. Формула для прямоугольника, позволяющая его вычислить, довольно проста и основана на знании стороны и высоты. Но при решении не всегда известны значения рёбер фигуры, поэтому приходится использовать свойства параллелограмма, а именно — способы нахождения площади.
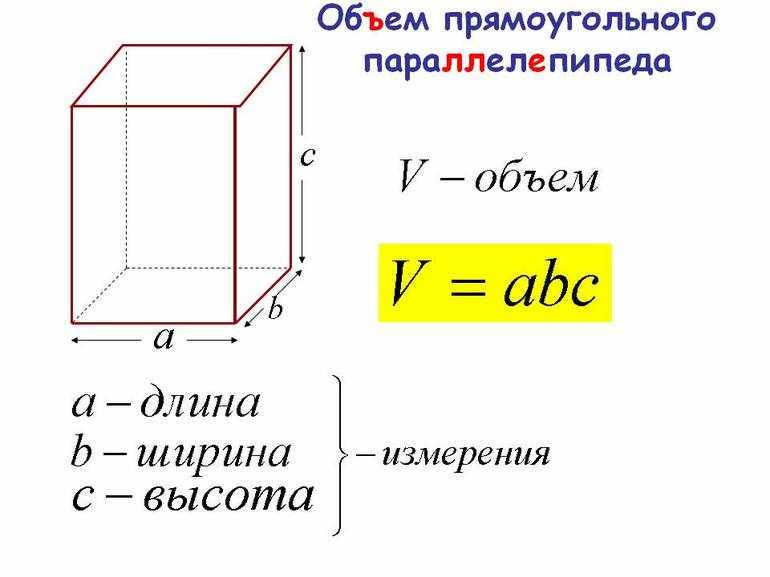
Общие сведения
По своей сути объём является количественной характеристикой пространства, которое занимает тело или вещество. Простыми словами, этот параметр показывает вместимость. В качестве единицы измерения, согласно СИ, принят кубический метр. За обозначение же объёма взята латинская буква V.
У тел, имеющих простую форму, характеристики находятся путём перемножения площади на высоту. Например, для куба он равен a3, прямоугольной призмы — h * b * a, пирамиды — (S * b * h) / 3. В эллипсоидных фигурах при расчётах используется радиус. Так, для конуса объём равен (p * R2 * h) / 3, сферы — (4 * p * R3) / 3, тора — 2 * p2 * R1 * R22.
Объём плоских фигур, таких как треугольник, круг, квадрат, прямоугольник, равен нулю. Но если их стороны или окружности имеют связанные с ними попарно параллельные линии, то они уже являются объёмными фигурами. Например, прямоугольник в пространстве называют параллелепипедом. Таким образом, чтобы найти объём прямоугольника, необходимо, чтобы он представлял собой прямоугольный параллелепипед, иначе действие будет бессмысленным.
Определить объём — значит, знать две основные величины фигуры:

- площадь — двумерная характеристика, определяющая размер фигуры,
- высоту — это длина перпендикуляра, опущенного из вершины на основание в трёхмерном пространстве.
Так как площадь измеряется в метрах квадратных, а высота просто в метрах, то перемножение площади и высоты как раз и даст единицу измерения объёма — метр кубический.
Решение задач
На самом деле вычисление объёма не только выполняют на уроках математики. Это знание востребовано в довольно многих специальностях и науках. Например, при строительстве, в архитектуре, инженерии, физике, химии. Поэтому знание нахождения параметра может пригодиться не только в школе. Теорию обязательно необходимо закреплять на практике. Вот некоторые задачи, которые помогут усвоить рассматриваемый материал:
- Пусть есть параллелепипед с прямыми сторонами. Его рёбра у основания равняются 19 и 20 сантиметрам. Размер же боковой грани составляет 10 сантиметров. Вычислить объём фигуры. Эта задача на одну формулу, все данные для подстановки в неё известны. Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.
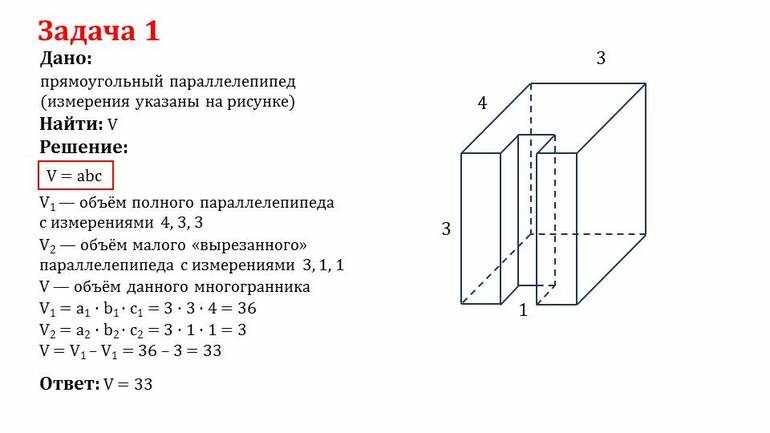
- Пусть имеется параллелепипед с основанием 1 см на 1,2 см и высотой 0,8 см. Из него был удалено другое прямоугольное тело с размерами 0,3 x 0,55 x 0,5. Найти объём получившейся фигуры. Так как искомый параметр новой фигуры равен разнице изначального и удалённого объёмов, то зная формулу найти ответ не составит труда: V = 0,8 * 1 * 1,2 — 0,3 * 0,5 * 0,55 = 0,877 см3.
- Дан прямоугольный параллелепипед с вершинами ABCD и A1B1C1D1. Сравнить объём образованного в середине пирамиды AA1BD тела со значением фигуры. Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.
- В гальванической ванне помещается три тысячи литров раствора. Высота наполнения ёмкости при этом достигает 75 сантиметров. В ванную поместили заготовку, после чего уровень поднялся на два сантиметра. Найти объём заготовки в метрах кубических. Итак, в одном кубическом метре содержится тысяча литров. Поэтому изначально в ёмкости было 3 м³ раствора. Значит, изначально в ванне раствор занимал: 3 = S * 75. Отсюда s = 3/75 = 1/25 см2. Объём детали составляет: V = S * 2 = (1/25) * 2 = 2 / 25 = 0,08 м³.
Использование калькулятора
Конечно же, на обычном калькуляторе объём прямоугольника не подсчитаешь. Разве что известны три его грани и формула нахождения параметра. Тогда нужно будет просто перемножить три числа. В других же случаях, когда нужно решить сложную задачу, связанную с громоздкими вычислениями, можно использовать математические сайты, имеющие название онлайн-калькуляторы.
Это интернет-сервисы, предлагающие своим пользователям бесплатно воспользоваться услугами по вычислению объёма геометрических фигур и выполнить другие математические операции. Для того чтобы воспользоваться сайтами-решателями, нужно иметь любой гаджет с возможностью подключения его к интернету и установленным на него веб-обозревателем.
После загрузки онлайн-калькулятора все действия пользователя сводятся к заполнению специальной формы в которую вносится условие задания. Конечно же, такое решение не может называться самостоятельным, но для проверки полученного результата или выявления ошибок в расчёте подходит идеально. Кроме, непосредственно автоматического вычисления объёма большинство сайтов содержат на своих страницах теоретический материал, а также примеры решений типовых заданий. Так что при обучении учащихся их использование на первых порах вполне оправданно.
