В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
-
Свойства куба
- Свойство 1
-
Свойство 2
- Свойство 3
-
Формулы для куба
- Диагональ
- Диагональ грани
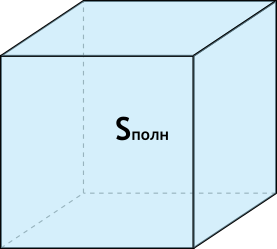
- Площадь полной поверхности
- Периметр ребер
-
Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.

- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
- a – ребро куба;
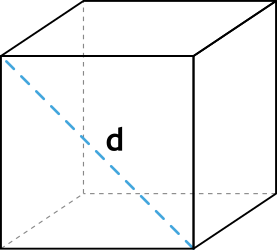
- d – диагональ куба или его грани.
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
![]()
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
![]()
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
![]()
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
![]()
Объем
Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
![]()
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
![]()
Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
Формула объёма куба через ребро
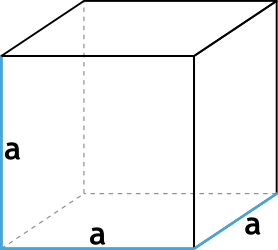
Формула объёма куба через диагональ грани
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d – диагональ грани куба
Формула объёма куба через периметр грани
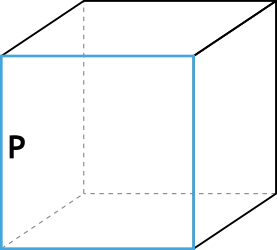
{V= Big( dfrac{P}{4} Big) ^3}
P – периметр грани куба
Формула объёма куба через диагональ куба
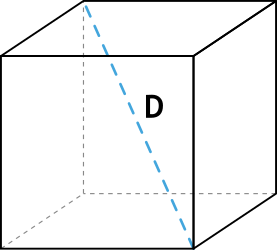
{V= dfrac{D^3}{3sqrt{3}}}
D – диагональ куба
Формула объёма куба через площадь полной поверхности
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн – диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
Загрузить PDF
Загрузить PDF
Кубические метры (м3) – это единица измерения объема, равная объему куба, стороны которого равны одному метру. Кубические метры являются предпочтительной единицей измерения при различных работах, например, при заливке бетона. Объем любого прямоугольного пространства длиной “L”, шириной “W” и высотой “Н” вычисляется по формуле: Объем = L × W × H.
-

1
Измерьте все необходимые расстояния в метрах. Объем многих трехмерных фигур легко вычислить по соответствующим формулам. Однако все значения, подставляемые в формулы, должны измеряться в метрах. Таким образом, перед подстановкой значений в формулу убедитесь, что все они измеряются в метрах, или что вы конвертировали другие единицы измерения в метры.
- 1 мм = 0,001 м
- 1 см = 0,01 м
- 1 км = 1000 м
-

2
Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = L × W × H (длину умножить на ширину умножить на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани.
- Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
- 4 × 3 × 2,5
- = 12 × 2,5
- = 30. Объем этой комнаты равен 30 м3.
- Куб – объемная фигура, у котрой все стороны равны. Таким образом, формулу для вычисления объема куба можно записать в виде: объем = L3 (или W3, или H3).
- Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
-

3
Для вычисления объема фигур в виде цилиндра используйте формулу: пи × R2 × H. Вычисление объема цилиндра сводится к умножению площади круглого основания на высоту (или длину) цилиндра. Найдите площадь круглого основания, умножив число пи (3,14) на квадрат радиуса круга (R) (радиус – расстояние от центра окружности до любой точки, лежащей на этой окружности). Затем полученный результат умножьте на высоту цилиндра (H), и вы найдете объем цилиндра. Все значения измеряются в метрах.
- Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
- (3,14) × 0,752 × 10
- = (3,14) × 0,5625 × 10
- = 17,66. Объем колодца равен 17,66 м3.
- Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
-

4
Для вычисления объема шара используйте формулу: 4/3 х пи × R3. То есть вам нужно знать только радиус (R) шара.
- Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
- 4/3 х пи × (5)3
- = 4/3 х (3,14) × 125
- = 4,189 × 125
- = 523,6. Объем воздушного шара равен 523,6 м3.
- Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
-

5
Для вычисления объема фигур в виде конуса используйте формулу: 1/3 х пи × R2 × H. Объем конуса равен 1/3 объема цилиндра, который имеет такую же высоту и радиус.
- Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см. Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
- 1/3 х (3,14) × 0,032 × 0,15
- = 1/3 х (3,14) × 0.0009 × 0,15
- = 1/3 × 0.0004239
- = 0,000141. Объем конуса мороженного равен 0,000141 м3.
- Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см. Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
-

6
Для вычисления объема фигур неправильной формы используйте несколько формул. Для этого попробуйте разбить фигуру на несколько фигур правильной формы. Затем найдите объем каждой такой фигуры и сложите полученные результаты.
- Например, вычислим объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиус 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Вычислив отдельно объем крыши и отдельно объем корпуса, мы можем найти общий объем зернохранилища:
- пи × R2 × H + 1/3 х пи × R2 × H
- (3,14) × 1,52 × 12 + 1/3 х (3,14) × 1,52 × 1
- = (3,14) × 2,25 × 12 + 1/3 х (3,14) × 2,25 × 1
- = (3,14) × 27 + 1/3 х (3,14) × 2,25
- = 84,822 + 2,356
- = 87,178. Объем зернохранилища равен 87,178 м3.
Реклама
- Например, вычислим объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиус 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Вычислив отдельно объем крыши и отдельно объем корпуса, мы можем найти общий объем зернохранилища:
-

1
Найдите площадь заливаемой бетоном поверхности. При заливке бетоном некоторого пространства (например, прямоугольной выемки в земле глубиной до нескольких десятков сантиметров) нет необходимости использовать сложные формулы для вычисления объема бетона, который вам потребуется. Вместо этого воспользуйтесь методом быстрого вычисления объема бетона. Начните с вычисления площади заливаемой поверхности.
- Все значения измеряются в метрах.
- Напомним, что площадь квадрата или прямоугольника вычисляется по формуле: площадь = длина × ширина. Площадь круга с радиусом r равна πr2.
-

2
Определите толщину бетонной заливки. Для этого просто измерьте глубину выемки в земле. Так как выемка относительно неглубокая, используйте значения, измеренные в сантиметрах.
-

3
Разделите площадь на коэффициент, основанный на толщине бетона. Все, что вам нужно сделать, чтобы определить точный объем, это разделить площадь на определенное число – если толщина бетона будет небольшой, эта цифра будет больше. Если толщина бетона будет большой, то это число будет меньше. Ниже даны самые распространенные значения. Если ваша толщина не соответствует ни одной из представленных, перейдите к следующему шагу.
- Если толщина бетона равна 10,16 сантиметрам (0,1016 м), разделите площадь на 205,74, чтобы определить объем.
- Если толщина бетона равна 15,24 сантиметрам (0,1524 м), разделите площадь на 137,16, чтобы определить объем.
- Если толщина бетона равна 20,32 сантиметрам (0,2032 м), разделите площадь на 101,6, чтобы определить объем.
- Если толщина бетона равна 30,48 сантиметрам (0,3048 м), разделите площадь на 68,58, чтобы определить объем.
-

4
Вычислите объем бетона с помощью быстрого метода. Если в вашем случае толщина бетона не соответствует ни одному из приведенных выше примеров, не волнуйтесь – вычислить объем можно достаточно просто. Для этого вычислите площадь заливаемой поверхности, разделите ее на 100, а затем умножьте полученный результат на толщину бетона (в сантиметрах).
- Допустим, выемка в земле имеет размеры 10 м × 15 м и глубину 20 см.
- 10 х 15 = 150
- 150/100 = 1,5
- 1,5 х 20 = 30. Нам понадобится 30 м3 бетона.
- Допустим, выемка в земле имеет размеры 10 м × 15 м и глубину 20 см.
-

5
Купите немного больше бетона, чем нужно. Он пригодится в том случае, если ваши измерения не были точными. В конце концов, сухую бетонную смесь, которая останется, можно сохранить,а затем использовать в другом проекте.
Реклама
Советы
- Метод быстрого вычисления объема бетона работает для заливаемых поверхностей любой правильной формы, но вычисляйте площадь заливаемой поверхности по соответствующей формуле.
Реклама
Об этой статье
Эту страницу просматривали 673 538 раз.
Была ли эта статья полезной?
Куб – это объемная геометрическая фигура, все грани которой, являются квадратами. Следовательно, все стороны, которые называются ребрами – равны. Все углы в кубе – прямые, т. е. 90 градусов

a – сторона (ребро) куба
Формула объёма куба, (V):

Прямоугольный параллелепипед – это объёмная геометрическая фигура, грани которой, являются прямоугольниками.
Противоположенные грани одинаковы и параллельны. Все углы в параллелепипеде – прямые, т. е. 90 градусов.

a, b, c – стороны параллелепипеда
Формула объёма параллелепипеда, (V):
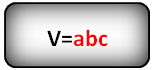

R– радиус шара
π ≈ 3,14
Формула объема шара, (V):

Калькулятор – вычислить, найти объем шара, сферы
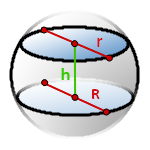
h– высота шарового слоя
R– радиус нижнего основания
r– радиус верхнего основания
π ≈ 3.14
Объем шарового слоя, (V):
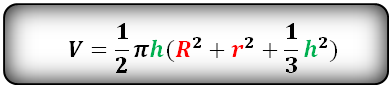
Калькулятор – вычислить, найти объем шарового слоя
h – высота сегмента
R – радиус шара
π ≈ 3.14
Объем шарового сектора, (V):

Калькулятор – вычислить, найти объем шарового сектора
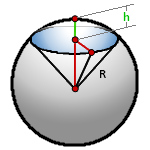
Шаровый сегмент – это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара
h – высота сегмента
π ≈ 3.14
Объем шарового сегмента, (V):
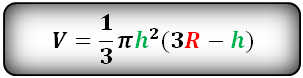
Калькулятор – вычислить, найти объем шарового сегмента
Прямой цилиндр – это геометрическое тело, полученное в результате вращения прямоугольника, вокруг его стороны. Цилиндр имеет два основания, верхнее и нижнее, которые одинаковы и имеют форму круга.
Высота цилиндра – это отрезок, соединяющий две любые точки оснований но обязательно расположенный перпендикулярно к ним обоим.
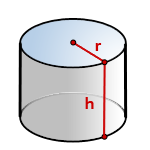
r – радиус основания
h – высота цилиндра
π ≈ 3.14
Формула для расчета объема цилиндра, (V):

Прямой круговой конус – это геометрическое тело, полученное вращением прямоугольного треугольника вокруг катета. Тогда этот катет, является высотой, другой катет – радиус основания, а гипотенуза это образующая.
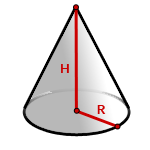
H – высота конуса
R – радиус основания
π ≈ 3.14
Формула объема конуса, (V):
Усеченный прямой конус – это конус, у которого отделена верхняя часть, плоскостью, параллельной основанию. В этом случае, появляется второе основание. Эти основания называют верхнее и нижнее, соответственно.
Высота усеченного конуса – это отрезок, соединяющий центры оснований и который расположен перпендикулярно к обоим основаниям.
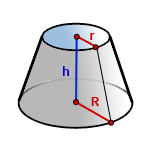
R – радиус нижнего основания
r – радиус верхнего основания
h – высота конуса
π ≈ 3.14
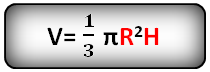
Формула объема усеченного конуса, (V):

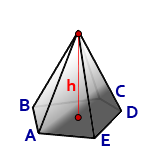
h – высота пирамиды
S – площадь основания ABCDE
Формула объема пирамиды, (V):
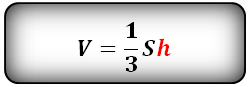
Калькулятор – вычислить, найти объем пирамиды
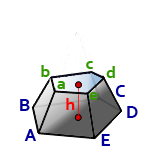
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

Калькулятор – вычислить, найти площадь поверхности прямоугольного параллелепипеда
Пирамида в основании, которой лежит правильный многоугольник и грани равные, равнобедренные треугольники, называется правильной.
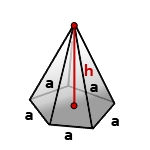
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
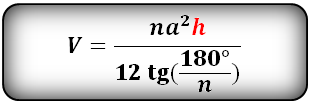
Формула объема правильной пирамиды, (V):
Калькулятор – вычислить, найти объем правильной пирамиды
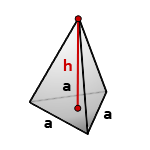
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
h – высота пирамиды
a – сторона основания
Формула объема правильной треугольной пирамиды, (V):

Калькулятор – вычислить, найти объем правильной треугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
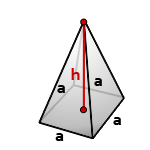
h – высота пирамиды
a – сторона основания
Формула объема правильной четырехугольной пирамиды, (V):
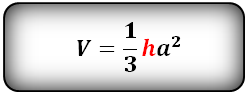
Калькулятор – вычислить, найти объем правильной четырехугольной пирамиды
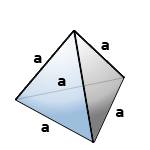
Правильный тетраэдр- пирамида у которой все грани, равносторонние треугольники.
а -ребро тетраэдра
Формула бъема правильного тетраэдра (V):
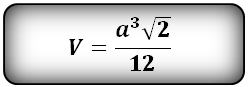
Калькулятор – вычислить, найти объем правильного тетраэдра
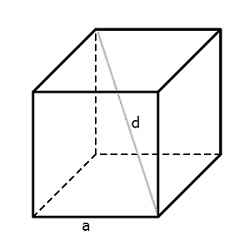
Куб – это прямоугольный параллелепипед, все стороны (ребра) которого равны.
Любой куб характеризуется ребром a и диагональю d (см. рисунок). Именно эти характеристики используются в формулах куба при вычислении объема и площади.
Диагональ куба – это отрезок, соединяющий противоположные вершины куба.
Формула диагонали куба
Диагональ d куба можно получить, зная его сторону:
d2 = 3a2
Формула площади куба
Площадь поверхности куба можно получить, зная его сторону:
S = 6a2
Формула объема куба
Объем куба можно вычислить, зная его сторону:
V = a3
Поделитесь статьей с одноклассниками «КУБ формулы объема, площади поверхности, диагональ куба».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
