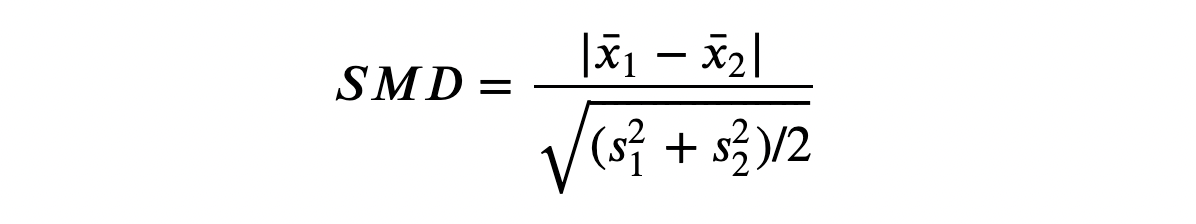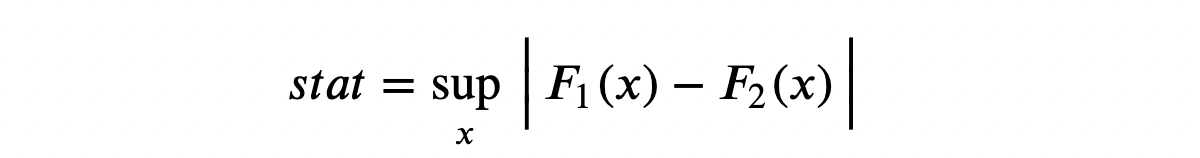From Wikipedia, the free encyclopedia
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable 




Every probability distribution supported on the real numbers, discrete or “mixed” as well as continuous, is uniquely identified by a right-continuous monotone increasing function (a càdlàg function) ![{displaystyle Fcolon mathbb {R} rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4c45b6faf38bb3fb300ab4678d3675afd172f56)


In the case of a scalar continuous distribution, it gives the area under the probability density function from minus infinity to 
Definition[edit]
The cumulative distribution function of a real-valued random variable 
|
|
(Eq.1) |
where the right-hand side represents the probability that the random variable 

The probability that 
![(a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)

|
|
(Eq.2) |
In the definition above, the “less than or equal to” sign, “≤”, is a convention, not a universally used one (e.g. Hungarian literature uses “<“), but the distinction is important for discrete distributions. The proper use of tables of the binomial and Poisson distributions depends upon this convention. Moreover, important formulas like Paul Lévy’s inversion formula for the characteristic function also rely on the “less than or equal” formulation.
If treating several random variables 






The probability density function of a continuous random variable can be determined from the cumulative distribution function by differentiating[3] using the Fundamental Theorem of Calculus; i.e. given 
as long as the derivative exists.
The CDF of a continuous random variable 

In the case of a random variable 

If 


Properties[edit]
From top to bottom, the cumulative distribution function of a discrete probability distribution, continuous probability distribution, and a distribution which has both a continuous part and a discrete part.
Example of a cumulative distribution function with a countably infinite set of discontinuities.
Every cumulative distribution function 
Every function with these four properties is a CDF, i.e., for every such function, a random variable can be defined such that the function is the cumulative distribution function of that random variable.
If 




If the CDF 




for all real numbers 




If 

and for any 
CDF plot with two red rectangles, illustrating 

as shown in the diagram.
In particular, we have
Examples[edit]
As an example, suppose 
![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
Then the CDF of 
Suppose instead that 
Then the CDF of 
Suppose 

Here λ > 0 is the parameter of the distribution, often called the rate parameter.
Suppose 

Here the parameter 

A table of the CDF of the standard normal distribution is often used in statistical applications, where it is named the standard normal table, the unit normal table, or the Z table.
Suppose 

Here 




Derived functions[edit]
Complementary cumulative distribution function (tail distribution)[edit]
Sometimes, it is useful to study the opposite question and ask how often the random variable is above a particular level. This is called the complementary cumulative distribution function (ccdf) or simply the tail distribution or exceedance, and is defined as
This has applications in statistical hypothesis testing, for example, because the one-sided p-value is the probability of observing a test statistic at least as extreme as the one observed. Thus, provided that the test statistic, T, has a continuous distribution, the one-sided p-value is simply given by the ccdf: for an observed value 
In survival analysis, 

- Properties
- For a non-negative continuous random variable having an expectation, Markov’s inequality states that[4]
- As
, and in fact
provided that
is finite.
Proof:[citation needed]
Assuminghas a density function
, for any
Then, on recognizing
and rearranging terms,
as claimed.
- For a random variable having an expectation,
and for a non-negative random variable the second term is 0.
If the random variable can only take non-negative integer values, this is equivalent to
Folded cumulative distribution[edit]
While the plot of a cumulative distribution 
where 
Inverse distribution function (quantile function)[edit]
If the CDF F is strictly increasing and continuous then ![F^{-1}(p),pin [0,1],](https://wikimedia.org/api/rest_v1/media/math/render/svg/b89fe1b58ff06ad5647ba178886bb6704d8da846)


Some distributions do not have a unique inverse (for example if 


Some useful properties of the inverse cdf (which are also preserved in the definition of the generalized inverse distribution function) are:
is nondecreasing
if and only if
- If
has a
distribution then
is distributed as
. This is used in random number generation using the inverse transform sampling-method.
- If
is a collection of independent
-distributed random variables defined on the same sample space, then there exist random variables
such that
is distributed as
and
with probability 1 for all
.[citation needed]
The inverse of the cdf can be used to translate results obtained for the uniform distribution to other distributions.
Empirical distribution function[edit]
The empirical distribution function is an estimate of the cumulative distribution function that generated the points in the sample. It converges with probability 1 to that underlying distribution. A number of results exist to quantify the rate of convergence of the empirical distribution function to the underlying cumulative distribution function[citation needed].
Multivariate case[edit]
Definition for two random variables[edit]
When dealing simultaneously with more than one random variable the joint cumulative distribution function can also be defined. For example, for a pair of random variables 

|
|
(Eq.3) |
where the right-hand side represents the probability that the random variable 



Example of joint cumulative distribution function:
For two continuous variables X and Y:
For two discrete random variables, it is beneficial to generate a table of probabilities and address the cumulative probability for each potential range of X and Y, and here is the example:[8]
given the joint probability mass function in tabular form, determine the joint cumulative distribution function.
| Y = 2 | Y = 4 | Y = 6 | Y = 8 | |
| X = 1 | 0 | 0.1 | 0 | 0.1 |
| X = 3 | 0 | 0 | 0.2 | 0 |
| X = 5 | 0.3 | 0 | 0 | 0.15 |
| X = 7 | 0 | 0 | 0.15 | 0 |
Solution: using the given table of probabilities for each potential range of X and Y, the joint cumulative distribution function may be constructed in tabular form:
| Y < 2 | 2 ≤ Y < 4 | 4 ≤ Y < 6 | 6 ≤ Y < 8 | Y ≥ 8 | |
| X < 1 | 0 | 0 | 0 | 0 | 0 |
| 1 ≤ X < 3 | 0 | 0 | 0.1 | 0.1 | 0.2 |
| 3 ≤ X < 5 | 0 | 0 | 0.1 | 0.3 | 0.4 |
| 5 ≤ X < 7 | 0 | 0.3 | 0.4 | 0.6 | 0.85 |
| X ≥ 7 | 0 | 0.3 | 0.4 | 0.75 | 1 |
Definition for more than two random variables[edit]
For 


|
|
(Eq.4) |
Interpreting the 

Properties[edit]
Every multivariate CDF is:
- Monotonically non-decreasing for each of its variables,
- Right-continuous in each of its variables,
-
Not every function satisfying the above four properties is a multivariate CDF, unlike in the single dimension case. For example, let 






The probability that a point belongs to a hyperrectangle is analogous to the 1-dimensional case:[9]
Complex case[edit]
Complex random variable[edit]
The generalization of the cumulative distribution function from real to complex random variables is not obvious because expressions of the form 

Complex random vector[edit]
Generalization of Eq.4 yields
as definition for the CDS of a complex random vector 
Use in statistical analysis[edit]
The concept of the cumulative distribution function makes an explicit appearance in statistical analysis in two (similar) ways. Cumulative frequency analysis is the analysis of the frequency of occurrence of values of a phenomenon less than a reference value. The empirical distribution function is a formal direct estimate of the cumulative distribution function for which simple statistical properties can be derived and which can form the basis of various statistical hypothesis tests. Such tests can assess whether there is evidence against a sample of data having arisen from a given distribution, or evidence against two samples of data having arisen from the same (unknown) population distribution.
Kolmogorov–Smirnov and Kuiper’s tests[edit]
The Kolmogorov–Smirnov test is based on cumulative distribution functions and can be used to test to see whether two empirical distributions are different or whether an empirical distribution is different from an ideal distribution. The closely related Kuiper’s test is useful if the domain of the distribution is cyclic as in day of the week. For instance Kuiper’s test might be used to see if the number of tornadoes varies during the year or if sales of a product vary by day of the week or day of the month.
See also[edit]
References[edit]
- ^ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Mathematics for Machine Learning. Cambridge University Press. p. 181. ISBN 9781108455145.
- ^ a b c d e f Park, Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3.
- ^ Montgomery, Douglas C.; Runger, George C. (2003). Applied Statistics and Probability for Engineers (PDF). John Wiley & Sons, Inc. p. 104. ISBN 0-471-20454-4. Archived (PDF) from the original on 2012-07-30.
- ^ Zwillinger, Daniel; Kokoska, Stephen (2010). CRC Standard Probability and Statistics Tables and Formulae. CRC Press. p. 49. ISBN 978-1-58488-059-2.
- ^ Gentle, J.E. (2009). Computational Statistics. Springer. ISBN 978-0-387-98145-1. Retrieved 2010-08-06.[page needed]
- ^
Monti, K. L. (1995). “Folded Empirical Distribution Function Curves (Mountain Plots)”. The American Statistician. 49 (4): 342–345. doi:10.2307/2684570. JSTOR 2684570. - ^ Xue, J. H.; Titterington, D. M. (2011). “The p-folded cumulative distribution function and the mean absolute deviation from the p-quantile” (PDF). Statistics & Probability Letters. 81 (8): 1179–1182. doi:10.1016/j.spl.2011.03.014.
- ^ “Joint Cumulative Distribution Function (CDF)”. math.info. Retrieved 2019-12-11.
- ^ “Archived copy” (PDF). www.math.wustl.edu. Archived from the original (PDF) on 22 February 2016. Retrieved 13 January 2022.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Sun, Jingchao; Kong, Maiying; Pal, Subhadip (22 June 2021). “The Modified-Half-Normal distribution: Properties and an efficient sampling scheme”. Communications in Statistics – Theory and Methods: 1–23. doi:10.1080/03610926.2021.1934700. ISSN 0361-0926. S2CID 237919587.
External links[edit]
Media related to Cumulative distribution functions at Wikimedia Commons
Кумулятивная функция распределения в нормально распределенных данных
Добавлено 30 августа 2020 в 11:43
В данной статье объясняется, как получить кумулятивную функцию распределения Гаусса и почему она полезна в статистическом анализе.
Если вы только присоединяетесь к нашему обсуждению статистики в электротехнике, возможно, вам будет интересно сначала просмотреть предыдущие статьи этой серии, список которых можно найти в оглавлении вверху над статьей.
Что мы знаем из предыдущих статей:
- мы можем получить функцию плотности вероятности нормально распределенных результатов измерений, вычислив стандартное отклонение и среднее значение набора данных;
- эта функция плотности вероятности является идеализированным математическим эквивалентом фигуры, которую мы наблюдаем на гистограмме набора данных;
- мы получаем вероятность (т.е. вероятность того, что определенные значения результатов измерений будут иметь место) путем интегрирования функции плотности вероятности по заданному интервалу.
Если участки интегрирования функции плотности вероятности являются ключом к извлечению вероятностей из измеренных данных, можно задаться вопросом о возможности простого интегрирования всей функции и тем самым создания новой функции, которая даст нам прямой доступ к информации о вероятности.
Как оказалось, это стандартный метод статистического анализа, и эта новая функция, которую мы получаем путем интегрирования всей функции плотности вероятности, называется кумулятивной функцией распределения.
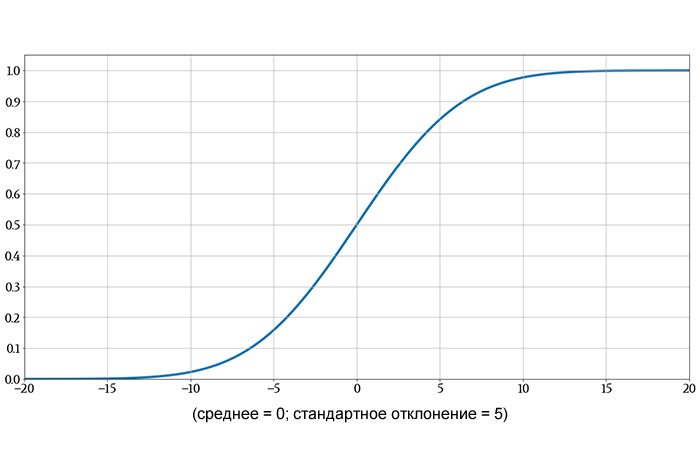
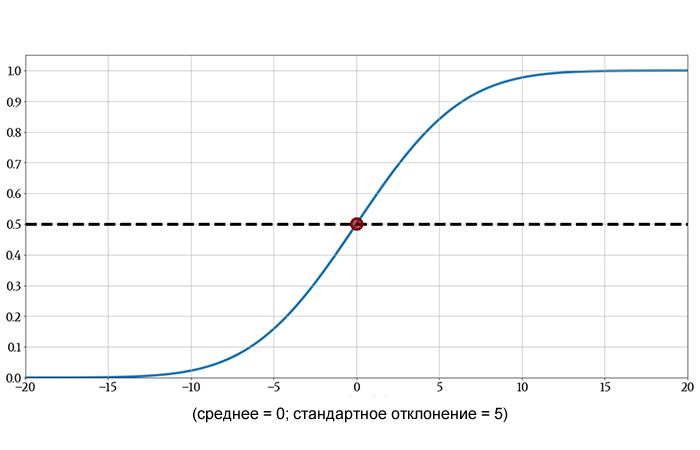
Кумулятивная функция нормального распределения
Использование кумулятивной функции распределения (CDF, cumulative distribution function) является особенно хорошей идеей, когда мы работаем с нормально распределенными данными, потому что интегрировать гауссову кривую не так-то просто.
Фактически, чтобы получить кумулятивную функцию распределения кривой Гаусса, даже математики должны прибегнуть к численному интегрированию (функция (e^{-x^2}) не имеет первообразной, которая может быть выражена в элементарной форме). Это означает, что кумулятивная функция распределения Гаусса на самом деле представляет собой последовательность дискретных значений, созданных из множества отдельных выборок, взятых вдоль гауссовой кривой.
В эпоху компьютеров мы можем легко обрабатывать огромное количество выборок, и, следовательно, дискретная кумулятивная функция распределения, полученная путем численного интегрирования, может быть вполне адекватной заменой непрерывной функции, полученной посредством символьного интегрирования.
Если мы отложим на графике большое количество значений гауссовой функции распределения, кривая будет выглядеть следующим образом:
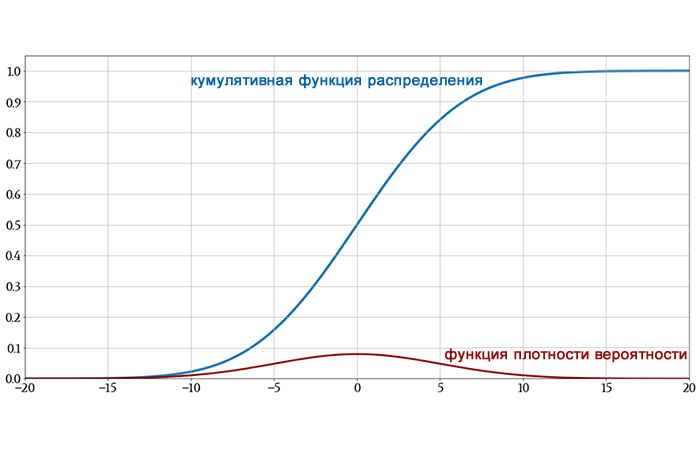
На следующем графике показаны как исходная гауссова функция плотности вероятности, так и ее функция распределения, чтобы вы могли увидеть, как интегрирование превращает одно в другое.
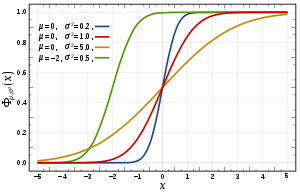
Одно небольшое замечание, прежде чем мы продолжим: в обсуждениях о статистике вы можете увидеть символ Φ (заглавная греческая буква фи). Когда нормальное распределение имеет среднее значение 0 и стандартное отклонение 1, оно называется стандартным нормальным распределением. Кумулятивная функция стандартного нормального распределения обозначается Φ; таким образом,
[Phi(z)=frac{1}{sqrt{2 pi}}int_{-infty}^{z}e^{-frac{x^2}{2}}dx]
Пример кумулятивной функции распределения
Когда мы интегрируем функцию плотности вероятности от отрицательной бесконечности до некоторого значения, обозначенного z, мы вычисляем вероятность того, что результат случайно выбранного измерения или нового измерения попадет в числовой интервал, который простирается от отрицательной бесконечности до z. Другими словами, мы вычисляем вероятность того, что измеренное значение будет меньше z.
Это именно та информация, которую мы получаем из кумулятивной функции распределения и без необходимости интегрирования. Если мы посмотрим на график кумулятивной функции распределения и найдем вертикальное значение, соответствующее некоторому числу z на горизонтальной оси, мы узнаем вероятность того, что измеренное значение будет меньше z.
Например:
Кумулятивная функция распределения при z = 0 равна 0,5. Это говорит нам о том, что результат выбранного случайным образом измерения имеет 50% вероятность быть меньше нуля. Это интуитивно понятно: нормальное распределение симметрично относительно среднего, и поскольку среднее значение в этом случае равно нулю, любое отдельное измерение имеет равные шансы быть меньше или больше нуля.
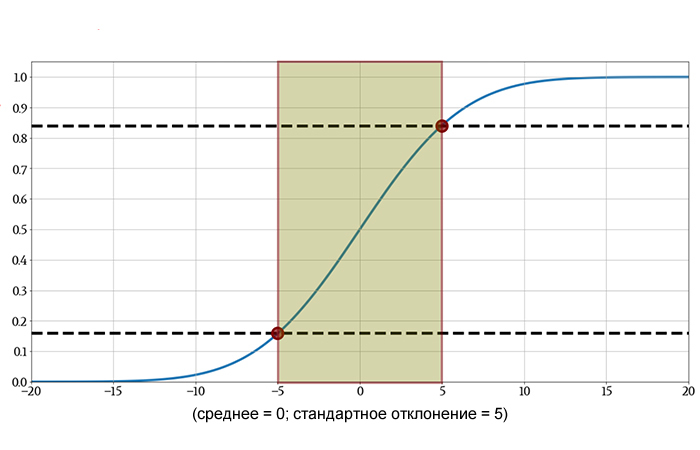
Кумулятивная функция распределения (CDF) также обеспечивает простой способ определения вероятности того, что результат измерения попадет в определенный диапазон. Если диапазон определяется двумя значениями z1 и z2, всё, что нам нужно сделать, это вычесть значение функции распределения в z2 из значения функции распределения в z1 (а затем при необходимости взять модуль полученного значения).
Вот еще один пример:
Вероятность того, что результат случайно выбранного измерения будет между –5 и +5, составляет приблизительно (0,84 – 0,16) = 0,68 (или 68%). Более точное значение – 68,27%.
Вероятность и стандартное отклонение
Вы могли заметить, что интервал, выбранный в предыдущем примере, был равен одному стандартному отклонению выше и ниже среднего. Когда мы обсуждаем вероятности со ссылкой на интервалы, представленные в единицах стандартного отклонения, эта информация применяется ко всем наборам данных, которые следуют нормальному распределению. Таким образом, мы можем определить вероятностные характеристики, используя кумулятивную функцию стандартного нормального распределения, а затем распространить эти тенденции на другие наборы данных, просто изменив стандартное отклонение (или размышляя относительно стандартных отклонений).
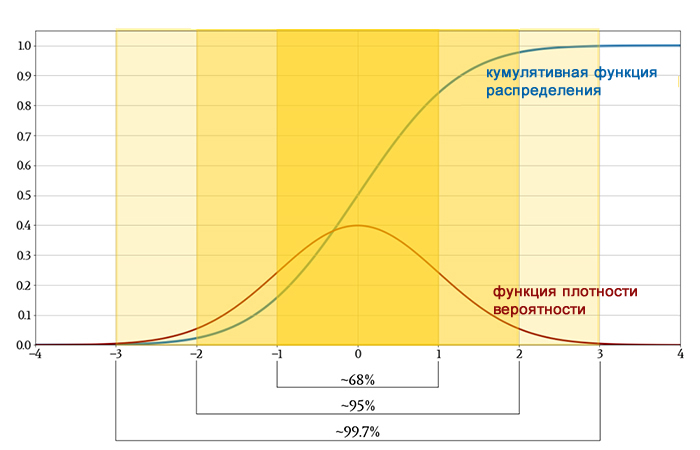
Выше мы видели, что в нормально распределенных данных измеренное значение имеет шанс 68,27% попасть в диапазон в пределах одного стандартного отклонения от среднего. Мы можем продолжить обобщение нормально распределенных данных следующим образом:
- вероятность того, что измеренное значение будет в пределах двух стандартных отклонений от среднего, составляет 95,45%;
- вероятность того, что измеренное значение будет в пределах трех стандартных отклонений от среднего, составляет 99,73%.
Эти три вероятности дают простое представление того, как будут вести себя нормально распределенные измерения.
Более приблизительная версия этого обобщения известна как правило 68-95-99,7: если набор данных демонстрирует нормальное распределение, около 68% значений будут в пределах одного стандартного отклонения от среднего, около 95% будут в пределах двух стандартных отклонений, и около 99,7% будут в пределах трех стандартных отклонений.
Заключение
Мы рассмотрели важный материал, и я надеюсь, что вам понравилось наше исследование нормального распределения и связанных с ним тем статистики. В следующей статье мы рассмотрим два малоизвестных описательных статистических показателя: асимметрию и эксцесс.
Теги
ВероятностьКумулятивная функция распределения / CDF (cumulative distribution function)Нормальное распределение / Гауссово распределениеСтандартное нормальное распределениеСтатистикаСтатистический анализФункция плотности вероятности
Вероятность того, что случайная величина X меньше или равна x. 
В теории вероятностей и статистика, кумулятивная функция распределения (CDF ) вещественной случайной величины X { displaystyle X}




В случае скалярного непрерывного распределения, это дает площадь под функцией плотности вероятности от минус бесконечности до x { displaystyle x}
Содержание
- 1 Определение
- 2 Свойства
- 3 Примеры
- 4 Производные функции
- 4.1 Дополнительная функция кумулятивного распределения (хвостовое распределение)
- 4.2 Свернутое кумулятивное распределение
- 4.3 Обратная функция распределения (функция квантиля)
- 4.4 Эмпирическая функция распределения
- 5 Многомерный случай
- 5.1 Определение для двух случайных величин
- 5.2 Определение для более двух случайных величин
- 5.3 Свойства
- 6 Сложный случай
- 6.1 Сложная случайная величина
- 6.2 Сложный случайный вектор
- 7 Использование в статистическом анализе
- 7.1 Критерии Колмогорова – Смирнова и Койпера
- 8 См. Также
- 9 Ссылки
- 10 Внешние ссылки
Определение
Кумулятивная функция распределения случайной величины с действительным знаком X { displaystyle X }
FX (x) = P (X ≤ x) { displaystyle F_ {X} (x) = operatorname { P} (X leq x)} |
(Eq.1) |
где правая часть представляет вероятность того, что случайная величина X { displaystyle X}


![( a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)

P (a < X ≤ b) = F X ( b) − F X ( a) {displaystyle operatorname {P} (a |
(Eq.2) |
В приведенном выше определении знак «меньше или равно», «≤», означает соглашение, которое не используется повсеместно (например, в венгерской литературе используется “<“), но различие важно для дискретных распределений. Правильное использование таблиц биномиальных и распределений Пуассона Кроме того, важные формулы, такие как Поль Леви, формула обращения для характеристической функции , также основываются на формулировке «меньше или равно».
При обработке нескольких случайных величин X, Y,… { displaystyle X, Y, ldots}


Функция плотности вероятности непрерывной случайной величины может быть определена из кумулятивной функции распределения путем дифференцирования с использованием Основная теорема исчисления ; т.е. задано F (x) { displaystyle F (x)}
- f (x) = d F (x) dx { displaystyle f (x) = {dF (x) over dx}}
до тех пор, пока существует производная.
CDF непрерывной случайной величины X { displaystyle X}

- FX (x) = ∫ – ∞ xf X (t) dt. { displaystyle F_ {X} (x) = int _ {- infty} ^ {x} f_ {X} (t) , dt.}
В случае случайной величины X { displaystyle X}

- P (X = b) = FX (b) – lim x → b – FX (x). { displaystyle operatorname {P} (X = b) = F_ {X} (b) – lim _ {x to b ^ {-}} F_ {X} (x).}
Если FX { displaystyle F_ {X}}


Свойства
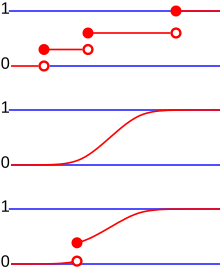
Каждое совокупное распределение функция FX { displaystyle F_ {X}}
- lim x → – ∞ FX (x) = 0, lim x → + ∞ FX (x) = 1. { displaystyle lim _ {x to – infty} F_ {X} (x) = 0, quad lim _ {x to + infty} F_ {X} (x) = 1.}
Каждая функция с этими четырьмя свойствами является функцией CDF, т. Е. Для каждой такой функции a случайная величина может быть определена так, что функция является кумулятивной функцией распределения этой случайной величины.
Если X { displaystyle X}




- FX (x) = P (X ≤ x) = ∑ xi ≤ x P (X = xi) = ∑ xi ≤ xp (xi). { displaystyle F_ {X} (x) = operatorname {P} (X leq x) = sum _ {x_ {i} leq x} operatorname {P} (X = x_ {i}) = сумма _ {x_ {i} leq x} p (x_ {i}).}
Если CDF FX { displaystyle F_ {X}}




- FX (b) – FX (a) = P (a < X ≤ b) = ∫ a b f X ( x) d x {displaystyle F_{X}(b)-F_{X}(a)=operatorname {P} (a
для всех действительных чисел a { displaystyle a}




Примеры
В качестве примера предположим, что X { displaystyle X}
![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
Тогда CDF для X { displaystyle X}
- FX (x) = {0: x < 0 x : 0 ≤ x ≤ 1 1 : x>1 { displaystyle F_ {X} (x) = { begin {cases} 0 : x <0\x: 0leq xleq 1\1: x>1 end {cases}}}
Предположим, что вместо этого X { displaystyle X}<169 принимает только дискретные значения 0 и 1 с равной вероятностью.
Тогда CDF X { displaystyle X}
- FX (x) = {0: x < 0 1 / 2 : 0 ≤ x < 1 1 : x ≥ 1 {displaystyle F_{X}(x)={begin{cases}0: x<0\1/2: 0leq x<1\1: xgeq 1end{cases}}}
Предположим, X { displaystyle X}

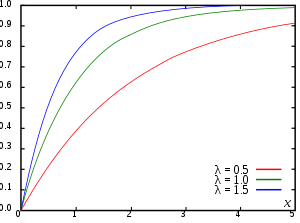
- FX (x; λ) = {1 – e – λ xx ≥ 0, 0 x < 0. {displaystyle F_{X}(x;lambda)={begin{cases}1-e^{-lambda x}xgeq 0,\0x<0.end{cases}}}
Здесь λ>0 – параметр распределения, часто называемый параметром скорости.
Предположим, что X { displaystyle X}

- F (x; μ, σ) = 1 σ 2 π ∫ – ∞ x exp (- (t – μ) 2 2 σ 2) dt. { Displaystyle F (х; му, sigma) = { frac {1} { sigma { sqrt {2 pi}}}} int _ {- infty} ^ {x} exp left (- { frac {(t- mu) ^ {2}} {2 sigma ^ {2}}} right) , dt.}
Здесь параметр μ { displaystyle mu}

Предположим, что X { displaystyle X}

- F (k; n, p) = Pr (X ≤ k) = ∑ i = 0 ⌊ k ⌋ (ni) пи (1 – п) N – я { Displaystyle F (к; п, р) = Pr (X Leq k) = сумма _ {я = 0} ^ { lfloor k rfloor} {п выберите i} p ^ {i} (1-p) ^ {ni}}
Здесь p { displaystyle p}




Производные функции
Дополнительная кумулятивная функция распределения (хвостовое распределение)
Иногда бывает полезно изучить противоположный вопрос и спросить, как часто случайная величина превышает определенный уровень. Это называется дополнительной кумулятивной функцией распределения (ccdf ) или просто хвостовым распределением или превышением и определяется как
- F ¯ X (x) = P (X>x) = 1 – FX (x). { displaystyle { bar {F}} _ {X} (x) = operatorname {P} (X>x) = 1-F_ {X} (x).}
Это имеет применения в статистической проверке гипотез, например, потому что одностороннее p-значение – это вероятность наблюдения статистической статистики при менее экстремально, чем наблюдаемое. Таким образом, при условии, что тестовая статистика, T, имеет непрерывное распределение, одностороннее p-значение просто дается ccdf: for наблюдаемое значение t { displaystyle t}
- p = P (T ≥ t) = P (T>t) = 1 – FT (t). { displaystyle p = operatorname {P} (T geq t) = operatorname {P} (T>t) = 1-F_ {T} (t).}
В анализе выживаемости, F ¯ X (x) { displaystyle { bar {F}} _ {X} (x)}

Z-таблице:
Одним из наиболее популярных приложений кумулятивной функции распределения является стандартная нормальная таблица, также называемая единичной нормальной таблицей или Z-таблицей, это значение кумулятивной функция распределения нормального распределения. Очень полезно использовать Z-таблицу не только для вероятностей ниже значения, которое является исходным приложением кумулятивной функции распределения, но также выше и / или между значениями стандартного нормального распределения, и в дальнейшем она была расширена до любого нормального распределения.
- Свойства
- Для неотрицательной непрерывной случайной величины, имеющей математическое ожидание, неравенство Маркова утверждает, что
-
- F ¯ X (x) ≤ E (X) x. { displaystyle { bar {F}} _ {X} (x) leq { frac { operatorname {E} (X)} {x}}.}
- F ¯ X (x) ≤ E (X) x. { displaystyle { bar {F}} _ {X} (x) leq { frac { operatorname {E} (X)} {x}}.}
- Доказательство: предположим, что X { displaystyle X}
имеет функцию плотности f X { displaystyle f_ {X}}
, для любого c>0 { displaystyle c>0}
- E (X) = ∫ 0 ∞ xf X (x) dx ≥ ∫ 0 cxf Икс (Икс) dx + с ∫ с ∞ е Икс (Икс) dx { Displaystyle OperatorName {E} (X) = int _ {0} ^ { infty} xf_ {X} (x) , dx geq int _ {0} ^ {c} xf_ {X} (x) , dx + c int _ {c} ^ { infty} f_ {X} (x) , dx}
- E (X) = ∫ 0 ∞ xf X (x) dx ≥ ∫ 0 cxf Икс (Икс) dx + с ∫ с ∞ е Икс (Икс) dx { Displaystyle OperatorName {E} (X) = int _ {0} ^ { infty} xf_ {X} (x) , dx geq int _ {0} ^ {c} xf_ {X} (x) , dx + c int _ {c} ^ { infty} f_ {X} (x) , dx}
- Затем при распознавании F ¯ X (c) = ∫ c ∞ f X (x) dx { displaystyle { bar {F}} _ {X} (c) = int _ {c} ^ { infty} f_ {X} (x) , dx}
и переставляя члены,
- 0 ≤ c F ¯ X (c) ≤ E (X) – ∫ 0 cxf X (x) dx → 0 как c → ∞ { displaystyle 0 leq c { bar {F}} _ {X} (c) leq operatorname {E} (X) – int _ {0} ^ {c} xf_ { X} (x) , dx to 0 { text {as}} c to infty}
- 0 ≤ c F ¯ X (c) ≤ E (X) – ∫ 0 cxf X (x) dx → 0 как c → ∞ { displaystyle 0 leq c { bar {F}} _ {X} (c) leq operatorname {E} (X) – int _ {0} ^ {c} xf_ { X} (x) , dx to 0 { text {as}} c to infty}
- как заявлено.
Свернутое кумулятивное распределение
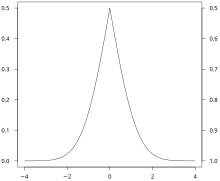
Хотя график кумулятивного распределения часто имеет S-образную форму, альтернативной иллюстрацией является свернутое кумулятивное распределение или горный график, который складывает верхнюю половину графика, таким образом используя две шкалы: одну для подъема, а другую – для спада. Эта форма иллюстрации подчеркивает медиану и дисперсию (в частности, среднее абсолютное отклонение от медианы) распределения или эмпирических результатов.
Обратная функция распределения (функция квантиля)
Если функция распределения F строго возрастает и непрерывна, то F – 1 (p), p ∈ [0, 1], { displaystyle F ^ {- 1} (p), p in [0,1],}![F ^ {- 1} (p), p in [0,1],](https://wikimedia.org/api/rest_v1/media/math/render/svg/b89fe1b58ff06ad5647ba178886bb6704d8da846)


Некоторые распределения не имеют уникального обратного распределения (например, в случае, когда f X (x) = 0 { displaystyle f_ {X} (x) = 0}


![p in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)
- F – 1 (p) = inf {x ∈ R: F (x) ≥ p}. { displaystyle F ^ {- 1} (p) = inf {x in mathbb {R}: F (x) geq p }.}
Некоторые полезные свойства обратного cdf (которые также сохраняются в определении обобщенной функции обратного распределения):
- F – 1 { displaystyle F ^ {- 1}}
неубывает
- F – 1 (F (x)) ≤ x { displaystyle F ^ {- 1} (F ( х)) leq x}
- F (F – 1 (p)) ≥ p { displaystyle F (F ^ {- 1} (p)) geq p}
- F – 1 (p) ≤ x { displaystyle F ^ {- 1} (p) leq x}
тогда и только тогда, когда p ≤ F (x) { displaystyle p leq F (x)}
- Если Y { displaystyle Y}
имеет распределение U [0, 1] { displaystyle U [0,1]}
, тогда F – 1 (Y) { displaystyle F ^ {- 1} (Y)}
распространяется как F { displaystyle F}
. Это используется в генерации случайных чисел с использованием метода выборки обратного преобразования.
- Если {X α} { displaystyle {X _ { alpha } }}
– это набор независимых F { displaystyle F}
-распределенных случайных величин, определенных в одном и том же пространстве выборки, тогда существуют случайные переменные Y α { displaystyle Y _ { alpha}}
такой, что Y α { displaystyle Y _ { alpha}}
распределяется как U [0, 1] { displaystyle U [0,1]}
и F – 1 (Y α) = X α { displaystyle F ^ {- 1} (Y _ { alpha}) = X _ { alpha}}
с вероятностью 1 для всех α { displaystyle alpha}
.
Обратное к cdf может использоваться для преобразования результатов, полученных для равномерного распределения, в другие распределения.
Эмпирическая функция распределения
эмпирическая функция распределения – это оценка кумулятивной функции распределения, которая сгенерировала точки в выборке. Он сходится с вероятностью 1 к этому базовому распределению. Существует ряд результатов для количественной оценки скорости сходимости эмпирической функции распределения к лежащей в основе кумулятивной функции распределения.
Многомерный случай
Определение для двух случайных величин
При одновременной работе с более чем одной случайной величиной также можно определить совместную кумулятивную функцию распределения . Например, для пары случайных величин X, Y { displaystyle X, Y}

FX, Y (x, y) = P (X ≤ x, Y ≤ y) { displaystyle F_ {X, Y} (x, y) = operatorname {P} (X leq x, Y leq y)} |
(Eq.3) |
где правая часть представляет вероятность того, что случайная величина X { displaystyle X}



Пример совместной кумулятивной функции распределения:
Для двух непрерывных переменных X и Y: Pr (a < X < b and c < Y < d) = ∫ a b ∫ c d f ( x, y) d y d x {displaystyle Pr(a
Для двух дискретных случайных величин, полезно создать таблицу вероятностей и рассмотреть совокупную вероятность для каждого потенциального диапазона X и Y, и вот пример:
с учетом совместной функции плотности вероятности в табличной форме, определить совместную совокупную расстояние функция распределения.
| Y = 2 | Y = 4 | Y = 6 | Y = 8 | |
| X = 1 | 0 | 0,1 | 0 | 0,1 |
| X = 3 | 0 | 0 | 0,2 | 0 |
| X = 5 | 0,3 | 0 | 0 | 0,15 |
| X = 7 | 0 | 0 | 0,15 | 0 |
Решение: используя данную таблицу вероятностей для каждого диапазона потенциалов X и Y, совместная кумулятивная функция распределения может быть построена в табличной форме:
| Y < 2 | 2 ≤ Y < 4 | 4 ≤ Y < 6 | 6 ≤ Y < 8 | Y ≤ 8 | |
| X < 1 | 0 | 0 | 0 | 0 | 0 |
| 1 ≤ X < 3 | 0 | 0 | 0,1 | 0,1 | 0,2 |
| 3 ≤ X < 5 | 0 | 0 | 0,1 | 0,3 | 0,4 |
| 5 ≤ X < 7 | 0 | 0,3 | 0,4 | 0,6 | 0,85 |
| X ≤ 7 | 0 | 0,3 | 0,4 | 0,75 | 1 |
.
Определение для более чем две случайные величины
Для N { displaystyle N}


FX 1,…, XN (x 1,…, x N) = P (X 1 ≤ x 1,…, XN ≤ xn) { displaystyle F_ {X_ {1}, ldots, X_ {N} } (x_ {1}, ldots, x_ {N}) = имя оператора {P} (X_ {1} leq x_ {1}, ldots, X_ {N} leq x_ {n})} |
(уравнение 4) |
Интерпретация N { displaystyle N}

- FX (x) = P (X 1 ≤ x 1,…, XN ≤ xn) { displaystyle F _ { mathbf {X}} ( mathbf {x}) = operatorname {P} (X_ {1} leq x_ {1}, ldots, X_ {N} leq x_ {n})}
Свойства
Каждая многомерная CDF:
- Монотонно неубывающая для каждой из своих переменных,
- Непрерывно справа по каждой из своих переменных,
- 0 ≤ FX 1… X n (Икс 1,…, xn) ≤ 1, { Displaystyle 0 leq F_ {X_ {1} ldots X_ {n}} (x_ {1}, ldots, x_ {n}) leq 1,}
- lim x 1,…, xn → + ∞ FX 1… X n (x 1,…, xn) = 1 и lim xi → – ∞ FX 1… X n (x 1,…, xn) = 0, для всех я. { displaystyle lim _ {x_ {1}, ldots, x_ {n} rightarrow + infty} F_ {X_ {1} ldots X_ {n}} (x_ {1}, ldots, x_ {n }) = 1 { text {и}} lim _ {x_ {i} rightarrow – infty} F_ {X_ {1} ldots X_ {n}} (x_ {1}, ldots, x_ {n }) = 0, { text {для всех}} i.}
Вероятность того, что точка принадлежит гипер прямоугольнику, аналогична одномерному случаю:
- FX 1, X 2 (a, c) + FX 1, X 2 (b, d) – FX 1, X 2 (a, d) – FX 1, X 2 (b, c) = P (a < X 1 ≤ b, c < X 2 ≤ d) = ∫… {displaystyle F_{X_{1},X_{2}}(a,c)+F_{X_{1},X_{2}}(b,d)-F_{X_{1},X_{2}}(a,d)-F_{X_{1},X_{2}}(b,c)=operatorname {P} (a
Сложный случай
Сложная случайная величина
Обобщение кумулятивной функции распределения от реальных до сложных случайных величин неочевидно, поскольку выражения вида P (Z ≤ 1 + 2 i) { displaystyle P (Z leq 1 + 2i)}

- FZ (z) = F ℜ (Z), ℑ (Z) (ℜ (z), ℑ (z)) = P (ℜ (Z) ≤ ℜ (z), ℑ (Z) ≤ ℑ (z)) { Displaystyle F_ {Z} (z) = F _ { Re {(Z)}, Im {(Z)}} ( Re {(z)}, Im {(z) }) = P ( Re {(Z)} leq Re {(z)}, Im {(Z)} leq Im {(z)})}
.
Комплексный случайный вектор
Обобщение Eq.4дает
- FZ (z) = F ℜ (Z 1), ℑ (Z 1),…, ℜ (Z n), ℑ (Z n) (ℜ (z 1), ℑ (z 1),…, ℜ (zn), ℑ (zn)) = P (ℜ (Z 1) ≤ ℜ (z 1), ℑ (Z 1) ≤ ℑ (Z 1),…, ℜ (Z N) ≤ ℜ (Zn), ℑ (Z N) ≤ ℑ (Zn)) { Displaystyle F _ { mathbf {Z}} ( mathbf {z}) = F _ { Re {(Z_ {1})}, Im {(Z_ {1})}, ldots, Re {(Z_ {n})}, Im {(Z_ {n})}} ( Re {(z_ {1})}, Im {(z_ {1})}, ldots, Re {(z_ {n})}, Im {(z_ {n})}) = operatorname {P} ( Re {(Z_ {1})} leq Re {(z_ {1})}, Im {(Z_ {1})} leq Im {(z_ {1})}, ldots, Re {(Z_ {n})} leq Re {(z_ {n})}, Im {(Z_ {n})} leq Im {(z_ {n})})}
как определение CDS комплексного случайного вектора Z = (Z 1,…, ZN) T { displaystyle mathbf {Z} = (Z_ {1}, ldots, Z_ {N}) ^ {T}}
Использование в статистическом анализе
Концепция кумулятивной функции распределения явно проявляется в статистический анализ двумя (похожими) способами. Кумулятивный частотный анализ – это анализ частоты появления значений явления, меньших контрольного значения. эмпирическая функция распределения представляет собой формальную прямую оценку кумулятивной функции распределения, для которой могут быть получены простые статистические свойства и которая может лечь в основу различных тестов статистических гипотез. Такие тесты могут оценить, есть ли свидетельства против выборки данных, полученных из данного распределения, или свидетельства против двух выборок данных, полученных из одного и того же (неизвестного) распределения населения.
Тесты Колмогорова-Смирнова и Койпера
Тест Колмогорова-Смирнова основан на кумулятивных функциях распределения и может использоваться для проверки того, являются ли два эмпирических распределения разными или отличается ли эмпирическое распределение от идеального. Тесно связанный критерий Койпера полезен, если область распределения является циклической, например, по дням недели. Например, тест Койпера можно использовать, чтобы увидеть, меняется ли количество торнадо в течение года или продажи продукта меняются в зависимости от дня недели или дня месяца.
См. Также
Ссылки
Внешние ссылки
СМИ, относящиеся к кумулятивным функциям распределения на Wikimedia Commons
Принимая инвестиционных решения, мы практически всегда мы работаем со случайными величины. Доходность акции и прибыль на акцию являются типичными примерами случайных величин.
Чтобы сделать вероятностные утверждения о случайной величине, нам нужно понять ее распределение вероятностей (англ. ‘probability distribution’). Распределение вероятностей определяет вероятности возможных исходов случайной величины.
В этом чтении мы представляем важные факты о четырех распределениях вероятности и их использовании в финансовом анализе. Эти четыре распределения – равномерное, биномиальное, нормальное и логнормальное (т.е. логарифмически нормальное) – широко используются в инвестиционной практике.
Они используются в таких базовых моделях оценки, как модель ценообразования опционов Блэка-Шоулза-Мертона, модель ценообразования биномиальных опционов и модель ценообразования долгосрочных активов (CAPM). Обладая практическими знаниями о распределении вероятностей, представленными в этом чтении, вы также будете лучше подготовлены к изучению и использованию других количественных методов, таких как проверка статистических гипотез, регрессионный анализ и анализ временных рядов.
После обсуждения распределения вероятностей мы заканчиваем чтение описанием метода моделирования Монте-Карло, компьютерным инструментом моделирования для получения ответов на сложные вопросы.
Например, инвестиционный аналитик может захотеть поэкспериментировать с инвестиционной идеей, фактически не реализовав ее. Или ему или ей может понадобиться оценка сложного опциона, для которого не существует простой формулы ценообразования.
В этих и многих других случаях метод Монте-Карло является важным инструментом в арсенале аналитика. Для проведения моделирования по методу Монте-Карло аналитик должен определить факторы риска, связанные с проблемой, и указать распределения вероятностей для них.
Следовательно, моделирование методом Монте-Карло является инструментом, который требует понимания распределения вероятностей.
Прежде чем мы обсудим конкретные распределения вероятностей, мы определим основные понятия и термины. Затем мы проиллюстрируем действие этих понятий через простейшее распределение, – равномерное распределение. После этого мы рассмотрим другие распределения вероятностей, которые имеют больше применений в инвестиционной практике, но также более сложны.
Дискретные случайные величины.
Случайная величина (англ. ‘random variable’) – это величина, будущие результаты которой неопределенны. Два основных типа случайных величин – это дискретные случайные величины (англ. ‘discrete random variables’) и непрерывные случайные величины (англ. ‘continuous random variables’). Дискретная случайная величина может принимать исчислимое количество возможных значений.
Например, дискретная случайная величина (X) может принимать ограниченное количество значений ( x_1, x_2, ldots, x_n ) (n возможных результатов), или дискретная случайная величина (Y) может принимать неограниченное количество значений ( x_1, x_2, ldots) ) (до бесконечности).
Мы придерживаемся соглашения, что заглавная буква представляет случайную величину, а строчная буква представляет результат (исход) или конкретное значение случайной величины. Таким образом, (X) обозначает случайную переменную, а x обозначает результат переменной (X). Мы подписываем результаты, как ( x_1, x_2 ), когда нам нужно различать отдельные результаты в списке значений случайной переменной.
Поскольку мы можем подсчитать все возможные результаты (X) и (Y) (даже если мы будем продолжать вечно в случае с (Y)), и (X), и (Y) удовлетворяют определению дискретной случайной величины. И напротив, мы не можем подсчитать результаты непрерывной случайной величины.
Мы не можем описать возможные результаты непрерывной случайной величины (Z) с исходами ( z_1, z_2, ldots ), когда возможный результат ( (z_1 + z_2)/2 ) отсутствует в списке результатов. Ставка доходности является примером непрерывной случайной величины.
Работая со случайной величиной, мы должны понимать ее возможные результаты.
Например, большинство акций, торгуемых на новозеландской фондовой бирже, котируются в тиках NZ$0.01. Таким образом, котируемая цена акций является дискретной случайной величиной с возможными значениями NZ$0, NZ$0.01, NZ$0.02, …
Но мы также можем смоделировать цену акций в виде непрерывной случайной величины (в качестве логнормальной случайной величины, которую мы рассмотрим позднее). Во многих практических ситуациях у нас есть выбор между использованием дискретного или непрерывного распределения. Обычно мы руководствуемся тем, какое распределение наиболее эффективно для стоящей перед нами задачи.
Эта возможность выбора не удивительна, так как многие дискретные распределения могут быть приблизительно равны непрерывным распределениям, и наоборот. В большинстве практических случаев распределение вероятностей – это всего лишь математическая идеализация или приблизительная модель относительных частот возможных результатов случайной величины.
Пример (1) распределения цены облигации.
Вы исследуете вероятностную модель цены облигации и анализируете характеристики облигаций, которые влияют на ее цену.
Каковы самые низкие и максимально возможные значения цены облигации? Почему?
Какие еще характеристики облигаций могут влиять на распределение цены облигаций?
Минимально возможное значение цены облигации равно 0, когда облигация бесполезна. Определение максимально возможного значения цены облигации является более сложной задачей. Обещанные платежи по купонной облигации – это купоны (процентные платежи) плюс номинальная сумма (основная сумма).
Цена облигации – это дисконтированная стоимость этих обещанных платежей. Поскольку инвесторы требуют возврата своих инвестиций, 0 процентов – это нижний предел ставки дисконта, который инвесторы будут использовать для дисконтирования обещанных платежей по облигациям.
При ставке дисконтирования 0% цена облигации представляет собой сумму номинальной стоимости и оставшихся купонов без какого-либо дисконта. Таким образом, ставка дисконта устанавливает верхний предел цены облигации.
Предположим, например, что номинальная стоимость составляет $1,000, и остались 2 купона на $40; интервал от $0 до $1,080 охватывает все возможные значения цены облигации. Этот верхний предел уменьшается со временем по мере уменьшения количества оставшихся платежей.
Прочие характеристики облигации также влияют на ее распределение цен. Привязка к номинальной стоимости является одной из таких характеристик: по мере приближения даты погашения стандартное отклонение цены облигации имеет тенденцию к уменьшению, когда цена облигации приближается к номинальной стоимости.
Встроенные опционы также влияют на цену облигации. Например, если облигации в текущий момент могут быть отозваны, эмитент может выкупить эти облигации с заранее установленной премией выше номинальной; этот опцион эмитента частично снижает рост цены облигации. Моделирование распределения цен облигаций является сложной задачей.
Каждая случайная величина связана с распределением вероятностей, которое полностью описывает переменную. Мы можем рассмотреть распределение вероятности двумя способами.
Основным представлением является функция вероятности, которая определяет вероятность того, что случайная величина принимает определенное значение:
( P(X = x) ) – это вероятность того, что случайная величина (X) принимает значение (x).
(Обратите внимание, что заглавная буква (X) обозначает случайную величину, а строчная буква x обозначает конкретное значение, которое может принимать случайная величина.)
Для дискретной случайной величины сокращенная запись для функции вероятности имеет вид:
( large p(x) = P(X = x) )
Для непрерывных случайных величин функция вероятности обозначается ( f(x) ) и называется функцией плотности вероятности (pdf, от англ. ‘probability density function’), или просто плотностью.
Другой технический термин для функции вероятности дискретной случайной величины – функция массы вероятности (pmf, от англ. ‘probability mass function’). Этот термин используется реже.
Функция вероятности имеет два ключевых свойства:
- ( 0 leq p(x) leq 1 ), потому что вероятность – это число от 0 до 1.
- Сумма вероятностей ( p(x) ) всех значений (X) равна 1. Если мы сложим вероятности всех различных возможных результатов случайной величины, эта сумма должна равняться 1.
Мы часто заинтересованы в поиске вероятности ряда результатов, а не конкретного результата. В этих случаях мы используем второе представление о распределении вероятностей, – кумулятивную (или накопленную) функцию распределения (cdf, англ. ‘cumulative distribution function’).
Кумулятивная функция распределения, или просто функция распределения, дает вероятность того, что случайная величина (X) меньше или равна определенному значению ( x ), ( P (X leq x) ).
Как для дискретных, так и для непрерывных случайных величин сокращенная запись следующий вид:
( large F(x) = P(X leq x) )
Как кумулятивная функция распределения связана с функцией вероятности?
Слово «кумулятивный» подразумевает накопленные исторические результаты. Чтобы найти ( F(x) ), мы суммируем или накапливаем значения функции вероятности для всех результатов, меньших или равных x.
Функция cdf параллельна функции кумулятивной (накопленной) относительной частоты, которую мы обсуждали в чтении о статистических концепциях и доходности рынка.
Далее мы проиллюстрируем эти концепции на примерах и покажем, как мы используем дискретные и непрерывные распределения. Начнем с простейшего распределения – дискретного равномерного распределения.
Дискретное равномерное распределение.
Простейшим из всех распределений вероятности является дискретное равномерное распределение. Предположим, что возможными результатами являются целые числа от 1 до 8 включительно, и вероятность того, что случайная переменная принимает любое из этих возможных значений, одинакова для всех результатов (то есть она является равномерной).
При восьми исходах ( p(x) = 1/8 ) или 0.125, для всех значений (X(X = 1, 2, 3, 4, 5, 6, 7, 8)); только что сделанное утверждение является полным описанием этой дискретной равномерной случайной величины. Распределение имеет конечное число указанных результатов, и каждый результат одинаково вероятен.
В Таблице 1 приведены два представления этой случайной величины: функция вероятности и кумулятивная функция распределения.
|
Функция вероятности |
Кумулятивная |
|
|---|---|---|
|
( X=x ) |
( p(x) = P(X = x) ) |
( F(x) = P(X leq x) ) |
|
1 |
0.125 |
0.125 |
|
2 |
0.125 |
0.250 |
|
3 |
0.125 |
0.375 |
|
4 |
0.125 |
0.500 |
|
5 |
0.125 |
0.625 |
|
6 |
0.125 |
0.750 |
|
7 |
0.125 |
0.875 |
|
8 |
0.125 |
1.000 |
Мы можем использовать Таблицу 1, чтобы найти три вероятности:
- ( P (X leq 7) ),
- ( P (4 leq X leq 6) ) и
- ( P (4 < X leq 6) ).
Следующие примеры иллюстрируют, как использовать cdf, чтобы найти вероятность того, что случайная переменная попадет в любой интервал (для любой случайной переменной, а не только для равномерной).
Вероятность того, что (X) меньше или равно 7, ( P (X leq 7) ), является ближайшей к последней записи в третьем столбце, 0.875 или 87.5%.
Чтобы найти ( P (4 leq X leq 6) ), нам нужно найти сумму трех вероятностей: (p(4)), (p(5)) и (p(6)). Мы можем найти эту сумму двумя способами. Мы можем сложить (p(4)), (p(5)) и (p(6)) из второго столбца. Или мы можем вычислить вероятность как разницу между двумя значениями кумулятивной функции распределения:
( F(6) = P(X leq 6) = p(6) + p(5) + p(4) + p(3) + p(2) + p(1) )
( F(3) = P(X leq 3) = p(3) + p(2) + p(1) )
поэтому
( begin{aligned} P(4 leq X leq 6) &= F(6) – F(3) \ &= p(6) + p(5) + p(4) = 3/8 end{aligned} )
Поэтому мы вычисляем вторую вероятность как:
( F(6) – F(3) = 3/8 )
Третья вероятность, ( P (4 < X leq 6) ), вероятность того, что (X) меньше или равно 6, но больше 4, равна (p(5) + p(6)). Мы вычисляем ее следующим образом, используя cdf:
( begin{aligned} P(4 < X leq 6) &= P(X leq 6) – P(X leq 4) \ &= F(6) – F(4) = p(6) + p(5) = 2/8 end{aligned} )
Таким образом, мы вычисляем третью вероятность как:
( F(6) – F(4) = 2/8 ).
Предположим, мы хотим проверить, что дискретная равномерная функция вероятности удовлетворяет общим свойствам функции вероятности, приведенным ранее.
Первое свойство – это ( 0 leq p(x) leq 1 ). Мы видим, что (p(x) = 1/8) для всех (x) в первом столбце таблицы. (Обратите внимание, что (p(x)) равно 0 для чисел (x), таких как -14 или 12.215, которых нет в этом столбце.)
Первое свойство удовлетворяется.
Второе свойство состоит в том, что вероятности составляют в сумме 1. Записи во втором столбце таблицы 1 тоже составляют в сумме 1.
У cdf есть два других характерных свойства:
- cdf лежит между 0 и 1 для любого x: ( 0 leq F(x) leq 1 ).
- По мере увеличения (x), cdf либо увеличивается, либо остается постоянным.
Проверьте эти утверждения, посмотрев на третий столбец в Таблице 1.
Теперь у нас есть некоторый опыт работы с вероятностными функциями и cdf для дискретных случайных величин. Позже в этом чтении мы обсудим моделирование методом Монте-Карло, методологию, основанную на случайных числах.
Как мы увидим, равномерное распределение имеет важное техническое применение: оно является основой для генерации случайных чисел, которые, в свою очередь, производят случайные наблюдения для всех других распределений вероятности.
Случайные числа, изначально генерируемые компьютерами, обычно представляют собой случайные положительные целые числа, которые преобразуются в приблизительные непрерывные равномерные случайные числа от 0 до 1. Затем непрерывные равномерные случайные числа используются для получения случайных наблюдений в других распределениях, таких как нормальное, с использованием различных методов.
Мы обсудим генерацию случайных наблюдений далее в разделе о методе моделирования Монте-Карло.
Как сравнивать распределения. От визуализации до статистических тестов
Время на прочтение
15 мин
Количество просмотров 21K

В подробном лонгриде к старту курса по анализу данных вы найдёте авторские визуализации, пояснения и комментарии об искусстве сравнивать распределения и делать выводы.
Сравнение эмпирического распределения переменной по разным группам — распространённая задача Data Science. Эта задача часто возникает при поиске причинно-следственных связей, когда нужно оценить качество рандомизации.
Золотой стандарт в выявлении причинно-следственных связей при оценке любой стратегии (функции UX, рекламной кампании, препарата и т. д.) — это рандомизированные контрольные испытания, известные как A/B-тесты. На практике выборка отбирается для исследования и случайным образом делится на группы — контрольную и экспериментальную, затем результаты этих групп сравниваются. Рандомизация гарантирует, что единственное различие двух группами — это выбранная независимая переменная, такая, что различия результатов можно объяснить именно её эффектом.
Несмотря на рандомизацию, эти группы никогда не бывают идентичными, а иногда их нельзя назвать даже «похожими». У нас может быть больше мужчин или пожилых людей в одной группе и т. д. (эти признаки обычно называются ковариатами — контрольными переменными). Когда такое случается, нельзя быть уверенным, что разница в результатах связана только с варьируемым нами эффектом и её нельзя приписать несбалансированным ковариатам. Поэтому после рандомизации всегда важно проверить сбалансированность всех наблюдаемых переменных между группами, а также проверить, нет ли систематических различий. Другой вариант, который позволяет заранее быть уверенным, что определённые ковариаты сбалансированы, — стратифицированная выборка.
Рассмотрим способы сравнения двух и более распределений, а также оценки величины и значимости их различий — визуальный и статистический. Эти подходы обычно сочетают интуицию и математическую точность: по диаграммам можно быстро оценить и изучить различия, но трудно сказать, систематические они или вызваны шумом.
Пример
Предположим, нужно провести эксперимент на группе людей, и мы случайным образом распределили их в экспериментальную (получает лечение) и контрольную группы (не получает его). Хотелось бы добиться наибольшей сопоставимости групп, чтобы объяснить любые различия между ними только эффектом от лекарства, который варьируется нами. Мы также разделили экспериментальную группу на разные группы для тестирования небольших вариаций одного и того же препарата.
Я смоделировал набор данных на 1000 человек, для которых мы наблюдаем набор характеристик, импортировал процесс генерации данных dgp_rnd_assignment() из src.dgp и некоторые графические функции и библиотеки из src.utils.
from src.utils import *
from src.dgp import dgp_rnd_assignment
df = dgp_rnd_assignment().generate_data()
df.head()У нас есть информация о 1000 человек, для которых мы наблюдаем переменные gender (пол), age (возраст) и income (доход за неделю). Каждый человек назначается либо в группу лечения, либо в контрольную группу (переменная group), и люди, получающие лечение, распределяются по четырём типам лечения (переменная arm).
Две группы — диаграммы
Начнём с самого простого: сравним распределение доходов в экспериментальной и контрольной группах. Сначала мы изучаем визуальные подходы, а затем статистические подходы. Преимущество первого — интуитивность, второго — математическая точность.
Для большинства визуализаций я буду использовать библиотеку Python seaborn.
Диаграмма размаха («ящик с усами»)
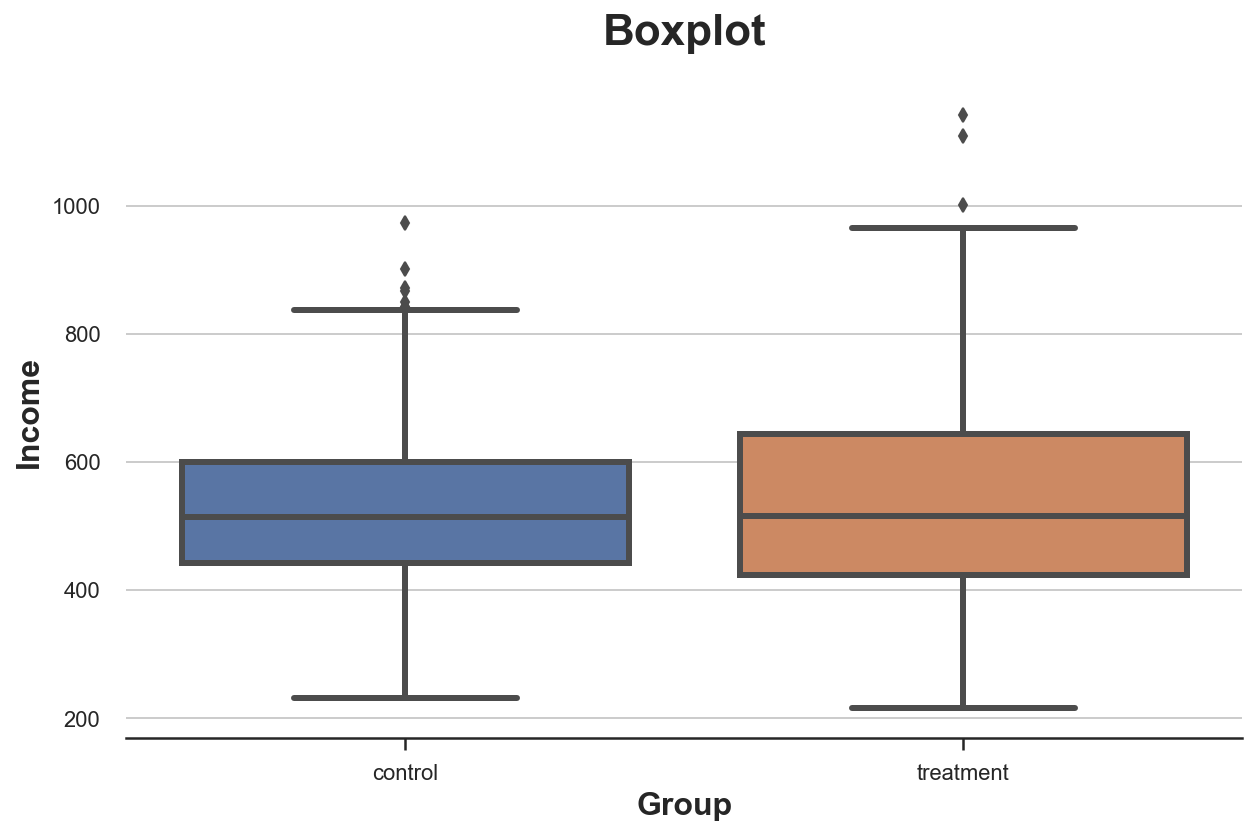
Первый визуальный подход — это диаграмма размаха. Такая диаграмма — это хороший компромисс между сводной статистикой и визуализацией данных. Центр «ящика» — медиана, а границы — первый (Q1) и третий квартиль (Q3) соответственно. «Усы» распространяются на первые точки данных, более чем в 1,5 раза превышающие межквартильный диапазон (Q3–Q1) вне «ящика». Точки за пределами «усов» наносятся на диаграмму отдельно и обычно считаются выбросами.
Эта диаграмма предоставляет сводную статистику (ящик и «усы»), а также прямую визуализацию данных — выбросы:
sns.boxplot(data=df, x='Group', y='Income');
plt.title("Boxplot");Кажется, распределение доходов в экспериментальной группе немного более рассеяно: оранжевый прямоугольник больше, а его «усы» охватывают более широкий диапазон. Но проблема ящика с усами в том, что он скрывает форму данных и сообщает некоторую сводную статистику, но не показывает фактическое распределение данных.
Гистограмма
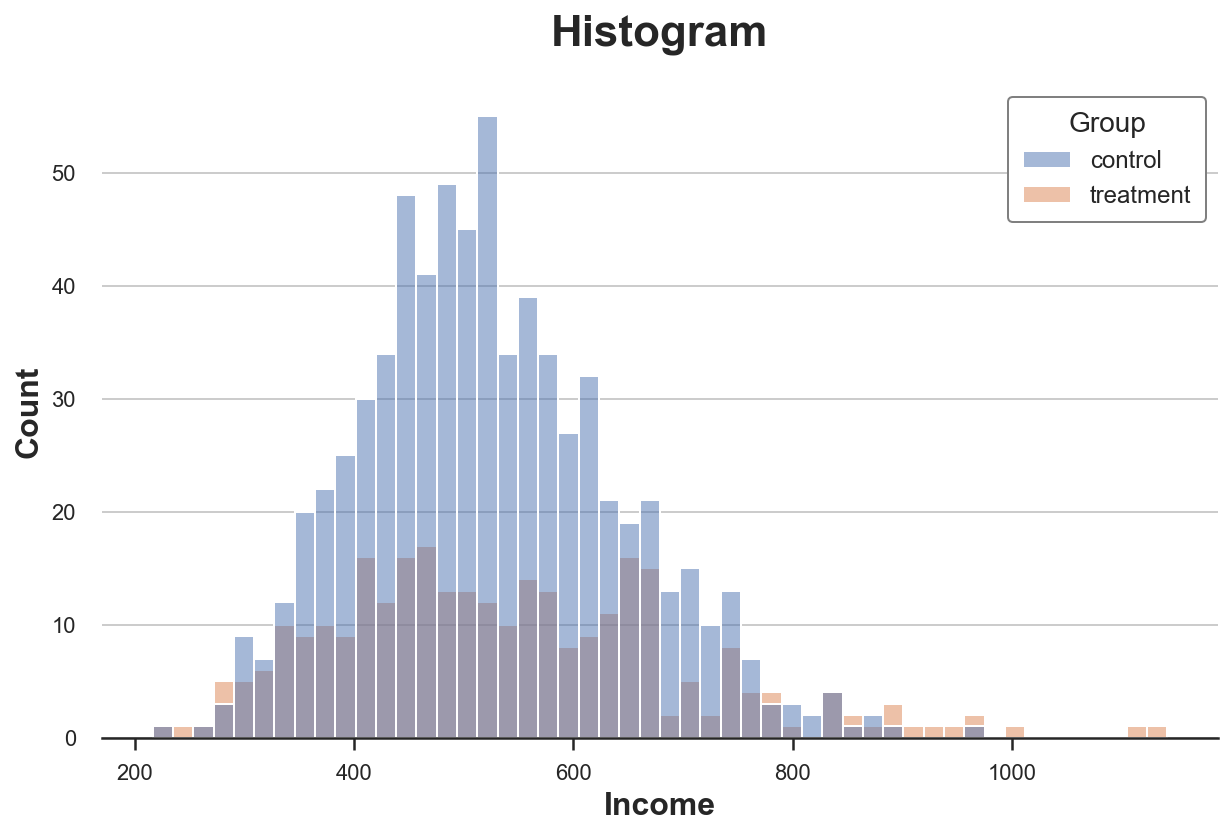
Наиболее интуитивно понятным способом построения диаграммы распределения является гистограмма. Гистограмма группирует данные в интервалы («бины») одинаковой ширины и отображает количество наблюдений в каждом интервале.
sns.histplot(data=df, x='Income', hue='Group', bins=50);
plt.title("Histogram");С этими диаграммами есть несколько проблем:
-
Количество наблюдений в группах разное, поэтому гистограммы несопоставимы.
-
Количество бинов произвольное.
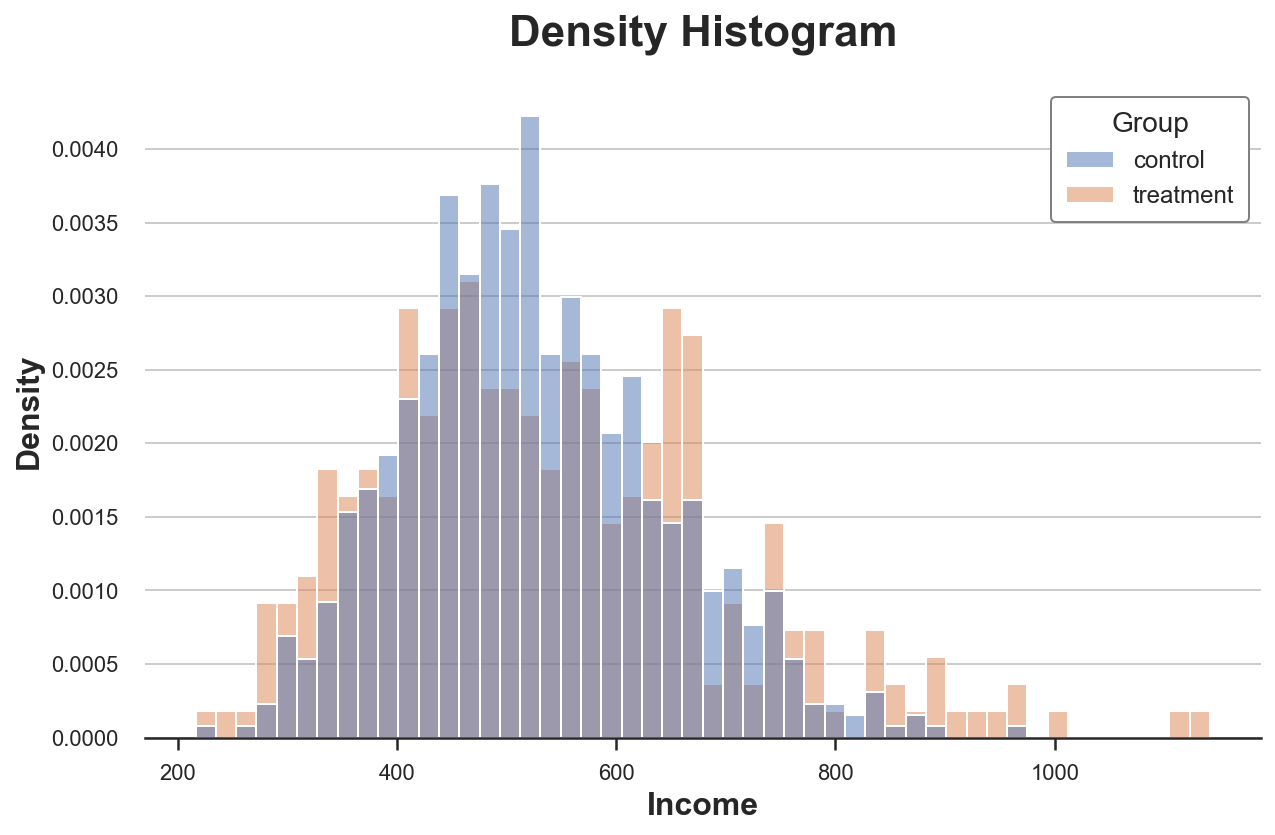
Решить первую проблему можно через параметр stat для построения диаграммы плотности вместо количества и установив для параметра common_norm значение False, чтобы нормализовать каждую гистограмму отдельно.
sns.histplot(data=df, x='Income', hue='Group', bins=50, stat='density', common_norm=False);
plt.title("Density Histogram");Теперь гистограммы сопоставимы!
Однако размер бинов по-прежнему произвольный. В крайнем случае, если сгруппировать меньше данных, мы получим бины не более чем с одним наблюдением, а если сгруппируем больше данных, то получим один бин. Так или иначе, если утрировать, диаграмма теряет информативность. Это — классический компромисс смещения и дисперсии.
Ядерная оценка плотности
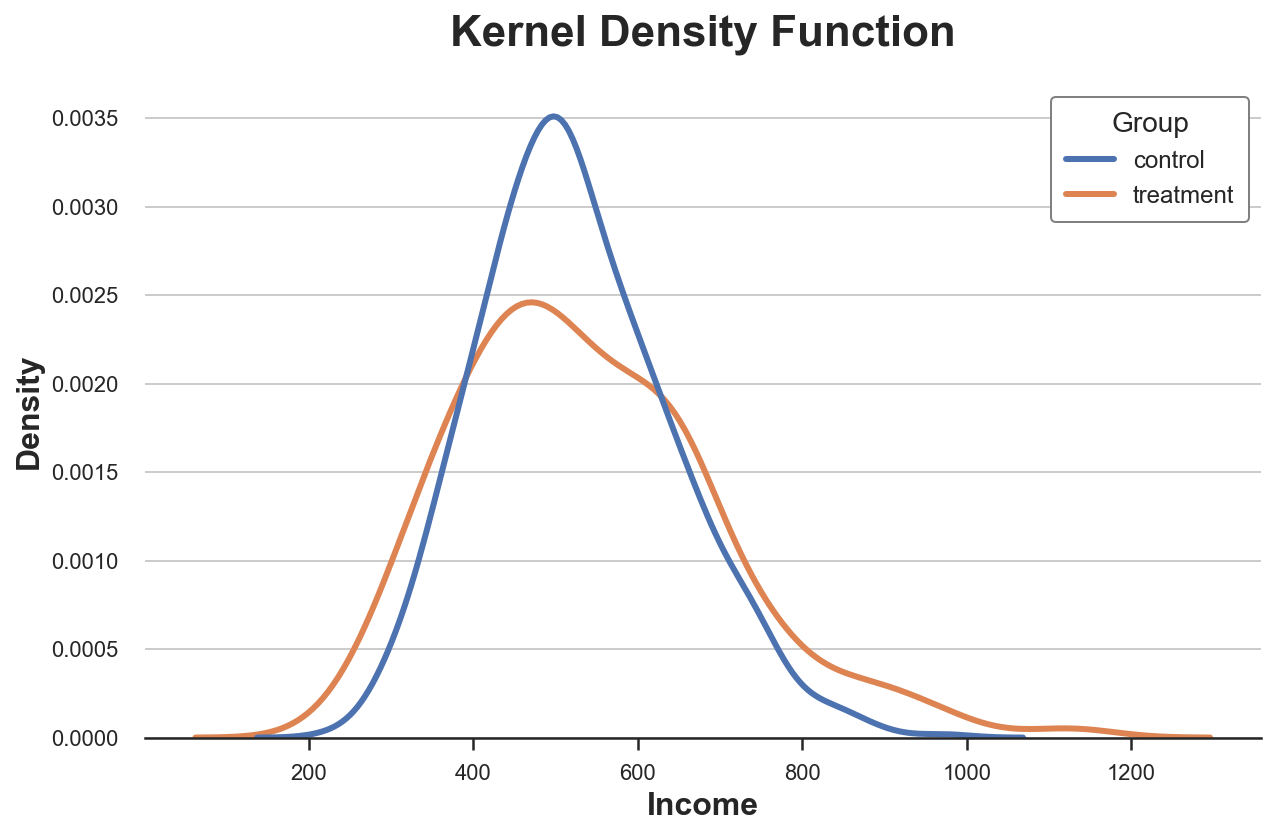
Одно из возможных решений — использовать метод ядерной оценки плотности, который пытается аппроксимировать гистограмму непрерывной функцией при помощи ядерной оценки плотности (KDE).
sns.kdeplot(x='Income', data=df, hue='Group', common_norm=False);
plt.title("Kernel Density Function");Выше видно, что ядерная оценка плотности дохода имеет «более толстые хвосты» (т. е. более высокую дисперсию) в экспериментальной группе, тогда как среднее значение по группам кажется одинаковым.
Проблема с ядерной оценкой плотности в том, что метод является чем-то вроде чёрного ящика, он может скрыть важные особенности данных.
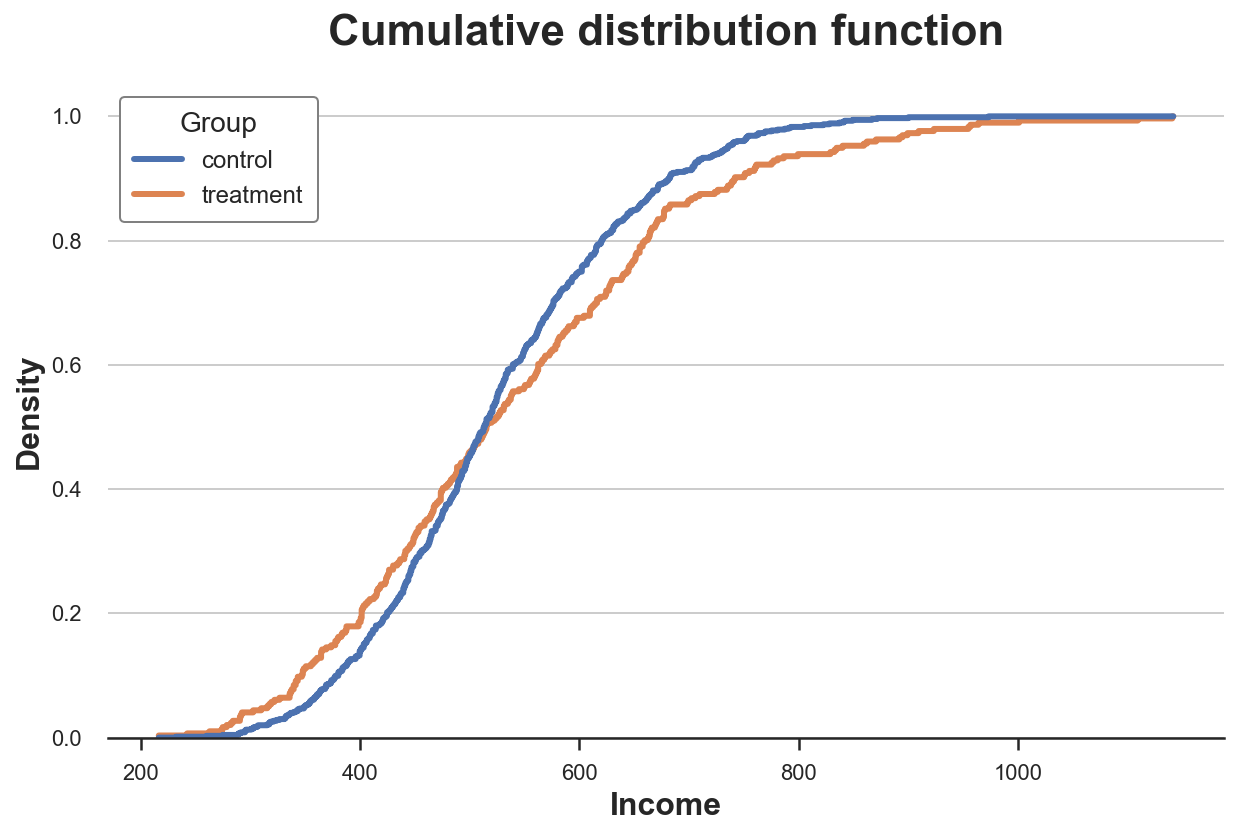
Кумулятивное распределение
Более прозрачное представление двух распределений — кумулятивная функция их распределения. В каждой точке оси x (доход) наносится процент точек данных, имеющих равное или меньшее значение. Основные преимущества кумулятивной функции распределения заключаются в том, что:
-
не нужно выбирать произвольно (например, количество бинов);
-
не нужна никакая аппроксимация (как с ядерной оценкой плотности), но мы представляем все точки данных.
sns.histplot(x='Income', data=df, hue='Group', bins=len(df), stat="density",
element="step", fill=False, cumulative=True, common_norm=False);
plt.title("Cumulative distribution function");Как же интерпретировать график?
-
Две линии пересекаются примерно в точке 0,5 (ось Y), а значит, их медианы cхожи.
-
Оранжевая линия выше синей линии слева и ниже этой линии справа: распределение экспериментальной группы имеет более толстые хвосты.
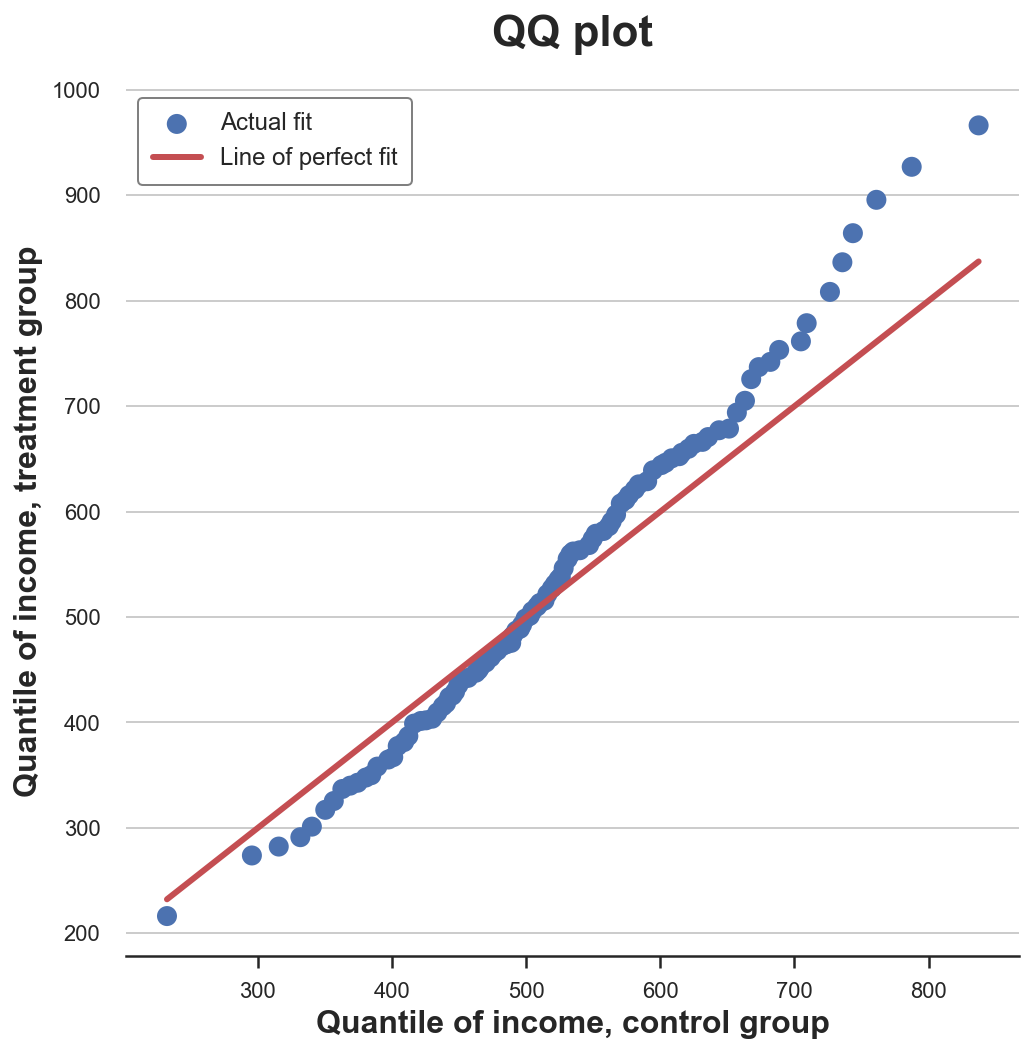
График квантиль-квантиль
Родственный метод — график квантиль-квантиль. Этот график отображает квантили двух распределений друг против друга. Если распределения совпадают, мы должны получить линию под углом в 45 градусов.
В Python нет встроенной функции графика квантиль–квантиль, и, хотя пакет statsmodels предоставляет функцию qqplot, он довольно громоздкий. Сделаем этот график вручную.
Во-первых, вычислим квартили двух групп функцией percentile.
income = df['Income'].values
income_t = df.loc[df.Group=='treatment', 'Income'].values
income_c = df.loc[df.Group=='control', 'Income'].values
df_pct = pd.DataFrame()
df_pct['q_treatment'] = np.percentile(income_t, range(100))
df_pct['q_control'] = np.percentile(income_c, range(100))Теперь можно построить два распределения квантилей относительно друг друга, а как эталон взять линию под углом в 45 градусов:
plt.figure(figsize=(8, 8))
plt.scatter(x='q_control', y='q_treatment', data=df_pct, label='Actual fit');
sns.lineplot(x='q_control', y='q_control', data=df_pct, color='r', label='Line of perfect fit');
plt.xlabel('Quantile of income, control group')
plt.ylabel('Quantile of income, treatment group')
plt.legend()
plt.title("QQ plot");График даёт представление, очень похожее на график кумулятивного распределения: доход в экспериментальной группе имеет ту же медиану (линии пересекаются в центре), но хвосты шире: точки ниже линии на левом конце и выше на правом.
Две группы — тесты
Итак, мы рассмотрели разные способы визуализации различий между распределениями. Главное преимущество визуализации — интуитивность.
Однако мы могли бы захотеть быть более точными и попытаться оценить статистическую значимость различия между распределениями, т. е. ответить на вопрос, «является ли наблюдаемое различие систематическим, или оно связано с шумом выборки?»
Проанализируем различные тесты, позволяющие сравнить два распределения.
T-тест
Первый и самый распространённый тест — t-критерий Стьюдента. T-тесты обычно используются для сравнения средних значений. Здесь хочется проверить, одинаковы ли средние значения распределения доходов в двух группах. Статистика теста для теста сравнения двух средних определяется таким образом:
x̅ — среднее значение выборки, s — стандартное отклонение выборки. В мягких условиях тестовая статистика асимптотически распределяется как t-распределение Стьюдента. Для выполнения t-теста воспользуемся функцией ttest_ind из scipy. Она возвращает тестовую статистику и предполагаемое p-значение.
from scipy.stats import ttest_ind
stat, p_value = ttest_ind(income_c, income_t)
print(f"t-test: statistic={stat:.4f}, p-value={p_value:.4f}")
t-test: statistic=-1.5549, p-value=0.1203Наше p-значение составляет 0,12, поэтому не отвергаем нулевую гипотезу об отсутствии различий в средних значениях в обеих группах.
Стандартизированная разность средних (SMD)
Как правило, при A/B-тестировании рекомендуется всегда проводить тест на различия средних значений всех переменных в экспериментальной и контрольной группах.
Однако знаменатель статистики t-критерия зависит от размера выборки, поэтому t-критерий критиковали из-за затруднения сравнения p-значений в разных исследованиях. На самом деле, мы можем получить значимый результат в эксперименте с очень малой величиной различия, но с большим размером выборки, в то время как получить незначимый результат можно в эксперименте с большой величиной различия, но с небольшим размером выборки.
Одно из предложенных решений — стандартизация разности средних (SMD). Как следует из названия метода, это не строго тестовая статистика, а просто стандартизированная разница, вычислить которую можно так:
Обычно значение ниже 0,1 считается «небольшой» разницей.
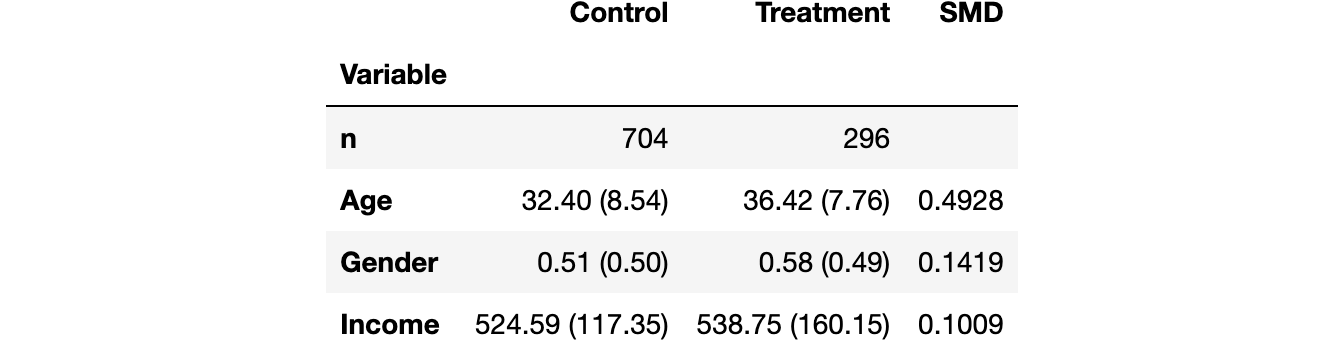
Хорошая практика — собрать средние значения всех переменных в экспериментальной и контрольной группах, а также измерить расстояния между ними — либо t-критерий, либо SMD — и занести в так называемую балансовую таблицу, для создания которой можно воспользоваться функцией create_table_one из библиотеки causalml. Как следует из названия функции, балансовая таблица всегда должна быть первой таблицей, которую вы представляете при выполнении A/B-тестирования.
from causalml.match import create_table_one
df['treatment'] = df['Group']=='treatment'
create_table_one(df, 'treatment', ['Gender', 'Age', 'Income'])В первых двух столбцах мы видим среднее значение различных переменных в экспериментальной и контрольной группах со стандартными ошибками в скобках. В последнем столбце значение SMD указывает на стандартизированную разницу более 0,1 для всех переменных, что позволяет предположить, что две группы, вероятно, различаются.
U-критерий Манна — Уитни
Альтернативный тест — U-критерий Манна — Уитни, который сравнивает медиану двух распределений. В частности, нулевая гипотеза для этого теста состоит в том, что две группы имеют одинаковое распределение, тогда как альтернативная гипотеза — в том, что одна группа имеет большие (или меньшие) значения, чем другая.
В отличие от тестов, которые мы видели до сих пор, U-критерий Манна — Уитни не зависит от выбросов и концентрируется на центре распределения.
И вот процедура расчёта критерия:
-
Объедините все точки данных и ранжируйте их в порядке возрастания или убывания.
-
Вычислите U₁ = R₁ − n₁(n₁ + 1)/2, где R₁ — сумма рангов точек данных в первой группе, а n₁ — количество точек в первой группе.
-
Аналогично вычислите U₂ для второй группы.
-
Тестовая статистика рассчитывается как stat = min(U₁, U₂).
При нулевой гипотезе об отсутствии систематических ранговых различий между двумя распределениями (т. е. об одинаковой медиане) тестовая статистика имеет асимптотическое нормальное распределение с известным средним значением и дисперсией.
Логика за вычислением R и U такова: если все значения в первой выборке больше, чем значения во второй выборке, то R₁ = n₁(n₁ + 1)/2 и, как следствие, U₁ будет тогда равным нулю (минимально достижимое значение). В противном случае, если бы две выборки были похожи, U₁ и U₂ были бы очень близки к n₁ n₂/2 (максимально достижимое значение).
Мы проводим тест при помощи mannwhitneyu из scipy:
from scipy.stats import mannwhitneyu
stat, p_value = mannwhitneyu(income_t, income_c)
print(f" Mann–Whitney U Test: statistic={stat:.4f}, p-value={p_value:.4f}")
Mann–Whitney U Test: statistic=106371.5000, p-value=0.6012Мы получаем p-значение 0,6, что означает, что мы не отвергаем нулевую гипотезу об отсутствии различий в медианах между экспериментальной и контрольной группами.
Пермутационные тесты
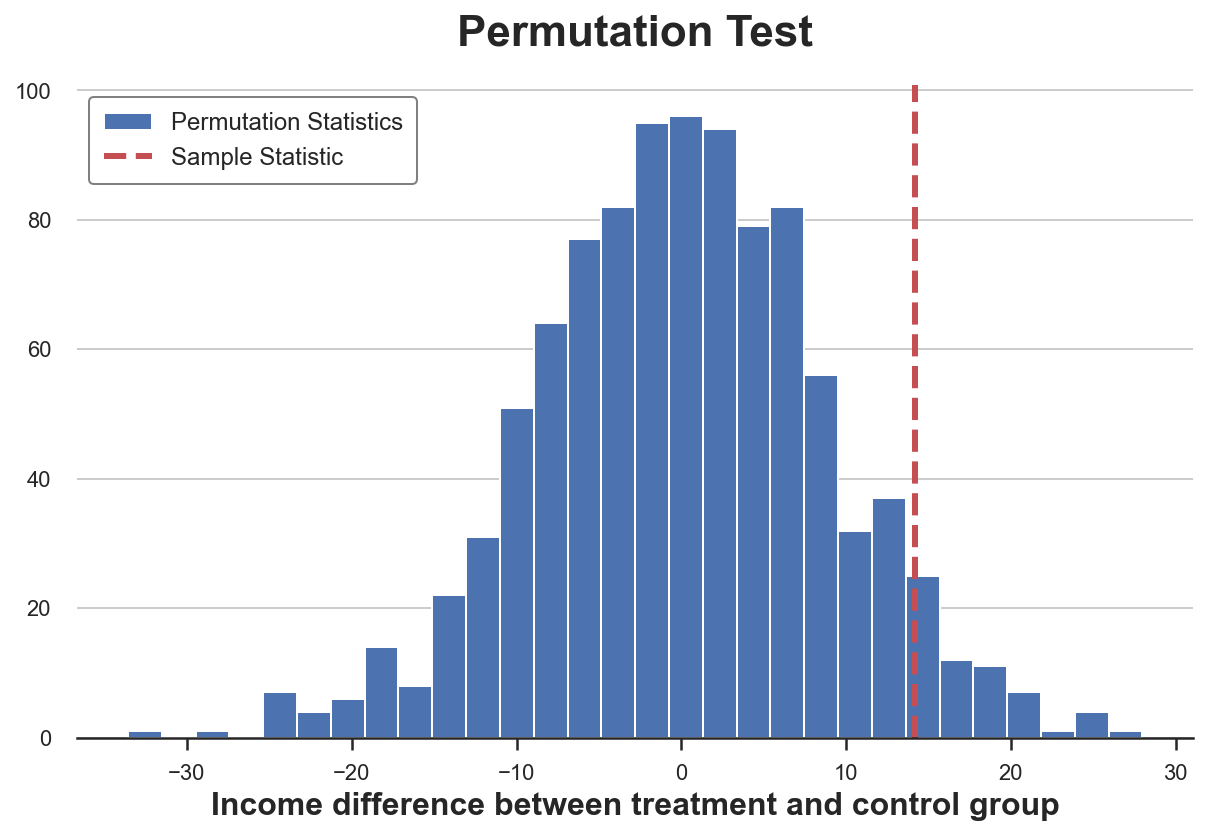
Непараметрическая альтернатива критерию Манна — Уитни — пермутационное (перестановочное) тестирование. Идея состоит в том, что при нулевой гипотезе два распределения должны быть одинаковыми, поэтому перетасовка меток групп не должна существенно изменить какую-либо статистику.
Мы можем выбрать любую статистику и проверить, как её значение в исходной выборке соотносится с её распределением по перестановкам групповых меток. Например, давайте использовать в качестве тестовой статистики разницу в выборочных средних между экспериментальной и контрольной группами.
sample_stat = np.mean(income_t) - np.mean(income_c)
stats = np.zeros(1000)
for k in range(1000):
labels = np.random.permutation((df['Group'] == 'treatment').values)
stats[k] = np.mean(income[labels]) - np.mean(income[labels==False])
p_value = np.mean(stats > sample_stat)
print(f"Permutation test: p-value={p_value:.4f}")
Permutation test: p-value=0.0530Пермутационный тест даёт нам p-значение 0,053, а это подразумевает слабое отклонение нулевой гипотезы на уровне 5%.
Как интерпретировать p-значение? Оно означает, что разница в средних значениях данных превышает 1 – 0,0560 = 94,4% различий в средних значениях по переставленным выборкам.
Тест можно визуализировать: построить диаграмму распределения статистики теста по перестановкам в зависимости от его выборочного значения.
plt.hist(stats, label='Permutation Statistics', bins=30);
plt.axvline(x=sample_stat, c='r', ls='--', label='Sample Statistic');
plt.legend();
plt.xlabel('Income difference between treatment and control group')
plt.title('Permutation Test');Как видим, выборочная статистика достаточно экстремальна по отношению к значениям в переставленных выборках, но не слишком.
Тест хи-квадрат
Тест хи-квадрат — это очень мощный тест, который в основном используется для проверки различий в частотах.
Одно из наименее известных применений критерия хи-квадрат — проверка сходства между двумя распределениями. Идея здесь — объединить наблюдения двух групп. Если бы два распределения были одинаковыми, можно было бы ожидать одинаковую частоту наблюдений в каждом бине. Важно отметить: чтобы тест был действительным, в каждом бине необходимо достаточное количество наблюдений.
Я генерирую ячейки, соответствующие децилям распределения дохода в контрольной группе, а затем вычисляю ожидаемое количество наблюдений в каждой ячейке в экспериментальной группе, если два распределения были одинаковыми.
# Init dataframe
df_bins = pd.DataFrame()
# Generate bins from control group
_, bins = pd.qcut(income_c, q=10, retbins=True)
df_bins['bin'] = pd.cut(income_c, bins=bins).value_counts().index
# Apply bins to both groups
df_bins['income_c_observed'] = pd.cut(income_c, bins=bins).value_counts().values
df_bins['income_t_observed'] = pd.cut(income_t, bins=bins).value_counts().values
# Compute expected frequency in the treatment group
df_bins['income_t_expected'] = df_bins['income_c_observed'] / np.sum(df_bins['income_c_observed']) * np.sum(df_bins['income_t_observed'])
df_binsТеперь мы можем выполнить тест, сравнив ожидаемое (E) и наблюдаемое (O) количество наблюдений в экспериментальной группе по бинам. Тестовая статистика задаётся следующим образом:
Бины индексируются как i, а O — наблюдаемое количество точек данных в бине i; E — ожидаемое количество точек данных бина i. Мы сгенерировали бины, используя децили распределения дохода в контрольной группе, поэтому ожидаем, что количество наблюдений на бин в экспериментальной группе будет одинаковым для всех бинов. Статистика теста асимптотически распределяется как распределение хи-квадрат.
Чтобы вычислить статистику теста и p-значение теста, воспользуемся функцией chisquare из scipy:
from scipy.stats import chisquare
stat, p_value = chisquare(df_bins['income_t_observed'], df_bins['income_t_expected'])
print(f"Chi-squared Test: statistic={stat:.4f}, p-value={p_value:.4f}")
Chi-squared Test: statistic=32.1432, p-value=0.0002В отличие от других тестов тест хи-квадрат решительно отвергает нулевую гипотезу об одинаковости двух распределений. Почему? Два распределения имеют похожий центр, но разные хвосты, и критерий хи-квадрат проверяет сходство по всему распределению, не только в центре, как в предыдущих тестах.
И этот результат предостерегает: прежде чем делать слепые выводы из p-значения, очень важно понять, что вы тестируете на самом деле!
Критерий Колмогорова — Смирнова
Идея критерия Колмогорова — Смирнова — сравнить кумулятивные распределения двух групп. В частности, статистика теста Колмогорова — Смирнова представляет собой максимальную абсолютную разницу между двумя кумулятивными распределениями.
Где F₁ и F₂ — две кумулятивные функции распределения, а x — значения базовой переменной. Асимптотическое распределение критерия Колмогорова — Смирнова имеет распределение Колмогорова.
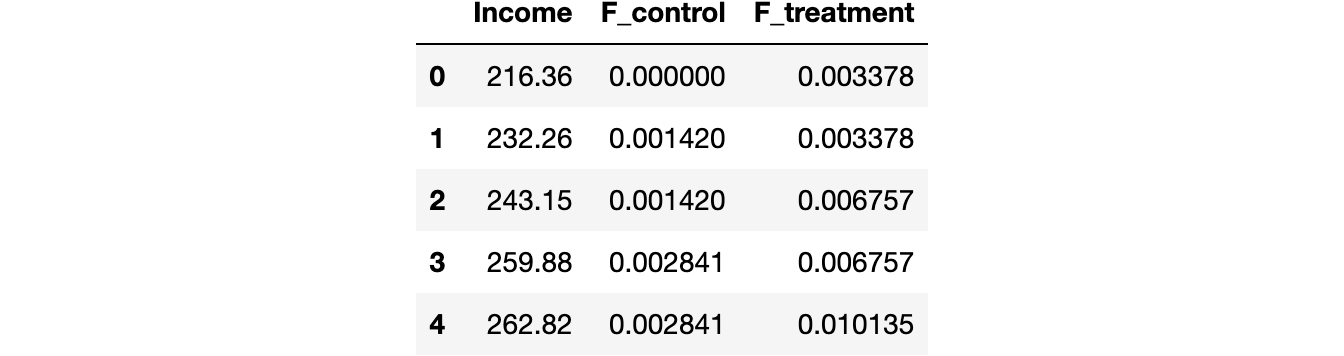
Чтобы лучше понять тест, построим кумулятивные функции распределения и статистику теста. Во-первых, вычислим кумулятивные функции распределения.
df_ks = pd.DataFrame()
df_ks['Income'] = np.sort(df['Income'].unique())
df_ks['F_control'] = df_ks['Income'].apply(lambda x: np.mean(income_c<=x))
df_ks['F_treatment'] = df_ks['Income'].apply(lambda x: np.mean(income_t<=x))
df_ks.head()Теперь нужно найти точку, где абсолютное расстояние между кумулятивными функциями распределения наибольшее.
k = np.argmax( np.abs(df_ks['F_control'] - df_ks['F_treatment']))
ks_stat = np.abs(df_ks['F_treatment'][k] - df_ks['F_control'][k])Можно также визуализировать значение тестовой статистики: построить две кумулятивные функции распределения и значение тестовой статистики.
y = (df_ks['F_treatment'][k] + df_ks['F_control'][k])/2
plt.plot('Income', 'F_control', data=df_ks, label='Control')
plt.plot('Income', 'F_treatment', data=df_ks, label='Treatment')
plt.errorbar(x=df_ks['Income'][k], y=y, yerr=ks_stat/2, color='k',
capsize=5, mew=3, label=f"Test statistic: {ks_stat:.4f}")
plt.legend(loc='center right');
plt.title("Kolmogorov-Smirnov Test");Видно, что значение тестовой статистики соответствует расстоянию между двумя кумулятивными распределениями при доходе ~650. Для этого значения дохода у нас самый большой дисбаланс между двумя группами.
А теперь можно выполнить сам тест, используя функцию kstest из scipy.
from scipy.stats import kstest
stat, p_value = kstest(income_t, income_c)
print(f" Kolmogorov-Smirnov Test: statistic={stat:.4f}, p-value={p_value:.4f}")
Kolmogorov-Smirnov Test: statistic=0.0974, p-value=0.0355Наше p-значение ниже 5%, поэтому с достоверностью 95% отвергаем нулевую гипотезу об одинаковости двух распределений.
Несколько групп — диаграммы
До сих пор рассматривался только случай двух групп: лечения и контроля. Но что, если групп несколько? Тогда некоторые методы выше масштабируются хорошо, а другие — нет. В качестве рабочего примера проверим, является ли распределение дохода одинаковым по типам лечения.
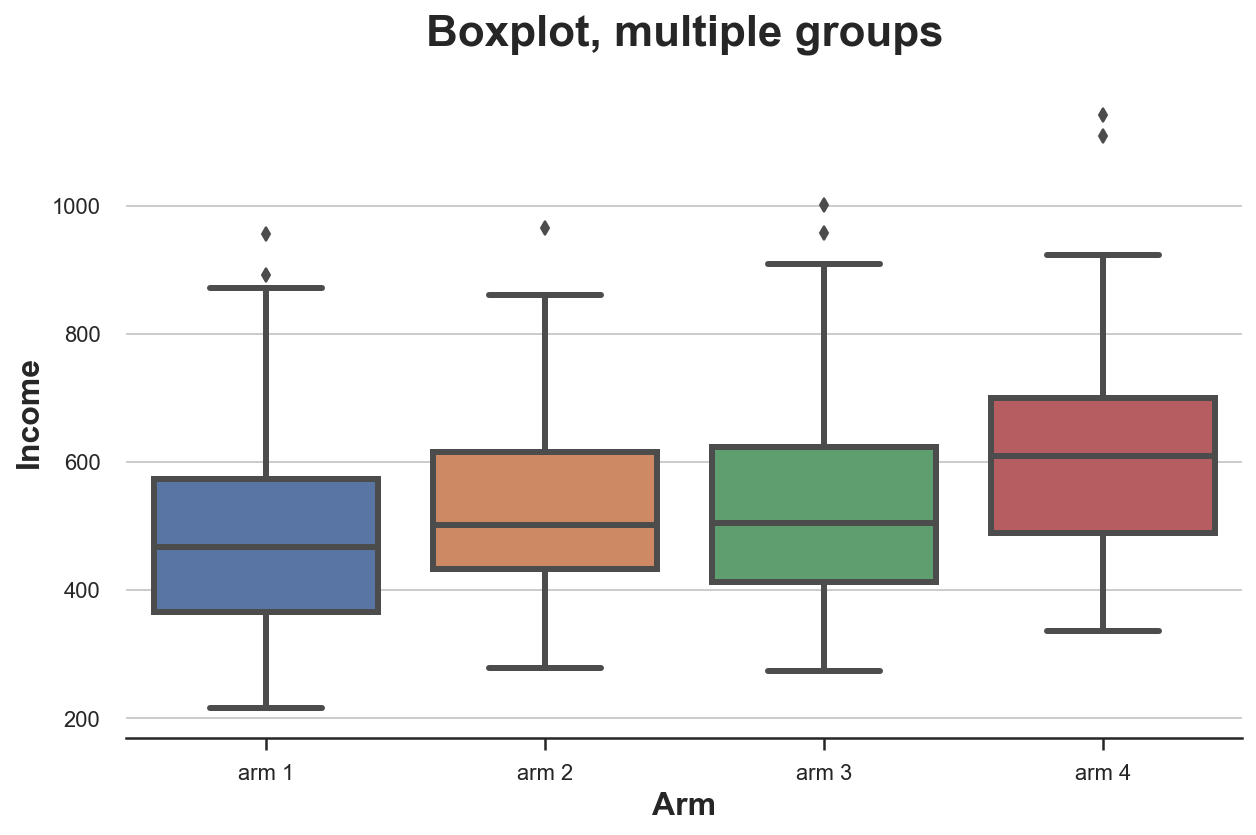
Диаграмма размаха («ящик с усами»)
Диаграмма размаха масштабируется очень хорошо, когда у нас есть несколько групп из однозначных чисел: разные блоки можно расположить рядом.
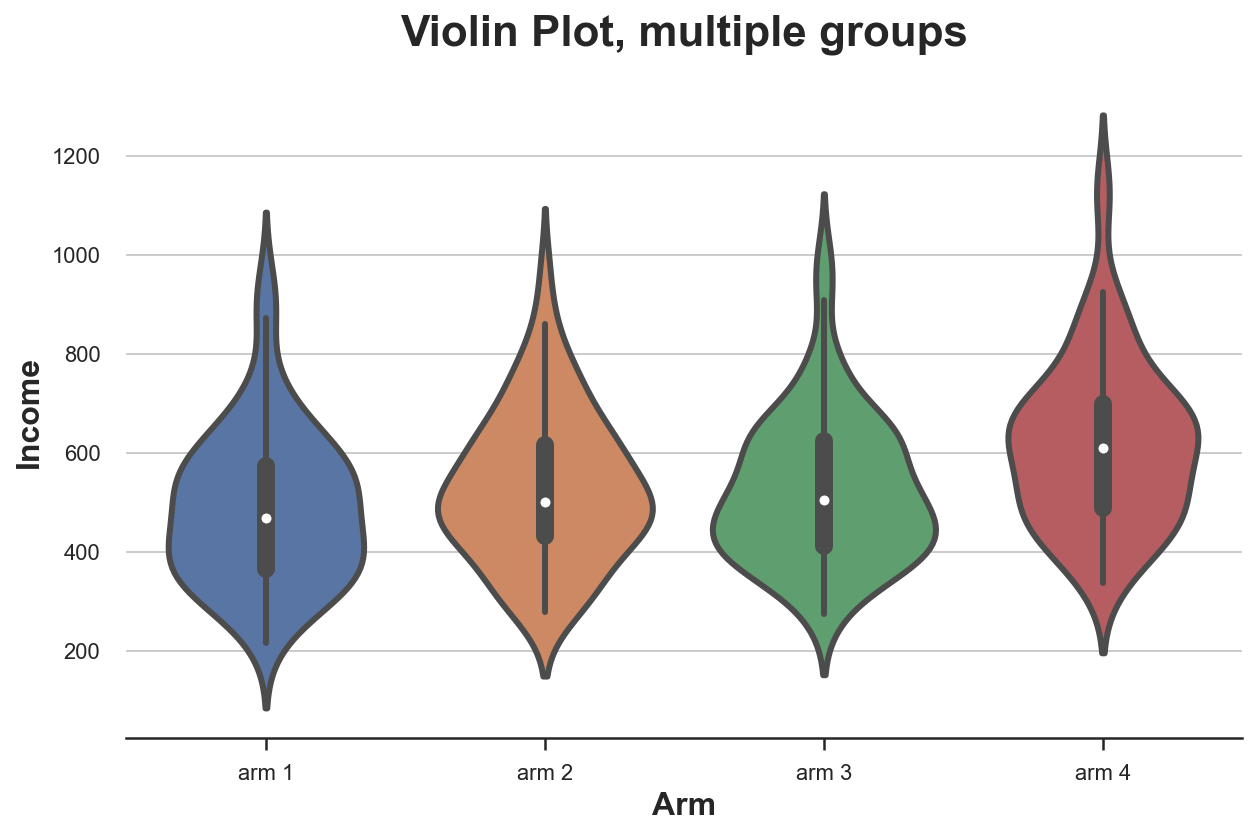
sns.boxplot(x='Arm', y='Income', data=df.sort_values('Arm'));
plt.title("Boxplot, multiple groups");Распределение доходов по типам лечения отличается: группы с более высокими номерами имеют более высокий средний доход.
Скрипичная диаграмма
Очень хорошее расширение для диаграмм вида «ящик с усами», который сочетает в себе сводную статистику и ядерную оценку плотности, — скрипичная диаграмма. Она отображает отдельные плотности по оси Y так, что они не перекрываются. По умолчанию внутри добавляется миниатюрная диаграмма.
sns.violinplot(x='Arm', y='Income', data=df.sort_values('Arm'));
plt.title("Violin Plot, multiple groups");Как и «ящик с усами», скрипичная диаграмма предполагает, что в группах с разным типом лечения доход различается.
Ridgeline (групповая хребтовая диаграмма)
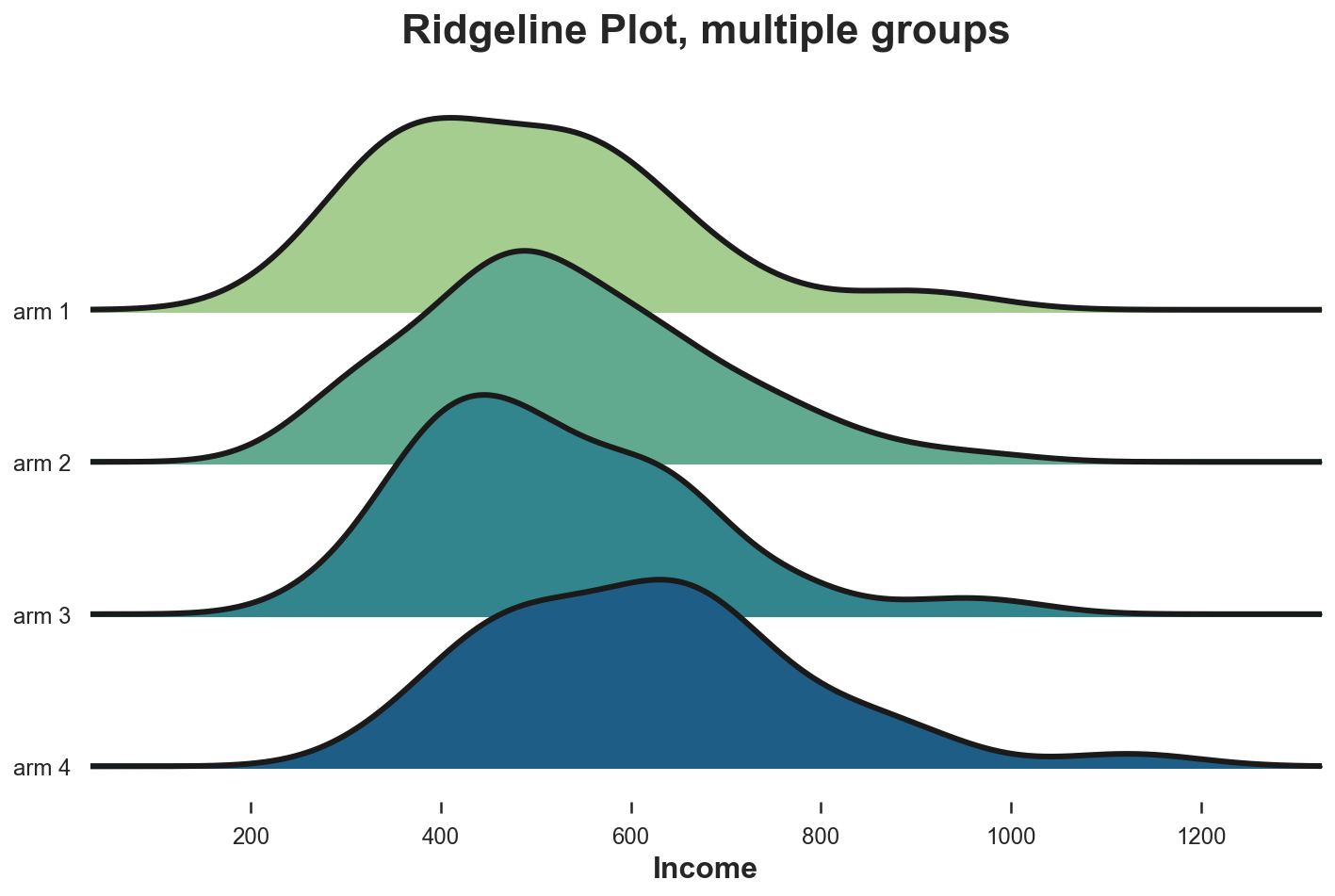
Эта диаграмма отображает несколько ядерных распределений плотности вдоль оси X, что делает их понятнее скрипичной диаграммы, но частично перекрывает распределения. К сожалению, ни в matplotlib, ни в seaborn нет групповой хребтовой диаграммы по умолчанию. Импортировать её нужно из joypy.
from joypy import joyplot
joyplot(df, by='Arm', column='Income', colormap=sns.color_palette("crest", as_cmap=True));
plt.xlabel('Income');
plt.title("Ridgeline Plot, multiple groups");Опять же, групповая хребтовая диаграмма показывает, что группы лечения с более высокими номерами имеют доход выше остальных. На этой диаграмме легче оценить формы распределений.
Несколько групп — тесты
Рассмотрим проверку гипотез для сравнения нескольких групп. Для упрощения сосредоточимся на самом популярном F-тесте.
F-тест
Этот тест сравнивает дисперсию переменной в разных группах и также называется дисперсионным анализом (ANOVA).
Статистика F-теста определяется как:
Здесь G — количество групп, N — количество наблюдений, x̅ — общее среднее, а x̅g — среднее значение в группе g. При нулевой гипотезе о независимости группы f-статистика обладает F-распределением.
from scipy.stats import f_oneway
income_groups = [df.loc[df['Arm']==arm, 'Income'].values for arm in df['Arm'].dropna().unique()]
stat, p_value = f_oneway(*income_groups)
print(f"F Test: statistic={stat:.4f}, p-value={p_value:.4f}")
F Test: statistic=9.0911, p-value=0.0000Тестовое p-значение практически равно нулю, что подразумевает решительное отклонение нулевой гипотезы об отсутствии различий в распределении доходов между типами лечения.
Код
Ссылка на Jupyter Notebook.
А пока вы сравниваете распределения, мы поможем вам прокачать навыки или с самого начала освоить профессию, актуальную в любое время:
-
Профессия Data Scientist
-
Профессия Data Analyst
Выбрать другую востребованную профессию.
Ссылки
[1] Student, The Probable Error of a Mean (1908), Biometrika.
[2] F. Wilcoxon, Individual Comparisons by Ranking Methods (1945), Biometrics Bulletin.
[3] B. L. Welch, The generalization of “Student’s” problem when several different population variances are involved (1947), Biometrika.
[4] H. B. Mann, D. R. Whitney, On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other (1947), The Annals of Mathematical Statistics.
[5] E. Brunner, U. Munzen, The Nonparametric Behrens-Fisher Problem: Asymptotic Theory and a Small-Sample Approximation (2000), Biometrical Journal.
[6] A. N. Kolmogorov, Sulla determinazione empirica di una legge di distribuzione (1933), Giorn. Ist. Ital. Attuar..
[7] H. Cramér, On the composition of elementary errors (1928), Scandinavian Actuarial Journal.
[8] R. von Mises, Wahrscheinlichkeit statistik und wahrheit (1936), Bulletin of the American Mathematical Society.
[9] T. W. Anderson, D. A. Darling, Asymptotic Theory of Certain “Goodness of Fit” Criteria Based on Stochastic Processes (1953), The Annals of Mathematical Statistics.







![{displaystyle mathbb {E} [X]=int _{-infty }^{infty }tdF_{X}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b8b269c99751edd630ab22c36aac1ffde3a4110)





















![{displaystyle F^{-1}(p)=inf{xin mathbb {R} :F(x)geq p},quad forall pin [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7f8d361fa630d92216975a16f12756a137f3d84)





![U[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4a82b2a883d751cf53e5ac11ea12b9e36298f0)

















 .
.