Как найти кумулятивную вероятность

Принимая инвестиционных решения, мы практически всегда мы работаем со случайными величины. Доходность акции и прибыль на акцию являются типичными примерами случайных величин.

Чтобы сделать вероятностные утверждения о случайной величине, нам нужно понять ее распределение вероятностей (англ. ‘probability distribution’). Распределение вероятностей определяет вероятности возможных исходов случайной величины.

В этом чтении мы представляем важные факты о четырех распределениях вероятности и их использовании в финансовом анализе. Эти четыре распределения – равномерное, биномиальное, нормальное и логнормальное (т.е. логарифмически нормальное) – широко используются в инвестиционной практике.

Они используются в таких базовых моделях оценки, как модель ценообразования опционов Блэка-Шоулза-Мертона, модель ценообразования биномиальных опционов и модель ценообразования долгосрочных активов (CAPM). Обладая практическими знаниями о распределении вероятностей, представленными в этом чтении, вы также будете лучше подготовлены к изучению и использованию других количественных методов, таких как проверка статистических гипотез, регрессионный анализ и анализ временных рядов.

После обсуждения распределения вероятностей мы заканчиваем чтение описанием метода моделирования Монте-Карло, компьютерным инструментом моделирования для получения ответов на сложные вопросы.

Например, инвестиционный аналитик может захотеть поэкспериментировать с инвестиционной идеей, фактически не реализовав ее. Или ему или ей может понадобиться оценка сложного опциона, для которого не существует простой формулы ценообразования.

В этих и многих других случаях метод Монте-Карло является важным инструментом в арсенале аналитика. Для проведения моделирования по методу Монте-Карло аналитик должен определить факторы риска, связанные с проблемой, и указать распределения вероятностей для них.

Следовательно, моделирование методом Монте-Карло является инструментом, который требует понимания распределения вероятностей.

Прежде чем мы обсудим конкретные распределения вероятностей, мы определим основные понятия и термины. Затем мы проиллюстрируем действие этих понятий через простейшее распределение, – равномерное распределение. После этого мы рассмотрим другие распределения вероятностей, которые имеют больше применений в инвестиционной практике, но также более сложны.

Дискретные случайные величины.

Случайная величина (англ. ‘random variable’) – это величина, будущие результаты которой неопределенны. Два основных типа случайных величин – это дискретные случайные величины (англ. ‘discrete random variables’) и непрерывные случайные величины (англ. ‘continuous random variables’). Дискретная случайная величина может принимать исчислимое количество возможных значений.

Например, дискретная случайная величина (X) может принимать ограниченное количество значений ( x_1, x_2, ldots, x_n ) (n возможных результатов), или дискретная случайная величина (Y) может принимать неограниченное количество значений ( x_1, x_2, ldots) ) (до бесконечности).

Мы придерживаемся соглашения, что заглавная буква представляет случайную величину, а строчная буква представляет результат (исход) или конкретное значение случайной величины. Таким образом, (X) обозначает случайную переменную, а x обозначает результат переменной (X). Мы подписываем результаты, как ( x_1, x_2 ), когда нам нужно различать отдельные результаты в списке значений случайной переменной.

Поскольку мы можем подсчитать все возможные результаты (X) и (Y) (даже если мы будем продолжать вечно в случае с (Y)), и (X), и (Y) удовлетворяют определению дискретной случайной величины. И напротив, мы не можем подсчитать результаты непрерывной случайной величины.

Мы не можем описать возможные результаты непрерывной случайной величины (Z) с исходами ( z_1, z_2, ldots ), когда возможный результат ( (z_1 + z_2)/2 ) отсутствует в списке результатов. Ставка доходности является примером непрерывной случайной величины.

Работая со случайной величиной, мы должны понимать ее возможные результаты.

Например, большинство акций, торгуемых на новозеландской фондовой бирже, котируются в тиках NZ$0.01. Таким образом, котируемая цена акций является дискретной случайной величиной с возможными значениями NZ$0, NZ$0.01, NZ$0.02, …

Но мы также можем смоделировать цену акций в виде непрерывной случайной величины (в качестве логнормальной случайной величины, которую мы рассмотрим позднее). Во многих практических ситуациях у нас есть выбор между использованием дискретного или непрерывного распределения. Обычно мы руководствуемся тем, какое распределение наиболее эффективно для стоящей перед нами задачи.

Эта возможность выбора не удивительна, так как многие дискретные распределения могут быть приблизительно равны непрерывным распределениям, и наоборот. В большинстве практических случаев распределение вероятностей – это всего лишь математическая идеализация или приблизительная модель относительных частот возможных результатов случайной величины.

Пример (1) распределения цены облигации.

Вы исследуете вероятностную модель цены облигации и анализируете характеристики облигаций, которые влияют на ее цену.

Каковы самые низкие и максимально возможные значения цены облигации? Почему?

Какие еще характеристики облигаций могут влиять на распределение цены облигаций?

Минимально возможное значение цены облигации равно 0, когда облигация бесполезна. Определение максимально возможного значения цены облигации является более сложной задачей. Обещанные платежи по купонной облигации – это купоны (процентные платежи) плюс номинальная сумма (основная сумма).

Цена облигации – это дисконтированная стоимость этих обещанных платежей. Поскольку инвесторы требуют возврата своих инвестиций, 0 процентов – это нижний предел ставки дисконта, который инвесторы будут использовать для дисконтирования обещанных платежей по облигациям.

При ставке дисконтирования 0% цена облигации представляет собой сумму номинальной стоимости и оставшихся купонов без какого-либо дисконта. Таким образом, ставка дисконта устанавливает верхний предел цены облигации.

Предположим, например, что номинальная стоимость составляет $1,000, и остались 2 купона на $40; интервал от $0 до $1,080 охватывает все возможные значения цены облигации. Этот верхний предел уменьшается со временем по мере уменьшения количества оставшихся платежей.

Прочие характеристики облигации также влияют на ее распределение цен. Привязка к номинальной стоимости является одной из таких характеристик: по мере приближения даты погашения стандартное отклонение цены облигации имеет тенденцию к уменьшению, когда цена облигации приближается к номинальной стоимости.

Встроенные опционы также влияют на цену облигации. Например, если облигации в текущий момент могут быть отозваны, эмитент может выкупить эти облигации с заранее установленной премией выше номинальной; этот опцион эмитента частично снижает рост цены облигации. Моделирование распределения цен облигаций является сложной задачей.

Каждая случайная величина связана с распределением вероятностей, которое полностью описывает переменную. Мы можем рассмотреть распределение вероятности двумя способами.

Основным представлением является функция вероятности, которая определяет вероятность того, что случайная величина принимает определенное значение:

( P(X = x) ) – это вероятность того, что случайная величина (X) принимает значение (x).

(Обратите внимание, что заглавная буква (X) обозначает случайную величину, а строчная буква x обозначает конкретное значение, которое может принимать случайная величина.)

Для дискретной случайной величины сокращенная запись для функции вероятности имеет вид:

( large p(x) = P(X = x) )

Для непрерывных случайных величин функция вероятности обозначается ( f(x) ) и называется функцией плотности вероятности (pdf, от англ. ‘probability density function’), или просто плотностью.

Другой технический термин для функции вероятности дискретной случайной величины – функция массы вероятности (pmf, от англ. ‘probability mass function’). Этот термин используется реже.

Функция вероятности имеет два ключевых свойства:

( 0 leq p(x) leq 1 ), потому что вероятность – это число от 0 до 1.
Сумма вероятностей ( p(x) ) всех значений (X) равна 1. Если мы сложим вероятности всех различных возможных результатов случайной величины, эта сумма должна равняться 1.

Мы часто заинтересованы в поиске вероятности ряда результатов, а не конкретного результата. В этих случаях мы используем второе представление о распределении вероятностей, – кумулятивную (или накопленную) функцию распределения (cdf, англ. ‘cumulative distribution function’).

Кумулятивная функция распределения, или просто функция распределения, дает вероятность того, что случайная величина (X) меньше или равна определенному значению ( x ), ( P (X leq x) ).

Как для дискретных, так и для непрерывных случайных величин сокращенная запись следующий вид:

( large F(x) = P(X leq x) )

Как кумулятивная функция распределения связана с функцией вероятности?

Слово «кумулятивный» подразумевает накопленные исторические результаты. Чтобы найти ( F(x) ), мы суммируем или накапливаем значения функции вероятности для всех результатов, меньших или равных x.

Функция cdf параллельна функции кумулятивной (накопленной) относительной частоты, которую мы обсуждали в чтении о статистических концепциях и доходности рынка.

Далее мы проиллюстрируем эти концепции на примерах и покажем, как мы используем дискретные и непрерывные распределения. Начнем с простейшего распределения – дискретного равномерного распределения.

Дискретное равномерное распределение.

Простейшим из всех распределений вероятности является дискретное равномерное распределение. Предположим, что возможными результатами являются целые числа от 1 до 8 включительно, и вероятность того, что случайная переменная принимает любое из этих возможных значений, одинакова для всех результатов (то есть она является равномерной).

При восьми исходах ( p(x) = 1/8 ) или 0.125, для всех значений (X(X = 1, 2, 3, 4, 5, 6, 7, 8)); только что сделанное утверждение является полным описанием этой дискретной равномерной случайной величины. Распределение имеет конечное число указанных результатов, и каждый результат одинаково вероятен.

В Таблице 1 приведены два представления этой случайной величины: функция вероятности и кумулятивная функция распределения.

Таблица 1. Функция вероятности и кумулятивная функция распределения для дискретной равномерной случайной величины.

	Функция вероятности	Кумулятивная функция распределения
( X=x )	( p(x) = P(X = x) )	( F(x) = P(X leq x) )
1	0.125	0.125
2	0.125	0.250
3	0.125	0.375
4	0.125	0.500
5	0.125	0.625
6	0.125	0.750
7	0.125	0.875
8	0.125	1.000

Мы можем использовать Таблицу 1, чтобы найти три вероятности:

( P (X leq 7) ),
( P (4 leq X leq 6) ) и
( P (4 < X leq 6) ).

Следующие примеры иллюстрируют, как использовать cdf, чтобы найти вероятность того, что случайная переменная попадет в любой интервал (для любой случайной переменной, а не только для равномерной).

Вероятность того, что (X) меньше или равно 7, ( P (X leq 7) ), является ближайшей к последней записи в третьем столбце, 0.875 или 87.5%.

Чтобы найти ( P (4 leq X leq 6) ), нам нужно найти сумму трех вероятностей: (p(4)), (p(5)) и (p(6)). Мы можем найти эту сумму двумя способами. Мы можем сложить (p(4)), (p(5)) и (p(6)) из второго столбца. Или мы можем вычислить вероятность как разницу между двумя значениями кумулятивной функции распределения:

( F(6) = P(X leq 6) = p(6) + p(5) + p(4) + p(3) + p(2) + p(1) )
( F(3) = P(X leq 3) = p(3) + p(2) + p(1) )

поэтому

( begin{aligned} P(4 leq X leq 6) &= F(6) – F(3) \ &= p(6) + p(5) + p(4) = 3/8 end{aligned} )

Поэтому мы вычисляем вторую вероятность как:

( F(6) – F(3) = 3/8 )

Третья вероятность, ( P (4 < X leq 6) ), вероятность того, что (X) меньше или равно 6, но больше 4, равна (p(5) + p(6)). Мы вычисляем ее следующим образом, используя cdf:

( begin{aligned} P(4 < X leq 6) &= P(X leq 6) – P(X leq 4) \ &= F(6) – F(4) = p(6) + p(5) = 2/8 end{aligned} )

Таким образом, мы вычисляем третью вероятность как:

( F(6) – F(4) = 2/8 ).

Предположим, мы хотим проверить, что дискретная равномерная функция вероятности удовлетворяет общим свойствам функции вероятности, приведенным ранее.

Первое свойство – это ( 0 leq p(x) leq 1 ). Мы видим, что (p(x) = 1/8) для всех (x) в первом столбце таблицы. (Обратите внимание, что (p(x)) равно 0 для чисел (x), таких как -14 или 12.215, которых нет в этом столбце.)

Первое свойство удовлетворяется.

Второе свойство состоит в том, что вероятности составляют в сумме 1. Записи во втором столбце таблицы 1 тоже составляют в сумме 1.

У cdf есть два других характерных свойства:

cdf лежит между 0 и 1 для любого x: ( 0 leq F(x) leq 1 ).
По мере увеличения (x), cdf либо увеличивается, либо остается постоянным.

Проверьте эти утверждения, посмотрев на третий столбец в Таблице 1.

Теперь у нас есть некоторый опыт работы с вероятностными функциями и cdf для дискретных случайных величин. Позже в этом чтении мы обсудим моделирование методом Монте-Карло, методологию, основанную на случайных числах.

Как мы увидим, равномерное распределение имеет важное техническое применение: оно является основой для генерации случайных чисел, которые, в свою очередь, производят случайные наблюдения для всех других распределений вероятности.

Случайные числа, изначально генерируемые компьютерами, обычно представляют собой случайные положительные целые числа, которые преобразуются в приблизительные непрерывные равномерные случайные числа от 0 до 1. Затем непрерывные равномерные случайные числа используются для получения случайных наблюдений в других распределениях, таких как нормальное, с использованием различных методов.

Мы обсудим генерацию случайных наблюдений далее в разделе о методе моделирования Монте-Карло.

См. далее:

CFA – Биномиальное распределение вероятностей
CFA – Непрерывные случайные величины и непрерывное равномерное распределение вероятностей
CFA – Нормальное распределение вероятностей
CFA – Критерий повышенной надежности Роя и применение нормального распределения вероятности
CFA – Логнормальное распределение вероятностей
CFA – Метод Монте-Карло

Источник

A cumulative probability curve is a visual representation of a cumulative distributive function, which is the probability that a variable will be less than or equal to a specified value. Since it is a cumulative function, the cumulative distributive function is actually the sum of the probabilities that the variable will have any of the values less than the stated value. For a function with a normal distribution, the cumulative probability curve will begin at 0 and rise to 1, with the steepest part of the curve in the center, representing the point with the highest probability for the function.

List all of the values for “x.” If “x” is a continuous function, select intervals for “x” and list them instead. The intervals should be evenly spaced, ranging from the least “x” to the highest. Smaller intervals will lead to a smoother and more accurate cumulative probability curve. For example, let the values of “x” equal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10.

Compute the probabilities for each value or interval of “x.” All of the probabilities should be between 0 and 1. If “x” has a normal distribution, the highest probabilities will be at the center of the range and the probabilities at either extreme will be near 0. For the example beginning in Step 1, the respective probabilities for “x” might be 0, 0, 0, .05, .25, .4, .25, .05, 0, 0 and 0.

Compute the cumulative sums for each probability of “x.” The cumulative probability for each value of “x” will be the probability of that “x” plus the probabilities of each preceding “x.” In this example, the respective cumulative probabilities for “x” would be 0, 0, 0, .05, .30, .70, .95, 1.0, 1.0, 1.0 and 1.0. If “x” has a normal distribution, the first values will always be 0. Regardless of the type of distribution, the last value of the cumulative probability function will be 1.

Graph the points for the cumulative distribution function. The horizontal axis should include all values or intervals of “x.” The vertical axis should range from 0 to 1. Connect the points as smoothly as possible. If “x” has a normal distribution, the curve will resemble a stretched “s” shape.

Things You’ll Need

Calculator
Graph paper

Источник

Кумулятивная функция распределения в нормально распределенных данных

Добавлено 30 августа 2020 в 11:43

В данной статье объясняется, как получить кумулятивную функцию распределения Гаусса и почему она полезна в статистическом анализе.

Если вы только присоединяетесь к нашему обсуждению статистики в электротехнике, возможно, вам будет интересно сначала просмотреть предыдущие статьи этой серии, список которых можно найти в оглавлении вверху над статьей.

Что мы знаем из предыдущих статей:

мы можем получить функцию плотности вероятности нормально распределенных результатов измерений, вычислив стандартное отклонение и среднее значение набора данных;
эта функция плотности вероятности является идеализированным математическим эквивалентом фигуры, которую мы наблюдаем на гистограмме набора данных;
мы получаем вероятность (т.е. вероятность того, что определенные значения результатов измерений будут иметь место) путем интегрирования функции плотности вероятности по заданному интервалу.

Если участки интегрирования функции плотности вероятности являются ключом к извлечению вероятностей из измеренных данных, можно задаться вопросом о возможности простого интегрирования всей функции и тем самым создания новой функции, которая даст нам прямой доступ к информации о вероятности.

Как оказалось, это стандартный метод статистического анализа, и эта новая функция, которую мы получаем путем интегрирования всей функции плотности вероятности, называется кумулятивной функцией распределения.

Кумулятивная функция нормального распределения

Использование кумулятивной функции распределения (CDF, cumulative distribution function) является особенно хорошей идеей, когда мы работаем с нормально распределенными данными, потому что интегрировать гауссову кривую не так-то просто.

Фактически, чтобы получить кумулятивную функцию распределения кривой Гаусса, даже математики должны прибегнуть к численному интегрированию (функция (e^{-x^2}) не имеет первообразной, которая может быть выражена в элементарной форме). Это означает, что кумулятивная функция распределения Гаусса на самом деле представляет собой последовательность дискретных значений, созданных из множества отдельных выборок, взятых вдоль гауссовой кривой.

В эпоху компьютеров мы можем легко обрабатывать огромное количество выборок, и, следовательно, дискретная кумулятивная функция распределения, полученная путем численного интегрирования, может быть вполне адекватной заменой непрерывной функции, полученной посредством символьного интегрирования.

Если мы отложим на графике большое количество значений гауссовой функции распределения, кривая будет выглядеть следующим образом:

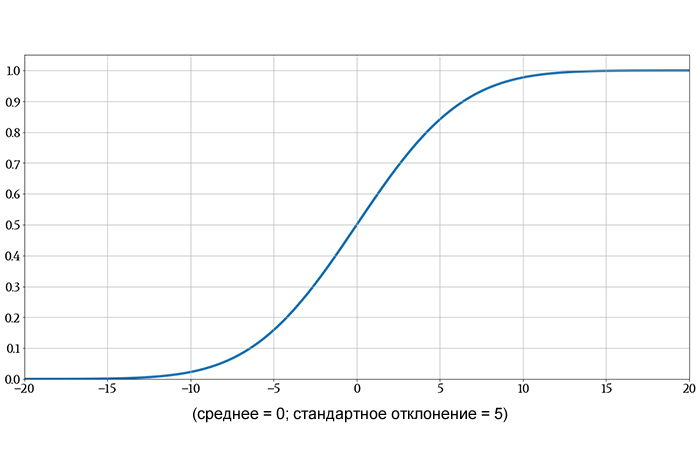
Рисунок 1 – Кумулятивная функция нормального распределения

На следующем графике показаны как исходная гауссова функция плотности вероятности, так и ее функция распределения, чтобы вы могли увидеть, как интегрирование превращает одно в другое.

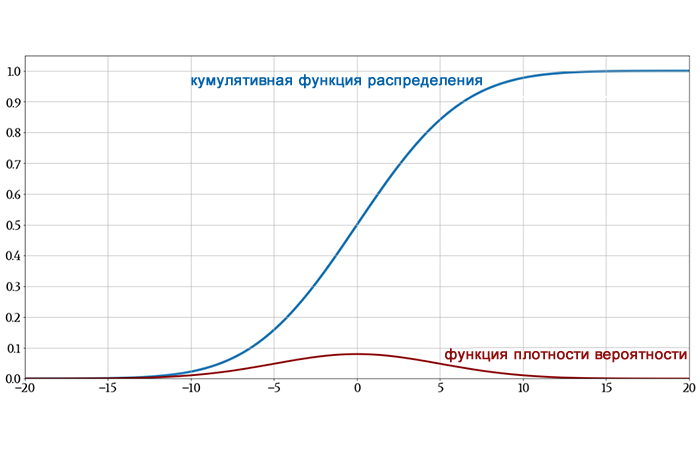
Рисунок 2 – Функция плотности вероятности нормально распределенной переменной и соответствующая функция распределения

Одно небольшое замечание, прежде чем мы продолжим: в обсуждениях о статистике вы можете увидеть символ Φ (заглавная греческая буква фи). Когда нормальное распределение имеет среднее значение 0 и стандартное отклонение 1, оно называется стандартным нормальным распределением. Кумулятивная функция стандартного нормального распределения обозначается Φ; таким образом,

[Phi(z)=frac{1}{sqrt{2 pi}}int_{-infty}^{z}e^{-frac{x^2}{2}}dx]

Пример кумулятивной функции распределения

Когда мы интегрируем функцию плотности вероятности от отрицательной бесконечности до некоторого значения, обозначенного z, мы вычисляем вероятность того, что результат случайно выбранного измерения или нового измерения попадет в числовой интервал, который простирается от отрицательной бесконечности до z. Другими словами, мы вычисляем вероятность того, что измеренное значение будет меньше z.

Это именно та информация, которую мы получаем из кумулятивной функции распределения и без необходимости интегрирования. Если мы посмотрим на график кумулятивной функции распределения и найдем вертикальное значение, соответствующее некоторому числу z на горизонтальной оси, мы узнаем вероятность того, что измеренное значение будет меньше z.

Например:

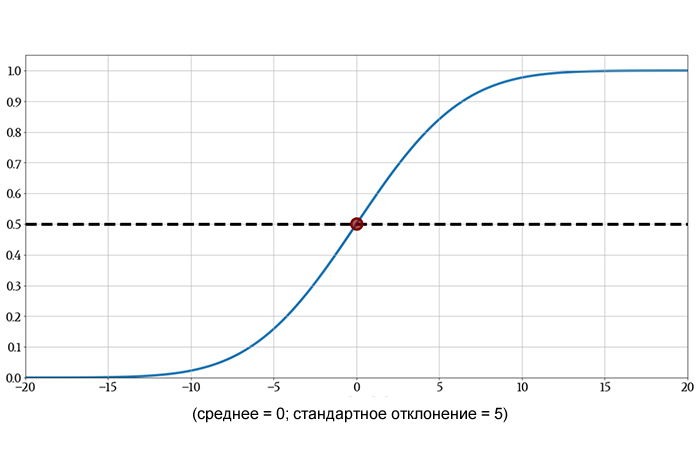
Рисунок 3 – Определение вероятности того, что измеренное значение будет меньше некоторой величины, с помощью кумулятивной функции распределения

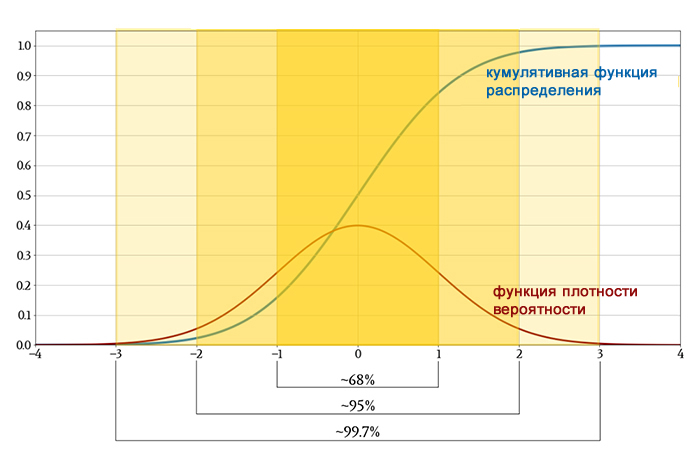
Кумулятивная функция распределения при z = 0 равна 0,5. Это говорит нам о том, что результат выбранного случайным образом измерения имеет 50% вероятность быть меньше нуля. Это интуитивно понятно: нормальное распределение симметрично относительно среднего, и поскольку среднее значение в этом случае равно нулю, любое отдельное измерение имеет равные шансы быть меньше или больше нуля.

Кумулятивная функция распределения (CDF) также обеспечивает простой способ определения вероятности того, что результат измерения попадет в определенный диапазон. Если диапазон определяется двумя значениями z₁ и z₂, всё, что нам нужно сделать, это вычесть значение функции распределения в z₂ из значения функции распределения в z₁ (а затем при необходимости взять модуль полученного значения).

Вот еще один пример:

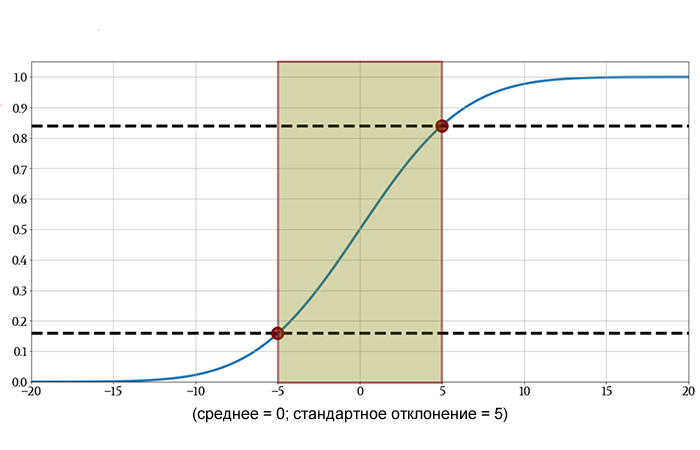
Рисунок 4 – Определение вероятности попадания результата измерения в определенный диапазон с помощью кумулятивной функции распределения

Вероятность того, что результат случайно выбранного измерения будет между –5 и +5, составляет приблизительно (0,84 – 0,16) = 0,68 (или 68%). Более точное значение – 68,27%.

Вероятность и стандартное отклонение

Вы могли заметить, что интервал, выбранный в предыдущем примере, был равен одному стандартному отклонению выше и ниже среднего. Когда мы обсуждаем вероятности со ссылкой на интервалы, представленные в единицах стандартного отклонения, эта информация применяется ко всем наборам данных, которые следуют нормальному распределению. Таким образом, мы можем определить вероятностные характеристики, используя кумулятивную функцию стандартного нормального распределения, а затем распространить эти тенденции на другие наборы данных, просто изменив стандартное отклонение (или размышляя относительно стандартных отклонений).

Выше мы видели, что в нормально распределенных данных измеренное значение имеет шанс 68,27% попасть в диапазон в пределах одного стандартного отклонения от среднего. Мы можем продолжить обобщение нормально распределенных данных следующим образом:

вероятность того, что измеренное значение будет в пределах двух стандартных отклонений от среднего, составляет 95,45%;
вероятность того, что измеренное значение будет в пределах трех стандартных отклонений от среднего, составляет 99,73%.

Эти три вероятности дают простое представление того, как будут вести себя нормально распределенные измерения.

Более приблизительная версия этого обобщения известна как правило 68-95-99,7: если набор данных демонстрирует нормальное распределение, около 68% значений будут в пределах одного стандартного отклонения от среднего, около 95% будут в пределах двух стандартных отклонений, и около 99,7% будут в пределах трех стандартных отклонений.

Рисунок 5 – Демонстрация правила 68-95-99,7 на графиках функции плотности вероятности и функции распределения

Заключение

Мы рассмотрели важный материал, и я надеюсь, что вам понравилось наше исследование нормального распределения и связанных с ним тем статистики. В следующей статье мы рассмотрим два малоизвестных описательных статистических показателя: асимметрию и эксцесс.

ВероятностьКумулятивная функция распределения / CDF (cumulative distribution function)Нормальное распределение / Гауссово распределениеСтандартное нормальное распределениеСтатистикаСтатистический анализФункция плотности вероятности

Источник

В этом руководстве дается простое объяснение разницы между PDF (функцией плотности вероятности) и CDF (кумулятивной функцией распределения) в статистике.

Случайные переменные

Прежде чем мы сможем определить PDF или CDF, нам сначала нужно понять случайные величины.

Случайная величина , обычно обозначаемая как X, представляет собой переменную, значения которой являются числовыми результатами некоторого случайного процесса. Случайные величины бывают двух типов: дискретные и непрерывные.

Дискретные случайные величины

Дискретная случайная величина — это та, которая может принимать только счетное число различных значений, таких как 0, 1, 2, 3, 4, 5…100, 1 миллион и т. д. Вот некоторые примеры дискретных случайных величин:

Количество раз, когда монета падает решкой после 20 подбрасываний.
Сколько раз игральная кость выпадает на число 4 после 100 бросков.

Непрерывные случайные величины

Непрерывная случайная величина — это такая, которая может принимать бесконечное число возможных значений. Некоторые примеры непрерывных случайных величин включают:

Рост человека
Вес животного
Время, необходимое, чтобы пробежать милю

Например, рост человека может быть 60,2 дюйма, 65,2344 дюйма, 70,431222 дюйма и т. д. Существует бесконечное количество возможных значений роста.

Полезное правило: если вы можете подсчитать количество результатов, то вы работаете с дискретной случайной величиной (например, подсчитывая, сколько раз монета падает орлом). Но если вы можете измерить результат, вы работаете с непрерывной случайной величиной (например, измерения, рост, вес, время и т. д.).

Функции плотности вероятности

Функция плотности вероятности (PDF) сообщает нам вероятность того, что случайная величина примет определенное значение.

Например, предположим, что мы бросаем кости один раз. Если мы обозначим через x число, на которое выпадет игральная кость, то функция плотности вероятности исхода может быть описана следующим образом:

Р (х < 1) : 0

Р(х = 1) : 1/6

Р(х = 2) : 1/6

Р(х = 3) : 1/6

Р(х = 4) : 1/6

Р(х = 5) : 1/6

Р(х = 6) : 1/6

Р(х > 6) : 0

Обратите внимание, что это пример дискретной случайной величины, поскольку x может принимать только целые значения.

Для непрерывной случайной величины мы не можем напрямую использовать PDF, поскольку вероятность того, что x примет любое точное значение, равна нулю.

Например, предположим, что мы хотим узнать вероятность того, что бургер из определенного ресторана весит четверть фунта (0,25 фунта). Поскольку вес — непрерывная переменная, он может принимать бесконечное число значений.

Например, данный бургер может на самом деле весить 0,250001 фунта, или 0,24 фунта, или 0,2488 фунта. Вероятность того, что данный бургер весит ровно 0,25 фунта, практически равна нулю.

Совокупные функции распределения

Кумулятивная функция распределения (cdf) говорит нам о вероятности того, что случайная величина примет значение, меньшее или равное x .

Например, предположим, что мы бросаем кости один раз. Если мы обозначим через x число, на которое выпадет игральная кость, то кумулятивную функцию распределения результата можно описать следующим образом:

Р (х ≤ 0) : 0

Р(х ≤ 1) : 1/6

Р(х ≤ 2) : 2/6

Р(х ≤ 3) : 3/6

Р(х ≤ 4) : 4/6

Р(х ≤ 5) : 5/6

Р(х ≤ 6) : 6/6

Р(х > 6) : 0

Обратите внимание, что вероятность того, что x меньше или равна 6 , равна 6/6, что равно 1. Это связано с тем, что кости выпадут на 1, 2, 3, 4, 5 или 6 с вероятностью 100%.

В этом примере используется дискретная случайная величина, но для непрерывной случайной величины можно также использовать непрерывную функцию плотности.

Кумулятивные функции распределения обладают следующими свойствами:

Вероятность того, что случайная величина примет значение меньше минимально возможного, равна нулю. Например, вероятность того, что на игральной кости выпадет значение меньше 1, равна нулю.
Вероятность того, что случайная величина примет значение, меньшее или равное максимально возможному значению, равна единице. Например, вероятность того, что на кубике выпадет значение 1, 2, 3, 4, 5 или 6, равна единице. Он должен приземлиться на одно из этих чисел.
cdf всегда не убывает. То есть вероятность того, что кубик выпадет на число, меньшее или равное 1, составляет 1/6, вероятность того, что он выпадет на число, меньшее или равное 2, составляет 2/6, вероятность того, что на нем выпадет число меньше или равно 3 — это 3/6 и т. д. Совокупные вероятности всегда не уменьшаются.

Связанный: вы можете использовать оживальный график для визуализации кумулятивной функции распределения.

Связь между CDF и PDF

С технической точки зрения, функция плотности вероятности (PDF) является производной от кумулятивной функции распределения (cdf).

Кроме того, площадь под кривой PDF между отрицательной бесконечностью и x равна значению x на cdf.

Подробное объяснение взаимосвязи между PDF и cdf, а также доказательство того, почему PDF является производной от cdf, см. в учебнике по статистике.

Источник

Кумулятивные функции распределения

Кумулятивная функция распределения дает интегральную картину распределения вероятности. Она рассматривает функцию вероятностной меры типа колоколообразной кривой и задает вопрос: «Какова вероятность того, что результат окажется меньше или равен такому-то?» Нормальная кривая показывает вероятность конкретного значения, a кумулятивная функция – вероятность данного спектра значений. Кумулятивная функция позволяет объединить понятие о неопределенности (теорию вероятности) с нашим инструментом для принятия решений (дерево решений). Она охватывает весь спектр возможных исходов при анализе переменных с множественными значениями.

Вернемся к примеру с нефтяной скважиной и посмотрим распределение значений возможной стоимости нефти (табл. 5.2):

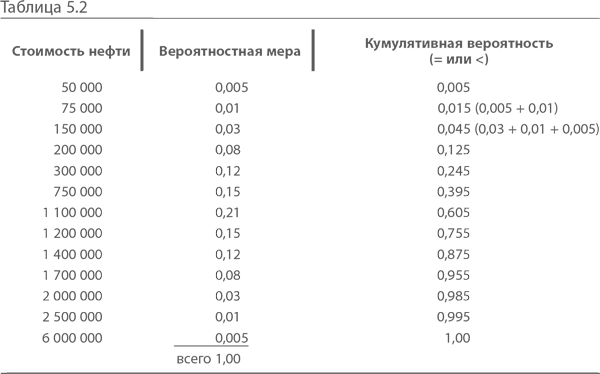
При построении дерева решений мы исходили из возможного выигрыша в миллион. Такова была ожидаемая стоимость нефти – я выбрал эту сумму ради удобства. При распределении мы получаем широкий спектр значений. Как видно из таблицы, с вероятностью 0,005 прибыль может оказаться равной $6 млн и $50 000. Если все эти суммы умножить на соответствующие вероятности, указанные во втором столбце, а затем сложить произведения, получится тот самый $1 млн, ожидаемая стоимость.

Построив функцию кумулятивного распределения, человек, принимающий решение, устанавливает среднее, то есть ожидаемую стоимость, и с этого может начать анализ. Построение кумулятивного распределения позволяет объединить оценки вероятности верхней границы, середины и нижней границы спектра исходов и установить ожидаемую стоимость, что позволит принять решение.

В графической форме кумулятивное распределение исходов в диапазоне напоминает большую букву «S». На такой кривой сразу видны все возможные исходы, а не только разрозненные статичные точки. Как показано на следующем графике, Сэм Хьюстон считает, что все возможные в данном случае исходы попадают в непрерывный диапазон значений от 0 до $6 000 000.

Диапазон вероятностей от 0 до 1,0 кумулятивного распределения разбивается на части – квантили – методом медиан интервального ряда. В таблице именно так разделена ожидаемая стоимость. Например, чтобы разделить диапазон вероятности ожидаемой стоимости на пять частей, нужно взять квантили 0,1; 0,3; 0,5; 0,7 и 0,9. Эти квантили будут представлять собой среднее арифметическое в диапазонах значений 0–0,2; 0,2–0,4; 0,4–0,6; 0,6–0,8 и 0,8–1,0 соответственно.

Квантиль 0,5 равнозначен медиане, поскольку с каждой его стороны находится ровно половина возможных значений. Медиана не обязательно совпадает со средним, то есть центром нормального распределения. Медиана – это просто центр диапазона значений. Среднее – это сумма произведений всех вероятностей на соответствующие значения: именно так мы получили ожидаемую стоимость обнаружения нефти $1 млн.

Чтобы объединить концепцию кумулятивного распределения с деревом решения и принимать существенные управленческие решения, нужно представить себе все вероятные значения прибыли от нефтяной скважины. Диапазон значений можно изобразить в виде веера событий. Кому-то может не хватить терпения для представления бесконечных возможностей в виде ветвей дерева, и тут выручит кумулятивная вероятность.

Рисуем кумулятивное распределение. Чтобы представить кумулятивное распределение в графической форме, как показано ниже, следует опираться на собственное суждение и данные исследований. Нужно задать себе ряд вопросов:

• При каком значении в 50 % случаев результат оказывается выше или ниже заданного значения (медиана)?

• Каким будет значение нижнего конца спектра (квантиль 0,10)?

• Каким будет значение верхнего конца спектра (квантиль 0,90)?

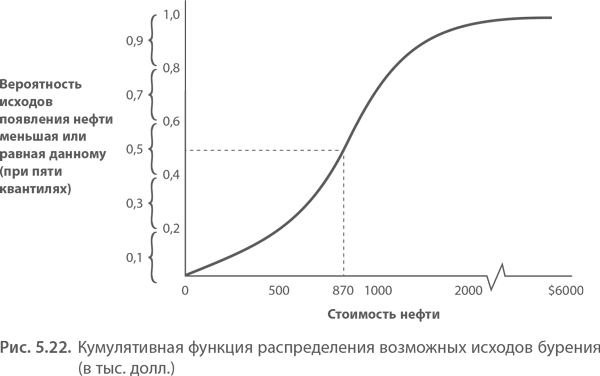
Ответив на эти вопросы, вы сможете представить кумулятивную стоимость возможных исходов. Ограничившись пятью исходами или пятью квантилями кумулятивного распределения, вы можете изобразить веер событий и их вероятностей на дереве решений в виде пяти ветвей.

Ожидаемый денежный эквивалент будет таким же, как при первом рассмотрении, но только потому, что с самого начала для удобства была задана правильная величина ожидаемой стоимости.

Сокращенный вариант такого анализа называют методом Тьюки – Пирсона. Вместо пяти квантилей используется всего три – 0,05; 0,5 и 0,95. Соответствующие этим квантилям вероятности – 0,185; 0,63 и 0,185.

Применительно к крупным задачам дерево решений строится с помощью компьютерных симулякров Монте-Карло, самый популярный из них – Oracle. Дерево и параметры «веера событий» кумулятивного распределения включены в компьютерную модель. Программа прогоняет множество сценариев событий, чтобы дать вам представление, чем может обернуться дело. Некоторые из компаний Fortune 500 используют этот метод.

Кумулятивное распределение и анализ методом квантилей можно применять к ситуациям, в которых ожидаемая стоимость ветви дерева решений неопределенна. Однако важнее всего суждение аналитика. Дерево – это всего лишь инструмент, который МВА обязан использовать в сочетании со своими знаниями и интуицией.

Данный текст является ознакомительным фрагментом.

Дискретные случайные величины.

Пример (1) распределения цены облигации.

Как кумулятивная функция распределения связана с функцией вероятности?