Что такое квадрант и как его найти?
Ученик
(162),
закрыт
12 лет назад
Дополнен 12 лет назад
Сделана :)) Спасибо за подсказку)
Дополнен 12 лет назад
Да да, все решено верно. В школе учился) просто что-то не сразу вспомнил, что такое квадрант. Когда в гугле искал (правда с телефона, вообще результаты другой тематики выдал).
stay-away
Гуру
(2963)
12 лет назад
Квадрант плоскости — любая из 4 областей (углов) , на которые плоскость делится двумя взаимно перпендикулярными прямыми, принятыми в качестве осей координат
Квадрант круга — сектор с центральным углом в 90°, четверть круга
Александр Потетнин
Мудрец
(19095)
12 лет назад
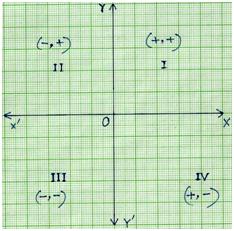
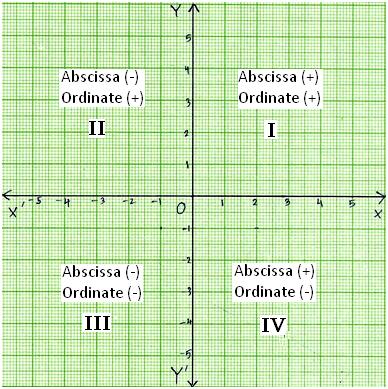
Попутно вопрос: а в курсе, что плюс для X – вправо, а для Y – вверх? От точки пересечения координатных осей. И первый квадрант – это у которого и х+, и у+; второй – х-, а у+; третий – и х-, и у-; и четвертый х+, а у-. Отсюда понятно, как по координатам проверить, в какой квадрант попадает точка.
Источник: 5 класс. Или шестой. Давно это было.
Что такое квадрант на графике?
Квадрант площадь, заключенная по осям x и y; таким образом, на графике четыре квадранта. Чтобы объяснить, двумерная декартова плоскость разделена осями x и y на четыре квадранта. В правом верхнем углу начинается квадрант I, а в направлении против часовой стрелки вы увидите квадранты со II по IV. 13 июля 2021 г.
Как найти квадрант графика?
То первый квадрант – верхний правый угол участка графика, где и x, и y положительны. Второй квадрант в верхнем левом углу включает отрицательные значения x и положительные значения y. Третий квадрант, нижний левый угол, включает отрицательные значения как x, так и y.
Что такое 4 квадранта на графике?
Квадранты координатной плоскости под номерами I, II, III и IV как показано на сетке ниже. В 5 классе учащимся обычно не нужно знать систему нумерации, но они должны понимать, что соответствующие квадранты для упорядоченных пар можно определить по знакам чисел.
Как определить квадранты?
Как вы делаете квадранты?
Если оба x и y положительны, то точка лежит в первом квадранте. Если x отрицательно, а y положительно, то точка лежит во втором квадранте. Если и x, и y отрицательны, то точка лежит в третьем квадранте. Если x положительный, а y отрицательный, то точка лежит в четвертом квадранте.
Как выглядит квадрант 4?
Квадрант IV: Четвертый квадрант находится в нижний правый угол. X имеет положительные значения в этом квадранте, а y имеет отрицательные значения.
Смотрите также, как долго вода испаряется
Что такое квадрант 3 на графике?
Квадрант III: Третий квадрант в левом нижнем углу самолета. Кроме того, и x, и y имеют отрицательные значения в этом квадранте.
Что такое квадрант или ось?
Квадрант область, ограниченная пересечением оси X и оси Y. На декартовой плоскости, когда две оси, ось X и ось Y, пересекаются друг с другом под углом 90º, вокруг нее образуются четыре области, и эти области называются квадрантами.
Что такое квадрант класса 9?
Квадрант область, определяемая двумя осями (ось x и ось y) системы координат. Когда две оси, ось x и ось y, пересекаются друг с другом под углом 90 градусов, четыре сформированные таким образом области представляют собой квадранты. Координаты представляют положение точки в квадранте. …
Чему равна площадь квадранта?
то есть пи (π), умноженное на квадрат радиуса (r2). Теперь, чтобы вычислить площадь квадранта, разделите площадь круга на 4 (так как четыре квадранта составляют круг). Получаем, площадь квадранта, A= (πr2)/4 Квадратные единицы.
Как нумеровать квадранты?
Эти четыре секции называются квадрантами. Квадранты названы с помощью римского цифры I, II, III и IV начиная с верхнего правого квадранта и двигаясь против часовой стрелки.
Где расположены квадранты?
Квадранты обозначены квадрантом I (римская цифра один), верхняя правая область, квадрант II (римская цифра два) представляет собой верхнюю левую область, квадрант III (римская цифра три) представляет собой нижнюю левую область, а квадрант IV (римская цифра четыре) представляет собой нижнюю правую область.
Квадрант какой формы?
что-то в форме как четверть круга, как часть машины.
Что такое квадрант числа 1 2?
Примеры алгебры
Точка находится в г. второй квадрант потому что x отрицательный, а y положительный.
Смотрите также, какое твердое тело представляет собой алмаз.
Что такое квадрант 0 4?
Примеры тригонометрии
Поскольку координата y положительна, а координата x равна 0, точка расположена на оси y между первой и четвертый квадранты.
Что такое квадрант 0 5?
Объяснение: Эта точка нев квадранте– он находится на положительной оси y, потому что точка, по сути, является точкой пересечения с осью y.
Что такое 4 квадранта на координатной плоскости?
Первый квадрант (QI) — это верхняя правая четверть координатной плоскости, где есть только положительные координаты. Второй квадрант (QII) — верхняя левая четвертая координатной плоскости. Третий квадрант (QIII) — нижний левый четвертый. Четвертый квадрант (QIV) — нижний правый четвертый..
Что означает координата Y?
Определение координаты Y
: координата, значение которой определяется измерением параллельно оси y-ось конкретно: ордината.
Что такое координата в 9 классе математики?
Координатные точки будут определить положение в декартовой плоскости. Первая точка (x) в координатах представляет собой горизонтальную ось, а вторая точка в координатах (y) представляет собой вертикальную ось.
Для чего используется координатная геометрия?
Ответ: Нужна координатная геометрия предложить связь между алгеброй и геометрией с использованием графиков линий и кривых. Это важный раздел математики, который обычно помогает нам находить точки на плоскости. Более того, он также имеет множество применений в областях тригонометрии, исчисления, размерной геометрии и других областях.
Что такое координата в математике?
более … Набор значений, показывающих точное положение. На графиках это обычно пара чисел: первое число показывает расстояние вдоль, а второе число показывает расстояние вверх или вниз. Пример: точка (12,5) находится на 12 единиц вперед и на 5 единиц вверх.
Что такое четверть в круге?
Квадрант четверть круга. Если круг равномерно разделить на четыре части двумя перпендикулярными линиями, то каждая из четырех частей является квадрантом. Таким образом, площадь круга делится на 4. … Квадрант круга — это сектор круга, секторальный угол которого равен 90 градусам.
Квадрант совпадает с сектором?
Квадрант одна четверть круга, и имеет угол 90. Сектор – это часть круга, которая может иметь любой угол и может быть любой частью круга, которая находится между двумя радиусами и центром.
Как найти площадь и периметр четверти?
потому что полуокружность – это сектор с секторальным углом 180°. Площадь квадранта круга = 14πr2. Периметр квадрант окружности = (π2 + 2)r.
Посмотрите также, как адаптируются пастбищные животные.
Какой номер имеет каждый квадрант на графике?
два
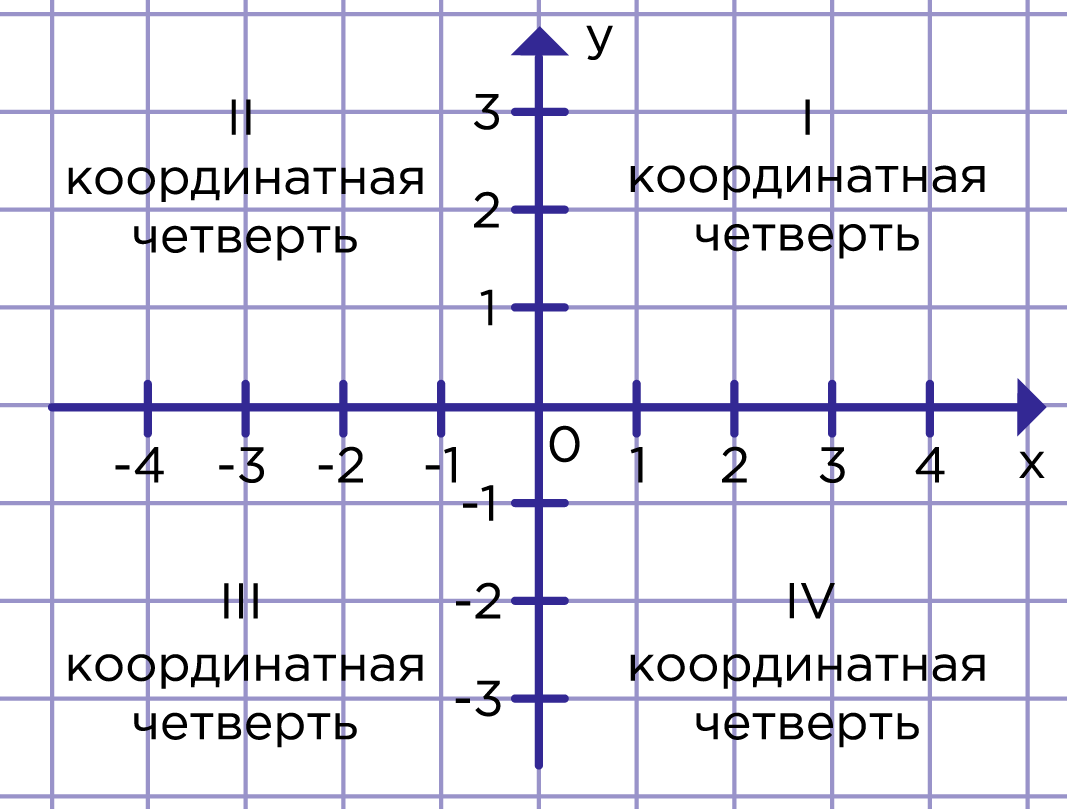
Оси двумерной декартовой системы делят плоскость на четыре бесконечные области, называемые квадрантами, каждая из которых ограничена двумя полуосями. Они часто нумеруются от 1-го до 4-го и обозначаются римскими цифрами: I (где знаки координат (x; y) I (+; +), II (-; +), III (-; -) и IV (+;-).
Какова роль квадрантов?
Знаки углов в квадрантах
Таким образом, в первом квадранте, где координаты x и y равны все положительные, все шесть тригонометрических функций имеют положительные значения. Во втором квадранте положительны только синус и косеканс (обратное значение синуса). В третьем квадранте положительны только тангенс и котангенс.
Чем отличаются квадранты?
Вот характеристики для каждого из четырех квадрантов координатной плоскости:
- Квадрант I: положительный x и положительный y.
- Квадрант II: отрицательный x и положительный y.
- Квадрант III: отрицательный x и отрицательный y.
- Квадрант IV: положительный x и отрицательный y.
Какой квадрант, если точка находится на оси?
Точки, лежащие на ось не лежит ни в одной четверти. Если точка лежит на оси x, то ее координата y равна 0. Аналогично для оси y.
Что такое квадрант, простое определение?
1 : четверть круга. 2: любая из четырех частей, на которые что-либо делится двумя воображаемыми или реальными линиями, пересекающими друг друга под прямым углом.
Что такое квадрант 10?
10 радиан — это примерно 6,4 угла на девяносто градусов, что удобно для третий квадрант.
В каком квадранте находится точка (- 3 4?
третий квадрант третий квадрант имеет точки вида (-x,-y), поэтому наша точка (-3,-4) лежит в третьем квадранте.
В каком квадранте лежит точка (- 3 5?
III квадрант
(v) Точка (-3,-5) лежит в III квадранте декартовой плоскости, поскольку и x, и y отрицательны. 23 февраля 2021 г.
В каком квадранте находится точка (- 2?
Эта точка находится на 3-й квадрант.
В каком квадранте находится точка 2 3?
третий квадрант Точка (2,−3) лежит в третий квадрант.
Квадранты и точки построения (упрощение математики)
Как построить график четырех квадрантов
Нанесение точек на координатную плоскость | Все 4 квадранта
Определение квадранта точки на координатной плоскости
Квадрант – это четверть круга. Итак, чтобы определить площадь квадранта, сначала определите площадь всего круга (используйте формулу A = π × r²), а затем разделите ответ на 4. В качестве альтернативы вы можете подставить радиус квадранта непосредственно в формула A = ¼ πr². Давайте посмотрим на несколько примеров проработки площади квадрантов:
Пример 1
Проработайте область этого квадранта (радиус 8 см).
Метод 1 (использование площади всего круга и деление на 4)
Сначала определите площадь всего круга, подставив радиус 8 см в формулу для площади круга:
A = π × r²
= π × 8²
= 64π (оставьте ответ как точное решение, так как его нужно разделить на 4).
Итак, все, что вам нужно сделать сейчас, это разделить ответ на 4:
Площадь квадранта = 64π ÷ 4 = 16π = 50,3 см² с точностью до 3 значащих цифр.
Метод 2 (с использованием ¼ πr²)
Подставляем r = 8 непосредственно в формулу A = ¼ πr².
A = ¼ πr².
A = ¼ × π × 8².
A = 50,3 см²
Как видите, он дает тот же ответ, что и метод 1.
Пример 2
Обсудите площадь этого квадранта (радиус 3,8 м).
Как и в примере 1, начните с подстановки радиуса 3,8 м в формулу для площади круга:
A = π × r²
= π × 3,8²
= 14,44π (оставьте ответ как точное решение, так как его нужно разделить на 4).
Опять же, все, что вам нужно сделать сейчас, это разделить ответ на 4:
Площадь квадранта = 14,44π ÷ 4 = 16π = 11,3 м² до 3 значащих цифр.
Способ 2
Подставляем r = 3,8 м непосредственно в формулу A = ¼ πr².
A = ¼ πr².
A = ¼ × π × 3,8².
A = 11,3 м²
Как видите, он дает тот же ответ, что и метод 1.
Вопросы и Ответы
Вопрос: Если площадь круга составляет 100 см2, какова площадь одного из его квадрантов?
Ответ: Все, что вам нужно сделать, это разделить 100 на 4, чтобы получить 25 см ^ 2.
Вопрос: Сможете ли вы найти площадь квадранта круга, длина окружности которого равна 22?
Ответ: Сначала найдите радиус окружности, разделив длину окружности на Пи и разделив ответ пополам, чтобы получить 3,501 до 3 десятичных знаков.
Теперь используйте 0,25 * Pi * радиус ^ 2, чтобы получить площадь квадранта 0,25 * Pi * 3,501 ^ 2 = 9,63 с точностью до 2 знаков после запятой.
Вопрос: Какова площадь квадранта радиусом 6 см, выраженная в Пи?
Ответ: Сначала возведите радиус 6 в квадрат, чтобы получить 36.
Теперь умножьте 36 на Пи, чтобы получить 36 Пи.
Затем разделите ответ на 4 и получите 9 Пи.
Вопрос: По какой формуле рассчитывается площадь квадранта?
Ответ: 0,25 * пи * r ^ 2.
Вопрос: Предполагается, что площадь четверти круга равна (8² x π) / 4?
Ответ: Да, формулу можно записать как (радиус² x π) / 4.
Думаю, вы показываете пример, когда радиус четверти круга равен 8.
Вопрос: Если колесо ворот находится на расстоянии 3 футов от стены и поворачивается на 90 градусов, какое расстояние преодолевает колесо?
Ответ: Сначала удвойте 3 фута, чтобы получить диаметр 6 футов.
Затем умножьте 3,14 на 6, чтобы получить длину окружности всего круга, равную 18,84 фута.
Теперь разделите ответ на 4, так как 90 градусов составляют 1/4 всей окружности, чтобы получить 4,7 фута с 1 десятичным знаком.
Вопрос: Сможете ли вы найти площадь квадранта радиусом 9 см?
Ответ: Квадрат 9, получаем 81.
Теперь умножьте 81 на 3,14, чтобы получить 254,34.
Наконец, разделите 254,34 на 4, чтобы получить 63,6 с точностью до 1 знака после запятой.
Вопрос: Какова площадь квадранта с радиусом 14 см?
Ответ: Площадь всего круга равна Pi, умноженному на 14, умноженному на 14, что дает 615,75… см ^ 2.
Теперь разделите этот ответ на 4, чтобы получить 153,9 см ^ 2 до 1 знака после запятой (или 49 Пи).
Вопрос: Какова площадь квадранта радиусом 4,3 см?
Ответ: Выполните 0,25, умноженные на Пи, умноженные на 4,3 ^ 2, чтобы получить 14,5 см ^ 2 с округлением до 1 знака после запятой.
Вопрос: Какова площадь 1/4 круга с радиусом 6?
Ответ: Сначала возведите радиус в квадрат, чтобы получить 36, и умножьте его на π, чтобы получить 36π.
Теперь разделите этот ответ на 4, чтобы получить 9π.
Вопрос: Радиус четверти круга составляет 3 миллиметра. Какова площадь четверти круга? (r = 3 мм, Pi = 3,14)
Ответ: Выполните 3 ^ 2, что равно 9.
Теперь умножаем 9 на 3,14, что составляет 28,26.
Теперь разделите 28,26 на 4, чтобы получить 7,065 мм ^ 2.
Конспект урока: Координатная плоскость
Координатная плоскость
План урока
- Координатная плоскость
Цели урока
- Знать понятия координатная плоскость, оси координат, координатные четверти, абсцисса и ордината точки, правила расположения координат точек на плоскости
- Знать свойство координат точек, симметричных относительно осей координат, начала отсчета
- Уметь находить координаты точки на координатной плоскости и строить точку по заданным координатам
Разминка
- Как задать координатную прямую?
- Что такое единичный отрезок?
- Как найти координату точки на координатной прямой?
Координатная плоскость
В речи взрослых вы могли слышать такую фразу: “Оставьте мне ваши координаты”. Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, которые и считаются в этом случае координатами человека.
Главное здесь в том, что по этим данным человека можно найти.
Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта.
Системы координат пронизывают всю практическую жизнь человека. Кроме почтовых адресов и номеров телефонов, вы знакомы с системой координат в зрительном зале кинотеатра (номер ряда и номер места), в поезде (номер вагона и номер места), с системой географических координат (долгота и широта).
Вы умеете задавать координаты на прямой. Для этого на прямой выбирают начало отсчета, положительное направление и единичный отрезок. После этого любая точка прямой получает свою собственную координату.
Рис. 1. Квадранты
Чтобы определить положение точки на плоскости проводят две перпендикулярные координатные прямые Х и У, которые пересекаются в точке О, и вводят на каждой из них обычные координаты. Эти координаты согласованы между собой. Точка пересечения прямых О называется
началом координат
. Сами координатные прямые называются
осями координат.
Горизонтальную ось называют
осью абсцисс
(осью х), вертикальную ось называют
осью ординат
(или осью у).
Плоскость, на которой задана система координат, называется
координатной плоскостью
.
Рис. 2. Координатная плоскость
Координатная плоскость делится осями на 4 части — 4
координатных четверти
(квадранта). Нумеруют четверти с верхней правой четверти (1 четверть) против часовой стрелки как показано на рис. 1.
Точке А на координатной плоскости (рис. 2) соответствует пара чисел: ее абсцисса и ордината. И, наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Прямая, проходящая через точку А параллельно оси абсцисс, пересекает ось ординат в координате 2 — это
ордината точки
А. Прямая, проходящая через точку А параллельно оси ординат, пересекает ось абсцисс в координате 3 — это
абсцисса точки
А. Запишем в скобках на первом месте абсциссу точки А, а на втором — ее ординату.
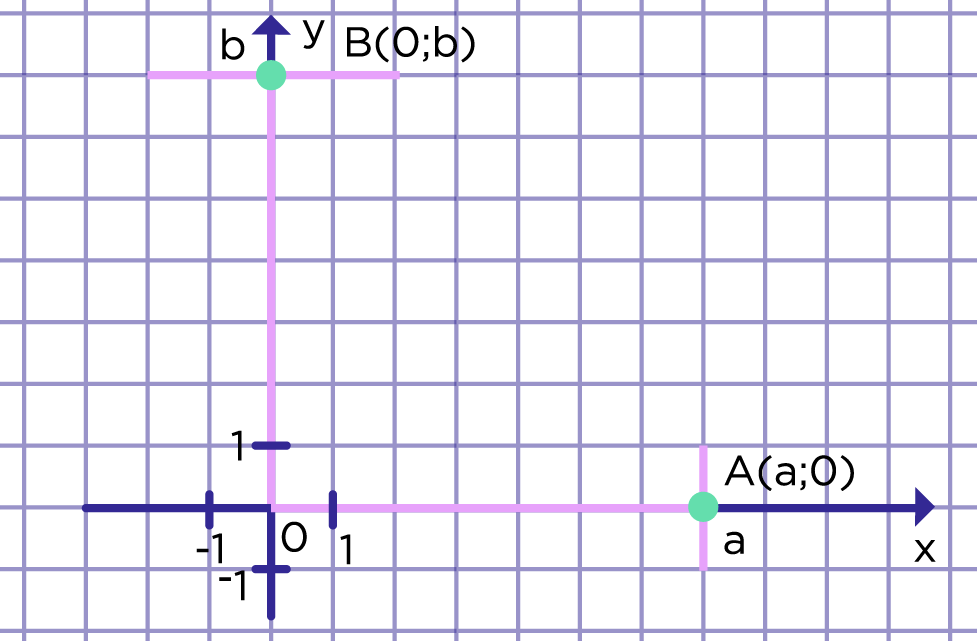
Рис. 3. Расположение точек на осях координат
Полученная запись будет
координатами
точки А в координатной плоскости:
А (3; 2).
Если точка лежит на оси ординат, то ее абсцисса равна нулю, если точка лежит на оси абсцисс, то ее ордината равна нулю. На рисунке 3 точка А имеет координаты (7; 0), а точка В (0; 7).
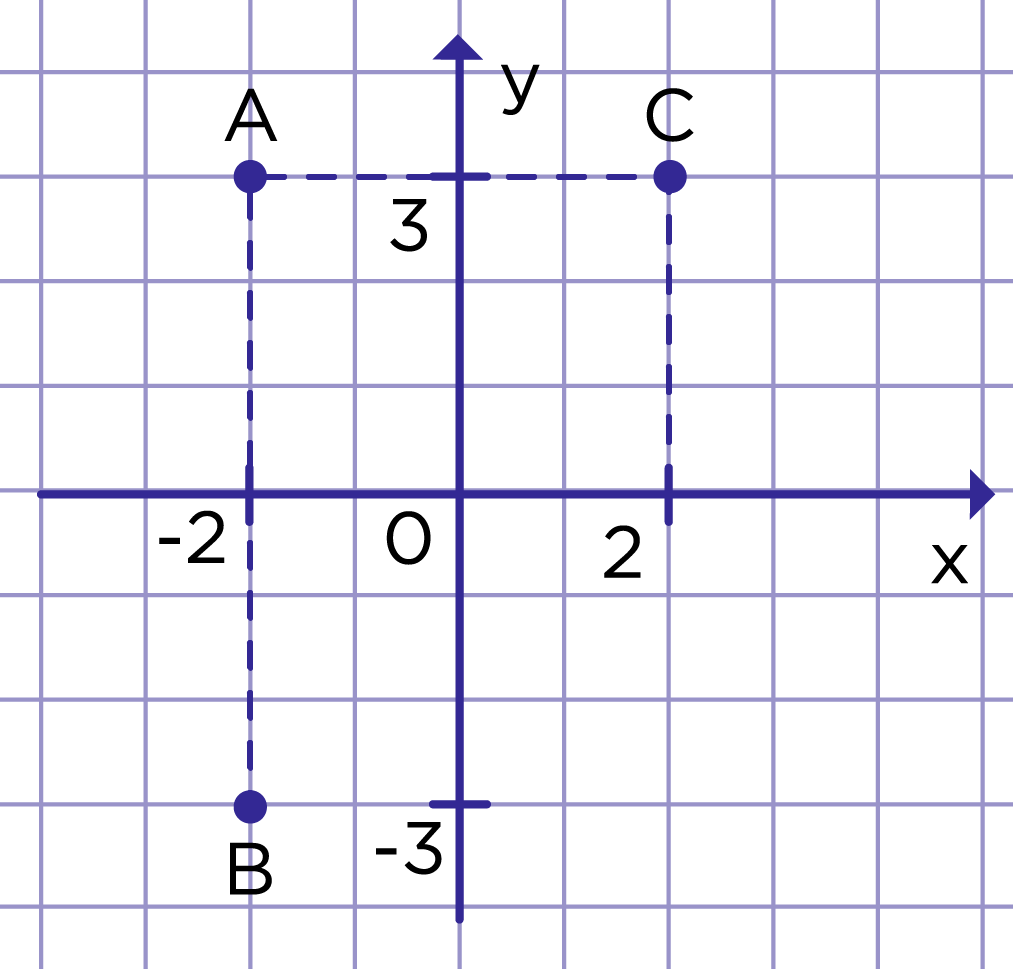
На рисунке 4 отмечены точки А (– 2; 3), В (– 2; – 3) и С (2; 3).
Рис. 4. Симметричные точки
Начало координат имеет координаты (0;0).
Обратим внимание, что абсциссы и ординаты точек B и С — противоположные числа. А сами точки симметричны относительно начала координат.
У точек А и С ордината одинаковая, а абсциссы — противоположные числа, сами точки симметричны относительно оси ординат.
Точки А и В симметричны относительно оси абсцисс, их абсциссы равны, а ординаты — противоположные числа.
Упражнения
Рис. 5
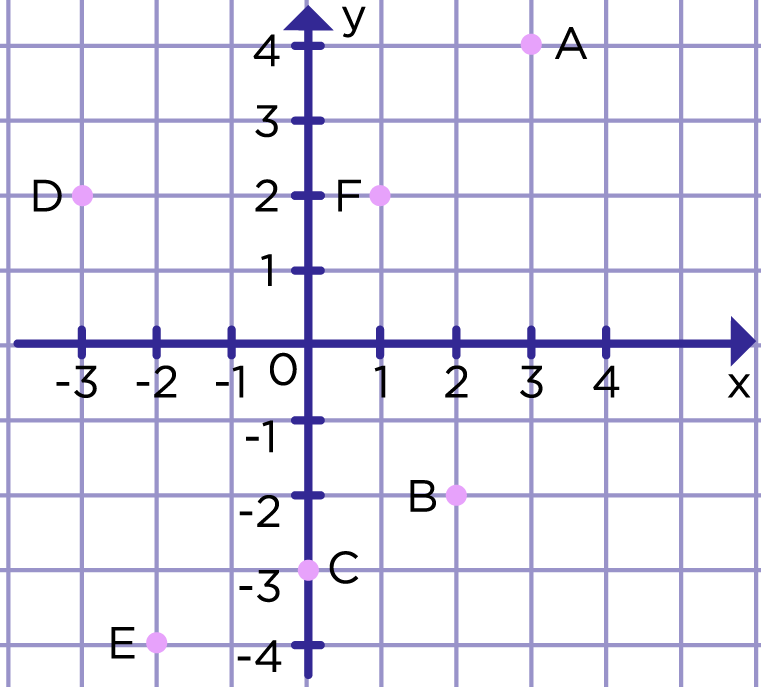
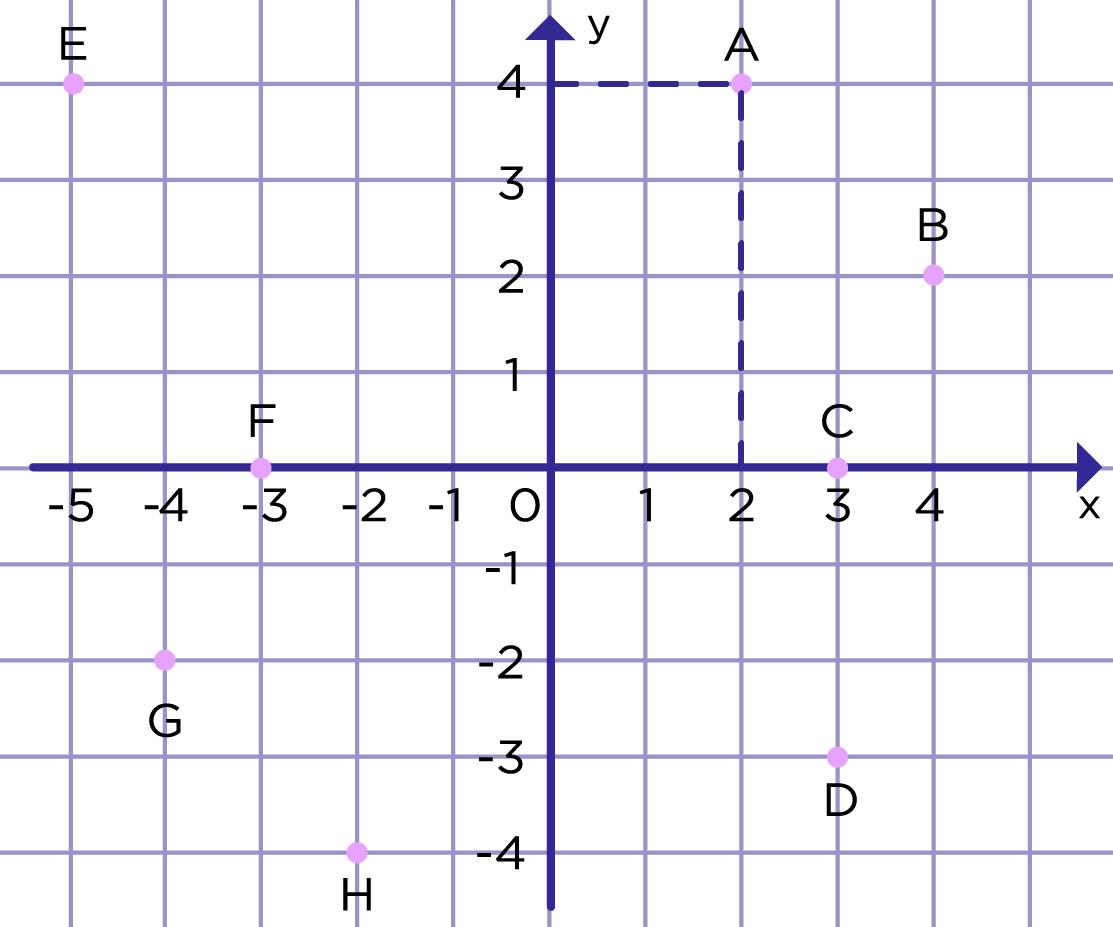
1. Найдите координаты точек на координатной плоскости на рис. 5.
2. Постройте координатную плоскость и отметьте на ней точки:
A (2; 4), В (4; 2), С (3; 0), D (3; – 3),
Е (– 5; 4); F (– 3; 0), G (– 4; – 2),
Н (– 2; – 4).
Контрольные вопросы
1. Как задать координатную плоскость?
2. Как еще можно назвать ось x? Ось y?
3. Под каким углом пересекаются оси?
4. Где на координатной плоскости находится точка, абсцисса которой равна нулю?
5. Как найти координату точки на координатной прямой?
Ответы
1. A(3; 4), B(2; – 2), C(0; – 3), D(– 3; 2), E(– 2; – 4), F(1; 2).
2.
Рис. 6. Упражнение. Ответ
Предыдущий урок
Бесконечные периодические десятичные дроби. Десятичное приближение обыкновенной дроби
Десятичные дроби
Следующий урок
Графики
Координатная плоскость
Learn all four quadrants of a coordinate system.
The
plane of the graph paper is divided into four regions by the coordinate axes
and the four regions are called quadrants.
What are the Quadrants
in the Coordinate Plane?
● The region XOY is called the I quadrant.
In first quadrant, both x and y co-ordinate are positive.
● The region X’OY’ is called the
II quadrant.
In second quadrant x co-ordinate is negative and y
co-ordinate is positive.
● The region X’OY’ is called the
III quadrant.
In third quadrant both x and y co-ordinate are negative.
● The region XOY’ is called the IV quadrant.
In fourth quadrant x co-ordinate is positive and y
co-ordinate is negative.
According to the quadrants the signs of the co-ordinate of a
point are of the form:
(+, +) in the first quadrant
(-, +) in the second quadrant
(-, -) in the third quadrant
(+, -) in the fourth quadrant
The table will help us to remember the region of the
quadrants and theirs signs of coordinates.
| Region | Quadrant | Signs of Coordinates |
|---|---|---|
| XOY | I | (+, +) |
| YOX’ | II | (-, +) |
| X’OY’ | III | (-, -) |
| Y’OX | IV | (+, -) |
Related Concepts:
● Coordinate Graph
● Ordered pair of a Coordinate System
● Plot Ordered Pairs
● Coordinates of a Point
● Signs of Coordinates
● Find the Coordinates of a Point
● Coordinates of a Point in a Plane
● Plot Points on Co-ordinate Graph
● Graph of Linear Equation
● Simultaneous Equations Graphically
● Graphs of Simple Function
● Graph of Perimeter vs. Length of the Side of a Square
● Graph of Area vs. Side of a Square
● Graph of Simple Interest vs. Number of Years
● Graph of Distance vs. Time
7th Grade Math Problems
8th Grade Math Practice
From All four Quadrants to HOME PAGE
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
|
Share this page: |
FacebookTwitterPinterestWhatsAppMessenger |