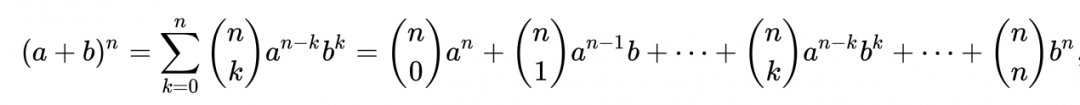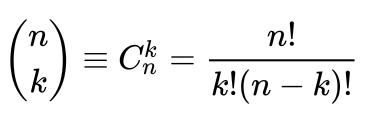Как найти квадрат бинома

How do
you get the square of a binomial?

For squaring a binomial we need to know
the formulas for the sum of squares and the difference of squares.

Sum of squares: (a + b)² = a² + b² + 2ab

Difference of squares: (a – b)² = a² + b² – 2ab

Worked-out
examples for the expansion of square of a binomial:

1.
(i) What should be added to 4m + 12mn to make it a perfect square?

(ii) What is the perfect square
expression?

Solution:

(i) 4m² + 12mn = (2m) ² + 2 (2m) (3n)

Thus, to make it a perfect square, (3n)² must be added.

(ii) Therefore, the new expression = (2m)² + 2 (2m) (3n) + (3n)² = (2m + 3n)²

2. What should be subtracted from 1/4 x² + 1/25 y² to make it a perfect square? What is the new expression formed?

Solution:

1/4 x² + 1/25 y² = (1/2 x) ² + (1/5 y)²

To make a perfect square, 2 (1/2 x) (1/5 y) must be subtracted.

Therefore, the new expression formed = (1/2 x)² + (1/5 y)² – 2 (1/2 x) (1/5 y)

                                                    = (1/2 x – 1/5 y)²

3. If x + 1/x = 9 then find the value of: x⁴ + 1/x⁴

Solution:

Give, x + 1/x = 9

Squaring both the sides we get,

(x + 1/x)² = (9)²

⇒ x² + 1/x² + 2 ∙ x ∙ 1/x = 81

⇒ x² + 1/x² = 81 – 2

⇒ x² + 1/x² = 79

Again, square both the sides we get,

⇒ (x² – 1/x²) ² = (79) ²

⇒ (x)⁴ + 1/x⁴ + (x⁴) × (1/x⁴) = 6241

⇒ (x)⁴ + 1/x⁴ + 2 = 6241

⇒ (x)⁴ + 1/x⁴ = 6241 – 2

⇒ (x)⁴ + 1/x⁴ = 6239

Therefore, (x)⁴ + 1/x⁴ = 6239

4. If x – 1/x = 5, find the value of x² + 1/x² and x⁴ + 1/x⁴

Solution:

Given, x – 1/x = 5

Square both sides

(x – 1/x)² = (5)²

x² + 1/x² – 2 (x) 1/x = 25

x² + 1/x² = 25 + 2

x² + 1/x² = 27

Again square both sides

(x² + 1/x²) = (27)²

(x)⁴ + 1/x⁴ + (x⁴) × (1/x⁴) = 729

(x)⁴ + 1/x⁴ = 729 – 2 = 727

5. If x + y = 8 and xy = 5, find the value of x² + y²

Solution:

Given, x + y = 10

Square both sides

(x + y)² = (8)²

x² + y² + 2xy = 64

x² + y² + 2 × 5 = 64

x² + y² + 10 = 64

x² + y² = 64 – 10

x² + y² = 50

Therefore, x² + y² = 54

6. Express 64x² + 25y² – 80xy as perfect square.

Solution:

(8x)² + (5y)² – 2(8x)(5y)

We know that (a – b)² = a² + b² – 2ab. Using this formula we get,

= (8x – 5y)², which is a required perfect square.

The explanation to find
the product of the square of a binomial will help us to expand the sum and difference
of binomial square.

Продолжаем рассказывать о разных формулах и подходах из математики, которые часто применяются в ИТ и в привычных алгоритмах. Сегодня будет про бином Ньютона — про него много кто слышал, но не все представляют, что это и зачем это нужно. Сейчас разложим по полочкам. 

Чтобы понять бином Ньютона, нам понадобится треугольник Паскаля.

Что такое треугольник Паскаля

Треугольник Паскаля — это одно из названий треугольной таблицы чисел. Его назвали в честь математика Блеза Паскаля, но про такой треугольник математики знали тысячу лет назад. 

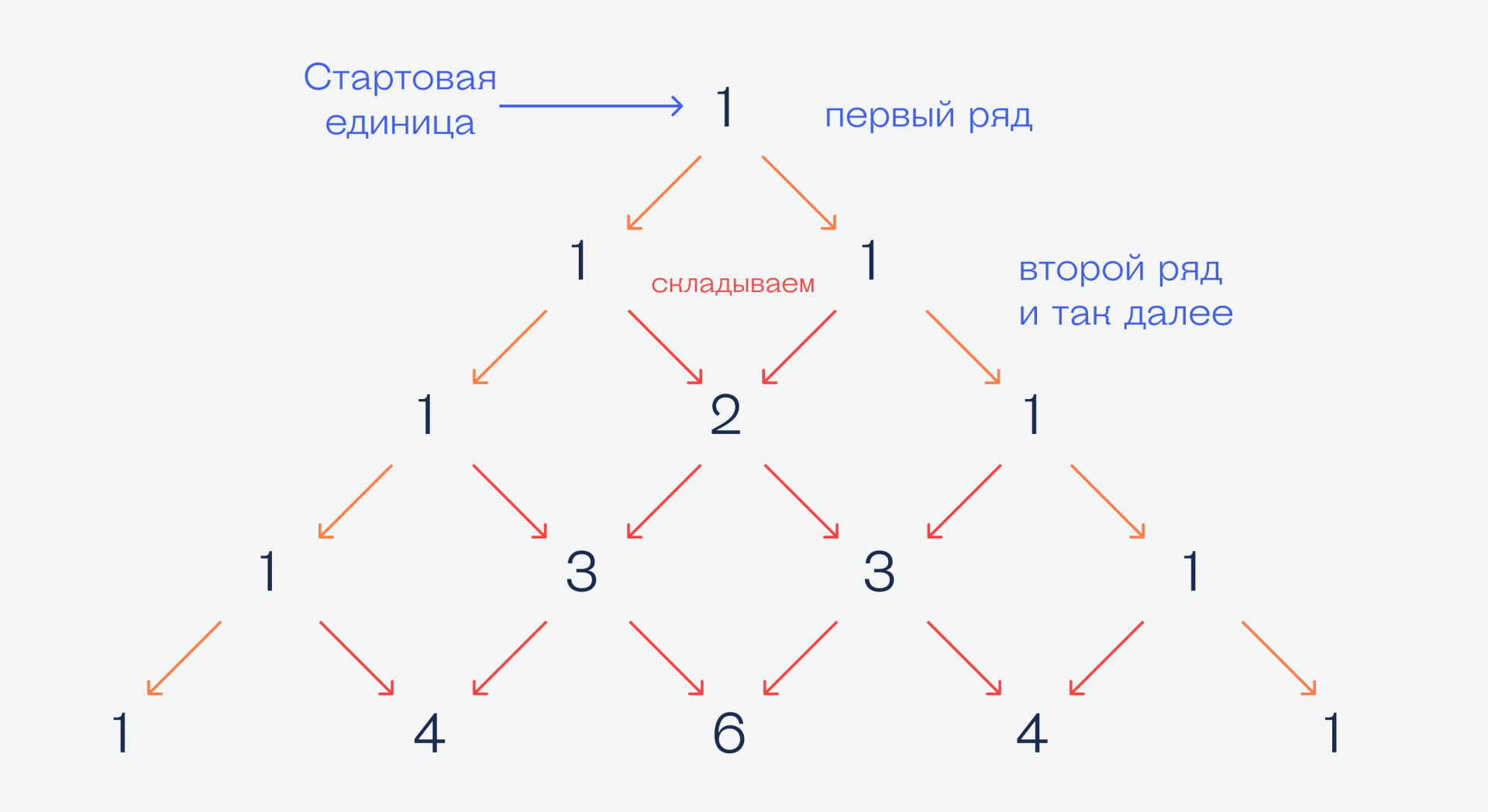
Работает треугольник так: берём единицу (это будет вершина треугольника), а все остальные числа в каждом ряду получаем сложением левых и правых чисел, которые стоят выше. Если нарисовать, то получится так:

Такой треугольник можно продолжать бесконечно. В математике этот треугольник обладает разными полезными свойствами, но нам он нужен для биномиальных коэффициентов в биноме Ньютона. Вот теперь поговорим про бином.

Что такое бином Ньютона (просто)

Бином Ньютона — это формула, которая помогает посчитать сумму двух чисел, возведенную в какую-то степень.

Разбираем по полочкам: 

Из школьной программы мы помним такую формулу: (a + b)² = a² + 2ab + b² — это частный случай бинома Ньютона для квадрата суммы. 

Может быть, вы помните сумму в кубе: (a + b)³ = a³ + 3a²b + 3ab² + b³ — это тоже бином Ньютона. 

А что если нам нужно возвести сумму не в квадрат, не в куб, а в сто сорок шестую степень? Какая тогда будет формула? Вот для этого нам нужна более обобщенная формула, которая опишет вообще все варианты биномов для любой степени.

Исходя из этой адской формулы для расчета бинома на компьютере нам нужно будет много раз посчитать факториал — это произведение всех целых чисел от единицы до заданного числа. Например, 5! = 1 × 2 × 3 × 4 × 5 = 120. А факториалы в силу своей цикличности жрут довольно много оперативной памяти. Может так получиться, что мы не сможем посчитать коэффициенты бинома, потому что закончилась оперативка.

Но, оказывается, необязательно считать факториалы — есть способ проще.

Биномиальные коэффициенты и треугольник Паскаля (простая теория в картинках)

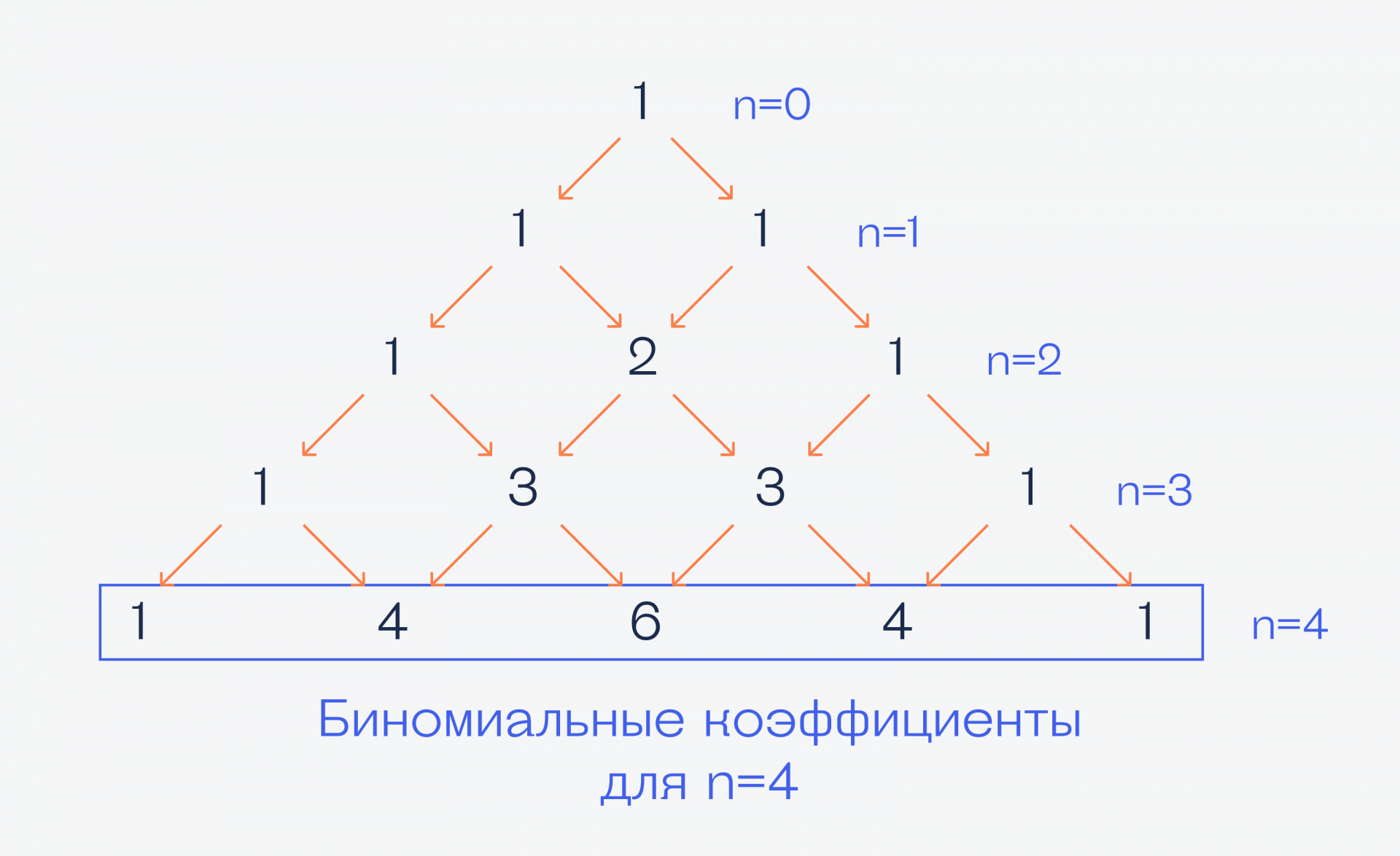
Тут нам приходит на помощь треугольник Паскаля. Оказывается, числа в каждом ряду — это биномиальные коэффициенты для каждой степени n:

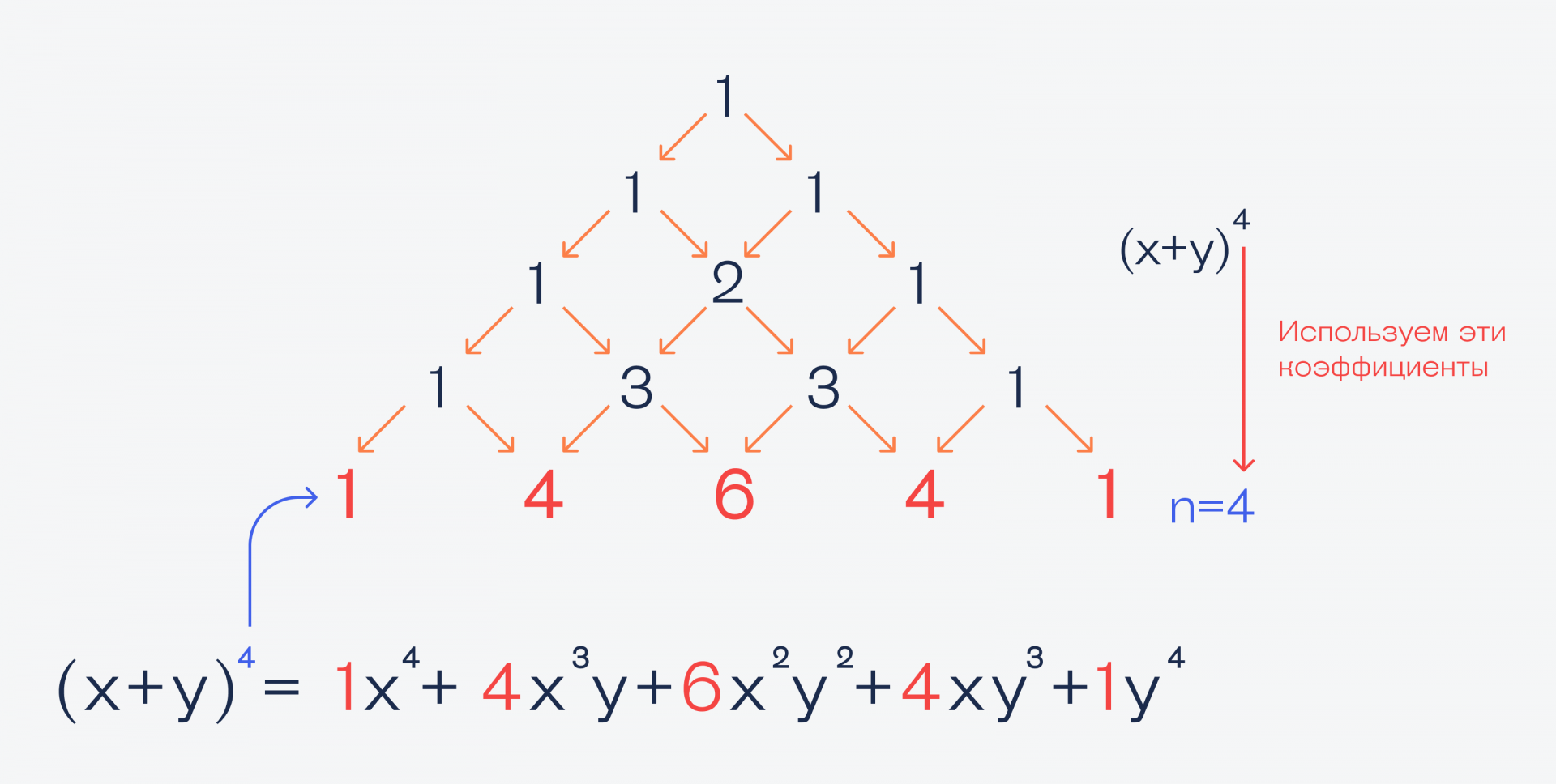
На практике это работает так: допустим, что по ходу работы алгоритма нам нужно раскрыть скобки и вычислить (x + y)⁴. Применим сюда бином Ньютона и треугольник Паскаля:

Получается, что с помощью этого треугольника можно не считать все эти формулы с факториалами, а быстро находить нужные коэффициенты, подставлять их в формулу бинома и сразу получать ответ. Так можно разложить любой бином и получить ответ гораздо быстрее, чем вычисляя все факториалы подряд.

Где используется бином Ньютона

Кроме математики, где бином нужен для комбинаторики и разных полезных формул, он часто применяется в программировании. Например, с его помощью можно обойти ограничение на размер оперативной памяти при возведении большого числа в степень: его можно разложить на сумму двух чисел поменьше и посчитать слагаемые через бином. 

Также биномиальные коэффициенты часто применяются в матрицах и операциях с векторами — а именно на матрицах построены почти все нейросети. Поэтому если мы сможем быстро находить нужный коэффициент и применять его к матрице, то сможем быстрее создавать дипфейки и генерировать реалистичные пейзажи. Строго говоря, для этого сейчас нужно просто знать команду import, потому что готовых библиотек на эту тему — вагон, без всяких биномов. 

А ещё на биномиальных коэффициентах работает отдельная непозиционная система счисления — её применяют в проектах, где надо быстро перебирать много различных вариантов и их возможных сочетаний.

Что дальше

Дальше мы попробуем применить эти знания и алгоритмы на практике: напишем код, который использует бином Ньютона для решения разных хитрых бытовых задач. 

Вы когда-нибудь слышали, чтобы ваш учитель или сокурсники говорили о методе FOIL? Они, вероятно, не говорят о типе фольги, которую вы используете для ограждения или на кухне. Вместо этого метод FOIL означает «первое, внешнее, внутреннее, последнее», мнемоническое устройство или устройство памяти, которое помогает вам вспомнить, как умножить два бинома вместе, и это именно то, что вы делаете, когда берете квадрат бинома.

TL; DR (слишком долго; не читал)

Чтобы возвести в квадрат бином, запишите умножение и используйте метод FOIL, чтобы сложить суммы первого, внешнего, внутреннего и последнего членов. Результатом является квадрат бинома.

Быстрое освежение в квадрате

Прежде чем идти дальше, потратьте секунду, чтобы освежить в памяти то, что означает возведение в квадрат числа, независимо от того, является ли оно переменной, константой, полиномом (включая двоичные числа) или чем-то еще. Когда вы возводите число в квадрат, вы умножаете его на себя. Таким образом, если вы возведете квадрат в квадрат x , у вас будет x × x, который также можно записать как x ² . Если вы возведете в квадрат бином, такой как x + 4, у вас будет ( x + 4) ² или, как только вы напишете умножение, ( x + 4) × ( x + 4). Имея это в виду, вы готовы применить метод FOIL к квадратным биномам.

1. Запишите умножение

Запишите умножение, подразумеваемое операцией возведения в квадрат. Таким образом, если ваша первоначальная проблема заключается в оценке ( y + 8) ², вы бы написали это как:

( у + 8) ( у + 8)

2. Применить метод фольги

Примените метод FOIL, начинающийся с «F», который обозначает первые члены каждого многочлена. В этом случае первыми являются оба y , поэтому, когда вы умножаете их вместе, вы получаете:

у ²

Затем, умножьте «O» или внешние члены каждого бинома вместе. Это y из первого бинома и 8 из второго бинома, так как они находятся на внешних краях умножения, которое вы выписали. Это оставляет вас с:

8_y_

Следующая буква в FOIL – «Я», поэтому вы умножите внутренние члены полиномов вместе. Это 8 из первого бинома и y из второго бинома, что дает вам:

8_y_

(Обратите внимание, что если вы возводите в квадрат многочлен, термины «O» и «I» для FOIL всегда будут одинаковыми.)

Последняя буква в FOIL – это «L», которая обозначает умножение последних членов биномов вместе. Это 8 из первого бинома и 8 из второго бинома, что дает вам:

8 × 8 = 64

3. Добавьте условия FOIL Вместе

Добавьте термины FOIL, которые вы только что рассчитали; результатом будет квадрат бинома. В этом случае термины были y ², 8_y_, 8_y_ и 64, поэтому у вас есть:

y ² + 8_y_ + 8_y_ + 64

Вы можете упростить результат, добавив оба условия 8_y_, в результате чего вы получите окончательный ответ:

y ² + 16_y_ + 64

Предупреждения

• FOIL – это быстрый и простой способ запомнить, как умножить биномы. Но это работает только для биномов. Если вы имеете дело с полиномами, которые имеют более двух терминов, вам придется применить свойство распределения.

Вы когда-нибудь слышали, чтобы ваш учитель или однокурсники говорили о методе FOIL? Вероятно, они не говорят о типе фольги, которую вы используете для ограждения или на кухне. Вместо этого метод FOIL означает «первый, внешний, внутренний, последний», мнемоническое устройство или устройство памяти, которое помогает вам помните, как умножить два бинома вместе, это именно то, что вы делаете, когда берете квадрат бином.