06
Фев 2014
Категория: Справочные материалы
Извлечение корня из большого числа
2014-02-06
2021-06-25
 А у вас есть зависимость от калькулятора? Или вы считаете, что кроме как с калькулятором или при помощи таблицы квадратов очень сложно вычислить, например,
А у вас есть зависимость от калькулятора? Или вы считаете, что кроме как с калькулятором или при помощи таблицы квадратов очень сложно вычислить, например, .
 Случается, школьники привязаны к калькулятору и даже
Случается, школьники привязаны к калькулятору и даже на
умножают, нажимая на заветные кнопочки. Говорят, ну я все равно знаю как посчитать, а сейчас сэкономлю время… Вот будет экзамен… тогда и напрягусь…
Так дело в том, что на экзамене и так будет предостаточно «напряжных моментов»… Как говорится, вода камень точит. Вот и на экзамене мелочи, если их много, способны подкосить…
Давайте минимизируем количество возможных неприятностей.
Извлекаем квадратный корень из большого числа
Мы будем говорить сейчас только о случае, когда результат извлечения корня квадратного – целое число.
Случай 1 + показать
Случай 2 + показать
Смотрите также «Отдельные случаи вычисления дискриминанта»
Автор: egeMax |
комментария 4
Это умение очень пригодится на ЕГЭ и ОГЭ, потому как калькулятором пользоваться нельзя, подбором, умножая в столбик, получается долго и муторно, а в восьмой раз в туалет уже никто не выпустит.
Так что смотрим и запоминаем, чтобы потом научить своих детей, которым наверняка не рассказывали это в школе, но это сильно сэкономит время на экзаменах.
Этот способ подойдет для тех чисел, из которых корень извлекается целым числом. Именно поэтому этот способ очень удобен как раз для ОГЭ и ЕГЭ, потому как там не дают корни, из которых корень не извлекается (часть С не в счет).
Покажу на примерах. Кому удобнее смотреть видео, смотрите.
Допустим нам надо извлечь корень из числа 54756. Дальше листаем галерею, смотрим подписи к фотографиям и запоминаем алгоритм.
Второй пример. Извлечем корень из числа 259081. Попробуйте сами. На втором слайде будет решение.
На первый взгляд схема весьма непростая, но стоит один-два раза попробовать извлечь корни таким образом самостоятельно и вы будете щелкать такие задачи, как семечки. Попробуйте извлечь корень из 112225; 210681 и 998001.
С числами поменьше, всё ещё проще, даже писать ничего не придется. Можно в уме вычислять. Вот, например, как извлечь корень из 3136? Понятно, что грани две, поэтому в ответе двухзначное число. Первая цифра в ответе — это 5, потому что 5²=25, а 6²=36>31. Так как 3136 заканчивается на 6, а при возведении в квадрат шестерку могут давать только 4 или 6, ответом будет либо 54, либо 56. Как выбрать? Давайте вспомним чему равен 55². Если не помните, то это легко посчитать (подробно читайте тут), надо в конце записать 25, а в начале 5•6=30 Итого 55²=3025. 3025<3136, а так как корень должен извлекаться нацело, значит ответ 56.
Аналогично извлекаем корень из 4624. 6²=36, а 7²=49, поэтому первая цифра ответа — 6. При возведении в квадрат четверку на конце дают только 2 и 8, то есть ответ 62 или 68. Чтобы выбрать, мы должны сравнить подкоренное число с 65². 6•7=42, дописываем в конце 25 и получаем 65²=4225. 4225<4624 следовательно √4624=68.
Ну и последний корень попробуйте снова извлечь самостоятельно. Чему равен √2116? Проверьте себя по картинке ниже.
И не забываем о том, что у меня появился канал на Ютубе. Заходите в гости и подписывайтесь.
Ещё интересно: Два простых способа быстрого сложения и вычитания в уме
Простой и очень быстрый способ возведения в квадрат чисел, оканчивающихся на 5. Будешь считать быстрее калькулятора
90% европейских выпускников не смогли решить задачу, которую решили российские восьмиклассники
При решении текстовых задач на составление уравнений очень часто приходится вычислять квадратный корень из больших чисел. Если говорить про стандартные задачи из ОГЭ и ЕгЭ , то в таких случаях обычно предполагается, что корень (из дискриминанта при решении квадратного уравнения) извлечь можно.
Но как без калькулятора вычислить корни больших чисел? Предположим, вам требуется найти корень из 1369. Есть простой и логичный алгоритм. Сначала надо определить десятки. Для этого ищем целые числа, в квадраты которых заключено число. Так квадрат 30- это 900, квадрат 40- 1600. Значит искомое число от 30 до 40.
Проверим теперь какие числа точно не подойдут. Т.к. произведение чётных чисел всегда четно, то отпадают все четные — 32, 34, 36, 38. Так как исходное число оканчивается не на 5, то 35 тоже отпадает. Теперь вспоминаем таблицу умножения. Число заканчивается на 9. 3 * 3 =9 и 7 * 7 = 49. Значит это либо 33, либо 37. Путем не сложной проверки можно убедиться, что искомое число — 37.
![]()
Извлечение корня из большого числа. Дорогие друзья! В этой статье мы с вами разберём как извлекать корень из большого числа без калькулятора. Это необходимо не только для решения некоторых типов задач ЕГЭ (есть такие — на движение), но и для общего математического развития этот аналитический приём знать желательно.
Казалось бы, всё просто: разложи на множители, да извлекай. Проблемы нет. Например число 291600 при разложении даст произведение:
![]()
Вычисляем:
![]()
Есть одно НО! Способ хорош если легко определяются делители 2, 3, 4 и так далее. А что делать если число, из которого мы извлекаем корень является произведением простых чисел? Например 152881 является произведением чисел 17, 17, 23, 23. Попробуй-ка сходу найди эти делители.
Суть рассматриваемого нами метода — это чистый анализ. Корень при наработанном навыке находится быстро. Если навык не отработан, а просто понят подход, то немного медленнее, но всё же определяется.
![]()
Извлечём корень из 190969.
Сначала определим — между какими числами (кратными ста) лежит наш результат.
Очевидно, что результат корня из данного числа лежит в пределах от 400 до 500, так как
4002=160000 и 5002=250000
Действительно:
![]()
Далее смотрим, где «стоит» это число:
посредине, ближе к 160 000 или к 250 000?
Число 190969 находится примерно посредине, но все же ближе к 160000. Можно сделать вывод, что результат нашего корня будет меньше 450. Проверим:
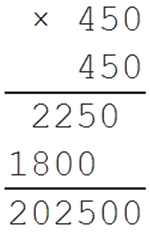
Действительно, он меньше 450, так как 190 969 < 202 500.
Теперь проверим число 440:
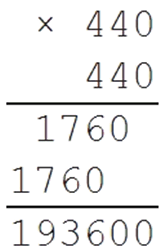
Значит наш результат меньше 440, так как 190 969 < 193 600.
Проверяем число 430:

Мы установили, что результат данного корня лежит в пределах от 430 до 440.
Далее используются свойства произведений чисел. Известно, что:
Произведение чисел имеющих на конце 1 или 9 дают число с 1 в конце. Например, 21 на 21 равно 441.
Произведение чисел имеющих на конце 2 или 8 дают число с 4 в конце. Например, 18 на 18 равно 324.
Произведение чисел имеющих на конце 5 дают число с 5 в конце. Например, 25 на 25 равно 625.
Произведение чисел имеющих на конце 4 или 6 дают число с 6 в конце. Например 26 на 26 равно 676.
Произведение чисел имеющих на конце 3 или 7 дают число с 9 в конце. Например, 17 на 17 равно 289.
Так как число 190969 заканчивается цифрой 9, то это произведение либо числа 433, либо 437.
*Только они при возведении в квадрат могут дать 9 в конце.
Проверяем:
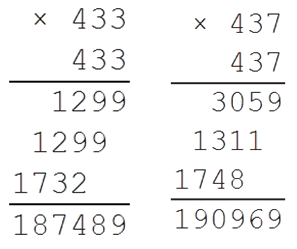
Значит результат корня будет равен 437.
То есть, мы как бы «нащупали» верный ответ.
Как видите, максимум что потребуется это осуществить 5 действий столбиком. Возможно, вы сразу попадёте в точку, или сделаете всего три действия. Всё зависит о того, как точно вы сделаете начальную оценку числа.
Извлеките самостоятельно корень из 148996
Такой дискриминант получается в задаче:
Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.
Результат корня находится между числами 300 и 400:
3002=90000 4002=160000
Действительно, 90000<148996<160000.
Суть дальнейших рассуждений сводится к тому, чтобы определить, как число 148996 расположено (отстоит) относительно этих чисел.
Вычислим разности 148996 — 90000=58996 и 160000 — 148996=11004.
Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360.
Далее пробуем возводить в квадрат, например число 370. Как бы «щупаем» результат:
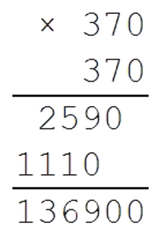
Можем сделать вывод, что наш результат больше 370. Далее ясно: так как 148996 оканчивается цифрой 6, то это означает, что в квадрат надо возводить число, оканчивающееся либо на 4, либо на 6. *Только эти числа при возведении в квадрат дают в конце 6.
Проверяем числа 374, 376, 384, 386, 394 …

Ответ: 386
Объективно говоря, вероятность того, что вам попадёт подобная задача, очень мала. Но пусть этот приём в вашем арсенале будет. Впереди вас ждёт много полезного, не пропустите!
Есть ещё метод по извлечению корня из большого числа, называют его алгоритмом Евклида. Его достоинство состоит в том, что можно извлекать корень из любого числа с необходимой точностью до десятых, сотых и тд. То есть корни неизвлекаемые в целых числах. *В будущем статья будет обязательно дополнена.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Как быстро извлекать квадратные корни
14 декабря 2012
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень. Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.
Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней.
Итак, алгоритм:
- Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.
Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
102 = 100;
202 = 400;
302 = 900;
402 = 1600;
…
902 = 8100;
1002 = 10 000.
Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
![]()
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:
![]()
Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа.
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
22 = 4;
82 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
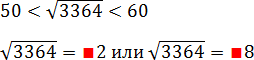
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
![]()
Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:
522 = (50 +2)2 = 2500 + 2 · 50 · 2 + 4 = 2704;
582 = (60 − 2)2 = 3600 − 2 · 60 · 2 + 4 = 3364.
Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный 🙂
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Для начала выясним, между какими числами лежит число 576:
400 < 576 < 900
202 < 576 < 302
Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
24; 26.
Осталось возвести каждое число в квадрат и сравнить с исходным:
242 = (20 + 4)2 = 576
Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Здесь и далее я буду писать только основные шаги. Итак, ограничиваем число:
900 < 1369 < 1600;
302 < 1369 < 402;
Смотрим на последнюю цифру:
1369 → 9;
33; 37.
Возводим в квадрат:
332 = (30 + 3)2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
372 = (40 − 3)2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Вот и ответ: 37.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
2500 < 2704 < 3600;
502 < 2704 < 602;
Смотрим на последнюю цифру:
2704 → 4;
52; 58.
Возводим в квадрат:
522 = (50 + 2)2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
3600 < 4225 < 4900;
602 < 4225 < 702;
Смотрим на последнюю цифру:
4225 → 5;
65.
Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:
652 = (60 + 5)2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Заключение
Многие спрашивают: зачем вообще считать такие корни? Не лучше ли взять калькулятор и не парить себе мозг?
Увы, не лучше. Давайте разберемся в причинах. Их две:
- На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
- Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.
В общем, учитесь считать. И все будет хорошо. Удачи!
Смотрите также:
- Выделение полного квадрата

- Преобразование выражений с корнем — часть 1

- Знаки тригонометрических функций

- Задача B1 — время, числа и проценты

- Как решать задачу 18: графический подход

- Задача B2 про комиссию в терминале

