Download Article
Download Article
Need to find the square of a number? Finding a number’s square is as simple as multiplying it by itself. To square fractions, find the squares of both the numerator and denominator. Then reduce or simplify the result. Keep reading for helpful tips and examples!
-

1
Learn how to do basic multiplication. When you square a number, you simply multiply the number by itself so it’s important to know how to multiply. To make it easier to square commonly used single digits, try to memorize basic times tables.[1]
- For example, learn how to multiply single digit times tables.
-

2
Multiply the single digit number by itself. Write down the number you want to square. Remember that when you’re squaring a number, you multiply it by the same number, not 2.[2]
- For example,
is not 5 x 2 = 10. Instead, it’s 5 x 5 = 25.
Advertisement
- For example,
-

3
Recognize other terms for squaring a number. If you read word problems asking you to square a number, keep in mind that they may also ask you to raise the number to the 2 power or factor. This is just another way of asking you to square the number.[3]
- You may also see a problem written as 6^2. This is another way of asking you to square 6.
-

4
Distinguish between squaring and finding the square root. It’s easy to get these terms mixed up, but remember that finding the square root of a number is the opposite of squaring a number. Finding the square root means that you’re looking for the number that can be multiplied by itself to get the number in the square.[4]
Advertisement
-

1
Write the problem out. To find the square of a number with more than 1 digit, it will help if you rewrite the problem as a double digit multiplication problem. Start by writing the same number on top of itself.[5]
- For example, to do
, write 24 x 24.
- For example, to do
-

2
Multiply the number on the bottom ones place by the 1 directly above it. Write a line below the numbers and place the result below the ones space.[6]
- For example, with 24 x 24, multiply the 4 by 4 to get 16. Write a 6 below the ones space and carry the 1 above the top tens number.
-

3
Multiply the bottom ones place by the top tens number. Take the same number on the bottom and multiply it by the top tens number. Remember to add the number you carried and write the result below the line.[7]
- For example, with 24 x 24, multiply 4 by 2 and add the 1 you carried. The result below the line should be 96.
-

4
Put a 0 under the result and multiply the bottom tens number by the top ones. The 0 will act as a placeholder. Write the result of multiplying the bottom tens number by the top ones number next to the 0.[8]
- For the 24 x 24 example, multiply 2 by 4. You should now see 80 below the 96.
-

5
Multiply the bottom tens number by the top tens number. If you carried any numbers, remember to add them to your result. Write the result below the line.[9]
- To finish multiplying 24 by 24, multiply the 2 by 2 to get 4. The result on this line should be 480.
-

6
Add the 2 results to get your answer. If you multiplied a number with 3 or more digits, you’ll have more lines to add together. Write the answer from your results to show the square of the number.
- Add 96 + 480 to get the answer for 24 x 24.
= 576.
- Add 96 + 480 to get the answer for 24 x 24.
Advertisement
-

1
Square the numerator. Multiply the top number of the fraction by itself to find its square. Write the result and place the fraction line below it.[10]
- For example, with (8/2)2, you’d multiply 8 by 8 to get a numerator of 64.
-

2
Square the denominator. Multiply the bottom number of the fraction by itself. Write the result of this square below the fraction line.[11]
- So for (8/2)2, multiply 2 by 2 to get a denominator of 4.
-

3
Simplify the result. While you could leave the fraction large or improper, most directions will tell you to simplify or reduce the result. If you have an improper fraction, turn it into a mixed number.[12]
- For example, (8/2)2 = (64/4) can be simplified to 16 because 4 goes into 64 16 times.
Advertisement
Add New Question
-
Question
How do I calculate the square root?

-
Question
√5 is the square of what number?

√5 is the square of plus-or-minus the fourth root of 5.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Remember that if you square a negative number, the answer will be positive because the 2 negatives cancel each other out.
-
To square a number using a calculator, enter the number x the number. For example, for
, enter 4 x 4 to get 16.
Advertisement
About This Article
Article SummaryX
To find the square of a number, multiply the number by itself. For example, if you’re trying to find the square of 5, you would multiply 5 by 5 and get 25, which is the square. To learn how to square fractions, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 120,392 times.
Did this article help you?
Как найти квадрат числа
Учитель на уроке диктует математическое выражение для того, чтобы учащиеся записали его в тетрадь: «Три в квадрате минус пять…» Один ученик не успевая, просит: «Подождите, не говорите слишком быстро, я еще квадрат не нарисовал». Так вот, дабы не рисовать квадраты и кубы на математике, нужно знать, что квадратом числа является его вторая степень, то есть когда число умножается на себя два раза. Вычислять квадраты учат в еще школе: дважды два – четыре, пятью пять – двадцать пять.

Вам понадобится
- – таблицы умножения;
- – таблица квадратов двузначных чисел;
- – калькулятор.
Инструкция
Чтобы найти квадрат любого числа достаточно только это число умножить на себя. Пример 1. 6*6 =36; 4*4 = 16; 7*7 = 49. Произведение чисел до 10, состоящих из одной цифры, размещено в таблице, знакомой всем еще с начальной школы: таблицы умножения. В ней по диагонали можно увидеть квадраты чисел: 1*1=1, 2*2=4, 3*3=9,4*4=16,5*5=25,6*6=36,7*7=49,8*8=64,9*9=81.
Вторая степень двузначных чисел (например, числа 16, 79, 54) определяется тем же способом: умножением числа на себя. Пример2. 20*20=400; 25*25=625; 40*40=1600. Существует специальная таблица квадратов двузначных чисел, размещенная в учебнике по алгебре для седьмого класса. В ней легко найти квадрат любого числа. Для этого разбейте число, возводимое в квадрат на десятки и единицы. Найдите пересечение строки-десятков и столбца-единиц по указанной таблице – ячейка на пересечении и будет содержать квадрат данного числа.
Если под рукой нет таблицы, квадрат числа можно найти произведением числа на само себя, выполненное в столбик. Этим способом находится и квадрат числа, состоящего из любого количества цифр. Однако квадрат большого числа лучше вычислить с помощью калькулятора. Для этого умножьте на нем заданное число само на себя. Сначала наберите нужное число с помощью цифровой клавиатуры, затем нажмите кнопку “*”. После этого еще раз наберите это же число и в заключении кнопку “=”. Калькулятор представит на экране точный ответ квадрата числа.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Когда надо найти квадрат какого-то двузначного числа, то в приницпе не так уж и сложно умножить его само на себя столбиком. Но что если надо найти много квадратов? Например, все квадраты чисел от 70 до 80? В этом случае умножать столбиком 11 раз будет не очень удобно. А если нужно найти квадраты чисел от 20 до 99, например?
В общем, показываю алгоритм, по которому все это находится буквально за секунды.
1. Нужно найти квадраты круглых чисел. В нашем случае квадраты 70 и 80 соответственно равны 4900 и 6400 — это легко. Плюс желательно вспомнить квадрат 75. У меня есть отдельная статья о том, как возводить в квадрат числа, заканчивающиеся на 5, но если коротко, то в конце надо написать 25, а в начале записать произведение 7•(7+1)=56. То есть 75²=5625. На картинке ниже изобразил схематично.
2. Дальше действуем по алгоритму. Числа 71 и 72 находятся ближе к 70, 73, 74, 76 и 77 ближе к 75, а 78 и 79 — к 80. На это мы будем опираться при вычислениях. Сейчас всё поймете. Чтобы считать быстрее, рекомендую прочитать мою статью о способах быстрого сложения и вычитания больших числе в уме.
71²=70²+70+71=4900+70+71=5041.
По такому же алгоритму считаем 76, но опираться будет не на 70, а на 75:
76²=75²+75+76=5625+75+76=5776.
С 74 и 79 почти точно так же, только мы не складываем, а отнимаем, так эти числа стоят слева от опорных 75 и 80.
74²=75²-75-74=5625-75-74=5550-74=5476.
79²=80²-80-79=6900-80-79=6320-79=6241.
3. Числа, которые стоят через одно от опорного, считаются чуть-чуть по-другому.
72²=70²+4•71=4900+284=5184
77²=75²+4•76=5625+304=5929
В числах, которые левее опорных, делаем вычитание вместо сложения:
73²=75²-4•74=5625-280-16=5329
78²=80²-4•79=640-320+4=6084.
На первый взгляд кажется сложно и громоздко, но стоит один раз понять, освоить и попробовать, как все сразу становится на свои места, и вы буквально за секунды сможете находить квадраты двухзначных чисел, немного потренировавшись и запомнив алгоритм.
Для простоты, постарался записать для вас алгоритм действий на одном листе. Сохраните картинку или лайкните этот пост. Можно будет поражать всех своим умением быстро считать в уме.
Напоминаю, тем кто ещё не подписался, что у меня появился одноименный канал на Ютубе, где я делюсь решениями интересных задач и всякими математическими и физическими хитростями.
Ещё интересно: Два простых способа быстрого сложения и вычитания в уме
90% европейских выпускников не смогли решить задачу, которую решили российские восьмиклассники
Простой и очень быстрый способ возведения в квадрат чисел, оканчивающихся на 5
В этой статье мы поговорим, что такое квадрат числа, как его найти, а также каким образом производятся подобные вычисления в программировании.
Квадратом Х называют произведение 2-х множителей, каждый из которых равен Х.
Обозначение квадрата осуществляется с помощью степени, то есть Х² читается «Х в квадрате».
Если говорить еще более простым языком, то квадратом можно назвать число, которое умножено само на себя. Таким образом, мы можем написать простейшую формулу вычисления Х2:
Х2 = Х ⋅ Х
Почему вообще такое выражение называют квадратом X? Дело в том, что именно данной формулой выражают площадь квадрата, сторона которого равна X, то есть геометрически это значение можно представить в виде площади квадрата, имеющего целочисленную сторону.
Вывод тут прост: для решение поставленной задачи следует требуемое значение взять в качестве множителя дважды, а потом вычислить произведение. Соответственно:
32 = 3 ⋅ 3 = 9
52 = 5 ⋅ 5 = 25
102 = 10 ⋅ 10 = 100
Это все элементарно и проходится в начальных классах средней школы. Решить такой пример в математике не проблема, а когда числовые значения выходят за рамки классической таблицы умножения, используют таблицу, ускоряющую расчеты.
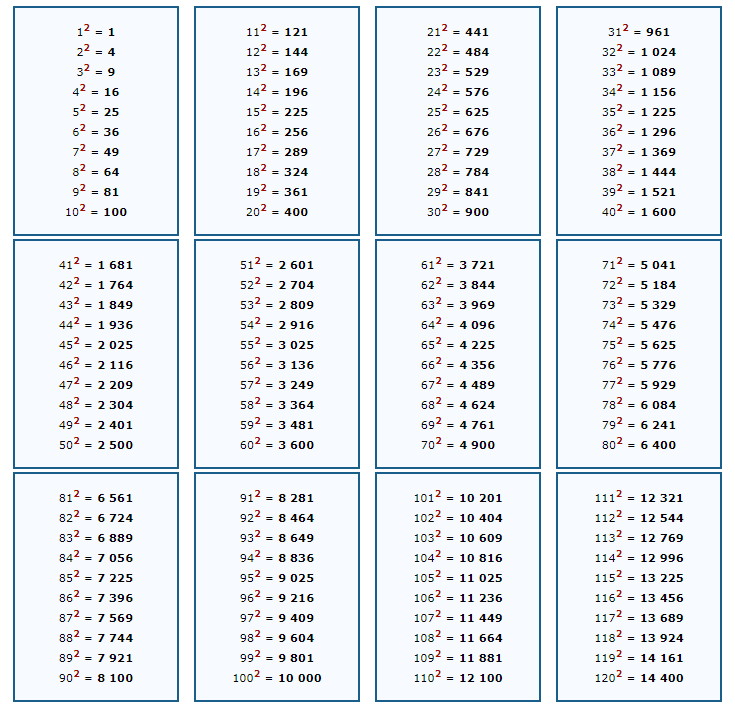
Также описанную математическую операцию можно рассматривать в контексте частного случая возведения в степень — ведь именно этим, по сути, она и является — возведением в степень 2.
Интерес представляет и числовая последовательность для квадратов целых чисел, являющихся неотрицательными (речь идет о последовательности A000290 в OEIS):
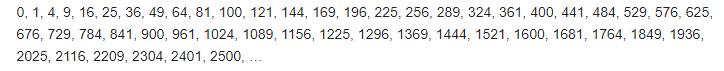
Нельзя не сказать и про график y=x², где представлены целые значения x на отрезке 1-25.
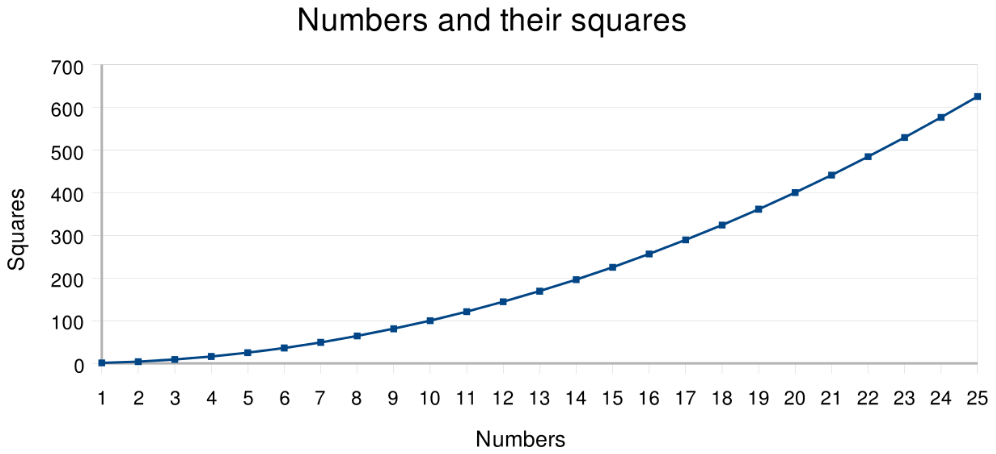
Квадратные числа
Если же говорить о натуральных числах из последовательности, упомянутой выше, в историческом контексте, то их всегда называли «квадратными». Квадратное числовое значение также называют полным либо точным квадратом, то есть целым значением, квадратный корень из которого можно извлечь нацело. К примеру, найти корень из 9 несложно (√9 = 3, т. к. 3 ⋅ 3 = 9). Не составляет проблем и вычислить корень из ста: (√100 = 10, ведь десять на десять равно сто).
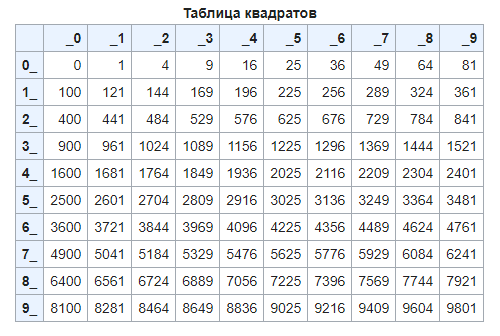
Легко понять, что сто — это квадратное число, так как его можно записать в виде 10 ⋅ 10, плюс оно может быть представлено, как было сказано выше, в качестве площади квадрата со стороной, равной десяти. Таким образом, можно сделать вывод, что квадратное число включено в категорию классических фигурных чисел, то есть чисел, которые мы можем представить в виде геометрических фигур. Но в эту тему углубляться пока не будем.
А что в программировании?
Теперь давайте посмотрим, как все это работает в программировании. Для примера возьмем такой язык программирования, как Java (кстати, статья о том, как выполнять возведение в степень в Java, уже была).
Напишем простой метод по возведению любых числовых значений в квадрат:
public class Main{
static int square(int x){
return x*x;
}
public static void main(String[] args){
System.out.println( square(10) );
}
}
Вы можете воспользоваться любым онлайн-компилятором для проверки этого кода. Также никто не мешает вписать любое число вместо десяти.
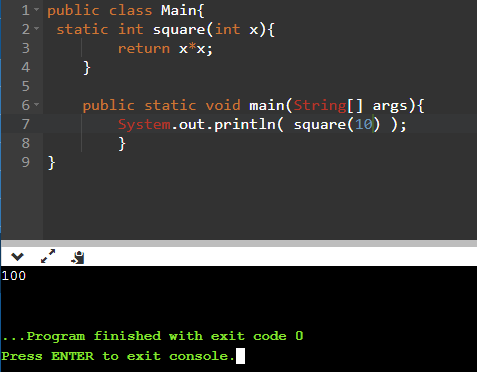
Теперь воспользуемся простейшей программой для того, чтобы найти квадратный корень из 100:
public class Main{
public static void main(String args[]){
double x = 100;
System.out.printf("sqrt(%.2f) = %.2f%n", x, Math.sqrt(x));
}
}
Программа позволяет извлекать корень и из неквадратных значений. Ниже мы находим корень из 167:
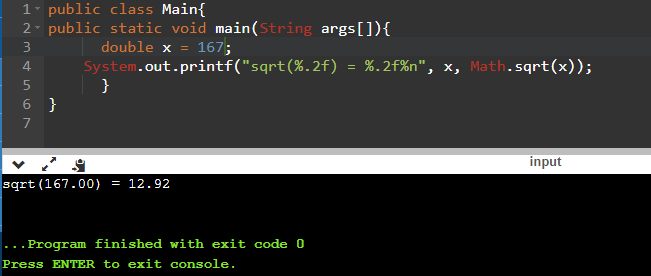
Да, в современную эпоху калькуляторов мало кто считает в уме. Вдобавок ко всему, сегодня даже не надо покупать настоящий калькулятор, так как калькулятор есть в любом мобильном телефоне, не говоря уже об онлайн-калькуляторах, коих существует огромное количество. Однако это не значит, что можно забыть азы алгебры. Не зря же великий русский ученый Михаил Ломоносов когда-то сказал:

По материалам:
- https://calculator888.ru/tablitsa-kvadratov;
- http://www.for6cl.uznateshe.ru/kvadrat-chisla/;
- https:/ru.wikipedia.org/.
Быстрое возведение чисел от 1 до 100 в квадрат
Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.
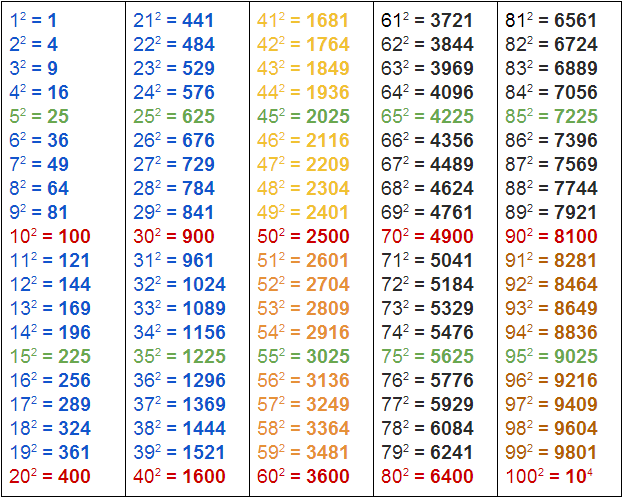
*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
В таблице отмечены красным.
Правило 2 (отсекает 10 чисел)
Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.
В таблице отмечены зеленым.
Правило 3 (отсекает 8 чисел)
Для чисел от 40 до 50.
Достаточно трудно, верно? Давайте разберем пример:
В таблице отмечены светло-оранжевым.
Правило 4 (отсекает 8 чисел)
Для чисел от 50 до 60.
Тоже достаточно трудно для восприятия. Давайте разберем пример:
В таблице отмечены темно-оранжевым.
Правило 5 (отсекает 8 чисел)
Для чисел от 90 до 100.
Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:
В таблице отмечены темно-темно-оранжевым.
Правило №6 (отсекает 32 числа)
Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 🙂
В таблице отмечены синим.
Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:
Формулы (осталось 24 числа)
Для чисел от 25 до 50
Для чисел от 50 до 100
Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):
UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»:
Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».
Для квадратов, соответственно, еще проще.
Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.
Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.
Таблица квадратов натуральных чисел. Формулы сокращенного умножения
Как научиться считать быстро и без калькулятора? Ведь и на ЕГЭ, и на ОГЭ по математике пользоваться калькулятором вы не можете.
Первое, что вам поможет, — это знание таблицы квадратов натуральных чисел. Учите наизусть, как таблицу умножения!

Все мы изучали в средней школе формулы сокращенного умножения. Правда, тогда мы не вполне понимали, зачем нам это надо. Все эти квадраты суммы и разности квадратов… А нужны они для того, чтобы быстро считать. И когда на ЕГЭ по математике на решение варианта у вас всего 3 часа 55 минут, а успеть надо очень много, — эти формулы просто незаменимы.

Как применять эти формулы на практике?
.
И более сложная ситуация. Она может вам встретиться в задании 7 Профильного ЕГЭ по математике, если вдруг придется считать площадь криволинейной под графиком функции как разность первообразных.
Правда, есть и более простое решение этой задачи. И в нем тоже используется одна из формул сокращенного умножения.
А вот и еще один полезный лайфхак:
Числа, оканчивающиеся на 5, в квадрат возводятся мгновенно.
Чтобы найти квадрат числа ( – не обязательно цифра, любое натуральное число), умножаем на и к результату приписываем 25.)
Таблица квадратов от 1 до 100

— Таблица квадратов — это таблица, содержащая квадраты чисел. Квадрат числа — это результат умножения какого-либо числа на самого себя, то есть число, возведенное во вторую степень.
В таблице пересечение цифр слева в столбце и сверху в строке дает квадрат искомого числа. Например, нужно найти квадрат числа 15. В столбце слева берем первую цифру данного числа «1». В самой верхней строке берем вторую цифру данного числа «5». На пересечении данных цифр получаем квадрат числа 15, то есть 225.
Таблицу квадратов также можно использовать для извлечения квадратного корня — обратной операции возведения в квадрат. Например, √225=15.
— Если мы говорим о сдаче ОГЭ и ЕГЭ базового уровня по математике, то учить таблицу квадратов необязательно, так как она будет в справочном материале. А вот для ЕГЭ по профильной математике это делать нужно: справочные материалы не предоставляются. Пригодится таблица квадратов и позже, при обучении в вузе. Вот несколько советов, как это сделать.
1. Если число заканчивается на 0, его легко возвести в квадрат — необходимо только дописать пару нулей: 60 х 60 = 3600.
2. Если число заканчивается на 5, то следует умножить первую цифру (x) на (x+1) и дописать к полученному числу «25». 65 х 65 = 6 х 7 = 42 приписываем 25 и получаем 4225.
3. Можно воспользоваться формулой (a + b) 2 = a 2 + 2ab + b 2 . Как мы уже выяснили, возводить в квадрат числа, оканчивающиеся на 0, очень просто. Следовательно, а — это число, которое делится на 10, а b — остаток от деления на 10. Приведем пример. Возведем в квадрат 32. 32 можно представить как 30 (число делится на 10) и 2 (остаток от деления на 10): (30+2) 2 = 30 2 + 2 х 30 х 2 + 2 2 = 900 + 120 + 4 =1024.
Для начала нужно выучить таблицу квадратов первого десятка, так как она используется чаще всего: 121, 144, 169, 196, 225, 256, 289, 324, 361. И важно запомнить, что не бывает квадратов, последняя цифра в которых 2, 3, 7, 8. Также часто используются квадраты таких чисел как 21, 24, 25, 26: они встречаются чаще других.
Выучить данные значения квадратов можно довольно быстро: попробуйте просто ежедневно выписывать значения в тетрадь.
