Как найти квадрат целого числа - Сайт, где вы сможете решить свои вопросы

Download Article

Need to find the square of a number? Finding a number’s square is as simple as multiplying it by itself. To square fractions, find the squares of both the numerator and denominator. Then reduce or simplify the result. Keep reading for helpful tips and examples!

1
Learn how to do basic multiplication. When you square a number, you simply multiply the number by itself so it’s important to know how to multiply. To make it easier to square commonly used single digits, try to memorize basic times tables.^[1]
- For example, learn how to multiply single digit times tables.
2
Multiply the single digit number by itself. Write down the number you want to square. Remember that when you’re squaring a number, you multiply it by the same number, not 2.^[2]
- For example, $5^{{2}}$ is not 5 x 2 = 10. Instead, it’s 5 x 5 = 25.
Advertisement
3
Recognize other terms for squaring a number. If you read word problems asking you to square a number, keep in mind that they may also ask you to raise the number to the 2 power or factor. This is just another way of asking you to square the number.^[3]
- You may also see a problem written as 6^2. This is another way of asking you to square 6.
4

Distinguish between squaring and finding the square root. It’s easy to get these terms mixed up, but remember that finding the square root of a number is the opposite of squaring a number. Finding the square root means that you’re looking for the number that can be multiplied by itself to get the number in the square.^[4]

1
Write the problem out. To find the square of a number with more than 1 digit, it will help if you rewrite the problem as a double digit multiplication problem. Start by writing the same number on top of itself.^[5]
- For example, to do $24^{{2}}$ , write 24 x 24.
2
Multiply the number on the bottom ones place by the 1 directly above it. Write a line below the numbers and place the result below the ones space.^[6]
- For example, with 24 x 24, multiply the 4 by 4 to get 16. Write a 6 below the ones space and carry the 1 above the top tens number.
3
Multiply the bottom ones place by the top tens number. Take the same number on the bottom and multiply it by the top tens number. Remember to add the number you carried and write the result below the line.^[7]
- For example, with 24 x 24, multiply 4 by 2 and add the 1 you carried. The result below the line should be 96.
4
Put a 0 under the result and multiply the bottom tens number by the top ones. The 0 will act as a placeholder. Write the result of multiplying the bottom tens number by the top ones number next to the 0.^[8]
- For the 24 x 24 example, multiply 2 by 4. You should now see 80 below the 96.
5
Multiply the bottom tens number by the top tens number. If you carried any numbers, remember to add them to your result. Write the result below the line.^[9]
- To finish multiplying 24 by 24, multiply the 2 by 2 to get 4. The result on this line should be 480.
6
Add the 2 results to get your answer. If you multiplied a number with 3 or more digits, you’ll have more lines to add together. Write the answer from your results to show the square of the number.
- Add 96 + 480 to get the answer for 24 x 24. $24^{{2}}$ = 576.

1
Square the numerator. Multiply the top number of the fraction by itself to find its square. Write the result and place the fraction line below it.^[10]
- For example, with (⁸/₂)², you’d multiply 8 by 8 to get a numerator of 64.
2
Square the denominator. Multiply the bottom number of the fraction by itself. Write the result of this square below the fraction line.^[11]
- So for (⁸/₂)², multiply 2 by 2 to get a denominator of 4.
3
Simplify the result. While you could leave the fraction large or improper, most directions will tell you to simplify or reduce the result. If you have an improper fraction, turn it into a mixed number.^[12]
- For example, (⁸/₂)² = (⁶⁴/₄) can be simplified to 16 because 4 goes into 64 16 times.

Add New Question

Question

How do I calculate the square root?
Question

√5 is the square of what number?

√5 is the square of plus-or-minus the fourth root of 5.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Remember that if you square a negative number, the answer will be positive because the 2 negatives cancel each other out.
To square a number using a calculator, enter the number x the number. For example, for $4^{{2}}$ , enter 4 x 4 to get 16.

About This Article

Article SummaryX

To find the square of a number, multiply the number by itself. For example, if you’re trying to find the square of 5, you would multiply 5 by 5 and get 25, which is the square. To learn how to square fractions, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 119,444 times.

Did this article help you?

Источник

Что такое квадрат числа? Как найти квадрат числа?

Определение.

Квадрат числа a — это произведение двух множителей, каждый из которых равен a.

Квадрат числа a обозначают a². Читают: «a в квадрате».

С помощью формулы определение квадрата числа a можно записать так:

$[{a^2} = a cdot a]$

Выражение a² назвали квадратом числа a, так как именно такой формулой выражается площадь квадрата со стороной a.

Таким образом, чтобы найти квадрат некоторого числа, надо это число взять множителем два раза и вычислить произведение.

Например,

$[{0^2} = 0 cdot 0 = 0;]$

$[{1^2} = 1 cdot 1 = 1;]$

$[{7^2} = 7 cdot 7 = 49;]$

$[{10^2} = 10 cdot 10 = 100;]$

$[{12^2} = 12 cdot 12 = 144.]$

Если числовое выражение содержит квадрат числа, значение квадрата вычисляют до выполнения остальных действий.

Например,

$[{9^2} + 2 cdot {(2 + 8)^2} = 81 + 2 cdot {10^2} = ]$

В математике находить квадраты чисел приходится достаточно часто. Для ускорения вычислений используется таблица квадратов.

Источник

Полный квадрат, также точный квадрат или квадратное число, — число, являющееся квадратом некоторого целого числа. Иными словами, квадратом является целое число, квадратный корень из которого извлекается нацело. Геометрически такое число может быть представлено в виде площади квадрата с целочисленной стороной.

Например, 9 — это квадратное число, так как оно может быть записано в виде 3 × 3, а также представляет площадь квадрата со стороной, равной 3.

Квадратное число входит в категорию классических фигурных чисел.

Примеры[править | править код]

Последовательность квадратов начинается так:

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, … (последовательность A000290 в OEIS)

Таблица квадратов

	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9
0_	0	1	4	9	16	25	36	49	64	81
1_	100	121	144	169	196	225	256	289	324	361
2_	400	441	484	529	576	625	676	729	784	841
3_	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4_	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5_	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6_	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7_	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8_	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9_	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Представления и свойства[править | править код]

Квадрат натурального числа можно представить в виде суммы первых нечётных чисел:

…

…

Ещё один способ представления квадрата натурального числа:
$n^{2}=1+1+2+2+...+(n-1)+(n-1)+n$
Пример:

…

…

Сумма квадратов первых натуральных чисел вычисляется по формуле^[1]:

$sum _{{k=1}}^{n}k^{2}=1^{2}+2^{2}+3^{2}+...+n^{2}={frac {n(n+1)(2n+1)}{6}}$

Ряд обратных квадратов сходится^[2]:

${displaystyle sum _{n=1}^{infty }{frac {1}{n^{2}}}={frac {1}{1^{2}}}+{frac {1}{2^{2}}}+dots +{frac {1}{n^{2}}}+dots ={frac {pi ^{2}}{6}}}$

Четыре различных квадрата не могут образовывать арифметическую прогрессию.^[3] Арифметические прогрессии из трёх квадратов существуют — например: 1, 25, 49.

Каждое натуральное число может быть представлено как сумма четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов).

4900 — единственное число > 1, которое является одновременно квадратным и пирамидальным.

Суммы пар последовательных треугольных чисел являются квадратными числами.

В десятичной записи квадратные числа имеют следующие свойства:

Последняя цифра квадрата в десятичной записи может быть равной 0, 1, 4, 5, 6 или 9 (квадратичные вычеты по модулю 10).
Квадрат не может оканчиваться нечётным количеством нулей.
Квадрат либо делится на 4, либо при делении на 8 даёт остаток 1. Квадрат либо делится на 9, либо при делении на 3 даёт остаток 1.
Две последние цифры квадрата в десятичной записи могут принимать значения 00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89 или 96 (квадратичные вычеты по модулю 100). Зависимость предпоследней цифры квадрата от последней можно представить в виде следующей таблицы:

последняя цифра	предпоследняя цифра
0	0
5	2
1, 4, 9	чётная
6	нечётная

Геометрическое представление[править | править код]

1

4

9

16

25

См. также[править | править код]

Многоугольное число
Автоморфное число
Квадратное пирамидальное число

Примечания[править | править код]

↑ Некоторые конечные числовые ряды. Math24.ru. Дата обращения: 14 июня 2019. Архивировано 14 июня 2019 года.
↑ Кохась К. П. Сумма обратных квадратов // Математическое просвещение. — 2004. — Вып. 8. — С. 142–163.
↑ K. Brown. No Four Squares In Arithmetic Progression (англ.)

Литература[править | править код]

Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М.: Просвещение, 1996. — С. 30. — 320 с. — ISBN 5-09-006575-6.
Деза Е., Деза М. Фигурные числа. — М.: МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.

Ссылки[править | править код]

Фигурные числа Архивная копия от 23 ноября 2018 на Wayback Machine
Figurate Numbers Архивная копия от 10 июня 2019 на Wayback Machine на сайте MathWorld (англ.)

Источник

В этой статье мы поговорим, что такое квадрат числа, как его найти, а также каким образом производятся подобные вычисления в программировании.

Квадратом Х называют произведение 2-х множителей, каждый из которых равен Х.

Обозначение квадрата осуществляется с помощью степени, то есть Х² читается «Х в квадрате».

Если говорить еще более простым языком, то квадратом можно назвать число, которое умножено само на себя. Таким образом, мы можем написать простейшую формулу вычисления Х²:

Х² = Х ⋅ Х

Почему вообще такое выражение называют квадратом X? Дело в том, что именно данной формулой выражают площадь квадрата, сторона которого равна X, то есть геометрически это значение можно представить в виде площади квадрата, имеющего целочисленную сторону.

Вывод тут прост: для решение поставленной задачи следует требуемое значение взять в качестве множителя дважды, а потом вычислить произведение. Соответственно:

3² = 3 ⋅ 3 = 9

5² = 5 ⋅ 5 = 25

10² = 10 ⋅ 10 = 100

Это все элементарно и проходится в начальных классах средней школы. Решить такой пример в математике не проблема, а когда числовые значения выходят за рамки классической таблицы умножения, используют таблицу, ускоряющую расчеты.

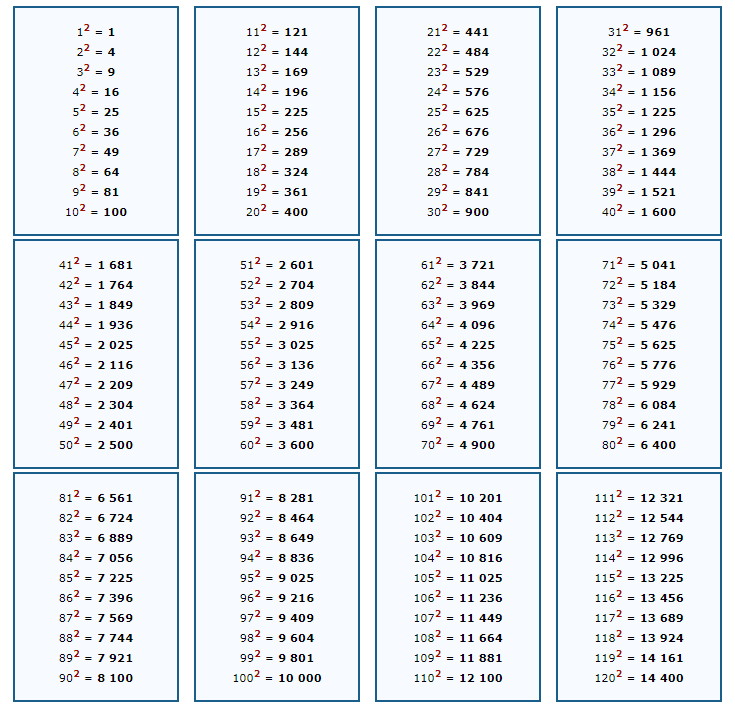
Также описанную математическую операцию можно рассматривать в контексте частного случая возведения в степень — ведь именно этим, по сути, она и является — возведением в степень 2.

Интерес представляет и числовая последовательность для квадратов целых чисел, являющихся неотрицательными (речь идет о последовательности A000290 в OEIS):

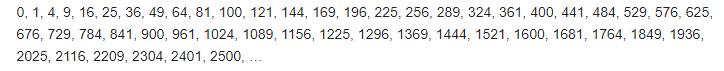
Нельзя не сказать и про график y=x², где представлены целые значения x на отрезке 1-25.

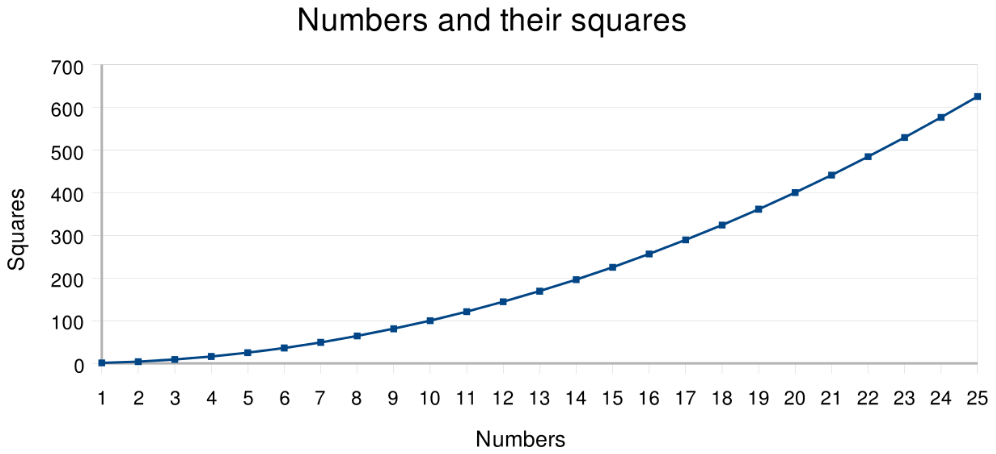
Квадратные числа

Если же говорить о натуральных числах из последовательности, упомянутой выше, в историческом контексте, то их всегда называли «квадратными». Квадратное числовое значение также называют полным либо точным квадратом, то есть целым значением, квадратный корень из которого можно извлечь нацело. К примеру, найти корень из 9 несложно (√9 = 3, т. к. 3 ⋅ 3 = 9). Не составляет проблем и вычислить корень из ста: (√100 = 10, ведь десять на десять равно сто).

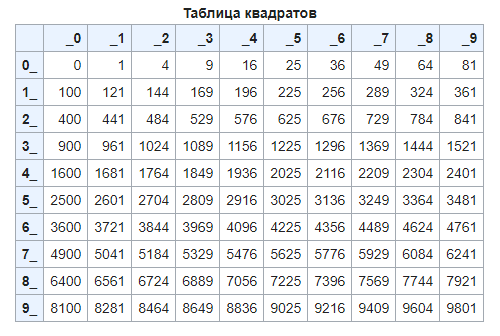
Легко понять, что сто — это квадратное число, так как его можно записать в виде 10 ⋅ 10, плюс оно может быть представлено, как было сказано выше, в качестве площади квадрата со стороной, равной десяти. Таким образом, можно сделать вывод, что квадратное число включено в категорию классических фигурных чисел, то есть чисел, которые мы можем представить в виде геометрических фигур. Но в эту тему углубляться пока не будем.

А что в программировании?

Теперь давайте посмотрим, как все это работает в программировании. Для примера возьмем такой язык программирования, как Java (кстати, статья о том, как выполнять возведение в степень в Java, уже была).

Напишем простой метод по возведению любых числовых значений в квадрат:

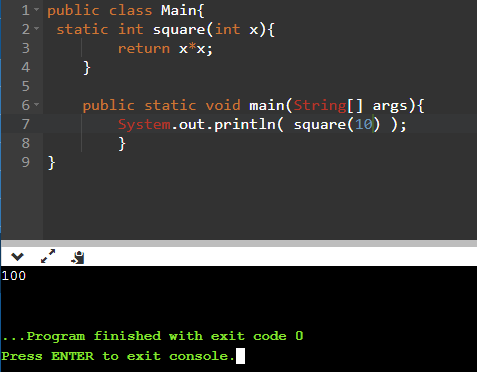
public class Main{

static int square(int x){

return x*x;

}

public static void main(String[] args){

System.out.println( square(10) );

}

Вы можете воспользоваться любым онлайн-компилятором для проверки этого кода. Также никто не мешает вписать любое число вместо десяти.

Теперь воспользуемся простейшей программой для того, чтобы найти квадратный корень из 100:

public class Main{

public static void main(String args[]){

double x = 100;

System.out.printf("sqrt(%.2f) = %.2f%n", x, Math.sqrt(x));

}

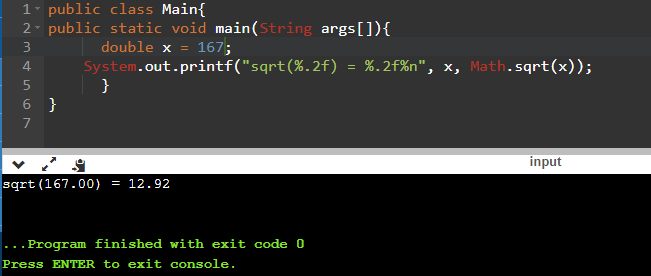
Программа позволяет извлекать корень и из неквадратных значений. Ниже мы находим корень из 167:

Да, в современную эпоху калькуляторов мало кто считает в уме. Вдобавок ко всему, сегодня даже не надо покупать настоящий калькулятор, так как калькулятор есть в любом мобильном телефоне, не говоря уже об онлайн-калькуляторах, коих существует огромное количество. Однако это не значит, что можно забыть азы алгебры. Не зря же великий русский ученый Михаил Ломоносов когда-то сказал:

По материалам:

https://calculator888.ru/tablitsa-kvadratov;
http://www.for6cl.uznateshe.ru/kvadrat-chisla/;
https:/ru.wikipedia.org/.

Источник

Как найти квадрат числа

Учитель на уроке диктует математическое выражение для того, чтобы учащиеся записали его в тетрадь: «Три в квадрате минус пять…» Один ученик не успевая, просит: «Подождите, не говорите слишком быстро, я еще квадрат не нарисовал». Так вот, дабы не рисовать квадраты и кубы на математике, нужно знать, что квадратом числа является его вторая степень, то есть когда число умножается на себя два раза. Вычислять квадраты учат в еще школе: дважды два – четыре, пятью пять – двадцать пять.

Вам понадобится

– таблицы умножения;
– таблица квадратов двузначных чисел;
– калькулятор.

Инструкция

Чтобы найти квадрат любого числа достаточно только это число умножить на себя. Пример 1. 6*6 =36; 4*4 = 16; 7*7 = 49. Произведение чисел до 10, состоящих из одной цифры, размещено в таблице, знакомой всем еще с начальной школы: таблицы умножения. В ней по диагонали можно увидеть квадраты чисел: 1*1=1, 2*2=4, 3*3=9,4*4=16,5*5=25,6*6=36,7*7=49,8*8=64,9*9=81.

Вторая степень двузначных чисел (например, числа 16, 79, 54) определяется тем же способом: умножением числа на себя. Пример2. 20*20=400; 25*25=625; 40*40=1600. Существует специальная таблица квадратов двузначных чисел, размещенная в учебнике по алгебре для седьмого класса. В ней легко найти квадрат любого числа. Для этого разбейте число, возводимое в квадрат на десятки и единицы. Найдите пересечение строки-десятков и столбца-единиц по указанной таблице – ячейка на пересечении и будет содержать квадрат данного числа.

Если под рукой нет таблицы, квадрат числа можно найти произведением числа на само себя, выполненное в столбик. Этим способом находится и квадрат числа, состоящего из любого количества цифр. Однако квадрат большого числа лучше вычислить с помощью калькулятора. Для этого умножьте на нем заданное число само на себя. Сначала наберите нужное число с помощью цифровой клавиатуры, затем нажмите кнопку “*”. После этого еще раз наберите это же число и в заключении кнопку “=”. Калькулятор представит на экране точный ответ квадрата числа.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

About This Article

Did this article help you?

Примеры[править | править код]

Представления и свойства[править | править код]

Геометрическое представление[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Квадратные числа

А что в программировании?

Как найти квадрат числа

Вам также может понравиться

Как найти пересечение прямой с осями координат

Как составить схему рассрочки

Как найти сериал лесник

Добавить комментарий Отменить ответ