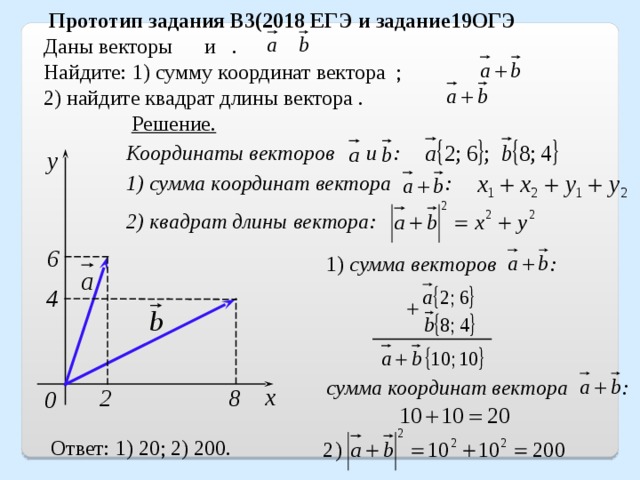
Введите в мир математики: встреча с различными концепциями и обозначениями, которые становятся фундаментом благоразумного понимания мира вокруг нас. Один из фундаментальных абстрактных объектов в математике – вектор. Вектор можно представить как направленное отрезок прямой, у которого есть явное направление, а также длина. В этой статье мы ознакомимся с одной из основных арифметических операций над векторами, а именно – определением квадрата длины вектора.
Что такое вектор? Вектор – это математическое понятие, которое описывает направление перемещения объекта или изменение состояния. Векторы широко используются в физике, инженерии, компьютерной графике и других отраслях. Важность векторов заключается в том, что они описывают движение и изменения в пространстве, позволяя максимально точно моделировать предметы и процессы к нам и вокруг нас.
Квадрат длины вектора – это математическая операция, которая позволяет получить информацию о “ширине”, “величине” или “величинности” вектора. Вне зависимости от того, какое воздействие применяет вектор, такие параметры как длина или площадь периодически зависят от квадрата размера вектора. В данной статье мы заглянем в мир поддержанных математических концепций и разберем, как напрямую найти квадрат длины вектора.
Разделим домашнее задание по статье на темы следующим образом:
- Определение: что такое вектор длины квадрата.
- Алгоритм: как определить квадрат длины.
- Примеры: аналитическое решение на основе принципа квадрата длины вектора.
Применение знания формулы квадрата длины вектора позволяет спокойно решать сложные математические расчеты и на излёт расширять рамки ваших знаний о двигающихся объектах во вселенной.
Это вверх от порадно – такое уроки начались. Не отказывайте себе в конституционных правах делать изучение математики увлекательным!
Основные понятия вектора

Вектор — это математический объект, обладающий как величиной (ориентиром), так и направлением. Векторы широко используются в физике (например, вектор скорости, вектор ускорения, вектор силы), а также в компьютерной графике и геометрии.
Координата вектора
Вектор может быть представлен в виде пары или более, состоящих из координат x, y, z и т.д., в зависимости от используемой системы координат. В двумерной пространственной системе координат (прямоугольной системе координат) вектор описывается двумя координатами (x, y). В трехмерной системе координат, два дополнительных элемента y и z, ко всем уже указанным координатам, требуется, что состоит из координат (x, y, z). В любом случае, эти x, y и z координаты используются для отображения местоположения или направления вектора.
Умножение вектора на число
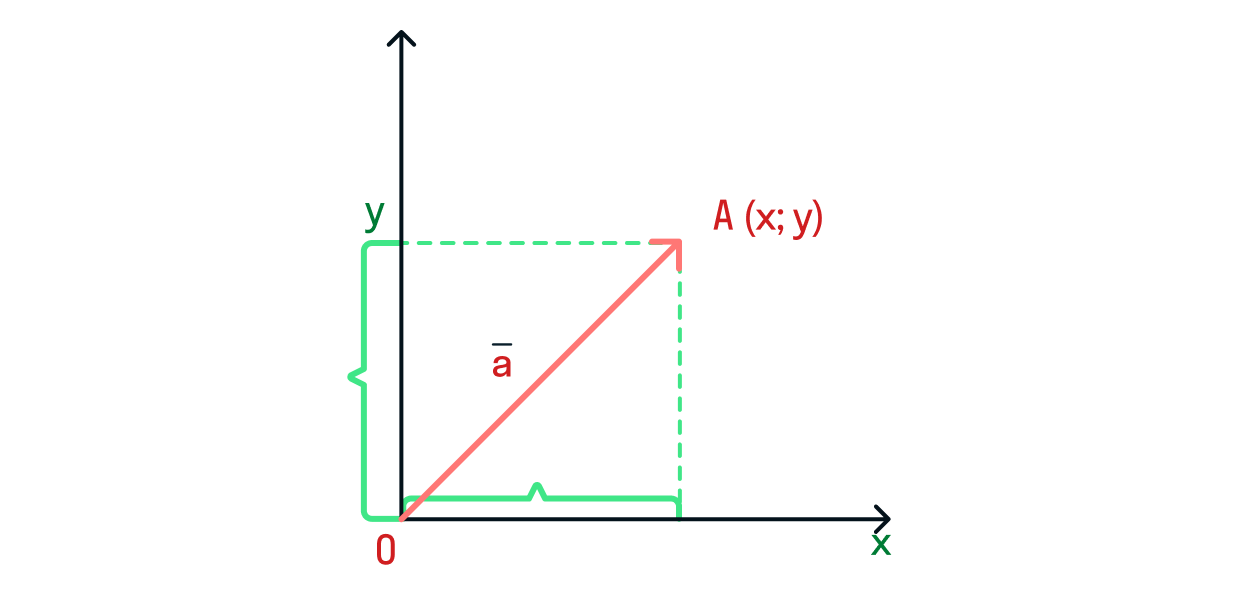
Когда вектор умножается на число, оно называется скаляром. Вектор, умноженный на скаляр, будет иметь ту же направленность, что и исходный вектор, если скаляр положительный, и противоположную, если он отрицательный. Величина вектора, умноженного на скаляр, будет пропорциональной скаляру. Такое математическое действие называется умножение вектора на число.
Например, если вектор A = (1, 2) и скаляр k = 3, то умножение вектора скаляром дает вектор A*k=3*(1, 2)=(3, 6).
Источник: [1] [2] [3]
Примечания: [1] Контрс, Р., “Интернет-ресурсы в области векторного анализа” (1997). Интернет ресурсы по математике. Доступны на сайте. [2] Вадимов, В. И., “Векторное исчисление для архитекторов” (2013). Исследовательские работы ВГАСА. Доступны на сайте. [3] Кузнецов, П. И., “Векторное исчисление для инженеров и геофизиков” (2015). Исследовательские работы СПбГАСУ. Доступны на сайте.
Применение векторов в физике

Векторы нашили широкое распространение в разных областях науки, включая физику, где они имеют важную функцию для решения различных задач и проблем. Благодаря компактной и эффективной символике векторы призваны представлять чётко различные физические величины, которым присущи размер и направление.
Одна из основных области применения векторов в физике – это динамика движения. Для описания направления и величины скорости движения объектов высвобождается понятие скорости, являющееся векторной величиной. Квадрат длины вектора скорости дает высокую энергию кинетической энергии тела, которая оказывает непосредственное воздействие на поведение тела в физических процессах.
Также векторы оказывают важное воздействие на теорию относительности, где их используют для описания различных полей скоростей и сил, влияющих на тела в движении. В классической электродинамике вектор напряжённости электрического поля используется для представления физического закономерства зоны, где действует электрическая сила. Более того, в современных физических исследованиях векторы находят применение в квантовой хромодинамике, где они могут описывать сильные взаимодействия между частицами, составляющими атомы.
Одним из ключевых приложений векторов в физике является сила, это векторная величина, которая направляется по траектории, описывающей движение объекта при воздействии этой силы. В природе сила, в исходном виде, вносит необходимый вклад для возникновения движения большинства физических тел в различных климатических условиях.
Таким образом, векторы – основополагающее ядро физических теорий и представленных массой формулирований и подходов, которые позволяют получить представление о направлении и величине различных физических величин для более удобного их использования основ. центра сервисных работ и исследований.
Вопрос-ответ:
Что такое вектор?
Вектор – это математический объект, представляющий собой направление и размер (или величину) движения или действия в пространстве. Векторы часто представляются в виде стрелок, указывающих направление, и длины, указывающих величину. Векторы используются для описания движений, сил, скоростей и других аспектов физического мира.
Какой алгоритм используется для нахождения квадрата длины вектора?
Для нахождения квадрата длины вектора используется следующий алгоритм: берем каждую координату вектора, увеличиваем каждую на квадрат, а затем складываем все результаты. Например, для вектора (3, 4) мы умножаем 3 на 3, получаем 9, умножаем 4 на 4, получаем 16, и складываем оба результата, что дает 9 + 16 = 25. Таким образом, квадрат длины вектора (3, 4) равен 25.
Что такое длина вектора и почему мы измерим квадрат длины, а не саму длину?
Длина вектора – это число, обозначающее его величину или модуль, которая определяет «длину» вектора. Вычисление квадрата длины вектора требует менее вычислительных операций, чем вычисление самой длины, что делает этот подход быстрее, когда оно важно, например, при выполнении каких-либо вычислений или проверка условий.
Какая задача требует нахождения квадрата длины вектора?
Такие задачи, как проверка точки на принадлежность многоугольнику (пользующихся методом решета), вычисление квадрата расстояния между двумя точками в пространстве и выполнение операций с векторами энергии, требуют нахождения квадрата длины вектора.
Можно ли найти квадрат длины вектора, используя только треугольных теоремы, без использования алгебры?
Да, можно измерить квадрат длины вектора, используя теорему Пифагора. В этом случае вычисление квадрата длины вектора представляет собой прямое применение теоремы Пифагора к основным координатам вектора.