Как найти квадрат дробного числа - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Возведение в квадрат дробей – это одна из самых простых операций с дробями. Она похожа на возведение в квадрат целых чисел – нужно умножить числитель и знаменатель на себя.^[1] В некоторых случаях дробь можно упростить, а потом возвести ее в квадрат, чтобы упростить процесс. Эта статья научит вас возводить в квадрат дроби.

1
Уясните, как возводить в квадрат целые числа. Если показатель степени равен 2, то число нужно возвести в квадрат. Для этого нужно умножить число на себя.^[2] Например:
- 5² = 5 × 5 = 25
2
Возведение в квадрат дробей похоже на возведение в квадрат целых чисел. Чтобы возвести в квадрат дробь, нужно умножить ее на себя, то есть нужно умножить числитель на себя, а затем умножить знаменатель на себя.^[3] Например:
- (⁵/₂)² = ⁵/₂ × ⁵/₂ = (^5²/_2²).
- Возведя каждое число в квадрат, вы получите: (²⁵/₄).
3
Умножьте числитель на себя и умножьте знаменатель на себя. Не имеет значения, какое число умножать в первую очередь – главное возвести в квадрат и числитель, и знаменатель. Чтобы упростить процесс, начните с числителя: умножьте его на себя. Затем умножьте знаменатель на себя.
- Числитель записывается над чертой, а знаменатель – под чертой.
- Например: (⁵/₂)² = (^{5 x 5}/_{2 x 2}) = (²⁵/₄).
4
Сократите дробь. В конце вычислений нужно сократить дробь до наименьших значений числителя и знаменателя, или преобразовать неправильную дробь в смешанное число.^[4] В нашем примере дробь ²⁵/₄ является неправильной, потому что числитель больше знаменателя.
- Чтобы преобразовать дробь в смешанное число, разделите 25 на 4. Вы получите 6 (6 х 4 = 24) и остаток 1. Таким образом, смешанное число: 6 ¹/₄.
Реклама

1
Обратите внимание на знак «минус» перед дробью. Если дана отрицательная дробь, перед ней стоит знак «минус». В некоторых случаях отрицательные дроби (и числа) заключают в круглые скобки, чтобы не перепутать отрицательную дробь (или число) с операцией вычитания.^[5]
- Например: (–²/₄)
2
Умножьте дробь на себя. То есть умножьте числитель на себя, а затем умножьте знаменатель на себя. Или просто умножьте дробь на себя.
- Например: (–²/₄)² = (–²/₄) x (–²/₄)
3
Помните, что при перемножении двух отрицательных чисел получается положительное число. Если перед дробью стоит знак «минус», то дробь отрицательная. Возводя в квадрат дробь, вы перемножаете два отрицательных числа. При перемножении двух отрицательных чисел получается положительное число.^[6]
- Например: (-2) x (-8) = (+16)
4
После возведения в квадрат избавьтесь от знака «минус» (-). Возведя в квадрат дробь, вы перемножили два отрицательных числа. То есть теперь дробь стала положительной. Не забудьте записать окончательный ответ без знака «минус».^[7]
- В нашем примере конечная дробь будет положительной.
- (–²/₄) x (–²/₄) = (+⁴/₁₆)
- В подавляющем большинстве случаев знак «плюс» (+) перед положительными дробями (и числами) не пишут.^[8]
5
Сократите дробь. В конце вычислений нужно сократить дробь до наименьших значений числителя и знаменателя, или преобразовать неправильную дробь в смешанное число, которое затем сокращается.
- Например: у числителя и знаменателя дроби (⁴/₁₆) есть общий делитель 4.
- Разделите дробь на 4: 4/4 = 1, 16/4 = 4
- Запишите сокращенную дробь: (¹/₄)
Реклама

1
Проверьте, можно ли сократить дробь перед тем, как возвести ее в квадрат. Как правило, легче сократить дробь до ее возведения в квадрат. Чтобы сократить дробь до наименьших значений числителя и знаменателя, нужно разделить и числитель, и знаменатель на общий делитель.^[9] Сокращение дроби до возведения в квадрат означает, что сокращать дробь после возведения в квадрат уже не нужно.
- Например: (¹²/₁₆)²
- Числа 12 и 16 можно разделить на 4: 12/4 = 3 и 16/4 = 4. Таким образом, дробь ¹²/₁₆ сокращается до ³/₄.
- Теперь возведите в квадрат дробь ³/₄.
- (³/₄)² = ⁹/₁₆. Эту дробь сократить нельзя.
- Чтобы доказать это, возведите в квадрат исходную дробь:
  - (¹²/₁₆)² = (^{12 x 12}/_{16 x 16}) = (¹⁴⁴/₂₅₆)
  - У числителя и знаменателя дроби (¹⁴⁴/₂₅₆) есть общий делитель 16. Разделив числитель и знаменатель на 16, вы сократите дробь до (⁹/₁₆), то есть получается такая же дробь, как при сокращении до возведения в квадрат.
2
Научитесь определять, когда нужно повременить с сокращением дроби. Работая с более сложными уравнениями, можно сократить один из множителей. В этом случае с сокращением дроби лучше подождать. Дробь, которая участвовала в приведенном выше примере, умножим на число:
- Например: 16 × (¹²/₁₆)²
- Степень запишите в виде произведения дроби на себя, а затем сократите множитель:16 * ¹²/₁₆ * ¹²/₁₆
  - Так как множитель равен 16, и один из знаменателей равен 16, можно сократить и множитель, и один из знаменателей – просто зачеркните их.
- Упрощенное уравнение запишется так: 12 × ¹²/₁₆
- Сократите дробь ¹²/₁₆, разделив числитель и знаменатель на 4. Вы получите дробь: ³/₄
- Перемножьте: 12 × ³/₄ = 36/4
- Разделите: 36/4 = 9
3
Научитесь упрощать степень. Упрощение степени – это другой способ решить ту же задачу. Вы получите тот же ответ, но процесс вычисления немного изменится.
- Например: 16 * (¹²/₁₆)²
- Запишите числитель и знаменатель в виде степеней: 16 * (^12²/_16²)
- Сократите множитель и показатель степени у знаменателя:16 * ^12²/_16²
  - Показатель степени множителя 16 равен 1: 16¹. По правилу деления степеней их показатели вычитаются: 16¹/16² = 16^1-2 = 16^-1 = 1/16.
- Вы получили дробь:^12²/₁₆
- Перепишите дробь в следующем виде и сократите ее: ^12*12/₁₆ = ¹² * ³/₄.
- Перемножьте: 12 × ³/₄ = 36/4
- Разделите: 36/4 = 9
Реклама

Что вам понадобится

Бумага или доска
Карандаш/ручка или мел

Об этой статье

Эту страницу просматривали 91 117 раз.

Была ли эта статья полезной?

Источник

Как выполнить возведение дроби в квадрат? Как возвести в квадрат смешанное число?

Чтобы найти квадрат дроби, нужно найти произведение двух множителей, каждый из которых равен этой дроби:

$[{(frac{a}{b})^2} = frac{a}{b} cdot frac{a}{b}]$

Например,

$[{(frac{1}{4})^2} = frac{1}{4} cdot frac{1}{4} = frac{1}{{16}};]$

$[{(frac{2}{9})^2} = frac{2}{9} cdot frac{2}{9} = frac{4}{{81}};]$

$[{(frac{7}{{16}})^2} = frac{7}{{16}} cdot frac{7}{{16}} = frac{{49}}{{256}};]$

$[{(frac{5}{{11}})^2} = frac{5}{{11}} cdot frac{5}{{11}} = frac{{25}}{{121}}.]$

Другой способ найти дробь в квадрате — возвести в квадрат отдельно числитель, отдельно — знаменатель:

$[{(frac{a}{b})^2} = frac{{{a^2}}}{{{b^2}}}]$

Например,

$[{(frac{3}{{10}})^2} = frac{{{3^2}}}{{{{10}^2}}} = frac{9}{{100}};]$

$[{(frac{5}{{12}})^2} = frac{{{5^2}}}{{{{12}^2}}} = frac{{25}}{{144}};]$

$[{(frac{6}{{17}})^2} = frac{{{6^2}}}{{{{17}^2}}} = frac{{36}}{{289}};]$

$[{(frac{{19}}{{30}})^2} = frac{{{{19}^2}}}{{{{30}^2}}} = frac{{361}}{{900}}.]$

Чтобы найти квадрат смешанного числа (смешанной дроби), надо сначала перевести это число в неправильную дробь, возвести ее в квадрат, а затем из полученной неправильной дроби выделить целую часть.

Например,

$[{(1frac{2}{3})^2} = {(frac{5}{3})^2} = frac{5}{3} cdot frac{5}{3} = frac{{25}}{9} = 2frac{7}{9};]$

$[{(2frac{3}{5})^2} = {(frac{{13}}{5})^2} = frac{{13}}{5} cdot frac{{13}}{5} = frac{{169}}{{25}} = 6frac{{19}}{{25}};]$

$[{(7frac{1}{2})^2} = {(frac{{15}}{2})^2} = frac{{15}}{2} cdot frac{{15}}{2} = frac{{225}}{4} = 56frac{1}{4};]$

$[{(4frac{1}{6})^2} = {(frac{{25}}{6})^2} = frac{{25}}{6} cdot frac{{25}}{6} = frac{{625}}{{36}} = 17frac{{13}}{{36}}.]$

Источник

Download Article

Squaring fractions is one of the simplest operations you can perform on fractions. It is very similar to squaring whole numbers in that you simply multiply both the numerator and the denominator by itself. There are also some instances in which simplifying the fraction before squaring makes the process easier. If you haven’t yet learned this skill, this article provides an easy overview that will improve your understanding quickly.

1
Understand how to square whole numbers. When you see an exponent of two, you know that you need to square the number. To square a whole number, you multiply it by itself.^[1] For example:
- 5² = 5 × 5 = 25
2
Realize that squaring fractions works the same way. To square a fraction, you multiply the fraction by itself. Another way to think about it is to multiply the numerator by itself and then the denominator by itself.^[2] For example:
- (⁵/₂)² = ⁵/₂ × ⁵/₂ or (^5²/_2²).
- Squaring each number yields (²⁵/₄).
Advertisement
3
Multiply the numerator by itself and the denominator by itself. The actual order that you multiply these numbers by themselves doesn’t matter as long as you have squared both numbers. To keep things simple, start with the numerator: simply multiply it by itself. Then, multiply the denominator by itself.^[3]
- The numerator will stay on top of the fraction and the denominator will stay at the bottom of the fraction.
- For example: (⁵/₂)² = (^{5 x 5}/_{2 x 2}) = (²⁵/₄).
4
Simplify the fraction to finish. When working with fractions, the last step is always to reduce the fraction to its most simple form or turn the improper fraction into a mixed number.^[4] For our example, ²⁵/₄ is an improper fraction because the numerator is larger than the denominator.
- To convert to a mixed number, divide 4 into 25. It goes in 6 times (6 x 4 = 24) with 1 leftover. Therefore, the mixed number is 6 ¹/₄.

1
Recognize the negative sign in front of the fraction. If you are working with a negative fraction, it will have a minus sign in front of it. It is good practice to always put parentheses around a negative number so you know that the “–“ sign is referring to the number and not telling you to subtract two numbers.^[5]
- For example: (–²/₄)
2
Multiply the fraction by itself. Square the fraction as you would normally by multiplying the numerator by itself and then multiplying the denominator by itself. Alternatively, you can simply multiply the fraction by itself.
- For example: (–²/₄)² = (–²/₄) x (–²/₄)
3
Understand that two negative numbers multiply to make a positive number. When a minus sign is present, the entire fraction is negative. When you square the fraction, you are multiplying two negative numbers together. Whenever two negative numbers are multiplied together, they make a positive number.^[6]
- For example: (-2) x (-8) = (+16)
4
Remove the negative sign after squaring. After you have squared the fraction, you will have multiplied two negative numbers together. This means that the squared fraction will be positive. Be sure to write your final answer without the negative sign.^[7]
- Continuing the example, the resulting fraction will be a positive number.
- (–²/₄) x (–²/₄) = (+⁴/₁₆)
- Generally, the convention is to drop the “+” sign for positive numbers.^[8]
5
Reduce the fraction to its simplest form. The final step when doing any calculations with a fraction is to reduce it. Improper fractions must first be simplified into mixed numbers and then reduced.^[9]
- For example: (⁴/₁₆) has a common factor of four.
- Divide the fraction through by 4: 4/4 = 1, 16/4= 4
- Rewrite simplified fraction: (¹/₄)

1
Check to see if you can simplify the fraction before you square it. It is usually easier to reduce fractions before squaring them. Remember, to reduce a fraction means to divide it by a common factor until the number one is the only number that can be evenly divided into both the numerator and denominator.^[10] Reducing the fraction first means you don’t have to reduce it at the end when the numbers will be larger.
- For example: (¹²/₁₆)²
- 12 and 16 can both be divided by 4. 12/4 = 3 and 16/4 = 4; therefore, ¹²/₁₆ reduces to ³/₄.
- Now, you will square the fraction ³/₄.
- (³/₄)² = ⁹/₁₆, which cannot be reduced.
- To prove this, let’s square the original fraction without reducing:
  - (¹²/₁₆)² = (^{12 x 12}/_{16 x 16}) = (¹⁴⁴/₂₅₆)
  - (¹⁴⁴/₂₅₆) has a common factor of 16. Dividing both the numerator and denominator by 16 reduces the fraction to (⁹/₁₆), the same fraction we got from reducing first.
2
Learn to recognize when you should wait to reduce a fraction. When working with more complex equations, you may be able to simply cancel one of the factors. In this case, it is actually easier to wait before you reduce the fraction. Adding an additional factor to the above example illustrates this.
- For example: 16 × (¹²/₁₆)²
- Expand out the square and cross out the common factor of 16: 16 * ¹²/₁₆ * ¹²/₁₆
  - Because there is one 16 whole number and two 16’s in the denominator, you can cross ONE of them out.
- Rewrite the simplified equation: 12 × ¹²/₁₆
- Reduce ¹²/₁₆ by dividing through by 4: ³/₄
- Multiply: 12 × ³/₄ = 36/4
- Divide: 36/4 = 9
3
Understand how to use an exponent shortcut. Another way to solve the same example is to simplify the exponent first. The end result is the same, it’s just a different way to solve.
- For example: 16 * (¹²/₁₆)²
- Rewrite with the numerator and denominator squared: 16 * (^12²/_16²)
- Cancel out the exponent in the denominator: 16 * ^12²/_16²
  - Imagine the first 16 has an exponent of 1: 16¹. Using the exponent rule of dividing numbers, you subtract the exponents. 16¹/16², yields 16^1-2 = 16^-1 or 1/16.
- Now, you are working with: ^12²/₁₆
- Rewrite and reduce the fraction: ^12*12/₁₆ = ¹² * ³/₄.
- Multiply: 12 × ³/₄ = 36/4
- Divide: 36/4 = 9

Add New Question

Question

How do I solve 2 (1/3)?

Multiply the fraction’s numerator by the whole number, and retain the denominator.
Question

How do I use exponential notation for a fraction raised to a power?

Use parentheses around the fraction, and ^ to raise it to any power. For example: one third, squared: (1/3)^2.
Question

How do I solve (3/16) divided by [(1/2+1/4)squared]?

(½ + ¼)² = (¾)² = 3² / 4² = 9/16. 3/16 divided by 9/16, which is the same as 3/16 multiplied by 16/9, which equals 48/144, which equals 1/3.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Thanks for submitting a tip for review!

Things You’ll Need

Paper or screen for working on
Pencil/Pen (for use w/ paper)

About This Article

Article SummaryX

To square a fraction, simplify the fraction as much as you can. Next, multiply the numerator by itself, then multiply the denominator by itself. If you are squaring a negative fraction, the result will be positive. Reduce the fraction to its simplest form. If you want to learn how to simplify your fractions before squaring them, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 822,286 times.

Did this article help you?

Источник

Тема сводится к тому, что нам необходимо производить умножение одинаковых дробей. Данная статья расскажет, какое необходимо использовать правило, чтобы верно возводить алгебраические дроби в натуральную степень.

Правило возведения алгебраической дроби в степень, его доказательство

Перед тем, как начать возводить в степень, необходимо углубить знания при помощи статьи про степень с натуральным показателем, где имеется произведение одинаковых множителей, которые находятся в основании степени, причем их количество определено показателем. К примеру, число 23=2·2·2=8.

При возведении в степень чаще всего используем правило. Для этого в отдельности возводят в степень числитель и отдельно знаменатель. Рассмотрим на примере 232=2232=49. Правило применимо для возведения дроби в натуральную степень.

При возведении алгебраической дроби в натуральную степень получаем новую, где числитель имеет степень исходной дроби, а знаменатель – степень знаменателя. Это все имеет вид abn=anbn , где а и b являются произвольными многочленами, b является ненулевым, а n натуральным числом.

Доказательство данного правила записывается в виде дроби, которую необходимо возвести в степень, основываясь на самом определении с натуральным показателем. Тогда получаем умножение дробей вида abn=ab·ab·…·ab=a·a·…·ab·b·…·b=anbn

Примеры, решения

Правило возведения алгебраической дроби в степень производится последовательно: сначала числитель , потом знаменатель. Когда в числителе и знаменателе имеется многочлен, тогда само задание сведется к возведению заданного многочлена в степень. После чего будет указана новая дробь, которая равна исходной.

Пример 1

Произвести возведение дроби x23·y·z3 в квадрат.

Решение

Необходимо зафиксировать степень x23·y·z32. По правилу возведения алгебраической дроби в степень получаем равенство вида x23·y·z32=x223·y·z32 . Теперь необходимо произвести преобразование полученной дроби к виду алгебраической, выполняя возведение в степень. Тогда получим выражение вида

x223·y·z32=x2·232·y2·z32=x49·y2·z6

Все случаи возведения в степень не предполагают подробного разъяснения, поэтому сам решение имеет краткую запись. То есть, получаем, что

x23·y·z32=x223·y·z32=x49·y2·z6

Ответ: x23·y·z32=x49·y2·z6.

Если числитель и знаменатель имеют многочлены, тогда необходимо возводить всю дробь в степень, после чего применять формулы сокращенного умножения для его упрощения.

Пример 2

Возвести дробь 2·x-1×2+3·x·y-y в квадрат.

Решение

Из правила имеем, что

2·x-1×2+3·x·y-y2=2·x-12×2+3·x·y-y2

Чтобы преобразовать выражение, необходимо воспользоваться формулой квадрата суммы трех слагаемых в знаменателе, а в числителе – квадратом разности, что позволит упростить выражение. Получим:

2·x-12×2+3·x·y-y2==2·x2-2·2·x·1+12×22+3·x·y2+-y2+2·x2·3·x·y+2·x2·(-y)+2·3·x·y·-y==4·x2-4·x+1×4+9·x2·y2+y2+6·x3·y-2·x2·y-6·x·y2

Ответ: 2·x-12×2+3·x·y-y2=4·x2-4·x+1×4+9·x2·y2+y2+6·x3·y-2·x2·y-6·x·y2

Заметим, что при возведении в натуральную степень дробь, которую не можем сократить, получаем также несократимую дробь. Это не упрощает ее для дальнейшего решения. Когда заданная дробь может быть сокращена, тогда при возведении в степень получаем, что необходимо выполнение сокращения алгебраической дроби, во избежание выполнения сокращения после того, как возведем в степень.

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Возведение дроби в степень

Возведение дроби в степень. Наш онлайн-калькулятор позволяет возводить в степень любую дробь. Чтобы задать смешанную дробь заполните поля, соответствующие целой части, числителю и знаменателю. Если дробь не имеет целой части, то тогда оставьте соответствующее поле незаполненным. Если необходимо задать отрицательную дробь – для этого нажмите кнопку [+/-].После нажатия на кнопку “Вычислить” калькулятор выдаст ответ. Ниже под калькулятором будет приведено подробное решение с последовательностью действий, которые необходимо совершить.

						=


			+/−

Вычислить

Для того, чтобы возвести дробь в степень, необходимо возвести её числитель и знаменатель в эту же степень.

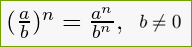
При возведение в степень смешанной дроби, сначала нужно эту дробь преобразовать в неправильную, а затем возвести в степень её числитель и знаменатель.

Источник

Что вам понадобится

Об этой статье

Была ли эта статья полезной?

Video

Things You’ll Need

About This Article

Did this article help you?

Правило возведения алгебраической дроби в степень, его доказательство

Примеры, решения

Вам также может понравиться

Как найти разность фаз колебаний волны

Как найти площадь квадрата понятие

Как найти нормаль прямой в пространстве

Добавить комментарий Отменить ответ