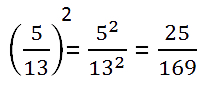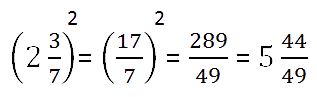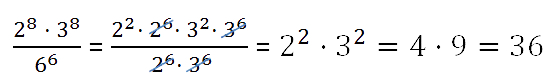Как найти квадрат обыкновенной дроби - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Возведение в квадрат дробей – это одна из самых простых операций с дробями. Она похожа на возведение в квадрат целых чисел – нужно умножить числитель и знаменатель на себя.^[1] В некоторых случаях дробь можно упростить, а потом возвести ее в квадрат, чтобы упростить процесс. Эта статья научит вас возводить в квадрат дроби.

1
Уясните, как возводить в квадрат целые числа. Если показатель степени равен 2, то число нужно возвести в квадрат. Для этого нужно умножить число на себя.^[2] Например:
- 5² = 5 × 5 = 25
2
Возведение в квадрат дробей похоже на возведение в квадрат целых чисел. Чтобы возвести в квадрат дробь, нужно умножить ее на себя, то есть нужно умножить числитель на себя, а затем умножить знаменатель на себя.^[3] Например:
- (⁵/₂)² = ⁵/₂ × ⁵/₂ = (^5²/_2²).
- Возведя каждое число в квадрат, вы получите: (²⁵/₄).
3
Умножьте числитель на себя и умножьте знаменатель на себя. Не имеет значения, какое число умножать в первую очередь – главное возвести в квадрат и числитель, и знаменатель. Чтобы упростить процесс, начните с числителя: умножьте его на себя. Затем умножьте знаменатель на себя.
- Числитель записывается над чертой, а знаменатель – под чертой.
- Например: (⁵/₂)² = (^{5 x 5}/_{2 x 2}) = (²⁵/₄).
4
Сократите дробь. В конце вычислений нужно сократить дробь до наименьших значений числителя и знаменателя, или преобразовать неправильную дробь в смешанное число.^[4] В нашем примере дробь ²⁵/₄ является неправильной, потому что числитель больше знаменателя.
- Чтобы преобразовать дробь в смешанное число, разделите 25 на 4. Вы получите 6 (6 х 4 = 24) и остаток 1. Таким образом, смешанное число: 6 ¹/₄.
Реклама

1
Обратите внимание на знак «минус» перед дробью. Если дана отрицательная дробь, перед ней стоит знак «минус». В некоторых случаях отрицательные дроби (и числа) заключают в круглые скобки, чтобы не перепутать отрицательную дробь (или число) с операцией вычитания.^[5]
- Например: (–²/₄)
2
Умножьте дробь на себя. То есть умножьте числитель на себя, а затем умножьте знаменатель на себя. Или просто умножьте дробь на себя.
- Например: (–²/₄)² = (–²/₄) x (–²/₄)
3
Помните, что при перемножении двух отрицательных чисел получается положительное число. Если перед дробью стоит знак «минус», то дробь отрицательная. Возводя в квадрат дробь, вы перемножаете два отрицательных числа. При перемножении двух отрицательных чисел получается положительное число.^[6]
- Например: (-2) x (-8) = (+16)
4
После возведения в квадрат избавьтесь от знака «минус» (-). Возведя в квадрат дробь, вы перемножили два отрицательных числа. То есть теперь дробь стала положительной. Не забудьте записать окончательный ответ без знака «минус».^[7]
- В нашем примере конечная дробь будет положительной.
- (–²/₄) x (–²/₄) = (+⁴/₁₆)
- В подавляющем большинстве случаев знак «плюс» (+) перед положительными дробями (и числами) не пишут.^[8]
5
Сократите дробь. В конце вычислений нужно сократить дробь до наименьших значений числителя и знаменателя, или преобразовать неправильную дробь в смешанное число, которое затем сокращается.
- Например: у числителя и знаменателя дроби (⁴/₁₆) есть общий делитель 4.
- Разделите дробь на 4: 4/4 = 1, 16/4 = 4
- Запишите сокращенную дробь: (¹/₄)
Реклама

1
Проверьте, можно ли сократить дробь перед тем, как возвести ее в квадрат. Как правило, легче сократить дробь до ее возведения в квадрат. Чтобы сократить дробь до наименьших значений числителя и знаменателя, нужно разделить и числитель, и знаменатель на общий делитель.^[9] Сокращение дроби до возведения в квадрат означает, что сокращать дробь после возведения в квадрат уже не нужно.
- Например: (¹²/₁₆)²
- Числа 12 и 16 можно разделить на 4: 12/4 = 3 и 16/4 = 4. Таким образом, дробь ¹²/₁₆ сокращается до ³/₄.
- Теперь возведите в квадрат дробь ³/₄.
- (³/₄)² = ⁹/₁₆. Эту дробь сократить нельзя.
- Чтобы доказать это, возведите в квадрат исходную дробь:
  - (¹²/₁₆)² = (^{12 x 12}/_{16 x 16}) = (¹⁴⁴/₂₅₆)
  - У числителя и знаменателя дроби (¹⁴⁴/₂₅₆) есть общий делитель 16. Разделив числитель и знаменатель на 16, вы сократите дробь до (⁹/₁₆), то есть получается такая же дробь, как при сокращении до возведения в квадрат.
2
Научитесь определять, когда нужно повременить с сокращением дроби. Работая с более сложными уравнениями, можно сократить один из множителей. В этом случае с сокращением дроби лучше подождать. Дробь, которая участвовала в приведенном выше примере, умножим на число:
- Например: 16 × (¹²/₁₆)²
- Степень запишите в виде произведения дроби на себя, а затем сократите множитель:16 * ¹²/₁₆ * ¹²/₁₆
  - Так как множитель равен 16, и один из знаменателей равен 16, можно сократить и множитель, и один из знаменателей – просто зачеркните их.
- Упрощенное уравнение запишется так: 12 × ¹²/₁₆
- Сократите дробь ¹²/₁₆, разделив числитель и знаменатель на 4. Вы получите дробь: ³/₄
- Перемножьте: 12 × ³/₄ = 36/4
- Разделите: 36/4 = 9
3
Научитесь упрощать степень. Упрощение степени – это другой способ решить ту же задачу. Вы получите тот же ответ, но процесс вычисления немного изменится.
- Например: 16 * (¹²/₁₆)²
- Запишите числитель и знаменатель в виде степеней: 16 * (^12²/_16²)
- Сократите множитель и показатель степени у знаменателя:16 * ^12²/_16²
  - Показатель степени множителя 16 равен 1: 16¹. По правилу деления степеней их показатели вычитаются: 16¹/16² = 16^1-2 = 16^-1 = 1/16.
- Вы получили дробь:^12²/₁₆
- Перепишите дробь в следующем виде и сократите ее: ^12*12/₁₆ = ¹² * ³/₄.
- Перемножьте: 12 × ³/₄ = 36/4
- Разделите: 36/4 = 9
Реклама

Что вам понадобится

Бумага или доска
Карандаш/ручка или мел

Об этой статье

Эту страницу просматривали 90 874 раза.

Была ли эта статья полезной?

Источник

Как выполнить возведение дроби в квадрат? Как возвести в квадрат смешанное число?

Чтобы найти квадрат дроби, нужно найти произведение двух множителей, каждый из которых равен этой дроби:

$[{(frac{a}{b})^2} = frac{a}{b} cdot frac{a}{b}]$

Например,

$[{(frac{1}{4})^2} = frac{1}{4} cdot frac{1}{4} = frac{1}{{16}};]$

$[{(frac{2}{9})^2} = frac{2}{9} cdot frac{2}{9} = frac{4}{{81}};]$

$[{(frac{7}{{16}})^2} = frac{7}{{16}} cdot frac{7}{{16}} = frac{{49}}{{256}};]$

$[{(frac{5}{{11}})^2} = frac{5}{{11}} cdot frac{5}{{11}} = frac{{25}}{{121}}.]$

Другой способ найти дробь в квадрате — возвести в квадрат отдельно числитель, отдельно — знаменатель:

$[{(frac{a}{b})^2} = frac{{{a^2}}}{{{b^2}}}]$

Например,

$[{(frac{3}{{10}})^2} = frac{{{3^2}}}{{{{10}^2}}} = frac{9}{{100}};]$

$[{(frac{5}{{12}})^2} = frac{{{5^2}}}{{{{12}^2}}} = frac{{25}}{{144}};]$

$[{(frac{6}{{17}})^2} = frac{{{6^2}}}{{{{17}^2}}} = frac{{36}}{{289}};]$

$[{(frac{{19}}{{30}})^2} = frac{{{{19}^2}}}{{{{30}^2}}} = frac{{361}}{{900}}.]$

Чтобы найти квадрат смешанного числа (смешанной дроби), надо сначала перевести это число в неправильную дробь, возвести ее в квадрат, а затем из полученной неправильной дроби выделить целую часть.

Например,

$[{(1frac{2}{3})^2} = {(frac{5}{3})^2} = frac{5}{3} cdot frac{5}{3} = frac{{25}}{9} = 2frac{7}{9};]$

$[{(2frac{3}{5})^2} = {(frac{{13}}{5})^2} = frac{{13}}{5} cdot frac{{13}}{5} = frac{{169}}{{25}} = 6frac{{19}}{{25}};]$

$[{(7frac{1}{2})^2} = {(frac{{15}}{2})^2} = frac{{15}}{2} cdot frac{{15}}{2} = frac{{225}}{4} = 56frac{1}{4};]$

$[{(4frac{1}{6})^2} = {(frac{{25}}{6})^2} = frac{{25}}{6} cdot frac{{25}}{6} = frac{{625}}{{36}} = 17frac{{13}}{{36}}.]$

Источник

Как возвести дробь в квадрат

При решении арифметических и алгебраических задач иногда требуется возвести дробь в квадрат. Проще всего это сделать, когда дробь десятичная – достаточно обычного калькулятора. Однако если дробь обыкновенная или смешанная, то при возведении такого числа в квадрат могут возникнуть некоторые затруднения.

Вам понадобится

калькулятор, компьютер, приложение Excel.

Инструкция

Чтобы возвести десятичную дробь в квадрат, возьмите инженерный калькулятор, наберите на нем возводимую в квадрат дробь и нажмите на клавишу возведения во вторую степень. На большинстве калькуляторов эта кнопка обозначена как «х²». На стандартном калькуляторе Windows функция возведения в квадрат выглядит как «x^2». Например, квадрат десятичной дроби 3,14 будет равен: 3,14² = 9,8596.

Чтобы возвести в квадрат десятичную дробь на обычном (бухгалтерском) калькуляторе, умножьте это число само на себя. Кстати, в некоторых моделях калькуляторов предусмотрена возможность возведения числа в квадрат даже при отсутствии специальной кнопки. Поэтому предварительно ознакомьтесь с инструкцией к конкретному калькулятору. Иногда примеры «хитрого» возведения в степень приведены на задней крышке или на коробке калькулятора. Например, на многих калькуляторах для возведения числа в квадрат достаточно нажать кнопки «х» и «=».

Для возведения в квадрат обыкновенной дроби (состоящей из числителя и знаменателя), возведите в квадрат по отдельности числитель и знаменатель этой дроби. То есть воспользуйтесь следующим правилом:(ч / з)² = ч² / з², где ч – числитель дроби, з – знаменатель дроби.Пример: (3/4)² = 3²/4² = 9/16.

Если возводимая в квадрат дробь – смешанная (состоит из целой части и обыкновенной дроби), то предварительно приведите ее к обыкновенному виду. То есть примените следующую формулу:(ц ч/з)² = ((ц*з+ч) / з)² = (ц*з+ч)² / з², где ц – целая часть смешанной дроби.Пример: (3 2/5)² = ((3*5+2) / 5)² = (3*5+2)² / 5² = 17² / 5² = 289/25 = 11 14/25.

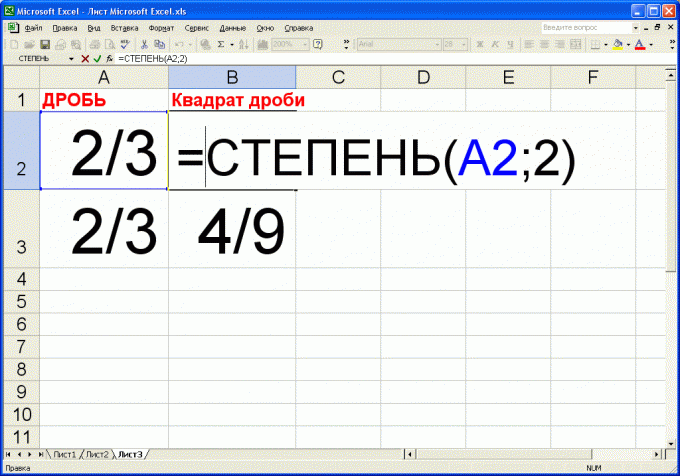
Если возводить в квадрат обыкновенные (не десятичные) дроби приходится постоянно, то воспользуйтесь программой MS Excel. Для этого введите в одну из клеток таблицы следующую формулу: =СТЕПЕНЬ(A2;2) где А2 – адрес ячейки, в которую будет вводиться возводимая в квадрат дробь.Чтобы сообщить программе, что с вводимым числом необходимо обращаться как с обыкновенной дробью (т.е. не преобразовывать ее в десятичный вид), наберите перед дробью цифру «0» и знак «пробел». То есть для ввода, например, дроби 2/3 нужно ввести: «0 2/3» (и нажать Enter). При этом в строке ввода отобразится десятичное представление введенной дроби. Значение и представление дроби непосредственно в клетке сохранится в исходном виде. Кроме того, при использовании математических функций, аргументами которых являются обыкновенные дроби, результат также будет представлен в виде обыкновенной дроби. Следовательно квадрат дроби 2/3 будет представлен как 4/9.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

как возвести обычную дробь в квадрат?

анастасия панюшкина

Ученик

(98),
закрыт

11 лет назад

Лучший ответ

Hermione

Гуру

(2550)

11 лет назад

И числитель, и знаменатель возводи в квадрат. Удачи!

Остальные ответы

Murka

Гуру

(3984)

11 лет назад

Числитель в квадрат и знаменатель тоже в квадрат.

Андрей Александров

Знаток

(388)

11 лет назад

умножить эту дробь саму на себя

Источник: алгебра 6 класс

Похожие вопросы

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Возведение дроби в степень

Поддержать сайт

Запомните!

При возведении в степень дроби нужно
возвести в степень и числитель, и знаменатель.

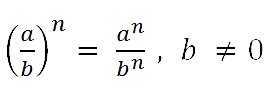
Данное свойство соответствует другой записи свойства № 5
«Степень частного», расмотренного на предыдущей странице.

Примеры возведения в степень дроби.

()² =

=

=

Как возвести в степень смешанное число

Чтобы возвести в степень смешанное число, сначала избавляемся от целой
части, превращая смешанное число в неправильную дробь. После этого
возводим в степень и числитель, и знаменатель.

Пример.

Формулу возведения в степень дроби применяют как
слева направо, так и справа налево, то есть, чтобы
разделить друг на друга степени
одинаковыми показателями, можно разделить одно основание на другое,
а показатель степени оставить неизменным.

Пример. Найти значение выражения рациональным способом.

На нашем сайте вы также можете проверить свои вычисления и
возвести число в степень онлайн.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Что вам понадобится

Об этой статье

Была ли эта статья полезной?

Как возвести дробь в квадрат

как возвести обычную дробь в квадрат?

Возведение дроби в степень

Как возвести в степень смешанное число

Ваши комментарии

Вам также может понравиться

Как найти катакомбы в грим соул

Как составить сравнительную таблицу по литературе 5 класс

Как найти работу в мелеузе

Добавить комментарий Отменить ответ