Как возвести подстановку в степень
Определение 1. Подстановкой (перестановкой) множества M= n > состоящего из n первых натуральных чисел, называется взаимно-однозначное отображение множества M на себя. Число n в этом случае называется степенью подстановки (не путать с порядком подстановки!).
Подстановки будем записывать в виде таблицы, состоящей из двух строк и n столбцов следующим образом:
Пример. Примерами подстановок 5-го порядка будут подстановки:
Заметим,что порядок чисел в верхней строчке является несущественным, например,рассмотрим подстановку четвертой степени:
Поэтому эти подстановки тождественные.
Каждую подстановку можно записывать так, чтобы все числа в первой строке располагались в порядке возрастания. При такой записи подстановок любые две подстановки одной степени будут отличаться только перестановками во второй строке.
Отсюда следует довольно простой и важный вывод:
существует n! различных подстановок n – ой степени.
Научный форум dxdy
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву , правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Возвести подстановку в степень.
Последний раз редактировалось qwertz 04.05.2013, 21:57, всего редактировалось 3 раз(а).

Последний раз редактировалось qwertz 05.05.2013, 10:09, всего редактировалось 2 раз(а).
Цикл 












В утверждении про остаток я говорил про один цикл, а вы применяете его к двум.
Если и
две подстановки, то
(50 раз). В общем случае это упростить нельзя, но непересекающиеся циклы коммутативны, поэтому если
и
непересекающиеся циклы, то
. Для получения остатка делить степень надо на длину цикла. Чтобы понять, почему, возьмите какой-нибудь цикл и возведите его в степень 1, 2, 3 и т.д., чтобы понять закономерность.
1
Тема: Как возвести подстановку в степень? (Прочитано 6515 раз)
0 Пользователей и 1 Гость просматривают эту тему.
1 2 3 4 5 6 7 8
1 7 8 5 6 2 3 4 возвести в 19-ую степень
(1)^19 (2738456)^19
« Последнее редактирование: 25 Октября 2011, 00:38:32 от Asix »
19 раз умножить саму на себя
1 2 3 4 5 6 7 8
1 7 8 5 6 2 3 4 возвести в 19-ую степень
(1)^19 (2738456)^19
А попонятней можно задачу объяснить?
За жизнью надо тщательно следить, все время избегая с ней разлуки.
А попонятней можно задачу объяснить?
Т.е.?
(1) так и остается
а вот (2738456)^19 вроде находится так:
я делю степень на длину цикла
197 и беру остаток,т.е 5
(2738456)^19=(2738456)^5
и как возвести этот цикл в 5ую степень?
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Возвести подстановку в степень.
|
|
08/04/13 |
Как это сделать?
|
|
|
|
|
AV_77 |
Re: Возвести подстановку в степень.
|
||
11/11/07 |
В виде произведения независимых циклов представьте. Или просто начните перемножать, заметите закономерность.
|
||
|
|
|||
|
qwertz |
Re: Возвести подстановку в степень.
|
|
08/04/13 |
|
|
|
|
|
devgen |
Re: Возвести подстановку в степень.
|
|
26/03/11 |
qwertz 1 это 4, 4 это 1, 1 это 4, 4 это 1..
|
|
|
|
|
_Ivana |
Re: Возвести подстановку в степень.
|
|
05/09/12 |
|
|
|
|
|
devgen |
Re: Возвести подстановку в степень.
|
|
26/03/11 |
|
|
|
|
|
arseniiv |
Re: Возвести подстановку в степень.
|
||
27/04/09 |
|||
|
|
|||
|
provincialka |
Re: Возвести подстановку в степень.
|
||
18/01/13 |
Почему равно? Вы имели в виду, что левую часть надо тоже в сотую степень возвести? Сегодняшнее пасхальное настроение привело меня к такому совету: будьте как дети! То есть попробуйте решить задачу без теории, экспериментально. Ну вот, цикл
|
||
|
|
|||
|
qwertz |
Re: Возвести подстановку в степень.
|
|
08/04/13 |
Цикл
|
|
|
|
|
provincialka |
Re: Возвести подстановку в степень.
|
||
18/01/13 |
|||
|
|
|||
|
bot |
Re: Возвести подстановку в степень.
|
||
21/12/05 |
Никогда не умножал подстановки разных размеров А почему разложению не удивлялись? Циклы-то ведь были “разных размеров”
|
||
|
|
|||
|
arseniiv |
Re: Возвести подстановку в степень.
|
||
27/04/09 |
Получилось, что тождественная подстановка Обычно такие
|
||
|
|
|||
|
provincialka |
Re: Возвести подстановку в степень.
|
||
18/01/13 |
Получилось, что тождественная подстановка Обычно такие Именно это я и имела в виду, сказав, что ответ верный. Впрочем, это мелочи – как человеку понятнее, так пусть и записывает.
|
||
|
|
|||
|
qwertz |
Re: Возвести подстановку в степень.
|
|
08/04/13 |
А почему разложению не удивлялись? Циклы-то ведь были “разных размеров” Совсем недавно начал изучать подстановки. Опыта мало, многие вещи становятся понятными не сразу. Но с вами процесс понимания идет быстрее, чем с литературой. Всем большое спасибо!
|
|
|
|
|
arseniiv |
Re: Возвести подстановку в степень.
|
||
27/04/09 |
(Оффтоп) Обычно такие Именно это я и имела в виду, сказав, что ответ верный. Впрочем, это мелочи – как человеку понятнее, так пусть и записывает. Я этого и не оспаривал. Знание, что не обязательно писать
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
|
10:24 Степень подстановки что это |
|
Определение 1. Подстановкой (перестановкой) множества M={1,2,3,…n} состоящего из n первых натуральных чисел, называется взаимно-однозначное отображение множества M на себя. Число n в этом случае называется степенью подстановки (не путать с порядком подстановки!). Подстановки будем записывать в виде таблицы, состоящей из двух строк и n столбцов следующим образом: Пример. Примерами подстановок 5-го порядка будут подстановки: Заметим,что порядок чисел в верхней строчке является несущественным, например,рассмотрим подстановку четвертой степени: Поэтому эти подстановки тождественные. Отсюда следует довольно простой и важный вывод: существует n! различных подстановок n – ой степени. P.S. Перестановку записанную в две строки обычно называют подстановкой. |
Категория: Комбинаторика | Просмотров: 4385 | | Теги: перестановки | Рейтинг: 3.0/2 |
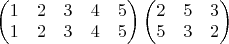


 а дальше?
а дальше? что означает? Что будет, если применить его 2 раза? Три раза? Во что перейдут 1 и 4?
что означает? Что будет, если применить его 2 раза? Три раза? Во что перейдут 1 и 4? умножается на цикл
умножается на цикл 
 — ничего же не меняется. При умножении на другие циклы и вовсе не пишут.
— ничего же не меняется. При умножении на другие циклы и вовсе не пишут. , не будет лишним.
, не будет лишним. 