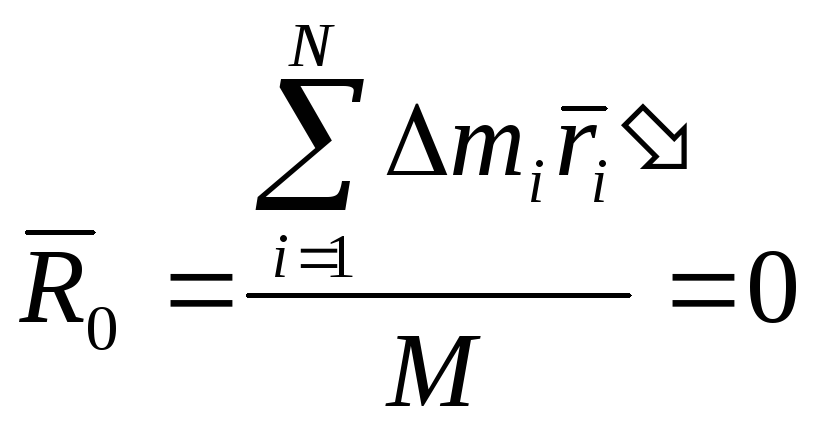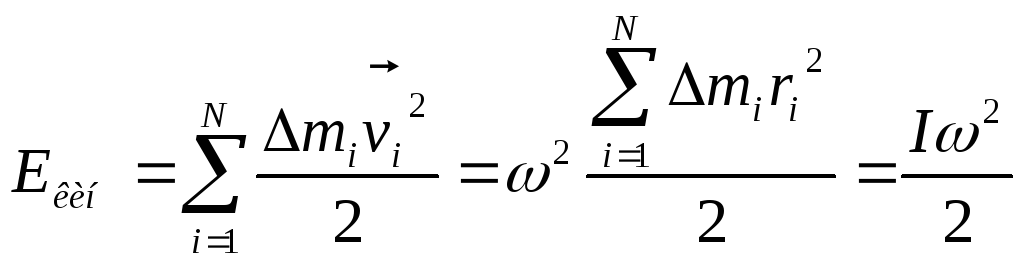Как найти квадрат расстояния между осями

Теорема Штейнера.

Имеется
тело массой М, разбиваем его на N
частей массой
– каждая. Имеется 2 оси О и О^/.
Вычислим момент инерции относительно
оси О.

пусть
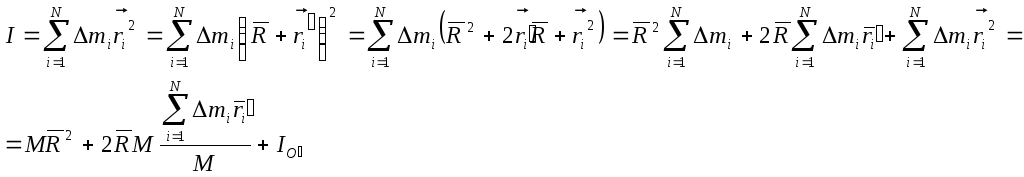
ось
проходит через центр масс и тогда

–
теорема Штейнера

Момент
инерции тела относительно производной
оси О равен сумме моментов инерции этого
же тела относительно оси, проходящей
через центр масс и произведения массы
тела на квадрат расстояния между осями.

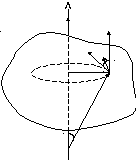
Основное уравнение динамики вращательного движения.

Рассмотрим
вращающееся вокруг оси Z
твердое тело. Выделим массу;– импульс i-той части тела;– момент импульса i-той части

.

Для
тела вращающегося вокруг оси симметрии

Дифференцируем
левую и правую часть этого соотношения
по t.

–
результирующий момент сил, действующий
на тело.

Данное
соотношение является основным уравнением
динамики вращающегося движения твердого
тела и является аналогом 2-ого закона
Ньютона

Поступательное движение	Вращательное движение
m	I

Кинетическая энергия вращающегося твердого тела.

Вопросы для самоконтроля

1. Что представляет
   момент импульса системы? Сформулируйте
   закон сохранения момента импульса?

2. Что называется
   моментом инерции тела относительно
   оси?

3. Что называется
   моментом инерции материальной точки?
   Моментом инерции твердого тела?

4. Сформулируйте
   теорему Штейнера.

5. В чем заключается
   основное уравнение вращательного
   движения твердого тела?

6. Как определяется
   кинетическая энергия при вращательном
   движении?

СПИСОК ЛИТЕРАТУРЫ

Основная

1. Детлаф, А.А.
   Курс физики учеб. пособие / А.А. Детлаф,
   Б.М. Яворский.-7-е изд. Стер.-М. : ИЦ
   «Академия».-2008.-720 с.

2. Савельев, И.В.
   Курс физики: в 3т.: Т.1: Механика .Молекулярная
   физика : учеб.пособие / И.В. Савельев.-4-е
   изд. стер. – СПб.; М. Краснодар:
   Лань.-2008.-352 с.

3. Трофимова, Т.И.
   курс физики: учеб. пособие/ Т.И. Трофимова.-
   15-е изд., стер.- М.: ИЦ «Академия», 2007.-560
   с.

Дополнительная

1. Фейнман,
   Р. Фейнмановскиелекции по физике /Р.
   Фейнман, Р. Лейтон, М. Сэндс.
   – М.: Мир.

Т.1.
Современная наука о природе. Законы
механики. – 1965. –232 с.

Т. 2. Пространство,
время, движение. – 1965. – 168 с.

Т. 3. Излучение. Волны.
Кванты. – 1965. – 240 с.

1. Берклеевский курс
   физики. Т.1,2,3. – М.: Наука, 1984

Т. 1. Китель,
Ч. Механика /
Ч. Китель, У. Найт, М. Рудерман. – 480 с.

Т. 2. Парселл,
Э. Электричество
и магнетизм / Э. Парселл. – 448 с.

Т. 3. Крауфорд,
Ф. Волны / Ф.
Крауфорд – 512 с.

1. Фриш, С.Э.
   Курс общей физики: в 3 т.: учеб. / С.Э. Фриш,
   А.В. Тиморева.- СПб.: М.; Краснодар:
   Лань.-2009.

Т. 1. Физические
основы механики. Молекулярная физика.
Колебания и волны: учебник – 480 с.

Т.2: Электрические
и электромагнитные явления: учебник. –
518 с.

Т. 3. Оптика. Атомная
физика : учебник– 656 с.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #

  25.03.20152.69 Mб2171.doc

Содержание:

1. Динамика системы материальных точек
2. Силы и их классификация и свойства
3. Силы внутренние и внешние
4. Активные силы и реакции связей
5. Дифференциальные уравнения движения свободной системы материальных точек
6. Дифференциальные уравнения движения несвободной системы материальных точек
7. Масса. Центр масс системы
8. Моменты инерции механической системы (геометрия масс)
9. Теоремы Гюйгенса – Штейнера о моментах инерции
10. Теорема 1 (о моментах инерции относительно параллельных осей)
11. Теорема 2 (о моменте инерции относительно двух параллельных не центральной осей)
12. Теорема 3 (о планарных моментах инерции)
13. Теорема 4 (о центробежных моментах инерции)
14. Вычисление моментов инерции некоторых тел простой формы
15. Момент инерции однородного цилиндра
16. Момент инерции шара
17. Момент инерции относительно произвольной оси, проходящей через данную точку
18. Эллипсоид инерции
19. Вычисления тензора инерции

Динамика (от греч. dinamikos – сильный) – раздел теоретической механики, в котором изучаются движения материальных объектов в зависимости от действующих на них сил. Материальной точкой называют простейшую модель материального тела любой формы, размеры которого достаточно малы и которое можно принять за геометрическую точку при изучении его движения.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Динамика системы материальных точек

В основу классической механики положены законы Ньютона, которые были получены им путём обобщений целого ряда опытных данных и теоретических исследований.

Основные понятия динамики системы материальных точек:
Системой материальных точек называется совокупность материальных точек, положения и движения которых взаимосвязаны.
 Различают свободные и несвободные системы. Если на движение точек системы не наложены заранее заданные ограничения, которые не зависят от закона движения, то система называется свободной. Иными словами, если точки системы в любой момент времени могут занимать произвольное положение и иметь произвольные скорости, то такая система материальных точек называется свободной. Примером свободной системы является Солнечная система, причем Солнце и планеты рассматриваются как материальные точки. Это объясняется тем, что расстояния между Солнцем и планетами очень большие по сравнению с их размерами.
Несвободной называется такая система материальных точек, на движение которых наложены связи. В задачах техники встречаются в основном несвободные системы (несвободные твердые тела).

Напомним, что связи делятся на геометрические и кинематические. Геометрические связи
накладывают ограничения на координаты точек системы, кинематические – на скорости точек системы.
 Условия, ограничивающие свободу движения материальных точек системы, выражаются некоторыми уравнениями, которые называются уравнениями связей. В общем случае эти уравнения устанавливают связи между координатами материальных точек, проекциями скоростей этих точек и временем.
 Уравнения геометрической связи имеют вид:

                                                                                                 (15.1)

Уравнение кинематической связи записывают в форме:

                                                                                                       (15.2)
Если на систему материальных точек одновременно наложены геометрические и кинематические связи, то общее количество связей будет  где – количество геометрических связей, – количество кинематических связей.
 Отметим, для того чтобы движение происходило, общее количество связей не должно превышать числа координат материальных точек системы.
 По классификации немецкого физика Г. Герца (1857 1894), связи делятся на голономные и неголономные.
Голономными называются связи, уравнения которых могут быть интегрированные. Неголономные, или не интегрированными, называются связи, в дифференциальные уравнения которых явно входят скорости так, что для этих уравнений не существует интегрирующего множителя.
 Классическим примером системы с неголономными связями является качение без скольжения абсолютно твердой шара радиусом по шершавой поверхности.
 Введем неподвижную систему координат (рис. 15.1, я), связанную с неподвижной
плоскостью, и подвижную , связанную с шаром с полюсом С в центре шара. Положение шара относительно системы координат зададим с помощью углов Эйлера (см. рис. 10.3, а). Точка Р является мгновенным центром скоростей, поэтому:

                                                                                                              (15.3)

где – скорость центра шара, – радиус-вектор точки Р,  – мгновенная угловая скорость шара.

Проецируя на оси неподвижной системы координат , обе части этого уравнения, получим:

                                                                                                         (15.4)

где  

Из рис. 10.3,а с помощью основной формулы сферической тригонометрии (10.20) найдем

                                                                                                      (15.5)

С учетом соотношений для   выражения для проекций линейной скорости
примут вид:

                                                                  

Эти уравнения не имеют интегрирующего множителя, поэтому связь является неголономной.

Плоский диск, который катится по прямой линии (рис. 15.1, б), является системой с голономными связями. Уравнения связей в этом случае имеют вид:

                                                                                                     (15.7)

Очевидно, эти уравнения интегрируются. Получим:

                                                                                                     (15.8)
Различают также связи не удерживающие и удерживающие. Связь называется удерживающей, если она ограничивает движение как в определенном направлении, так и в обратном. Удерживающая связь выражается уравнением (15.2). Связь называется не удерживающейся, если она ограничивает движение в определенном направлении, но не ограничусь в обратном. Неудерживающими связями определяется неравенством:

                                                                                                  (15.9)

В механике чаще всего  рассматривают удерживающие связи. Различают также связи стационарные и нестационарные. Если в уравнение связи явно  не входит, то связь называется стационарной. В противном случае связь называется нестационарной.

Силы и их классификация и свойства

В динамике, так же как и в статике, используют две классификации сил, приложенных к системе материальных точек, а именно:

1) силы внутренние и внешние;

2) активные силы и реакции связей.
 

Силы внутренние и внешние

Напомним, что внутренними называются силы взаимодействия между материальными точками одной и той самой системы. Внутренние силы обозначим . Они имеют следующие свойства:
главный вектор и главный момент внутренних сил  относительно некоторой точки, например О, равны нулю:

                                                                                               (15.10)

Условие (15.10) получаем на основе третьего закона Ньютона. Следует отметить, что эти условия нельзя рассматривать как достаточные условия равновесия внутренних сил. При рассмотрении движения изменяемой системы материальных точек вопрос о равновесии внутренних сил не имеет физического смысла, поскольку эти силы приложены к разным телам и к них нельзя применять аксиому 1 о двух силах, хотя внутренние силы действуют попарно, имеют общую линию действия, равны по модулю и противоположно направлены. Например, между Солнцем и Землей действуют внутренние силы взаимного притяжения, но одна из них приложена к Земле, а другая – к Солнцу, “Равновесие” таких сил не имеет физического содержания.
 Как показано в статике, внутренние силы уравновешиваются или образуют нулевую систему только тогда, когда они приложены к абсолютно твердому телу.
Внешними называются силы взаимодействия между материальными точками определенной системы и другими физическими телами, которые входят в систему. Внешние силы обозначим . Эта классификация сил применяется в основном в условиях свободной системы материальных точек. В зависимости от состава системы одни и те же силы могут быть или внешними, либо внутренними. Обратимся к такому примеру. Поезд состоит
 из вагонов и тепловоза.  Внутренними силами здесь являются силы сцепления между вагонами, внешними – силы притяжения, реакции рельсов, силы сопротивления воздуха. Если в рассматриваемую систему ввести рельсы, то реакции рельсов будут внутренними силами.
 

Активные силы и реакции связей

По второй классификации, силы делятся на активные и реакции связей. Активную силу обозначим , а реакцию связи . Эта классификация применяется в случае несвободной системы материальных точек. Реакциями связей
называют силы, с которыми в связи действуют на систему материальных точек.

Реакции связей, в отличие от активных сил, является неизвестными величинами, и в общем случае зависят от закона движения механической системы.
 Разработка методов определения реакций связей является одной из задач динамики несвободной системы. Отметим, что реакции связей вводятся на основе аксиомы об освобождении от связей.
Таким образом, с помощью аксиомы о освобождение от связей несвободная система превращается в свободную, но на которую наряду с активными силами действуют дополнительные силы -реакции связей.
 Следует отметить, что введенные классификации сил являются относительными. Так, в зависимости от того, что мы принимаем за систему, одна и та же сила может быть как внутренней, так и внешней. Метод, с помощью которого происходит изменение состава системы и переклассификация сил, является методом сечений. Для иллюстрации введенных понятий и условности классификации сил рассмотрим, например, силы, приложенные к автомобилю, который движется по горизонтальной дороге (рис. 15.2). На автомобиль действует сила притяжения . Эта сила внешняя, поскольку она вызвана действием Земли – тела, которые не входят в данную материальную систему (автомобиля). Одновременно эта сила   является активной силой, поскольку не зависит от связей. К активным внешних сил относится также аэродинамическая сила сопротивления воздуха Она тоже не зависит от связей и обусловлена ​​сопротивлением окружающей среды. Применим теперь принцип освобождения от связей и заменим действие связи (дороги)  его реакциями . Первые две силы и  с равнодействующими нормальных составляющих реакций дороги к передним и задним колесам, а силы F2 – равнодействующие силы трения, вызванные вращением ведущих и ведомых колес. Силы – внешние, поскольку они обусловлены действием дороги, которая в систему не входит. Таким образом, к автомобилю приложено шесть внешних сил
Сила давления газов на поршни двигателя, силы давления поршней на шатуны и шатунов на кривошипы коленчатого вала, силы трения на осях колес и тому подобное – это все внутренние силы системы.

Возникает вопрос: как же тогда автомобиль движется под действием внутренних сил?
Оказывается, что причиной движения автомобиля есть внешняя сила – сила трения скольжения между задними ведущими колесами и дорогой. Но внешняя сила трения возникнет только тогда, когда двигателем будут созданы внутреннего силы, которые вызывают эту внешнюю силу. Понятно, что когда эта сила трения недостаточная или отсутствует, то задние колеса пробуксовывать и автомобиль не будет двигаться.
 Точно такой же механизм движения человека при ходьбе. Внешние силы трения между
подошвами обуви и полом или дорой не могут возникнуть без внутренних мышечных
усилий человека. Если не создавать мышечных усилий, то соответствующие внешние силы
трения не проявляют своего действия.

Дифференциальные уравнения движения свободной системы материальных точек

Как отмечалось в п. 13.2, основной задачей динамики системы материальных точек является исследование ее движения при заданных силах, действующих на систему. Рассмотрим систему материальных точек, на которые действуют внутренние и внешние силы. Для произвольной материальной точки системы уравнения движения имеет следующий вид:

                                                                                                     (15.11)

Этим уравнением движения в векторной форме соответствуют дифференциальных уравнения в координатной форме:

                                                                                                                 (15.12)

Уравнения (15.12) составляют систему обыкновенных дифференциальных уравнений второго
порядке. При интегрировании этой системы уравнений получим  постоянных интегрирования, которые определим из начальных условий движения. Нахождение неизвестных функций , из системы уравнений (15.12), в общем, связано с
значительными, а иногда и непреодолимыми математическими трудностями, которые связаны с тем, что в эти уравнения могут входить неизвестные внутренние силы, которые предварительно нужно определить. Кроме того, сложности решения системы уравнений могут возникать из-за ее высокий порядок и взаимосвязь отдельных уравнений системы, поскольку силы, входящие в эти уравнения, могут зависеть от координат не только одной материальной точки системы. Если допустить, что дифференциальное уравнение движения хотя бы одной материальной точки системы, например интегрируется независимо от остальных уравнений, то это означает, что движение точки не зависит от движения точек системы.
Поэтому, если материальная точка принадлежит системе, то хотя бы одна из проекций сил, приложенная к этой точке, будет функцией хотя бы одной из координат остальных точек системы. Преодолеть эти трудности помогают общие теоремы динамики, которые дают возможность получить зависимости между различными характеристиками движения точек системе, не интегрируя дифференциальные уравнения движения системы (15.12).

Дифференциальные уравнения движения несвободной системы материальных точек

Если
система материальных точек несвободна, то на нее действуют активные силы и реакции связей . Пусть несвободная система состоит из  материальных точек, массы которых соответственно равны  Освободив эту систему от связей, заменив их реакциями и формально превратив ее в свободную, составим дифференциальное уравнение движения несвободной системы в векторной форме:

                                                                                                              (15.13)

или

                                                                                                               (15.14)

где – равнодействующая активных сил, приложенных к i-й точки системы; – равнодействующая реакций связей, приложенных в i-й точке системы.
 Уравнением (15.14) в векторной форме соответствуют уравнения движения несвободной системы в координатной форме :

                                                                                                           (15.15)

где – проекции равнодействующей активных или устанавливаемых сил на оси декартовых координат, a – проекции равнодействующей реакций на те же оси координат.
 Аналогично указанному в п. 13.6, неизвестных величин в (15.15) больше, чем уравнений. Не дает возможности решить вторую основную задачу динамики, то есть по известным
массам и силам, действующими на точки системы, определить закон движения точек системы.
Действительно, как видно из (15.15), дифференциальных уравнений , а неизвестных , то есть  координат и  проекций реакций связей, что действуют на точки системы.
Итак, в общем виде задачу о движение несвободной системы материальных точек
без дополнительных соотношений, которым удовлетворяют связи, решить нельзя. При
этом задача может быть решена только для идеальных связей с помощью уравнений
Лагранжа первого рода, которые будут приведены в части IV ( “Основы аналитической механики”) и представляют собой обобщение уравнений п. 13.6).

Масса. Центр масс системы

Массой системы, состоящей из материальных точек, называется сумма масс точек системы.

                                                                                                            (15.16)

Предположим, что все точки системы движутся с одинаковыми ускорениями  которые по второму закону Ньютона можно считать вызванными действием приложенной к
ним системы параллельных сил . Центром масс или центром инерции системы
материальных точек называется центр параллельных сил предоставляющих движение точкам системы с одинаковым ускорением или поступательное движение неизменной системе. На основании формул (6.12) определим координаты центра масс:

                                                                                                       (15.17)

где – масса -й точки системы,  – координаты й точки системы. Поскольку  одновременно являются проекциями радиус-вектора  центра масс, то получим:

                                                                                                     (15.18)

Дифференцируя соотношение (15.18) по времени, найдем скорость и ускорение центра масс в неподвижной системе координат:

                                                                                                         (15.19)

                                                                                                          (15.20)

Понятие центра масс более широкое, чем понятие центра масс системы. Геометрически
центр тяжести системы совпадает с его центром масс, однако отождествлять центр
тяжести с центром масс нельзя, потому что между ними есть глубокие физические отличия. Известно, что понятие о центре тяжести связано с предположением об однородности поля сил тяжести в незначительных областях вблизи поверхности Земли. На самом деле, силы тяжести непараллельные.
Следовательно, понятие центра тяжести вводится приближенно на основе гипотезы о параллельности сил тяжести. Понятие центра масс не зависит от такого рода предположений.

Введение понятия центра масс позволяет в ряде случаев свести задачу о движении системы материальных точек к задаче о движении одной точки – центра масс.
 Как видно из формул (15.17), координаты центра масс зависят только от распределения масс. Заметим, что положение центра масс в теле или неизменной системе является неизменным и не зависит от выбора системы координат и закона ее движения.
Если массы системы размещены симметрично относительно некоторой плоскости, то центр масс лежит в этой плоскости. Если массы точек системы распределены симметрично относительно двух плоскостей, то центр масс расположен на линии их пересечения. При симметричном распределении масс относительно трех плоскостей центр масс находится в точке пересечения этих плоскостей.
 В завершение отметим, что для нахождения координат центра масс сложной системы можно применить компьютерные технологии. Для этого формулы (15.17) и (15.18) целесообразно записать в матричной форме.

                                                                                                       (15.21)

или 

                                                                                                       (15.22)

Если эти формулы использовать для определения центра масс системы твердых тел, то под т. д. нужно понимать координаты центров масс тел механической системы. при этом:

                                                                                                       (15.23)

Моменты инерции механической системы (геометрия масс)

В этом параграфе приведены основные определения и классификации моментов инерции.
Понятие момента инерции тела относится к основных и важных понятий в динамике.
Его ввел Л. Эйлер. Заметим, что в этом  параграфе будем изучать не движение твердого
тела, а только характер распределения масс. В теоретической механике принимается гипотеза о том, что масса твердого тела распределяется непрерывно. Приведем такие определения.
 1. Моментом инерции материальной точки относительно оси называют произведение массы этой точки в квадрат ее расстояния к этой оси, например

                                                                                                                   (15.24)

2. Моментом инерции системы, состоящей из материальных точек относительно оси
называют сумму произведений масс точек системы на квадраты расстояний от точек до оси:

                                                                                                          (15.25)

В случае непрерывного распределения массы вместо суммы будет интеграл, распространенный на всю массу.
 3. Моментом инерции твердого тела относительно оси, например называют интеграл, распространенный на всю массу и имеет вид:

                                                                                                       (15.26)

В ряде случаев для вычисления моментов инерции пользуются понятием радиуса
инерции, или плеча инерции. Радиусом инерции называют расстояние, на котором от оси вращения надо разместить массу тела, которое  рассматривается, сосредоточив ее в одной точке, чтобы она имела тот самый момент инерции, что и рассматриваемое тело:

                                                                                                  (15.27)

Радиус или плечо, инерции – это радиус такого полого кругового цилиндра, который, будучи описан вокруг оси, имеет момент инерции, одинаковый с моментом инерции данного тела, если массу тела равномерно распределить по боковой поверхности цилиндра.
 Различают моменты инерции осевые, или аксиальные, полярные, планарные и центробежные.

Для вычисления осевого момента инерции точки ее массу умножают на квадрат расстояния до оси, полярного – до заданной точки (полюса), планарного – до заданной плоскости.
Осевой момент инерции тела – это физическая величина, характеризующая меру инертности тела во время вращательного движения твердого тела вокруг неподвижной оси. В случае вращения твердого тела вокруг неподвижной точки степени инертности этого тела является момент инерции относительно мгновенной оси, проходящей через неподвижную точку.

Выведем формулы для определения перечисленных моментов инерции. Рассмотрим
точку М тела, элементарная масса которой (рис. 15.3). Координаты точки М обозначим
. Согласно определению соответствующих моментов инерции их вычисляют по таким формулам:

осевые моменты инерции тела

                                                                                          (15.28)

полярный момент инерции тела

                                                                                     (15.29)

планарные моменты инерции тела относительно координатных плоскостей:

                                                                                                           (15.30)

относительно моментов инерций тела:

                                                                                                      (15.31)

Центробежные моменты инерции зависят от направления координатных осей и выбора
начала координат. Поэтому, говоря о центробежном моменте инерции в данной точке,
понимают, что начало координат совпадает с этой точкой. Центробежные моменты инерции могут равняться нулю и иметь любой знак (плюс или минус). Если центробежные моменты инерции равны нулю, то оси называют главными осями инерции тела в данной точке. если это точка размещается в центре масс, то оси являются главными и центральными осями инерции.

Выведем зависимость между полярными, осевыми и пленарных моментами инерции.
Составляя левые и правые части выражений (15.28) и учитывая (15.29), получим:

                                                                                                     (15.32)

то есть сумма осевых моментов инерции равна удвоенному полярному моменту инерции. Составим левые и правые части выражений (15.30):

                                                                                                      (15.33)

то есть сумма пленарных моментов инерции равна полярному моменту инерции.
 С выражений (15.28) – (15.31) следует также ряд неравенств. Например,

                                                                                                 (15.34)

Нетрудно заметить, что осевые моменты инерции удовлетворяют соотношению между
сторонами треугольника. То есть на осевых моментах инерции как на сторонах можно построить треугольник.

Теоремы Гюйгенса – Штейнера о моментах инерции

Теорема Гюйгенса – Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями.

Теорема 1 (о моментах инерции относительно параллельных осей)

Момент инерции системы материальных точек или твердого тела относительно некоторой оси равен моменту инерции относительно центральной оси, параллельной данной, составленный из произведений массы системы (тела) на квадрат расстояния между осями.

 Доказательство. Пусть центр масс С является началом координат (рис. 15.4), ось параллельная центральной оси . Рассмотрим произвольную точку системы расстояние которой от оси равно   а от оси Расстояние между осями равно  h. вычислим момент инерции системы относительно оси

                                     (15.35)

Однако, поскольку  а  то получим  где по определению осевого момента инерции:  Откуда, 

                                                                                                           (15.36)

что и нужно было доказать.

С (15.36) также видно, что ось, которая проходит через центр масс, является осью наименьшего момента инерции всех параллельных осей.
 

Теорема 2 (о моменте инерции относительно двух параллельных не центральной осей)

(рис. 15.5). Момент инерции тела относительно произвольно центральной оси равна
момента инерции относительно другой параллельной ей не центральной оси составленном из произведением массы тела на разность квадратов расстояний от осей и до параллельной им центральной оси

 Если воспользоваться рис. 15.5, то математически эта теорема запишется так:

                                                                                             (15.37)
Доказательство. Пусть относительно центральной оси тело имеет момент инерции . Вот   параллельная заданным осям , и , моменты относительно которых обозначим соответственно и . Обозначим расстояние между осью , а между и  Тогда, согласно первой теореме Гюйгенса – Штейнера, получим  соотношение:

                                                                                           (15.38)

Отняв от первого равенства второе, получим соотношение (15.37), что отражает содержание теоремы 2. Таким образом теорема доказана. Отметим, что когда речь идет о параллельных оси систем координат – центральной системы координат и системы координат с началом в произвольной точке О, то на основе первой теоремы Гюйгенса – Штейнера, учитывая расстояния между этими параллельными осями, имеем

                                                                                              (15.39)

Очевидно, аналогичные зависимости будут иметь место и между радиусами инерции

                                                                                            (15.40)
 

Теорема 3 (о планарных моментах инерции)

Планарный момент инерции тела относительно произвольной плоскости равен планарному момента инерции относительно параллельной плоскости, проходящий через центр масс, и составленном из произведения массы тела на квадрат расстояния между плоскостями. Если за такие плоскости взять координатные плоскости, показаны на рис. 15.6, то математически эта теорема запишется так:

                                                                                                  (15.41)

Доказательство. обозначим координаты центра масс (точка Q в системе координат   (рис. 15.6). Эти координаты являются постоянными и они характеризуют расстояние между параллельными плоскостями: расстояние между плоскостями  и   и и 

Координаты произвольной точки М, масса которой  в системе координат  будут:  а в системе координат соответственно:

                                                                                              (15.42)

По определению, например, планарный момент  равен:

                                                                                         (15.43)

а планарный момент  соответственно:

                                                                                             (15.44)

Интеграл в правой части (15.43) можно изобразить в форме:

                                                         (15.42)

Рассмотрим каждый из интервалов в (15.45) отдельно.

Поскольку  то 

                                                                                                   (15.46)

Дальше

                                                                                                    (15.47)

поскольку координата С, центра масс (точка С тела в системе координат  равна
нулю (начало координат помещено именно в центр масс). И наконец:

                                                                                         *15.48)

Подставив значения выражений (15.46) -(15.48) в (15.43), получим первое соотношение теоремы (15.41). Аналогично приходятся два других соотношения (15.41).

Теорема 4 (о центробежных моментах инерции)

Центробежные моменты инерции тела
относительно заданных произвольных осей координат равны центробежным моментам инерции относительно центральных осей координат, которые параллельные осям заданной системе координат, составленных из произведений   массы тела на соответствующие координаты центра масс в заданной системе координат. Математически эта теорема (рис. 15.6) запишется так:

                                                                                                     (15.49)

Доказательство. Воспользуемся обозначениями, приведенными в теореме 3, и соотношениями (15.42). По определению центробежных моментов инерции в этих системах координат (рис. 15.6) получим:

                                                                                                (15.50)

Воспользовавшись соотношениями, которые приведены при доказательстве предыдущей теоремы, получим равенства (15.49), выражающих содержание теоремы 4.

Вычисление моментов инерции некоторых тел простой формы

Вычислим моменты инерции однородного тонкого стержня, однородного цилиндра и
шара (рис. 15.7).

Момент инерции однородного тонкого стержня (длина его  постоянное поперечное сечение ) относительно оси , которая перпендикулярна к стержню и проходит через его конец О, равна трети произведения массы на квадрат длины стержня (рис. 15.7, а). Для доказательства этого выделим на расстоянии от оси элемент стержня . Тогда элементарная масса , где – плотность материала стержня, а – площадь поперечного сечения стержня. Момент инерции стержня:

                                                                      (15.5)

Поскольку масса стержня  то

                                                                                                      (15.52)

Момент инерции однородного цилиндра

(Высота его и, радиус основания R, плотность материала ) относительно продольной центральной оси (рис. 15.7, б), проходящей через центр масс цилиндра, равна половине
произведению массы цилиндра на квадрат радиуса основы. По определению осевого момента инерции:

                                                                                                         (15.53)

Как элементарный объем цилиндра выберем соосный с ним кольцевой цилиндр такой же высоты h, радиус которого г и толщина . Масса этого элементарного объема:

                                                                                                  (15.54)

Подставив в выражение (15.53), получим:

                                                                                               (15.55)

Окончательно:

Выведем также выражение для момента инерции этого цилиндра относительно одной из поперечных центральных осей, например оси  Поскольку оси и лежат в плоскости симметрии цилиндра, то  Очевидно, что:

                                                                                               (15.56)

                                                                  (15.57)

Вычислим  Для этого рассмотрим элемент цилиндра в виде тонкого диска толщиной  что удаленный от плоскости  на расстояние z. Масса этого  диска  Итак:

                                                                                        (15.58)

Подставляя выражения интегралов (15.57) и (15.58) в (15.56), получим:

                                                                                                (15.59)

Момент инерции шара

При вычислении момента инерции однородного шара радиусом R
относительно одной из центральных осей, которые являются осями симметрии, учтем, что Итак, момент инерции шара относительно ее центра С (рис. 15.7, в)

                                                                                              (15.60)

откуда  Кроме того полярный момент инерции шара:

                                                                                                 (15.61)

Как элемент шара выделим объем, лежащий между двумя сферическими поверхностями
радиусов и Масса этого элемента следовательно:

                                                                                                   (15.62)

где  масса шара. Окончательно получим:

                                                                                                           (15.63)

Выражения для моментов инерции других тел простейшей формы можно найти в справочной литературе по механике (табл. 15.1).

Таблица 15.1 Момент инерции однородных тел.

Момент инерции относительно произвольной оси, проходящей через данную точку

Установим зависимость между моментами инерции твердого тела (материальной системы)
относительно произвольной оси , проходящей через начало координат, и моментами инерции относительно координатных осей (рис. 15.8).
 Обозначим направляющие косинусы оси через

Выберем любую точку тела (системы опустим с нее перпендикуляр на ось и обозначим  

По определению момента инерции относительно оси:

                                                                                                              (15.64)

Следовательно, необходимо выразить  через заданные величины 

Учитывая, что  откуда 

Поскольку  Тогда 

                                                                                                                        (15.65)

Введем обозначения:

Подставляя теперь в выражение (15.64) значения , с учетом введенных обозначений
(15.66), получим равенство:

                                                                         (15.67)

которое можно представить также в виде

                                                                                 (15.68)

или

                             (15.69)

Теоремы о моментах инерции относительно параллельных осей и тех, которые пересекаются, характеризуют изменение осевого момента инерции в зависимости от положения оси. Итак, девять величин – три статических моменты  инерции  (которые устанавливают положение центра масс), три момента инерции относительно координатных осей

                                                                                                 (15.70)

и три центробежных моменты инерции

                                                                                                            (15.71)
полностью характеризуют распределение масс системы (твердого тела).
 Используем теперь комбинацию теорем Гюйгенса – Штейнера и выражение (15.69)
для вычисления моментов инерции относительно произвольной оси. Пусть имеем произвольную ось , которая не является центральной и не проходит через точку С, в которой известные моменты инерции (рис. 15.9). Выберем главную систему координат, в которой ось удалена от центра масс (точки С) на расстояние d и имеет с координатными осями углы
Проведем через центр масс прямую , которая параллельная . Тогда, используя теорему Гюйгенса – Штейнера и последнюю теорему, получим:

                                                                                              (15.72)

Эллипсоид инерции

Закон изменение момента инерции  (15.69) с изменением параметров что определяют направление оси , допускает простую геометрическую интерпретацию, на которую указал французский ученый О. Коши (1789-1857). Следует, однако, заметить, что идея о эллипсоид инерции есть в исследованиях Л. Эйлера (1765 p.).
 Выберем на оси (рис. 15.10) точку N, расположенную на расстоянии от начала координат. Координаты этой точки , откуда   следовательно формула (15.69) примет вид:

                                                                                         (15.73)

Таким образом, геометрическое место точек – это поверхность второго порядка,
выраженная уравнением (15.73).  Поскольку и расстояния всех точек N от начала координат конечные, то уравнение (15.73) определяет эллипсоид с центром в начала координат. Этот эллипсоид называют эллипсоидом инерции, его оси симметрии  – главные оси инерции с началом в точке А. Если начало координат размещается в центре инерции системы (тела), то эллипсоид инерции называют центральным, его
оси симметрии – главными центральными осями инерции, а соответствующие моменты инерции – главными центральными моментами инерции.
 Если за координатные оси взять главные оси инерции, то уравнение эллипсоида инерции имеет вид:

                                                                                                          (15.75)

в котором нет членов, содержащих произведение координат. Главные моменты инерции системы (тела) соответственно равны  а центробежные моменты инерции равны
нулю:

                                                                                              (15.75)

Каждой точке О системы (тела) соответствует  определенный эллипсоид инерции. Если эллипсоид инерции известен, то формула (15.73) позволяет определить момент инерции  относительно любой оси, проходящей через точку О.
Следовательно, необходимым и достаточным условием того, чтобы ось была главной осью инерции системы (тела) в точке О, является равенство нулю соответствующих центробежных моментов Инерции

Знание главных осей инерции позволяет упростить уравнения движения твердого тела.
Если оси координат являются главными осями инерции, то формула (15.69) примет вид:

                                                                                          (15.76)

Вычисления тензора инерции

При решении многих задач динамики, в частности при определении динамических реакций твердого тела, вращающегося вокруг неподвижной оси, при определении погрешностей гироскопов на подвижной основе, при разработке законов управления высокоманевренных подвижными объектами – самолетами, управляемыми снарядами и т.п., необходимо знать не только осевые, но и центробежные моменты инерции в системе координат, жестко связанной с тем или иным телом.

То есть возникает задача об изучении общих свойств определенных величин при преобразованиях координат. Величины, имеющие общие свойства по преобразованию координат, называют тензорами.

Рангом тензора называют закон, который является общим для всех тензоров, принадлежащих к одной категории. Так, в законе преобразования компонент векторных величин при изменении координатных систем, направляющие косинусы входят в первый степень, то есть формулы преобразования линейные по направляющим косинусам новых осей, а в формулы преобразования моментов инерции направляющие косинусы входят во второй степень, то есть эти тензоры – квадратичные по указанным косинусам.

Обычно при исчислении тензора инерции можно пользоваться восходящими формулами для моментов инерции и вычислять каждый раз соответствующие интегралы в той или иной системе координат. Но это достаточно трудоемкая операция. Ее можно значительно упростить, если знать формулы преобразования моментов инерции как тензоров.

Пусть требуется определить тензор инерции 1 тела для прямоугольной системы координат
. Будем считать, что нам известны координаты центра масс (точка С) в
системе координат направления главных центральных осей инерции соответствующие моменты инерции (рис. 15.11).

Построим вспомогательную систему координат , оси которой параллельны соответствующим осям системы координат . Тогда направления главных центральных осей определяться направляющими косинусами:

                                                                                                  (15.77)

Моменты инерции  по формуле (15.76) равны:

                                                                                                (15.78)

Квадрат расстояния между осями и , очевидно, равна расстоянию точки С до оси х, то есть   аналогичные формулы имеем для расстояния между осями   и   и Тогда, воспользовавшись соотношениями (15.39), что определяются первой теореме Гюйгенса – Штейнера, и соотношениями (15.78), получим:

                                                                                         (15.79)

Перейдем теперь к вычислению центробежных моментов инерции тела относительно осей 

Рассмотрим произвольную точку М (рис. 15.11). Пусть ее координаты в системе  будут  а в системе координат  Эти координаты связаны следующими формулами преобразования:

                                                                                    (15.80)

Поскольку оси  являются главными центральными моментами инерции, то все центробежные моменты инерции относительно этих осей и все статические моменты равны нулю:

                                                                                     (15.81)

По определению центробежных моментов инерций относительно осей  получим:

                                                                                                         (15.82)

Подставив сюда значения  в (15.80), (ограничимся рассмотрением только )

                                                                  (15.83)

и, учитывая равенство (15.81), получим:

                                                  (15.84)

Поскольку оси  и  ортогональные, то  Отсюда

                                                                                       (15.85)

Подставим (15.85) в последнее слагаемое (15.84) для  получим:

                                                                 (15.86)

Прибавляя и вычитая в интеграле (15.86)  где есть разность и соответственно  где есть разность  с учетом перегруппирования получим:                                       (15.87)

В результате получим следующие формулы для центробежных моментов инерци1:

                                                                               (15.88)

Следовательно, формулы (15.79) и (15.88) определяют элементы тензора инерции твердого тела. Формулы (15.79) и (15.88) можно объединить и записать в форме такого матричного
соотношение

                                                                                                                               (15.89)

где 

Пример 1. Найти момент инерции прямого кругового конуса относительно образующей SB (рис. 15.12), если радиус основания конуса равен R, а высота Н.

 Решение. Построим центральную систему координат . Центр масс конуса находится на  его высоте  причем . Ось  направим по оси конуса, ось, параллельно основе так, чтобы она пересекла образующую , ось – перпендикулярно к плоскости . Координатные плоскости и  являются плоскостями симметрии, поэтому оси главные центральные оси инерции конуса. Проведем в конусе
прямую sb параллельно образующей SB, тогда мы сведем задачу к  схеме, изображенной на рис. 15.9. 

Углы между прямой и осями соответственно равны  где  -угол между образующей  и высотой  конуса.

Подставляя значения этих углов  в формулу (15.76), получим:

По таблице моментов инерции находим:

Непосредственно с рис. 15.12 определим:

Подставив эти выражения в формулы для  получим:

Расстояние  от центра масс С конуса до его образующей найдем из треугольника 

Теперь по формуле (15.13) найдем 

Предлагаем самостоятельно решить эту задачу, воспользовавшись формулами для преобразования тензора инерции.
 Пример 2. Ротор гироскопа, изготовленный в форме тонкого диска радиусом R, который выполненный с технологическими погрешностями так, что его центр масс С не совпадает с осью вращения Ох и смещен относительно точки О в направлении координат у и z на величины  и . При этом плоскость симметрии ротора не перпендикулярна оси
вращения и наклонена к ней на небольшой угол . Найти компоненты моментов инерции ротора в системе координат , которая связана с валом вращения ротора.
 Решение. По аналогии с рис. 15.11 введем три системы координат: – связана с
валом; – система координат связана с ротором так, что оси являются главными центральными осями инерции; – система координат с полюсом в центре масс, оси которой параллельны осям системы координат  (рис. 15.13). Учитывая, что ротор – это тонкий диск по формулам п. 15.7 получим:

Матрица преобразования осей (15.77) будет иметь вид:

Тогда по формулам (15.79) и (15.88) получим

Центробежный момент инерции  запишем в виде:

Подставив в эти формулы значение получим:

Если учесть, что угол мал, то   получим приближенно:

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Сосредоточенные силы и распределенные нагрузки
20. Кинематика
21. Кинематика твердого тела
22. Движения твердого тела
23. Динамика материальной точки
24. Динамика механической системы
25. Динамика плоского движения твердого тела
26. Динамика относительного движения материальной точки
27. Динамика твердого тела
28. Кинематика простейших движений твердого тела
29. Общее уравнение динамики
30. Работа и мощность силы
31. Обратная задача динамики
32. Поступательное и вращательное движение твердого тела
33. Плоскопараллельное (плоское) движение твёрдого тела
34. Сферическое движение твёрдого тела
35. Движение свободного твердого тела
36. Сложное движение твердого тела
37. Сложное движение точки
38. Плоское движение тела
39. Статика твердого тела
40. Равновесие составной конструкции
41. Равновесие с учетом сил трения
42. Центр масс
43. Колебания материальной точки
44. Относительное движение материальной точки
45. Статические инварианты
46. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Сопротивление материалов

Геометрические характеристики плоских сечений



При некоторых видах деформаций прочность и жесткость (способность противостоять деформации) элементов конструкций зависит не только от величины поперечного сечения, но и от формы этого сечения.

Самый простой пример – обыкновенную школьную линейку можно легко изогнуть относительно широкой стороны поперечного сечения и совершенно невозможно изогнуть относительно его короткой стороны. При этом общая площадь сечения в обоих случаях одинакова. На основании этого примера становится очевидным, что на сопротивление некоторым видам деформации оказывает влияние (иногда – решающее) не только величина площади сечения бруса, но и его геометрическая форма.
При изучении деформаций изгиба и кручения нам потребуется знание некоторых геометрических характеристик плоских сечений, которые оказывают влияние на способность конструкций сопротивляться деформациям относительно той или иной оси либо полюса (точки).

Чтобы понять суть явления и влияния этих геометрических характеристик на сопротивление бруса, например, изгибу, следует обратиться к основополагающим постулатам сопромата. Как известно из установленного в 1660 году английским физиком Робертом Гуком закона, напряжение в сечениях бруса прямо пропорционально его относительному удлинению. Очевидно, что волокна, расположенные дальше от оси изгиба, растягиваются (или сжимаются) сильнее, чем расположенные вблизи оси. Следовательно, и напряжения возникающие в них будут бόльшими.
Можно привести условную сравнительную аналогию между напряжением в разных точках сечения бруса с моментом силы – чем больше плечо силы – тем больше ее момент (относительно оси или точки). Аналогично – чем дальше от какого-либо полюса (оси) отстоит точка в сечении, тем большее напряжение в ней возникает при попытке изогнуть или скрутить брус относительно этого полюса (оси).

***

Статический момент площади

Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок (S_i) на расстояния (r_i)от них до этой оси.

Если упростить это определение, то статический момент инерции плоской фигуры относительно какой-либо оси (лежащей в той же плоскости, что и фигура) можно получить следующим образом:

• разбить фигуру на крохотные (элементарные) площадки (рис. 1);
• умножить площадь каждой площадки на расстояние r_i от ее центра до рассматриваемой оси;
• сложить полученные результаты.

Статический момент площади плоской фигуры обозначают S с индексом оси, относительно которой он рассматривается: S_x, S_y, S_z.

Примечание: в разных учебниках или других источниках информации обозначение тех или иных физических величин может отличаться от приведенных на этом сайте. Как вы понимаете, от условного обозначения величин суть описываемых явлений и закономерностей не изменяется.

S_x = Σ y dA;        S_y = Σ x dA.

Анализ этих формул позволяет сделать вывод, что статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние от ее центра тяжести до этой оси.
Из этого вывода следует еще один вывод – если рассматриваемая ось проходит через центр тяжести плоской фигуры, то статический момент этой фигуры относительно данной оси равен нулю.

Единица измерения статического момента площади – метр кубический (м³).
При определении статического момента площади сложной фигуры можно применять метод разбиения, т. е. определять статический момент всей фигуры, как алгебраическую сумму статических моментов отдельных ее частей. При этом сложная геометрическая фигура разбивается на простые по форме составные части – прямоугольники, треугольники, окружности, дуги и т. п., затем для каждой из этих простых фигур подсчитывается статический момент площади, и определяется алгебраическая сумма этих моментов.

***

Полярный момент инерции

Полярным моментом инерции плоской фигуры относительно полюса (точки), лежащего в той же плоскости, называется сумма произведений элементарных площадок (S_i) этой фигуры на квадрат их расстояний (r²_i) до полюса.
Полярный момент инерции обозначают I_ρ (иногда его обозначают J_ρ), а формула для его определения записывается так:

I_ρ = Σ ρ² dA.

Единица измерений полярного момента инерции – м⁴, из чего следует, что он не может быть отрицательным.
Понятие полярного момента инерции понадобится при изучении деформаций кручения круглых валов, поэтому приведем формулы для определения полярного момента квадратного, круглого и кольцевого сечения.

Очевидно, что полярный момент инерции кольцевого сечения равен разности полярных моментов инерции большого и малого кругов, ограничивающих это сечение.

***

Осевой момент инерции

Осевым моментом инерции плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат расстояний от них до этой оси (рис).

Осевой момент инерции обозначается I (иногда – J)с индексом, соответствующим оси:

I_x = Σ y² dA;        I_y = Σ x² dA.

Если при этом площадь элементарных площадок принять стремящимися к минимуму, то можно использовать методы интегрального исчисления, заменив знак суммы Σ на знак интеграла ∫.
Очевидно, что осевой и полярный момент инерции выражаются в одинаковых единицах – м⁴. Осевой момент инерции величина всегда положительная и не равна нулю (м⁴ не может быть отрицательным, а площадь не может быть равной нулю, иначе пропадает и сама фигура, как площадка).
Если сложить осевые моменты инерции плоской фигуры относительно перпендикулярных осей, то получим полярный момент инерции этой фигуры относительно точки пересечения этих осей (начала координат), т. е. :

I_x + I_y = I_ρ.

Так как интеграл суммы равен сумме интегралов, то момент инерции сложной фигуры можно вычислить как сумму моментов инерции простых фигур, на которые разбивают сложную фигуру.
Понятие осевого момента инерции понадобится при изучении теории изгиба.

Приведем формулы для определения осевых моментов инерции наиболее часто встречающихся при расчетах форм сечений:

	Для прямоугольника размером b × h:	Ix = bh3 /12
	Для квадрата со стороной а:	Ix = a4 / 12
	Для круга диаметром d:	Ix = Iy ≈ 0,05 d4
	Для кольцевого сечения размером D × d:	Ix = Iy ≈ 0,05 (D4 – d4)

***

Момент инерции при параллельном переносе осей

Оси, проходящие через центр тяжести плоской фигуры, называют центральными осями.
Момент инерции относительно центральной оси называется центральным моментом инерции.

Для доказательства этой теоремы рассмотрим произвольную плоскую фигуру, площадь которой равна А, центр тяжести расположен в точке С, а центральный момент инерции относительно оси x будет I_x.
Вычислим момент инерции фигуры относительно некоторой оси x₁, параллельной центральной оси и отстоящей от нее на расстоянии а (рис. 2).

I_x1 = Σ y₁² dA + Σ (y + a)² dA =
= Σ y² dA + 2a Σ y dA + a² Σ dA.

Анализируя полученную формулу, отмечаем, что первое слагаемое – осевой момент инерции относительно центральной оси, второе слагаемое – статический момент площади этой фигуры относительно центральной оси (следовательно, он равен нулю), а третье слагаемое после интегрирования может быть представлено в виде произведения a² A, т. е. в результате получим формулу:

I_x1 = I_x + а² А – теорема доказана.

На основании теоремы можно сделать вывод, что из ряда параллельных осей осевой момент инерции плоской фигуры будет наименьшим относительно центральной оси.

***



Главные оси и главные моменты инерции

Представим себе плоскую фигуру, моменты инерции которой относительно осей координат I_x и I_y, а полярный момент инерции относительно начала координат равен I_ρ. Как было установлено ранее,

I_x + I_y = I_ρ.

Если оси координат поворачивать в своей плоскости вокруг начала координат, то полярный момент инерции останется неизменным, а осевые моменты будут изменяться, при этом их сумма останется величиной постоянной. Поскольку сумма переменных величин постоянна, то одна из них уменьшается, а другая увеличивается, и наоборот.
Следовательно, при определенном положении осей один из осевых моментов достигнет максимального значения, а другой – минимального.

Оси, относительно которых моменты инерции имеют минимальное и максимальное значения, называют главными осями инерции.
Момент инерции относительно главной оси называется главным моментом инерции.

Если главная ось проходит через центр тяжести фигуры, она называется главной центральной осью, а момент инерции относительно такой оси – главным центральным моментом инерции.
Можно сделать вывод, что если фигура симметрична относительно какой-нибудь оси, то эта ось всегда будет одной из главных центральных осей инерции этой фигуры.

***

Центробежный момент инерции

Центробежным моментом инерции плоской фигуры называют взятую по всей площади сумму произведений элементарных площадок на расстояние до двух взаимно перпендикулярных осей:

I_xy = Σ xy dA,

где x, y – расстояния от площадки dA до осей x и y.
Центробежный момент инерции может быть положительным, отрицательным и равным нулю.

Центробежный момент инерции входит в формулы для определения положения главных осей несимметричных сечений.
В таблицах стандартных профилей содержится характеристика, которая называется радиусом инерции сечения, вычисляемая по формулам:

i_x = √ (I_x / A),        i_y = √ (I_y / A),        (здесь и далее знак “√” – знак корня)

где I_x, I_y – осевые моменты инерции сечения относительно центральных осей; А – площадь сечения.
Эта геометрическая характеристика используется при изучении внецентрального растяжения или сжатия, а также продольного изгиба.

***

Материалы раздела “Сопротивление материалов”:

• Основные понятия и определения
• Растяжение и сжатие
• Смятие. Контактные напряжения
• Деформация сдвига (среза)
• Деформация кручения
• Деформация изгиба

Растяжение и сжатие

Правильные ответы на вопросы Теста № 2

№ вопроса	1	2	3	4	5	6	7	8	9	10
Правильный вариант ответа	2	3	2	1	1	3	3	2	2	2

Зачем нужен момент инерции сечения

Несмотря на то, что наука о прочности давно уже шагнула вперёд, и давно уже развиваются многие её направления (строительная механика, механика разрушения, теория упругости и другие), а также несмотря на то, что всё чаще расчеты сложных конструкций выполняются при помощи метода конечного элемента посредством специализированных программных комплексов, прикидочные расчеты на основе методов сопромата не утратили своей актуальности. Ведь именно они, во-первых, позволяют дать оценку прочности конструкции «в полевых условиях» (без трудоёмкого построения конечно-элементной модели, без сложных математических выкладок), а во-вторых — позволяют это сделать достаточно быстро.

В основном, расчеты в сопротивлении материалов имеют целью проверить общую (а не местную) прочность балок. Поэтому расчетная схема принимается упрощенной, и многими конструктивными элементами, даже являющимися концентраторами напряжений, в ней пренебрегают. Тем не менее, несмотря на ряд упрощений в схеме и принятые допущения (гипотезы, принятые для построения теории сопротивления материалов), в этой науке разработаны методы, позволяющие с довольно большой точностью определить опасные сечения и напряжения, возникающие в них.

Вообще, поперечное сечение балки может представлять собой тавр, швеллер, двутавр, круг, прямоугольник, кольцо, полый прямоугольник и т.п. или может быть составным, т.е. составленным из нескольких однотипных или различных профилей. От его формы и размеров зависит прочность и жесткость балки. Площадь поперечного сечения является важной характеристикой, но знать только лишь её достаточно разве что для задач на центральное растяжение. Если же балка испытывает изгиб или кручение, то знать только лишь площадь поперечного сечения оказывается недостаточно. Балка может «проходить» (т.е. обладать достаточной прочностью и жесткостью) с одним типом сечения и «не проходить» с другим типом сечения такой же площади. В процессе решения задач по сопромату, касающихся определения напряжений в балке при её изгибе или кручении, проверке устойчивости сжатых стержней, а также при решении некоторых других задач требуется знать не только площадь, но и другие геометрические характеристики сечения (момент инерции площади сечения, момент сопротивления площади сечения, полярный момент инерции площади сечения). Во-первых, они требуются для решения конкретной задачи об определении напряжений в данной балке с заданными размерами поперечного сечения. Во-вторых, они нужны для выполнения сравнительного анализа разных типов сечений (например, выбора среди нескольких различных сечений с одинаковой площадью именно того сечения, которое будет лучше сопротивляться изгибу или кручению), для подбора оптимального сечения для балки, работающей в конкретно заданных условиях. Поскольку нахождение геометрических характеристик сечения требует определенных знаний и практических навыков, в любом учебнике или справочнике по сопромату выделен раздел, посвященный определению этих характеристик, а в любом задачнике по сопромату приведены задачи по нахождению момента инерции или момента сопротивления сечения.

Что такое момент инерции сечения

Обычно, когда речь идёт о геометрических характеристиках сечения, слово «площадь» опускают, чтобы не было нагромождения слов, и говорят не «момент инерции площади сечения», «момент сопротивления площади сечения», а просто «момент инерции сечения», «момент сопротивления сечения» или даже просто «момент инерции», «момент сопротивления». При этом различают осевой, полярный и центробежный момент инерции площади сечения.

Осевой момент инерции площади фигуры (сечения) — это интеграл произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси. Другое, менее распространенное его название – экваториальный момент инерции. Величина осевого момента инерции всегда положительна.

Полярный момент инерции площади фигуры (сечения) относительно данной точки (полюса) — это интеграл произведений элементарных площадок на квадраты их расстояний от полюса. Величина полярного момента инерции всегда положительна.

Центробежный момент инерции площади фигуры — это интеграл произведений элементарных площадок на их расстояния от координатных осей. В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным, а также равным нулю. При повороте осей вокруг начала координат на 90 градусов знак центробежного момента инерции меняется на обратный.

Задавая вопросы «в чем измеряется момент инерции», «какова единица измерения момента инерции», «как обозначается момент инерции» необходимо четко представлять, что именно имеется в виду: момент инерции сечения (о котором идёт речь в сопромате и, в частности, в настоящей статье) или же момент инерции тела (который упоминается в физике и в теории механизмов и машин). Размерность момента инерции сечения – это размерность длины в четвертой степени (например, см⁴, м⁴, мм⁴). Моменты инерции сечений стандартных профилей (швеллеров, уголков, тавров, двутавров) приведены в справочных таблицах в размерности «см⁴». При необходимости, данную в таблице величину можно представить в другой единице измерения. Обычно при решении задач возникает необходимость перевода этой величины в «мм⁴». Обозначается момент инерции сечения буквой I с нижним индексом, который указывает, относительно какой оси вычислена данная характеристика (например, I_x, I_y). Момент сопротивления сечения обозначается буквой W, также с нижним индексом, указывающим на ось, относительно которой дана эта величина (например, W_x, W_y). 

Что такое главные оси

Главные оси инерции – оси, относительно которых центробежный момент инерции равен нулю.

Главные центральные оси — главные оси, проходящие через центр тяжести сечения.

Как найти момент инерции сечения

При вычислении момента инерции сечения можно воспользоваться непосредственно определением момента инерции и вычислить эту характеристику сечения путём нахождения интеграла по площади. Так и поступают при нахождении момента инерции треугольника, круга, прямоугольника, кругового сектора и других простых фигур.

Обозначив характерные размеры сечения через параметры (т.е. буквами) и выполнив соответствующее интегрирование по площади, получают формулы для определения моментов инерции этих сечений. Ход решения показан, например, в учебнике по сопромату Г.С. Писаренко на примере вывода формул для определения момента инерции прямоугольника, треугольника, кругового сектора и эллипса. Такие формулы приведены во многих справочниках по сопромату (например, в книге Писаренко Г.С., Яковлев А.П. Матвеев В.В. Справочник по сопротивлению материалов. – К: Наукова думка, 1975, на страницах 24 — 77) для многих типов сечений (квадрат, полый квадрат, прямоугольник, полый прямоугольник, прямоугольник с круглым отверстием, прямоугольник с двумя отверстиями, прямоугольник с полукруглыми вырезами, повернутый прямоугольник, крестовина, корытное сечение, треугольник, трапеция, круг, кольцо, круговое незамкнутое тонкостенное кольцо, полукруг, четверть круга, круговой сектор, круговой сегмент, полукольцо, сектор кольца, круг с лыской, правильный шестиугольник, правильный многоугольник, круговое сечение с одной или с двумя шпоночными канавками, эллипс, полуэллипс, четверть эллипса, полый эллипс, параболический сегмент, параболический полусегмент, круговой треугольник, сечение железнодорожного рельса). Готовыми формулами из справочника пользоваться намного проще, чем выводить каждый раз нужную формулу самостоятельно путём интегрирования.

В этом же справочнике приведены и формулы для приближенного вычисления геометрических характеристик (F, I, W) сечений стандартных прокатных профилей: уголков (равнобокого и неравнобокого), швеллера, тавра, двутавра, однако на практике этими формулами пользуются весьма редко, т.к. все необходимые характеристики стандартных сечений уже вычислены и приведены в соответствующих нормативных документах (см. ГОСТ 8240-97 для швеллеров, ГОСТ 8509-93 для равнополочных уголков, ГОСТ 8510-86 для неравнополочных уголков, ГОСТ 26020-83 и ГОСТ 8239-89 для двутавров). Выдержки из перечисленных выше стандартов приведены во многих справочниках, учебниках и решебниках по сопромату.

Скачать примеры решения задач, касающиеся того, как найти момент инерции и момент сопротивления, можно здесь (бесплатно, без регистрации):

При вычислении моментов инерции сложных сечений их разбивают на отдельные простые части, моменты инерции которых известны.

Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.

Центробежный момент инерции относительно любой системы прямоугольных осей равен центробежному моменту инерции относительно системы центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях.

При повороте прямоугольных осей сумма осевых моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.

Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции.

Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки поперечного сечения.

Размерность моментов сопротивления – единица длины в кубе (например, см³, м³, мм³).

Практическое значение имеют моменты сопротивления относительно главных центральных осей, которые обычно называются просто моментами сопротивления. Полярным моментом сопротивления называется отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения.

Источники:

• Н.М. Беляев. Сопротивление материалов.
•  Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. Справочник по сопротивлению материалов.
• А.В. Александров, В.Д. Потапов, Б.П. Державин. Сопротивление материалов.
• reshusam.ucoz.ru — Примеры определения моментов инерции сечений.

Дополнительно на Геноне:

• Что такое сопромат

Моменты инерции тел

Инерционные свойства твердого тела характеризуются не только его массой , определяющей инерционность при поступательном движении, но и моментом инерции, определяющим инерционность вращательного движения тела.

Моментом инерции тела относительно оси называется сумма произведений массы каждой точки на квадрат расстояния от точки до оси

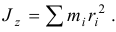
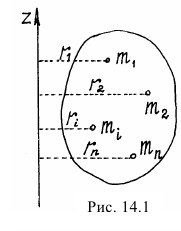
Заметим сразу, что момент инерции тела — это геометрическая характеристика тела, не зависящая от его движения (рис. 14.1).

Для однородных тел простой симметричной формы момент инерции можно найти в справочниках. А моменты инерции некоторых тел, которые чаще всего встречаются при исследовании движения материальных систем, даны на рис. 14.2.

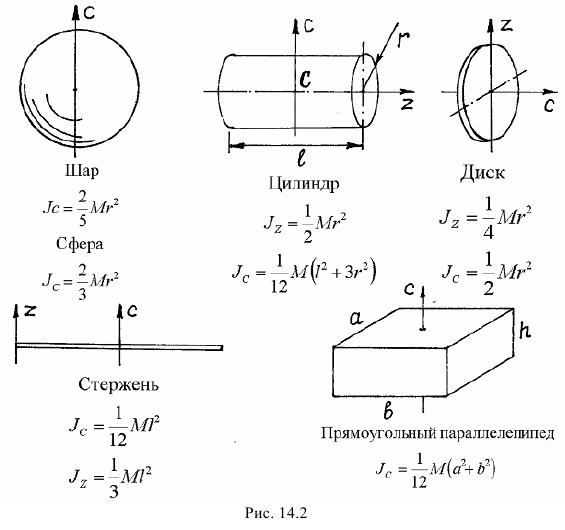
На рисунке даны моменты инерции тел относительно осей симметрии. Но нередко при исследовании движения реальных механизмов приходится определять моменты инерции относительно осей, не совпадающих с осями симметрии. Этому помогают следующие теоремы.

Теорема Гюйгенса-Штейнера о моментах инерции тела относительно параллельных осей

Найдем зависимость между моментами инерции тела относительно параллельных осей и (рис. 14.3). Ось , проходящая через центр масс тела, называется центральной осью. Расстояние между осями — .

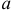
По определению (14.3)

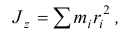
причем

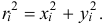
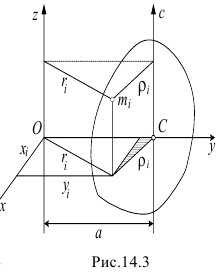
Но из заштрихованного прямоугольного треугольника (см. рис. 14.3) следует, что

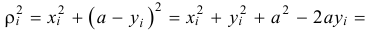
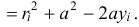
Значит

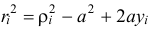
и момент инерции относительно оси

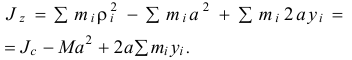
Но по формуле (14.2) сумма

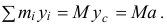
Поэтому

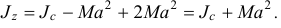
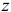
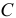
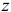
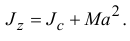
Следовательно, момент инерции тела относительно оси равен сумме момента инерции тела относительно центральной оси , параллельной оси , и произведения массы тела на квадрат расстояния между осями

Так, например, момент инерции стержня относительно оси

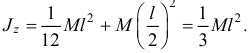
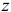
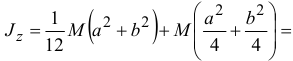
А момент инерции прямоугольного параллелепипеда относительно оси , проведенной по какому-нибудь вертикальному ребру

Момент инерции тела относительно произвольной оси

Найдем момент инерции тела относительно оси 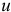, проходящей через некоторую точку (рис. 14.4).

По определению момент инерции

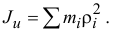
Поместим в точку начало координатных осей . Из прямоугольного треугольника следует

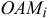
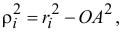
где

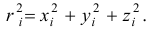
И так как радиус-вектор точки равен

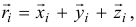
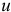
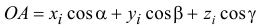
то, проектируя это равенство на ось , получим

Как известно из тригонометрии

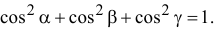
Поэтому

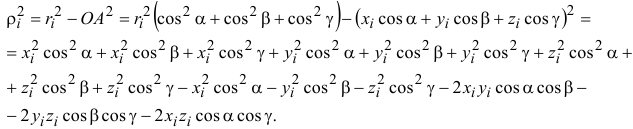
И, группируя подобные члены, содержащие косинусы одинаковых углов,

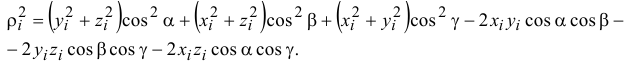
Но

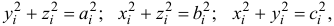
где

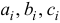
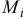
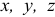
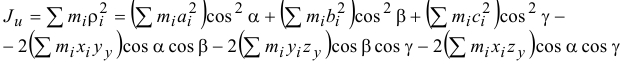
расстояние от точки до осей соответственно. Поэтому

или

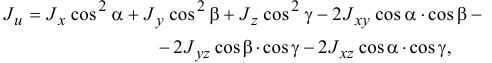
где 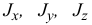— моменты инерции тела относительно осей координат; — центробежные моменты инерции относительно осей, отмеченных в индексах.

Если два центробежных момента инерции, оба содержащих в индексах названия какой-нибудь одной оси, равны нулю, то эта ось называется

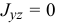
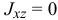
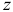
главной осью инерции. Например, если и , то ось — главная ось инерции.

Так как все моменты инерции зависят от того, где находится точка , от выбора начала координат, то обязательно надо указать, для какой точки определены эти моменты инерции. Если начало координат взято в центре масс , то все главные оси инерции называются главными центральными осями инерции.

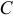
Если в данной точке координатные оси являются главными осями инерции (центробежные моменты инерции относительно их равны нулю), то формула (14.5) упрощается

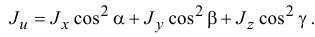
Иногда по некоторым признакам нетрудно найти главные оси инерции тела.

• Если у однородного тела имеется ось симметрии, то эта ось является главной центральной осью инерции.

Действительно. Направим координатную ось по оси симметрии. Тогда для каждой точки тела с координатами можно отыскать точку с координатами и поэтому центробежные моменты инерции и . Значит ось — главная ось инерции и центральная ось, так как центр масс, как известно, находится на оси симметрии. Причем, эта ось будет главной для любой точки, расположенной на оси симметрии.

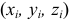
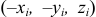
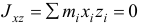
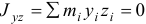
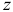
• Если у однородного тела имеется плоскость симметрии, то любая ось, перпендикулярная ей, будет главной осью инерции для всех точек этой плоскости.

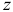
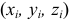
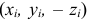
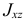
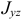
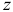
Направим ось перпендикулярно плоскости симметрии из любой ее точки , назначив там начало координат. Тогда для каждой точки тела с координатами можно найти симметричную ей точку с координатами . Поэтому центробежные моменты инерции и будут равны нулю. Значит ось — главная ось инерции.

Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:

Помощь по теоретической механике

Кстати возможно вам будут полезны эти страницы: