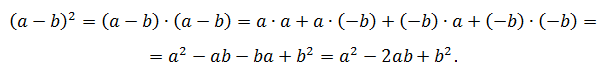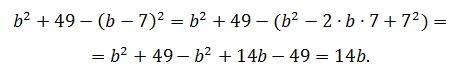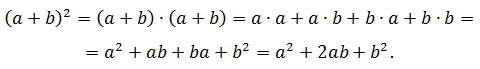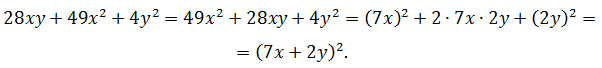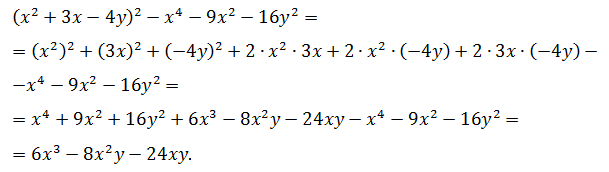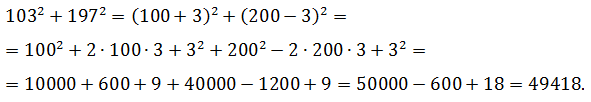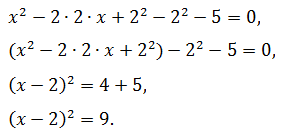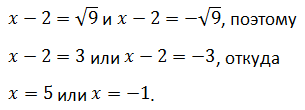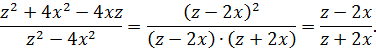Алгебра
7 класс
Урок № 27
Квадрат разности
Перечень вопросов, рассматриваемых в теме:
- Квадрат числа.
- Квадрат разности двух чисел.
- Квадрат двучлена.
Тезаурус:
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого и второго чисел, плюс квадрат второго числа.
Основная литература:
- Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
- Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
- Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
- Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения:
Для того чтобы выяснить, как выглядит формула квадрата разности, выполним возведение в степень. Возвести выражение во вторую степень, значит умножить его само на себя. Выполнив необходимые действия, получим формулу квадрата разности.
Сформулируем правило: квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого и второго чисел, плюс квадрат второго числа.
Эта формула также используется для упрощения вычислений.
Девяносто восемь можно представить в виде разности сто минус два. И далее использовать формулу квадрата разности.
Такое разложение делает возведение в квадрат двузначного числа доступным для устного вычисления.
Представьте многочлен в виде квадрата разности:
Теперь, используя формулу, можем записать квадрат разности:
Преобразуйте выражение в многочлен стандартного вида.
Первым действием всегда выполняется возведение в степень. Поэтому сначала разложим квадраты разностей по формуле. Затем выполняем умножение, внимательно определяя знак каждого произведения. Выполним приведение подобных слагаемых и получим многочлен стандартного вида.
Справа мы видим трехчлен, напоминающий нам разложение разности квадратов.
Рассмотрим слагаемые этого трёхчлена.
Но слева у нас сумма, а не разность, значит, одночлен 4у нужно взять со знаком минус. И одночлен b является квадратом одночлена a.
Разбор заданий тренировочного модуля.
1. Квадрат суммы и квадрат разности.
Решите уравнение:
Решение.
Выполним возведение в квадрат и умножение числа на разность:
- Формула квадрата суммы
- Формула квадрата разности
- Примеры
Формула квадрата суммы
Возведем в квадрат сумму (a+b):
$$ (a+b)^2 = (a+b)(a+b) = a(a+b)+b(a+b) = a^2+ab+ab+b^2 = a^2+2ab+b^2 $$
Мы получили формулу квадрата суммы двух выражений:
$$(a+b)^2 = a^2+2ab+b^2$$
Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого и второго выражения, плюс квадрат второго выражения.
Формула помогает нам избавиться от лишней работы: не перемножать скобки каждый раз и не приводить постоянно подобные, получая из четырёх слагаемых три.
Вместо a и b в формуле могут быть любые одночлены (и даже многочлены), которые нужно подставить. Поэтому в правиле и говорится о «выражениях», а не просто о «переменных». Например:
$$ (5x^2+7y)^2 = (5x^2 )^2+2cdot5x^2cdot7y+(7y)^2 = 25x^2+70x^2 y+49y^2 $$
Геометрическое объяснение
Рассмотрим квадрат со стороной (a+b). Он состоит из двух квадратов и двух прямоугольников. Для площади можем записать: $$ S = (a+b)^2 = a^2+b^2+2ab $$
Откуда $$ (a+b)^2 = a^2+2ab+b^2 $$
И формула квадрата суммы замечательно подтверждается геометрическими соображениями.
Формула квадрата разности
Теперь возведём в квадрат разность:
$$ (a-b)^2 = (a-b)(a-b) = a(a-b)-b(a-b) = a^2-ab-ab+b^2 = a^2-2ab+b^2 $$
Мы получили формулу квадрата разности двух выражений:
$$ (a-b)^2 = a^2-2ab+b^2$$
Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого и второго выражения, плюс квадрат второго выражения.
Геометрическое объяснение
Рассмотрим квадрат со стороной a, в один из углов которого вписан квадрат поменьше со стороной $b lt a$.
Для его площади можем записать: $$a^2 = (a-b)^2+b^2+2(a-b)b$$ Откуда $$(a-b)^2 = a^2-b^2-2(a-b)b = $$ $$a^2-b^2-2ab+2b^2 = a^2-2ab+b^2 $$
И формула квадрата разности также подтверждается геометрией.
Внимание!
Не забывайте о втором слагаемом в формулах квадрата двучленов!
Не путайте знаки «+» и «-» перед слагаемыми!
Неправильно: $(a+b)^2$ ≠ $a^2+b^2 или (a-b)^2 $≠$ a^2-b^2$
Правильно: $(a+b)^2 = a^2+$ 2ab $+b^2 и (a-b)^2 = a^2$ -2ab+$ b^2$
Примеры
Пример 1. Найдите квадрат суммы:
а) $(x+y)^2 = x^2+2xy+y^2$
б) $(3+t)^2 = 3^2+2cdot3t+t^2 = 9+6t+t^2$
в) $(3a+4b)^2 = (3a)^2+2cdot3acdot4b+(4b)^2 = 9a^2+24ab+16b^2$
г) $(4k^2 m+5n)^2 = (4k^2 m)^2+2cdot4k^2 mcdot5n+(5n)^2 = 16k^4 m^2+40k^2 mn+25n^2$
Пример 2. Найдите квадрат разности:
а) $(m-n)^2 = m^2-2mn+n^2$
б) $(x-5)^2 = x^2-2xcdot5+5^2 = x^2-10x+25$
в) $(7y-9z)^2 = (7y)^2-2cdot7ycdot9z+(9z)^2 = 49y^2-126yz+81z^2$
г) $(3km^2-8n^2 )^2 = (3km^2 )^2-2cdot3km^2cdot8n^2+(8n^2 )^2 = 9k^2 m^4-48km^2 n^2+64n^4$
Пример 3. Выполните действия:
а) $(10m-1)^2+20m = (10m)^2-2cdot10mcdot1+1+20m =$
$= 100m^2-20m+1+20m = 100m^2+1 $
б) $36k^2-(1-6k)^2 = 36k^2-(1-2cdot6k+(6k)^2 ) = 36k^2-1+12k-36k^2 = 12k-1 $
в) $4(x-1)-(2x+1)^2 = 4x-4-((2x)^2+2cdot2x+1) = 4x-4-4x^2-4x-1 = -4x^2-5$
г) $ frac{1}{3} (3y+4)^2-8y = frac{1}{3} ((3y)^2+2cdot3ycdot4+4^2 )-8y = frac{1}{3} (9y^2+24y+16)-8y =$
$=3y^2+8y+frac{16}{3}-8y=3y^2+5 frac{1}{3}$
Пример 4. Решите уравнение:
а) $(7-x)^2-(x+8)^2 = 45$
$49-14x+x^2-(x^2+16x+64) = 45 $
49-14x-16x-64 = 45
-30x = 45-49+64
-30x = 60
x = -2
б) $(2x-15)^2-x(4x+3) = 153$
$(2x)^2-2cdot2xcdot15+15^2-4x^2-12x = 153 $
-60x+225-12x = 153
-72x = 153-225
-72x = -72
x = 1
Чтобы разность возвести в квадрат, можно от суммы квадратов первого и второго выражений вычесть удвоенное их произведение:
.
Так как:
a−b2=a−b⋅a−b=a⋅a+a⋅−b−b⋅a−b⋅−b==a2−ab−ba+b2=a2−2ab+b2.
Пример:
представить квадрат в виде многочлена:
6z−92
.
Применим формулу квадрата разности:
.
Можно раскрыть квадрат как произведение одинаковых многочленов, но вычисления будут более трудоёмкими:
6z−92=6z−9⋅6z−9=6z⋅6z+6z⋅−9−9⋅6z−9⋅−9==36z2−54z−54z+81=36z2−108z+81.
Для успешного решения математических задач часто бывает необходимо уметь преобразовывать созданные выражения. Для этого применяют базовые знания, формулы сокращённого умножения, в том числе, квадрат суммы и квадрат разности.
Они помогают упрощать громоздкие записи, более рационально подходить к приведению дробей к одному знаменателю, решению уравнений и задач по геометрии, тригонометрии, математическому анализу, физике, химии, экономическим дисциплинам и многим другим наукам.
Поэтому среди многих разделов математики школьная алгебра занимает базовую приоритетную позицию, дающую основы вычислений для смежных предметов.
Формула квадрата разности
Для получения формулы применяют правило умножения многочлена на многочлен: нахождение суммы произведений каждого слагаемого одной скобки на каждое слагаемое второй скобки, учитывая, что квадрат отрицательного числа равен квадрату положительного:
Если запомнить правило, то необходимость постоянно прописывать эту цепочку равенств исчезает.
Квадрат разности двух выражений равен сумме квадратов каждого из выражений без их удвоенного произведения:
Примеры задач с решением
Задача №1
Требуется возвести в квадрат разность (8x – 3y).
Решение.
При использовании формулы получается:
Ответ: 64x2 – 48xy + 9y2.
Задача №2
Упростить выражение:
b2 + 49 – (b – 7)2
Решение.
Ответ: 14b.
Формула квадрата суммы и неполного квадрата суммы
Также легко, как и в предыдущем случае, выводится эта формула:
Квадрат суммы двух выражений равен сумме квадратов каждого из них плюс их удвоенное произведение:
Многие школьники, начинающие знакомиться с этим материалом, часто теряют двойку во втором слагаемом правой части, получая
Однако, в этом случае, возникает неполный квадрат суммы (или разности), который на множестве действительных чисел не раскладывается на множители.
Обе формулы применяются не только для раскрытия скобок, но и для разложения на множители, что в свою очередь упрощает приведение к одному знаменателю, сокращение дробей, решение уравнений высоких степеней.
Примеры задач с решением
Задача №3
Преобразовать трёхчлен в квадрат двучлена:
28xy + 49x2 + 4y2
Решение.
Поскольку квадраты находятся на втором и третьем местах, поменяем слагаемые между собой и подготовим выражение для применения формулы:
Ответ: (7x + 2y)2.
Возведение во вторую степень суммы трёх и более слагаемых выполняется аналогично: необходимо возвести в квадрат каждый элемент, записать все возможные удвоенные произведения и сложить полученные результаты.
Правила возведения в степени более высоких порядков возникают, когда выполняется умножение одинаковых многочленов несколько раз.
Возможность выполнять возведение в квадрат больших чисел, не используя калькулятор, является одним из преимуществ сокращённого умножения.
Задача №4
Выполнить раскрытие скобок и упростить:
(x2 + 3x – 4y)2 – x4 – 9x2 – 16y2
Решение.
Ответ: 6x3 – 8x2 – 24xy.
Задача №5
Вычислить:
1032 + 1972
Решение.
Для каждого слагаемого применяется одно из правил возведения в квадрат, затем производится суммирование результатов:
Решая квадратные уравнения, вместо поиска дискриминанта выделяют полный (точный) квадрат среди слагаемых, расположенных в левой части. В правую сторону собираются оставшиеся элементы.
Задача №6
Решить уравнение:
x2 – 4x – 5 = 0
Решение.
Первые два слагаемых левой части полностью удовлетворяют формуле квадрата суммы. Соотнеся их с соответствующими элементами правила, определяют, прибавляют и вычитают третье, затем сворачивают в точный квадрат, остальные члены алгебраической суммы переносят в правую сторону:
Решениями исходного уравнения являются корни уравнений
Ответ: x = 5 или x = -1.
Разность квадратов
Ещё одной формулой сокращённого умножения является разность квадратов. Она получается при умножении суммы двух выражений на их разность.
Читается справа налево.
Разность квадратов двух выражений равна произведению разности этих выражений на их сумму:
Применение последней записи справа налево есть раскрытие скобок более удобным способом, чем простое умножение многочленов.
Разложение на множители позволяет судить о наличии целых или натуральных корней квадратного уравнения.
Пример задачи с решением
Задача №7
Сократить дробь:
Решение.
В числителе записан квадрат разности, а в знаменателе – разность квадратов двух выражений. Применяя соответствующие формулы, получается искомый результат:
Ответ:
.
В большинстве случаев разницы, как сворачивать квадрат двучлена, не существует. Однако в данной ситуации, благодаря выражению в знаменателе, на первое место лучше поставить
, чтобы избежать игры с минусом при сокращении.
Онлайн калькуляторы помогают выполнять преобразования. Однако, поскольку формулы сокращённого умножения являются базовым материалом школьного курса, то лучше не просто получить результат, но и понять, каким образом к нему пришли.
При расчёте алгебраических многочленов для упрощения вычислений используются
формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.
Следует также помнить, что вместо
«a» и «b» в формулах могут стоять как числа, так и любые другие
алгебраические многочлены.
Разность квадратов
Запомните!
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
a2 − b2 = (a − b)(a + b)
Примеры:
- 152 − 22 = (15 − 2)(15 + 2) = 13 · 17 = 221
- 9a2 − 4b2с2 = (3a − 2bc)(3a + 2bc)
Квадрат суммы
Запомните!
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе
плюс квадрат второго числа.
(a + b)2 =
a2 + 2ab + b2
Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить
квадраты больших чисел, не используя калькулятор или умножение в столбик. Поясним на примере:
Найти 1122.
- Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.
112 = 100 + 1 - Запишем сумму чисел в скобки и поставим над скобками квадрат.
1122 = (100 + 12)2 - Воспользуемся формулой квадрата суммы:
1122 = (100 + 12)2 = 1002 +
2 · 100 · 12 + 122 = 10 000 + 2 400 + 144 = 12 544
Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.
- (8a + с)2 = 64a2 + 16ac + c2
Предостережение!
(a + b)2 не
равно (a2 + b2)
Квадрат разности
Запомните!
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе
плюс квадрат второго числа.
(a − b)2 =
a2 − 2ab + b2
Также стоит запомнить весьма полезное преобразование:
(a − b)2 = (b − a)2
Формула выше доказывается простым раскрытием скобок:
(a − b)2 =
a2 −2ab + b2 = b2 − 2ab + a2 = (b − a)2
Куб суммы
Запомните!
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа
на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
(a + b)3 =
a3 + 3a2b + 3ab2 + b3
Как запомнить куб суммы
Запомнить эту «страшную» на вид формулу довольно просто.
- Выучите, что в начале идёт «a3».
- Два многочлена посередине имеют коэффициенты
3. - Вспомним, что любое число в нулевой степени есть 1.
(a0 = 1, b0 = 1). Легко заметить, что в формуле
идёт понижение
степени «a» и увеличение степени
«b». В этом можно убедиться:
(a + b)3 =
a3b0 +
3a2b1 + 3a1b2 +
b3a0 = a3 + 3a2b + 3ab2 + b3
Предостережение!
(a + b)3
не равно a3 + b3
Куб разности
Запомните!
Куб разности двух чисел равен кубу первого числа минус утроенное
произведение квадрата первого числа на второе
плюс утроенное произведение первого числа на квадрат второго минус куб второго.
(a − b)3 =
a3 − 3a2b + 3ab2 − b3
Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и
«−».
Перед первым членом «a3 »
стоит «+» (по правилам математики мы его не пишем).
Значит, перед следующим членом будет
стоять «−», затем опять «+» и т.д.
(a − b)3 =
+ a3 −
3a2b
+ 3ab2 −
b3
=
a3 − 3a2b + 3ab2 − b3
Сумма кубов
Не путать с кубом суммы!
Запомните!
Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
a3 + b3 =
(a + b)(a2 − ab + b2)
Сумма кубов — это произведение двух скобок.
- Первая скобка — сумма двух чисел.
- Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
(a2− ab + b2)
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.
Разность кубов
Не путать с кубом разности!
Запомните!
Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
a3 − b3 =
(a − b)(a2 + ab + b2)
Будьте внимательны при записи знаков.
Применение формул сокращенного умножения
Следует помнить, что все формулы, приведённые выше, используется также и справа налево.
Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.
Примеры:
- a2 + 2a + 1 = (a + 1)2
- (aс − 4b)(ac + 4b) = a2c2 − 16b2
Таблицу со всеми формулами сокращённого умножения вы можете скачать в разделе
«Шпаргалки».
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
15 ноября 2015 в 10:23
Кристина Костенко
Профиль
Благодарили: 0
Сообщений: 1
Кристина Костенко
Профиль
Благодарили: 0
Сообщений: 1
(x+y+z)3=
0
Спасибо
Ответить
12 июня 2016 в 1:59
Ответ для Кристина Костенко
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Перемножить тупо лень?
0
Спасибо
Ответить
6 сентября 2015 в 19:02
Артур Хорішко
Профиль
Благодарили: 0
Сообщений: 1
Артур Хорішко
Профиль
Благодарили: 0
Сообщений: 1
(3ч-4)в квадрате=0,25
0
Спасибо
Ответить
2 сентября 2016 в 15:41
Ответ для Артур Хорішко
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
полагаю, что имеется ввиду пример:
(3 · x ?4)2=0,25
Применим формулу «разность квадратов» и решим квадратное уравнение, найдя корни.
9 · x2 ? 2 · 3 · 4 · x + 16 = 0,25
9x2-24x+15,75=0
D=9
x1=1,5
x2=1
Произведем проверку подставив в исходное выражение каждый из получившихся корней:
1) (3 · 1,5 ?4)2=0,25
0,52=0,25
2) (3 ·
?4)2=0,25
-0,52=0,25
0
Спасибо
Ответить