Как найти квадратичную форму в базисе - Сайт, где вы сможете решить свои вопросы

Е.Б. Павельева, В.Я. Томашпольский. Линейная алгебра.

2.Пусть Α – кососимметрический оператор в евклидовом

пространстве, т.е. Α = −A. Доказать, что для любого вектора x имеет место равенство (Ax, x)= 0 .

3. Найти все симметрические ортогональные матрицы размера 2 ×2 .
Указание. Общий вид симметрической матрицы размера 2 ×2 :	a	b
A =	.

	b	c

Из ортогональности получаем A2 = E . Далее нужно составить и исследовать систему уравнений с переменными a , b и c .

4.Доказать, что если λ является собственным значением ортогонального оператора, то λ =1.

5.Привести матрицу линейного самосопряженного оператора к

диагональному	виду ортогональным преобразованием. Указать матрицу
	0	2	−3
	2	3	−6
перехода. A =	.
	−3	−6	8

5.1. Определение квадратичной формы, матрица квадратичной формы, преобразование матрицы квадратичной формы при переходе к новому базису

Определение. Квадратичной формой называется однородный многочлен второй степени от n переменных с действительными

n
коэффициентами f (x1,x2 ,…, xn ) = ∑aij xi x j , где aij = a ji	i, j =1,2,…,n .
i, j=1

Пример. f (x , x	2	) =8x2	−3x x	2
1	1	1
Замечание. Учитывая, что
форму можно записать в виде	f (x1,x

+ 6x22 – квадратичная форма ( n = 2). aij = a ji i, j =1,2,…,n , квадратичную

n
2 ,…, xn ) = ∑aii xi2 + 2 ∑aij xi x j .
i=1	1≤i< j≤n

				a	…	a
				11		1n
Определение.	Симметрическая	матрица	A = …	…	…	,
					…
				an1	ann
составленная	из	коэффициентов квадратичной	формы,	называется
матрицей квадратичной формы.

Е.Б. Павельева, В.Я. Томашпольский. Линейная алгебра.

Утверждение. Квадратичную

форму

можно

записать

в матричном

виде:

f (x ,x

,…, x

) =X T A X ,

где

X =

–

столбец

переменных,

–

…

матрица квадратичной формы.

Задача 1.

Записать

квадратичную

форму

матричном

виде:

f (x ,x

, x ) = x2 − 2x2

+ 4x2

+ 6x x

−8x

x .

Решение. Учитывая,

что

–

это

коэффициенты

при

i =1,2,3 ,

aij + a ji

= 2aij

= 2a ji

–

коэффициенты

при

xi x j ,

1 ≤i < j ≤3,

получим

матрицу

квадратичной

формы

− 2

− 4

A =

− 4

f (x ,x

, x ) =X T

A X =

(x x

)

3 − 2

− 4

Задача 2.

Зная

матрицу

квадратичной

формы

A =

−1 ,

−1

записать квадратичную форму в виде многочлена.

Решение. f (x ,x

, x ) =3x2

+ 4x2 + 5x2

+ 2x x

+ 4x x

− 2x

x .

Замечание. Пусть L – n -мерное линейное пространство.

Квадратичную форму можно трактовать как отображение

f : L → R ,

сопоставляющее каждому элементу

x L

с координатами (x1, x2 ,…, xn )

некотором базисе

действительное число

∑aij xi x j :

f ( x) =

∑aij xi x j .

i, j=1

Тогда матрица коэффициентов квадратичной формы называется матрицей

квадратичной формы в базисе e и обозначается Ae .
Утверждение. При переходе от	базиса e	к базису	f матрица
квадратичной формы меняется по закону
	A	f	=T T	A T	,
		e→ f	e	e→ f
где Te→ f	– матрица перехода от базиса	e к базису	f .
Действительно, пусть X −столбец	координат вектора x L в базисе e ,	Y −
столбец	координат вектора x L в базисе	f .	Координаты вектора	x в
базисах	e и f связаны между собой соотношением X =Te→ f	Y . Запишем

квадратичную форму в матричном виде:

Е.Б. Павельева, В.Я. Томашпольский. Линейная алгебра.

f ( x) =X T Ae X =(Te→ f Y )T Ae (Te→ f Y ) =Y T (TeT→ f Ae Te→ f ) Y =Y T Af Y .

результате

получим

квадратичную

форму

матрицей

=T T

A T

e→ f

Замечание. Изменение базиса в линейном пространстве L приводит к

линейной замене переменных

X =Te→ f

Y в квадратичной форме.

Задача 1.

Найти

квадратичную

форму,

полученную

из

f ( x) = f (x , x

) = x2

− 4x x

+ 5x2

невырожденным

преобразованием

переменных:

x = 2 y

−3y

2 .

способ.

x2 = y1 + y2

Сделав замену

переменных

квадратичной

форме,

получим:

f ( x) = f (x , x

) =

(2 y −3y

)2 − 4(2 y −3y

)(y + y

)+ 5(y + y

= y2

+ 2 y y

+ 26 y2 .

− 2

способ.

–

матрица

квадратичной

формы

некотором

− 2

базисе e . Запишем невырожденное преобразование переменных в матричной

форме:	x		2	−3	y		. Матрицу	2	−3	можем трактовать, как
1		=		1		U =
								1
	x2		1	1	y2			1
матрицу перехода от старого базиса к новому.	Тогда A		=U T A		1	1
f	e	U =		.
											26
												1

Зная матрицу квадратичной формы, запишем квадратичную форму в виде

многочлена	f ( x) = f ( y , y	2	) = y2	+ 2 y y	2	+ 26 y	2 .
			Задача 2.			1				1	1		2
							Написать		квадратичную				форму
f ( x) = f (x , x	2	) = x2	+ 4x x	2	+ 2x2 в новом базисе f	1	= (1, 3) ,	f	2		= (−1, 2) .
					1				1		1			2
Решение.	A				1	2
=			– матрица квадратичной формы в исходном базисе e .
					e				2	2

T				1	−1	– матрица перехода от базиса		e к базису	f . При переходе
		=
e→ f		3		2
				e						f
от базиса	к базису		матрица квадратичной формы меняется по закону
A		=T T		A		T			1 3	1 2 1 −1	31 9			Квадратичная
f				=									=		.
		e→ f		e		e→ f		−1 2				3 2
													2 2		9 1
форма в новом базисе имеет вид	f ( x) = f ( y , y	2	) =31y2 +18y y	2	+y2 .
																1	1	1	2

Е.Б. Павельева, В.Я. Томашпольский. Линейная алгебра.

5.2. Приведение квадратичной формы к каноническому виду. Закон инерции квадратичных форм

			n
Определение.	Квадратичная	форма	f (x1,x2 ,…, xn ) = ∑aii xi2 ,
			i=1

содержащая только квадраты переменных, называется квадратичной формой канонического вида. Коэффициенты aii , i =1,2,…,n , квадратичной

формы канонического вида называются каноническими коэффициентами. Замечание. Матрица квадратичной формы канонического вида

является диагональной.

Теорема. Для любой квадратичной формы существует базис, в котором она имеет канонический вид.

Определение. Базис, в котором квадратичная форма имеет канонический вид, называется каноническим базисом.

Рассмотрим методы приведения квадратичной формы к каноническому виду: метод Лагранжа и метод ортогональных преобразований.

I. Метод Лагранжа.

Метод Лагранжа приведения квадратичной формы к каноническому виду состоит в последовательном выделении полных квадратов переменных. Коротко опишем этот метод. Если a11 ≠ 0 , то вынесем a11 за скобку, в скобке

соберем все слагаемые, содержащие x1 , и дополним полученное выражение до полного квадрата. В результате получим

f (x1, x2 ,…, xn ) = a11				n					2	+ f1(x2 ,…, xn ) ,		где			f1(x2 ,…,xn ) –
x1	+ ∑bj x j
																	j=2									x1 .	Выполнив линейную
квадратичная форма, не содержащая переменную
													n									f (x1, x2 ,…, xn ) = a11 y12 + f1(x2 ,…, xn ) .
замену			y1 = x1 + ∑b j x j ,	получим	С
													j=2
квадратичной формой	f1(x2 ,…,xn ) поступим аналогично. Проиллюстрируем
этот метод на конкретном примере.
Задача.								Привести						квадратичную			форму
f ( x) = f (x	,x	2	, x ) = x2	+ x2 −3x x	2	+ 4x x	3	+ 2x	x	к		каноническому виду
						1						3		1		3			1	1				2	3
методом Лагранжа.		a11 =1 ≠0,															содержащие x1 ,
Решение.		Поскольку			соберем	слагаемые,	и
дополним полученное выражение до полного квадрата:
x2 −3x x	2	+ 4x x = x2 + 2x (−		3	x	2	+ 2x ) + (−	3	x	2	+ 2x )2	− (−	3	x	2	+ 2x )2 =
2
1	1					1		3	1			1				3		2			3	2	3
= (x −		3	x	2	+ 2x	3	)2 − (	9 x2	− 6x	2	x + 4x	2 ) = y2	−	9 x2 + 6x	2	x − 4x2 ,
2
1											4	2			3		3	1			4	2	3		3
где y = x		−	3	x	2	+ 2x .

1				1		2				3

Е.Б. Павельева, В.Я. Томашпольский. Линейная алгебра.

Итак,	f ( x) = y2	−	9	x	2		+ 6x			x		− 4x2	+ x2 + 2x			x		= y2	−	9	x2 −3x	2	+8x		x .
4	2		2			2	3				2
													1									3		3			3						1		4		2		3					3
Поскольку коэффициент при x22	не равен нулю,	вынесем этот коэффициент
за скобку, в скобке соберем все слагаемые, содержащие		x2 ,	и дополним
полученное выражение до полного квадрата:
−	9	x2	+8x	2	x = −9	(x2	− 32 x	2	x ) = −	9 (x2 − 2x	2		16 x + (16 x )2 − (16 x )2 ) =
4
		2								3		4			2			9						3		4		2				9		3		9		3			9	3
= −9	(x	2	− 16 x )2	+	64 x	2	=−		9			y2 +	64 x2	,	где y	2	= x	2	−	16 x .
	4						9			3			9	3				4			2	9	3									9	3
Итак,	f ( x) = y2	−	9 y2	+ 64 x2		−3x	2 = y	2	− 9	y2		+	37 x2	= y2 −	9	y2	+	37	y2 ,	где
													1		4		2			9				3			3		1	4	2				9	3		1	4	2				9	3
y	= x		−	3		x	2	+ 2x		,		y	2	= x	2		− 16 x ,	y	3	= x .			Найдем	матрицу		перехода	от

1			1		2					3											9	3			3														x1,	x2 ,	x3
старого базиса к новому. Для этого выразим переменные	через
																		3		y2 +		2			y3																1		3		2
																2		3																	2		3
										x1 = y1 +
y1, y2	, y3 :		x2 = y2 + 169	y3								. Итак,		X =UY , где U =	0	1	169		– матрица
										x = y	3																														0	0	1
												3														e к новому базису		f .
перехода от старого базиса			Учитывая,	что матрица

перехода состоит из координат векторов нового базиса в старом, записанных

по столбцам, получим	координаты	векторов	нового	базиса	f1 = (1,0,0) ,
f2 = (	3	,1,0), f3 = (	2	,	169 ,1).
2	3	f ( x) = y2		y2			y2 .
	Окончательно		получим:	− 9	+	37	Указанный
							1	4	2	9	3

канонический вид квадратичная форма имеет в каноническом базисе f1 = e1 , f2 = 32 e1 + e2 , f3 = 32 e1 + 169 e2 + e3 .

Замечание 1. Если коэффициент a11 = 0 , т.е. нет слагаемого x12 , но

отличен от нуля коэффициент при квадрате какой-либо другой переменной, то надо начинать выделение полного квадрата с этой переменной.

Замечание 2. Если все коэффициенты при квадратах переменных равны нулю, то сначала надо выполнить промежуточную замену переменных. Пусть, например, a12 ≠ 0 , т.е. присутствует слагаемое 2a12 x1x2 .

Сделаем линейную замену переменных:	x1	′	′	,	′	′	,	′	,
= x1	+ x2	x2 = x1	− x2	xi = xi
i =3,4,…,n , тогда	′	′	′	′			′ 2	′	2	). После
2a12 x1x2 = 2a12 (x1	+ x2 )(x1	− x2 )= 2a12	((x1 ) − (x2 )

замены переменных получим квадратичную форму, у которой коэффициент

при (x1′)2	отличен от нуля.
II. Метод ортогонального преобразования.
e		Пусть E –		n -мерное евклидово пространство. При переходе от базиса
	к базису		f		матрица	квадратичной формы меняется по закону
A	f	=T T	A T		,	где T	– матрица перехода от базиса e к базису f
	e→ f	e	e→ f		e→ f

(гл. V, п. 5.1). Поскольку матрица квадратичной формы является симметрической, она может быть приведена ортогональным

Е.Б. Павельева, В.Я. Томашпольский. Линейная алгебра.

преобразованием к диагональному виду, т.е. для матрицы Ae существует такая ортогональная матрица U (U −1 =U T ), что U T Ae U = Λ. Здесь Λ –

диагональная матрица, диагональными элементами которой являются собственные значения матрицы Ae , повторяющиеся столько раз, какова их

кратность. При этом матрица U является матрицей перехода из старого ортонормированного базиса к новому ортонормированному базису,

состоящему из собственных векторов матрицы Ae

(гл. IV, п. 4.3).

0 …

λ2 …

Квадратичная

форма с

матрицей

Af = Λ =

имеет

…

… … …

0 …

λn

канонический вид:

f ( x) = λ y2

+… + λ

y2 .

Ортонормированный базис f ,

1 1

состоящий из собственных векторов матрицы Ae ,

является каноническим

базисом квадратичной формы.

Задача 1.

Найти

ортогональное

преобразование,

приводящее

квадратичную

форму

f ( x) = f (x , x

) = x

+ 4x x

+ x2

к каноническому

виду. Написать канонический вид.

– матрица

квадратичной формы

в исходном

Решение. а) A =

ортонормированном базисе e . Найдем собственные значения матрицы A. Для этого решим характеристическое уравнение

A − λE

1 − λ

= (1 − λ)2 − 4 = 0 .

λ = −1,

–

корни

2 1 − λ

−1

характеристического

уравнения.

–

матрица

квадратичной

Λ =

базисе f

формы в новом

(ортонормированном

базисе из

собственных

векторов матрицы A ). В базисе f

квадратичная форма имеет канонический

вид

f ( x) = f ( y

, y

) = −y2

+ 3y2 .

б) Чтобы построить базис из собственных векторов, надо для каждого собственного значения λ решить СЛАУ (A − λE) X =O . Координаты собственного вектора, отвечающего собственному значению λ1 = −1, найдем

из

СЛАУ

Общее

решение системы

имеет вид:

α . Вектор

= (1,−1)

является собственным вектором

=α

−α

A ,

−1

значению λ1 = −1.

матрицы

отвечающим

собственному

Координаты

собственного вектора, отвечающего собственному значению λ2 =3 , найдем

Е.Б. Павельева, В.Я. Томашпольский. Линейная алгебра.

из

СЛАУ

− 2 2

. Общее

решение системы

имеет

вид:

2 − 2

α .

Вектор

= (1,1)

является

собственным

вектором

матрицы

отвечающим

собственному

значению

λ2 =3 .

Нормируя

собственные векторы,

получим

ортонормированный базис, состоящий из

собственных векторов матрицы A :

f1 = (

, −

f2 = (

), в котором

квадратичная

форма

имеет

указанный

канонический

вид.

Матрица

является ортогональной матрицей перехода от базиса

e к

U =

−

базису

f ,

причем

Λ =U T A U .

Изменение базиса привело

линейной

замене переменных

X =U Y в квадратичной форме: x

= −

y .

Задача 2.

Найти

ортогональное

преобразование,

приводящее

квадратичную форму к каноническому виду. Написать канонический вид.

	f ( x) = f ( x	1	, x	2	, x	3	) =11x 2	+ 5 x 2	+ 2 x 2	+ 16 x x	2	+ 4 x x	3	− 20 x	2	x	3	.
										1			2	3		1		1
								11	8		2
									8		5	−10		– матрица квадратичной формы в исходном
Решение. а) A =
									2		−10	2

ортонормированном базисе	e .	Найдем собственные значения матрицы A.
Для	этого					решим			характеристическое				уравнение
	A − λE			11 − λ				8		2

		=		8			5 − λ	−10	= 0 .	λ1 =18 ,		λ2 =9 ,	λ3 = −9		– корни

					2				−10	2 − λ
																	18	0	0
характеристического уравнения.		0	9	0
Λ =		– матрица квадратичной
																		0	0 −9
формы в новом базисе	f
(в ортонормированном базисе из собственных
векторов матрицы A ). В базисе	f квадратичная форма имеет канонический

вид f ( x) = f ( y1, y2 , y3 ) =18y12 + 9 y22 −9 y32 .

Е.Б. Павельева, В.Я. Томашпольский. Линейная алгебра.

− 7

−13

−10

. Общее решение системы имеет вид:

из СЛАУ:

−10 −16

− 2α

− 2

α .

Вектор

a1 = (− 2,−2,1) является собственным

X =

− 2α =α

вектором матрицы

отвечающим

собственному

значению

λ1 =18 .

Координаты собственного

вектора, отвечающего

собственному значению

λ2 =9 , найдем из

СЛАУ

− 4

−10

. Общее

решение

2 −10

− 7

	− 2α		− 2
системы имеет вид: X =	α	=α	1	α . Вектор a2 = (− 2,1,−2) является
			− 2
	− 2α

собственным вектором матрицы A,	отвечающим собственному значению
λ2 =9 .		Аналогично найдем координаты собственного вектора, отвечающего
собственному				значению		λ		= −9,	a	3	= (− 1 , 1, 1).	Нормируя собственные
																						3	2
векторы,	получим	ортонормированный базис, состоящий из собственных
векторов матрицы	A:	f1 = (−	2	,−	2	, 13 ),	f2 = (−	2	, 13 ,−	2	), f3 = (− 13 ,	2	,	2	). В
3	3	3	3	3	3
этом базисе			квадратичная		форма	имеет указанный	канонический	вид.
												−	2				−	2		− 1
											3				3
																		3
Матрица U =		−	2				1				2		является ортогональной матрицей перехода от
3						3
																3
											1						−	2			2
																	3		3
											3
базиса				e	к базису		f ,	причем Λ =U T A U .	Изменение базиса привело к
линейной		замене	переменных	X =U Y			в	квадратичной форме:
x1 = −	2		y1 −	2	y2 − 13 y3
3	3
				2	y1 + 13 y2 +	2
x2	= −	y3 .
3	3
x	= 1	y	−	2	y	2	+		2	y	3
	3
	3	3	1	3

Замечание. Ни канонический базис, ни канонический вид квадратичной формы не определены однозначно. Возникает вопрос: что общего у различных канонических видов одной и той же квадратичной формы?

Определение. Ранг матрицы квадратичной формы в произвольном базисе называется рангом квадратичной формы.

Теорема. Ранг квадратичной формы не меняется при невырожденных линейных преобразованиях и равен 1) числу отличных от нуля канонических коэффициентов;

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому п, а коэффициенты квадратичной формы не всегда являются вещественными числами.

Понятие квадратичной формы

Квадратичной формой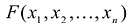

Пример:

Сумма 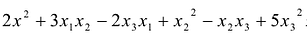является квадратичной формой от трех неизвестных .

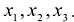Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приводятся подобные в квадратичной форме, затем коэффициенты при 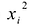обозначаются через 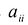а коэффициенты при 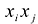через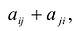 причем 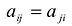„ Член 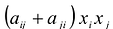записывается в виде 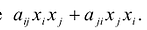После этих преобразований квадратичную форму можно записать в виде: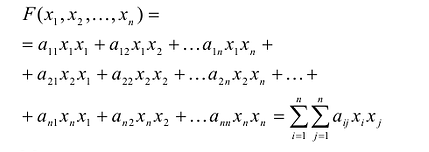

Матрица: 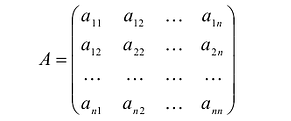называется матрицей квадратичной формы F. Так как 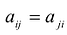то А – симметричная матрица.

С учетом правила умножения матриц можно вывести матричную форму записи квадратичной формы.

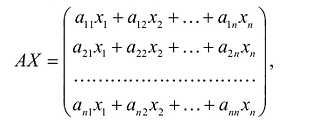
где А – матрица квадратичной формы, X – матрица-столбец неизвестных:

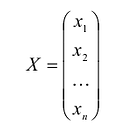
Приведенные выкладки показывают, в частности, что если А -симметрическая матрица, то выражение 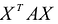является квадратичной формой от неизвестных 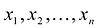,т.е. квадратичная форма является

результатом скалярного произведения матриц X и АХ. Матричная форма записи квадратичной формы имеет вид 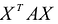. Если 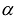– произвольный n— мерный вектор, то после подстановки в квадратичную форму 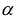вместо X получится число 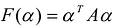, которое называется значением квадратичной формы F(X) на векторе .

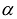Канонический базис квадратичной формы

Принято считать, что квадратичная форма F(X) имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е. 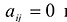при 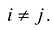. При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами 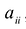,т.е.:

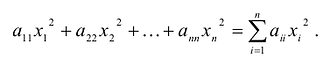
В этом случае матрица квадратичной формы имеет диагональный вид:

Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.

Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.

Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.

Пусть дана квадратичная форма 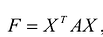, Поскольку А -симметрическая матрица, для нее существует диагонализирующая ортогональная матрица S, такая что:

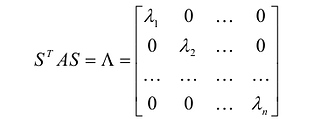
где 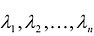-собственные значения матрицы А.

Применим к квадратичной форме линейное преобразование 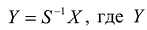– матрица-столбец новых переменных 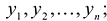– матрица, обратная к S.

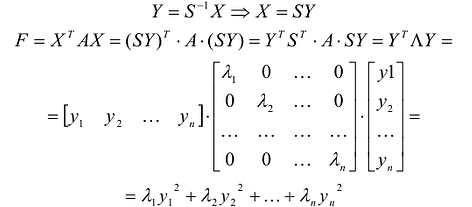
Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.

Наиболее удобным для исследования является канонический вид, в котором коэффициенты при новых переменных равны +1 или -1, т.е. квадратичная форма имеет вид:

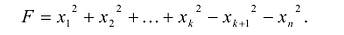
Такую запись называют нормальным видом квадратичной формы. В нем общее число квадратов равно рангу r квадратичной формы.

Квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями. При этом справедлива следующая теорема.

Теорема, Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная вещественная квадратичная форма вещественным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.

Эту теорему называют законом инерции квадратичных форм.

Базис пространства R” называется каноническим базисом квадратичной формы 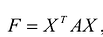, если в этом базисе квадратичная форма имеет канонический вид, т.е. 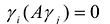при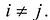

Если канонический базис F(X), то выражение: 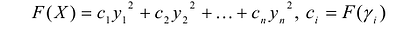называется каноническим видом F(X) в базисе где – новый набор неизвестных.

Теорема. Если 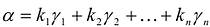– разложение вектора а по каноническому базису квадратичной формы 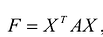то значение F(X) на векторе а вычисляется по формуле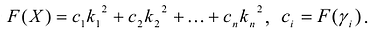

Доказательство:

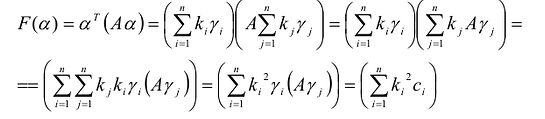
Эта теорема утверждает, что если известны канонический базис квадратичной формы F(X) и ее канонический вид 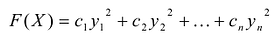в этом базисе, то для вычисления значения F(a) квадратичной формы F(X) на векторе а достаточно:

разложить вектор а по каноническому базису :
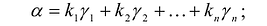
коэффициенты разложения 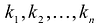подставить вместо неизвестных в канонический вид квадратичной формы: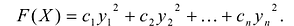

Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется приведением квадратичной формы к сумме квадратов.

Наиболее часто используются: канонический базис из собственных векторов матрицы А и канонический базис Якоби.

Канонический базис из собственных векторов матрицы квадратичной формы

Теорема. Ортонормированный базис пространства Rсостоящий из собственных векторов симметрической матрицы 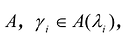, является каноническим базисом квадратичной формы 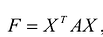, а выражение 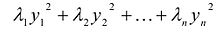– ее каноническим видом в базисе ,

Доказательство:

Канонический базис Якоби квадратичной формы 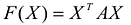. Будем говорить, что матрица 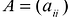удовлетворяет условию Якоби, если определители:

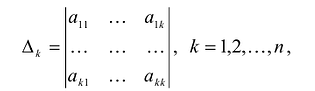
называемые угловыми минорами матрицы А, не равны нулю. Очевидно, что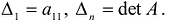

Обозначим через 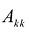матрицу:

Вычислим определитель этой матрицы, разлагая ее по последнему столбцу, затем также по последнему столбцу разложим полученный определитель и т.д. 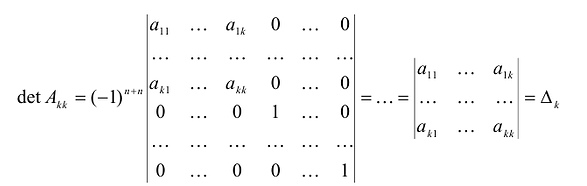Из условия следует, что и, значит, каждая система уравнений 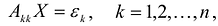, где 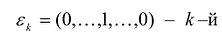вектор диагональной системы, имеет единственное решение 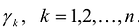. Система векторов называется системой векторов Якоби матрицы А, которая удовлетворяет условию Якоби.

Теорема. матрица А квадратичной формы 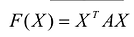удовлетворяет условию Якоби, система векторов Якоби матрицы А является каноническим базисом квадратичной формы 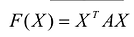, а выражение:

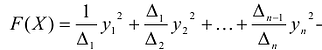ее каноническим видом в базисе .

Положительно и отрицательно определенные квадратичные формы

Квадратичная форма F{X) называется положительно определенной, если значение F(X) на каждом ненулевом значении а больше нуля, т.е.:

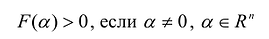
Если же F(a) < 0 на каждом , то квадратичная форма называется отрицательно определенной.

Теорема. Дана квадратичная форма 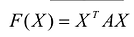, ее канонический базис, л выражение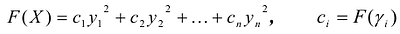

канонический вид 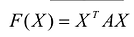в базисе . Тогда справедливы следующие утверждения:

Квадратичная форма F(X) положительно определена тогда и только тогда, когда .
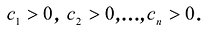Квадратичная форма F{X) отрицательно определена тогда и только тогда, когда

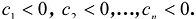
Доказательство:

Необходимость. Дано, что F(X) – положительно определенная форма. Так как 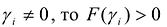и поэтому .

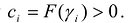Достаточность. Дано, что в каноническом виде все коэффициенты 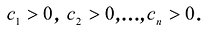Нужно доказать, что F(X) положительно определена. Рассмотрим произвольный ненулевой вектор а и разложим его по базису :

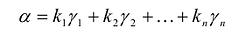
Так как 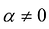, то в разложении 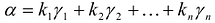не все коэффициенты равны нулю. Следовательно 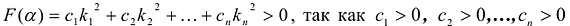и среди чисел 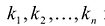хотя бы одно отлично от нуля.

Аналогично доказывается и второе утверждение.

Эта теорема дает два наиболее употребляемых критерия положительной и отрицательной определенности квадратичной формы.

Теорема. Дана квадратичная форма 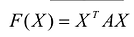. Тогда справедливы следующие утверждения:

Квадратичная форма F(X) положительно определена тогда и только тогда, когда все собственные значения матрицы А положительны.
Квадратичная форма F(X) отрицательно определена тогда и только тогда, когда все собственные значения матрицы А отрицательны.

Заказать решение задач по высшей математике

Доказательство:

Докажем первое утверждение. Рассмотрим ортонормированный базис пространства R”, состоящий из собственных векторов симметрической матрицы А, и пусть 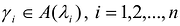. Тогда канонический базис квадратичной формы F(X), а выражение 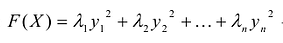– ее канонический вид в базисе . Теперь первое утверждение этой теоремы вытекает из первого предложения предыдущей теоремы.

Второе предложение доказывается аналогично.

Лемма. Если какой-нибудь угловой минор 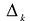матрицы А равен нулю у то найдется такой ненулевой вектор 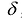, что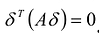

Теорема (Критерий Сильвестра). Справедливы следующие утверждения:

Квадратичная форма 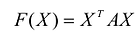положительно определена тогда и только тогда, когда главные миноры матрицы А положительны.
Квадратичная форма 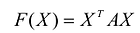отрицательно определена тогда и только тогда, когда главные миноры матрицы А четного порядка положительны, а главные миноры матрицы А нечетного порядка отрицательны.

Доказательство: Докажем первое утверждение.

Необходимость. Дано, что F(X) положительно определена. Покажем, что все угловые миноры матрицы А отличны от нуля. Допустим обратное, и пусть 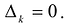. Тогда согласно Лемме найдется такой ненулевой вектор 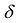, что 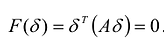. Однако это противоречит положительной определенности квадратичной формы.

Итак, матрица А удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби , которая является каноническим базисом F(X), причем выражение 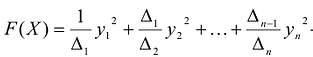– ее канонический вид в базисе . Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует,

что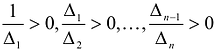, и значит, что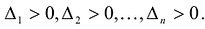

Достаточность. Если 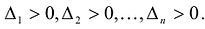, то угловые миноры матрицы А отличны от нуля, и можно построить канонический базис квадратичной формы F(X), в котором 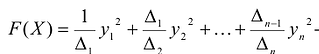– канонический вид квадратичной формы F(X). Поскольку 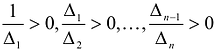, то F(X) положительно определена.

Аналогично доказывается второе утверждение теоремы.

Применение квадратичных форм к исследованию кривых второго прядка

В общем случае кривая второго порядка в базисе описывается уравнением 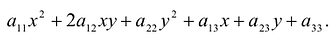. Ее первые три слагаемые образуют квадратичную форму 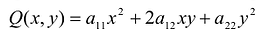с матрицей:

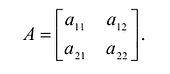
Задача о приведении кривой 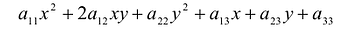, к каноническому виду сводится к задаче о приведении к каноническому виду квадратичной формы Q (х,у) этой кривой.

Пусть 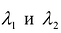– собственные значения матрицы 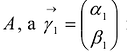и 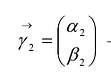ортонормированные собственные векторы матрицы А, соответствующие собственным значениям .

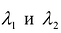Ортонормированные векторы 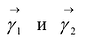называются главными направлениями этой кривой.

Пусть 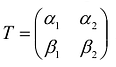является матрицей перехода от ортонормированного базиса к ортонормированному базису 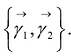Тогда ортогональное преобразование: 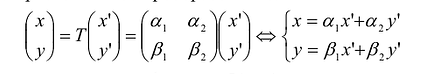приводит квадратичную форму Q (х,у) к каноническому виду 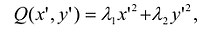, а уравнение кривой – к виду 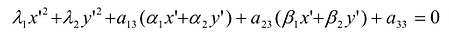в прямоугольной декартовой системе координат 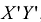, оси которой направлены вдоль векторов, а начало совпадает с точкой О системы координат XY.

Выделив в этом уравнении полные квадраты, получим 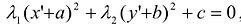, где а,Ь,с – некоторые числа. Осуществив параллельный перенос системы координат 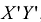в новое начало 0 = (-а—Ь), получим канонический вид уравнения

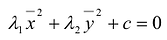в системе координат 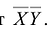. В зависимости от чисел 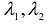,с эта кривая будет эллипсом, гиперболой, параболой, парой прямых, точкой или мнимой кривой.

Системы линейных уравнений с примерами
Линейное программирование
Дифференциальное исчисление функций одной переменной
Исследование функции
Евклидово пространство
Матрица – виды, операции и действия с примерами
Линейный оператор – свойства и определение
Многочлен – виды, определение с примерами

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 сентября 2021 года; проверки требуют 3 правки.

Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.

Определение[править | править код]

Пусть есть векторное пространство над полем и $e_{1},e_{2},dots ,e_{n}$ — базис в .

Функция Q:Lto K называется квадратичной формой,
если её можно представить в виде

$Q(x)=sum _{{i,j=1}}^{n}a_{{ij}}x_{i}x_{j},$

где $x=x_{1}e_{1}+x_{2}e_{2}+cdots +x_{n}e_{n}$ , а $a_{{ij}}$ — некоторые элементы поля .

Связанные определения и свойства[править | править код]

${displaystyle Q(x_{1},x_{2})=a_{11}x_{1}^{2}+2a_{12}x_{1}x_{2}+a_{22}x_{2}^{2}}$

${displaystyle A'=C^{T}A,C,}$

где

— матрица квадратичной формы в новом базисе.

Из формулы ${displaystyle A'=C^{T}A,C}$ следует, что определитель матрицы квадратичной формы не является её инвариантом (т.е. не сохраняется при замене базиса, в отличие, например, от матрицы линейного отображения), но её ранг — является. Таким образом, определено понятие ранга квадратичной формы.
Если матрица квадратичной формы имеет полный ранг , то квадратичную форму называют невырожденной, в противном случае — вырожденной.
Для любой квадратичной формы существует единственная симметричная билинейная форма , такая, что . Билинейную форму называют полярной к , если она может быть вычислена по формуле

$B(x,y)={frac {1}{2}},(Q(x+y)-Q(x)-Q(y)).$

Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.

Знакоопределённые и знакопеременные формы[править | править код]

В случае, когда (поле вещественных чисел), важную роль, в том числе, для различных приложений, играют понятия положительно и отрицательно определённой квадратичной формы.

Для решения вопроса о том, является ли данная квадратичная форма положительно (отрицательно) определённой, используется критерий Сильвестра:

Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.

Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.

Канонический вид[править | править код]

Вещественный случай[править | править код]

В случае, когда (поле вещественных чисел), для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид, то есть содержит только квадраты переменных:

${displaystyle Q(x)=a_{1}x_{1}^{2}+cdots +a_{p}x_{p}^{2}-a_{p+1}x_{p+1}^{2}-cdots -a_{p+q}x_{p+q}^{2},quad 0leq p,qleq r,quad p+q=r,qquad (*)}$

где — ранг квадратичной формы. . В этом случае коэффициенты $a_{{i}}$ называются каноническими коэффициентами. В случае невырожденной квадратичной формы , а в случае вырожденной — .

Существует также нормальный вид квадратичной формы:
${displaystyle Q_{n}(x)=x_{1}^{2}+cdots +x_{p}^{2}-x_{p+1}^{2}-cdots -x_{p+q}^{2},quad 0leq p,qleq r,quad p+q=r,qquad (*)}$ .

Для приведения квадратичной формы к каноническому виду обычно используются метод Лагранжа или ортогональные преобразования базиса, причем привести данную квадратичную форму к каноническому виду можно не одним, а многими способами.

Число (отрицательных членов) называется индексом инерции данной квадратичной формы, а число p-q (разность между числом положительных и отрицательных членов) называется сигнатурой квадратичной формы. Отметим, что иногда сигнатурой квадратичной формы называют пару (p,q) . Числа являются инвариантами квадратичной формы, то есть не зависят от способа её приведения к каноническому виду (закон инерции Сильвестра).

Комплексный случай[править | править код]

В случае, когда (поле комплексных чисел), для любой квадратичной формы существует базис, в котором форма имеет канонический вид

${displaystyle Q(x)=x_{1}^{2}+cdots +x_{r}^{2},qquad (**)}$

где — ранг квадратичной формы. Таким образом, в комплексном случае (в отличие от вещественного) квадратичная форма имеет один единственный инвариант — ранг, и все невырожденные формы имеют один и тот же канонический вид (сумма квадратов).

Примеры[править | править код]

См. также[править | править код]

Теорема Витта
Метод Лагранжа приведения квадратичной формы к каноническому виду

Примечания[править | править код]

Литература[править | править код]

Беклемишев Д. В. Аналитическая геометрия и линейная алгебра.-М.: Высш. шк. 1998, 320с.
Гельфанд И. М., Линейная алгебра. Курс лекций.
Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
Конвей Дж. Квадратичные формы, данные нам в ощущениях. — М.: МЦНМО, 2008. — 144 с. — 1000 экз. — ISBN 978-5-94057-268-8.
Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.

Источник

5.1. Определение квадратичной формы, матрица квадратичной формы, преобразование матрицы квадратичной формы при переходе к новому базису

5.2. Приведение квадратичной формы к каноническому виду. Закон инерции квадратичных форм

Понятие квадратичной формы

Канонический базис квадратичной формы

Канонический базис из собственных векторов матрицы квадратичной формы

Положительно и отрицательно определенные квадратичные формы

Применение квадратичных форм к исследованию кривых второго прядка

Определение[править | править код]

Связанные определения и свойства[править | править код]

Знакоопределённые и знакопеременные формы[править | править код]

Канонический вид[править | править код]

Вещественный случай[править | править код]

Комплексный случай[править | править код]

Примеры[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Форд фокус 2 неисправность системы esp как исправить ошибку

Как найти сохраненный документ на компе

Как найти задолженность по коммунальным платежам

Добавить комментарий Отменить ответ