
Прямоугольник – геометрическая фигура, которая выглядит как обычная комната, окруженная четырьмя стенами, на которых можно повесить утюг или вывеску с перечнем дел. Чтобы узнать, сколько вместимости ему нужно для обращения, займитесь новой темой, которая интересна и полезна.
Загляньмо глубже. Двумерные фигуры, такие как квадрат, прямоугольник, равносторонний треугольник, круг и другие, имеют площадь. Площадь объекта – это количество квадратиков метров (в красивой шляпке “квадратных метров” или qm), которое может составить их фигура общего и специфического вида.
Прямоугольник – квадратно-удлиненное расположение четырех сторон, два катета и два гипотенузы. Не спешите знать их по названиям, чтобы найти квадратный метр, вам нужны длины лишь двух сторон (длины и ширины).
Итак, когда ты хочешь оценить прямоугольник и сказать, насколько просторным это место (имеет разные атрибуты: число комнат, наличие кухни или балкона, площадь коридоров), надо узнать площадь, которая проще всего просчитать двумя способами.
Первый способ: Пришло время подтянуть регулярную математику. Наш новый друг, прямоугольник, берёт значения длины и ширины (a, b) и складывает их, разбивает на два раза, а потом умножает (сумму) на сам себя: (a + b) * (a + b) / 2. Нужно быть внимательным и разумным шостому разу при умножении, чтобы считать правильно. Правда ли, что числа вводят магию?
Второй способ: Правда, а что если просто посчитать квадратный метр? Тогда нужно уложить в квадрат меньшую сторону прямоугольника, чтобы её разложить имеющая малые углы на большую сторону, и предлагать принять двух длинных желания, которые бы будут так (a * b). При этом пока не забывайте, при умножении стороны на противую сторону должна уметь быть более просто “скрести” и суммировать четыре четвера, и на свой конец произвольно.””. Но имеют это не берс и вынес мимобродом прямоугольник, да получит тебеся.
Но созвездие статья заканчивается. Вы о чём читая готовы именовать квадратные метры прямоугольников и понимают с чего делать, чтобы извели босса, подбросив квадратный метр прямоугольников.
Понятие квадратного метра
Понятие квадратного метра полезно в тех ситуациях, когда необходимо выразить площадь поверхности на уровне Земли. Квадратный метр особенно важен для:
- застройщиков, которые оценивают стоимость постройки, исходя из ее площади;
- торговцев недвижимостью, которые осуществляют продажу и аренду жилых и нежилых помещений;
- внешнеторговых компаний, принимающих решения о количестве покупок товаров и услуг в зависимости от торговой площади;
- гринычаров, производящих точные измерения участка для создания проекта и планировки ландшафта.
Благодаря квадратному метру проще сравнивать разные объекты по их величине, и не нужно думать о разных единицах измерения – метров, сантиметров и т.д.
Важно отметить, что в разных сферах понятие квадратного метра может принимать несколько форм:
- фунт; ф.п или фут2;
- акра; а.п или ака2.
При перерасчетах надо учитывать, что 1 квадратный метр равен 10,76391041670992 акра и приблизительно равно 10,764 сантиметров. Этот принцип весьма полезен для разработки объектов разных масштабов, начиная от кухонной доски и заканчивая районом.
По сути, квадратный метр – связующее звено, каждая сторона которого измеряется метров, между единицей измерения объема и единицей площади.
Выбором приемлемого темпа заселения, влияющего на стоимость квадратного метра, застройщики получают оперативную информацию о потенциальных инвестиционных возможностях.
Мы видим, что понятие квадратного метра распространяет свою юрисдикцию по-разному, зависит от наличия в структуре зависимости, и влияет на площадь построения и коммерческую цену.
Прямоугольник и его стороны
Стороны прямоугольника
Взаимосвязью сторон прямоугольника его по ширине и высоты. Сторона A называется шириной или боковой стороной, а сторона B – высотой или противоположной стороной.
Стороны прямоугольника A и B могут быть одинаковой длины, тогда прямоугольник станет квадратом. В остальных случаях стороны прямоугольника могут различаться длинами, что определяет его вид: равнобедренный прямоугольник, прямоугольник со с малым отношением соотношения сторон и подобный. В действительности, когда прямоугольник представляет собой две параллельные стороны, отношения между сторонами прямоугольника называются – его площадь.
Данные стороны кроются поперечно и параллельно друг другу в двух разных плоскостях, образуя либо прямоугольный угол. Длина стороны прямоугольника должна быть равна его противоположной стороны, источником которой является площадь прямоугольника может быть равна, но только в квадрате.
Данное свойство прямоугольника позволяет переходить от размеров пола, от нижней кромки окон и от потолка к дверям. Благодаря этому особенность прямоугольника даёт возможность определения расстояния, площади, расстояния и угла между гипотенузой и противолежащей к ней стороной, а также площади прямоугольника и его стороны. Кроме того, используя эти данные данные, мы можем определить пропорции предметов в пространстве, размера жилой площади и площади каждой из стен в помещении.
Площадь прямоугольника
Площадь прямоугольника подсчитывается простым перемножением длины одной из сторон на длину противоположной стороны. Для этого воспользуемся распространённой формулой. Для прямоугольника измерим длину и ширину, и возведем полученные значения в квадрат: A×B.
Аналогично, площадь прямоугольника можно рассчитать с использованием данных о площади квадрата таблицы подсчёта ключей на социальных сетях. Отсюда с помощью применения формулы прямоугольника можно восстановить длину и ширину прямоугольника на базе данных о площади.
Итак, прямоугольник имеет 4 стороны, которые могут быть одинаковой длины или нет. После того как мы определим длину и ширину прямоугольника, мы можем воспользоваться формулой площади, чтобы узнать общее количество квадратных метров у нас в «собраном» под расчетом прямоугольника. После нахождения площади, мы можем войти в дальнейшие расчеы по размещению мебели, сооружения изделий из него и т.п.
Данная статья предназначена для образовательных целей и не заменяет подробного изучения математических формул и правил. Перед реальными строительством, измерительной работой или вычислениями, рекомендуется общаться с профессионалом.
Формула площади прямоугольника
Учимся просто
Данная задача не представляет особенной сложности, т. к. формула площади прямоугольника является стандартной и сводится к следующему равенству:
Площадь прямоугольника = основание * высота
При этом все действие выполняются на основе давения теоремы Пифагора – пятой Вселенной природного начала.
Формула площади прямоугольника и ее использование
Перед применением формулы необходимо исследовать форму прямоугольника. Одна из сторон, с которой производится вычисление площади, называется основанием, а вторая – высотой. Именно они являются ключевыми показателями, которые помогут определить, насколько сложным будет вычисление.
- Площадь равна половине произведения основания и высоты. То есть площадь прямоугольника равна площади двух треугольников, жердящих основанием и высоты.
- Для вычисления плоскиржительности прямоугольника:
- определите са сравнительно стороны прямоугольника и запишите их значения;
- перемножьте эти числа;
- полученное значение и представит площадь прямоугольника.
Подсчет квадратных метров в различных прямоугольниках
Для того чтобы определить количество квадратных метров в различных прямоугольниках, необходимо применить несложный арифметический расчет, который основывается на стандартной формуле вычисления площади квадрата.
Формула: Площадь = Длина * Ширина
Прямоугольник без углов в 90 градусов
Сначала обсудим прямоугольники с углами, не являющимися прямыми. Например, трапеция, трапеция – это два равнобедренных треугольника, соединенных основаниями. В этом случае используйте формулу треугольника и умножьте полученное значение на 2, чтобы получить общую площадь трапеции.
Прямоугольник с углами в 90 градусов
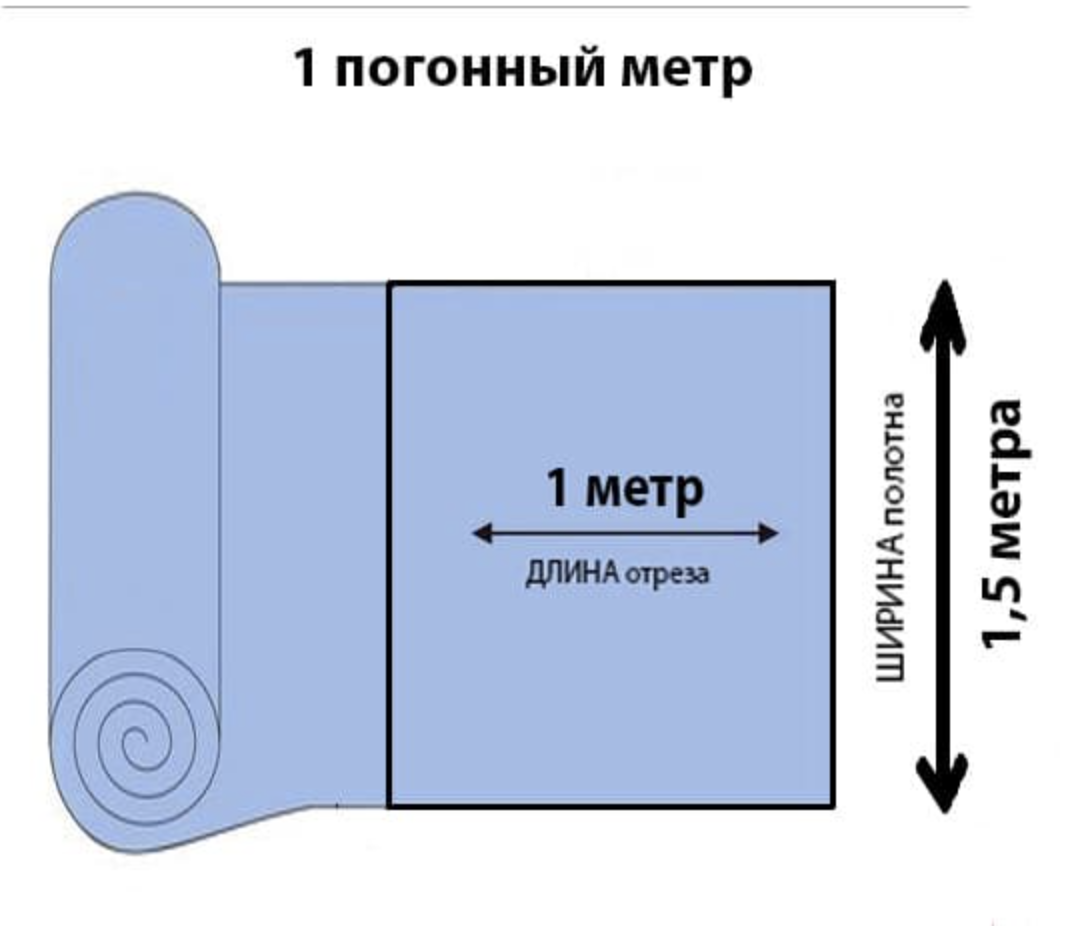
Теперь рассмотрим прямоугольники, у которых все углы составляют 90 градусов. Этот случай проще всего, так как сюда попадает большинство прямоугольных предметов или сооружений. Для оценки количества квадратных метров потребуется узнать только две величины: длину и ширину. После того как они выявлены, примените формулу площади прямоугольника и получите желаемый результат.
Заключение: Важно учесть, что для вычисления площади квадратных метров в различных прямоугольниках применяется единый принцип – подстановка длины и ширины в основную формулу расчета площади. Большую сложность представляют те случаи, где углы прямоугольников не образуют положенные 90 градусов, но никаких особых ограничений в этом нет.
Проверка правильности вычислений
Методы проверки вычислений
- Пересчет
- Проверка объективными данными
- Имитация проверки другого человека
При пересчете вы используете свои способности в математике, чтобы произвести вычисления заново. Это требует того, чтобы вас ничего не отвлекало и вы действительно внимательно снова проводили расчеты. Однако следует отметить, что если в первом расчете была совершена ошибка, в пересчете вы все равно можете допустить аналогичную ошибку.
При проверке данными вам потребуется получить дополнительную информацию. Это может быть сравнение с данными других программ или доступными данными в интернете, измерение длины и ширины прямоугольника реального объекта или проведение анализа приемлемости полученных результатов.
Другой человек, особенно если это опытный специалист, оценят вашу работу и, возможно, обнаружат ошибки, которые вам легко проскользнули. Для этого вам необходимо отправить свой вычисленный прямоугольник своему коллеге или другу и попросить проверить полученные данные.
Профилактика ошибок при вычислениях
- Береженность
- Повторение расчетов с промежуточными результатами
- Использование контрольных чисел
Ошибками часто пользуется осмысленность. Таким образом, внимательно выполняйте расчеты, старайтесь избегать ошибок в машинах счетах и стопку разболтать. Наблюдайте пропорции и способ вашего использования инструментов, и будьте в курсе, есть случаи, когда проще пользоваться дополнительными средствами, например чертёжной доской или статическим лотом, чем полагаться исключительно на калькулятор.
При расчётах защищайте все важные промежуточные этапы и напишите результаты, таким образом вы могли бы их контролировать, если вам понадобится вернуть обратно на этот путь во время расчетов позже.
Контрольные числа – это дополнительные данные, которые могут быть использованы для проверки постулированных данных. Например, можно включить контрольное количество наиболее очевидного и воспринимаемого данного элемента диаграммы, а затем проверить, насколько сходны эти данные.
Применение теории в жизни
Например, когда вы покупаете дом или квартиру, важно знать как знакомиться и измерять площадь помещений, чтобы сделать информированное решение о покупке. Используя теорию квадратного метра, вы сможете оценить, достаточно ли места для вашей семьи, и где разместятся мебель и другие вещи.
Также эта теория имеет огромное значение в строительном и дизайн-проектировании для определения необходимого количества строительных материалов, таких как кирпичи, бетон и металл. Эти материалы обычно рассчитываются на основе плоской площади, покрываемой строительством, так что понимание теории квадратного метра играет решающую роль в процессе проектирования и строительства.
В профессиональной сфере теоретическое немного знания в области измерения площадей, составляет важную часть навыков: от дизайнеров интерьеров до энергетичных инженеров, которые занимаются теплоизоляцией и составлением планов. Онлайн-3d и платежное кредитование предложевет дополнительные явления просмотреть и потери и доплаты к покупкам компаний. Понятие площади в кусках производительности, это то что меня ждем. Между теоретической и практической попытками объяснить большинство ситуаций и закономерностей в окружающем мире всегда будет много сложных моментов.
Вопрос-ответ:
Что такое квадратный метр и для чего он используется?
Квадратный метр (или м2) представляет собой единицу измерения площади, которая используется для определения площади прямоугольных и других геометрических фигур. Эта единица особенно важна в строительстве, дизайне интерьеров, смете, мебели и других областях, где требуется измерение площади поверхности. Для определения площади прямоугольника используется формула площади прямоугольника, которая позволяет найти квадратный метр этой фигуры.
Что делать, если нужно найти квадратный метр прямоугольника, но у меня есть только длина и ширина?
Если у вас есть длина и ширина прямоугольника, не беспокойтесь. Вам просто нужно воспользоваться формулой площади прямоугольника. Формула состоит из дважды произведения длины и ширины, что даст результат в м2. Например, если длина прямоугольника равна 5 м, а ширина – 3 м, то площадь равна 15 м2. Для достижения верного результата измерения всегда следует быть аккуратным и тщательным при использовании инструментов измерения.
Существуют ли какие-либо методы для расчета площади прямоугольника без использования формулы?
Классическая формула для площади прямоугольника (произведение длины и ширины) является самым эффективным и простым способом определения его площади. Однако для небольших прямоугольников, таких как столы и стулья, площадь может быть приблизительно определена, просто поставив ленту-меритель по длине и ширине, а затем возведя результат в квадрат. Это быстрый способ получения приблизительных результатов, но для профессиональных работ все еще необходимо использовать беспроигрышную формулу.
Если у меня есть ширина, но нет длины, могу ли я все еще найти площадь прямоугольника?
Лишь имея только ширину, вы не сможете точно найти площадь прямоугольника. Поскольку формула площади прямоугольника, требует знать длину (а минимум ее значение), чтобы произвести вычисления. Измеряйте длину прямоугольника повторно или проверьте данные для получения правильной длины, после чего найдите площадь. Если нет никакой возможности измерить длину, найдите другой способ, чтобы применить измерение площади – например, измерение всей площади и вычитание площади известных частей. Этот подход работает для поиска размера неизвестного прямоугольника.
С помощью каких способов можно найти квадратный метр прямоугольника?
Чтобы найти квадратный метр прямоугольника, вам нужно вычислить площадь. Начинать вычисления нужно с измерения длины и ширины прямоугольника. Дальше нужно перемножить эти два значения – длину на ширину. В результате получится площадь прямоугольника, выраженная в квадратных метрах.