Как найти квадратное уравнение по его графику

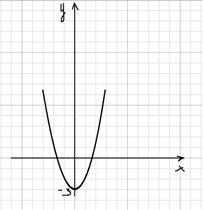
Как определить a, b и c по графику параболы

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

– Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим (9a) вместо (b):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение (a):

Получается квадратичная функция: (y=-x^2-9x-15).

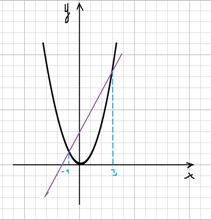
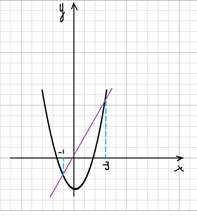
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа – вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
– График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

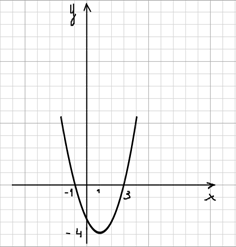
У вас наверно остался вопрос – как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

Квадратичная функция и ее график

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где 0″ title=”a<>0″/> называется квадратичной функцией.

В уравнении квадратичной функции:

a – старший коэффициент

b – второй коэффициент

с – свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками – это, так называемые “базовые точки”. Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.

График функции имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .

Если старший коэффициент a , то ветви параболы напрaвлены вниз .

Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции – это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если 0″ title=”a>0″/>,то график функции выглядит как-то так:

2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если 0″ title=”a>0″/>,то график функции выглядит примерно так:

3 . Если 0″ title=”D>0″/>,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

,

Если 0″ title=”a>0″/>,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции – координаты вершины параболы:

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции – точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как 0″ title=”a=2>0″/>,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

0″ title=”D=b^2-4ac=9-4*2*(-5)=49>0″/>

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

,

3. Координаты вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2 . Уравнение квадратичной функции имеет вид – в этом уравнении – координаты вершины параболы

или в уравнении квадратичной функции , и второй коэффициент – четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,
• затем одинаты всех точек графика умножить на 2,
• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент – четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции – точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы:

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
– ширины графика функции от значения коэффициента ,
– сдвига графика функции вдоль оси от значения ,

– сдвига графика функции вдоль оси от значения
– направления ветвей параболы от знака коэффициента
– координат вершины параболы от значений и :

И.В. Фельдман, репетитор по математике.

Алгоритм нахождения коэффициентов a, b, c квадратичной функции по графику

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

нахождения значений коэффициентов a , b , c

по графику квадратичной функции

Автор: Храмова Ирина Михайловна

МБОУ Луговская ООШ

Источники : алгебра 9 класс, Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под редакцией А.С.Теляковского,

Москва «Просвещение», 2013г.

I . Нахождение коэффициента a :

1) по графику параболы определяем координаты вершины ( m , n )

2) по графику параболы определяем координаты любой точки А(х₁;у₁)

3) подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

4) решаем полученное уравнение.

Сначала находим значение коэффициента a (шаг I , смотри выше)

В формулу для абсциссы параболы m = – b /2 a подставляем значения m и a

Находим значение коэффициента b .

III . Нахождение коэффициента с:

Находим ординату у точки пересечения параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;с) – точка пересечения параболы с осью Оу.

Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I , II (находим коэффициенты a , b )

Краткое описание документа:

В модуле «Алгебра» ГИА – 2013 есть задание на нахождение коэффициентов квадратичной функции с помощью графика – параболы. Но в материалах учебника «Алгебра – 9» Ю.Н. Макарычева под редакцией С.А. Теляковского таких заданий нет и нет объяснения этого. Поэтому тему «Алгоритм нахождения коэффициентов а, в и с квадратичной функции» я включила в программу кружка по математике для учащихся 8 – 9 классов. Это позволяет учащимся научиться определять коэффициенты. Кружок посещают все учащиеся 9 класса и часть учащихся 8 класса. Программа кружка рассчитана на 68 часов, то есть 2 часа в неделю.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 939 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 587 772 материала в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 15.02.2015
• 1853
• 2

• 15.02.2015
• 15293
• 43

• 15.02.2015
• 1463
• 0

• 15.02.2015
• 1312
• 1

• 15.02.2015
• 1039
• 0

• 15.02.2015
• 1001
• 0

• 15.02.2015
• 667
• 1

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 15.02.2015 56563
• DOCX 34.5 кбайт
• 376 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Храмова Ирина Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет
• Подписчики: 0
• Всего просмотров: 61904
• Всего материалов: 5

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Школьник из Сочи выиграл международный турнир по шахматам в Сербии

Время чтения: 1 минута

В школах Хабаровского края введут уроки спортивной борьбы

Время чтения: 1 минута

Минобрнауки создаст для вузов рекомендации по поддержке молодых семей

Время чтения: 1 минута

Каждый второй ребенок в школе подвергался психической агрессии

Время чтения: 3 минуты

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Только 23 февраля!
Получите новую
специальность
по низкой цене

Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки

[spoiler title=”источники:”]

http://ege-ok.ru/2012/05/21/kvadratichnaya-funktsiya-i-ee-grafik

http://infourok.ru/algoritm_nahozhdeniya_koefficientov_a_b_c_kvadratichnoy_funkcii_po_grafiku-389899.htm

[/spoiler]

Здравствуйте. В данной статье я попытаюсь показать вам возможные способы решения квадратных уравнений с помощью графиков.

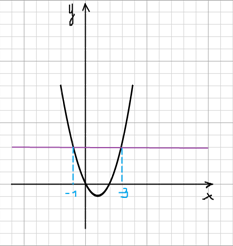
Допустим, надо решить уравнение х² ‒ 2х ‒ 3 = 0. На этом примере мы рассмотрим варианты решения квадратного уравнения графически.

1) Можно представить наше уравнение в виде х² = 2х + 3. Далее построим в одной системе координат графики функций у = х² и у = 2х + 3. График у = х² представлен на рисунке 1, а оба графика на рисунке 2. 

Рисунок 1                                 Рисунок 2

Графики пересекаются в двух точках, наше уравнение имеет решение х = – 1 и х = 3.

2) А ведь можно представить уравнение и по – другому, например х² ‒ 2х = 3 и построить в одной системе координат графики функций  у = х² ‒ 2х и у =3. Вы их можете увидеть на рисунках 3 и 4. На рисунке 3 изображен график у = х² ‒ 2х, а на рисунке 4 оба графика у = х² ‒ 2х и у =3.

Рисунок 3                                         Рисунок 4

Как мы видим, эти два графика так же пересекаются в двух точках, где х = -1 и х = 3. Значит ответ: – 1; 3.

3) Есть и другой вариант представления этого уравнения х² ‒ 3 = 2х. И снова строим графики функций у = х² ‒ 3 и у = 2х в одной системе координат. Первый у = х² ‒ 3 на рисунке 5 и оба графика на рисунке 6.

Рисунок 5                                 Рисунок 6

Они также пересекаются в двух точках, в которых х = -1 , х = 3.

Ответ: – 1; 3.

4) Можно построить параболу у = х² ‒ 2х ‒ 3.

Вершина параболы  х₀ = – b/2а = 2/2=1, у₀ = 1² ‒ 2·1 ‒ 3 = 1 – 2 – 3 = ‒ 4. Это точка (1; ‒ 4). Тогда наша парабола симметрична относительно прямой х =1. Если взять две точки симметричные относительно прямой х = 1 например: х = – 2 и х = 4, то мы получим две точки через которые проходят ветви графика.

Если х = -2, то у =(- 2)² ‒ 2( -2) ‒ 3 = 4 + 4 – 3 = 5.

Аналогично х =4, у = 4² ‒ 2 · 4 ‒ 3= 16 – 8 – 3 = 5. Полученные точки ( -2; 5); (1; 4) и (4; 5) отмечаем в на плоскости и проводим параболу рисунок 7.

Рисунок 7

Парабола пересекает ось абсцисс в точках – 1 и 3. Это и есть корни уравнения х² ‒ 2х ‒ 3 = 0.

Ответ: – 1 и 3.

5) А можно выделить квадрат двучлена:

х² ‒ 2х ‒ 3= 0

(х² ‒ 2х + 1) ‒1 ‒ 3= 0

(х -1)² – 4 = 0

(х – 1)² = 4

Затем построить в одной системе координат графики функций у = (х – 1)² и у = 4. Первый график у = (х – 1)² на рисунке 8, а оба графика у = (х – 1)² и у = 4 на рисунке 9.

Рисунок 8                                     Рисунок 9

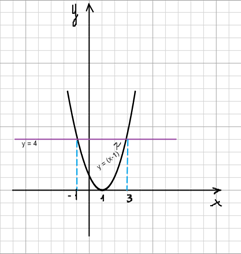
Они также пересекаются в двух точках, в которых х = -1 , х = 3.

Ответ: – 1; 3.

6) Так как х = 0 не является корнем уравнения х² ‒ 2х ‒ 3 = 0 (иначе выполнялось бы равенство 0² – 2· 0 –3 = 0), то можно все члены уравнения разделить на х. В результате мы получим уравнение х – 2 – 3/х = 0. Перенесем 3/х вправо и получаем уравнение х – 2 = 3/х Тогда можно построить в одной системе координат графики функций у = 3/х и у = х – 2.

На рисунке 10 изображен график функции у = 3/х, а на рисунке 11 оба графика функций у = 3/х и у = х – 2.

Рисунок 10                           Рисунок 11

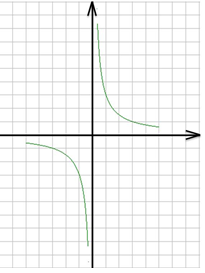
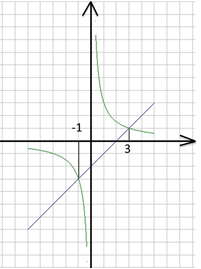
Они также пересекаются в двух точках, в которых х = -1 , х = 3.

Ответ: – 1; 3.

Если вы были внимательны, то обратили внимание, что каким бы образом вы не представили бы уравнение в виде двух функций, у вас всегда будет один и тот же ответ (разуметься, что вы не допустите ошибок при переносе выражений из одной части уравнения в другую и при построении графиков). Поэтому, решая графически уравнение, выбирайте способ представления функций графики которых вам легче построить. И еще одно замечание если корни уравнения не целые числа, то ответ получится не точным.

Репетитор Валентина Галиневская.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Инфоурок

›

Алгебра

›Презентации›Графическое решение квадратных уравнений

Графическое решение квадратных уравнений

Решение уравнений с помощью графиков

Решение линейных уравнений

Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.

Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.

Сейчас же я покажу тебе, как это сделать графическим способом.

Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)

Как его решить?

Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:

Иными словами, у нас будет:

Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:

Наш ответ: ( displaystyle x=6)

Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!

Вариант 1. Напрямую

Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)

Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:

Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:

И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).

Ты знаешь, что парабола симметрична относительно своей вершины, например:

Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:

Возвращаемся к нашей параболе.

Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?

Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).

Как ты думаешь, что является решением уравнения?

Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).

И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).

Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!

Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.

Что у тебя получилось? То же самое?

Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!

Решение смешанных неравенств

Теперь перейдем к более сложным неравенствам!

Как тебе такое:

Первое, с чего мы начнем, – это с построения двух графиков:

Расписал? Теперь строй два графика.

Сравним наши рисунки?

У тебя так же? Отлично!

Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).

Смотри, что получилось в итоге:

А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!

На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).

Это и есть ответ!

Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!