Как найти квадратную единицу фигуры

Рассмотрим фигуру ниже:

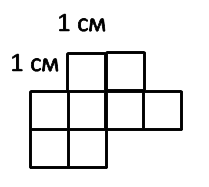
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.

Площадь одного такого квадрата называют квадратным сантиметром и записывают:
1 см².

Площадь всей фигуры 8 см².

В математике для нахождения площади геометрических фигур используют специальные формулы,
в которых площадь обозначается заглавной латинской буквой «S».

Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.

Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата,
равна 1 м, то его площадь равна 1
квадратному метру (1 м²); если длина
его стороны равна 1 см, то его площадь
равна 1 квадратному сантиметру
(1 см²).

Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.

Как перевести квадратные единицы

Рассмотрим квадрат со стороной 1 см.

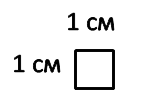
Его площадь равна:

S = 1 см · 1 см = 1см²

Рассмотрим квадрат со стороной 1 м.

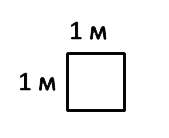
Его площадь равна:

S = 1 м · 1 м = 1 м²

Известно, что: 1 м = 100 см

1 м² = 1 м · 1 м = 100 см · 100 см = 10 000 см²

Увеличим сторону квадрата равную 1 м в
10 раз. Получим квадрат со
стороной 10 м.

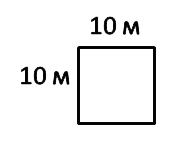
Площадь такого квадрата называют ар или сотка.

S = 10 м · 10 м = 100 м²

В одном аре — сто квадратных метров.

Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».

1 ар (сотка) = 100 м²

Чтобы выразить ар в cм², вспомним, что 1 м² = 10 000 см².

Значит: 1 ар (сотка) = 100 м² = 100 · 10 000 см² = 1 000 000 см²

Увеличим сторону квадрата равную 10 м в 10 раз.
Получим квадрат со
стороной 100 м.

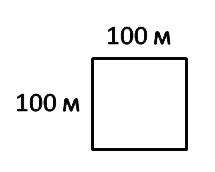
Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование
проговаривается полностью.

Выразим гектар в квадратных метрах.

1 га = 100 м · 100 м = 10 000 м²

Теперь определим, сколько в одном гектаре аров.

1 ар = 100 м²

Значит: 10 000 м² : 100 м² = 100 (ар)

1 га = 100 ар

Для измерения больших площадей, например, территорий государств, материков используют квадратный километр.
То есть квадрат со стороной 1 км и
площадью 1 км².

1 км = 1000 м

1 км² = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м²

Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.

Таблица переводов квадратных единиц

Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.

	га	ар	м2	cм2
1 км2	100 га	10 000 ар	1 000 000 м2	1 000 000 000 cм2
1 га	1 га	100 ар	10 000 м2	100 000 000 cм2
1 ар	0,01 га	1 ар	100 м2	1 000 000cм2
1 м2	0,000 1 га	0,01 ар	1 м2	10 000 cм2

---

Ваши комментарии

Оставить комментарий:

---

Как найти квадратные сантиметры

Квадратные сантиметры – это метрическая единица измерения площади различных плоских геометрических фигур. Она имеет повсеместное применение, начиная со школьной скамьи и кончая вычислениями на уровне архитектуры и механики. Найти квадратные сантиметры не очень трудно

Инструкция

Квадратный сантиметр образно представляет собой квадрат, у которого длина стороны составляет 1 см. Треугольники, прямоугольники, ромбы и другие геометрические фигуры могут включить в себя далеко не один такой квадрат. Таким образом, квадратный сантиметр, по своей сути, является одной из самых часто применяемых единиц измерения площади фигур в школьной программе.

Площади различных плоских геометрических фигур вычисляется по разному:

S = a² – это площадь квадрата, где a – длина любой из его сторон;

S = a*b – площадь прямоугольника, где a и b – стороны данной фигуры;

S = (a*b*sinα)/2 – площадь треугольника, a и b – стороны данного треугольника,α – угол между данными сторонами. На самом деле, формул для исчисления площади треугольника чрезвычайно много;

S = ((a + b)*h)/2 – площадь трапеции, a и b – основания трапеции, h – ее высота. Формул по вычислению площади трапеции также существует несколько;

S = a*h – площадь параллелограмма, а – сторона параллелограмма, h – проведенная к данной стороне высота.
Приведенные выше формулы – далеко не все, с помощью которых можно вычислить площади различных геометрических фигур.

Для того, чтобы было понятнее, как найти квадратные сантиметры, можно привести несколько примеров:

Пример 1: Дан квадрат, у которого длина стороны составляет 14 см, необходимо вычислить ее площадь.

Решить задачу можно при помощи одной из данных выше формул:

S = 14² = 196 см²

Ответ: площадь квадрата составляет 196 см²

Пример 2: Имеется прямоугольник, длина которого 20 см, а ширина 15 см, опять же требуется найти его площадь. Решить поставленную задачу можно при помощи второй формулы:

S = 20*15 = 300 см²

Ответ: площадь прямоугольника 300 см²

Если же в задаче единицами измерения сторон и других частей фигуры являются не сантиметры, а, к примеру, метры или дециметры, то выразить площадь данной фигуры в сантиметрах опять же очень легко.

Пример 3: Пусть дана трапеция, основания которой равны 14 м и 16 м, высота ее 11 м. Требуется вычислить площадь фигуры. Для этого придется воспользоваться четвертой формулой:

S = ((14+16)*11)/2 = 165 м² = 16500 см² (1 м = 100 см)

Ответ: площадь трапеции 16500 см²

Источники:

• квадратный сантиметр

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Единичный квадрат — квадрат, стороной которого является единичный отрезок. Единичный квадрат является единицей измерения площади. Иногда требуют, чтобы в прямоугольных координатах левый нижний угол единичного квадрата находился бы в начале координат и его стороны были бы параллельны осям координат. В этом случае его вершины имеют координаты , , и .

Определения[править | править код]

Часто под единичным квадратом подразумевается любой квадрат со стороной 1.

Если задана прямоугольная система координат, то этот термин часто используют в более узком смысле: единичный квадрат — это множество точек, обе координаты которых (x и y) лежат между 0 и 1:

.

Иными словами, единичный квадрат — это прямое произведение I × I, где I — единичный отрезок .

В комплексной плоскости под единичным квадратом подразумевается квадрат с вершинами 0, 1, 1 + i и i^[1].

Единица площади[править | править код]

Единичный квадрат является единицей измерения площади фигуры. Измерить площадь фигуры — значит найти отношение площади фигуры к площади единичного квадрата, то есть сказать, сколько раз единичный квадрат может быть уложен в данной фигуре^[2]. Есть все основания предполагать, что так определяли площадь математики Древнего Вавилона^[3].
В «Началах» Евклида не было единицы измерения длины, а значит, не было понятия единичный квадрат. Евклид не измерял площади числами, вместо этого он рассматривал отношения площадей друг к другу^[4].

Свойства[править | править код]

• Площадь единичного квадрата равна 1, периметр — 4, диагональ — .
• Единичный квадрат является «кругом» диаметра 1 в смысле равномерной нормы (), то есть множество точек, которые расположены на расстоянии 1/2 в смысле равномерной нормы от центра с координатами (1/2, 1/2), является единичным квадратом^[5].
• Кантор доказал, что существует взаимнооднозначное соответствие между единичным отрезком и единичным квадратом. Этот факт настолько противоречит интуиции, что Кантор в 1877 году писал Дедекинду: «Я вижу это, но не верю»^[6][7].
• Ещё более удивительный факт был открыт Пеано в 1890 году: оказывается существует непрерывное отображение отрезка на квадрат. Примером такого отображения является кривая Пеано, первый пример заполняющей пространство кривой. Кривая Пеано задаёт непрерывное отображение единичного отрезка на квадрат, так, что для каждой точки квадрата найдется соответствующая точка отрезка^[8].
• Тем не менее, не существует взаимнооднозначного непрерывного отображения отрезка в квадрат. Кривая Пеано содержит кратные точки, то есть она проходит через некоторые точки квадрата более одного раза. Таким образом, кривая Пеано не задаёт взаимнооднозначного соответствия. В действительности легко доказать, что отрезок не гомеоморфен квадрату, значит, избежать кратных точек невозможно^[9].

Открытая проблема[править | править код]

Неизвестно (на 2011 год), существует ли точка на плоскости такая, что расстояние до любой вершины единичного квадрата является рациональным числом. Однако известно, что такой точки не существует на границе квадрата^[10][11].

См. также[править | править код]

• Единичная сфера
• Единичный круг
• Единичный куб

Примечания[править | править код]

Ссылки[править | править код]

• Weisstein, Eric W. Unit Square (англ.) на сайте Wolfram MathWorld.

Этапы урока	Деятельность учителя	Деятельность учащихся
I. Мотивирование к учебной деятельности.  1. Организационный момент.	Здравствуй, мой любимый класс, Очень рада видеть вас! Ты готов начать урок? Всё ль на месте? Всё ль в порядке? Ручки, книжки и тетрадки?	Приветствуют учителя. Проверяют свою готовность к уроку.
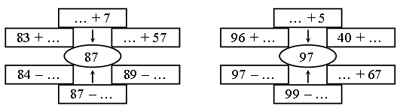
II. Актуализация знаний. Устный счёт.	1)Вставьте пропущенные числа. 2) Решите задачу. В аллее 28 каштанов, а ясеней в 4 раза меньше. Сколько ясеней растёт в аллее?	Повторяют правила нахождения неизвестных компонентов сложения и вычитания, закрепляют таблицу умножения.
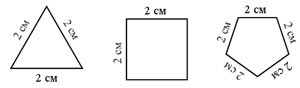
III. Определение темы урока. 1. Целеполагание. 2. Постановка проблемы.	– Как называются данные на доске фигуры? – Что их объединяет? (Это многоугольники, стороны которых равны 2 см.) – Как найти периметр каждого многоугольника? 2 + 2 + 2 = 6 (см) 2 + 2 +2 + 2 = 8 (см). 2 + 2 + 2 + 2 + 2 = 10 (см). – Как найти площадь этих фигур? – Какие трудности у вас возникли? – Сегодня на уроке мы узнаем, что называют площадью фигуры.	Фиксируют затруднение.
IV. Открытие нового знания.	Какая фигура меньше занимает места на плоскости? Говорят, что треугольник имеет меньшую площадь, четырёхугольник. – Площадь какой фигуры больше? Площадь – свойство фигуры, занимать место на плоскости.  Площадь – это внутренняя часть фигуры. – Площадь квадрата больше, чем площадь круга? – Площадь какой фигуры больше красной или жёлтой? – Сможем ли мы сравнить площади фигур наложением? – Наложить мы не сможем эти фигуры, но можем разделить на квадраты и узнать, сколько квадратов занимают фигуры. Площадь фигуры можно измерять и другими мерками. Сравните жёлтый и красный прямоугольники по количеству квадратов. – Сколько квадратов в первом прямоугольнике, во втором? – Почему так получилось? Чтобы этого не было вводятся специальные размеры квадратов. Длина стороны квадрата 1 см.	Работают с презентацией. Треугольник занимает меньше места. Площадь четырёхугольника больше, чем площадь треугольника. Это видно на глаз. Площадь квадрата больше, чем площадь круга. Проверим способом наложения. Площадь двух кругов одинаковая. Сравнивают прямоугольники по количеству квадратов. Т.к. фигуры разбиты на квадраты разных размеров.
V. Первичное закрепление. Работа в парах.	– Образуйте фигуры, площадь которой 3 кв. см.(5,4 кв.см) Назовите площадь. Фигуры у всех разные, но что у них одинаковое? -Образуйте фигуры, площадь которой 5 кв. см. (4 кв.см) Назовите площадь. Чтение правила по учебнику стр. 27. (Квадратным сантиметром называют площадь квадрата с длиной стороны 1 см.) – Сформулируйте определение квадратного метра. – Квадратный сантиметр, квадратный дециметр, квадратный метр – это единицы площади. Их обозначают так: см2, дм2, м2. – Рассмотрите вырезанные из бумаги квадраты площадью 1 дм2, 1 см2 и 1 м2. – Сравните попарно площади этих квадратов. – В квадрате площадью 1 дм2 может уместиться ровно 100 квадратов площадью 1 см2, а в квадрате площадью 1 м2 – ровно 100 квадратов площадью 1 дм2.	Работают в парах. У учащихся модели 1кв. см. У наших фигур одинаковые площади. Читают определение квадратного дециметра, формулируют определение квадратного сантиметра, метра. Сравнивают попарно площади этих квадратов, накладывая меньший квадрат на больший.
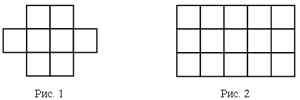
Физминутка.	Определите площади фигур на экране. 1) Площадь одного такого квадрата называют квадратным сантиметром. Пишут: 1 см2. 2) Прямоугольник на рисунке состоит из 3 полос, каждая из которых разбита на 5 квадратов со стороной 1 см.	1) Фигура состоит из 8 квадратов со стороной 1 см каждый. Значит, площадь всей фигуры равна 8 см2. 2) Весь прямоугольник состоит из 5 * 3 = 15 таких квадратов, и его площадь равна 15 см2.
VI. Самостоятель ная работа. Работа в группах.	Дополни высказывание. 1 группа. Квадратной единицей называют не квадрат, а его (площадь). 2 группа. Квадратным сантиметром называют площадь квадрата с длиной стороны (1 см). 3 группа. Квадратным дециметром называют площадь квадрата с длиной стороны (1 дм). 4 группа. Квадратным метром называют площадь квадрата с длиной стороны (1 м).	Работают в группах. Дополняют высказывание.
VIII. Систематизация и повторение.	Задание № 3 (с. 28). Работа в печатной тетради № 2. Задание № 3,стр.13. Напиши площадь данных фигур.	Читают величины, записанные единицами площади. Устанавливают взаимосвязь между изученными единицами площади: 1 дм2 = 100см2. Записывают площадь фигур.
VII. Итог урока.	Выбери правильное утверждение: 1. Единицы измерения площади: а) см б) кв.см в) кг 2. Площадь – это … а) сумма длин всех сторон б) внутренняя часть фигуры в) всё, что находится вокруг фигуры Что нового узнали на уроке? – Назовите единицы измерения площади фигуры. Пригодится ли вам в жизни умение  находить площадь фигур? – Где и зачем?	Выбирают правильное утверждение.
Рефлексия деятельности.	Покажите своё настроение в конце урока смайликом. – Что не получилось? Почему?

Комментарии преподавателя

 Наблюдение за измерением площади фигуры разными мерками

Мы уже знаем, что такое пло­щадь фи­гу­ры. Вспом­ни­те, ка­ки­ми спо­со­ба­ми можно срав­нить пло­ща­ди фигур. Пра­виль­но. Можно срав­нить пло­ща­ди на глаз, спо­со­бом на­ло­же­ния одной фи­гу­ры на дру­гую и с по­мо­щью мерок.

Рас­смот­рим, какие спо­со­бы для срав­не­ния пло­ща­ди фигур вы­бра­ли Оля, Соня и Мак­сим (рис. 1).

Рис. 1. Ил­лю­стра­ция к за­да­че

Для из­ме­ре­ния пло­ща­ди квад­ра­та Оля, Соня и Мак­сим вы­бра­ли раз­ные мерки.

Оля вы­бра­ла мерку – квад­рат, Мак­сим из­ме­рял пло­щадь квад­ра­та ше­сти­уголь­ни­ка­ми, а Соня – кру­га­ми.         

 Знакомство с единицей измерения площади – квадратным сантиметром

Как вы ду­ма­е­те, какая мерка самая удоб­ная? Ко­неч­но, самая удоб­ная мерка – квад­ра­ты. Они по­ме­сти­лись в фи­гу­ре целое число раз (рис. 2).

Рис. 2. Квад­ра­ты

У Мак­си­ма не все ше­сти­уголь­ни­ки по­ме­сти­лись пол­но­стью. По краям квад­ра­та мы видим толь­ко часть ше­сти­уголь­ни­ков. Зна­чит, из­ме­ре­ния будут неточ­ны­ми (рис. 3).

Рис. 3. Ше­сти­уголь­ни­ки

У Сони круги по­ме­сти­лись целое число раз, но между кру­га­ми есть про­бе­лы, ко­то­рые оста­лись не за­кры­ты кру­га­ми. По­это­му и эти из­ме­ре­ния будут неточ­ны­ми (рис. 4).

Рис. 4. Круги

Итак, самая удоб­ная мерка – квад­рат.

Срав­ни­те. По­че­му, в квад­ра­те Оли по­ме­сти­лось 9 мерок, а в таком же квад­ра­те у учи­те­ля по­ме­сти­лось толь­ко 4 мерки (рис. 5)?

ОЛЯ

УЧИ­ТЕЛЬ

Рис. 5. Ил­лю­стра­ция к за­да­че

Пра­виль­но. По­то­му что обе мерки – квад­ра­ты, но они раз­но­го раз­ме­ра.

Ма­те­ма­ти­ки всего мира до­го­во­ри­лись из­ме­рять пло­ща­ди фигур оди­на­ко­вы­ми мер­ка­ми. По­зна­ко­мим­ся с одной из квад­рат­ных еди­ниц (рис. 6).

Рис. 6. Квад­рат­ный сан­ти­метр

 Измерение площади фигур с помощью квадратных сантиметров

Пло­щадь квад­ра­та, сто­ро­на ко­то­ро­го 1 см, – это еди­ни­ца пло­ща­ди, квад­рат­ный сан­ти­метр.

По­тре­ни­ру­ем­ся из­ме­рять пло­ща­ди фигур в квад­рат­ных сан­ти­мет­рах, чтобы срав­нить их пло­ща­ди (рис. 7).

Рис. 7. Ил­лю­стра­ция к за­да­че

Для этого со­счи­та­ем, сколь­ко квад­рат­ных сан­ти­мет­ров в каж­дой фи­гу­ре (рис. 8).

Рис. 8. Ил­лю­стра­ция к за­да­че

В жёл­той фи­гу­ре 8 квад­рат­ных сан­ти­мет­ров, а в зе­лё­ной фи­гу­ре – 11 квад­рат­ных сан­ти­мет­ров. Зна­чит пло­щадь зе­лё­ной фи­гу­ры боль­ше, чем пло­щадь жёл­той фи­гу­ры (рис. 9).

Рис. 9. Ил­лю­стра­ция к за­да­че

 Выполнение арифметических действий с квадратными сантиметрами

Вы­пол­ни­те за­да­ние. Срав­ни­те дан­ные ве­ли­чи­ны и по­ставь­те знак срав­не­ния.

5 см2 … 8 см2

3 см2 + 6 см2….10 см2 – 1 см2

14 см2 – 6 см2 … 5 см2 + 4 см2

Про­верь­те себя.

Рас­смот­ри­те гео­мет­ри­че­скую фи­гу­ру. Можно ли сразу опре­де­лить пло­щадь дан­но­го квад­ра­та (рис. 10)?

Рис. 10. Ил­лю­стра­ция к за­да­че

Дан­ный квад­рат раз­де­ли­ли на квад­рат­ные сан­ти­мет­ры. По­это­му мы можем узнать пло­щадь дан­но­го квад­ра­та. Она равна 9 см2.

Те­перь этот квад­рат раз­де­ли­ли на гео­мет­ри­че­ские фи­гу­ры и со­ста­ви­ли из них домик. Ка­ко­ва пло­щадь до­ми­ка, со­став­лен­но­го из гео­мет­ри­че­ских фигур (рис. 11)? 

Рис. 11. Ил­лю­стра­ция к за­да­че

Рас­суж­да­ем так: пло­щадь квад­ра­та – 9 см2, а домик со­став­лен из фигур этого квад­ра­та, зна­чит, пло­щадь до­ми­ка будет равна 9 см2.

 Выполнение тренировочных упражнений по измерению и сравнению площади фигуры

Вы­пол­ни­те за­да­ние. Среди фигур, пред­став­лен­ных на ри­сун­ке, сна­ча­ла най­ди­те фи­гу­ры, рав­ные по форме, а затем фи­гу­ры, рав­ные по пло­ща­ди (рис. 12).

Рис. 12. Ил­лю­стра­ция к за­да­че

Про­верь­те себя.

Фи­гу­ры, рав­ные по форме: № 1, № 4.

Фи­гу­ры, рав­ные по пло­ща­ди: № 1, № 3, № 4 (рис. 13).

Рис. 13. Ил­лю­стра­ция к за­да­че

Как вы­ду­ма­е­те, чему будет равна пло­щадь фи­гу­ры, со­став­лен­ной из 1 и 2 фигур?

Можно рас­суж­дать так. Пло­щадь пер­вой фи­гу­ры – 7 см2, а пло­щадь вто­рой фи­гу­ры – 5 см2. Чтобы узнать пло­щадь со­став­лен­ной фи­гу­ры, надо эти ве­ли­чи­ны сло­жить. Тогда пло­щадь новой фи­гу­ры будет равна 12 см2 (рис. 14).

Рис. 14. Ил­лю­стра­ция к за­да­че

Се­год­ня на уроке мы по­зна­ко­ми­лись с еди­ни­цей пло­ща­ди, квад­рат­ным сан­ти­мет­ром, по­тре­ни­ро­ва­лись вы­чис­лять и срав­ни­вать пло­ща­ди фигур в квад­рат­ных сан­ти­мет­рах.

ИСТОЧНИКИ

http://interneturok.ru/ru/school/matematika/3-klass/tema/edinitsa-ploschadi-kvadratnyy-santimetr?seconds=0&chapter_id=1779