Как найти квадратный корень способы – Сайт, где вы сможете решить свои вопросы

Методы вычисления квадратных корней — это вычислительные алгоритмы для вычисления приближённых значений главных (или неотрицательных) квадратных корней (обычно обозначаемых как ${displaystyle {sqrt {S}}}$ , ${displaystyle {sqrt[{2}]{S}}}$ или ${displaystyle S^{1/2}}$ ) вещественного числа. Арифметически это означает, что если дано число $S$ , процедура находит число, которое при умножении на себя даёт $S$ . Алгебраически это означает процедуру нахождения неотрицательного корня уравнения ${displaystyle x^{2}-S=0}$ . Геометрически это означает построение стороны квадрата с заданной площадью.

Любое вещественное число имеет два корня^[1]. Главное значение квадратного корня большинства чисел является иррациональным числом с бесконечной последовательностью десятичных цифр. Как результат, десятичное представление любого такого квадратного корня может быть вычислено только приближённо с конечной точностью (знаков после запятой). Однако, даже если мы берём корень от полного квадрата целого числа, так что результат имеет конечное представление, некоторые процедуры, используемые для вычисления корня, могут вернуть лишь ряд приближений с возрастающей точностью.

Представление вещественного числа в виде цепной дроби может быть использовано вместо десятичного или двоичного разложения и это представление имеет свойство, что квадратный корень любого рационального числа (который не является полным квадратом) имеет период, то есть периодическое разложение, похожее на то, как рациональные числа имеют повторяющееся разложения десятичной системе счисления.

Большинство общепризнанных аналитических методов являются итеративными и состоят из двух шагов: нахождения подходящего начального значения с последующим итеративным уточнением пока не будет достигнут определённый критерий остановки. Начальным значением может быть любое число, но если оно ближе к конечному значению, число требуемых итераций потребуется меньше. Наиболее известным таким методом, да ещё и удобным для программирования, является метод Ньютона, который основывается на вычислении производной. Несколько методов, такие как обычное деление вручную по схеме Горнера или разложение в ряд, не требуют задание начального значения. В некоторых приложениях требуется найти целочисленный квадратный корень, который является квадратным корнем, округлённым до ближайшего целого (в этом случае может быть использована модифицированная процедура).

Используемый метод зависит от того, как результат будет использован (то есть, насколько точен должен быть результат) и какие средства есть под рукой. Методы можно грубо разбить на те, которые можно выполнить в уме, которые требуют карандаша и листа бумаги, или те, которые реализуются в виде программы и выполняются на компьютерах или других вычислительных устройствах. Могут приниматься в расчёт скорость сходимости (сколько итераций потребуется для достижения заданной точности), вычислительной сложности отдельных операций (таких как деление) или итераций, и распределение ошибок (точность результата).

Процедуры поиска квадратных корней (в частности, корня из 2) известны по меньшей мере со времён древнего Вавилона (17-й век до нашей эры). Метод Герона из Египта первого века был первым проверяемым алгоритмом для вычисления квадратного корня. Современные аналитические методы начались разрабатываться после принятия арабских цифр в Западной Европе в Раннем Ренессансе. В настоящие дни почти все вычислительные устройства имеют функцию быстрого и точного вычисления квадратного корня в виде встроенной конструкции языка программирования, библиотечной функции или аппаратного оператора, которые основываются на описанных ниже процедурах.

Начальная оценка[править | править код]

Многие итеративные алгоритмы вычисления квадратного корня требуют задания начального случайного значения. Это значение должно быть ненулевым положительным числом. Оно должно быть между 1 и $S$ , числом, квадратным корень которого мы ищем, поскольку квадратный корень должен быть в этих пределах. Если начальное значение очень далеко от корня, алгоритму потребуется больше итераций. Если начать с ${displaystyle x_{0}=1}$ (или с $S$ ), будет отработано лишних примерно ${displaystyle {tfrac {1}{2}}vert log _{2}Svert }$ итераций просто для получения порядка корня. Поэтому полезно иметь грубую оценку корня, которая может иметь слабую точность, но зато легко вычисляется. В общем случае чем точнее оценка, тем быстрее сходимость. Для метода Ньютона (называемого также вавилонским или методом Герона), начальное значение несколько большее корня даёт более быструю сходимость, по сравнению с начальным значением, меньшим корня.

Вообще говоря, оценка рассматривается на произвольном интервале, в котором известно, что в нём содержится корень (таком как ${displaystyle [x_{0},S/x_{0}]}$ ). Получение лучшей оценки вовлекает либо получение более узких границ интервала, либо лучшего функционального приближения к ${displaystyle f(x).}$ Последнее обычно означает использование для аппроксимации многочленов более высокого порядка, хотя не все аппроксимации используют многочлены. Общие методы оценки бывают скалярные, линейные, гиперболические и логарифмические. Десятичная система счисления обычно используется для оценки в уме или на бумаге. Двоичная система счисления более пригодна для компьютерных оценок. При оценке экспонента и мантисса обычно обрабатываются отдельно.

Десятичная оценка[править | править код]

Обычно число $S$ выражается в экспоненциальном виде как ${displaystyle atimes 10^{2n}}$ , где ${displaystyle 1leqslant a<100}$ , а n — целое число, тогда оценкой возможного квадратного корня может быть ${displaystyle {sqrt {a}}times 10^{n}}$ , где ${displaystyle 1leqslant {sqrt {a}}<10}$ .

Скалярные оценки[править | править код]

Скалярные методы делят весь диапазон на интервалы и оценка в каждом интервале представлена одним числом. Если диапазон рассматривается как один интервал, то арифметическое среднее (5,5) или геометрическое среднее ( ${displaystyle {sqrt {10}}approx 3{,}16)times 10^{n}}$ являются приемлемыми оценками. Абсолютная и относительная оценка для этих оценок будет отличаться. В общем случае отдельное число будет очень неточно. Более точные оценки разбивают диапазон на два и более интервалов, но скалярная оценка продолжает оставаться очень грубой.

Для двух интервалов, разбитых геометрически, квадратный корень ${displaystyle {sqrt {S}}={sqrt {a}}times 10^{n}}$ можно оценить как^[2].

${displaystyle {sqrt {S}}approx {begin{cases}2cdot 10^{n}&{text{если }}a<10,\6cdot 10^{n}&{text{если }}ageqslant 10.end{cases}}}$

Эта оценка имеет максимальную абсолютную погрешность ${displaystyle 4cdot 10^{n}}$ в точке = 100 и максимальную относительную ошибку в 100% в точке = 1.

Например, для ${displaystyle S=125348}$ с разложением ${displaystyle 12{,}5348times 10^{4}}$ , оценка будет ${displaystyle {sqrt {S}}approx 6cdot 10^{2}=600}$ . ${displaystyle {sqrt {125348}}=354{,}0}$ , с абсолютной ошибкой 246 и относительной ошибкой почти 70%.

Линейная оценка[править | править код]

Лучшей оценкой и стандартным методом является линейное приближение функции $y = x^2$ на малой дуге. Если, как и выше, степень выделена из числа $S$ , а интервал сокращён до ${displaystyle [1,100]}$ , можно использовать секущую или касательную где-то вдоль дуги для аппроксимации, но прямая регрессии метода наименьших квадратов будет более точной.

Прямая, получающаяся методом наименьших квадратов, минимизирует среднее расстояние между оценкой и значением функции. Её уравнение — ${displaystyle y=8{,}7x-10}$ . После преобразования ${displaystyle x=0{,}115y+1{,}15}$ и округления коэффициентов для упрощения вычислений получим

${displaystyle {sqrt {S}}approx (a/10+1{,}2)cdot 10^{n}}$

Это лучшая оценка в среднем, которую можно получить одной попыткой линейной аппроксимации функции $y=x^2$ в интервале ${displaystyle [1,100]}$ . Оценка имеет максимальную абсолютную ошибку 1,2 в точке a=100 и максимальную относительную ошибку в 30% в точках S=1 и 10^[3].

Чтобы разделить на 10, вычитаем единицу из показателя степени $a$ или, образно говоря, передвигаем десятичную запятую на одну позицию влево. Для этой формулы любая добавленная константа, равная 1 плюс маленькое приращение, даёт удовлетворительную оценку, так что запоминать точное число нет необходимости. Аппроксимация (округлённая или не округлённая) с помощью одной прямой, стягивающей область ${displaystyle [1,100]}$ по точности даёт не более одного верного знака. Относительная ошибка более чем 1/2², так что даёт менее 2 битов информации. Точность сильно ограничена, поскольку область охватывает два порядка, что достаточно большая величина для такого рода оценок.

Существенно лучшую оценку можно получить при помощи кусочно–линейной аппроксимации, то есть с помощью нескольких отрезков, которые приближают поддугу исходной дуги. Чем больше отрезков используется, тем лучше приближение. Наиболее употребительно применение касательных. Критичным моментом является как делить дугу и где располагать точки касания. Действенным методом деления дуги от y=1 до y=100 является геометрический — для двух интервалов границей интервалов является квадратный корень исходного интервала, 1*100, то есть ${displaystyle [1,{sqrt[{2}]{100}}]}$ и ${displaystyle [{sqrt[{2}]{100}},100]}$ . Для трёх интервалов будут кубические корни — ${displaystyle [1,{sqrt[{3}]{100}}],[{sqrt[{3}]{100}},({sqrt[{3}]{100}})^{2}]}$ , и ${displaystyle [({sqrt[{3}]{100}})^{2},100]}$ , и так далее. Для двух интервалов ${displaystyle {sqrt[{2}]{100}}=10}$ является очень удобным числом. Легко получить касательные прямые в точках касания ${displaystyle x={sqrt {1*{sqrt {10}}}}}$ и ${displaystyle x={sqrt {10*{sqrt {10}}}}}$ . Их уравнения: ${displaystyle y=3{,}56x-3{,}16}$ и ${displaystyle y=11{,}2x-31{,}6}$ . Обращая уравнения, получим, что квадратные корни равны ${displaystyle x=0{,}28y+0{,}89}$ и ${displaystyle x=0{,}089y+2{,}8}$ . Тогда для ${displaystyle S=acdot 10^{2n}}$ :

${displaystyle {sqrt {S}}approx {begin{cases}(0{,}28a+0{,}89)cdot 10^{n}&{text{если }}a<10,\(0{,}089a+2{,}8)cdot 10^{n}&{text{если }}ageqslant 10.end{cases}}}$

Максимальные абсолютные значения оказываются в правых границах интервалов, в точках a=10 и 100, и равны 0,54 и 1,7 соответственно. Максимальные относительные ошибки появляются на концах интервалов, в точках a=1, 10 и 100, и равны 17%. 17% или 0,17. Они больше, чем 1/10, так что метод даёт точность менее одной значащей цифры.

Гиперболическая оценка[править | править код]

В некоторых случаях может оказаться действенной гиперболическая оценка, поскольку гипербола также является выпуклой кривой и может лежать вдоль дуги Y = x² лучше, чем прямая. Гиперболическая оценка вычислительно более сложная, поскольку для неё нужно деление на число с плавающей запятой. Почти оптимальной гиперболической аппроксимацией к x² на интервале ${displaystyle [1,100]}$ является ${displaystyle y=190/(10-x)-20}$ . После преобразования получим ${displaystyle x=-190/(y+20)+10}$ . Тогда для ${displaystyle S=acdot 10^{2n}}$ :

${displaystyle {sqrt {S}}approx left({frac {-190}{a+20}}+10right)cdot 10^{n}}$

Деление с плавающей запятой должно быть с точностью до одного десятичного знака, поскольку вся оценка даёт такую точность, и такое деление можно выполнить в уме. Гиперболическая оценка в среднем лучше, чем скалярная или линейная оценка. Её максимальная абсолютная ошибка составляет 1,58 в точке 100, а максимальная относительная ошибка составляет 16,0% в точке 10. Для худшего случая a=10 оценка равна 3,67. Если начать с 10 и применять итерации Нютона-Рапсона напрямую, требуется две итерации, которые дают 3,66, прежде чем достичь точности гиперболической оценки. Для более типичного случая наподобие 75 гиперболическая оценка даёт 8,00 и требуется 5 итераций Ньютона-Рапсона с начальным значением 75, чтобы получить более точный результат.

Арифметическая оценка[править | править код]

Метод, аналогичный кусочно-линейной аппроксимации, но использующий лишь арифметические операции вместо алгебраических уравнений, использует таблицу умножения в обратную сторону — квадратный корень чисел между 1 и 100 где-то между 1 и 10, так что, поскольку мы знаем, что 25 является точным квадратом (5 × 5) и 36 является точным квадратом (6 × 6), то квадратный корень из числа, которое больше 25, но меньше 36, начинается с цифры 5. Аналогично для чисел между другими квадратами. Этот метод даёт правильный первый знак, но точность его всего одна цифра — первая цифра квадратного корня из 35, например, равна 5, но сам корень из 35 почти равен 6.

Лучше делить интервал между двумя квадратами пополам. Так что корень любого числа между 25 и половины пути до 36 (что есть 30,5) оценивается как 5, остальные числа, большие 30,5 вплоть до 36 оцениваются как 6^[4]. Процедура требует очень мало арифметики для нахождения середины двух произведений из таблицы. Вот таблица таких чисел:

a	nearest square	${displaystyle k={sqrt {a}}}$ est.
1 to 2,5	1 (= 1²)	1
2,5 to 6,5	4 (= 2²)	2
6,5 to 12,5	9 (= 3²)	3
12,5 to 20,5	16 (= 4²)	4
20,5 to 30,5	25 (= 5²)	5
30,5 to 42,5	36 (= 6²)	6
42,5 to 56,5	49 (= 7²)	7
56,5 to 72,5	64 (= 8²)	8
72,5 to 90,5	81 (= 9²)	9
90,5 to 100	100 (= 10²)	10

Конечной операцией будет умножение оценки k на степень десятки, делённой пополам, так что для ${displaystyle S=acdot 10^{2n}}$ ,

${displaystyle {sqrt {S}}approx kcdot 10^{n}}$

Метод даёт точность в одну значащую цифру, поскольку он округляет до лучшей первой цифры.

Метод можно распространить до 3 значащих цифр в большинстве случаев, интерполируя между ближайшими квадратами. Если ${displaystyle k^{2}leqslant a<(k+1)^{2}}$ , то ${sqrt {a}}$ примерно равен k плюс дробь, равная разности a и $k^{2}$ , делённой на разность между двумя квадратами:

${displaystyle {sqrt {a}}approx k+R}$ где ${displaystyle R={frac {(a-k^{2})}{(k+1)^{2}-k^{2}}}}$

Конечной операцией, как и выше, служит умножение результата на степень десятки, делённой пополам

${displaystyle {sqrt {S}}={sqrt {a}}cdot 10^{n}approx (k+R)cdot 10^{n}}$

Число k есть десятичная цифра, а R есть дробь, которую следует превратить в десятичную. Дробь имеет обычно одну цифру в числителе и одну или две цифры в знаменателе, так что преобразование в десятичную дробь можно провести в уме.

Пример: найти квадратный корень из 75. ${displaystyle 75=75times 10^{2cdot 0}}$ , так что a равно 75, а n равно 0. Исходя из таблицы умножения квадратный корень мантиссы должен быть 8 с дробью, поскольку ${displaystyle 8times 8=64}$ , а ${displaystyle 9times 9=81}$ , слишком велико. Так что k равно 8 с дробью является десятичным представлением R. Дробь R имеет ${displaystyle 75-k^{2}=11}$ в числителе и ${displaystyle 81-k^{2}=17}$ в знаменателе. 11/17 чуть меньше, чем 12/18, что равно 2/3 или 0,67, так что 0,66 является хорошим предположением (здесь можно ограничиться и предположением поскольку ошибка мала). Так что оценка корня равна ${displaystyle 8+0{,}66=8{,}66}$ . √75 до трёх значащих цифр будет 8,66, так что оценка до трёх значащих цифр хорошая. Не все оценки с помощью такого метода столь точны, но они довольно близки.

Двоичная оценка[править | править код]

Когда работа ведётся в двоичной системе счисления (скажем, в процессоре компьютера), $S$ выражается как ${displaystyle atimes 2^{2n}}$ , где ${displaystyle 0{,}1_{2}leqslant a<10_{2}}$ , квадратный корень ${displaystyle {sqrt {S}}={sqrt {a}}times 2^{n}}$ можно оценить величиной

${displaystyle {sqrt {S}}approx (0{,}485+0{,}485cdot a)cdot 2^{n}}$

что является регрессией методом наименьших квадратов по 3 старшим битам. ${sqrt {a}}$ имеет максимальную абсолютную ошибку 0,0408 в точке $a$ =2 и максимальную относительную ошибку в 3,0% в точке $a$ =1. Для вычислений удобна округлённая оценка (поскольку коэффициенты являются степенями 2)

${displaystyle {sqrt {S}}approx (0{,}5+0{,}5cdot a)cdot 2^{n}}$ ^[5]

которая имеет максимальную абсолютную ошибку 0,086 в точке 2 и максимальную относительную ошибку в 6,1% в точках ${displaystyle a=0{,}5}$ и ${displaystyle a=2{,}0}$ .

Для ${displaystyle S=125348=1;1110;1001;1010;0100_{2}=1{,}1110;1001;1010;0100_{2}times 2^{16},}$ двоичное приближение даёт ${displaystyle {sqrt {S}}approx (0{,}5+0{,}5cdot a)cdot 2^{8}=1{,}0111;0100;1101;0010_{2}cdot 1;0000;0000_{2}=1{,}456cdot 256=372{,}8.}$ Поскольку ${displaystyle {sqrt {125348}}=354{,}0}$ , оценка даёт абсолютную ошибку в 19 и относительную ошибку 5,3%. Относительная ошибка чуть меньше 1/2⁴, так что приближение даёт точность до 4+ бит.

Оценку для $a$ с точностью до 8 бит можно получить путём просмотра таблицы по старшим 8 битам $a$ , учитывая, что старший бит задаётся неявно в большинстве представлений чисел с плавающей запятой, а младшие биты после 8 бит должны быть округлены. Таблица содержит 256 байт заранее вычисленных 8-битных квадратных корней. Например, для индекса 11101101₂, что в десятичной системе равно 1,8515625₁₀, значение в таблице равно 10101110₂, что в десятичной системе равно 1,359375₁₀, квадратному корню числа 1,8515625₁₀ с точностью до 8 бит (2+ десятичных знака).

Вавилонский метод[править | править код]

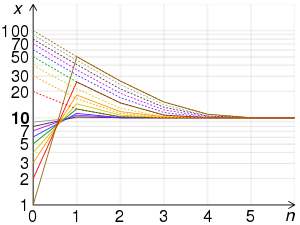
Полулогарифмические графики сравнения скорости сходимости вавилонского метода нахождения квадратного корня для 100 различных начальных значений. Отрицательное начальное значение приводит к отрицательному корню. Заметим, что более близкие к корню значения сходятся быстрее, и все приближения являются завышенными. В SVG файле наведите курсор мыши на конкретный график, чтобы видеть точки этого графика.

Возможно первым алгоритмом, используемым для аппроксимации ${displaystyle {sqrt {S}}}$ , является метод, известный как вавилонский метод, несмотря на то, что нет никаких прямых свидетельств, за исключением гипотетических умозаключений, что вавилонские математики использовали этот метод^[6]. Метод известен также как метод Герона, по имени греческого математика первого столетия Герона, который дал первое явное описание метода в своей работе 60 года Метрика^[7].Основная методика заключается в том, что если x больше квадратного корня неотрицательного вещественного числа S то ${displaystyle {tfrac {S}{x}}}$ будет меньше корня и наоборот. Так что среднее этих двух чисел резонно ожидать более близким к корню (формальное доказательство этого факта основывается на неравенстве о среднем арифметическом, геометрическом и гармоническом, которое показывает, что это среднее всегда больше квадратного корня, что обеспечивает сходимость). Метод эквивалентен использованию метода Ньютона для решения уравнения ${displaystyle x^{2}-S=0}$ .

Точнее, если x является начальным приближением для ${displaystyle {sqrt {S}}}$ , а $varepsilon$ ошибка в нашей оценке, такая что ${displaystyle S=(x+varepsilon )^{2}}$ , мы можем раскрыть скобки и получим

${displaystyle varepsilon ={frac {S-x^{2}}{2x+varepsilon }}approx {frac {S-x^{2}}{2x}},}$ поскольку ${displaystyle varepsilon ll x}$ .

Следовательно, мы можем компенсировать ошибку и обновить нашу старую оценку

${displaystyle x+varepsilon approx x+{frac {S-x^{2}}{2x}}={frac {S+x^{2}}{2x}}={frac {{frac {S}{x}}+x}{2}}equiv x_{text{обновлённый}}}$

Поскольку вычисленная ошибка не была точной, она станет нашим следующим приближением. Процесс обновления продолжается пока не достигнем нужной точности. Это алгоритм с квадратичной сходимостью, что означает, что число верных цифр приближения (грубо говоря) удваивается с каждой итерацией. Работает он так:

Начинаем с любого положительного начального значения $x_{0}$ (чем ближе к истинному квадратному корню числа S, тем лучше).
Положим $x_{{n+1}}$ равным среднему между $x_{n}$ и ${displaystyle {tfrac {S}{x_{n}}}}$ (используем среднее арифметическое для аппроксимации среднего геометрического).
Повторяем шаг 2 пока не достигнем нужной точности.

Алгоритм можно представить следующим образом:

${displaystyle x_{0}approx {sqrt {S}},}$

${displaystyle x_{n+1}={frac {1}{2}}left(x_{n}+{frac {S}{x_{n}}}right),}$

${displaystyle {sqrt {S}}=lim _{nto infty }x_{n}.}$

Алгоритм работает также хорошо и для p-адических чисел, но не может быть использован для отождествления вещественных квадратных корней с p-адичными квадратными корнями. Можно, например, построить последовательность рациональных чисел, полученных этим методом, которая сходится к +3 в случае вещественных чисел, но к -3 в 2-адичных числах.

Пример[править | править код]

Для вычисления √S, где S = 125348, с точностью до шести значащих цифр используем метод грубой оценки, описанный выше

${displaystyle {begin{aligned}{begin{array}{rlll}x_{0}&=6cdot 10^{2}&&=600{,}000\[0,3em]x_{1}&={frac {1}{2}}left(x_{0}+{frac {S}{x_{0}}}right)&={frac {1}{2}}left(600{,}000+{frac {125348}{600{,}000}}right)&=404{,}457\[0.3em]x_{2}&={frac {1}{2}}left(x_{1}+{frac {S}{x_{1}}}right)&={frac {1}{2}}left(404{,}457+{frac {125348}{404{,}457}}right)&=357{,}187\[0.3em]x_{3}&={frac {1}{2}}left(x_{2}+{frac {S}{x_{2}}}right)&={frac {1}{2}}left(357{,}187+{frac {125348}{357{,}187}}right)&=354{,}059\[0.3em]x_{4}&={frac {1}{2}}left(x_{3}+{frac {S}{x_{3}}}right)&={frac {1}{2}}left(354{,}059+{frac {125348}{354{,}059}}right)&=354{,}045\[0.3em]x_{5}&={frac {1}{2}}left(x_{4}+{frac {S}{x_{4}}}right)&={frac {1}{2}}left(354{,}045+{frac {125348}{354{,}045}}right)&=354{,}045end{array}}end{aligned}}}$

Поэтому ${displaystyle {sqrt {125348}}approx 354{,}045}$ .

Сходимость[править | править код]

Предположим, что x₀ > 0 и S > 0. Тогда для любого n x_n > 0. Относительная ошибка^[en] x_n определена как

${displaystyle varepsilon _{n}={frac {x_{n}}{sqrt {S}}}-1>-1}$

а тогда

${displaystyle x_{n}={sqrt {S}}cdot (1+varepsilon _{n}).}$

Теперь можно показать, что

${displaystyle varepsilon _{n+1}={frac {varepsilon _{n}^{2}}{2(1+varepsilon _{n})}}geqslant 0.}$

а следовательно

${displaystyle varepsilon _{n+2}leqslant min left{{frac {varepsilon _{n+1}^{2}}{2}},{frac {varepsilon _{n+1}}{2}}right}}$

а отсюда следует гарантированная сходимость и эта сходимость квадратичная.

Сходимость в худшем случае[править | править код]

Если использовать метод грубой оценки с вавилонским методом, то наихудшие случаи точности в нисходящей последовательности:

${displaystyle {begin{aligned}S&=1;&x_{0}&=2;&x_{1}&=1{,}250;&varepsilon _{1}&=0{,}250.\S&=10;&x_{0}&=2;&x_{1}&=3{,}500;&varepsilon _{1}&<0{,}107.\S&=10;&x_{0}&=6;&x_{1}&=3{,}833;&varepsilon _{1}&<0{,}213.\S&=100;&x_{0}&=6;&x_{1}&=11{,}333;&varepsilon _{1}&<0{,}134.end{aligned}}}$

А тогда в любом случае

${displaystyle varepsilon _{1}leqslant 2^{-2}.,}$

${displaystyle varepsilon _{2}<2^{-5}<10^{-1}.,}$

${displaystyle varepsilon _{3}<2^{-11}<10^{-3}.,}$

${displaystyle varepsilon _{4}<2^{-23}<10^{-6}.,}$

${displaystyle varepsilon _{5}<2^{-47}<10^{-14}.,}$

${displaystyle varepsilon _{6}<2^{-95}<10^{-28}.,}$

${displaystyle varepsilon _{7}<2^{-191}<10^{-57}.,}$

${displaystyle varepsilon _{8}<2^{-383}<10^{-115}.,}$

Ошибки округления ослабляют сходимость. Рекомендуется хранить по меньшей мере одну лишнюю цифру выше желаемой точности x_n, чтобы минимизировать ошибки округления.

Метод Бакхшали[править | править код]

Этот метод для поиска приближения квадратного корня был написан в древнеиндийской рукописи, называемой манускриптом Бакхшали. Метод эквивалентен двум итерациям вавилонского метода с начальным значением x₀. Таким образом, алгоритм является квадратично сходящимся, что означает, что число верных знаков приближения увеличивается примерно в четыре раза с каждой итерацией^[8]. Представление алгоритма в современной нотации следующее: Следует вычислить ${displaystyle {sqrt {S}}}$ , пусть x₀² будет начальным приближением к корню S. Последовательно выполняются итерации

${displaystyle {begin{aligned}a_{n}&={frac {S-x_{n}^{2}}{2x_{n}}},\b_{n}&=x_{n}+a_{n},\x_{n+1}&=b_{n}-{frac {a_{n}^{2}}{2b_{n}}}=(x_{n}+a_{n})-{frac {a_{n}^{2}}{2(x_{n}+a_{n})}}.end{aligned}}}$

Это можно использовать для построения рационального приближения к квадратному корню, начав с целого числа. Если ${displaystyle x_{0}=N}$ — это целое число, выбранное так, что $N^2$ близко к S, и ${displaystyle d=S-N^{2}}$ — это разность, абсолютная величина которой минимизируется, то первую итерацию можно записать следующим образом:

${displaystyle {sqrt {S}}approx N+{frac {d}{2N}}-{frac {d^{2}}{8N^{3}+4Nd}}={frac {8N^{4}+8N^{2}d+d^{2}}{8N^{3}+4Nd}}={frac {N^{4}+6N^{2}S+S^{2}}{4N^{3}+4NS}}={frac {N^{2}(N^{2}+6S)+S^{2}}{4N(N^{2}+S)}}.}$

Метод Бакхшали может быть обобщён для вычисления произвольного корня, включая дробные корни^[9].

Пример[править | править код]

Используем тот же пример, что был приведён для вавилонского метода. Пусть ${displaystyle S=125348.}$ Тогда первая итерация даёт

${displaystyle {begin{aligned}x_{0}&=600\a_{1}&={frac {125348-600^{2}}{2times 600}}&&=&-195{,}543\b_{1}&=600+(-195{,}543)&&=&404{,}456\x_{1}&=404{,}456-{frac {(-195{,}543)^{2}}{2times 404{,}456}}&&=&357{,}186end{aligned}}}$

Аналогично вторая итерация даёт

${displaystyle {begin{aligned}a_{2}&={frac {125348-357{,}186^{2}}{2times 357{,}186}}&&=&-3{,}126\b_{2}&=357{,}186+(-3{,}126)&&=&354{,}060\x_{2}&=354{,}06-{frac {(-3{,}1269)^{2}}{2times 354{,}06}}&&=&354{,}046end{aligned}}}$

Цифра за цифрой[править | править код]

Это метод последовательного поиска каждой цифры квадратного корня. Метод медленнее вавилонского, но имеет некоторые преимущества

Он проще для вычислений вручную.
Каждый найденный знак корня заведомо верный, то есть он не будет изменён на следующих итерациях.
Если представление квадратного корня имеет конечное число цифр, алгоритм завершается после последней найденной цифры. Таким образом, он может быть использован для проверки, что данное число является полным квадратом.
Алгоритм работает в любой системе счисления, и естественно, работа алгоритма зависит от выбранной системы счисления.

Палочки Непера включают дополнительные средства для выполнения этого алгоритма. Алгоритм вычисления n-го корня цифра за цифрой^[en] является обобщением этого метода.

Основной принцип[править | править код]

Рассмотрим сначала случай нахождения квадратного корня из числа Z, являющегося квадратом двузначного числа XY, где X — это цифра десятков, а Y — цифра единиц. Имеем:

${displaystyle Z=(10X+Y)^{2}=100X^{2}+20XY+Y^{2}}$

Сначала определим значение X. X — это наибольшая цифра, такая что X² не превосходит Z, от которого отброшены две последние цифры.

На следующей итерации соединяем пару цифр, умножая X на 2 и помещая результат в позицию десятков, а затем пытаемся найти, чему же равно Y.

Поскольку в нашем случае ответом является точный квадратный корень, алгоритм останавливается.

Та же идея может быть распространена на вычисление произвольного квадратного корня. Представим, что мы можем найти квадратный корень из N как сумму n положительных чисел, таких что

${displaystyle N=(a_{1}+a_{2}+a_{3}+dotsb +a_{n})^{2}.}$

Путём многократного использования тождества

${displaystyle (x+y)^{2}=x^{2}+2xy+y^{2},}$

правую часть можно представить в виде

${displaystyle {begin{aligned}&(a_{1}+a_{2}+a_{3}+dotsb +a_{n})^{2}\=&,a_{1}^{2}+2a_{1}a_{2}+a_{2}^{2}+2(a_{1}+a_{2})a_{3}+a_{3}^{2}+dotsb +a_{n-1}^{2}+2left(sum _{i=1}^{n-1}a_{i}right)a_{n}+a_{n}^{2}\=&,a_{1}^{2}+[2a_{1}+a_{2}]a_{2}+[2(a_{1}+a_{2})+a_{3}]a_{3}+dotsb +left[2left(sum _{i=1}^{n-1}a_{i}right)+a_{n}right]a_{n}.end{aligned}}}$

Это выражение позволяет нам найти квадратный корень последовательным подбором значений $a_{i}$ . Предположим, что числа ${displaystyle a_{1},ldots ,a_{m-1}}$ уже подобраны, тогда m-й член задаётся выражением ${displaystyle Y_{m}=[2P_{m-1}+a_{m}]a_{m},}$ , где ${displaystyle P_{m-1}=sum _{i=1}^{m-1}a_{i}}$ является найденным приближением к квадратному корню. Теперь каждый новый подбор $a_m$ должен удовлетворять рекурсии

${displaystyle X_{m}=X_{m-1}-Y_{m},}$

так что ${displaystyle X_{m}geqslant 0}$ для всех ${displaystyle 1leqslant mleqslant n,}$ при начальном значении ${displaystyle X_{0}=N.}$ Если ${displaystyle X_{n}=0,}$ найден точный квадратный корень. Если нет, то сумма $a_{i}$ даёт подходящую аппроксимацию к квадратному корню и $X_n$ будет ошибкой аппроксимации.

Например, в десятичной системе мы имеем

${displaystyle N=(a_{1}cdot 10^{n-1}+a_{2}cdot 10^{n-2}+cdots +a_{n-1}cdot 10+a_{n})^{2},}$

где ${displaystyle 10^{n-i}}$ являются указателями положения цифр, а коэффициенты ${displaystyle a_{i}in {0,1,2,ldots ,9}}$ . На каждом m-м шаге вычисления квадратного корня находится приближённый квадратный корень. Величина ${displaystyle P_{m-1}}$ и суммируемые члены $Y_{m}$ задаются формулами

${displaystyle P_{m-1}=sum _{i=1}^{m-1}a_{i}cdot 10^{n-i}=10^{n-m+1}sum _{i=1}^{m-1}a_{i}cdot 10^{m-i-1},}$

${displaystyle Y_{m}=[2P_{m-1}+a_{m}cdot 10^{n-m}]a_{m}cdot 10^{n-m}=left[20sum _{i=1}^{m-1}a_{i}cdot 10^{m-i-1}+a_{m}right]a_{m}cdot 10^{2(n-m)}.}$

Поскольку указатели положения $Y_{m}$ имеют чётную степень 10, нам нужно работать только с парой старших цифр в оставшемся члене ${displaystyle X_{m-1}}$ на любом m-м шаге. Раздел ниже систематизирует эту процедуру.

Очевидно, что подобный метод может быть использован для вычисления квадратного корня в любой системе счисления, не обязательно в десятичной. Например, нахождение цифра за цифрой квадратного корня в двоичной системе довольно эффективно, поскольку значение $a_{i}$ ищется в малом наборе цифр {0,1}. Это делает вычисление более быстрым, поскольку на каждом шаге значение $Y_{m}$ либо равно ${displaystyle Y_{m}=0}$ для ${displaystyle a_{m}=0}$ , либо ${displaystyle Y_{m}=2P_{m-1}+1}$ для ${displaystyle a_{m}=1}$ . Факт, что имеется всего две возможности для $a_m$ также делает проще процесс выбора значения $a_m$ на m-м шаге вычислений. Это потому, что нам нужно лишь проверить, что ${displaystyle Y_{m}leqslant X_{m-1}}$ для ${displaystyle a_{m}=1.}$ Если это условие выполняется, мы берём ${displaystyle a_{m}=1}$ ; а если не выполняется, то берём ${displaystyle a_{m}=0.}$ Также факт, что умножение на 2 осуществляется сдвигом влево, помогает при вычислениях.

Десятичная система счисления[править | править код]

Запишем исходное число в десятичном виде. Числа, записываются по аналогии алгоритму деления столбиком, и, как и в длинном делении, квадратный корень будет писаться в верхней строке. Теперь разобьём цифры на пары, начиная с запятой, в обе стороны от неё. Десятичная запятая квадратного корня будет на десятичной запятой квадрата. Одна цифра квадратного корня записывается над парой цифр квадрата.

Начиная с крайне левой позиции выполняем следующую процедуру для каждой пары цифр:

Сносим вниз старшую пару ещё неиспользованных цифр (если все цифры использованы, пишем “00”) и записываем их справа от остатка предыдущего шага (на первом шаге остатка нет). Другими словами, умножаем остаток на 100 и добавляем две цифры. Это будет текущим значением c.
Находим p, y и x следующим образом:
Вычитаем y из c для образования нового остатка.
Если остаток равен нулю и нет больше цифр, которые можно спустить вниз, алгоритм останавливается. В противном случае возвращаемся на шаг 1 и выполняем следующую итерацию.

Примеры[править | править код]

Находим квадратный корень из 152,2756.

          1  2. 3  4 
       /
     /  01 52,27 56

         01                   1*1 <= 1 < 2*2                 x = 1
         01                     y = x*x = 1*1 = 1
         00 52                22*2 <= 52 < 23*3              x = 2
         00 44                  y = (20+x)*x = 22*2 = 44
            08 27             243*3 <= 827 < 244*4           x = 3
            07 29               y = (240+x)*x = 243*3 = 729
               98 56          2464*4 <= 9856 < 2465*5        x = 4
               98 56            y = (2460+x)*x = 2464*4 = 9856
               00 00          Алгоритм останавливается: Ответ 12,34

Двоичная система счисления[править | править код]

Этот раздел использует формализм раздела «Вычисление цифра за цифрой» с небольшими изменениями, что ${displaystyle N^{2}=(a_{n}+dotsb +a_{0})^{2}}$ , а каждое $a_m$ равно $2^{m}$ или ${displaystyle 0}$ .
Теперь мы пробегаем по всем $2^{m}$ от $2^{n}$ вниз до $2^0$ и строим приближённое решение ${displaystyle P_{m}=a_{n}+a_{n-1}+ldots +a_{m}}$ в виде суммы всех $a_{i}$ , для которых мы найдём значение.
Чтобы определить, равно ли $a_m$ значению $2^{m}$ или ${displaystyle 0}$ , мы берём ${displaystyle P_{m}=P_{m+1}+2^{m}}$ . Если ${displaystyle P_{m}^{2}leqslant N^{2}}$ (то есть квадрат нашего приближения включая $2^{m}$ не превосходит исходного квадрата), то полагаем ${displaystyle a_{m}=2^{m}}$ , в противном случае полагаем ${displaystyle a_{m}=0}$ и ${displaystyle P_{m}=P_{m+1}}$ .
Чтобы избежать возведения в квадрат ${displaystyle P_{m}}$ на каждом шаге, мы запоминаем разность ${displaystyle X_{m}=N^{2}-P_{m}^{2}}$ и обновляем её на каждой итерации, полагая ${displaystyle X_{m}=X_{m+1}-Y_{m}}$ с ${displaystyle Y_{m}=P_{m}-P_{m+1}=2P_{m+1}a_{m}+a_{m}^{2}}$ .
Первоначально мы устанавливаем ${displaystyle a_{n}=P_{n}=2^{n}}$ для наибольшего $n$ с ${displaystyle (2^{n})^{2}=4^{n}leqslant N^{2}}$ .

В качестве дополнительной оптимизации сохраняем ${displaystyle P_{m+1}2^{m+1}}$ и ${displaystyle (2^{m})^{2}}$ , два члена $Y_{m}$ в случае, когда $a_m$ не нуль, в отдельных переменных ${displaystyle c_{m}}$ , ${displaystyle d_{m}}$ :

${displaystyle c_{m}=P_{m+1}2^{m+1}}$

${displaystyle d_{m}=(2^{m})^{2}}$

${displaystyle Y_{m}={begin{cases}c_{m}+d_{m}&{text{если }}a_{m}=2^{m}\0&{text{если }}a_{m}=0end{cases}}}$

${displaystyle c_{m}}$ и ${displaystyle d_{m}}$ можно эффективно обновлять на каждом шаге:

${displaystyle c_{m-1}=P_{m}2^{m}=(P_{m+1}+a_{m})2^{m}=P_{m+1}2^{m}+a_{m}2^{m}={begin{cases}c_{m}/2+d_{m}&{text{если }}a_{m}=2^{m}\c_{m}/2&{text{если }}a_{m}=0end{cases}}}$

${displaystyle d_{m-1}={frac {d_{m}}{4}}}$

Заметим, что

${displaystyle c_{-1}=P_{0}2^{0}=P_{0}=N}$ , что является конечным результатом, возвращаемым функцией, представленной ниже.

Реализация алгоритма на языке C^[10]:

int32_t isqrt(int32_t n) 
{ assert(("входное значение должно быть неотрицательным", n > 0));
  int32_t x = n;    // 
  int32_t c = 0;    // 
  //  начинается с наибольшей степени четырёх <= n
  int32_t d = 1 << 30; // Второй старший бит устанавливаем в 1.
                        // То же самое, что ((unsigned)INT32_MAX + 1) / 2.
  while (d > n) d >>= 2;
  while (d != 0)    // для 
  { if (x >= c + d) // если , то 
    { x -= c + d;       // 
     c = (c >> 1) + d;  // 
   } else
          c >>= 1;      // 
    d >>= 2;            // 
  }
  return c;             // 
}

Можно реализовать более быстрый алгоритм как в двоичной, так и в десятичной системе счисления, если использовать таблицы для выбора, то есть реализация принципа использование больше памяти сокращает время исполнения^[11].

Экспоненциальное тождество[править | править код]

Карманные калькуляторы обычно реализуют хорошие программы вычисления экспоненты и натурального логарифма. Вычисление квадратного корня S тогда производится с помощью свойств логарифмов ( ${displaystyle ln x^{n}=nln x}$ ) и экспоненты ( ${displaystyle e^{ln x}=x}$ ):

${displaystyle {sqrt {x}}=e^{{frac {1}{2}}ln x},,x>0.}$

Или в более общем случае:

${displaystyle {sqrt[{n}]{x}}=e^{{frac {1}{n}}ln x},,x>0.}$

Знаменатель дроби n соответствует степени корня. В случае квадратного корня знаменатель равен 2. То же самое тождество используется для вычисления квадратного корня с помощью таблиц логарифмов или логарифмических линеек.

Такой метод вычисления квадратного корня удобен для калькуляторов, поскольку они обычно не критичны ко времени выполнения операции. Однако ресурсоемкость данного метода делает его малопригодным для использования в ЭВМ, где простые арифметические операции должны обладать минимальными задержками. Тем не менее описанный метод вычисления квадратного корня применялся в ЭВМ ZX Spectrum.

Итеративный метод с двумя переменными[править | править код]

Этот метод применим для поиска квадратного корня из ${displaystyle 0<S<3,!}$ и лучше всего сходится для ${displaystyle Sapprox 1}$ .
Это, однако, не является существенным ограничением для вычислений на компьютерах, поскольку в представлениях двоичных чисел с плавающей запятой и с фиксированной запятой тривиально умножить ${displaystyle S,!}$ на целую степень числа 4, с последующей коррекцией ${displaystyle {sqrt {S}}}$ на нужную степень 2 путём изменения экспоненты или сдвигом соответственно. Таким образом, ${displaystyle S,!}$ может быть сдвинуто в пределы ${displaystyle {frac {1}{2}}leqslant S<2}$ . Более того, приведённый ниже метод не использует делений общего вида, а только сложение, вычитание, умножение и деление на степень двойки. Последнее из этих действий тривиально реализуется. Недостатком метода является накопление ошибки, в отличие от итеративных методов с одной переменной, таких как вавилонский.

Начальный шаг метода

${displaystyle a_{0}=S,!}$

${displaystyle c_{0}=S-1,!}$

Итерационные шаги

${displaystyle a_{n+1}=a_{n}-a_{n}c_{n}/2,!}$

${displaystyle c_{n+1}=c_{n}^{2}(c_{n}-3)/4,!}$

Тогда ${displaystyle a_{n}rightarrow {sqrt {S}}}$ (при ${displaystyle c_{n}rightarrow 0}$ ).

Заметим, что сходимость ${displaystyle c_{n},!}$ , а потому и ${displaystyle a_{n},!}$ , квадратична.

Доказательство метода достаточно простое. Сначала перепишем итерационное определение ${displaystyle c_{n},!}$ как

${displaystyle 1+c_{n+1}=(1+c_{n})(1-c_{n}/2)^{2},!}$ .

Теперь «в лоб» доказывается, что

${displaystyle S(1+c_{n})=a_{n}^{2}}$

а потому сходимость ${displaystyle a_{n},!}$ к желаемому результату ${displaystyle {sqrt {S}}}$ обеспечивается сходимостью ${displaystyle c_{n},!}$ к 0, что, в свою очередь, вытекает из ${displaystyle -1<c_{0}<2,!}$ .

Этот метод разработали около 1950 года М. В. Уилкс, Д. Дж. Уилер и С. Гилл^[12] для использования в EDSAC, одном из первых электронных компьютеров^[13]. Позднее метод был обобщён на неквадратные корни^[14].

Итеративные методы вычисления обратного к квадратному корню числа[править | править код]

Далее приведены итеративные методы вычисления обратного к квадратному корню из S числа, то есть ${displaystyle 1/{sqrt {S}}}$ . Если такое значение найдено, находим ${displaystyle {sqrt {S}}}$ просто умножением: ${displaystyle {sqrt {S}}=Scdot (1/{sqrt {S}})}$ . Эти итерации используют только умножение и не используют деления. Потому методы быстрее, чем вавилонский метод. Однако методы нестабильны, если начальное значение не близко к обратному к корню значению, итерации расходятся. Поэтому может быть выгодным сначала сделать итерацию вавилонским методом для грубой оценки корня перед началом использования этих методов.

Алгоритм Гольдшмидта[править | править код]

Некоторые компьютеры используют алгоритм Гольдшмидта для одновременного вычисления ${displaystyle {sqrt {S}}}$ и ${displaystyle 1/{sqrt {S}}}$ .
Алгоритм Гольдшмидта находит ${displaystyle {sqrt {S}}}$ быстрее, чем итерация Ньютона-Рапсона, на компьютерах с операциями совмещённого умножения-сложения и имеющих либо конвейерный процессор плавающей запятой, либо два независимых процессора плавающей запятой^[15].

Первый способ записи алгоритма Гольдшмидта начинается с

${displaystyle b_{0}=S}$

${displaystyle Y_{0}approx 1/{sqrt {S}}}$ (обычно используется поиск в таблице)

${displaystyle y_{0}=Y_{0}}$

${displaystyle x_{0}=Sy_{0}}$

и осуществляются итерации

${displaystyle b_{n+1}=b_{n}Y_{n}^{2}}$

${displaystyle Y_{n+1}=(3-b_{n+1})/2}$

${displaystyle x_{n+1}=x_{n}Y_{n+1}}$

${displaystyle y_{n+1}=y_{n}Y_{n+1}}$

пока $b_{i}$ не окажется достаточно близко к 1 или не будет проведено фиксированное число итераций. Итерации сходятся к

${displaystyle lim _{nto infty }x_{n}={sqrt {S}}}$ ,

${displaystyle lim _{nto infty }y_{n}=1/{sqrt {S}}}$ .

Заметим, что можно опустить вычисление $x_{n}$ или $y_{n}$ , а если оба значения желательны, то ${displaystyle x_{n}=Sy_{n}}$ можно использовать в конце вместо вычисления на каждой итерации.

Второй способ, использующий операции совмещённого умножения-сложения начинается с

${displaystyle y_{0}approx 1/{sqrt {S}}}$ (обычно используется поиск в таблице)

${displaystyle x_{0}=Sy_{0}}$

${displaystyle h_{0}=y_{0}/2}$

и осуществляются итерации

${displaystyle r_{n}=0{,}5-x_{n}h_{n}}$

${displaystyle x_{n+1}=x_{n}+x_{n}r_{n}}$

${displaystyle h_{n+1}=h_{n}+h_{n}r_{n}}$

пока $r_{i}$ не станет достаточно близко к 0, либо не будет осуществлено фиксированное число итераций. Значения сходятся к

${displaystyle lim _{nto infty }x_{n}={sqrt {S}}}$

${displaystyle lim _{nto infty }2h_{n}=1/{sqrt {S}}}$ .

Ряды Тейлора[править | править код]

Если N является приближением к ${displaystyle {sqrt {S}}}$ , лучшее приближения может быть найдено использованием ряда Тейлора функции квадратного корня:

${displaystyle {sqrt {N^{2}+d}}=Nsum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{(1-2n)n!^{2}4^{n}}}{frac {d^{n}}{N^{2n}}}=Nleft(1+{frac {d}{2N^{2}}}-{frac {d^{2}}{8N^{4}}}+{frac {d^{3}}{16N^{6}}}-{frac {5d^{4}}{128N^{8}}}+cdots right)}$

Порядок сходимости равен числу используемых членов ряда. При использовании двух членов метод эквивалентен вавилонскому методу. При использовании трёх членов каждая итерация использует почти столько же операций, сколько использует приближение Бакхшали, но сходимость слабее. Поэтому этот метод не является особенно эффективным способом вычисления. Для максимизации скорости сходимости, следует выбрать N так, чтобы ${displaystyle {frac {|d|}{N^{2}}},}$ было как можно меньше.

Разложение в цепную дробь[править | править код]

Квадратичные иррациональности (числа вида ${displaystyle {frac {a+{sqrt {b}}}{c}}}$ , где a, b и c целые числа), и, в частности, квадратные корни из целых чисел, имеют периодические цепные дроби^[en]. Иногда целью является не нахождение численного значения квадратного корня, а его разложение в цепную дробь, а следовательно его рационального приближения. Пусть S будет положительным числом, корень из которого требуется найти. Теперь пусть a будет начальным приближением, а r будет остаточным членом, тогда мы можем записать ${displaystyle S=a^{2}+r.}$ Поскольку мы имеем ${displaystyle S-a^{2}=({sqrt {S}}+a)({sqrt {S}}-a)=r}$ , мы можем выразить квадратный корень из S как

${displaystyle {sqrt {S}}=a+{frac {r}{a+{sqrt {S}}}}.}$

Применяя это выражение для ${displaystyle {sqrt {S}}}$ к знаменателю дроби, получим

${displaystyle {sqrt {S}}=a+{frac {r}{a+(a+{frac {r}{a+{sqrt {S}}}})}}=a+{frac {r}{2a+{frac {r}{a+{sqrt {S}}}}}}.}$

Компактная запись

Числитель/знаменатель разложения для непрерывных дробей (см. слева) затруднительно записывать, а также трудно укладывается в существующую систему форматирования документов. По этой причине была разработана специальная нотация для компактного представления целой и периодической частей непрерывных дробей. Одно из таких соглашений использует лексическую «ломаную линию» для представления черты между числителем и знаменателем, что позволяет записывать дробь горизонтально, а не вертикально:

${displaystyle {sqrt {S}}=a+{frac {r|}{|2a}}+{frac {r|}{|2a}}+{frac {r|}{|2a}}+cdots }$

Здесь каждая горизонтальная черта (в дроби) представлена тремя чертами — двумя вертикальными и одной горизонтальной, которые отделяют $r$ от $2a$ .

Ещё более компактная нотация имеет специальный вид

${displaystyle [a;2a,2a,2a,...]}$

Для периодических непрерывных дробей (которыми являются все квадратные корни), повторяющаяся часть указывается лишь один раз с чертой над повторяющейся частью:

${displaystyle [a;{overline {2a}}]}$

Для √2 значение $a$ равно 1, так что представлением будет

${displaystyle [1;{overline {2}}]}$

Следуя этим путём мы получаем обобщённую непрерывную дробь^[en] для квадратного корня
${displaystyle {sqrt {S}}=a+{cfrac {r}{2a+{cfrac {r}{2a+{cfrac {r}{2a+ddots }}}}}}}$

Первым шагом вычисления такой дроби для получения квадратного корня является подстановки для корня и выбор числа знаменателей. Например, в канонической форме $r$ равен 1 и для √2, $a$ равен 1, так что численно непрерывной дробью для 3 знаменателей будет

${displaystyle {sqrt {2}}approx 1+{cfrac {1}{2+{cfrac {1}{2+{cfrac {1}{2}}}}}}}$

Шаг 2. Непрерывная дробь свёртывается снизу вверх, один знаменатель за раз, чтобы получить рациональную дробь, числитель и знаменатель которой являются целыми числами. Процесс свёртывания тогда выглядит следующим образом (беря первые три знаменателя):

${displaystyle 1+{cfrac {1}{2+{cfrac {1}{2+{cfrac {1}{2}}}}}}=1+{cfrac {1}{2+{cfrac {1}{frac {5}{2}}}}}}$

${displaystyle =1+{cfrac {1}{2+{cfrac {2}{5}}}}=1+{cfrac {1}{frac {12}{5}}}}$

${displaystyle =1+{cfrac {5}{12}}={frac {17}{12}}}$

Наконец (шаг 3), делим числитель на знаменатель рациональной дроби, чтобы получить приближённое значение корня:

${displaystyle 17div 12=1{,}42}$ округлено до трёх знаков.

Действительное значение корня √2 равно 1,41 с точностью до трёх значащих цифр. Относительная ошибка равна 0,17%, так что рациональная дробь хороша почти до трёх знаков. Если брать больше знаменателей, получим последовательное улучшение приближения — четыре знаменателя дают дробь ${displaystyle {frac {41}{29}}=1{,}4137}$ , что даёт почти 4 цифры точности, и т.д.

Непрерывные дроби доступны в таблицах по меньшей мере для малых чисел и общеизвестных констант. Для произвольных чисел в десятичной системе счисления предварительно вычисленные значения, скорее всего, бесполезны. Следующая таблица малых рациональных дробей, называемых подходящими дробями, полученных из канонических непрерывных дробей для нескольких констант:

√S	цепная дробь	~десятичное	Подходящие дроби
√2	${displaystyle [1;{overline {2}}]}$	1,41421	${displaystyle {frac {3}{2}},{frac {7}{5}},{frac {17}{12}},{frac {41}{29}},{frac {99}{70}}}$
√3	${displaystyle [1;{overline {1,2}}]}$	1,73205	${displaystyle {frac {2}{1}},{frac {5}{3}},{frac {7}{4}},{frac {19}{11}},{frac {26}{15}},{frac {71}{41}},{frac {97}{56}}}$
√5	${displaystyle [2;{overline {4}}]}$	2,23607	${displaystyle {frac {9}{4}},{frac {38}{17}},{frac {161}{72}}}$
√6	${displaystyle [2;{overline {2,4}}]}$	2,44949	${displaystyle {frac {5}{2}},{frac {22}{9}},{frac {49}{20}},{frac {218}{89}}}$
√10	${displaystyle [3;{overline {6}}]}$	3,16228	${displaystyle {frac {19}{6}},{frac {117}{37}}}$
${displaystyle {sqrt {pi }}}$	${displaystyle [1;1,3,2,1,1,6...]}$	1,77245	${displaystyle {frac {2}{1}},{frac {7}{4}},{frac {16}{9}},{frac {23}{13}},{frac {39}{22}}}$
${displaystyle {sqrt {e}}}$	${displaystyle [1;1,1,1,5,1,1...]}$	1,64872	${displaystyle {frac {2}{1}},{frac {3}{2}},{frac {5}{3}},{frac {28}{17}},{frac {33}{20}},{frac {61}{37}}}$
${displaystyle {sqrt {phi }}}$	${displaystyle [1;3,1,2,11,3,7...]}$	1,27202	${displaystyle {frac {4}{3}},{frac {5}{4}},{frac {14}{11}}}$

Примечание: Перечислены все подходящие дроби вплоть до знаменателя 99.

В общем виде чем больше знаменатель рациональной дроби, тем лучше аппроксимация. Также можно доказать, что отсечение непрерывной дроби приводит к рациональной дроби, с лучшим приближением к корню любой дроби со знаменателем, меньшим или равным знаменателю этой дроби. Например, никакая дробь со знаменателем, не превосходящем 70, не будет так же хороша, как аппроксимация к √2 числом 99/70.

Метод последовательности Люка[править | править код]

Последовательность Люка первого рода ${displaystyle U_{n}(P,Q)}$ определяется рекуррентным отношением

${displaystyle U_{n}(P,Q)={begin{cases}0&{text{если }}n=0\1&{text{если }}n=1\Pcdot U_{n-1}(P,Q)-Qcdot U_{n-2}(P,Q)&{text{в противном случае}}end{cases}}}$

и его характеристическим многочленом является

${displaystyle x^{2}-Pcdot x+Q=0}$

, он имеет дискриминант ${displaystyle D=P^{2}-4Q}$ и корни

${displaystyle {begin{matrix}x_{1}={dfrac {P+{sqrt {D}}}{2}},&x_{2}={dfrac {P-{sqrt {D}}}{2}}end{matrix}}}$

Всё это даёт следующее положительное значение

${displaystyle lim _{nto infty }{dfrac {U_{n+1}}{U_{n}}}=x_{1}}$

. Так что если мы хотим получить ${sqrt {a}}$ , мы можем выбрать ${displaystyle P=2}$ и ${displaystyle Q=1-a}$ , а затем вычислить ${displaystyle x_{1}=1+{sqrt {a}}}$ используя ${displaystyle U_{n+1}}$ и $U_{n}$ для больших значений $n$ .
Наиболее эффективный способ вычисления ${displaystyle U_{n+1}}$ и $U_{n}$ —

${displaystyle {begin{bmatrix}U_{n}\U_{n+1}end{bmatrix}}={begin{bmatrix}0&1\-Q&Pend{bmatrix}}cdot {begin{bmatrix}U_{n-1}\U_{n}end{bmatrix}}={begin{bmatrix}0&1\-Q&Pend{bmatrix}}^{n}cdot {begin{bmatrix}U_{0}\U_{1}end{bmatrix}}}$

Итог:

${displaystyle {begin{bmatrix}0&1\a-1&2end{bmatrix}}^{n}cdot {begin{bmatrix}0\1end{bmatrix}}={begin{bmatrix}U_{n}\U_{n+1}end{bmatrix}},}$

а тогда при $nto infty$ :

${displaystyle {sqrt {a}}={frac {U_{n+1}}{U_{n}}}-1}$

Аппроксимации, зависящие от представления в виде числа с плавающей запятой[править | править код]

Число представляется в виде числа с плавающей запятой как ${displaystyle mtimes b^{p}}$ . Этот формат записи называется также экспоненциальной записью. Квадратный корень из этого числа равен ${displaystyle {sqrt {m}}times b^{tfrac {p}{2}}}$ и аналогичные формулы могут быть представлены для кубических корней и логарифмов. Это не упрощает задачу, но если требуется только аппроксимация, то ${displaystyle b^{tfrac {p}{2}}}$ является хорошей оценкой порядка мантиссы. Далее, понимаем, что некоторые степени p могут оказаться нечётными, тогда для ${displaystyle 3141{,}59=3{,}14159{times }10^{3}}$ вместо работы с дробными степенями основания умножаем на него и вычитаем единицу из степени, делая её чётной. Уточнённое представление превращается в ${displaystyle 31{,}4159{times }10^{2}}$ , так что квадратный корень будет равен ${displaystyle {sqrt {31,4159}}{times }10^{1}}$ .

Если взять лишь целую часть мантиссы, она может принимать значения от 1 до 99 и это можно использовать в качестве индекса в таблице из 99 предварительно вычисленных корней для завершения оценки. Компьютер, использующий шестнадцатеричное основание может потребовать большей таблицы, но при использовании основания 2 таблица будет состоять лишь из трёх величин — возможными битами целой части уточнённого представления мантиссы могут быть 01 (если степень чётная, так что нет никакого сдвига, и заметим, что нормализованное число с плавающей точкой всегда имеет ненулевую старшую цифру), или, если степень была нечётной, 10 или 11, это два первых бита исходной мантиссы. Тогда 6,25 (= 110,01 в двоичном представлении) нормализуется к ${displaystyle 1{,}1001times 2^{2}}$ с чётной степенью, так что парой битов мантиссы будет 01, в то время как 0,625 (= 0,101 в двоичном представлении) нормализуется к ${displaystyle 1{,}01times 2^{-1}}$ с нечётной степенью, так что требуется преобразование числа к ${displaystyle 10{,}1times 2^{-2}}$ , а тогда парой бит будет 10. Заметим, что младший бит порядка отражается в старший бит сгруппированной парами мантиссы. Чётная степень имеет нулевой младший бит и уточнённая мантисса будет начинаться с нуля, в то время как нечётная степень имеет 1 в младшем бите и уточнённая мантисса будет начинаться с 1. Таким образом, когда степень делится пополам, это эквивалентно тому, что младший бит порядка сдвигается в первый бит попарно сгруппированной мантиссы.

Таблица с тремя элементами может быть расширена для включения дополнительных бит мантиссы. Однако в случае компьютеров вместо вычисления интерполяции в таблице часто лучше искать более простой способ вычислений, дающий те же результаты. Всё теперь зависит от точных деталей формата представления чисел и от операций, которые доступны для получения частей числа и работы с ними. Например, Фортран содержит функцию EXPONENT(x) для получения степени. Усилия, потраченные на получение хорошего начального приближения окупаются за счёт исключения дополнительных итераций процесса уточнения, которые потребовались бы в случае плохого приближения.

Многие компьютеры следуют стандарту IEEE для чисел с плавающей запятой^[en] (или достаточно близкое представление) и очень быстрое приближение для квадратного корня может быть получено в качестве стартового значения метода Ньютона. Техника данного приближения вытекает из факта, что формат плавающего числа (по основанию два) аппроксимирует логарифм по основанию 2. То есть, ${displaystyle log _{2}(mtimes 2^{p})=p+log _{2}(m)}$

Так что для 32-битного числа с плавающей запятой в формате IEEE (в котором степень имеет смещение^[en] на 127^[16]) вы можете получить приближённый логарифм путём интерпретации числа как 32-битного целого, умножения его на ${displaystyle 2^{-23}}$ и вычета смещения 127, то есть

${displaystyle x_{text{int}}cdot 2^{-23}-127approx log _{2}(x).}$

Например, число 1,0 в шестнадцатеричной системе имеет вид 0x3F800000, что можно представить как ${displaystyle 1065353216=127cdot 2^{23}}$ , если рассматривать его как целое. Используя вышеприведённую формулу вы получите ${displaystyle 1065353216cdot 2^{-23}-127=0}$ , как и ожидалось от ${displaystyle log _{2}(1{,}0)}$ . Аналогичным образом вы получите 0,5 из 1,5 (=0x3FC00000).

Чтобы получить квадратный корень, делим логарифм на 2 и преобразуем результат обратно. Ниже программа демонстрирует идею. Заметим, что младший бит порядка намеренно переводится в мантиссу. Одним из способов обоснования шагов этой программы, в предположении что $b$ является смещением степени, а $n$ является числом запоминаемых бит в мантиссе, заключается в доказательстве

${displaystyle (((x_{text{int}}/2^{n}-b)/2)+b)cdot 2^{n}=(x_{text{int}}-2^{n})/2+((b+1)/2)cdot 2^{n}.}$

/* Предполагаем, что плавающее число имеет формат IEEE 754 */
#include <stdint.h>
float sqrt_approx(float z)
{
	union { float f; uint32_t i; } val = {z};	/* Преобразуем тип не меняя битового представления */
	/*
	 * Для обоснования работы кода докажите, что
	 * ((((val.i / 2^m) - b) / 2) + b) * 2^m = ((val.i - 2^m) / 2) + ((b + 1) / 2) * 2^m)
	 * где
	 * b = смещение степени
	 * m = число бит в мантиссе
	 */
	val.i -= 1 << 23;	/* Вычитаем 2^m. */
	val.i >>= 1;		/* Делим на 2. */
	val.i += 1 << 29;	/* Добавляем ((b + 1) / 2) * 2^m. */

	return val.f;		/* Интерпретируем снова как плавающее */
}

Три арифметические операции, образующие ядро функции можно представить в одну строку. Дополнительное уточнение может быть добавлено для уменьшения максимальной относительной ошибки. Таким образом, три операции, не включая приведение к вещественному, можно переписать как

	val.i = (1 << 29) + (val.i >> 1) - (1 << 22) + a;

где a — смещение для уменьшения ошибок аппроксимации. Например, с a = 0 результаты точны для чётных степеней двойки 2 (например, 1,0), но для других чисел результат будет несколько великоват (например, 1,5 для 2,0 вместо 1,414… с ошибкой 6%). При a = −0x4B0D2 максимальная относительная ошибка сокращается до ±3,5%.

Если приближение нужно использовать как начальное значение для метода Ньютона в уравнении ${displaystyle (1/x^{2})-S=0}$ , то обратная форма, показанная в следующем разделе, предпочтительнее.

Обратное значение квадратного корня[править | править код]

Вариант описанной выше процедуры представлен ниже и он может быть использован для вычисления обратного к квадратному корню, то есть ${displaystyle x^{-{1 over 2}}}$ . Этот вариант написал Грег Уолш. Приближение сдвигом даёт относительную ошибку менее 4% и ошибка уменьшается до 0,15% после одной итерации метода Ньютона^[17]. В компьютерной графике это очень эффективный способ нормализации вектора.

float invSqrt(float x) {
    float xhalf = 0.5f * x;
    union {
        float x;
        int i;
    } u;
    u.x = x;
    u.i = 0x5f375a86 - (u.i >> 1);
    /* Следующая строка может быть повторена произвольное число раз для увеличения точности */
    u.x = u.x * (1.5f - xhalf * u.x * u.x);
    return u.x;
}

Некоторые СБИС реализуют нахождение обратной величины к квадратному корню с помощью полиномиальной оценки с последующей итерацией Голдшмидта^[18].

Корень из отрицательного или комплексного числа[править | править код]

Если $S<0$ , то его главный корень равен

${displaystyle {sqrt {S}}={sqrt {vert Svert }},,i,.}$

Если ${displaystyle S=a+bi}$ , где a и b вещественные числа и $bneq 0$ , то его главный корень равен

${displaystyle {sqrt {S}}={sqrt {frac {vert Svert +a}{2}}},+,operatorname {sgn}(b){sqrt {frac {vert Svert -a}{2}}},,i,.}$

Это можно проверить возведением в квадрат^[19]^[20]. Здесь

${displaystyle vert Svert ={sqrt {a^{2}+b^{2}}}}$

является модулем числа S. Главный корень комплексного числа определяется как корень с неотрицательной вещественной частью.

См. также[править | править код]

Алгоритм альфа max плюс бета min^[en]
Целочисленный квадратный корень

Примечания[править | править код]

↑ Кроме главного корня имеется отрицательный квадратный корень, равный по модулю главному корню, но с противоположным знаком, за исключением случая нуль, когда имеется два одинаковых корня, равных нулю.
↑ Множители два и шесть используются ввиду того, что они аппроксимируют среднее геометрическое нижнего и верхнего возможных значений с заданным числом знаков: ${displaystyle {sqrt {{sqrt {1}}cdot {sqrt {10}}}}={sqrt[{4}]{10}}approx 1{,}78,}$ и ${displaystyle {sqrt {{sqrt {10}}cdot {sqrt {100}}}}={sqrt[{4}]{1000}}approx 5{,}62,}$ .
↑ Неокруглённая оценка имеет максимальную абсолютную ошибку 2,65 в точке 100 и максимальную относительную ошибку в 26,5% в точках y=1, 10 и 100
↑ Если число находится ровно посередине между двумя квадратами, наподобие 30,5, берём большее число, которое в нашем случае 6
↑ Это уравнение касательной прямой к y=x² в точке y=1.
↑ Fowler, Robson, 1998, с. 376.
↑ Heath, 1921, с. 323–324.
↑ Bailey, Borwein, 2012, с. 646–657.
↑ Bucking down to the Bakhshali manuscript. Simply Curious blog (5 июня 2018). Дата обращения: 21 декабря 2020. Архивировано 26 октября 2020 года.
↑ Fast integer square root by Mr. Woo’s abacus algorithm (archived)
↑ Integer Square Root function. Дата обращения: 30 декабря 2021. Архивировано 30 сентября 2007 года.
↑ Wilkes, Wheeler, Gill, 1951.
↑ Campbell-Kelly, 2009.
↑ Gower, 1958, с. 142–143, 1958.
↑ Markstein, Peter (November 2004). Software Division and Square Root Using Goldschmidt’s Algorithms (PDF). 6th Conference on Real Numbers and Computers. Dagstuhl, Germany. CiteSeerX 10.1.1.85.9648. Архивировано (PDF) из оригинала 2022-04-28. Дата обращения 2021-12-30.
↑ К экспоненте числа добавляется 127, что позволяет интерпретировать экспоненту как число без знака.
↑ Fast Inverse Square Root Архивная копия от 6 февраля 2009 на Wayback Machine by Chris Lomont
↑
“High-Speed Double-Precision Computation of Reciprocal, Division, Square Root and Inverse Square Root”
by José-Alejandro Piñeiro and Javier Díaz Bruguera 2002 (abstract)
↑ Abramowitz, Stegun, 1964, с. 17.
↑ Cooke, 2008, с. 59.

Литература[править | править код]

David Fowler, Eleanor Robson. Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context // Historia Mathematica. — 1998. — Т. 25, вып. 4. — doi:10.1006/hmat.1998.2209.
Thomas Little Heath. A History of Greek Mathematics. — Oxford: Clarendon Press, 1921. — Т. 2. — С. 323–324.
David Bailey, Jonathan Borwein. Ancient Indian Square Roots: An Exercise in Forensic Paleo-Mathematics // American Mathematical Monthly. — 2012. — Т. 119, вып. 8.
Miltonn Abramowitz, Irene A. Stegun. Section 3.7.26 // Handbook of mathematical functions with formulas, graphs, and mathematical tables. — Courier Dover Publications, 1964. — С. 17. — ISBN 978-0-486-61272-0.
J. C. Gower. A Note on an Iterative Method for Root Extraction // The Computer Journal. — 1958. — Т. 1 1, вып. 3.
M. Campbell-Kelly. Origin of Computing // Scientific American. — 2009. — Сентябрь.
Roger Cooke. Classical algebra: its nature, origins, and uses. — John Wiley and Sons, 2008. — ISBN 978-0-470-25952-8.
M. V. Wilkes, D. J. Wheeler, S. Gill. The Preparation of Programs for an Electronic Digital Computer. — Addison-Wesley, 1951.

СсылкиWeisstein, Eric W. Square root algorithms (англ.) на сайте Wolfram MathWorld.[править | править код]

Square roots by subtraction
Integer Square Root Algorithm by Andrija Radović
Personal Calculator Algorithms I : Square Roots (William E. Egbert), Hewlett-Packard Journal (may 1977) : page 22
Калькулятор для обучения квадратному корню

Источник

#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳

Авторские права на изображение принадлежат медиагруппе “Хакнем” и защищены товарным знаком ®️

УНИВЕРСАЛЬНЫЕ СПОСОБЫ (ПРИЁМЫ) ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ

ЧАСТЬ II (часть I по ссылке)

Здравствуйте, уважаемые читатели канала Хакнем Школа!

Прежде чем перейти к рассмотрению универсальных способов (приёмов) извлечения квадратного корня из любого неотрицательного рационального числа, к слову сказать, весьма трудоёмких, необходимо разобраться со следующей теоремой, утверждение которой будет нами широко использоваться.

ТЕОРЕМА. Если a > b >0 , то √ a >√ b .

ДОКАЗАТЕЛЬСТВО.

Способы, позволяющие вычислить квадратный корень из любого числа без таблиц и калькуляторов

Из (1) и (2) следует (√ a – √ b )×(√ a + √ b ) > 0 . (3)

Из неравенств a >0 и b >0 по определению квадратного корня имеем √ a >0 и √ b >0 , но тогда √ a + √ b > 0 . (4)

Произведение двух множителей положительно тогда и только тогда, когда либо оба множителя больше 0, либо оба множителя меньше 0.

Из (1) и (4) следует, что √ a – √ b > 0 ó √ a > √ b , что и требовалось доказать.

Приступим к рассмотрению приёмов непосредственного извлечения квадратного корня из натуральных чисел. Прежде всего обратимся к хорошо нам известному приёму разложения натурального числа на множители, который основан на признаках делимости, которые можно при необходимости повторить по статье «Признаки делимости чисел: где мы их применяем в жизни», автор #ирина_чудневцева .

СПОСОБ I

ЗАДАЧА 1. Вычислить √91728.

РЕШЕНИЕ. Под знаком радикала стоит пятизначное число, которого нет в четырёхзначных таблицах квадратов, и нельзя использовать калькулятор. В этом случае нам поможет разложение этого числа на простые множители. Получим:

Поскольку квадратный корень произведения равен произведению квадратных корней сомножителей, то

Если под знаком корня стоит десятичная дробь, то её следует представить в виде произведения целого числа, убрав запятую, и десятичной дроби с числителем, равным единице, и числом знаков после запятой, равным числу знаков после запятой в заданной дроби, при этом число этих знаков должно быть чётным, например:

√917,28=√(91728×0,01)=√91728 × √0,01=84√13 × 0,1=8,4√13.

Прежде чем перейти к следующему способу непосредственного вычисления квадратного корня необходимо рассмотреть следующую лемму:

ЛЕММА (об опорных квадратах).

Пусть нам известен квадрат одного из двух последовательных натуральных чисел m и n , таких, что n = m +1 или, что то же, m = n – 1 .

В этом случае становятся верными два тождества:

ДОКАЗАТЕЛЬСТВО.

Отдельный интерес представляет случай использования этих тождеств, когда n и т дроби, отличающиеся друг от друга на единицу самого младшего разряда, например:

Следующий способ, опирающийся на метод подбора каждой цифры результата путём последовательных приближений с использованием средних арифметических значений, позволяет извлекать квадратный корень с наперёд заданной точностью.

СПОСОБ II

При решении предыдущей задачи осталась одна неясность: чему же равен √13 ? Попытаемся ответить на этот вопрос. Восьмиклассники уже знают, что значения квадратных корней из чисел, не являющихся точными квадратами, относятся к так называемым иррациональным числам , которые могут быть представлены в виде бесконечных непериодических десятичных дробей . Поэтому в различного рода расчётах их представляют округлёнными до конкретного разряда числами.

ЗАДАЧА 2. Найти значение √13 с точностью до сотых.

РЕШЕНИЕ. Рассмотренная в начале статьи теорема позволяет опереться на следующее неравенство:

Среднее арифметическое чисел 0 и 1, между которыми может находится значение цифры, стоящей в разряде десятых искомого значения корня квадратного, равно числу 5 , и это число является первым кандидатом на то, чтобы соответствующая ему цифра была проверена соответствующей подстановкой. Однако можно заметить, что число 13 находится дальше от числа 9 нежели от числа 16 . Поэтому проверку можно начать с цифры 6, и заодно покажем интересный способ вычисления квадратов таких чисел с помощью так называемых опорных квадратов.

Подбор цифры в разряд сотых начнём с квадрата числа 3,61:

С целью получения наименьшей погрешности необходимо найти цифру для разряда тысячных для последующего округления…

Выберем цифру 5 из середины интервала (0, 9) :

Для разряда тысячных необходимо ещё проверить цифру 6 :

СПОСОБ III

Этот способ, значительно облегчающий подбор цифр-кандидатов, является удачной формализацией второго способа.

ЗАДАЧА III. Найти значение √13 с точностью до сотых.

РЕШЕНИЕ. Поскольку квадрат однозначного числа равен однозначному или двузначному числу, то натуральное число надо разбить на грани по две цифры в каждой, начиная с разряда единиц а десятичную дробь — от запятой, причём последнюю грань при необходимости следует дополнить цифрой 0 .

Предварительный результат будет содержать три цифры после запятой — значит, десятичная часть числа, из которого будем извлекать квадратный корень будет содержать три грани:

13,00 | 00 | 00.

Ищем наибольшее число, квадрат которого не превосходит числа 13, стоящего в первой грани. Этим числом будет 3. Записываем его в ответ — это будет первая цифра результата. Поскольку следующая грань находится после запятой, то ставим запятую в ответ.

Возводим число 3 в квадрат и результат вычитаем из первой грани.

К найденной разности приписываем справа вторую грань и получаем число 400 . Слева от этого числа ставим вертикальную чёрточку на две строчки и слева от неё записываем удвоенную цифру полученного результата (цифру 6 ), оставляя между этой цифрой и вертикальной чертой место для ещё одной цифры, обозначенной литерой а .

Эту цифру подбираем таким образом, чтобы произведение двузначного числа 6а на это число 6а× a было наибольшим, но не больше числа 400 справа от вертикальной черты. Таким числом будет число 6 .

Вычтем (столбиком) произведение 66×6=396 из числа 400 и запишем разность под горизонтальной чертой, проставив слева от неё вертикальную черту на две строчки. Слева от этой черты запишем сумму 66+6=72, оставив место для ещё одной цифры между полученной суммой и вертикальной чертой.

Повторяем действия описанные в предыдущих двух абзацах пока не получим цифры в разряде тысячных результата. В итоге мы получим следующую запись:

Вычисление √13.

Осталось провести округление: √13 = 3,603…≈3,61.

Попробуйте самостоятельно найти √2374,6129 и сверить свои действия с приведённым образцом.

Вычисление √2374,6129

Помните, что дорогу осилит идущий! Желаю успехов и не только в учёбе!

Продолжение следует…

Не забудьте подписаться на канал Хакнем Школа и хэштег #хакнем_математика

Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.

Читайте наш канал в телеграм – по этой ссылке

Другие статьи автора:

Источник

Загрузить PDF

До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.

1
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число.^[1] Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
- Записать это можно следующим образом: √400 = √(25 х 16).
2
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b.^[2] Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
  - √(25 х 16)
  - √25 х √16
  - 5 х 4 = 20
3
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
  - √147
  - = √(49 х 3)
  - = √49 х √3
  - = 7√3
4
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
  - Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 – мы были правы.
5
Еще один способ – разложите подкоренное число на простые множители. Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
  - √88
  - = √(2 х 44)
  - = √ (2 х 4 х 11)
  - = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
  - = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Реклама

При помощи деления в столбик

1
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как “7 95 20 78 91 82, 47 89 70”.
- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде “7 80, 14”. Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
2
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4 < 7, то есть 2² < 7 и n = 2. Напишите 2 сверху справа – это первая цифра в искомом квадратном корне. Напишите 2×2=4 справа снизу; вам понадобится это число для последующих вычислений.
3
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.
4
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением “_×_=”.
- В нашем примере второй парой чисел является “80”. Запишите “80” после 3. Затем, удвоенное число сверху справа дает 4. Запишите “4_×_=” снизу справа.
5
Заполните прочерки справа. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 – слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа – это вторая цифра в искомом квадратном корне числа 780,14.
6
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
7
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением “_×_=”.
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите “54_×_=” снизу справа.
8
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 – 4941 = 173.
9

Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).

Реклама

Понимание процесса

1

Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
2

Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C – третьей и так далее.
3

Задайте букву для каждой пары первых цифр. Обозначим через S_a первую пару цифр в значении S, через S_b – вторую пару цифр и так далее.
4

Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
5
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S_a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa < (A+1)²). В нашем примере, S1 = 7, и 2² ≤ 7 < 3²; таким образом A = 2.
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8 < 7×(d+1). В этом случае d будет равно 1.
6
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C – цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B². Запомните, что 10A+B – это такое число, у которого цифра B означает единицы, а цифра A – десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² – это площадь всего квадрата, 100A² – площадь большого внутреннего квадрата, B² – площадь малого внутреннего квадрата, 10A×B – площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
7

Вычтите A² из S_a. Для учета множителя 100 снесите одну пару цифр (S_b) из S: вам нужно, чтобы “SaSb” было равным общей площади квадрата, и из нее вычтите 100A² (площадь большого квадрата). В результате получите число N1, стоящее слева в шаге 4 (N = 380 в нашем примере). N1 = 2×10A×B + B² (площадь двух прямоугольников плюс площадь малого квадрата).
8

Выражение N1 = 2×10A×B + B² можно записать как N1 = (2×10A + B) × B. В нашем примере вам известно значение N1 (=380) и A(=2) и необходимо вычислить B. Скорее всего, B не является целым числом, поэтому необходимо найти наибольшее целое B, удовлетворяющее условию: (2×10A + B) × B ≤ N1. При этом B+1 будет слишком большим, поэтому N1 < (2×10A + (B+1)) × (B+1).
9

Решите уравнение. Для решения умножьте A на 2, переведите результат в десятки (что эквивалентно умножению на 10), поместите B в положение единиц, и умножьте это число на B. Это число (2×10A + B) × B и это выражение абсолютно идентичны записи “N_×_=” (где N=2×A) сверху справа в шаге 4. А в шаге 5 вы находите наибольшее целое B, которое ставится на место прочерков и соответствует неравенству: (2×10A + B) × B ≤ N1.
10

Вычтите площадь (2×10A + B) × B из общей площади (слева в шаге 6). Так вы получите площадь S-(10A+B)², которая еще не учитывалась (и которая поможет вычислить следующие цифры).
11

Для вычисления следующей цифры C повторите процесс. Слева снесите следующую пару цифр (Sc) из S для получения N2 и найдите наибольшее C, удовлетворяющее условию (2×10×(10A+B)+C) × C ≤ N2 (что эквивалентно двукратному написанию числа из пары цифр “A B” с соответствующим “_×_=”, и нахождению наибольшего числа, которое можно подставить вместо прочерков).

Реклама

Советы

Перемещение десятичного разделителя при увеличении числа на 2 цифры (множитель 100), перемещает десятичный разделить на одну цифру в значении квадратного корня этого числа (множитель 10).
В нашем примере, 1,73 может считаться остатком: 780,14 = 27,9² + 1,73.
Данный метод верен для любых чисел.
Записывайте процесс вычисления в том виде, который вам наиболее удобен. Например, некоторые записывают результат над исходным числом.
Альтернативный метод с использованием непрерывных дробей включает формулу: √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x + …))). Например, для вычисления квадратного корня из 780,14, целым числом, квадрат которого близок к 780,14 будет число 28, поэтому z=780,14, x=28, y=-3,86. Подставляя эти значения в уравнение и решая его в упрощении до х+у/(2x), уже в младших членах получаем результат 78207/2800 или около 27,931(1), а в следующих членах 4374188/156607 или около 27,930986(5). Решение каждого последующего члена добавляет около 3 цифр к дробной доли по сравнению с предыдущем членом.

Предупреждения

Не забудьте разделить число на пары, начиная с дробной части числа. Например, разделяя 79520789182,47897 как “79 52 07 89 18 2,4 78 97″, вы получите бессмысленное число.

Источники

Об этой статье

Эту страницу просматривали 927 271 раз.

Была ли эта статья полезной?

Источник

Из этой статьи вы узнаете:

что такое «извлечение корня»;
в каких случаях он извлекается;
принципы нахождения значения корня;
основные способы извлечения корня из натуральных и дробных чисел.

Что такое «извлечение корня»

Для начала введем определение «извлечение корня».

Определение 1

Извлечение корня — процесс нахождения значения корня.

При извлечении корня n-ной степени из числа a, мы находим число b, n-ная степень которого равняется a. Если мы нашли такое число b, можно утверждать, что корень извлечен.

Замечание 1

Выражения «извлечение корня» и «нахождение значения корня» равнозначны.

В каких случаях извлекается корень?

Определение 2

Корень n-ной степени можно извлечь из числа a точно в случае, если a можно представить в виде n-ной степени некоторого числа b.

Пример 1

4=2×2, следовательно, из числа 4 можно точно извлечь квадратный корень, который равен 2

Определение 3

Когда корень n-ной степени из числа a невозможно представить в виде n-ной степени числа b, то такой корень не извлекается, либо извлекается только приближенное значение корня с точностью до любого десятичного разряда.

Пример 2

2≈1,4142.

Принципы нахождения значения корня и способы их извлечения

Использование таблицы квадратов, таблицы кубов и т.д.
Разложение подкоренного выражения (числа) на простые множители
Извлечение корней из дробных чисел
Извлечение корня из отрицательного числа
Поразрядное нахождение значения корня

Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.

Определение 4

Главный принцип нахождения значения корней — основываться на свойствах корней, в том числе на равенстве: bnn=b, которое является справедливым для любого неотрицательного числа b.

Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.

Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).

Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.

Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.

И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.

Использование таблицы квадратов, кубов и т.д.

Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.

Таблица квадратов

Таблица квадратов	единицы
0	1	2	3	4	5	6	7	8	9
десятки	0	0	1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2041
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Существуют также таблицы кубов, четвертой степени и т.д., которые созданы по принципу, аналогичному таблице квадратов.

Таблица кубов

Таблица кубов		единицы
0	1	2	3	4	5	6	7	8	9
десятки	0	0	1	8	27	64	125	216	343	512	729
1	1000	1 331	1 728	2 197	2 744	3 375	4 096	4 913	5 832	6 859
2	8000	9 261	10 648	12 167	13 824	15 625	17 576	19 683	21 952	24 389
3	27000	29 791	32 768	35 937	39 304	42 875	46 656	50 653	54 872	59 319
4	64000	68 921	74 088	79 507	85 184	91 125	97 336	103 823	110 592	117 649
5	125000	132 651	140 608	148 877	157 464	166 375	175 616	185 193	195 112	205 379
6	216000	226 981	238 328	250 047	262 144	274 625	287 496	300 763	314 432	328 509
7	343000	357 911	373 248	389 017	405 224	421 875	438 976	456 533	474 552	493 039
8	512000	531 441	551 368	571 787	592 704	614 125	636 056	658 503	681 472	704 969
	729000	753 571	778 688	804 357	830 584	857 375	884 736	912 673	941 192	970 299

Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.

Разложение подкоренного числа на простые множители

Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.

Определение 5

Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.

Пример 3

Извлечем квадратный корень из 144.

Разложим 144 на простые множители:

Таким образом: 144=2×2×2×2×3×3=(2×2)2×32=(2×2×3)2=122. Следовательно, 144=122=12.

Также при использовании свойств степени и корней можно записать преобразование немного по-другому:

144=2×2×2×2×3×3=24×32=24×32=22×3=12

144=12 – окончательный ответ.

Извлечение корней из дробных чисел

Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.

Определение 6

Следуя свойству корня из частного, справедливым является следующее равенство:

pqn=pnqn. Исходя из этого равенства, необходимо воспользоваться правилом извлечения корня из дроби: корень из дроби равен от деления корня числителя на корень знаменателя.

Пример 4

Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.

Необходимо извлечь кубический корень из 474,552. Первым делом, представим десятичную дробь в виде обыкновенной: 474,552 = 474552/1000. Из этого следует: 47455210003=474552310003. Затем можно приступить к процессу извлечения кубических корней в числителе и знаменателе:

474552=2×2×2×3×3×3×13×13×13=(2×3×13)3=783 и 1000=103, то

4745523=7833=78 и 10003=1033=10.

Завершаем вычисления: 474552310003=7810=7,8.

Извлечение корня из отрицательных чисел

Если знаменатель является нечетным числом, то число под знаком корня может оказаться отрицательным. Из этого следует: для отрицательного числа -a и нечетного показателя корня 2n-1 справедливо равенство:

-a2×n-1=-a2×n-1

Определение 7

Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.

Пример 5

-122092435. Для начала необходимо преобразовать выражение, чтобы под знаком корня оказалось положительно число:

-122092435=12209243-5

Затем следует заменить смешанное число обыкновенной дробью:

12209243-5=3125243-5

Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:

3125243-5=-312552435

Вычисляем корни в числителе и знаменателе:

-312552435=-555355=-53=-123

Краткая запись решения:

-122092435=12209243-5=3125243-5=-312552435=-555355=-53=-123.

Ответ: -122092435=-123.

Поразрядное нахождение значения корня

Бывают случаи, когда под корнем находится число, которое не получается представить в виде n-ной степени некоторого числа. Но необходимо знать значение корня с точностью до некоторого знака.

В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.

Пример 6

Как это происходит, разберем на примере извлечения квадратного корня из 5.

Сперва необходимо найти значение разряда единиц. Для этого начнем перебирать значения 0,1,2,…,9, вычисляя при этом 02, 12, …, 92 до необходимого значения, которое больше, чем подкоренное число 5. Все это удобно представить в виде таблицы:

Возможное значение корня	0	1	2	3
Это значение в степени	0	1	4	9

Значение ряда единиц равняется 2 (так как 22<5, а 23>5). Переходим в разряду десятых — будем возводить в квадрат числа 2,0, 2,1, 2,2,…,2,9, , сравнивая полученные значения с числом 5.

Возможное значение корня	2,0	2,1	2,2	2,3
Это значение в степени	4	4,41	4,84	5,29

Поскольку 2,22<5, а 2,32>5, то значение десятых равняется 2. Переходим к нахождению значения сотых:

Возможное значение корня	2.20	2,21	2,22	2,23	2,24
Это значение в степени	4,84	4,8841	4,8294	4,9729	5,0176

Таким образом, найдено значение корня из пяти — 2,23. Можно находить значения корня дальше:

2,236, 2,2360, 2, 23606, 2,236067,…

Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.

Источник

Download Article

In the days before calculators, students and professors alike had to calculate square roots by hand. Several different methods have evolved for tackling this daunting process, some giving a rough approximation, others giving an exact value. To learn how to find a number’s square root using only simple operations, please see Step 1 below to get started.

1
Divide your number into perfect square factors. This method uses a number’s factors to find a number’s square root (depending on the number, this can be an exact numerical answer or a close estimate). A number’s factors are any set of other numbers that multiply together to make it.^[1] For instance, you could say that the factors of 8 are 2 and 4 because 2 × 4 = 8. Perfect squares, on the other hand, are whole numbers that are the product of other whole numbers. For instance, 25, 36, and 49 are perfect squares because they are 5², 6², and 7², respectively. Perfect square factors are, as you may have guessed, factors that are also perfect squares. To start finding a square root via prime factorization, first, try to reduce your number into its perfect square factors.^[2]
- Let’s use an example. We want to find the square root of 400 by hand. To begin, we divide the number into perfect square factors. Since 400 is a multiple of 100, we know that it’s evenly divisible by 25 – a perfect square. Quick mental division lets us know that 25 goes into 400 16 times. 16, coincidentally, is also a perfect square. Thus, the perfect square factors of 400 are 25 and 16 because 25 × 16 = 400.
- We would write this as: Sqrt(400) = Sqrt(25 × 16)
- You can also try multiplying different numbers by themselves and see if they give you the correct answer. Let’s say you were trying to find the square root of 81—you could multiply 7 by 7 to get 49, which is too low. You could go a little higher and multiply 10 by 10 to get 100, which is too high. You could then go a little lower and multiply 9 by 9. This would give you 81, making 9 your square root.
2
Take the square roots of your perfect square factors. The product property of square roots states that for any given numbers a and b, Sqrt(a × b) = Sqrt(a) × Sqrt(b). Because of this property, we can now take the square roots of our perfect square factors and multiply them together to get our answer.^[3]
- In our example, we would take the square roots of 25 and 16. See below:
  - Sqrt(25 × 16)
  - Sqrt(25) × Sqrt(16)
  - 5 × 4 = 20
Advertisement
3
Reduce your answer to simplest terms, if your number doesn’t factor perfectly. In real life, more often than not, the numbers you’ll need to find square roots for won’t be nice round numbers with obvious perfect square factors like 400. In these cases, it may not be possible to find the exact answer as an integer. Instead, by finding any perfect square factors that you can, you can find the answer in terms of a smaller, simpler, easier-to-manage square root. To do this, reduce your number to a combination of perfect square factors and non-perfect square factors, then simplify.^[4]
- Let’s use the square root of 147 as an example. 147 isn’t the product of two perfect squares, so we can’t get an exact integer value as above. However, it is the product of one perfect square and another number – 49 and 3. We can use this information to write our answer in simplest terms as follows:
  - Sqrt(147)
  - = Sqrt(49 × 3)
  - = Sqrt(49) × Sqrt(3)
  - = 7 × Sqrt(3)
4
Estimate, if necessary. With your square root in simplest terms, it’s usually fairly easy to get a rough estimate of a numerical answer by guessing the value of any remaining square roots and multiplying through. One way to guide your estimates is to find the perfect squares on either side of the number in your square root. You’ll know that the decimal value of the number in your square root is somewhere between these two numbers, so you’ll be able to guess in between them.
- Let’s return to our example. Since 2² = 4 and 1² = 1, we know that Sqrt(3) is between 1 and 2 – probably closer to 2 than to 1. We’ll estimate 1.7. 7 × 1.7 = 11.9 If we check our work in a calculator, we can see that we’re fairly close to the actual answer of 12.13.
  - This works for larger numbers as well. For example, Sqrt(35) can be estimated to be between 5 and 6 (probably very close to 6). 5² = 25 and 6² = 36. 35 is between 25 and 36, so its square root must be between 5 and 6. Since 35 is just one away from 36, we can say with confidence that its square root is just lower than 6. Checking with a calculator gives us an answer of about 5.92 – we were right.
5
Reduce your number to its lowest common factors as a first step. Finding perfect square factors isn’t necessary if you can easily determine a number’s prime factors (factors that are also prime numbers). Write your number out in terms of its lowest common factors. Then, look for matching pairs of prime numbers among your factors. When you find two prime factors that match, remove both these numbers from the square root and place one of these numbers outside the square root.^[5]
- As an example, let’s find the square root of 45 using this method. We know that 45 = 9 × 5 and we know that 9 = 3 × 3. Thus, we can write our square root in terms of its factors like this: Sqrt(3 × 3 × 5). Simply remove the 3’s and put one 3 outside the square root to get your square root in simplest terms: (3)Sqrt(5). From here, it’s simple to estimate.
- As one final example problem, let’s try to find the square root of 88:
  - Sqrt(88)
  - = Sqrt(2 × 44)
  - = Sqrt(2 × 4 × 11)
  - = Sqrt(2 × 2 × 2 × 11). We have several 2’s in our square root. Since 2 is a prime number, we can remove a pair and put one outside the square root.
  - = Our square root in simplest terms is (2) Sqrt(2 × 11) or (2) Sqrt(2) Sqrt(11). From here, we can estimate Sqrt(2) and Sqrt(11) and find an approximate answer if we wish.

Using a Long Division Algorithm

1
Separate your number’s digits into pairs. This method uses a process similar to long division to find an exact square root digit-by-digit. Though it’s not essential, you may find that it’s easiest to perform this process if you visually organize your workspace and your number into workable chunks. First, draw a vertical line separating your work area into two sections, then draw a shorter horizontal line near the top of the right section to divide the right section into a small upper section and a larger lower section. Next, separate your number’s digits into pairs, starting from the decimal point. For instance, following this rule, 79,520,789,182.47897 becomes “7 95 20 78 91 82. 47 89 70”. Write your number at the top of the left space.^[6]
- As an example, let’s try calculating the square root of 780.14. Draw two lines to divide your workspace as above and write “7 80. 14” at the top of the left space. It’s O.K. that the leftmost chunk is a lone number, rather than a pair of numbers. You will write your answer (the square root of 780.14.) in the top right space.
2
Find the largest integer n whose square is lesser than or equal to the leftmost number (or pair). Start with the leftmost “chunk” of your number, whether this is a pair or a single number. Find the largest perfect square that’s less than or equal to this chunk, then take the square root of this perfect square. This number is n. Write n in the top right space and write the square of n in the bottom right quadrant.
- In our example, the leftmost “chunk” is the number 7. Since we know that 2² = 4 ≤ 7 < 3² = 9, we can say that n = 2 because it’s the largest integer whose square is less than or equal to 7. Write 2 in the top right quadrant. This is the first digit of our answer. Write 4 (the square of 2) in the bottom right quadrant. This number will be important in the next step.
3
Subtract the number you just calculated from the leftmost pair. As with long division, the next step is to subtract the square we just found from the chunk we just analyzed. Write this number underneath the first chunk and subtract, writing your answer underneath.^[7]
- In our example, we would write 4 below 7, then subtract. This gives us an answer of 3.
4
Drop down the next pair. Move the next “chunk” in the number whose square root you’re solving for down next to the subtracted value you just found. Next multiply the number in the top right quadrant by two and write it in the bottom right quadrant. Next to the number you just wrote down, set aside space for a multiplication problem you’ll do in the next step by writing ‘”_×_=”‘.
- In our example, the next pair in our number is “80”. Write “80” next to the 3 in the left quadrant. Next, multiply the number in the top right by two. This number is 2, so 2 × 2 = 4. Write “‘4″‘ in the bottom right quadrant, followed by _×_=.
5
Fill in the blank spaces in the right quadrant. You must fill each blank space you’ve just written in the right quadrant with the same integer. This integer must be the largest integer that allows the result of the multiplication problem in the right quadrant to be lower than or equal to the current number on the left.^[8]
- In our example, filling in the blank spaces with 8, gives us 4(8) × 8 = 48 × 8 = 384. This is greater than 380. Therefore, 8 is too big, but 7 will probably work. Write 7 in the blank spaces and solve: 4(7) × 7 = 329. 7 checks out because 329 is less than 380. Write 7 in the top right quadrant. This is the second digit in the square root of 780.14.
6
Subtract the number you just calculated from the current number on the left. Continue with the long-division style chain of subtraction. Take the result of the multiplication problem in the right quadrant and subtract it from the current number on the left, writing your answer below.
- In our example, we would subtract 329 from 380, which gives us 51.
7
Repeat step 4. Drop the next chunk of the number you’re finding the square root of down. When you reach the decimal point in your number, write a decimal point in your answer in the top right quadrant. Then, multiply the number in the top right by 2 and write it next to the blank multiplication problem (“_ × _”) as above.
- In our example, since we are now encountering the decimal point in 780.14, write a decimal point after our current answer the top right. Next, drop the next pair (14) down in the left quadrant. Two times the number on the top right (27) is 54, so write “54 _×_=” in the bottom right quadrant.
8
Repeat step 5 and 6. Find the biggest digit to fill in the blanks on the right that gives an answer lesser than or equal to the current number on the left. Then, solve the problem.^[9]
- In our example, 549 × 9 = 4941, which is lower than or equal to the number on the left (5114). 549 × 10 = 5490, which is too high, so 9 is our answer. Write 9 as the next digit in the top right quadrant and subtract the result of the multiplication from the number on the left: 5114 minus 4941 is 173.
9

Continue to calculate digits. Drop a pair of zeros on the left, and repeat steps 4, 5 and 6. For added accuracy, continue repeating this process to find the hundredth, thousandth, etc. places in your answer. Proceed through this cycle until you find your answer to the desired decimal place.

Understanding the Process

1

Consider the number you are calculating the square root of as the area S of a square. Because a square’s area is L² where L is the length of one of its sides, therefore, by trying to find the square root of your number, you are trying to calculate the length L of the side of that square.
2

Specify letter variables for each digit of your answer. Assign the variable A as the first digit of L (the square root we are trying to calculate). B will be its second digit, C its third, and so on.
3

Specify letter variables for each “chunk” of your starting number. Assign the variable S_ato the first pair of digits in S (your starting value), S_b the second pair of digits, etc.
4

Understand this method’s connection to long division. This method of finding a square root is essentially a long division problem that divides your starting number by its square root, thus giving its square root as an answer. Just like in a long division problem, in which you are only interested by the next one digit at a time, here, you are interested by the next two digits at a time (which correspond to the next digit at a time for the square root).
5
Find the biggest number whose square is less than or equal to S_a. The first digit A in our answer is then the biggest integer where the square does not exceed S_a (meaning A so that A² ≤ Sa < (A+1)²). In our example, S_a = 7, and 2² ≤ 7 < 3², so A = 2.
- Note that, for instance, if you wanted to divide 88962 by 7 via long division, the first step would be similar: you would be looking at the first digit of 88962 (8) and you would want the biggest digit that, when multiplied by 7, is lower than or equal to 8. Essentially, you’re finding d so that 7×d ≤ 8 < 7×(d+1). In this case, d would be equal to 1.
6
Visualize the square whose area you are beginning to solve. Your answer, the square root of your starting number, is L, which describes the length of a square with area S (your starting number). Your values for A,B,C, represent the digits in the value L. Another way of saying this is that, for a two-digit answer, 10A + B = L, while for a three-digit answer, 100A +10B + C = L, and so on.
- In our example, (10A+B)² = L² = S = 100A² + 2×10A×B + B². Remember that 10A+B represents our answer L with B in the units position and A in the tens position. For instance, with A=1 and B=2, 10A+B is simply the number 12. (10A+B)² is the area of the whole square, while 100A² the area of the biggest square inside, B² is the area of the smallest square, and 10A×B is the area of each of the two remaining rectangles. By performing this long, convoluted process, we find the area of the entire square by adding up the areas of the squares and rectangles inside it.
7

Subtract A² from S_a. Drop one pair (S_b) of digits from S. S_a S_b is nearly the total area of the square, which you just subtracted the area of the bigger internal square from. The remainder is can be though of as the number N1, which we obtained in step 4 (N1 =380 in our example). N1 is equal to 2×10A×B + B² (area of the two rectangles plus area of the small square).
8

Look for N1 = 2×10A×B + B², also written as N1 = (2×10A + B) × B. In our example, you already know N1 (380) and A (2), so you need to find B. B is most likely not going to be an integer, so you must actually find the biggest integer B so that (2×10A + B) × B ≤ N1. So, you have: N1 < (2×10A + (B+1)) × (B+1).)
9

Solve. To solve this equation, multiply A by 2, shift it in the position of the tens (which is equivalent to multiplying by 10), place B in the position of the units, and multiply the resulting number by B. In other words, solve (2×10A + B) × B. This is exactly what you do when you write “N_×_=” (with N=2×A) in the bottom right quadrant in step 4. In step 5, you find the biggest integer B that fits on the underscore so that (2×10A + B) × B ≤ N1.
10

Subtract the area (2×10A + B) × B from the total area. This gives you the area S-(10A+B)² not yet accounted for (and which will be used to calculate the next digits in a similar fashion).
11

To calculate the next digit C, repeat the process. Drop the next pair (S_c) from S to obtain N2 on the left, and look for the biggest C so you have (2×10×(10A+B)+C) × C ≤ N2 (equivalent to writing two times the two-digit number “A B” followed by “_×_=” . Look for the biggest digit that fits in the blanks that gives an answer that is less than or equal to N2, as before.

Add New Question

Question

Is 28 a perfect number?

Yes. A “perfect” number is a positive integer which is the sum of all of its positive divisors (except itself). Thus, 28 = 1 + 2 + 4 + 7 + 14.
Question

What is the square root of 0.000121?

.011. If you are calculating it by hand, here’s what to do: 121’s sqrt is 11. To get .000121, you simply find an amount of 0’s after the decimal point and the number 11 afterwards. Then multiply by itself. .011*.011= .000121.
Question

Can I write the cube root of x as (1/x)^1/3?

No, it’s (x)^1/3.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

This method works for any base, not just in base 10 (decimal).
In the example, 1.73 can be considered to be a “remainder” : 780.14 = 27.9² + 1.73.
Moving the decimal point by an increment of two digits in a number (factor of 100), moves the decimal point by increments of one digit in its square root (factor of 10).

Show More Tips

Be sure to separate the digits into pairs from the decimal point. Separating 79,520,789,182.47897 as “79 52 07 89 18 2.4 78 97″ will yield a useless number.

Calculator

References

About This Article

Article SummaryX

To calculate a square root by hand, first estimate the answer by finding the 2 perfect square roots that the number is between. A perfect square root is any square root that’s a whole number. For example, if you’re trying to find the square root of 7, first you’d need to find the first perfect square below 7, which is 4, and the first perfect square above 7, which is 9. Then, find the square root of each perfect square. The square root of 4 is 2, and the square root of 9 is 3. Therefore, you know that the square root of 7 falls somewhere between 2 and 3. Now, divide your number by one of the perfect square roots you found. For example, you would divide 7 by either 2 or 3. If you were to choose 3, your answer would be 2.33. Next, find the average of that number and the perfect square root. To find the average in this example, add 2.33 and 2, then divide by 2 and get 2.16. Repeat the process using the average you got. First, divide the number you’re trying to find the square root of by the average. Then, find the average of that number and the original average by adding them together and dividing by 2. For example, first you would divide 7, the number you started with, by 2.16, the average you calculated, and get 3.24. Then, you’d add 3.24 to 2.16, the old average, and divide by 2 to find the new average, which is 2.7. Now, multiply your answer by itself to see how close it is to the square root of the number you started with. In this example, 2.7 multiplied by itself is equal to 7.29, which is 0.29 away from 7. To get closer to 7, you would just repeat the process. Keep dividing the number you started with by the average of that number and the perfect square, using that number and the old average to find the new average, and multiplying the new average by itself until it equals your starting number. If you want to learn how to use the long division algorithm to find the square root, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 2,545,476 times.

Reader Success Stories

“I needed a refresher. This was great! I went to give a quick Google search on how to solve X-roots by hand, and it…” more

Did this article help you?

Источник

Начальная оценка[править | править код]

Десятичная оценка[править | править код]

Скалярные оценки[править | править код]

Линейная оценка[править | править код]

Гиперболическая оценка[править | править код]

Арифметическая оценка[править | править код]

Двоичная оценка[править | править код]

Вавилонский метод[править | править код]

Пример[править | править код]

Сходимость[править | править код]

Сходимость в худшем случае[править | править код]

Метод Бакхшали[править | править код]

Пример[править | править код]

Цифра за цифрой[править | править код]

Основной принцип[править | править код]

Десятичная система счисления[править | править код]

Примеры[править | править код]

Двоичная система счисления[править | править код]

Экспоненциальное тождество[править | править код]

Итеративный метод с двумя переменными[править | править код]

Итеративные методы вычисления обратного к квадратному корню числа[править | править код]

Алгоритм Гольдшмидта[править | править код]

Ряды Тейлора[править | править код]

Разложение в цепную дробь[править | править код]

Метод последовательности Люка[править | править код]

Аппроксимации, зависящие от представления в виде числа с плавающей запятой[править | править код]

Обратное значение квадратного корня[править | править код]

Корень из отрицательного или комплексного числа[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

СсылкиWeisstein, Eric W. Square root algorithms (англ.) на сайте Wolfram MathWorld.[править | править код]

СПОСОБ I

СПОСОБ II

СПОСОБ III

Другие статьи автора:

При помощи деления в столбик

Понимание процесса

Советы

Предупреждения

Похожие статьи

Источники

Об этой статье

Была ли эта статья полезной?

Что такое «извлечение корня»

В каких случаях извлекается корень?

Принципы нахождения значения корня и способы их извлечения

Использование таблицы квадратов, кубов и т.д.

Таблица квадратов

Таблица кубов

Разложение подкоренного числа на простые множители

Извлечение корней из дробных чисел

Извлечение корня из отрицательных чисел

Поразрядное нахождение значения корня

Using a Long Division Algorithm

Understanding the Process

Calculator

References

About This Article

Reader Success Stories

Did this article help you?

Вам также может понравиться

Как найти где подключена подписка яндекс плюс

Как найти чернильный мешок в майнкрафте

Как найти сберпэй в сбербанк онлайн

Добавить комментарий Отменить ответ