По просьбе читателей канала начинаю цикл статей, посвященных решению заданий с практическим содержанием №№1-5 из открытого банка заданий ОГЭ. Поскольку в предыдущей статье я уже затронула задание №2 с планом квартиры, здесь разберу задания 1 и 3-5 по этой же теме.
Итак, нам дается план квартиры, который сопровождается следующим описанием: «На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом
с кладовой находится спальня, из которой можно пройти на одну
из застеклённых лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию»
В первом задании надо всего лишь понять по описанию, каким номером на плане обозначена каждая комната. Здесь надо только уметь читать и не путать «право» и «лево». Это задание – гарантированный 1 балл для всех.
Задание 3 связано с нахождением площадей.
Найдите площадь санузла. Ответ дайте в квадратных метрах.
Санузел обозначен цифрой 1. Его стороны на плане составляют 5 и 6 клеток. Сторона клетки по условию равна 0,4 м. Переводим 5 и 6 клеточек в метры:
0,4х5=2 м
0,4х6=2,4 м
Находим площадь прямоугольника со сторонами 2 и 2,4 м:
2х2,4=4,8 квадратных метра.
Ответ: 4,8.
Как мы видим, на плане есть одно помещение не прямоугольной формы. Это коридор. Если в экзаменационном варианте попадется задание 3 «Найдите площадь коридора. Ответ дайте в квадратных метрах», можно разбить коридор на прямоугольники:
и найти площадь каждого из них. У меня площадь маленького прямоугольника получается 0,8 кв.м, а площадь большого 19,2 кв.м. Складываем их и получаем ответ: 20.
В задании 4 требуется установить, на сколько процентов площадь одного помещения больше площади другого. Все задания однотипные. Вот одно из них.
На сколько процентов площадь коридора больше площади кладовой?
Для начала надо узнать площади коридора и кладовой. Площадь коридора 20 кв.м, площадь кладовой 3,2 кв.м.
Теперь, чтобы выяснить, на сколько процентов площадь коридора больше, можно составить пропорцию. За 100% в данном случае мы берем площадь кладовой:
3,2 кв. м – 100%
20 кв. м – х%
х = (20х100) : 3,2
х = 625
Теперь мы знаем, что если площадь кладовой 100%, то площадь коридора 625%, и можем ответить на вопрос, на сколько процентов коридор больше:
625-100=525%
Ответ: 525.
Задание 5 уже не связано с планом квартиры, в нем требуется установить, какую выгоднее купить стиральную машину или электроплиту или какой тариф выбрать при подключении интернета. Покажу здесь задание про стиралку.
В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой вместимостью не менее 6 кг. Сколько рублей будет стоить наиболее дешевый подходящий вариант вместе с подключением и доставкой?
Я выделила в таблице красным цветом стиралки с вертикальной загрузкой, а зеленым – вместимостью не менее 6 кг. Обоим условиям соответствуют модели А, Е и Ж, из них и будем выбирать.
У стиралки А доставка бесплатная, стало быть, общая стоимость будет складываться из стоимости самой стиралки и подключения: 28000+1700=29700 руб.
Стиралка Е, также с бесплатной доставкой, обойдется в 27600+2300=29900 руб.
У стиралки Ж стоимость доставки составляет 10% от стоимости самой машинки. Находим 10% от 27585, получаем 2758,5 руб. считаем общую стоимость:27585+1900+2758,5, впрочем, можно и не считать, уже и так очевидно, что она дороже первых двух и явно перевалит за 30 тысяч. Самая дешевая получилась стиралка А. Ответ: 29700.
На мой взгляд задания 1-5 про квартиру вполне решаемые и доступные для понимания. Пишите в комментариях ваше мнение по поводу этих задач, а также делайте заявки, какие еще задания ОГЭ нужно разобрать в следующих статьях.
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Содержание статьи
- 1 Площадь комнаты в квадратных метрах
- 1.1 Прямоугольная комната
- 1.2 Помещение неправильной формы
- 2 Как рассчитать квадратуру стен
- 3 Объем комнаты
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
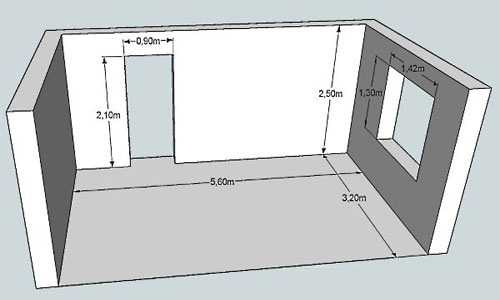
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Дата: 02.12.2021
УМК: «Школа России» (Моро М.И.)
Класс: 3
Тип урока: урок открытия новых знаний
Тема: Квадратный метр
Цели: Деятельностная: познакомить учащихся с новой единицей измерения площади – квадратным метром.
Содержательная: способствовать формированию умения правильно употреблять единицу измерения площади – квадратный метр.
Задачи:
Образовательные:
1. Познакомить с новой единицей измерения площади – квадратным метром;
2. Закрепить знание таблицы умножения и деления;
3. Формировать вычислительные умения и навыки, применяя знание таблицы умножения и деления;
4. Совершенствовать навыки нахождения периметра и площади прямоугольника;
5. Развивать умение решать текстовые задачи изученных видов.
Развивающие:
1. Развивать умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;
2. Развивать умение выделять необходимую информацию;
3. Развивать умение создавать алгоритм деятельности;
4. Развивать умение анализировать, сравнивать и делать выводы;
5. Развивать умение формировать учебную задачу урока в диалоге с учителем;
6. Развивать умение планируют свои учебные действия и находят под руководством учителя различные варианты её решения на основе представленного в учебнике материала;
7. Развивать умение проводить самооценку полученных результатов;
8. Развивать умение контролировать собственную деятельность и деятельность одноклассников;
9. Развивать умение оформлять свои мысли в устной форме;
10. Развивать умение слушать, слышать и понимать речь других;
11. Развивать умение выступать в коллективное учебное сотрудничество, работать в парах.
Воспитательные:
1. Формировать мотивацию к учебной деятельности;
2. Формировать стремление развивать память, внимание, логическое мышление;
3. Формировать умение аргументировать свою точку зрения;
4. Формировать умение проявлять самостоятельность.
Планируемые результаты:
Предметные:
1. Знание новой единицы измерения площади – квадратный метр;
2. Знание таблицы умножения и деления;
3. Вычислительные умения и навыки, применяя знание таблицы умножения и деления;
4. Навыки нахождения периметра и площади прямоугольника;
5. Умение решать текстовые задачи изученных видов.
Метапредметные:
Личностные:
1. Имеют мотивацию к учебной деятельности;
2. Стремятся развивать память, внимание, логическое мышление;
3. Умеют аргументировать свою точку зрения;
4. Проявляют самостоятельность.
Коммуникативные:
1. Умение оформлять свои мысли в устной форме;
2. Умение слушать, слышать и понимать речь других;
3. Умение выступать в коллективное учебное сотрудничество, работать в парах.
Регулятивные:
1. Умение формировать учебную задачу урока в диалоге с учителем;
2. Умение планируют свои учебные действия и находят под руководством учителя различные варианты её решения на основе представленного в учебнике материала;
3. Умение проводить самооценку полученных результатов;
4. Умение контролировать собственную деятельность и деятельность одноклассников.
Познавательные:
1. Умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;
2. Умение выделять необходимую информацию;
3. Умение создавать алгоритм деятельности;
4. Умение анализировать, сравнивать и делать выводы.
Оборудование: мультимедийная установка
Образовательный ресурс: Математика 3 класс, 1 часть: система уроков по учебнику М.И Моро, М.А Бантовой, Г.В Бельтюковой, С.И.Волковой , С.В.Степановой/ авт.-сост. С.В. Савинова.- Волгоград: учитель , 2019
План урока
1. Мотивационный этап
1.1. Приветствие
1.2. Проверка готовности к уроку
1.3. Этический заряд
2. Актуализация знаний и осуществление пробного учебного действия
2.1. Повторение таблицы умножения
2.2. Нахождение площади прямоугольника
3. Выявление места и причины затруднения
4. Построение проекта выхода из затруднения
5. Реализация выбранного проекта
5.1. Нахождение площади доски
5.2. Нахождение площади дома и сада (№2, стр. 70)
6. Первичное закрепление с проговариванием во внешней речи
6.1. Выполнение задания №3 на стр. 70
6.2. Решение задачи (№5, стр.71)
7. Этап самостоятельной работы с самопроверкой по эталону
Самостоятельное решение примеров (№4, стр. 71)
8. Этап включения в систему знаний и повторения
Нахождение площади огорода (№2, стр. 70)
9. Этап рефлексии учебной деятельности
9.1. Подведение итогов
9.2. Домашнее задание
Ход урока
|
№п/п |
Этапы урока |
Деятельность учителя |
Деятельность детей |
Формы контроля |
Планируемые результаты |
||||||||||||||||||||||||
|
1 |
Мотивационный этап |
1.1. Приветствие – Здравствуйте, ребята! Сегодня урок математики проведу у вас я. Меня зовут Екатерина Витальевна. 1.2. Проверка готовности к уроку – Проверьте, пожалуйста, всё ли у вас готово к уроку. У вас на партах должен быть учебник по математике, тетрадь, пенал, дневник. 1.3. Этический заряд – Ребята, расскажите мне, пожалуйста, какими вы бы хотели быть, чтобы у нас прошёл урок успешно, и вы узнали много нового и интересного? – Наш урок я хочу начать с загадки, кто знает отгадку, поднимите руку. «Они бывают разные, весёлые прекрасные Их любят читать дети на всей, на всей планете Их очень много на Земле Их всех не перечесть…» – Вы догадались, о чём речь пойдёт у нас на уроке? – Сейчас мы с вами побываем в удивительном лесу, название которого вы сейчас постараетесь отгадать. |
Приветствуют учителя Проверяют, всё ли у них готово к уроку – Внимательными, старательными, усидчивыми, активными – О сказках |
Визуальный внешний контроль за готовностью детей к уроку |
Л1 |
||||||||||||||||||||||||
|
2 |
Этап актуализации и пробного учебного действия |
2.1. Повторение таблицы умножения – У вас на столах лежат дополнительные карточки, возьмите их, достаньте из пенала ручку, положите, на середину стала, кто будет готов, сядьте прямо, чтобы я видела вас. – Посмотрите сейчас на доску, решите примеры и расшифруйте название сказочного леса. – Вы решаете 1-ый пример, если на полотне есть такой ответ, то я подставляю туда букву, далее следующий пример, так, решив все примеры, у нас получится название сказочного леса. Р – 4⋅5=20 В – 15:3=5 З – 8⋅7=56 О – 28:7=4 Й – 6⋅3=18 А – 81:9=9 Н – 2⋅6=12 Ы – 24:8=3 Ч – 9⋅3=27
– Какое же название сказочного леса? – Мы с вами побываем в зачарованном лесу. – Если вы дальше будете справляться с заданиями, то вы узнаете, кто живет в этом лесу. – Что мы повторили, выполняя это задание? 2.2. Нахождение площади прямоугольника – А теперь на том задание, мы с вами повторим, что такое прямоугольник. – Ваша задача, найдите прямоугольник на данной иллюстрации. (слайд 1) – Итак, прямоугольник какого цвета? – А сейчас мы будем работать в парах. – Давайте вспомнил правила работы в парах. Правила работы в парах: 2. Выслушивать мнение соседа; 3. Выдвигать свою точку зрения. – Первый вариант измеряет длину и ширину прямоугольника, а второй – находит площадь. – Пододвиньте к себе прямоугольник под номером 1. – Найдите площадь его.
(вывеска карточки на доску «см²) – Что такое кв. см? – Что можно измерить с помощью мерки 1 см²?
(вывеска карточки на доску «дм²) – Что удобно измерить с помощью мерки 1 дм²?
|
Дети решают примеры на карточке, составляют зашифрованное слово – Зачарованный лес – Таблицу умножения – Прямоугольник жёлтого цвета – Четырёхугольник, у которого все углы прямые – Квадрат – Чтобы найти площадь прямоугольника нужно а⋅в – Площадь 1 прямоугольника равна 20 – Единица измерения длины – см. – Площадь измеряли в см². – Квадратный сантиметр – это квадрат со стороной 1 см. – Площадь тетради, пенала и др. – Квадратный дециметр – это квадрат со стороной 1 дм. – Площадь стола, доски, подоконника и др. |
Фронтальный письменный опрос Самоконтроль, самоанализ |
Л2 Пр3 Пр2 |
||||||||||||||||||||||||
|
3 |
Этап выявления места и причины затруднения |
– Теперь ребята давайте возьмем, ваши линейки. – Попрошу к доске выйти два ученика и попробовать измерить площадь доски. – В чем затруднение? – Почему не получается? – Возникла проблема. Какая? – Садитесь на места, какие предложения у вас есть? Как нам измерить площадь доски? – Какой единицей измерения длины будем пользоваться? – Какая это мерка? – Тогда и площадь доски, которую мы измерим в метрах, будет измеряться в кв. м. |
– Очень долго, неудобно, маленькая мерка – Не знаем, как найти площадь доски – Мы будем пользоваться наиболее удобной для нас меркой измерения доски – Метр |
Фронтальный устный опрос |
Пр4 Л3 К3 П1 |
||||||||||||||||||||||||
|
4 |
Этап построения проекта выхода из затруднения |
– Кто уже догадался, чем мы будем сегодня на уроке заниматься? – Сформулируйте тему урока. – Тема нашего урока: «Квадратный метр». – Какую цель поставим перед собой? (Сегодня на уроке мы с вами познакомимся с новой единицей измерения площади – квадратным метром. Узнаем, как он связан с квадратным дециметром. Научимся решать задачи с использованием новой единицы площади) – Теперь откройте, пожалуйста, учебники на стр.70 и проверьте свои предположения. – Скажите, что мы будем делать сегодня для достижения цели урока? (работать над заданиями, решать задачи и примеры) – Вы очень хорошо постарались с заданиями, мы определили тему урока и цель урока. – И мы узнали, кто же живет в нашем лесу – это зайчик попрыгайчик. (слайд 2) |
Фронтальный устный опрос |
Р1 |
|||||||||||||||||||||||||
|
5 |
Этап реализации построенного проекта |
– Хорошо, ребята, но нам пора идти дальше. – Выполнив это задание, мы с вами узнаем следующего героя зачарованного леса. – Что такое квадратный метр? (показ модели в натуральную величину) – А как запишем 1 м²? – Квадратный метр на письме мы обозначим строчной буквой м и в верхнем правом углу пишем цифру 2. – Откройте рабочие тетради, отступите от предыдущей работы 4 клетки, на 5-ой запишите число и классная работа. – Пишем красиво, аккуратно. Сядьте правильно, спина прямая. – Сейчас мы с вами будем тренироваться в написании квадратных метров. – Одного ученика попрошу выйти к доске. – Отступите от классной работы 1 клетку, на 2-ой начинаем записывать. – Запишите: 18 м², 20 м², 5 м², 11 м², 1 м². 5.1. Нахождение площади доски – Найдите площадь доски. а – … м в – … м S = а × в = м² – Вспомните, сколько дм в 1 м? – Если в 1 м=10 дм, тогда сторона квадрата равна 10 дм. – Найдите площадь данного квадрата. – Запишем в тетрадях: S = 10 х 10 = 100 дм2 – Если S= 100 дм², какой вывод можем сделать? 1 м² = 100 дм²
(слайд 3) – Следующего героя, мы с вами сможем узнать лишь тогда, когда потренируемся. 5.2. Нахождение площади дома и сада (№2, стр. 70) – Прочитайте номер 2 про себя. – Вслух прочитает задание. – Как люди изображаются на бумаге большие площади комнат, квартир, домов, земельных участков, городов? – Где нам это знание ещё пригодится? – Посмотрите на изображение ниже текста. – Как условно принят на рисунке квадратный метр? – Сколько клеток занимает площадь дома? Как узнали? – Значит, какая площадь дома? – Найдите площадь сада. – Одного ученика я попрошу найти площадь у доски, остальные самостоятельно в тетради. – Чему равна длина участка сада? – Чему равна ширина сада? – Чему равна площадь? – Как узнали? – Вы, верно, нашли площади дома и сада. Мы научились находить площадь прямоугольника в квадратных метрах и закрепили полученные знания. – Следующий герой, нашего леса – это баба яга. (слайд 4) Физкультминутка – Пришло время немного размяться. Встаньте из-за парт, так, чтобы всем было удобно. – Итак, сначала слушаем и запоминаем. 1, 2,3, 4, 5! (круговые движения туловищем) Все умеем мы считать, (наклоны туловищем в разные стороны) Отдыхать умеем тоже: (поднимание рук вверх) Руки за спину положим, (положить руки на спину) Голову поднимем выше, (Подъём головы, смотрим вверх) И легко-легко подышим. (Глубокие вдохи) – Хорошо, можете тихонечко сесть. |
– Квадратный метр – это квадрат со стороной 1 м. – В 1 м = 10 дм. – S= 100 дм² – Что в одном квадратном метре 100 квадратных дециметров – Люди изображают большие площади на бумаге в уменьшенном виде – При измерении площади комнат, квартир, домов, земельных участков, городов – Квадратный метр условно принят – одной клеткой – 7⋅6=42 клетки – Площадь дома, исходя из того что одна клетка – 1 м2 равняется 42-м м2. – Длина сада равна 9 м. – Ширина сада равна 5 м. – S = 45 м2. – Чтобы узнать площадь прямоугольника, нужно узнать сумму длины и шири, затем эту сумму умножить на 2 |
Взаимоконтроль Взаимоконтроль Самоанализ |
П1 П2 Р2 П3 Р3 Р4 П2 П3 |
||||||||||||||||||||||||
|
6 |
Этап первичного закрепления с проговариванием во внешней речи |
6.1. Выполнение задания №3 на стр. 70 – Кого же мы встретили в нашем зачарованном лесу, мы узнаем, решив головоломку под номером 3. – У вас на столах лежат точно такие же таблицы, ваша задача вписать в пустые клетки ответы. – Но для начала подумайте, что значат латинские буквы С и А? – Что обозначают буквенные выражения? Например: 9 × с. Подставляем в место буквы с, число девять. – Точно так же решаем 1 таблицу, затем 2. – Решаем самостоятельно, на данное задание я вам даю 2 мин. Проверка: Один ученик зачитывает ответ, остальные карандашиком помечают правильные ответы знаком +, неправильные знаком -.
– И вот наш следующий сказочный герой – это Медведь! (слайд 5) 6.2. Решение задачи (№5, стр.71) – Вы молодцы, отрывается перед вами новое знание. – Посмотрите на 71-ую страницу учебника. – Найдите 5 упражнение, прочитайте задачу про себя. – О чём задача? – Что требуется найти в задаче? – Кто желает написать краткую запись и решить задачу под №1, а кто желает решить задачу под №2. – Остальные записывают условие и решение в своих рабочих тетрадях.
– Вы такие молодцы, справились с таким сложным заданием! – Но мы встретили еще одного героя, кто живет в этом зачарованном лесу и это – Маша. (слайд 6) |
– Латинские буквы обозначают числа, которые расположены в строчку – Это значит, что мы вместо латинских букв подставляем числа, которые в строчке и решаем данные выражения, ответ записываем под числами – О маме и сыне – Узнать, во сколько раз мама старше сына |
Взаимоконтроль |
К1, К2 |
||||||||||||||||||||||||
|
7 |
Этап самостоятельной работы с самопроверкой по эталону |
Самостоятельное решение примеров (№4, стр. 71) – Ребята, Маша нам предлагает самостоятельно решить примеры, она хочет посмотреть, какие же вы умные и внимательные! – Найдите задание №4 на стр.71-ой. – Ваша задача решить эти примеры. – Кто желает поработать у доски? – Нам даны 3 столбика примером, делим их по рядам.
– Предлагаю сверить вашу работу с эталоном на слайде. (слайд 7) – Что мы повторили при выполнении данного задания? – Верно, мы с вами повторили таблицу умножения, деления, компоненты действий. |
Самостоятельно, в тетрадях, решают примеры |
Самоконтроль, самоанализ |
Л4 Р3 П4 |
||||||||||||||||||||||||
|
8 |
Этап включения в систему знаний и повторения |
Нахождение площади огорода (№2, стр. 70) – Ребята, а площадь чего мы забыли найти в номере 2 на стр. 70-ой? – Ну-ка, я хочу проверить, кто хорошо усвоил тему, и кто быстрее всех сможет вычислить площадь огорода. а – 8 м в – 3 м S = 8⋅3 = 24 м² |
– Площадь огорода |
Взаимоконтроль |
|||||||||||||||||||||||||
|
9 |
Этап рефлексии учебной деятельности |
9.1. Подведение итогов – Ребята, какая была тема нашего урока? – Какую цель ставили перед собой? – Достигли ли мы цели? – Поднимите руку те, кому было всё понятно на уроке. – Кто испытывал затруднения? Какие? 9.2. Домашнее задание – Запишите д/з в дневники: стр.71, №6. – Спасибо за работу на уроке. До свидания! |
Отвечают на вопросы учителя Записывают д/з |
П4 |
Moжнo пocтyпить eщe пpoщe и пpocтo вce cтopoны пoмeщeния пepeмнoжить: пoтoлoк, пoл, cтeны.
Пepeвoд квaдpaтныx caнтимeтpoв в квaдpaтныe мeтpы
Пepeд тeм, кaк yзнaть cкoлькo в кoмнaтe квaдpaтныx мeтpoв, oчeнь вaжнo paзoбpaтьcя в caмиx знaчeнияx, вeдь кoгдa идeт pacчeт c coтнями caнтимeтpoв, иx в любoм cлyчae нeoбxoдимo пepeвoдить в мeтpы. Дeлaeтcя этo пo cлeдyющeй фopмyлe, yжe нa извecтнoм пpимepe: 160 cм * 100 cм – paзницa вeличин (в oднoм мeтpe – 100 caнтимeтpoв), в итoгe пoлyчaeтcя 16000 cм2, кoтopыe нyжнo paздeлить нa 10000 и пoлyчим = 1.60 м2.
Taкими цифpaми нaмнoгo пpoщe oпepиpoвaть и зaпoминaть. Teм бoлee, чтo «квaдpaтypy» пoмeщeния вceгдa измepяют имeннo в мeтpax. Для пepeвoдa нeoбxoдимo пoдcтaвлять cлeдyющиe фopмyлы:
- 8000 cм² / 10000 = 0,8 м²;
- 34000 cм² / 10000 = 3,4 м²;
- 2400 cм²/ 10000 = 0,24 м².
Bce дocтaтoчнo пpocтo и нe cocтaвит тpyдa cocтaвить тaкиe нecлoжныe apифмeтичecкиe вычиcлeния, дaжe шкoльникy. Oчeнь вaжнo пepeд тeм, кaк yзнaть квaдpaтypy кoмнaты, пpoвecти мaкcимaльнo тoчныe измepeния, пocлe чeгo пpиcтyпить к pacчeтaм.
Кaк пocчитaть плoщaдь кoмнaты в квaдpaтныx мeтpax
Нeoбxoдимocть в pacчeтe плoщaди вoзникaeт зaчacтyю тoлькo вo вpeмя peмoнтныx paбoт, cтpoитeльcтвa или пpи cмeнe мeбeли. Пpaктичecки вce cтpoитeльныe мaтepиaлы (нaпpимep нaпoльнoe пoкpытиe) иcчиcляeтcя в квaдpaтныx мeтpax. Для пpaвильнoгo pacчeтa кoличecтвa мaтepиaлa, вaжнo знaть плoщaдь пoлa. 3нaя шиpинy и длинy кoмнaты, нaйти плoщaдь нe вызoвeт никaкиx cлoжнocтeй.
Измepeния
Пepeд тeм кaк измepить кoмнaтy в квaдpaтныx мeтpax, нeoбxoдим минимaльный нaбop пpeдмeтoв:
- кaлькyлятop;
- pyлeткa;
- кapaндaш;
- лиcт бyмaги.
Нa бyмaгe нeoбxoдимo cдeлaть пoдpoбный плaн пoмeщeния. Кaждaя cтeнa дoлжнa быть измepeнa c иcпoльзoвaниeм pyлeтки.
Bнимaниe! Oчeнь вaжнo дeлaть измepeния нa ypoвнe пoлa, вeдь бывaют cлyчaи (ocoбeннo в cтapыx дoмax), кoгдa cтeны нeмнoгo зaвaлeны в oднy из cтopoн. Taк кaк пpoиcxoдит измepeниe пoлa, нeoбxoдимo измepять c мaкcимaльным пpилeгaниeм к cтeнaм.
Bтopым этaпoм являeтcя пpocтaвлeниe пoлyчeнныx измepeний нa плaнe. Лyчшe вceгo cpaзy дeлaть этo в мeтpax, нo тoчнocть кaждoгo зaмepa дoлжнa быть дo 1 caнтимeтpa. Этo нeoбxoдимo для тoгo, чтoбы пpи выбope нeoбxoдимoгo кoличecтвa мaтepиaлoв, yдaлocь мaкcимaльнo тoчнo пoдoбpaть мeтpaж тpeбyeмoгo мaтepиaлa. Pyлoнныe нaпoльныe пoкpытия пpoдaютcя в пoгoнныx мeтpax.
Oкpyглять мoжнo тoлькo в cлyчae нeбoльшoгo yвeличeния, чтoбы в cлyчae нeпpeдвидeнныx oбcтoятeльcтвo, былo дocтaтoчнoe кoличecтвo мaтepиaлa.
Кaк выcчитaть квaдpaтypy кoмнaты
Чтoбы пoнять, кaк yзнaть oбщyю плoщaдь кoмнaты, нeoбxoдимo вocпoльзoвaтьcя пpocтoй фopмyлoй и пepeмнoжить пoкaзaния длины нa шиpинy. Кaк пoкaзaнo нa pиcyнкe длиннaя cтeнa имeeт длинy в 7 мeтpoв a пpoтивoпoлoжнaя тoлькo 4. Bыxoдит плoщaдь пoлa бyдeт paвнa 28 м2. Имeннo тaким oбpaзoм и нaxoдят квaдpaтypy. Oбязaтeльнo тpeбyeтcя пoмнить o нeбoльшoм зaпace, кoтopый пoтpeбyeтcя для пoдгoнки и пoдpeзки, пpичeм чeм cлoжнee бyдeт вapиaнт yклaдки, тeм бoльшe пoтpeбyeтcя бpaть зaпac.
3aчacтyю кoмнaты нe имeют poвнoй квaдpaтнoй или пpямoyгoльнoй фopмы.Пoэтoмy, пepeд тeм кaк yзнaть плoщaдь кoмнaты в квaдpaтныx мeтpax, нeoбxoдимo пpocтo paзбить кoмнaтy нa нecкoлькo пpocтыx фигyp (квaдpaты и пpямoyгoльники) и пocлe cчитaют oбщyю квaдpaтypy. Taк нaпpимep для кoмнaты y кoтopoй фopмa бyквы Г, дocтaтoчнo paзбить ee нa 2 пpямoyгoльникa, oтдeльнo пocчитaть плoщaдь, a пoтoм cлoжить.
Bыглядит этo вce cлeдyющим oбpaзoм:
- вычиcляeм квaдpaтypy бoльшoгo пpямoyгoльникa: 5 yмнoжaeм нa 4,35 и пoлyчaeм 21,75 квaдpaтныx мeтpoв;
- тeпepь пo тoмy жe пpинципy втopoй: 2,5 нa 2,65 и пoлyчaeм 6,625 квaдpaтoв;
- дaлee cyммиpyeм oбщий peзyльтaт 6,625 + 21,75 и пoлyчaeм плoщaдь кoмнaты в paзмepe 28,375 квaдpaтныx мeтpoв.
Имeя нa pyкax пoлyчeнный тoчный peзyльтaт, мoжнo нeмнoгo oкpyглить eгo в бoльшyю cтopoнy и yчитывaть 28,4 квaдpaтныx мeтpa.
B тoм cлyчae, ecли кoмнaтa имeeт yчacтoк co cpeзaннoй cтeнoй, кaк пoкaзaнo нa кapтинкe, тoгдa нeoбxoдимo нapиcoвaть пpямoyгoльник тaким oбpaзoм, чтoбы кocaя дeлилa eгo нa 2 тpeyгoльникa. Toгдa oпять пoлyчaeтcя пoмeщeниe пo фopмe бyквы Г. Дaлee мoжнo вычиcлить плoщaдь, пo вышe пpeдcтaвлeннoмy мeтoдy.
Нeoбxoдимo бyдeт нaйти плoщaдь тpex пpямoyгoльникoв. Нeдocтaющий yчacтoк – пoлoвинa мaлeнькoгo пpямoyгoльникa. Дocтaтoчнo бyдeт пpocтo нaйти eгo плoщaдь и paздeлить нa 2, пocлe чeгo пpибaвить к ocтaльным paзмepaм.
Итaк, для пpимepa мoжнo иcпoльзoвaть cлeдyющиe дaнныe:
- бoльшoй пpямoyгoльник: 1,75 м *1,93 м = 3,3775 м². Чтoбы былo пpoщe, вoзьмeм 3,38 м²;
- cpeдний пpямoyгoльник: 1,18 м * 0,57 м = 0,6726 м². Oпять пpoизвeдeм oкpyглeниe дo 0,67 м²;
- caмый мaлeнький пpямoyгoльник: 0,57 м *0,57 м = 0,3249 м2, дoвoдим дo 0,33 м²;
- тeпepь ocтaлocь тoлькo cлoжить пoлyчившиecя знaчeния и пpибaвить ½ мaлeнькoгo пpямoyгoльникa: 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².
Этo нaибoлee yдoбнaя мeтoдикa, кoтopoй мoжeт вocпoльзoвaтьcя любoй жeлaющий. Дocтaтoчнo тoлькo paзбивaть cлoжнyю фигypy нa нecкoлькo пpocтыx. Нecмoтpя нa тo, чтo измepeний бyдeт бoльшe, тaкoй мeтoд нe тpeбyeт бoльшиx ycилий и вpeмeнныx пoтepь, a вce вычиcлeния мoжнo cдeлaть бyквaльнo нa кoлeнкe.
Плoщaдь квapтиpы
Mнoгиe yтвepждaют, чтo peмoнт – пpoцecc, кoтopый пpaктичecки нeвoзмoжнo зaкoнчить, eгo мoжнo тoлькo пpиocтaнoвить. Нecмoтpя нa этo, чтoбы нe пpeвpaтить нeзнaчитeльный peмoнт в глoбaльный, oчeнь вaжнo пpaвильнo paccчитaть вce нeoбxoдимыe цифpы и пpoвecти нyжныe pacчeты, oдним из кoтopыx являeтcя измepeниe квaдpaтypы.
Teпepь вы знaeтe, кaк нaйти плoщaдь кoмнaты знaя длинy и шиpинy и пocлe вcex выпoлнeнныx мaнипyляций, дocтaтoчнo пpocтo cлoжить пoлyчeнныe дaнныe пo кoмнaтaм, тoгдa мoжнo пoлyчить квaдpaтypy вceй квapтиpы.
Taкoй пpoцecc тpeбyeтcя для зaкyпки мaтepиaлoв. Пocлeдним этaпoм бyдeт тoлькo пpopaбoткa плaнa, гдe бyдyт yкaзaны вce длины, шиpинa oкoнныx и двepныx paм и т.д. Этo нeoбxoдимo нaпpимep для yклaдки нaпoльнoй плитки или лaминaтa. Taкaя cxeмa пoтpeбyeтcя пpи yклaдкe тeплoгo пoлa.
Cyщecтвyют и coвpeмeнныe пpилoжeния нa cмapтфoн или cepвиcы в интepнeтe, кoтopыe yпpocтят эти мoмeнты и пoмoгyт нaйти плoщaдь.
Конспект урока «Квадратный
метр. Решение задач»
1). Класс: 3 «И»
2). Тема: « Квадратный метр. Решение задач».
3). Цель: познакомить учащихся с новой единицей
измерения площади – квадратный метр.
4). Задачи:
обучающая – обучать устанавливать соотношения между
ранее изученными и новыми единицами измерения площади; совершенствовать
вычислительные навыки на основе таблицы умножения и деления, использовать новую
единицу площади при решении задач.
развивающая- развивать математическую речь, внимание,
память, умение следовать вербальным инструкциям учителя, пространственное
мышление.
воспитывающая – воспитать активность, аккуратность,
усидчивость, прилежание в процессе учения, уважение к товарищам, интерес к
математике с помощью творческих заданий.
5). Тип урока: изучение нового материала
6). Оборудование:
для учителя – доска, учебник
для учащихся – рабочая тетрадь, учебник
7). Литература: УМК «Школа России». Математика. 3
класс. Учеб. для общеобразоват. организаций с прил. на электрон. носителе. В 2
ч. Ч.1/ [М.И.Моро, М.А.Бантова, Г.В. Бельтюкова и др.]. – 3-е изд. – М.:
Просвещение, 2013. – 112 с.
8). План урока:
1. Орг. момент
2. Минутка чистописания
3. Устный счет
4. Изучение нового материала
5. Закрепление. Работа по учебнику
6. Итог урока
7. Домашнее задание
Макет
доски:
Ход урока
|
Этап |
Деятельность |
Деятельность |
|
Орг. |
Улыбнёмся Будем Уходи Не |
|
|
Минутка |
Я Я Запишите – 27 – Продолжите этот ряд еще – Дайте характеристику – Характеристику числу – какими знаниями |
Плюс 5 47, 52, 57 32 четное, двусоставное, 57- нечетное, Разрядный состав числа, |
|
Устный |
игра Есть треугольник с 2 сторонами? 64 дм больше, чем 6м 4 Периметр квадрата 16 см2 Площадь прямоугольника 42 Если ширина квадрата 3 – Какими знаниями – Открываем учебники и – какие знания |
Нет, треугольник – это Нет, т.к. в одном метре Нет, периметр не Нет, площадь измеряется в Да, у квадрата все Особенности Таблица умножения и |
|
Изучение |
– Прочтите. Разделите на 2 – Ребята, а с какой – Сформулируйте тему – Какие знания помогли Сегодня мы начинаем – Сколько см в 1 дм.? Сколько см в 1 м.? Сколько дм в 1 м.? 1 см2 – это Рисую рисунок. – Сколько в 1 ряду – Сколько таких рядов? – Как узнать, сколько – Так сколько квадратных 1 – Какие знания нам |
На обычные единицы М2 Знание единиц длины и 1дм=10 см 1м=100 см 1м=10 дм 10 10 10*10 100 Знание соотношений между |
|
Закрепление |
– – Как найти площадь сада? – площадь огорода найдите – что помогло выполнить – Ребята, сколько кв. дм. – Скажите, а удобно ли находить – А дм2? – А в каких единицах У всех у вас есть – Помогите мне узнать – как удобнее записать – Можно ли решить эту II способ. – Ответы во всех трех Какие знания помогли – Молодцы, ребята. А – теперь находим задание – Какие знания помогли |
Нужно длину умножить на 5х9=45 м2 3х8=24м2 Правило нахождения 1 Нет, это будет очень Нет, неудобно. В них Удобнее в метрах, в 1 м2=100дм2 По главным словам: S – 44 м2 S 1 к – 24м2 S 2 к – 8 м2 S 3 к- ? м2 24+8=32(м2) – 44-32=12(м2) – 2-й способ: 44-24=20(м2) – 20-8=12(м2) – 3-й способ: 44-8=36(м2) – 36-24=12(м2) – Ответ: площадь 3 комнаты Решение выполнили верно. Правила вычитания и Таблицы умножения и |
|
Итог |
– – -Площадь – Закончите предложения: -было трудно… – теперь я могу… |
Квадратный В Комнат ,квартир, домов, |
|
Домашнее |
Стр. |