Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.

Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
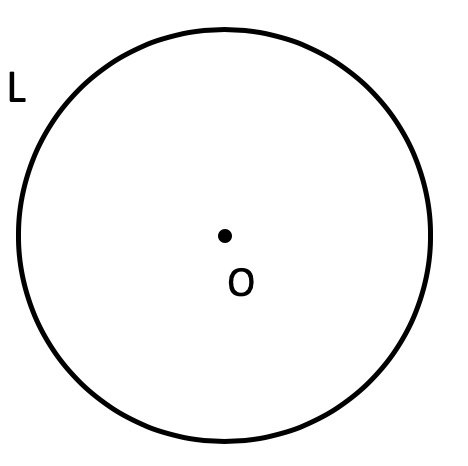
S = L2 : (4 × π), где L — это длина окружности.
Важно!
Задачку не решить, если длина и ширина даны в разных единицах. Для правильного решения переведите все данные к одной единице измерения, и все получится.
Популярные единицы измерения площади:
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Как решаем:
-
Диаметр окружности равен двум радиусам.
-
Используем формулу: S = π × d2 : 4.
-
Подставим известные значения: S = 3,14 × 122 : 4.
S = 113,04 см2.
Ответ: 113,04 см2.
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Как решаем:
-
Используем формулу: S = π × d2 : 4.
-
Подставим известные значения: S = 3,14 × 902 : 4.
S = 6358,5 мм2.
Ответ: 6358,5 мм2.
Задание 3. Найти длину окружности при радиусе 3 см.
Как решаем:
-
Отношение длины окружности к диаметру является постоянным числом.
π = L : d
-
Получается: L = d × π.
-
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
-
Подставим значение радиуса: L = 2 × 3,14 × 3.
L = 18,84 см2.
Ответ: 18,84 см2.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
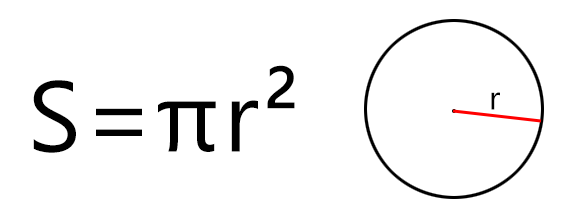
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):
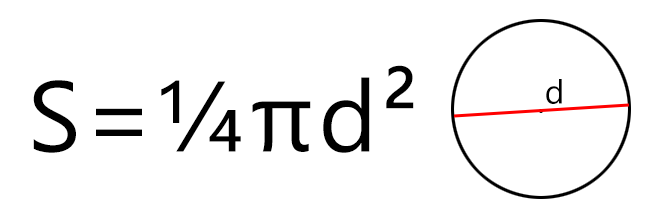
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):
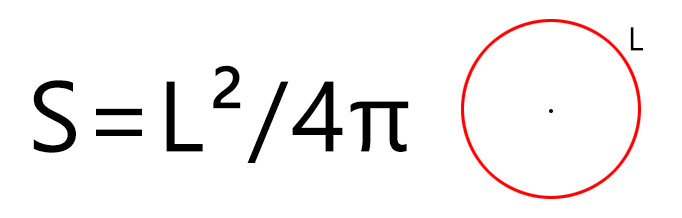
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
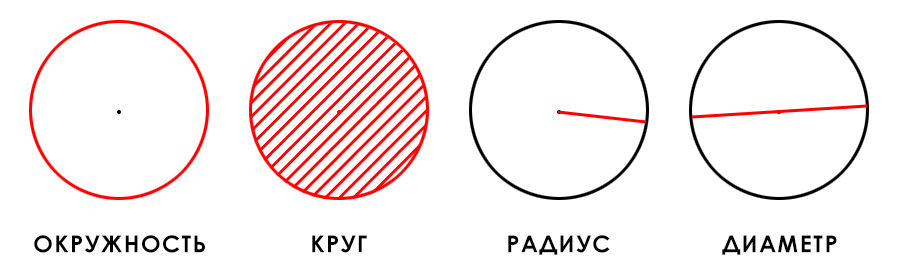
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
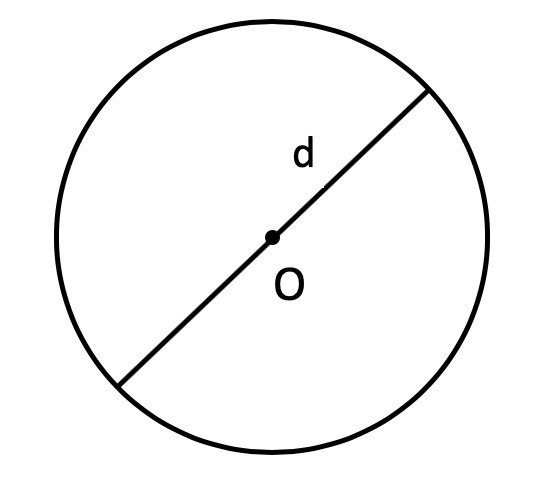
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:

Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
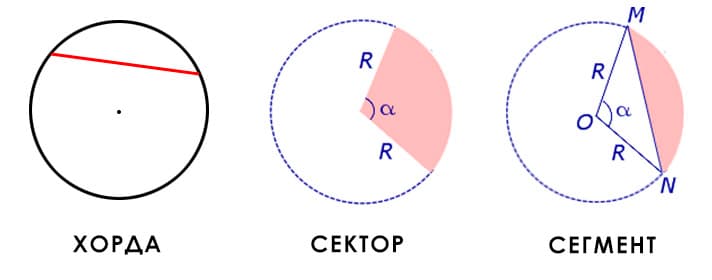
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
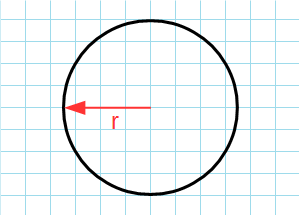
Формула для нахождения площади круга через радиус:
π – константа равная (3.14); r – радиус круга.
Через диаметр
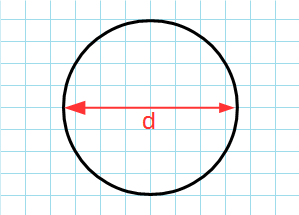
Формула для нахождения площади круга через диаметр:
π – константа равная (3.14); d – диаметр.
Через длину окружности

Формула для нахождения площади круга через длину окружности:
π – константа равная (3.14); l – длина окружности.
Площадь круга с радиусом r равна 


Связанные понятия[править | править код]
-

Сектор круга (закрашен зелёным)
-

Сегмент круга (закрашен жёлтым)
Площадь сектора круга равна 

Площадь сегмента круга равна 

История[править | править код]
Современные математики могут получить площадь круга с помощью методов интегрирования или вещественного анализа. Однако площадь круга изучалась ещё в Древней Греции. Гиппократ Хиосский (в своих попытках квадрирования гиппократовых луночек) первым сформулировал утверждение: площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение[2][3]. Однако они не установили значения коэффициента пропорциональности.
Античные математики также безуспешно пытались решить задачу «квадратуры круга», то есть построения с помощью циркуля и линейки квадрата, равновеликого по площади заданному кругу. Проблемой занимались крупнейшие античные учёные — Анаксагор, Антифон, Брисон Гераклейский, Архимед и другие; неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа 
Архимед в III веке до н. э. использовал методы евклидовой геометрии, чтобы показать в своей книге «Измерение круга[en]», что площадь круга равна площади прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу окружности. В современных обозначениях, длина окружности равна 


Для доказательства Архимед построил для круга вписанный и описанный 96-угольники и вычислил длины их сторон (см. ниже).

Круг, развёрнутый в треугольник
Средневековые европейские математики использовали для обоснования формулы площади круга метод неделимых. Представим себе разворачивание концентричных кругов бесконечно малой толщины в отрезки, получим прямоугольный треугольник с высотой r и основанием 
- Площадь =
основание
высота =
.
Доказательства[править | править код]
Предельный переход[править | править код]
Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к кругу, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус[5], то есть 
Доказательство Архимеда[править | править код]
Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.
Не больше[править | править код]

Круг с вписанными квадратом и восьмиугольником. Показан зазор
Предположим, что площадь круга C больше площади треугольника T = 1⁄2cr. Пусть E означает превышение площади. Впишем[en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G4 больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G8. Продолжаем деление, пока общий зазор Gn не станет меньше E. Теперь площадь вписанного многоугольника Pn = C − Gn должна быть больше площади треугольника.
Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1⁄2nhs. Но h < r и ns < c, так что площадь многоугольника должна быть меньше площади треугольника 1⁄2cr, получили противоречие.
Не меньше[править | править код]

Окружность с описанным квадратом и восьмиугольником. Показан зазор
Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G4 больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника Pn должна быть меньше T.
Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.
Таким образом, площадь круга в точности равна площади треугольника.
Доказательство перегруппировкой[править | править код]

Площадь круга после перегруппировки

Следуя Сато Мошуну [6] и Леонардо да Винчи [7], мы можем использовать вписанные правильные многоугольники другим способом. Положим, мы вписали шестиугольник. Разрежем шестиугольник на шесть треугольников, делая сечения через центр. Два противоположных треугольника содержат общие диаметры. Сдвинем теперь треугольники, чтобы радиальные стороны стали смежными. Теперь пара треугольников образует параллелограмм, в котором стороны шестиугольника образуют две противоположные стороны длиной s. Две радиальные стороны становятся боковыми сторонами, а высота параллелограмма равна h (как в доказательстве Архимеда). Фактически, мы можем собрать все треугольники в один большой параллелограмм, располагая в ряд полученные параллелограммы (из двух треугольников). То же самое будет верно, если мы будем увеличивать число сторон. Для многоугольника с 2n сторонами параллелограмм будет иметь основание ns и высоту h. С ростом числа сторон длина основания параллелограмма увеличивается, стремясь к половине окружности, а высота стремится к радиусу. В пределе параллелограмм становится прямоугольником с шириной πr и высотой r.
-
Приближения площади круга единичного радиуса перегруппировкой треугольников.
многоугольник параллелограмм n сторона основание высота площадь 4 1,4142136 2,8284271 0,7071068 2,0000000 6 1,0000000 3,0000000 0,8660254 2,5980762 8 0,7653669 3,0614675 0,9238795 2,8284271 10 0,6180340 3,0901699 0,9510565 2,9389263 12 0,5176381 3,1058285 0,9659258 3,0000000 14 0,4450419 3,1152931 0,9749279 3,0371862 16 0,3901806 3,1214452 0,9807853 3,0614675 96 0,0654382 3,1410320 0,9994646 3,1393502 ∞ 1/∞ π 1 π
Интегрирование[править | править код]

Площадь круга путём интегрирования
Используя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице. Площадь бесконечно тонкого «слоя» радиуса t будет равна 2πt dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.
Можно разбивать круг не на кольца, а на треугольники с бесконечно малым основанием. Площадь каждого такого треугольника равна 1/2 * r * dt. Суммируя (интегрируя) все площади этих треугольников, получим формулу круга:
Быстрая аппроксимация[править | править код]
Для применения формулы площади круга необходимо знать с нужной точностью значение числа 
Метод удвоения Архимеда[править | править код]
Если задан круг, пусть un будет периметром вписанного правильного n-угольника, а Un — периметром описанного правильного n-угольника. Тогда un и Un являются нижней и верхней границей длины окружности, которые становятся точнее с ростом n, а их среднее значение (un + Un)/2 становится особенно хорошей аппроксимацией длины окружности. Чтобы вычислить un и Un для больших n, Архимед вывел следующие формулы:
(среднее геометрическое)
(среднее гармоническое).
Начав с шестиугольника, Архимед удваивал n четыре раза, дойдя до 96-угольника, который дал ему хорошую аппроксимацию длины окружности круга.
В современных обозначениях можно воспроизвести эти вычисления (и пойти дальше).
Для единичной окружности вписанный шестиугольник имеет периметр u6 = 6, а описанный шестиугольник имеет периметр U6 = 4√3.
Удваиваем семь раз, получаем
-
Удвоения Архимеда семь раз; n = 6×2k.
k n un Un (un + Un)/4 0 6 6,0000000 6,9282032 3,2320508 1 12 6,2116571 6,4307806 3,1606094 2 24 6,2652572 6,3193199 3,1461443 3 48 6,2787004 6,2921724 3,1427182 4 96 6,2820639 6,2854292 3,1418733 5 192 6,2829049 6,2837461 3,1416628 6 384 6,2831152 6,2833255 3,1416102 7 768 6,2831678 6,2832204 3,1415970
(здесь (un + Un)/2 аппроксимирует длину единичной окружности, которая равна 2π, так что (un + Un)/4 аппроксимирует π)
Последняя строка таблицы содержит число, близкое к 355⁄113 — отличному рациональному приближению числа π; лучшие приближения имеют знаменатели на несколько порядков больше[9].
Улучшение Снелла-Гюйгенса[править | править код]
Снелл предложил (а Гюйгенс доказал) более тесные границы, чем у Архимеда:
Для n = 48 формула даёт приближение лучше (около 3,14159292), чем метод Архимеда для n = 768.
Развитие формулы удваивания Архимеда[править | править код]

Круг с подобными треугольниками, описанным, вписанным и дополнительным
Пусть одна сторона вписанного правильного n-угольника имеет длину sn и пусть точки A и B — её концы. Пусть A′ — противоположная A точка на окружности, так что A′A является диаметром, а A′AB является вписанным треугольником, опирающимся на этот диаметр. По теореме Фалеса этот треугольник является прямоугольным (угол B прямой). Пусть длина A′B равна cn и эту длину будем называть дополнением sn. Тогда cn2+sn2 = (2r)2. Пусть точка C делит дугу AB пополам, и пусть C′ является противоположной C точкой окружности. Тогда длина CA равна s2n, длина C′A равна c2n, а C′CA снова является прямоугольным треугольником, опирающимся на диаметр C′C. Поскольку C делит дугу AB пополам, диаметр C′C перпендикулярен хорде AB, которую он пересекает, скажем, в точке P. Треугольник C′AP тогда прямоуголен и подобен C′CA, поскольку у них общий угол C′. Получаем, что все три соответствующие стороны находятся в одной и той же пропорции. В частности, мы имеем C′A : C′C = C′P : C′A и AP : C′A = CA : C′C. Центр окружности O делит A′A пополам, так что треугольник OAP подобен A′AB и длина OP равна половине длины A′B. В результате получаем
В первом равенстве отрезок C′P равен сумме C′O+OP, что равно r+1⁄2cn, а отрезок C′C является диаметром и его длина равна 2r. Для единичного круга получаем знаменитую формулу удвоения Людольфа Ван Цейлена
Если мы теперь построим правильный описанный n-угольник со стороной ″B″, параллельной AB, то OAB и OA″B″ являются подобными с отношением подобия A″B″ : AB = OC : OP. Обозначим описанную сторону Sn, тогда отношение превращается в Sn : sn = 1 : 1⁄2cn. (Мы снова используем факт, что OP равен половине A′B.) Получаем
Обозначим периметр вписанного многоугольника через un = nsn, а описанного через Un = nSn. Комбинируя равенства, получим
так что
Получили среднее геометрическое.
Можно также вывести
или
Получили среднее гармоническое.
Аппроксимация случайными бросаниями[править | править код]

Площадь единичного круга методами Монте-Карло. После 900 бросаний получаем 4×709⁄900 = 3,15111…
Если более эффективные методы недоступны, можно прибегнуть к «бросанию дротиков». Этот метод Монте-Карло использует факт, что при случайных бросаниях точки равномерно распространяются по площади квадрата, в котором расположен круг, число попаданий в круг приближается к отношению площади круга на площадь квадрата. Следует принимать этот метод как последнюю возможность вычисления площади круга (или фигуры любой формы), поскольку для получения приемлемой точности требует огромного числа испытаний. Для получения точности 10−n необходимо около 100n случайных испытаний [10].
Конечная перегруппировка[править | править код]
Как мы видели, разбив диск на бесконечное число кусков мы можем из них затем собрать прямоугольник. Интересный факт был открыт относительно недавно Лацковичем [11], что мы можем разбить круг на большое, однако конечное число кусков, а затем перегруппировать их в квадрат той же площади. Сам вопрос о таком конечном разбиении носит название «Квадратура круга Тарского».
Обобщения[править | править код]
Мы можем растянуть круг до формы эллипса. Поскольку это растяжение является линейным преобразованием плокости, оно изменяет площадь, но сохраняет отношения площадей. Этот факт можно использовать для вычисления площади произвольного эллипса, отталкиваясь от площади круга.
Пусть единичный эллипс описан квадратом со стороной 2. Преобразование переводит круг в эллипс путём сжатия или растяжения горизонтального и вертикального диаметров до малой и большой оси эллипса. Квадрат становится прямоугольником, описанным вокруг эллипса. Отношение площади круга к площади квадрата равно π/4, и отношение площади эллипса к площади прямоугольника будет тоже π/4. Если a и b — длины малой и большой осей эллипса. Площадь прямоугольника будет равна ab, а тогда площадь эллипса — πab/4.
Мы можем распространить аналогичные техники и на большие размерности. Например, если мы хотим вычислить объём внутри сферы, и мы знаем формулу для площади сферы, мы можем использовать приём, аналогичный «луковичному» подходу для круга.
Примечания[править | править код]
- ↑ 1 2 Справочник по элементарной математике, 2006, с. 342.
- ↑ Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М.: Наука, 1959. — С. 204. — 456 с.
- ↑ История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 102.
- ↑ Белозеров С. Е. Пять знаменитых задач древности. История и современная теория. — Ростов: изд-во Ростовского университета, 1975. — С. 144—168. — 320 с.
- ↑ Hill, George. Лекции по геометрии для начинающих Архивная копия от 7 января 2014 на Wayback Machine, страница 124 (1894).
- ↑ Smith, Mikami, 1914.
- ↑ Beckmann, 1976.
- ↑ Gerretsen, Verdenduin, 1983.
- ↑ Не все лучшие рациональные приближения сводятся к непрерывным дробям! Дата обращения: 14 января 2015. Архивировано 28 августа 2014 года.
- ↑ Thijsse, 2006.
- ↑ Laczkovich, 1990.
Литература[править | править код]
- Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6.
- Archimedes в переводе Томаса Хита. The Works of Archimedes. — Dover, c. 260 BCE, год публикации 2002. — С. 91–93. — ISBN 978-0-486-42084-4.
- Petr Beckmann. A History of Pi. — St. Martin’s Griffin, 1976. — ISBN 978-0-312-38185-1.
- J. Gerretsen, P. Verdenduin. Fundamentals of Mathematics, Volume II: Geometry. — MIT Press, 1983. — С. 243–250. — ISBN 978-0-262-52094-2.
- Serge Lang. Math! : Encounters with High School Students. — Springer-Verlag, 1985. — ISBN 978-0-387-96129-3.
- Miklós Laczkovich. Equidecomposability and discrepancy: A solution to Tarski’s circle squaring problem // Journal für die reine und angewandte Mathematik. — 1990. — Т. 404. — С. 77–117.
- David Eugene Smith, Yoshio Mikami. A history of Japanese mathematics. — Chicago: Open Court Publishing, 1914. — С. 130–132. — ISBN 978-0-87548-170-8.
- J. M.Thijsse. Computational Physics. — Cambridge University Press, 2006. — С. 273. — ISBN 978-0-521-57588-1.
Ссылки[править | править код]
- Area of a Circle Calculator
- Area enclosed by a circle Архивная копия от 4 декабря 2008 на Wayback Machine (with interactive animation)
- Science News on Tarski problem Архивная копия от 13 апреля 2008 на Wayback Machine
Загрузить PDF
Загрузить PDF
Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала нужно запомнить формулу, по которой вычисляется площадь круга: 
-

1
Найдите радиус круга. Радиус – это отрезок, соединяющий центр круга с любой точкой внешней окружности круга. Радиус можно измерить в любом направлении: он будет одним и тем же. Радиус также равен половине диаметра круга. Диаметр – это отрезок, который проходит через центр круга и соединяет две точки внешней окружности круга.[1]
- Как правило, значение радиуса дано в условиях задачи. Довольно трудно найти точный центр круга, если только он не обозначен на круге, который нарисован на бумаге.
- Например, радиус круга равен 6 см.
-

2
Возведите радиус в квадрат. Формула для вычисления площади круга:
, где
– радиус, который возведен во вторую степень (в квадрат).[2]
-

3
Полученный результат умножьте на число Пи. Это число обозначается греческой буквой
и представляет собой математическую константу, которая характеризует взаимосвязь радиуса и площади круга. Число Пи приблизительно равно 3,14. Точное значение числа Пи включает бесконечное количество цифр. Иногда ответ (площадь круга) записывается с постоянной
.[3]
- В нашем примере (r = 6 см) площадь вычисляется так:
-

4
Запишите ответ. Помните, что площадь измеряется в квадратных единицах. Если радиус дан в сантиметрах, площадь измеряется в квадратных сантиметрах. Если радиус дан в миллиметрах, площадь измеряется в квадратных миллиметрах. Уточните у преподавателя, нужно ли представить ответ с постоянной
или в числовой форме, используя приблизительное значение числа Пи. Если требование не ясно, запишите оба варианта ответа.[4]
- В нашем примере (r = 6 см) S = 36
см2 или S = 113,04 см2.
Реклама
- В нашем примере (r = 6 см) S = 36
-

1
Измерьте или запишите диаметр. В некоторых задачах радиус не дан. Вместо радиуса указывается диаметр. Если диаметр нарисован на бумаге, измерьте его с помощью линейки. Скорее всего, числовое значение диаметра будет задано.
- Например, диаметр круга равен 20 мм.
-

2
Разделите диаметр пополам. Помните, что диаметр равен удвоенному радиусу. Поэтому разделите любое значение диаметра на 2, чтобы найти радиус.
- Таким образом, если диаметр круга равен 20 мм, то радиус круга равен 20/2 = 10 мм.
-

3
-

4
Запишите ответ. Помните, что площадь измеряется в квадратных единицах. В нашем примере диаметр дан в миллиметрах, поэтому радиус тоже измеряется в миллиметрах, а площадь в квадратных миллиметрах. В нашем примере S =
мм2.
- Также ответ можно представить в численной форме, используя вместо
приблизительное значение 3,14. В этом случае S = (100)(3,14) = 314 мм2.
Реклама
- Также ответ можно представить в численной форме, используя вместо
-

1
Запишите преобразованную формулу. Если известна длина окружности круга, можно воспользоваться преобразованной формулой для вычисления его площади. Такая формула включает длину окружности, а не радиус, и записывается так:
-

2
Измерьте или запишите длину окружности. В некоторых ситуациях нельзя точно измерить диаметр или радиус. Если диаметр не нарисован или центр не отмечен, очень сложно найти точный центр круга. Длину окружности некоторых предметов (например, сковороды) довольно легко измерить с помощью рулетки, то есть можно найти более точное значение длины окружности, чем диаметра.[5]
- Например, длина окружности круга (или круглого предмета) равна 42 см.
-

3
-

4
Запишите формулу для вычисления площади круга. Запишите преобразованную формулу на основе соотношения между длиной окружности и радиусом. Подставьте последнее равенство в стандартную формулу для вычисления площади круга:[7]
-

5
Воспользуйтесь преобразованной формулой, чтобы решить задачу. Теперь в формуле вместо радиуса присутствует длина окружности, поэтому можно вычислить площадь круга по известной длине окружности. Подставьте значение длины окружности и выполните вычисления следующим образом:[8]
-

6
Запишите ответ. Если длина окружности дана в виде числа, а не произведения числа и
, ответ можно записать с
в знаменателе. Или вместо числа Пи подставьте его приблизительное значение (3,14).[9]
Реклама
-

1
Запишите известные величины. В некоторых задачах дана площадь сектора круга, по которой нужно найти площадь всего круга. Внимательно прочитайте такую задачу; ее условие может выглядеть так: «Площадь сектора круга равна 15
см2. Найдите площадь всего круга».[10]
-

2
Запомните определение сектора. Сектор круга – это часть круга, которая ограничена дугой и двумя радиусами. Пространство между такими радиусами и дугой называется сектором.[11]
-

3
Измерьте центральный угол сектора. Воспользуйтесь транспортиром, чтобы измерить угол между двумя радиусами. Линейку (прямолинейную шкалу) совместите с одним из радиусов, причем центр линейки должен совпадать с центром круга. Затем найдите величину угла; для этого посмотрите на точку пересечения второго радиуса с угломерной шкалой.[12]
- Не перепутайте внутренний и внешний угол между двумя радиусами. В задаче должно быть указано, с каким углом работать. Помните, что сумма внутреннего и внешнего углов равна 360 градусов.
- Во многих задачах центральный угол дан, то есть измерять его не нужно. Например, в задаче может быть сказано: «Центральный угол сектора равен 45 градусов»; если это не так, измерьте центральный угол.
-

4
Используйте преобразованную формулу для вычисления площади круга. Если известны площадь сектора и его центральный угол, используйте следующую преобразованную формулу, чтобы найти площадь круга: [13]
-

5
-

6
Запишите ответ. В нашем примере сектор составлял одну восьмую полного круга. Поэтому площадь полного круга равна 120
см2. Так как площадь сектора дана с постоянной
, скорее всего, ответ тоже можно представить с этой постоянной.[15]
- Чтобы записать ответ в численной форме, умножьте 120 x 3,14 = 376,8 см2.
Реклама
Об этой статье
Эту страницу просматривали 264 783 раза.
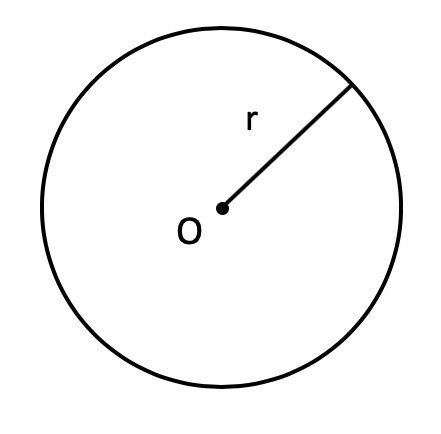



![{begin{aligned}mathrm {Area} (r)&{}=int _{0}^{r}2pi t,dt\&{}=left[(2pi ){frac {t^{2}}{2}}right]_{t=0}^{r}\&{}=pi r^{2}.end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7732a8e7d081596042d1a4f09556b2ad246bfbfd)
![{begin{aligned}mathrm {Area} (r)&{}=int _{0}^{2pi r}{frac {1}{2}}r,dt\&{}=left[{frac {1}{2}}rtright]_{t=0}^{2pi r}\&{}=pi r^{2}.end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58bae552dd0e0d1fa22ae837f150b88b5b6d3781)
![n{frac {3sin {frac {pi }{n}}}{2+cos {frac {pi }{n}}}}<pi <n[2sin {frac {pi }{3n}}+tan {frac {pi }{3n}}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2d64d2436fb5b1a761c0251cdce8ef519ce59a4)








