Сумма квадратов диагоналей параллелограмма
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

Пусть AC и BD – диагонали параллелограмма ABCD.
Докажем, что .
Противоположные стороны параллелограмма равны , поэтому равенство, которое нужно доказать, можно записать в виде:
.
Самый простой способ – воспользоваться теоремой косинусов.
Из треугольника ABC:
Из треугольника BDC:
Сложим полученные равенства:
![]()
AB=CD, BC=AD (по свойству параллелограмма), тогда
![]()
(как односторонние углы при параллельных сторонах AB и CD), поэтому
.
![]()
, что и требовалось доказать.
Теорема косинусов помогает найти решение многих задач по планиметрии из вариантов ЕГЭ по математике.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Сумма квадратов диагоналей параллелограмма» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023
Теорема. (Свойства диагоналей параллелограмма).
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
![]()
Так как противолежащие стороны параллелограмма равны: AB=CD, AD=BC, то сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон:
![]()
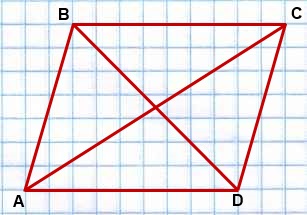
Дано:
ABCD — параллелограмм,
AC и BD — диагонали.
Доказать:
![]()
Доказательство:
I споссоб.

1) Опустим перпендикуляры BK и CF на прямую, содержащую сторону AD.
2) Рассмотрим прямоугольный треугольник BDK.
По теореме Пифагора
![]()
3) Аналогично, из прямоугольного треугольника ACF
![]()
4) Сложим почленно полученные равенства:
![Rendered by QuickLaTeX.com [begin{array}{l} B{D^2} = B{K^2} + K{D^2}\ underline {A{C^2} = C{F^2} + A{F^2}} \ A{C^2} + B{D^2} = B{K^2} + C{F^2} + K{D^2} + A{F^2} end{array}]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-9097ac166774298003b917d601c588e8_l3.png)
BK=CF (как высоты параллелограмма, проведенные к одной стороне), поэтому
![]()
5) Из прямоугольного треугольника ABK по теореме Пифагора
![]()
6) KD=AD-AK, AF=AD+FD, поэтому
![]()
![]()
7) BK=CF, AB=CD. Значит, прямоугольные треугольники ABK и DCF равны (по катету и гипотенузе).
Следовательно, их соответствующие стороны равны: AK=DF. Отсюда,
![]()
![]()
Раскрываем скобки:
![]()
![]()
![]()
Упрощаем
![]()
![]()
Что и требовалось доказать.
II способ.
Свойство диагоналей параллелограмма можно рассматривать как следствие из теоремы косинусов.
Этот способ доказательства будет рассмотрен в следующий раз.
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
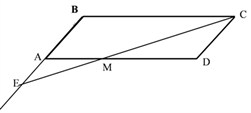
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
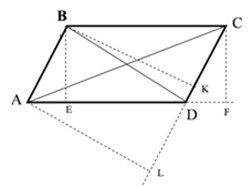
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О; <ВМD = 95о , <DНС = 90о, <ВОD = 155о. Найдите отношение длин отрезков АВ и НD и углы параллелограмма.
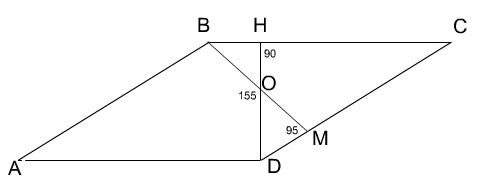 Решение.
Решение.
1. В треугольнике DОМ <МОD = 25о (Он смежный с <ВОD = 155о); <ОМD = 95о. Тогда <ОDМ = 60о.
2. В прямоугольном треугольнике DНС
(<DНС = 90о по условию) <НDС = 60о.
Тогда <НСD = 30о. СD : НD = 2 : 1
(Так как в прямоугольном треугольнике катет, который лежит против угла в 30о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ : НD = 2 : 1.
3. <С = 30о, <D = 150о (Так как сумма углов прилегающих к стороне параллелограмма составляет 180о).
4. <А = <С = 30о, <В = <D = 150о (Противоположные углы параллелограмма равны).
Ответ: АВ : НD = 2 : 1, <А = <С = 30о, <В = <D = 150о
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60о, а вторая диагональ составляет с тем же основанием угол 45о. Найти вторую диагональ.
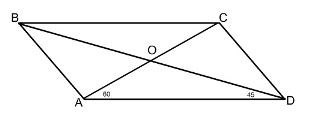
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45о = OD/sin 60о.
ОD = (2√6sin 60о) / sin 45о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
3. ВD = 12.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d1, d2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными 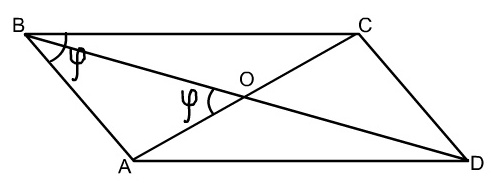 способами его площадь.
способами его площадь.
SABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
SABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d1 d2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d1 d2 sin ф или
2 · 5√2 · 7√2 = d1 d2;
d1 d2 = 140.
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ2 + АD2) · 2 = АС2 + ВD2.
((5√2)2 + (7√2)2) · 2 = d12 + d22.
d12 + d22 = 296.
3. Составим систему:
{d12 + d22 = 296,
{d1 + d2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d1 + d2)2 = 576. Отсюда Id1 + d2I = 24.
Так как d1, d2 – длины диагоналей параллелограмма, то d1 + d2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45о. Найдите площадь параллелограмма.
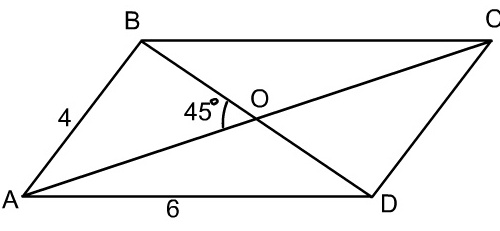
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ2 = АО2 + ВО2 2 · АО · ВО · cos АОВ.
42 = (d1/2)2 + (d2/2)2 – 2 · (d1/2) · (d2/2)cos 45о;
d12/4 + d22/4 – 2 · (d1/2) · (d2/2)√2/2 = 16.
d12 + d22 – d1 · d2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что <АОD = 135о и cos 135о = -cos 45о = -√2/2.
Получим уравнение d12 + d22 + d1 · d2 √2 = 144.
3. Имеем систему
{d12 + d22 – d1 · d2 √2 = 64,
{d12 + d22 + d1 · d2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d1 · d2 √2 = 80 или
d1 · d2 = 80/(2√2) = 20√2
4. SABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d1 d2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
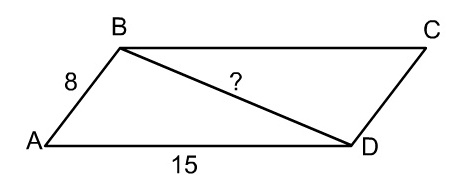
Решение.
1. SABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4/5.
2. Найдём cos ВАD. sin2 ВAD + cos2 ВАD = 1.
(4/5)2 + cos2 ВАD = 1. cos2 ВАD = 9/25.
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3/5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD2 = АВ2 + АD2 – 2 · АВ · ВD · cos ВАD.
ВD2 = 82 + 152 – 2 · 8 · 15 · 3/5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Параллелограмм и его свойства
- Противоположные углы параллелограмма равны.
- Высота перпендикулярно основанию параллелограмма.
- Cумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: (d_1^2+d_2^2=2(a^2+b^2));
- Диагонали параллелограмма пересекаются в точке: (AO = OC, BO = OD)
- Сумма углов четырехугольника прилегающих к любой стороне равна (180°).
- Сумма квадратов диагоналей равна сумме квадратов сторон в параллелограмме: (d^2_1+d_2^2=2a^2+2b^2.)
- Биссектрисы противоположных углов параллелограмма всегда параллельны.
- Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°).
- Сторону параллелограмма можно найти по диагонали и углу между ними:
(a= sqrt{d_1^2 + d^2_2 – 2d_1d_2cosa } )
- Также сторону параллелограмма можно найти по диагоналям и другой стороне:
(a = { sqrt{2d_1^2+ 2d_1^2 – 4b_2^2 } over 2} )
(b = { sqrt{2d_1^2+ 2d_1^2 – 4a_2^2 } over 2} )
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Формулы суммы квадратов диагоналей и разности квадратов сторон параллелограмма:
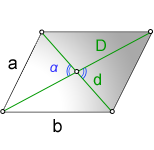
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
Формула суммы квадратов диагоналей:
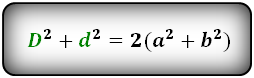
Формула разности квадратов сторон:
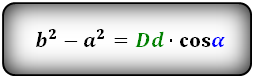
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
