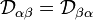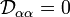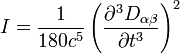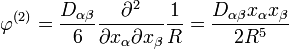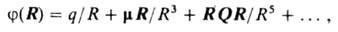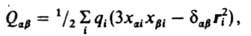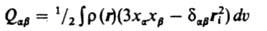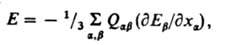Как найти квадрупольный момент системы зарядов

1.7Дипольный момент. Тензор квадрупольного момента. Поле системы зарядов на больших расстояниях

1.8 Силы и энергия в электростатическом поле

Электрический квадруполь[править | править код]

Поле квадруполя[править | править код]

Магнитный квадруполь[править | править код]

Гравитационный квадруполь[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Содержание

Электрический квадруполь

Поле квадруполя

Магнитный квадруполь

Гравитационный квадруполь

См. также

Литература

КВАДРУПОЛЬНЫЙ МОМЕНТ

1.7Дипольный момент. Тензор квадрупольного момента. Поле системы зарядов на больших расстояниях

1.8 Силы и энергия в электростатическом поле

Электрический квадруполь[править | править код]

Поле квадруполя[править | править код]

Магнитный квадруполь[править | править код]

Гравитационный квадруполь[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Содержание

Электрический квадруполь

Поле квадруполя

Магнитный квадруполь

Гравитационный квадруполь

См. также

Литература

КВАДРУПОЛЬНЫЙ МОМЕНТ

1.7Дипольный момент. Тензор квадрупольного момента. Поле системы зарядов на больших расстояниях

1.8 Силы и энергия в электростатическом поле

Электрический квадруполь[править | править код]

Поле квадруполя[править | править код]

Магнитный квадруполь[править | править код]

Гравитационный квадруполь[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Содержание

Электрический квадруполь

Поле квадруполя

Магнитный квадруполь

Гравитационный квадруполь

См. также

Литература

КВАДРУПОЛЬНЫЙ МОМЕНТ

Реклама

Добавить комментарий Отменить ответ

Реклама

Вам также может понравиться

Как составить резюме для работы секретарем

Арбитражный суд московской области как найти дело

Как найти сяоми с другого сяоми

Добавить комментарий Отменить ответ

Соответственно выражение для напряженности поля есть

E~ =

grad ϕ =

~ar ∂

+ ~aϕ

∂ + ~aθ

1 ∂

(

Er cos θ) 1

R33 =

−

“

−

∂r

r sin ϕ

∂ϕ

r ∂θ

1 + 2

cos θ

sin θ.

= ~arE0

−

~aθE0

− r

Поверхностная плотность заряда равна: σ = −41π ∂ϕ∂r |r=R = 43π E0 cos θ.

Комментарий: так как интеграл от поверхностной плотности заряда равен нулю, безразлично, заряжена сфера или изолирована.

Задание на дом: решить задачи 2.16–2.18 на стр. 33.

Скалярный потенциал произвольной системы зарядов на больших расстояниях определяется следующим выражением:

(dr~ )

(84)

ϕ =

Qαβxαxβ + . . .

2r5

α,β=1

Здесь q — полный заряд системы, d — дипольный момент системы:

~d = Z ~rρ(~r )dV

→

(85)

=1 qi~rl,

Qαβ — тензор квадрупольного момента.

Qαβ = Z (3xαxβ − r2δαβ)ρ(r)dV

→

− r(i)2

δαβ

(86)

=1 qi 3xα(i)xβ(i)

Пример 1.7.1 Плотность заряда в одном из возбужденных состояний атома водорода в сферических координатах имеет вид:

ρ = ρ0r4e−λr sin4 θ,

где , . Вычислить ~ и .

ρ0 λ = const d Qα,β

По определению дипольного момента (85):

Z Z 3

~ ~ ~ ~ ~ X ~

d = ρ(r)r dV = ρ[ix + jy + kz] dV = eαdα.

α=1

Вычисление компонент dα дает значение, равное нулю, т.к. вычисляются

интегралы от нечетных функций в симметричных пределах, т.е. ~ . d = 0

Для вычисления компонент тензора квадрупольного момента воспользуемся формулой (86). При α = β = 1 получим:

В результате для (87) после интегрирования по ϕ и замены переменных интегрирования u = λr, x = cos θ находим:

	ρ	+1	ρ0		32
Qxx =		Z0∞ u8e−u du Z−1 (1 − x2)2[3π(1 − x2) − 2π]dx =		8! 2π		.
λ9	λ9	15 · 7

Аналогичные вычисления для Qyy дают: Qyy = Qxx, а для Qzz = −2Qxx при α 6= β Qαβ равен нулю.

Пример 1.7.2. Полусфера радиуса R заряжена с постоянной объемной плотностью ρ. Определить компоненты дипольного и тензора квадрупольного моментов.

Выбирая систему координат в центре полусферы, получим dx = dy = 0. Соответственно для dz:

	R	2π	π/2		3
dz = Z	ρzr2dr sin θ dθ dϕ = ρ Z0	r3 dr Z0	dϕ Z0	cos θ sin θ dθ =		QR,
8

где Q — полный заряд полусферы: Q = ρ23 πR3, Qxx — компонента тензора квадрупольного момента:

Z R Z π/2 Z 2π

Qxx = ρ(3x2 − r2)r2dr sin θ dθ dϕ =

0 0 0

= ρ Z R r4dr Z π/2 Z 2π(3 sin2 θ cos2 ϕ − 1) sin θ dθ dϕ = 0.

00 0

Аналогично находим, что равны нулю и другие компоненты тензора Qαβ.

Пример 1.7.3 Цилиндр высоты H и радиуса R заряжен с объемной плотностью ρ = ρ0 = const. Определить Qxx элемент тензора квадрупольного момента такой системы зарядов.

По определению для Qxx в системе координат, связанной с осью цилиндра, находим:

Qxx = ρ0

2π[3ρ2 cos2 α

(ρ2+z2)]ρ dρ dz dα =

ρ0πHR4

2 .

−

Пример 1.7.4. Определить поле системы точечных зарядов (см. рис.12) на больших расстояниях.

Для нахождения поля необходимо определить, какой величиной характеризуется данное распределение зарядов. В данном случае полный заряд системы равен нулю. Дипольный момент также равен нулю:

		~	~	~	~	~
		d = q(−ia) − q(ja) + q(ia) − q(ja) = 0.
		Определим компоненты квадрупольного момента,
Рис. 12:		для примера:

Q11 = Qxx =	4	3xi2 − ri2	= q2a2	+ qa2 + q2a2 + qa2 = 6a2q.
=1 qu
iX

Аналогично вычисляются другие компоненты. В результате Q22 = −Q11, а остальные компоненты равны нулю. Таким образом, на больших расстояниях поле имеет вид:

ϕ =	1	(x2Qxx + y2Qyy) = −	3a2q	sin2 θ(1 − 2 cos2 ϕ),
2r5	r3

где r, θ, ϕ — переменные сферической системы координат.

Пример 1.7.5. Начало декартовой системы координат совпадает с центром тонкого кольца радиуса R. Найти поле на больших расстояниях от кольца с точностью до квадрупольных слагаемых, если кольцо заряжено с линейной плотностью τ.

Полный заряд кольца равен: q = 2πτR. Дипольный момент

~ Z ~ Z 2π ~ ~

d = rρdV = (ix + jy)τR dα = 0.

Компоненты тензора квадрупольного момента:

Z Z

Qxx = [3x2 − R2]τR dα = [3R2 cos α − R2]τR dα = τR3π.

Аналогично Qyy = τR3π, Qzz = −τR32π и Qαβ = 0 при α 6= β. В результате

для скалярного потенциала находим:

ϕ(~r ) =

1 3

[x2Qxx + y2Qyy] =

2r5

Qαβxαxβ ‘ r

2r5

αβ=1

=Q + τR3π h1 − cos2 θi r 2r3

Пример 1.7.6. Найти поле		точечного	диполя	~		= const,
	d
расположенного в начале координат.
~	~
В этом случае P =	dδ(~r ), и из решения уравнения (10) получим для
вектора Герца электрического типа:	~	~
Π = d/r. Отсюда:
	~					~		~
E~ = 4π~dδ(~r ) + rot rot	d	=	−	4π~dδ(~r ) +	3~n(~nd) − d	.

−		r					r3

Задание на дом: решить задачи 2.19–2.24 на стр. 34.

Величина

Формула

Энергия

единицы

объема

~ ~

; ε = Z

w и полная энергия ε

w =

w dV.

(88)

8π

электростатического поля

Сила,

действующая

на

(89)

F = qE

точечный заряд E

Сила,

действующая

на

F~ = Z

ρE~ dV

(90)

распределенный в пространстве

заряд

Сила, действующая на единицу

(91)

поверхности

проводника

~p =

8π

(давление)

~n – нормаль к поверхности

Величина

Формула

Выражение

для

силы

F= I

MklnkdS,

(92)

использованием

тензора

натяжений Максвелла

Mkl — тензор натяжений;

Mkl =

“EkEi −

E2 δki#

4π

~n — нормаль к dS.

Сила,

действующая

на

(93)

дипольный момент в поле

F = (d

grad )E

Знергия

заряда во

внешнем

qϕ

ρ(~r )ϕ(~r 0)dV

(94)

поле

Энергия системы зарядов

qiqj

(95)

=j ~ri

~rj

−

Энергия системы проводников

Xi qiϕi

(96)

Энергия

диполя во

внешнем

(97)

поле

− (d

· E)

Энергия

квадрупольного

ϕ(0)

Qα,β

∂

(98)

момента

во

внешнем

поле

со

α,β=1

∂x

∂xβ

скалярным потенциалом ϕ

Пример 1.8.1. Заряд Q равномерно распределен по поверхности

сферы радиуса R. Найти абсолютную величину силы, разрывающей

сферу на две равные половины. Решить задачу двумя методами с использованием формул (91) и (92).

Данная система зарядов создает поле, равное нулю для r < R, и поле, совпадающее с полем точечного заряда Q/r2 для r > R.

1 способ решения. Выделим произвольную половину сферы. На элемент поверхности dS действует сила E2~n dS/8π. Результирующая сила равна:

	E2	π/2	2π E2
F~ = Z		~n dS =	Z0	Z0	~nR2 sin θ dθ dϕ.
8π	8π

Вычислим проекции этой силы на декартовы оси с учетом: nx = sin θ cos ϕ,

ny = sin θ sin ϕ. Например, для Fz имеем:

π/2	2π E2	Q2
fz = Z0	Z0		cos θR2 sin θ dθ dϕ =	.
8π	8R2

Проекции Fx = Fy = 0.

2 способ решения. В соответствии с (92) имеем:

Fz = [Mxznx + Myzny + Mzznz] dS.

Поверхность интегрирования включает половину сферы и основание. Однако интеграл по основанию равен нулю в силу Mik=0 для точек r < R. Таким образом,

Fz =	π	2π		ExEz	sin θ cos ϕ +	EyEz	sin θ sin ϕ +	Ez2 − 21 E2
Z0	Z0	4π	4π	4π

cos θ sin θ dθ dϕ.

		(99)
По определению на сфере Ex =	Q sin θ cos ϕ/R2, Ey	= Q sin θ sin ϕ/R2,
Ez = Q cos θ/R2. Подставляя	Ek в (99), находим	после выполнения

интегрирования: Fz = Q2/8R2, как и при первом способе решения.

Пример 1.8.2. Шар радиуса R заряжен с объемной плотностью ρ = const. Найти силу, разрывающую шар на две равные половины. Решить задачу двумя методами.

На основании решения примера 1.2.2 известно, что поле такой системы

зарядов есть
~	4	πρ~r,	~	Q~r		(100)
E =	3	r < R; E =	r2		r	, r > R

1 способ решения. В соответствии с (90) сила, действующая на единицу

объема равна	~
ρE. Следовательно, для определения суммарной силы,

действующей на полусферу, надо проинтегрировать данное выражение по объему полусферы. При интегрировании получим, что Fx и Fy равны нулю. Соответственно для Fz находим:

R	π/2	2π		3 Q2
Fz = Z0	Z0	Z0	ρE(r) cos θr2dr sin θ dθ dϕ =		,
16	R2

где Q — полный заряд шара.

2 способ решения. На основании (92) необходимо интегрировать по замкнутой поверхности, которая в данном случае состоит из основания и поверхности полусферы. То есть интеграл разбивается на сумму двух

интегралов. При интегрировании по основанию для нормали к поверхности


имеем nx	= 0, ny = 0, nz	= −1. Интегрирование удобно выполнять в
цилиндрической системе координат, в которой dS = ρ dρ dα,
	1		R	2π	1
Fz(1)	= Z MzznzdS = −		Z0	Z0	“Ez2 −	(Ex2 + Ey2 + Ez2)# ρ dρ dα.
4π	2

С учетом (100) и соотношений Ex = E0 cos α, Ey = E0 sin α, Ez = 0, E0 = 43 πρ2, θ = π/2 находим после интегрирования: Ez(1) = Q2/16R2.

При интегрировании выражения (92) по поверхности сферы необходимо подставить nx = sin θ cos ϕ, ny = sin θ sin ϕ, nz = cos θ. В результате

	π/2 2π	Q
Fz(2) =	Z	Z [Mxz sin θ cos ϕ + Myz sin θ sin ϕ + Mzz cos θ]2R sin θ dθ dϕ =	,

8R2
	0	0

где использованы выражения для тензора натяжений Максвелла:

Mxz =

E12

sin θ cos ϕ cos θ; Myz =

E12

sin θ sin ϕ cos θ; Mzz = “cos2

−

4π

Суммарная сила: Fz = F (1)

+ F (2)

= 3Q2/16R2.

Комментарий: может показаться, что метод, основанный на использовании тензора натяжений Максвелла, весьма громоздок и неудобен. Однако преимущество этого метода проявляется там, где нет простой симметрии.

Пример 1.7.3 Шар радиуса R однородно заряжен с объемной плотностью ρ = const. Определить энергию поля, создаваемого зарядами шара.

Напряженность поля определяется выражением (100). В соответствии с

(88) полная энергия поля равна:

ε =

R π 2π

2 r2dr sin θdθdϕ +

∞ π 2π

2 r2dr sin θdθdϕ

8π

” r3

Z Z Z

“r2

Z Z Z

0 0 0

R 0 0

Пример 1.8.4. Потенциал внешнего электростатического поля имеет вид ϕ(x, y) = α exp[−β(x2 − y2)] и мало меняется по размеру квадруполя (см. рис.12 на стр 27). Найти энергию квадруполя во внешнем поле.

В соответствии с (98) и решением, приведенном в примере (1.7.4) , находим:

ε = 61

∂2ϕ

Qxx

∂2ϕ(0)

= 4αβa2q.

Qαβ ∂x ∂x(0)

∂x2

+ Qyy ∂y2

α β

αβ

Соседние файлы в папке Хасанов лекции

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 мая 2021 года; проверки требуют 2 правки.

В теории поля представление системы зарядов в виде некоторых квадрупо́лей, аналогично представлению её в виде системы диполей, используется для приближённого расчёта создаваемого ей поля и излучения. Более общим представлением является разложение системы на мультиполи, соответствующее разложению потенциалов в ряд Тейлора по некоторым переменным. Квадруполь — частный случай мультиполя. Квадрупольное рассмотрение системы оказывается особенно важным в том случае, когда её дипольный момент и заряд равны 0.

Электрический квадруполь (от лат. quadrum — четырёхугольник, квадрат и др.-греч. πόλος — полюс), система заряженных частиц, полный электрический заряд и электрический дипольный момент которой равны нулю. Квадруполь можно рассматривать как совокупность двух одинаковых диполей с равными по величине и противоположными по направлению дипольными моментами, расположенных на некотором расстоянии друг от друга (см. рис.). На больших расстояниях от квадруполя напряженность его электрического поля убывает обратно пропорционально четвёртой степени $(Esim 1/R^{4})$ , а зависимость от зарядов и их расположения описывается в общем случае набором из пяти независимых величин, которые, вместе составляют квадрупольный момент системы. Квадрупольный момент определяет также энергию квадруполя во внешнем электрическом поле. Квадруполь является мультиполем 2-го порядка.

Квадрупольный момент (произвольной) системы зарядов является тензором 2-го ранга в $mathbb {R} ^{3}$ . Он представляется интегралом по пространству

${mathcal {D}}_{{alpha beta }}=iiint limits _{V}rho (x,y,z)(3x_{alpha }x_{beta }-R^{2}delta _{{alpha beta }})dV$

где — плотность зарядов в данной точке, — модуль радиус-вектора, $(x_{1},x_{2},x_{3})=(x,y,z)$ , — индексы, нумерующие координаты.

Тензор квадрупольного момента симметричен:

${mathcal {D}}_{{alpha beta }}={mathcal {D}}_{{beta alpha }}$

Его след равен нулю:

${mathcal {D}}_{{alpha alpha }}=0$

Здесь и далее используется соглашение Эйнштейна о суммировании.

Если полный заряд системы и её дипольный момент равны 0, то квадрупольный момент не зависит от выбора начала координат. В противном случае необходимо также указывать центр квадруполя — начало координат при его вычислении.

На больших расстояниях поле любой в целом нейтральной системы зарядов, дипольный момент которой равен нулю, выглядит как поле некоторого (возможно, изменяющегося со временем) квадруполя или более высокого мультиполя (октуполя и т.д.). Рассмотрение системы как некоторого квадруполя может иметь смысл и тогда, когда дипольный момент и/или заряд системы не равны нулю, если раскладывать создаваемый потенциал в ряд по мультиполям. Квадрупольное излучение системы на больших расстояниях равно (в СГС)

$I={frac {1}{180c^{5}}}left({frac {partial ^{3}D_{{alpha beta }}}{partial t^{3}}}right)^{2}$

Здесь — скорость света, — полная мощность излучения. Во многих случаях достаточно считать, что излучение системы складывается из дипольного, квадрупольного и магнитодипольного.

Квадрупольный потенциал имеет вид (при определении квадрупольного момента так, как описано выше):

$varphi ^{{(2)}}={frac {D_{{alpha beta }}x^{alpha }x^{beta }}{2r^{5}}}$

Здесь $x_{alpha }=(x_{1},x_{2},x_{3})$ — радиус-вектор точки, в которой берётся потенциал, относительно центра квадруполя. $varphi ^{{(2)}}$ является вторым членом разложения потенциала в ряд по расстоянию до начала координат.

Поле электрического квадруполя имеет ярко выраженный нецентральный характер, и его удобно представлять, используя тензорную форму записи^[1]:

${displaystyle E_{alpha }^{(2)}=-{frac {partial varphi ^{(2)}}{partial x^{alpha }}}={frac {5}{2}}{frac {x_{alpha }D_{beta mu }x^{beta }x^{mu }}{r^{7}}}-{frac {D_{alpha beta }x^{beta }}{r^{5}}}}$

Катушки создают поле квадруполя

Все известные магнитные источники дают поля диполя. Однако, возможно создать магнитный квадруполь путём помещения четырёх идентичных стержневых магнитов перпендикулярно друг другу таким образом, что северный полюс одного магнита находится рядом с южным полюсом другого. Такая конфигурация убирает дипольный момент и даёт квадрупольный момент, а поля системы убывают на больших расстояниях быстрее, чем поля диполя.

Пример магнитного квадруполя, содержащего постоянные магниты, представлен на картинке справа. Электромагниты подобного концептуального дизайна (квадрупольные линзы) обычно используются для фокусировки пучков заряженных частиц в ускорителях заряженных частиц. Метод известен под названием сильная фокусировка.

Изменяющийся магнитный квадрупольный момент вызывает электромагнитное излучение.

Букингем (единица измерения)
Диполь (электродинамика)
Мультиполь
высокочастотный квадруполь, см. Квадрупольный масс-анализатор#Принцип действия

↑ В.И. Денисов, Лекции по электродинамике §11 (2007)

Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7. — § 41.

Источник

1 Электрический квадруполь
2 Поле квадруполя
3 Магнитный квадруполь
4 Гравитационный квадруполь
5 См. также
6 Литература

Квадруполь

Электрический квадруполь (от лат. quadrum — четырёхугольник, квадрат и греч. pólos — полюс), система заряженных частиц, полный электрический заряд и электрический дипольный момент которой равны нулю. Квадруполь можно рассматривать как совокупность двух одинаковых диполей с равными по величине и противоположными по направлению дипольными моментами, расположенных на некотором расстоянии друг от друга (см. рис.). На больших расстояниях R от квадруполя напряженность его электрического поля E убывает обратно пропорционально четвёртой степени R 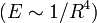, а зависимость E от зарядов и их расположения описывается в общем случае набором из пяти независимых величин, которые, вместе составляют квадрупольный момент системы. Квадрупольный момент определяет также энергию квадруполя во внешнем электрическом поле. Квадруполь является мультиполем 2-го порядка.

Квадрупольный момент (произвольной) системы зарядов является тензором 2-го ранга в 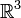R^3 . Он представляется интегралом по пространству

$mathcal{D}_{alpha beta} = iiintlimits_V rho(x,y,z) (3 x_alpha x_beta - R^2 delta_{alpha beta}) dV$

где ρ(x,y,z) — плотность зарядов в данной точке, R — модуль радиус-вектора, (x₁,x₂,x₃) = (x,y,z), α,β = 1,2,3 — индексы, нумерующие координаты.

Тензор квадрупольного момента симметричен:

$mathcal{D}_{alpha beta} = mathcal{D}_{beta alpha}$

Его след равен нулю:

$mathcal{D}_{alpha alpha} = 0$

Здесь и далее используется соглашение Эйнштейна о суммировании.

На больших расстояниях поле любой системы зарядов, дипольный момент которой равен 0, выглядит как поле некоторого квадруполя, возможно, изменяющегося со временем. Рассмотрение системы как некоторого квадруполя может также иметь смысл при неравном нулю дипольном моменте системы, если раскладывать создаваемый потенциал в ряд по мультиполям. Квадрупольное излучение системы на больших расстояниях равно (в СГС)

$I = frac{1}{180 c^5} left( frac{partial^3 D_{alphabeta}}{partial t^3} right)^2$

Здесь c — скорость света, I — полная мощность излучения. Во многих случаях достаточно считать, что излучение системы складывается из дипольного, квадрупольного и магнитодипольного.

Квадрупольный потенциал имеет вид

$varphi^{(2)} = frac{D_{alphabeta}}{6} frac{partial^2}{partial x_alpha partial x_beta} frac{1}{R} = frac{D_{alphabeta}x_alpha x_beta}{2R^5}$

Здесь x_α = (x₁,x₂,x₃) — радиус-вектор точки, в которой берётся потенциал, относительно центра квадруполя. 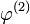$varphi^{(2)}$ является вторым членом разложения потенциала в ряд по расстоянию до начала координат.

Диполь
Мультиполь

Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7 — § 41.

Wikimedia Foundation.
2010.

Источник

КВАДРУПОЛЬНЫЙ МОМЕНТ электрический, тензор Q, характеризующий электростатич. потенциал j(R) системы зарядов (атома, молекулы, кристалла) на большом расстоянии R от нее (по сравнению с размерами системы). Простейшая модель системы с квадрупольным моментом – квадруполь, представляет собой два диполя с равными по величине, но противоположно направленными дипольными моментами. Если система зарядов электрически нейтральна и ее дипольный момент равен нулю, квадрупольный момент не зависит от выбора начала системы координат, в к-рой рассматриваются заряды.
Квадрупольный момент Q появляется в третьем члене разложения j(R) в ряд по обратным степеням расстояния от начала системы координат, связанной с системой зарядов, до точки, определяемой концом вектора R. Это разложение для системы частиц с зарядами q_i и радиусами-векторами r_i(i-номер частицы) имеет вид:

где 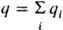– полный заряд системы, -дипольный
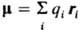
момент системы, Q-квадрупольный момент, компоненты к-рого Q_ab равны:

x_a_i и x_b_i– декартовы координаты вектора r_i, т.е. x_1i=x_i, x_2i=y_i x_3i=z_i; d_ab принимает значение 1 при a=b и 0 при a№b (a,b=1,2,3).

Для системы с непрерывным распределением заряда с плотностью r(r) заряд 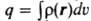(dv – элемент объема), дипольный момент m=, компоненты тензора квадрупольного момента равны:

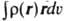
Размерность квадрупольного момента в СИ-Кл^.м². Для молекул часто используют в качестве единиц квадрупольного момента величину 10^-26 единиц заряда СГС^.см² ~ 3,3^.10^-40 Кл^.м²; для квадрупольных моментов ядер – величину 10^-34 единиц заряда СГС^.см². Часто квадрупольные моменты ядер выражают в единицах абс. заряда электрона е: Q/e=10^-24см², что соответствует ~ 4,803^.10^-34 единиц заряда СГС^.см².
Квадрупольный момент для сферически симметричного распределения заряда (а также для распределений кубич. и тетраэдрич. симметрии) равен нулю, тогда как для систем с более низкой симметрией распределения заряда квадрупольных моментов, как правило, отличен от нуля. Поэтому квадрупольный момент есть характеристика распределения заряда в системах заряженных частиц. При этом всегда Q_xx+Q_yy+Q_zz=0, а система координат м. б. выбрана так, что Q_ab=0 при a№b.
Во внеш. электрич. поле напряженности Е(Е_x, Е_у, Е_z) энергия Е электрически нейтральной системы зарядов при m=0 равна:

причем производные РE_b/Рx_a предполагаются постоянными в области распределения зарядов.
В химии рассматривают квадрупольное взаимод. атомов, молекул на сравнительно больших расстояниях. Энергия такого взаимод. для частиц, не обладающих дипольным моментом, убывает с увеличением расстояния R пропорционально 1/R⁵ (см. Поляризуемость). Квадрупольные моменты молекул м. б. определены экспериментально (напр., по компонентам мол. g-фактора, по главным моментам инерции и анизотропии магн. восприимчивости, по величинам двойного лучепреломления при наличии градиента электрич. поля), а также м. б. рассчитаны методами квантовой механики. Так, для молекулы фторацетилена 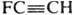Q_zz=3,96, Q_xx=Q_yy=-1,98^.10^-26 единиц заряда СГС^.см² (ось z совпадает с осью молекулы), для молекулы СО Q_zz=-4,3, Q_xx-Q_yy=2,15^.10^-26 (в тех же единицах).
Квадрупольным моментом обладают мн. атомные ядра. Если ядро с равномерно распределенным зарядом вытянуто вдоль нек-рой оси 2, Q>0; если ядро сплюснуто, то Q<0. Квадрупольные моменты ядер изменяются в широких пределах, напр. в единицах 10^-24 см² для ядер ¹⁷O Q=-0,021, ³⁵С1 Q=-0,0789, ²⁷Аl Q=0,149. Как правило, большие квадрупольные моменты ядер положительны, т. е. распределение заряда в них соответствует вытянутому эллипсоиду вращения.
Взаимодействие квадрупольного момента ядра с электрич. полем кристалла или молекулы приводит к появлению различных по энергии состояний ядра, соответствующих разл. ориентации ядерного спина относительно осей симметрии кристалла или молекулы. Число разрешенных ядерных ориентации определяется ядерным магн. моментом, связанным со спином ядра, и равно 2I+1, где I – спиновое квантовое число ядра (см. Ядро атомное). Низший по энергии уровень отвечает такой ориентации ядра, при к-рой положит. заряд на сплюснутом или вытянутом ядре располагается ближе всего к наиб. плотности отрицат. заряда в электронном окружении этого ядра. Резонансное поглощение энергии
электромагн. поля, обусловленное квантовыми переходами между уровнями энергии, связанными с ядерными ориентациями, наз. ядерным квадруполышм резонансом.

===
Исп. литература для статьи «КВАДРУПОЛЬНЫЙ МОМЕНТ»: Гречишкин B.C., Ядерные квадрупольные взаимодействия в твердых телах, М., 1973; Флайгер У., Строение и динамики молекул, пер. с англ., т. 1-2, М., 1982. См. также лит. при ст. Ядерный квадрутмьпый резонанс. И. Ф. Степанов.

Страница «КВАДРУПОЛЬНЫЙ МОМЕНТ» подготовлена по материалам химической энциклопедии.

Источник

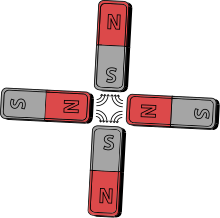
КВАДРУПОЛЬНЫЙ МОМЕНТ, мультипольный момент 2-го порядка (ранга), характеризующий источники какого-либо поля. Квадрупольным моментом системы электрических зарядов, распределённых в объёме V с плотностью ρ(r), называется симметричный тензор

где x_i, x_k — компоненты радиус-вектора r, δ_ik– символ Кронекера, i, k = 1,2,3. Поскольку ∑³_i₌₁Q^e_ii = 0, то в общем случае имеется всего пять независимых составляющих электрического квадрупольного момента; из них собственно квадрупольным моментом иногда называют только диагональную составляющую Q^e₃₃. Если электрический дипольный момент р^е и суммарный электрический заряд q системы равны нулю, то тензор электрического квадрупольного момента не зависит от выбора начала отсчёта (точки r = 0). Потенциал электростатического поля стационарной системы зарядов на расстояниях R, больших по сравнению с её размерами l (R >> l), с учётом первых трёх мультипольных моментов имеет вид φ = q/R + p^en/R² + 3Q^e_ikn_in_k/R³ (по повторяющимся индексам i и k производится суммирование). Здесь используется система единиц Гаусса, вектор n = R/R задаёт направление от центра системы (r = 0) в точку наблюдения R. Квадрупольная составляющая потенциала соответствует полю сосредоточенного (точечного, l → 0) электрического квадруполя.

Аналогично для описания магнитостатического поля стационарной системы электрических токов с плотностью j(r) вводится симметричный псевдотензор магнитного квадрупольного момента

где × – знак векторного произведения, с – скорость света. В случае изменяющихся во времени систем электрических зарядов и токов тензоры электрического Q^e_ik и магнитного квадрупольных моментов характеризуют полное электромагнитное поле, создаваемое этими системами (смотри Квадрупольное излучение).

Лит.: Джексон Дж. Классическая электродинамика. М., 1965; Терлецкий Я. П., Рыбаков Ю. П. Электродинамика. 2-е изд. М., 1990; Ландау Л. Д., Лифшиц Е. М. Теория поля. 8-е изд. М., 2003.

В. В. Кочаровский, Вл. В. Кочаровский.

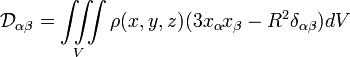Источник

Q11 = Qxx = Z0∞ Z0π Z02π ρ(r)[3x2 − r2]r2dr sin θ dθ dϕ =

Z0∞ r8e−λrdr Z0π Z02π sin4 θ(3 sin2 θ cos2 ϕ − 1) sin θ dθ dϕ.

Для интегрирования по углу ϕ воспользуемся выражением:

cos2 ϕ dϕ =

(1 + cos 2ϕ) = π.