На нынешнем ликбезе мы вынесем мозг рядовому гуманитарию темой, которая давно его интересует, но любые попытки почитать научно-познавательную литературу оканчивается зависанием над первой же формулой. Сейчас мы попросим всех физиков закрыть глаза и уши и расскажем остальным, что такое кванты. Наверняка, вы все постоянно встречаете это слово в литературе, телевизорах, интернетах, шаражкиных конторах и нанотехнолохотронах. Пора уже восполнить пробел и немножко врубиться в тему.

Самый простой способ объяснить, что такое кванты – это аналогия.
Возьмем расстояние между вашими глазами и монитором. Чисто математически это расстояние можно разделить на несколько отрезков. Сначала вполовину, потом еще на четыре, затем на восемь частей. И так, например, до бесконечности. И может показаться, что если вы захотите ткнуть пальцем в монитор, то не сможете это сделать, потому что это расстояние делится до бесконечности. Но вы знаете, что физически вы это сделаете без проблем, потому что, по-видимому, существует мельчайшая единица расстояния, меньше которой уже ничего нет.
Раньше считали, что мельчайший размер имеет атом, но нынче ученые докопались аж до кварков и суперструн. Но вопрос определения мельчайшего расстояния оставим физикам – рано или поздно нам предъявят эталон. Факт в том, что наш опыт подтверждает, что деление отрезка в реальности не бесконечно.
Эти рассуждения близки известному парадоксу Ахиллеса и черепахи. Древние тоже задумывались о бесконечности деления пространства. Так то!

Теперь возьмем другой пример из жизни. Энергию как она есть. Вы поджарили шашлык, и он, стало быть, теперь горячий. Излучает тепло, которое в общем случае является тем, что мы называем энергией, а физики – электромагнитными волнами. Жизненный опыт нам подсказывает, что энергия существует в виде непрерывных волн (помните, непонятные синусоиды на уроках алгебры). То есть энергия, как мы считаем, излучается непрерывно. До начала XX века все ученые мира тоже так думали.
А вот и нет. Выяснилось, что существует конечный кусочек энергии. Самая маленькая порция энергии, меньше которой не существует. Как и в случае с расстоянием, передачу энергии можно делить на кусочки (или пакеты, если вы вэб-программист, и вам так понятнее). Самый крошечный кусочек энергии и называют квантом.

Собственно на этом можно и закончить. Но ведь вам наверняка интересно, как это было обнаружено, да и почему из такого пустяка родилась целая наука – квантовая физика.
О том, что кванты существуют, никто не догадывался. Пока физики чисто из интереса не решили попрактиковаться в расчетах на всяких идеальных ситуациях. Они заморочились на так называемом абсолютно черном теле. Это такая выдуманная фиговина, типа духовки, которую нагревают, а она при этом не теряет (не отражает) ни капельки энергии – все тепло забирает себе без остатка.
Эта гипотетическая духовка после нагревания, разумеется, тоже начнет излучать тепло. Физики стали считать, сколько тепла (энергии) будет излучать такая духовка. И неожиданно у них по тогдашним, казалось бы логичным, формулам умника Максвелла выходила бесконечная энергия. Это была засада – практика показывала, что в реальности подобные бесконечности не наблюдается вообще нигде и тем более в духовках. И вот на этой ерунде вся классическая физика пошла лесом.

Первым что-то путное высказал Макс Планк – дедушка квантовой физики. Он чисто по-студенчески подогнал результат под задачу, придумав формулу, из которой следовало, что энергия излучается порциями. То есть каждая электромагнитная волна несет в себе определенное количество энергии, пропорциональное частоте этой волны. Чем больше частота волны, тем больше энергии несет в себе один квант. Коэффицент пропорциональности назвали постоянной Планка, которая впоследствии оказалась не просто какой-то случайной цифрой, а фундаментальной физической величиной.
Хорошая аналогия: когда мы играем на скрипке, и плавно увеличиваем громкость, то на самом деле громкость растет не непрерывно, а скачками, но такими маленькими, что мы не замечаем этого.

Планк, к сожалению, сам не понял, что открыл – до конца жизни он был противник квантовой физики. Квантование энергии было вообще очень оскорбительным для классиков. Один известный ученый-шутник (Гамов) объяснял квантование энергии так: это все равно, что природа разрешила либо пить целый литр пива сразу, либо вообще не пить ничего, не допуская промежуточных доз. Ну или аналогия от нас: вы покупаете пиво только в бутылках (разной емкости), но никакого розливного пива! Так получается и с энергией.
Формула Планка для излучения абсолютно черного тела выдала адекватный результат без всяких бесконечностей. Потому что кусочки энергии в отличие от бесконечно малых величин можно подсчитать. После этого научный мир замер в нехорошем предчувствии.

Окончательно добил классическую физику Эйнштейн. Его первым открытием была совсем не теория относительности. А объяснение фотоэффекта. За что он получил нобелевскую премию (а совсем не за ТО).
Фотоэффект – это когда свет падает на пластинку и выбивает из нее электроны. Только вот энергия выбитых электронов не зависит от увеличения мощности (яркости) света, хоть ставь сто ламп, но увеличивается только число электронов, а не их скорость. Энергия же выбитых из пластинки электронов растет, если увеличить частоту волны света, уменьшая ее длину: то есть посветить не красным, а, например, фиолетовым светом. Свет с малой частотой, типа очень красного, вообще не производит эффекта. Это, кстати, напрямую касается великой тайны, почему фотографии проявляют при красном свете – только этот цвет не засвечивает пленку, улавливаете?
Явление фотоэффекта вообще никто не мог объяснить в рамках классической физики. На картинке, походу, нарисован прибор для изучения фотоэффекта.

Никто не мог, кроме Эйнштейна. Чтобы объяснить, почему цвет падающего луча света, а не его энергия, определяет скорость выбиваемых электронов, Эйнштейн решил перенести идейки о порциях энергии Планка на световую волну. Ведь озадаченный Планк применял свою теорию только к тепловым излучениям.
Для начала Эйнштейн впервые озвучил идею, что свет можно и нужно рассматривать не как волну, а как частицу (впоследствии ее назовут фотоном, а Эйнштейн называл ее световым квантом). Для любознательных: обычная лампочка в 100 Ватт излучает в секунду примерно сто миллиардов миллиардов фотонов (это 10 в 20 степени).
При фотоэффекте в силу размеров сражение между электроном и фотоном идет один на один. Чтобы фотон при столкновении с электроном вырвал последний из металлической пластинки, он должен иметь для этого достаточное количество энергии. А если применить формулу Планка именно для света, то выходило, что энергия каждого фотона пропорциональна частоте световой волны, то есть отдельно взятый фотон обладает определенной энергией, зависящей от собственной частоты. Вот и получалось, что частота света (его цвет) определяет скорость вылетающих электронов, а интенсивность (яркость) света влияет только на количество выбитых электронов. Это как сотни детишек будут сбивать снежками сосульки, но никто не сможет докинуть, а потом придет переросток из старшей группы и метнет снежок до самой крыши и собьет цель.
>
Таким образом, Эйнштейн показал, что электромагнитная волна (свет) состоит из маленьких частиц – фотонов, которые в свою очередь представляют собой маленькие порции или кванты света.

И после этого мир уже никогда не был прежним. Физики столкнулись с невероятным для макромира явлением, что материя может быть одновременно и частицей и волной, что энергия не делится бесконечно, а очень даже кратна некоему значению (постоянной Планка), что эти самые кванты обладают такими свойствами, что расскажи кому в приличной компании – не поверят и вызовут санитаров.
Эйнштейн был злостным противником квантовой физики. Он до самой смерти держал оборону, считая, что квантовые явления можно как-то нормально объяснить. Но разные там Нильсы Боры, Гейзенберги, Ландау и прочие открывали все новые и новые свойства квантов. А в 50-е годы, уже после смерти Эйнштейна квантовые штучки были подтверждены экспериментально и окончательно.
Может быть, в дальнейших наших ликбезах мы заглянем в парадоксы квантовой физики, если нам хватит слов и умения объяснить их человеческим гуманитарным языком.
Благодарим за внимание!
NB: Все изображения взяты из гугла (поиск по картинкам) – авторство определяется там же.
Незаконное копирование текста преследуется, пресекается, ну, и сами знаете...
Если Вы вдруг поняли, что подзабыли основы и постулаты квантовой механики или вообще не знаете, что это за механика такая, то самое время освежить в памяти эту информацию. Ведь никто не знает, когда квантовая механика может пригодиться в жизни.
Зря вы усмехаетесь и ехидствуете, думая, что уж с этим предметом вам в жизни вообще никогда не придется сталкиваться. Ведь квантовая механика может быть полезной практически каждому человеку, даже бесконечно далекому от нее. Например, у Вас бессонница. Для квантовой механики это не проблема! Почитайте перед сном учебник – и Вы спите крепчайшим сном странице уже эдак на третьей. Или можете назвать так свою крутую рок группу. Почему бы и нет?
Шутки в сторону, начинаем серьезный квантовый разговор.
С чего начать? Конечно, с того, что такое квант.
Квант
Квант (от латинского quantum – ”сколько”) – это неделимая порция какой-то физической величины. Например, говорят – квант света, квант энергии или квант поля.
Что это значит? Это значит, что меньше быть уже просто не может. Когда говорят о том, что какая-то величина квантуется, понимают, что данная величина принимает ряд определенных, дискретных значений. Так, энергия электрона в атоме квантуется, свет распространяется «порциями», то есть квантами.
Сам термин «квант» имеет множество применений. Квантом света (электромагнитного поля) является фотон. По аналогии квантами называются частицы или квазичастицы, соответствующие иным полям взаимодействия. Здесь можно вспомнить про знаменитый бозон Хиггса, который является квантом поля Хиггса. Но в эти дебри мы пока не лезем.

Как механика может быть квантовой?
Как Вы уже заметили, в нашем разговоре мы много раз упоминали о частицах. Возможно, Вы и привыкли к тому, что свет – это волна, которая просто распространяется со скоростью с. Но если посмотреть на все с точки зрения квантового мира, то есть мира частиц, все изменяется до неузнаваемости.
Квантовая механика – это раздел теоретической физики, составляющая квантовой теории, описывающая физические явления на самом элементарном уровне – уровне частиц.
Действие таких явлений по величине сравнимо с постоянной Планка, а классическая механика Ньютона и электродинамика оказались совершенно непригодными для их описания. Например, согласно классической теории электрон, вращаясь с большой скоростью вокруг ядра, должен излучать энергию и в конце концов упасть на ядро. Этого, как известно, не происходит. Именно поэтому и придумали квантовую механику – открытые явления нужно было как-то объяснить, и она оказалась именно той теорией, в рамках которой объяснение было наиболее приемлемым, а все экспериментальные данные “сходились”.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Немного истории
Зарождение квантовой теории произошло в 1900 году, когда Макс Планк выступил на заседании немецкого физического общества. Что тогда сообщил Планк? А то, что излучение атомов дискретно, а наименьшая порция энергии этого излучения равна
,
Где h – постоянная Планка, ню – частота.
Затем Альберт Эйнштейн, введя понятие “квант света” использовал гипотезу Планка для объяснения фотоэффекта. Нильс Бор постулировал существование у атома стационарных энергетических уровней, а Луи де Бройль развил идею о корпускулярно-волновом дуализме, то есть о том, что частица (корпускула) обладает также и волновыми свойствами. К делу присоединились Шредингер и Гейзенберг, и вот, в 1925 году публикуется первая формулировка квантовой механики. Собственно, квантовая механика – далеко не законченная теория, она активно развивается и в настоящее время. Также следует признать, что квантовая механика с ее допущениями не имеет возможности объяснить все стоящие перед ней вопросы. Вполне возможно, что на смену ей придет более совершенная теория.

При переходе от мира квантового к миру привычных нам вещей законы квантовой механики естественным образом трансформируются в законы механики классической. Можно сказать, что классическая механика – это частный случай квантовой механики, когда действие имеет место быть в нашем с Вами привычном и родном макромире. Здесь тела спокойно движутся в неинерциальных системах отсчета со скоростью, гораздо меньшей скорости света, и вообще – все вокруг спокойно и понятно. Хочешь узнать положение тела в системе координат – нет проблем, хочешь измерить импульс – всегда пожалуйста.
Совершенно иной подход к вопросу имеет квантовая механика. В ней результаты измерений физических величин носят вероятностный характер. Это значит, что при изменении какой-то величины возможно несколько результатов, каждому из которых соответствует определенная вероятность. Приведем пример: монетка крутится на столе. Пока она крутится, она не находится в каком-то определенном состоянии (орел-решка), а имеет лишь вероятность в одном из этих состояний оказаться.
Здесь мы плавно подходим к уравнению Шредингера и принципу неопределенности Гейзенберга.
Уравнение Шредингера
Согласно легенде Эрвин Шредингер, в 1926 году выступая на одном научном семинаре с докладом на тему корпускулярно-волнового дуализма, был подвергнут критике со стороны некоего старшего ученого. Отказавшись слушать старших, Шредингер после этого случая активно занялся разработкой волнового уравнения для описания частиц в рамках квантовой механики. И справился блестяще! Уравнение Шредингера (основное уравнение квантовой механики) имеет вид:
Данный вид уравнения – одномерное стационарное уравнение Шредингера – самый простой.
Здесь x – расстояние или координата частицы, m – масса частицы, E и U – соответственно ее полная и потенциальная энергии. Решение этого уравнения – волновая функция (пси)
Волновая функция – еще одно фундаментальное понятие в квантовой механике. Так, у любой квантовой системы, находящейся в каком-то состоянии, есть волновая функция, описывающая данное состояние.
Например, при решении одномерного стационарного уравнения Шредингера волновая функция описывает положение частицы в пространстве. Точнее говоря, вероятность нахождения частицы в определенной точке пространства. Иными словами, Шредингер показал, что вероятность может быть описана волновым уравнением! Согласитесь, до этого нужно было додуматься!

Принцип неопределенности Гейзенберга
Но почему? Почему мы должны иметь дело с этими непонятными вероятностями и волновыми функциями, когда, казалось бы, нет ничего проще, чем просто взять и измерить расстояние до частицы или ее скорость.
Все очень просто! Ведь в макромире это действительно так – мы с определенной точностью измеряем расстояние рулеткой, а погрешность измерения определяется характеристикой прибора. С другой стороны, мы можем практически безошибочно на глаз определить расстояние до предмета, например, до стола. Во всяком случае, мы точно дифференцируем его положение в комнате относительно нас и других предметов. В мире же частиц ситуация принципиально иная – у нас просто физически нет инструментов измерения, чтобы с точностью измерить искомые величины. Ведь инструмент измерения вступает в непосредственный контакт с измеряемым объектом, а в нашем случае и объект, и инструмент – это частицы. Именно это несовершенство, принципиальная невозможность учесть все факторы, действующие на частицу, а также сам факт изменения состояния системы под действием измерения и лежат в основе принципа неопределенности Гейзенберга.
Приведем самую простую его формулировку. Представим, что есть некоторая частица, и мы хотим узнать ее скорость и координату.
В данном контексте принцип неопределенности Гейзенберга гласит: невозможно одновременно точно измерить положение и скорость частицы. Математически это записывается так:
Здесь дельта x – погрешность определения координаты, дельта v – погрешность определения скорости. Подчеркнем – данный принцип говорит о том, что чем точнее мы определим координату, тем менее точно будем знать скорость. А если определим скорость, не будем иметь ни малейшего понятия о том, где находится частица.
На тему принципа неопределенности существует множество шуток и анекдотов. Вот один из них:
Полицейский останавливает квантового физика.
– Сэр, Вы знаете, с какой скоростью двигались?
– Нет, зато я точно знаю, где я нахожусь

Надеемся, что эта статья помогла Вам немного размять мозги, вспомнить хорошо забытое старое, а может быть и узнать что-то новое. Здесь мы постарались рассказать о квантовой механике просто, понятно и по возможности интересно. Конечно, данная тема не может быть раскрыта в рамках одной статьи, поэтому о парадоксах, нерешенных задачах, черных дырах и котах Шредингера мы поговорим в самое ближайшее время. А пока, чтобы закрепить знания, предлагаем посмотреть тематическое видео. Возможно вас также заинтересуют правила оформления чертежей по ЕСКД.
И, конечно, напоминаем Вам! Если вдруг по какой-то причине решение уравнения Шредингера для частицы в потенциальной яме не дает Вам уснуть, обращайтесь к нашим авторам – профессионалам, которые были взращены с квантовой механикой на устах!
Фундаментальные константы
(атом, ядро, элементарные частицы, кварки, кванты)
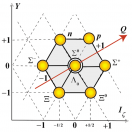
|
Физика, свободная от метафизических гипотез, невозможна. ( Макс Борн) |
Разделы микроскопической физики (микрофизики или физики микромира):
- Базовые единицы измерения в природе и их кванты
- Универсальные физические постоянные (фундаментальные константы)
- Ресурсы о фундаментальных постоянных
- Литература об универсальных константах
Базовые единицы измерения в природе и их кванты
В разделе ниже даются “первичные” физические константы, от которых завсисят другие, “вторичные”.
Эти первичные константы (или их часть) можно считать некими “квантами”.
Авторские рассуждения о квантах мира и вычисления кванта массы
Поскольку материя в нашем мире мыслится в понятии массы, а располагается в пространственно-временных координатах,
то нам интересны, прежде всего, “кванты” пространства и времени:
- hu = 7,69558071(63)·10–37 Дж·с.
- tu = 0,939963701(11)·10–23 с.
- lu = 2,817940285(31)·10–15 м.
А вот какое значение у минимально возможной массы – “кванта материи”? Можно ли его вычислить?
Давайте попробуем сделать это несколькими способами:
- на основе постоянной Планка ħ = 6,626176·10-34 Дж·с.
- на основе указанных “первичных” констант tu, lu
и hu = 7,69558071(63)·10–37 Дж·с. - на основе III закона Кеплера, показывающего соотношение пространства и времени рядолм с неизменной массой,
в формуле которого участвует гравитационная постоянная G (или γ) = 6,6720·10-11 Н·м2·кг-2.
Вычисление кванта массы на основе постоянной Планка
Джоуль - единица энергии. Т.к. E = ħ·ν = m·c2, то m = ħ·ν / c2. Частота ν имеет размерность с-1. Значит, m0 = ħ / tu / c2 = 6,626176·10-34 / (0,939963701(11)·10–23 · (2,99792458·108)2) ~ 7,8435·10-27 кг - это примерно 5 масс протона (4,7).
Вычисление кванта массы на основе первичных констант
Алаверды: m0 = hu / (tu · c2) = 7,69558071(63)·10–37 / 0,939963701(11)·10–23 / (2,99792458·108)2 ~ 0,911·10-30 ~ 9,11·10-31 кг - это Масса покоя электрона me!
Вычисление кванта массы на основе гравитационной постоянной
Согласно 3-му закону Кеплера (упрощенному): (T1/T2)2 = (a1/a2)2, где T - период планеты, a - её расстояние до Солнца. Отсюда масса Солнца пропорциональна a3/T2, а, точнее, равна этому соотношению, умноженному на гравитацонную постоянную γ = 2,56696941·10–45. Следовательно, квантом массы можно считать lu3/tu2 = (2,817940285·10–15)3 / (0,939963701·10–23)2 ~ 7,941·10–45 / 0,884·10–46 ~ 89,83. Если это число умножить на γ, то получим 230,6·10–45 = 2,306·10–43 кг. Поскольку, по недавним расчётам масса электронного нейтрино примерно в миллион раз меньше, чем самого электрона, — 1,5×10-37 килограммов, то вычисленный "квант массы" примерно в миллион раз меньше массы нейтрино!
Универсальные физические постоянные (фундаментальные константы)

Можно было бы думать, что свойства мира определяются такими универсальными постоянными,
как скорость света, заряд электрона или постоянная Планка, но это не так.
Если бы даже каждая из этих постоянных изменилась, но изменилась так, что численное значение “альфа”
[постоянная тонкой структуры α] по-прежнему осталось бы равным 1/137, мир тоже остался бы прежним,
и мы никогда не смогли бы опознать, что в нем что-то изменилось.
Но если “альфа” изменится хотя бы на одну миллионную, свойства нашего мира станут совершенно другими —
например, в нем не сможет существовать жизнь.
(физик Джон Бэрроу)
Первичные физические постоянные
Свет от квазаров на своем пути длиной в миллиарды лет проходит через межзвездные облака металлов (железа, никеля, хрома).
В 1997 при его исследовании обнаружили, что он поглотил некоторые из фотонов света квазара. Но не те, которые ожидалось.
Единственное непроверенное разумное объяснение состоит в том, что постоянная тонкой структуры, или альфа (α),
имела различное значение в то время, когда свет проходил через облака.
Но ведь альфа определяет, как свет взаимодействует с материей, и не должна меняться.
Ее значение зависит от заряда электрона, скорости света и постоянной Планка. Какая же постоянная изменилась?
Согласно Н. Косинову, проведенные исследования показали, что используемые в современной физике
фундаментальные физические константы непосредственно происходят от перечисленных ниже констант вакуума:
- hu = 7,69558071(63)·10–37 Дж·с.
- Gu = 2,56696941(21)·10–45 Н·с2.
- Ru = 29,9792458 Ом.
- tu = 0,939963701(11)·10–23 с.
- lu = 2,817940285(31)·10–15 м.
[А я бы не исключил возможность, что некоторые физические константы зависят не только от этих первичных,
которые можно назвать “квантами” и которые по сему относятся к области микромира,
но и от значений, которые относятся к области мегамира, например, возраста и радиуса Вселенной.]
Вторичные физические постоянные
Установлено, что современные фундаментальные физические постоянные имеют вторичный статус по отношению к найденным константам
и представляют собой различные комбинации констант hu, tu, lu и чисел π и α.
Константам, входящим в hu-tu-lu-π-α-базис, определен специальный статус – как универсальные суперконстанты.
На основе универсальных суперконстант получено новое значение гравитационной постоянной Ньютона, планковских констант
и найдена универсальная формула силы [?].
Новые фундаментальные физические константы дают широкие возможности для установления новых физических законов
и поиска констант взаимодействия для различных физических законов.
Все фундаментальные физические постоянные:
- Основные механические константы:
- Постоянная тонкой структуры α = 0,072973506; 1/α = 137,03604.
- Гравитационная постоянная G = 6,6720·10-11 Н·м2·кг-2.
- Скорость света в вакууме с = 2,99792458·108 м·с-1.
- Постоянная Планка ħ = 6,626176·10-34 Дж·с.
- Наименьшие из известных расстояний:
- Радиус первой боровской орбиты a0 = 0,52917706·10-10 м.
- Классический радиус электрона re = 2,8179380·10-15 м.
- Постоянная Ридберга R∞ = 10973731,77 м-1. [или ей лучше к энергетическим константам отнести?]
- Массы и энергии стабильных частиц:
- Масса покоя электрона me = 9,109534·10-31 кг 5,4858026·10-4 а.е.м.
- Энергия покоя электрона me·c2 = 0,5110034 МэВ.
- Масса покоя протона mp = 1,6726485·10-27 кг = 1,007276470 а.е.м.
- Энергия покоя протона mp·c2 = 938,2796 МэВ.
- Масса покоя нейтрона mn = 1,6749543·10-27 кг = 1,008665012 а.е.м.
- Энергия покоя нейтрона mn·c2 = 939,5731 МэВ.
- Отношение массы протона к массе электрона mp/me = 1836,15152.
- Атомная единица массы (10-3 кг·моль-1)/NA,
а.е.м. = 1,6605655(86)·10-27 кг. -
Массы атомов в а.е.м.:
водород 1H – 1,007825036;
дейтерий 2H – 2,014101795;
гелий-4 4He – 4,002603267. - Энергетические эквиваленты:
а.е.м. = 931,5016 МэВ;
1 электронвольт = 1,6021892·10-19 Дж. -
Энергия kT (при 25 °C) – энергетические эквиваленты:
4,11·10-21 Дж;
9,83·10-22 Кал;
0,0256 эВ;
2,479 кДж/моль;
0,593 кКал/моль.
- Магнитно-электрические константы:
- Магнитная постоянная μ0 = 4π·10-7 Гн·м-1 = 1,25663706144·10-6 Гн·м-1.
- Электрическая постоянная ε0 = (μ0c2)-1 8,85418782·10-12 Ф·м-1.
- Заряд электрона (абс. величина) e = 1,6021892·10-19 Кл = 4,803242·10-10 уд. СГСЭ.
- Отношение заряда электрона к его массе e/me = 1,7588047·1011 Кл·кг-1.
- Магнетон Бора μБ = 9,274078·10-24 Дж·Тл-1.
- Ядерный магнетон μN = 5,050824·10-24 Дж·Тл-1.
- Магнитный момент нейтрона в ядерных магнетонах μn/μN = 1,91315.
- Магнитный момент протона в ядерных магнетонах μp/μN = 2,7928456.
- Отношение Джозефсона 2e/h = 4,835939·1014 Гц·В-1.
- Квант магнитного потока Ф0 = h/2e = 2,0678506·10-15 Вб.
- Аэродинамические константы:
- Постоянная Авогадро NA = 6,022045·1023 моль-1.
- Постоянная Фарадея F = NA·e = 96484,56 Кл·моль-1.
- Молярная газовая постоянная R = 8,31441 Кл·моль-1·K-1.
- Объем моля идеального газа при нормальных условиях (1 атм, T0 = 273,15 К)
Vm = 22,41383·10-3 м3·моль-1. - Постоянная Больцмана k = R/NA = 1,380662·10-23 Дж·К-1.
Ресурсы о фундаментальных постоянных
Сетевые статьи и новости о физических константах:
Литература об универсальных константах
- 1. Peter J. Mohr and Barry N. Taylor. «CODATA Recommended Values of the Fundamental Physical Constants: 1998»;
NIST Physics Laboratory. Constants in the category «All constants»; Reviews of Modern Physics, (2000), v. 72, No. 2. - 2. D.C. Cole and H.E. Puthoff, «Extracting Energy and Heat from the Vacuum», Phys. Rev. E, v. 48, No. 2, 1993.
- 3. Ю.И. Манин. Математика и физика. М.: «Знание», 1979.
- 4. В.Л. Гинзбург. «Какие области физики и астрофизики представляются важными и интересными». УФН, №4, т. 169, 1999.
- 5. Н.В. Косинов. «Электродинамика физического вакуума». Физический вакуум и природа, №1, 1999.
- 6. Н.В. Косинов. «Физический вакуум и гравитация». Физический вакуум и природа, №4, 2000.
- 7. Н.В. Косинов. «Законы унитронной теории физического вакуума и новые фундаментальные физические константы».
Физический вакуум и природа, №3, 2000. - 8. N. Kosinov. «Five Fundamental Constants of Vacuum, Lying in the Base of all Physical Laws, Constants and Formulas».
Physical Vacuum and Nature, №4, 2000. - 9. Н.В. Косинов. «Пять универсальных физических констант, лежащих в основе всех фундаментальных rонстант, законов и формул физики».
Шестая Международная конференция «Современные проблемы естествознания». Программа и тезисы. С-Петербург, август, 2000 г. - 10. Н.В. Косинов. «Разгадка причин поразительного сходства формул законов Кулона и всемирного тяготения Ньютона».
Шестая Международная конференция «Современные проблемы естествознания». Программа и тезисы. С-Петербург, август, 2000 г. - 11. Н.В. Косинов. «Эманация вещества вакуумом и проблема структурогенеза». Идея, №2, 1994.
- 12. Н.В. Косинов. «Энергия вакуума». Энергия будущего века, №1, 1998.
- 13. Н.В. Косинов. «Универсальные физические суперконстанты».
- 14. Н.В. Косинов. «Новая фундаментальная физическая константа, лежащая в основе постоянной Планка».
- 15. N.V. Kosinov, Z.N. Kosinova. «Tie of Gravitational Constant G and Planck Constant h».
51st International Astronautical Congress 2…6 Oct. 2000 / Rio de Janeiro, Brazil. - 16. A. Пуанкаре. Наука и гипотеза. A. Пуанкаре. О науке. М., 1983.
- 17. В.А. Фирсов. «Философско-методологический анализ проблемы единства физики в концепции калибровочных полей».
Философия науки, №1(3), 1997.
|
На русском языке: фундаментальные константы, универсальные физические постоянные, кванты природы,
На английском языке: Fundamental constants.
|
Страница обновлена 20.08.2022
|
|
|
|
Основные формулы по физике – КВАНТОВАЯ ФИЗИКА
Начало развития квантовой физики связано с решением немецким ученым Максом Планком проблемы излучения абсолютно черного тела. Необходимо знать гипотезу Планка о квантовании энергии осцилляторов и уяснить, что на основании формулы Планка могут быть получены законы Стефана- Больцмана и Вина.
Развитие гипотезы Планка привело к созданию представлений о квантовых свойствах света. Кванты света называются фотонами. С позиций квантовой теории света объясняется такое явление как фотоэффект. Здесь следует знать формулу Эйнштейна для фотоэффекта.
Дальнейшее развитие квантовой физики связано с построением теории строения атома. О сложном строении атома говорят исследования спектров излучения разряженных газов.
Смотрите также основные формулы механике
Таблица сновных формул квантовой физики
|
Физические законы, формулы, переменные |
Формулы квантовой физики |
||
|
Закон Стефана-Больцмана: |
|
||
|
Энергетическая светимость (излучательность) серого тела: |
|
||
|
Закон смещения Вина: |
|
||
|
Импульс фотона: |
|
||
|
Энергия фотона: |
|
||
|
Формула Эйнштейна для фотоэффекта: |
|
||
|
Красная граница фотоэффекта: |
|||
|
Сериальные формулы спектра водородоподобного атома |
|
||
|
Длина волны де Бройля: где р – импульс частицы. В классическом приближении (при v<<c): p = mv; m – масса частицы; v – скорость частицы; с – скорость света в вакууме. В релятивистском случае (при |
|||
|
Связь импульса с кинетической энергией Wк в релятивистском приближении: |
|
||
|
Плотность вероятности нахождения частицы в соответствующем месте пространства |
|
||
|
Волновая функция, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме |
|
||
|
Энергия частицы в бесконечно глубокой одномерной потенциальной яме |
|
||
|
Электропроводность собственных полупроводников |
|
||
|
Постоянная Холла для полупроводников типа алмаза, германия, кремния |
|
Фотон в современной физике считается разновидностью элементарных частиц. В частности, он представляет собой квант электромагнитного излучения (квант — неделимая частица чего-либо).
Энергия и импульс фотона
Фотоны обладают определенной энергией и импульсом. Когда свет испускается или поглощается, он ведет себя подобно не волне, а потоку частиц, имеющих энергию Е = hν, которая зависит от частоты. Оказалось, что порция света по своим свойствам напоминает то, что принято называть частицей. Поэтому свойства света, обнаруживаемые при его излучении и поглощении, стали называть корпускулярными. Сама же световая частица была названа фотоном, или квантом электромагнитного излучения.
Как частица, фотон обладает определенной порцией энергии, которая равна hν. Энергию фотона часто выражают не через частоту v, а через циклическую частоту:ω = 2πν
При этом в формуле для энергии фотона в качестве коэффициента пропорциональности (постоянной Планка) используется другая величина, обозначаемая ℏ и равная:
ℏ=h2π≈1,0545726·10−34 (Дж·с)
Учитывая это, формула для определения энергии фотона примет вид:
Е=ℏω
Согласно теории относительности, энергия частиц связана с массой следующим соотношением:
Е=mс2
Так как энергия фотона равна hν, то, следовательно, его масса m получается равной:
m=hνс2
У фотона нет собственной массы, поскольку он не может существовать в состоянии покоя. Появляясь, он уже имеет скорость света. Поэтому формула выше показывает только массу движущегося фотона.
По известной массе и скорости фотона можно найти его импульс:
p=mc=hνc=hλ
Внимание! Вектор импульса фотона всегда совпадает с направлением распространения луча света.
Чем больше частота ν, тем больше энергия Е и импульс р фотона и тем отчетливее свет проявляет свои корпускулярные свойства. Из-за того что постоянная Планка мала, энергия фотонов видимого излучения крайне незначительна. К примеру, фотоны, свойственные зеленому свету, имеют энергию, равную всего 4∙10–19 Дж. Несмотря на это, человеческий глаз способен различать изменение освещенности, даже если оно измеряется единичными квантами.
Пример №1. Каков импульс фотона, если длина световой волны λ = 5∙10–7 м?
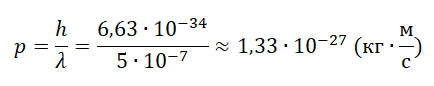
Корпускулярно-волновой дуализм
Законы теплового излучения и фотоэффекта объясняются только при условии, если начать считать свет потоком частиц. Однако нельзя отрицать тот факт, что свету присущи такие явления как интерференция и дифракция света. Но эти явления встречаются только у волновых процессов. Поэтому в современной физике принято считать свет с дуализмом, иначе — двойственностью свойств.
Когда свет распространяется в средах, он проявляет волновые свойства. Когда он начинает взаимодействовать с веществом (поглощаться или излучаться), проявляются корпускулярные свойства (свойства частицы).
Гипотеза де Бройля
Длительное время электромагнитное поле представлялось как материя, которая распределена в пространстве непрерывно. Электроны же представлялись как очень маленькие частицы материи. Не нет ли здесь ошибки, обратной той, которая была допущена при определении света? Может быть, электрон и другие частицы тоже обладают волновыми свойствами. Такую мысль высказал в 1923 г. французский ученый Луи де Бройль.
Он предположил, что с движением частиц связано распространение некоторых волн. И ученому удалось найти длину волны этих волн. Связь длины волны с импульсом частицы оказалась точно такой же, как и у фотонов. Если длину волны обозначить через λ, а импульс — через р, то получится, что:
λ=hp
Эта формула носит название формулы де Бройля, которая является одной из основных в разделе квантовой физики.
В будущем волновые свойства частиц, о которых предположил де Бройль, были обнаружены экспериментально. Так, удалось получить дифракцию электронов и других частиц на кристаллах. В этих случаях получалась почти такая же картина, как в случае с рентгеновскими и другими лучами. И формула де Бройля также нашла экспериментальное доказательство. Волновые свойства микрочастиц описываются квантовой механикой.
Квантовая механика — раздел физики, изучающий теорию движения микрочастиц.
Внимание! Законы Ньютона в квантовой физике в большинстве случаем не могут быть применены.
Давление света
В 1873 г. Максвелл, исходя из представлений об электромагнитной природе света, пришел к выводу: свет должен оказывать давление на препятствия. Предсказанное Максвеллом существование светового давления было экспериментально подтверждено Лебедевым, который в 1900 г. измерил давление света на твердые тела, используя чувствительные крутильные весы. Оно оказалось чрезвычайно малым, около 4∙10-7 Па.
Световое давление, обусловленное солнечным излучением у поверхности Земли, составляет менее 0,0001 Па. Этим и объясняется тот факт, что в обычных условиях давление света заметным образом себя не проявляет. Но давлением света объясняет следующие факты:
- хвосты комет направлены от ядра кометы в сторону, противоположную Солнцу;
- изменение орбит искусственных спутников Земли.
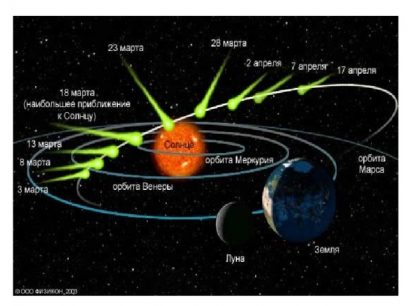
Свет — это поток фотонов с импульсом:
p=mc
При поглощении веществом фотон перестает существовать, но импульс его, по закону сохранения импульса, не может исчезнуть бесследно. Он предается телу, значит, на тело действует сила.
Приведенное рассуждение будет абсолютно верным, если считать, что свет только веществом поглощается. Но разве это всегда так, свет еще может отражаться телами, а если тело прозрачно, то может проходить сквозь него. В реальных условиях свет частично отражается телом, частично поглощается, а если это, например, стекло, то свет проходит сквозь него. Как будет обстоять дело, если поверхность зеркальная? Возникает световое давление в данном случае?
Для простоты предположим, что свет падает перпендикулярно к поверхности зеркала. Мы знаем, что при абсолютном ударе какого-либо тела о стенку она получает импульс, модуль которого равен удвоенному модулю импульса тела, то есть 2mv. Отражаясь, фотон летит с той же скоростью, но в противоположном направлении. Значит, при отражении фотона от зеркала его импульс изменяется на 2mc. Такое же изменение импульса, но в противоположном направлении, получит зеркало. Импульс, получаемый телом при отражении фотона, будет в 2 раза больше импульса, получаемого телом при поглощении фотона.
Задание EF17985
За время t=4 с детектор поглощает N=6⋅105 фотонов падающего на него монохроматического света. Поглощаемая мощность P=5⋅10−14 Вт. Какова длина волны падающего света?
Ответ:
а) 0,4 мкм
б) 0,6 мкм
в) 520 нм
г) 780 нм
Алгоритм решения
1.Записать исходные данные.
2.Установить взаимосвязь между энергией фотонов и поглощаемой детектором мощностью.
3.Выполнить решение в общем виде.
4.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Количество фотонов: N = 6∙105 шт.
• Поглощенная мощность: P = 5∙10–14 Вт.
Вся энергия фотонов будет поглощена детектором. Согласно закону сохранения энергии:
Nhν=Pt
Длина волны определяется формулой:
λ=cν
Отсюда частота равна:
ν=cλ
Подставим это выражение в записанный закон сохранения энергии:
Nhcλ=Pt
Отсюда длина волны равна:
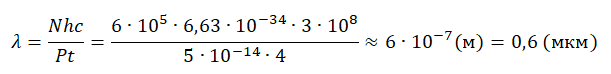
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17986
При изучении давления света проведены два опыта с одним и тем же лазером. В первом опыте свет лазера направляется на пластинку, покрытую сажей, а во втором – на зеркальную пластинку такой же площади. В обоих опытах пластинки находятся на одинаковом расстоянии от лазера и свет падает перпендикулярно поверхности пластинок.
Как изменится сила давления света на пластинку во втором опыте по сравнению с первым? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.
Алгоритм решения
1.Описать процессы, происходящие во время обоих опытов.
2.С помощью физических формул установить, как изменяется сила давления света.
Решение
В обоих опытах происходит поглощение световой волны. Этот процесс можно рассматривать как поглощение за время t большого числа световых квантов — N >>1 (фотонов). Фотоны поглощаются пластинкой. Причем каждый фотон передает этой пластинке свой импульс, равный:
pф=hνc
Поэтому импульс пластинки становится равным сумме импульсу всех поглощенных фотонов:
pп=Nhνc
В результате поглощения света пластинкой, покрытой сажей, она приобретает за время t импульс pп в направлении распространения света от лазера. Согласно закону изменения импульса, тела в инерциальной системе отсчета скорость изменения импульса тела равна силе, действующей на него со стороны других тел или полей:
F1=pпt=Nthνc
В результате отражения света от зеркальной пластины отраженный фотон имеет импульс, противоположный импульсу фотона падающей волны:
pф=∣∣−pфп∣∣
Поэтому отраженная волна будет иметь импульс:
pов=−N´pф=−N´hνc
N´ — количество отраженных фотонов.
В итоге за время t импульс волны под действием зеркальной пластинки изменился. Это изменение будет равно разности импульса отраженной волны и импульса пластинки:
Δp=pов−pп=−Npф−N´pф=−(N+N´)pф
Согласно закону сохранения импульса, импульс системы, состоящей из световой волны и зеркальной пластинки, сохраняется:
Δ(pп+pпл)=0
Отсюда:
Δpпл=Δpп
Но изменение импульса тела в инерциальной системе отсчета происходит только под действием других тел или полей и характеризуется силой:
F2=pплt=N+N´thνc
Если зеркала отражает хорошо, то N ≈ N´. Тогда:
F2≈2F1
Отсюда видно, что сила давления света увеличится вдвое.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18201
Излучением лазера с длиной волны 3,3⋅10−7 м за время 1,25⋅104 с был расплавлен лёд массой 1 кг, взятый при температуре 0 °С, и полученная вода была нагрета на 100 °С. Сколько фотонов излучает лазер за 1 с? Считать, что 50% излучения поглощается веществом.
Алгоритм решения
1.Записать исходные данные.
2.Установить, какое количество тепла было сообщено льду для его расплавления и нагревания до температуры кипения.
3.Установить, какая энергия была выделена лазером при условии, что лишь половина этой энергии была сообщена льду.
4.Из полученного выражения выразить количество фотонов, излученных лазером за время t.
5.Записать формулу для количества фотонов, выделяемых за время 1 с.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем не только те данные, что есть в условии задачи, но и табличные данные, которые нам понадобятся в ходе решения задачи:
• Удельная теплота плавления льда: λльда = 3,4∙105 Дж/кг.
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙оС).
• Начальная температура льда/воды: t1 = 0 оС.
• Конечная температура воды: t2 = 100 оС.
• Коэффициент полезного действия: η = 50%.
• Длина световой волны: λсвета = 3,3∙10–7.
• Время проведения всего опыта: t = 1,25∙104.
Чтобы лед расплавился, а образовавшаяся вода нагрелась до температуры кипения, нужно сообщить ему следующее количество энергии:
Q=Q1+Q2=mλльда+mc(t2−t1)
Так как КПД равен 50% (0,5), то это количество теплоты равно половине энергии, выделенной лазером:
Q=ηE
mλльда+mc(t2−t1)=ηE
Энергия, выделенная лазером, равна сумме энергий каждого из излученных фотонов, количество которых будет равно N:
E=Nhν
Но частота световой волны равна:
ν=cλсвета
Тогда:
E=Nhcλсвета
Отсюда:
Nhcλсвета
Теперь мы можем записать:
mλльда+mc(t2−t1)=ηNhcλсвета
Выразим количество излученных фотонов за все время:
N=λсвета(mλльда+mc(t2−t1))ηhc
Если разделить это выражение на время проведения опыта, то мы найдем количество фотонов, излученных за 1 секунду:
N1с=λсвета(mλльда+mc(t2−t1))ηhct
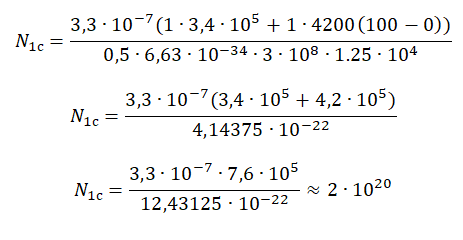
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 2.7k





 – максимальная кинетическая энергия фотоэлектрона.
– максимальная кинетическая энергия фотоэлектрона.





